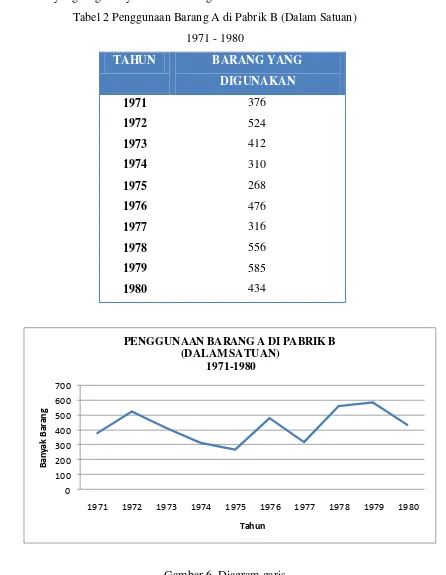
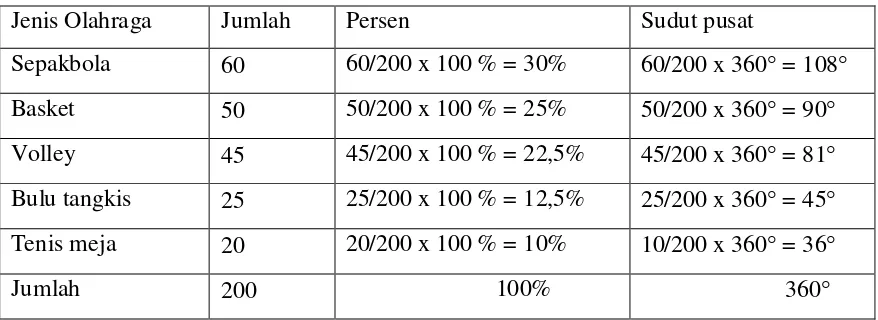
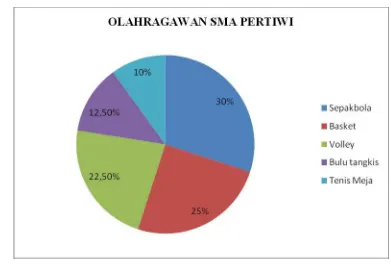
BAB 3 PENYAJIAN DATA DALAM BENTUK DIAGRAM A. Penyajian Data dalam Bentuk Diagram 1. Pengertian grafik atau diagram - 3 penyajian data dalam diagram
Teks penuh
Gambar


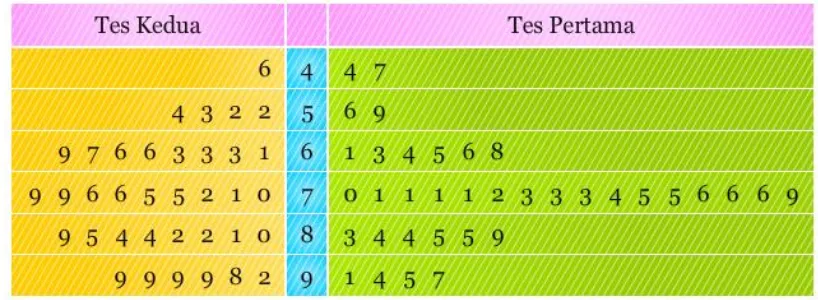
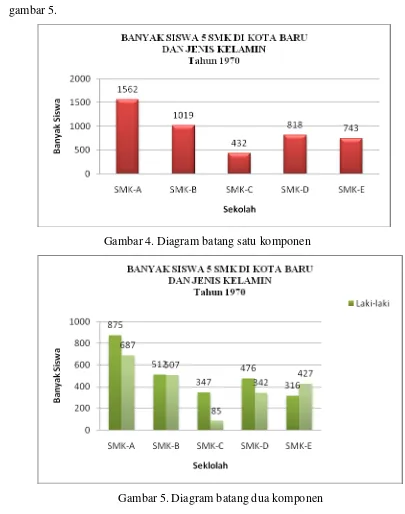
Dokumen terkait
Untuk data berkelompok, distribusi frekwensi kumulatif kurang dari mengambil patokan pada tepi atas, dan untuk distribusi freekwensi kumulatif lebih dari mengambil patokan pada
Peserta didik dapat menyajikan menyelesaikan masalah yang berkaitan dengan penyajian data dalam bentuk tabel distribusi kumulatif dan ogive dengan tepat..
Pengertian Tabel Distribusi Frekuensi menurut Sudijono (1987:36) adalah alat penyajian data statistik berbentuk kolom dan lajur, yang di dalamnya dimuat angka yang dapat
Dipergunakan Dipergunakan untuk untuk menyajikan menyajikan suatu suatu distribusi distribusi frekuensi frekuensi dari dari data yang data yang
Penyajian data Penyajian data Tabel Tabel Biasa Biasa Kontingensi Kontingensi Distribusi Frekuensi Distribusi Frekuensi Grafik Grafik Histogram Histogram Poligon Frekuensi Poligon
Data yang digunakan untuk ogif positif berasal dari tabel distribusi kumulatif kurang dari dengan tambahan tepi bawah dari kelas terendah.. Ciri dari ogif positif adalah grafiknya
Selanjutnya untuk membuatnya menjadi data dalam bentuk distribusi frekuensi bergolong, maka beberapa langkah berikut ini perlu ditempuh. 1) Mengurutkan data dari yang terkecil ke
Distribusi Frekuensi Kumulatif lebih dari, adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai lebih dari nilai batas kelas suatu