MAKALAH SEMINAR MATEMATIKA KAJIAN LANJUT

MAKALAH SEMINAR MATEMATIKA

KAJIAN LANJUT TENTANG

SEGIEMPAT HARMONIK

Oleh:

NI LUH SUDIARTINI

NIM. 1113011072

Dosen Pembimbing:

I Putu Pasek Suryawan, S.Pd, M.Pd

NIP. 19880617 201404 1 001

JURUSAN PENDIDIKAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS PENDIDIKAN GANESHA

KAJIAN LANJUT TENTANG SEGIEMPAT HARMONIK

Ni Luh Sudiartini

1113011072

ABSTRAK

Segiempat harmonik adalah segiempat siklik yang memiliki perbandingan sisi yang unik. Segiempat ini merupakan segiempat konveks yang keempat titik sudutnya berada pada sebuah lingkaran dan perbandingan dua sisinya yang berurutan bersesuaian. Segiempat harmonik memiliki beberapa sifat antara lain, sifat pertama simedian segitiga, sifat kedua diagonal dari segiempat harmonik merupakan simedian dari segitiga yang dibentuk oleh dua sisi yang berurutan dan panjang diagonal lainnya, dan sifat ketiga jika suatu segiempat konveks dengan keempat titik sudutnya berada pada sebuah lingkaran dan diagonalnya terbentuk dari simedian dua buah segitiga yang berhadapan maka segiempat tersebut adalah segiempat harmonik. Panjang diagonal segiempat harmonik adalah sebagai berikut





cd ab

bc ad ac p

 

 2 dan





bc ad

cd ab ac q

   (2 )

dan luas daerah dari segiempat harmonik adalah sebagai berikut L=b.datauL=a.c

Yang didapatkan dari penurunan rumus panjang diagonal dan luas daerah segiempat siklik yang memiliki perbandingan dua sisi yang berurutan bersesuaian.

BAB I

PENDAHULUAN

1.1 Latar Belakang

Matematika merupakan salah satu ilmu yang sangat penting untuk dikuasai, terutama tentang geometri. Studi tentang geometri dapat membantu peserta didik merepresentasikan kemampuannya dan mencapai pandangan tertentu tentang dunianya. Penguasaan tentang model-model geometri serta sifat-sifatnya dapat memberikan suatu perspektif bagi peserta didik, sehingga peserta didik dapat menganalisa dan mengkomunikasikan hal yang terkait dengan bangun-bangun geometri (Muabuai, 2010).

Geometri merupakan bagian yang tak terpisahkan dalam pembelajaran matematika. Geometri menempati posisi khusus dalam kurikulum matematika tingkat sekolah menengah, karena banyaknya konsep-konsep yang termuat di dalamnya. Menurut sudut pandang psikologi, geometri merupakan penyajian abstraksi dari pengalaman visual dan spasial misalnya bidang, pola, pengukuran dan pemetaan. Namun, berdasarkan sudut pandang matematika, geometri menyediakan pendekatan-pendekatan untuk pemecahan masalah, misalnya gambar-gambar, diagram, sistem koordinat, vektor, dan transformasi (Muabuai, 2010).

Perkembangan ilmu matematika terutama bidang geometri sangat penting dan menarik untuk diikuti, salah satunya mengenai segiempat, karena secara tidak langsung segiempat yang sering ditemui dikehidupan sehari-hari. Sesuai dengan definisinya, “segiempat adalah bangun datar yang memiliki empat buah sisi (Wisna, 2008)”. Beberapa bentuk segiempat yang biasa dikenal yaitu persegi, persegi panjang, trapesium, layang-layang, jajar genjang dan belah ketupat. Namun, ditelusuri lebih lanjut lagi, terdapat banyak segiempat yang memiliki sifat khusus tetapi belum banyak dikenal. Salah satu segiempat yang memiliki sifat khusus adalah segiempat harmonik.

yang berurutan bersesuaian (Smarandache dan Patrascu, 2014). Segiempat harmonik ini merupakan segiempat yang belum banyak dikenal baik dari segi sifat-sifat, panjang diagonal dan luas daerahnya. Sehubungan dengan hal tersebut, penulis merasa perlu dan tertarik untuk mengkaji lebih lanjut tentang segiempat harmonik yang berjudul “Kajian Lanjut tentang Segiempat Harmonik”. Nantinya diharapkan kajian makalah ini mampu memberikan pengetahuan lebih dan manfaat bagi perkembangan ilmu matematika terutama pada cabang geometri.

1.2 Rumusan Masalah

Berdasarkan dari latar belakang di atas dapat dirumuskan permasalahan sebagai berikut.

1. Bagaimanakah sifat-sifat dari segiempat harmonik?

2. Bagaimanakah cara menentukan panjang diagonal segiempat harmonik? 3. Bagaimanakah rumus luas daerah segiempat harmonik?

1.3 Tujuan

Tujuan dari penulisan makalah ini berdasarkan rumusan masalah di atas sebagai berikut.

1. Untuk mengetahui beberapa sifat dari segiempat harmonik

2. Untuk mengetahui cara menentukan panjang diagonal segiempat harmonik 3. Untuk menentukan rumus luas daerah segiempat harmonik

1.4 Manfaat

a. Bagi Pembaca

Pembaca dapat memperoleh informasi mengenai geometri bidang terutama tentang keunikan dari segiempat harmonik.

b. Bagi Penulis

1.5 Batasan Masalah

BAB II

LANDASAN TEORI

2.1 Segiempat

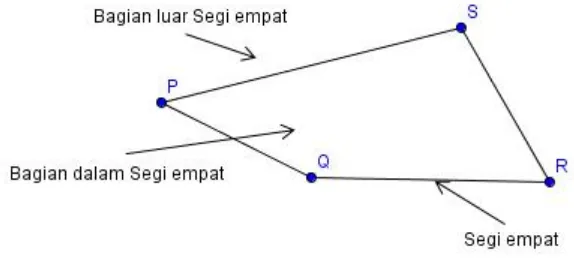
“Segiempat sederhana adalah bangun datar yang bersisi empat dan mempunyai perpotongan sisi hanya pada titik sudutnya. Suatu bangun segiempat sederhana pada dasarnya adalah bangun yang memisahkan suatu bidang kedalam tiga bagian yaitu: bagian pertama bagian dalam segiempat, bagian kedua bagian luar segiempat, dan bagian ketiga bangun segiempat itu sendiri” (Prayoga, Skripsi, 2011, Hal. 37). Contoh bangun segiempat sederhana adalah sebagai berikut.

Segiempat PQRS sederhana yang membagi bidang menjadi tiga bagian

Gambar. 1 Segiempat Sederhana

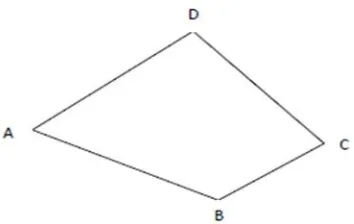
Definisi 2.1.1:

Gambar. 2 Segiempat Konveks

2.2 Segiempat Siklik

Perhatikan gambar berikut ini :

Gambar. 3 Segiempat Siklik

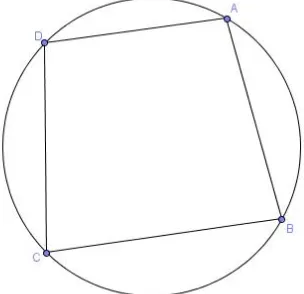
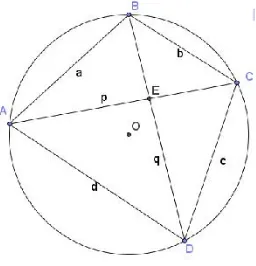
Pada gambar di atas titik O adalah titik pusat lingkaran dan titik A, B, C, serta D terletak pada keliling lingkaran tersebut. Ruas garis AB, BC, CD, dan AD adalah tali-tali busur lingkaran. Tali-tali busur tersebut membentuk Segiempat ABCD, dan selanjutnya disebutSegiempat siklik.Sehingga dapat disimpulkan bahwa Segiempat siklik adalah Segiempat yang titik-titik sudutnya terletak pada lingkaran(Jossefson, 2015, Vol. 99).

Kemudian sesuai dengan Theorema 14 pada Martin Josefsson,

Teorema 2.2.1

‘Sebuah segiempat konveks ABCD dengan sisi a, b, c, d adalah trapesium dengan sisi a // c serta ac jika dan hanya jika panjang diagonal AC dan BD adalah:





c a

cb ad c a ac p

   

 2 2 dan





c a

cd ab c a ac q

   

 2 2 ’.

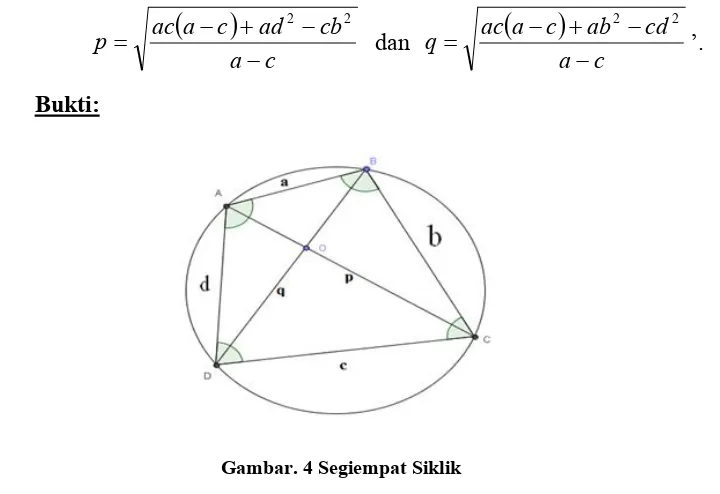
Bukti:

Gambar. 4 Segiempat Siklik

Dengan menggunakan rumus aturan cosinus pada DAB diperoleh:



DBA



aq q

a

d2  2 22 cos





2 2 2

cos

2aq DBA a q d





aq d q a DBA

2 cos

2 2 2_{ }



 …(1)

Dengan menggunakan cara yang analog pada DCB diperoleh:



BDC



cq q c

b2  2 22 cos 





2 2 2

cos

2cq BDC c q b





cq b q c BDC

2 cos

2 2 2 _{ }



 …(2)

Sebuah segiempat merupakan trapesium jika dan hanya jika a // c maka haruslah mDBAmBDC yang menyebabkan cos



DBA



cos



BDC



, sehingga diperoleh:









Dengan cara yang analog diperoleh







a c



2.3 Simedian Segitiga

Simedian segitiga merupakan hasil refleksi dari garis berat terhadap garis bagi yang melalui satu titik sudut yang sama pada sebuah segitiga. Perhatikan Gambar berikut.

Gambar 5 Simedian Segitiga

2.4 Cevian

Gambar 6 Cevian

2.4 Segiempat Harmonik

“Segiempat Harmonik merupakan segiempat konveks yang keempat titik sudutnya berada pada sebuah lingkaran dan perbandingan dua sisinya yang berurutan bersesuaian” (Smarandache dan Patrascu, 2014). Misalnya segiempat Siklik ABCD merupakan segiempat harmonik jika memenuhi perbandingan sisi AB.CD = BC.AD.

BAB III

PEMBAHASAN

3.1 Beberapa Sifat Segiempat Harmonik

Sifat 1. Pada ∆ ABC cevian AF dengan F berada pada ruas garis BC merupakan simedian jika dan hanya jika

2

      

AC AB CF

BF

(=>) Jika cevian AF dengan F berada pada ruas garis BC merupakan simedian maka memenuhi

2

      

AC AB CF

BF

Bukti:

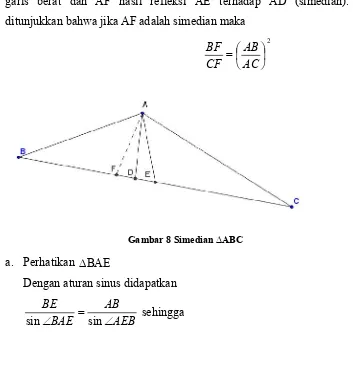
Diketahui pada ∆ ABC, dengan AD merupakan garis bagi, AE merupakan garis berat dan AF hasil refleksi AE terhadap AD (simedian). Akan ditunjukkan bahwa jika AF adalah simedian maka

2

      

AC AB CF

BF

Gambar 8 Simedian ∆ABC

a. Perhatikan BAE

Dengan aturan sinus didapatkan

AEB AB BAE

BE

 

 sin

AEB

b. Perhatikan EAC

Dengan aturan sinus didapatkan

AEC

sin sehingga

AEC

c. Perhatikan FAC

Dengan aturan sinus didapatkan

AFC

sin sehingga

AFC

d. Perhatikan BAF

Dengan aturan sinus didapatkan

AFB

sin sehingga

AFB

Dari persamaan (1) dan (2) didapatkan:

EAC

Dari persamaan (3) dan (4) didapatkan

FAC

2

(<=) Jika

2

dengan F berada pada ruas garis BC maka cevian AF

merupakan simedian.

Diketahui: AD merupakan garis bagi maka mBADmDAC, AE

. Akan ditunjukkan bahwa jika

2

merupakan simedian dari ∆ABC.

Bukti: jika AF simedian ∆ABC maka mFADmDAEserta FD = DE.

dari bukti di atas (=>) diketahui

FAC

dan sesuai dengan yang diketahui

)

Dari persamaan (2) didapat

EAC m BAF m  

Dari persamaan (1) dan (2) diketahui bahwa mBAF mEAC sehingga dapat disimpulkan bahwa AF merupakan simedian ∆ABC.

Sifat 2. Pada Segiempat Harmonik diagonal dari segiempat tersebut merupakan simedian dari segitiga yang dibentuk oleh dua sisi yang berurutan dan panjang diagonal lainnya.

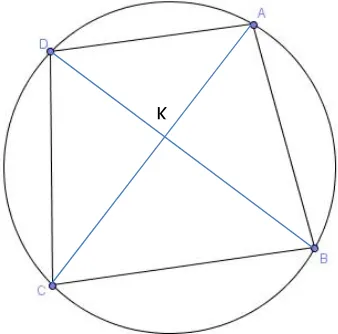
Gambar 9 Segiempat Harmonik ABCD

Bukti:

Misalkan segiempat ABCD merupakan segiempat Harmonik dan K merupakan titik perpotongan dari AC dan BD. Akan ditunjukkan bahwa BK merupakan simedian dari ∆ABC. Perhatikan ∆ABK dan ∆DCK, dari

)

Kemudian perhatikan ∆BCK dan ∆ADK, dari kesamaan kedua segitiga tersebut didapatkan pula,

2)

Dari persamaan (1) dan (2) didapatkan,

AK

Karena segiempat ABCD merupakan segiempat Harmonik maka diketahui,

...(4)

Dari persamaan (3) dan (4) didapatkan bahwa,

CK

Dari persamaan diatas dan merujuk dari Dalil 1, dapat disimpulkan bahwa BK merupakan simedian dari ∆ABC, dengan menggunakan teknik pembuktian yang sama dapat pula diketahui bahwa AK simedian dari ∆ABD, CK simedian ∆BCD dan DK merupakan simedian ∆ADC.

Gambar 10 Simedian dari ABCdan ADC

Misalkan segiempat ABCD bukan merupakan segiempat harmonik. DK dan BK merupakan simedian segitiga ADC dan ABC maka berlaku untuk:

Kasus I

a. Pada ADC dengan DK simedian ADC maka berlaku :

CK AK CD

AD



2 2

…. (1)

b. Pada ABC dengan BK simedian ABCmaka berlaku :

CK AK BC

AB



2 2

…. (2)

Dari persamaan (1) dan (2) maka :

AD BC CD AB CD

AD BC AB CD

AD BC

AB

x x

sehingga

2 2 2

2

 

 

Karena AB xCDBC xAD maka segiempat ABCD merupakan segiempat harmonik.

Kasus II

a. Pada BAD dengan AK simedian BAD maka berlaku :

) 1 ...(

2 2

DK BK AD

AB



b. Pada BCD dengan CK simedian ΔBCD maka berlaku :

) 2 ...(

2 2

DK BK CD

BC

Dari persamaan (1) dan (2) maka

BC AD CD AB CD

BC AD AB CD

BC AD

AB

x x

sehingga

2 2 2

2

 

 

Karena berlaku AB xCD AD xBC maka segiempat ABCD merupakan segiempat harmonik

Sehingga dari kasus I dan II dapat disimpulkan segiempat ABCD merupakan segiempat harmonik.

3.2 Panjang Diagonal Segiempat Harmonik

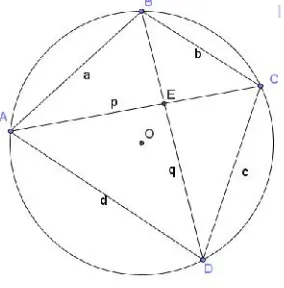
Untuk mengkaji panjang diagonal segiempat harmonik, perhatikan gambar berikut.

Gambar 11 Diagonal Segiempat Harmonik

Dengan melihat ACD dan menerapkan dalil Cosinus, maka diperoleh persamaanp2 c2 d2 2cdcos



ADC



...(1)

Kemudian dengan melihat ABC dan menerapkan dalil Cosinus lagi, maka didapatkan persamaan p2a2 b2 2abcos



ABC



. Namun kita ketahui bahwa mABCmADC1800 (sifatquadilateral), maka persamaannya dapat ditulis ulang sebagai berikut:









...

 

2

cos 2

180 cos 2 2 2 2

0 2

2 2

ADC ab

b a p

ADC ab

b a p

 

 

  

 

Kalikan persamaan (1) denganabsehingga menjadi:

Kalikan persamaan (2) dengancdsehingga menjadi,

 

cd p2 a2cd b2cd 2abcdcos



ADC



...(4)

Kemudian jumlahkan persamaan (3) dan (4), sehingga diperoleh:





Karena diketahui pada segiempat harmonikac = bdmaka :









Salah satu panjang diagonal p dapat diperoleh dari keempat sisi quadirateral. Maka dengan cara yang sama kita dapatkan formula untuk menentukan panjang diagonalqyaitu:





Maka dari pemaparan di atas diperoleh formula,





3.3 Luas Daerah Segiempat Harmonik

Berdasarkan aturan cosinus pada segitiga maka :

PadaABC berlaku :

PadaADC berlaku :

Dari persamaaan (1) dan (2) maka diperoleh :

)

Dari persamaan Teorema Pitot maka :

d Dari persamaan (3) dan (4) sehingga :

cd

Luas daerah segiempat pada gambar di atas (gambar 12) terbentuk dari dua buah segitiga yakniABC dan ADC yang menyebabkan :

D

Karena segiempat harmonik memiliki perbandingana . c = b . dmaka:

Untukb . d = a . c

c a L

c a L

c c a a L

c a c a L

d c b a L

. ) . (

. . .

. . .

. . .

2

    

Untuka . c = b . d

d b L

d b L

d d b b L

d b d b L

d c b a L

. ) . (

. . .

. . .

. . .

2

    

BAB IV

PENUTUP

4.1 Simpulan

Berdasarkan hasil pembahasan dapat disimpulkan sebagai berikut. 1. Beberapa sifat segiempat harmonik

Sifat 1. Pada ∆ABC (Gambar 8) cevian AF dengan F berada pada ruas garis BC merupakan simedian jika dan hanya jika

2

      

AC AB CF

BF

Sifat 2. Pada segiempat Harmonik diagonal dari segiempat tersebut merupakan simedian dari segitiga yang dibentuk oleh dua sisi yang berurutan dan panjang diagonal lainnya.

Sifat 3. Jika suatu segiempat konveks dengan keempat titik sudutnya

berada pada sebuah lingkaran dan diagonalnya terbentuk dari simedian dua buah segitiga yang berhadapan maka segiempat tersebut adalah segiempat harmonik.

2. Panjang diagonal segiempat harmonik (Gambar 11)









bc ad

cd ab ac q

cd ab

bc ad ac p

  

 

 2 dan (2 )

3. Rumus luas daerah dari segiempat harmonik (Gambar 12)

L = a.catauL = b.d

Untuk segiempat harmonik dengan masing-masing panjang sisinya a, b, c dan d.

4.2 Saran

DAFTAR PUSTAKA

Johnson R.A. 2007. Advanced Euclidean Geometry, New York: Dover Publications Inc. Mineola

Josefsson M. 2013. “Characterizations of Trapesoids” Forum Geometricorum, Volume 13

---, 2015. “Minimal Area of A Bicentric Quadrilateral” The Mathematical Gazette, Volume 99 (hlm.237)

Muabuai, Y. (2010). Pembelajaran Geometri melalui Model Kooperatif Tipe STAD Berbasis Program Cabri Geometry II Plus dalam Upaya Peningkatan Kemampuan Komunikasi Matematis Siswa SMP. Tesis (Tidak Diterbitkan) pada SPS UPI.

Prayoga, Tambah. 2008. Perbandingan Segiempat Saccheri Pada Geometri Euclid Dan Geometri Non Euclid. Skripsi (Tidak diterbitkan). Pendidikan Matematika, FMIPA UNY.

Smarandache, F dan I. Patrascu (Eds). 2012. The Geometry of Homological Triangles, Ohio:The Education Publisher Inc. Columbus

---, 2013. Variance on Topics of plane Geometry, Ohio: The Education Publisher Inc. Columbus

---, 2014. “Some Properties of the Harmonic Quadrilateral” International Frontier Science Letters(IFSL), Volume 1, Nomor 1 (hlm. 12-17)

Lampiran 2

Lampiran 3

Lampiran 1