Soal dan pembahasan latihan UN th. 2010
Teks penuh
Gambar
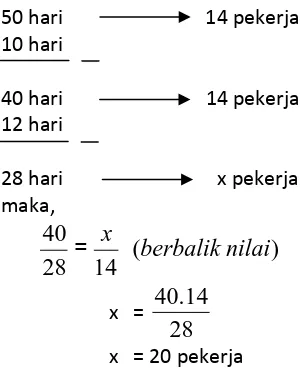
Garis besar
Dokumen terkait
Penetapan kebijakan harga yang terjangkau dari kemampuan yang dimiliki konsumen serta tingkat harga yang sesuai dengan kualitas dan manfaat barang atau jasa yang
Tujuan penyelenggaran Pendidikan Sistem Ganda adalah: (1) menghasilkan tenaga kerja yang memiliki keahlian profesional, (2) Memperkokoh link and match antara
Untouchability – “a key problem of Indian anthropology”, as Robert Deliège mentions in Introduction, closely bound with culture, religion, history and contemporary
2) Pekerja kebersihan alat kesehatan yang kontak dengan darah atau cairan tubuh (semen, vagina, serebospinal, sinovia, pleura, peritoneal, pericardial). 4) Pekerja di
pemesanan, barang jadi, bahan baku, proses, mesin, tenaga kerja dan jenis.
Tujuan dari penelitian ini adalah untuk mengetahui efek pemberian minyak buah merah terhadap perkembangan palatum (palatogenesis) pada mencit galur Swiss Webster.. Penelitian
Universitas Kristen Maranatha sarian (galenik), atau campuran dari bahan tersebut yang secara turun temurun telah digunakan untuk pengobatan, dan dapat diterapkan sesuai norma
organisasi seragam nasional yang mewakili operasi dan / atau keluaran spesifik, seperti layanan untuk lansia, pengendalian lalu lintas, personil manajemen, dan hampir 50