EL 2002 Probabilitas dan Statistik

2. Peubah

Acak

(Random Variable)

EL2002-Probabilitas dan

S

tatistik

Dosen:

Isi

0. Review dari EL2009

•

Konsep Peubah Acak

•

Sebaran Peluang Diskrit

•

Sebaran Peluang Kontinyu

•

Sebaran Empiris

•

Sebaran Peluang Gabungan

•

Nilai Harap

•

Hukum Nilai Harap

•

Sifat Variansi

Konsep Pubah Acak

• Eksperimen statistik dipakai untuk menyatakan proses dimana pengukuran peluang dilakukan.

• Seringkali, yang lebih penting bukanlah detail dari hasil eksperimen, tetapi gambaran numerik terkait eksperimen tsb. Contoh: pelantunan koin 3 kali memberikan hasil

S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

• Gambaran umum mengenai jumlah H yang muncul dapat dilakukan jika nilai-nilai 0, 1, 2, atau 3 bisa dikaitkan

Definisi

• Def.2.1: Suatu fungsi yang nilainya berupa bilangan riil yang ditentukan oleh setiap anggota dari ruang cuplikan disebut sebagai peubah acah (random variable).

• Peubah acak dinyatakan dengan huruf besar, misalnyaX, sedangkan nilainya dengan huruf kecil-nya, yakni x untuk kasus ini. Untuk kasus pelantunan koin tsb diatas, X akan bernilai 2 untuk peristiwa: E = {HHT, HTH, THH}

0 1

-2

S

R

Contoh

• Contoh 2.1 Dua bola diambil berturutan secara acak, tanpa penggantian, dari suatu wadah yang berisi empat bola

merah (R) dan tiga bola hitam (B). Hasil dapat muncul dan nilai y dari peubah acak Y, dimana Y menyatakan

banyaknya bola merah adalah

Peristiwa y

RR 2

RB 1

BR 1

…

• Contoh 2.2: Petugas penyimpanan helm mengembalikan helm dari tiga orang pegawai Smith, Jones, dan Brown dalam urutan spt itu. Jika helm diambil acak dan

dikembalikan sesuai urutan pegawai diatas, dan m menyatakan jumlah helm yang kembali ke pemilik sebenarnya , kemungkinan berikut bisa terjadi:

Peristiwa m

SJB 3

SBJ 1

JSB 1

JBS 0

BSJ 0

Peubah acak diskrit dan kontinyu

•

Def.2.2: Ruang cuplikan yang mengandung

sejumlah berhingga titik cuplikan, atau sejumlah

tak berhingga titik sebanyak seluruh bilangan

bulat, disebut sebagai ruang cuplikan diskrit, dan

peubah acak yang didefinisikan dalam ruang ini

disebut sebagai peubah acak diskrit.

•

Def.2.3: Ruang cuplikan yang mengandung

sejumlah takberhingga titik cuplikan, sebanyak

seluruh titik dalam segmen garis, disebut sebagai

ruang cuplikan kontinyu, dan peubah acak yang

didefinisikan dalam ruang ini disebut sebagai

Sebaran

Peluang

Sebaran peluang diskrit

• Dalam kasus pelantunan koin tiga kali, peubahX yang menyatakan banyaknya H muncul akan memberikan peluang 3/8 untuk x=2.

• Untuk kasus pengembalian helm, peluang tidak satupun pegawai mendapatkan helm yang benar, yakni m=0, adalah 2/6=1/3. Kita bisa membuat tabel berikut:

m 0 1 3

P(M=m) 1/3 1/2 1/6

• Nilaim menyatakan semua kasus yang mungkin terjadi, sehingga seluruh peluang akan berjumlah 1.

• Seringkali lebih praktis menyatakan semua kemungkinan peubah acak X kedalam formula. Jadi kita tuliskan

Fungsi atau sebaran peluang

• Def.2.4: Fungsif(x) adalah suatu fungsi peluang atau sebaran

peluang dari peubah acak X jika, untuk setiap hasil yang muncul x berlaku:

1. f(x) ≥ 0 2. Σ_x f(x) = 1 3. P(X =x) = f(x)

• Contoh 2.3: Tentukan sebaran peluang dari jumlah sepasang

mata dadu jika dilantunkan.

• Jawab: AndaikanX peubah acak yang nilainya x merupakan

..

Mata Dadu

1 2 3 4 5 6

1 2 3 4 5 6 7

2 3 4 5 6 7 8

3 4 5 6 7 8 9

4 5 6 7 8 9 10

5 6 7 8 9 10 11

6 7 8 9 10 11 12

x 2 3 4 5 6 7 8 9 10 11 12

f(x) 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36

Sebaran kumulatif

• Def.2.5: Sebaran kumulatifF(x) dari peubah acak diskrit X dengan sebaran peluang f(x) adalah

F(x) = P(X ≤ x) = Σ_t≤x f(t)

• Contoh 2.4 dan 2.5: Suatu koin dilantunkan empat kali. Tentukan: 1) formula sebaran peluang munculnya H yaitu f(x), dan

2) sebaran kumulatif F(x) nya. • Jawab:

1. Jumlah titik cuplikan ada 24 _{= 16. Jika x menyatakan banyaknya} muncul H, akan ada kombinasi sebanyak C(4,x). Dengan

demikian f(x) = C(4, x)/16, dimana x = 0, 1, 2, 3, 4 f(0) = (4!/4!)/16 = 1/16 ; f(1)=(4!/3!)/16 = 4/16; f(2) = (4!/(2!2!))/16 = 6/16; f(3) = f(1); f(4)= f(0); 1. Berdasarkan Def.2.5, diperoleh : F(0) = f(0) = 1/16;

…

• Dengan demikian

( )

⎪⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎪ ⎨ ⎧ ≥ < ≤ < ≤ < ≤ < ≤ < = 4 , 1 4 3 , 3 2 , 2 1 , 1 0 , 0 , 0 16 15 16 11 16 5 16 1 x untuk x untuk x untuk x untuk x untuk x untuk x F 1/4 1/2 3/4 1

0 _{1 2 3 4} x F(x)

Sebaran peluang dlm bentuk grafis

• Dari contoh 2.4: f(x) = C(4, x)/16

X 0 1 2 3 4

f(x) 1/16 4/16 6/16 4/16 1/16

1/16 2/16 3/16 4/16

0 1 2 3 x f(x)

5/16 6/16

4

1/16 2/16 3/16 4/16

0 1 2 3 x

f(x)

5/16 6/16

4

Luas=f(x)

2.3 Sebaran

peluang

Arti kerapatan peluang (kontinyu)

• Tinjau sebaran tinggi badan dari orang berumur 21 thn. Antara sebarang dua nilai, mis. 163.5 – 164.5, ada tak hingga macam tinggi badan.

– Peubah acak kontinyu memiliki peluang nol untuk suatu nilai eksak dari peubah acak ini.

P(a<X≤b) = P(a<X<b) + P(X=b) = P(a<X<b) + 0

– Jadi, tidak ada bedanya mengikutkan titik ujung dalam perhitungan ini ataupun tidak.

• Peubah acak kontinyu tidak dapat ditampilkan secara tabular, namun bisa dinyatakan dalam rumus.

Fungsi rapat peluang kontinyu

•

Suatu fungsi rapat peluang dibentuk sedemikian

hingga integrasi daerah dibawah kurva ke seluruh

X memberikan luas sebesar satu.

a _b x

f(x)

(

<

<

)

=

∫

b

( )

a

dx

x

f

b

X

a

P

Def. fungsi rapat peluang kontinyu

• Def.2.6: Suatu fungsif(x) adalah fungsi rapat peluang untuk peubah acak kontinyu X yang didefinisikan ke seluruh himpunan bilangan riil R, jika

1. f(x) ≥ 0 untuk semua x∈R 2. ∫∞_-∞ f(x) dx = 1.

3. P(a<X<b) = ∫b

a f(x) dx

• Contoh: andaikan peubah acakX memiliki fungsi rapat peluang: f(x) = x2_{/3; -1<x<2 dan f(x)=0 selain itu.}

Tentukan: (1) kondisi 2 pada Def.2.6, dan (2) Tentukan P(0< X ≤1)

• Jawab:

1) ∫∞_-∞ f(x) dx = ∫2

-1(x2/3)dx = x3/9|2-1 =(8/9) + (1/9) = 1

2) P(0< X ≤1) = ∫1

Sebaran peluang kumulatif kontinyu

•

Def.2.7: Sebaran peluang kumulatifF(x) dari suatu

peubah acak kontinyu X dengan fungsi kerapatan f(x)

diberikan oleh

( ) (

)

∫

( )

∞ −

=

≤

=

P

X

x

x

f

t

dt

x

F

•

Ada dua hasil langsung dari Def.2.7, yaitu:

Contoh

•

Soal: Untuk fungsi pada contoh 2.6., tentukanF(x)

dan gunakan untuk menghitung P(0< X

≤

1)

•

Jawab:

F(x) =

∫

∞_-∞

f(t) dt =

∫

x_-1

(t

2

/3)dt

= t

3

/9|

x_-1

= (x

3

+1)/9

Oleh karena itu,

2.4 Sebaran

Sebaran frekuensi relatif

• Dalam percobaan, seringkali fungsi rapat peluangf(x) untuk peubah acak kontinyu X tidak diketahui.

• Pemilihanf(x) harus mempertimbangkan setiap informasi yang tersedia dari data.

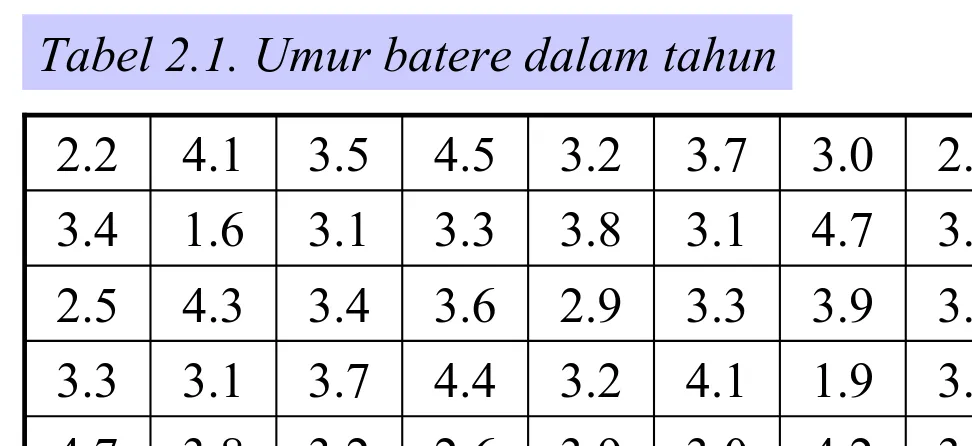
• Tinjau sebaran frekuensi relatif dari 40 buah umur batere mobil dalam Tabel 2.1. Pabrik menjamin umur batere

adalah 3 tahun.

2.2 4.1 3.5 4.5 3.2 3.7 3.0 2.6

3.4 1.6 3.1 3.3 3.8 3.1 4.7 3.7

2.5 4.3 3.4 3.6 2.9 3.3 3.9 3.1

3.3 3.1 3.7 4.4 3.2 4.1 1.9 3.4

4.7 3.8 3.2 2.6 3.9 3.0 4.2 3.5

Lanjutan …

• Andaikan diambil 7 kelas, dng demikian besar interval adalah (max-min)/kelas = (4.7-1.6)/7=0.443. Tabel 2.2 menunjukkan sebaran frekuensi relatif-nya.

Interval Kelas Titik tengah kelas

Frekuensi (f) Frekuensi relatif

1.5 - 1.9 1.7 2 0.050

2.0 - 2.4 2.2 1 0.025

2.5 – 2.9 2.7 4 0.100

3.0 – 3.4 3.2 15 0.375

3.5 – 3.9 3.7 10 0.250

4.0 – 4.4 4.2 5 0.125

4.5 – 4.9 4.7 3 0.075

Histogram dan estimasi fungsi rapat peluang

1.7 2.2 2.7 3.2 3.7 4.2 4.7 0.125

0.250 0.375

• Bentuk kurva: lingkaran? Hiperbola? Elips? Parabola

f(x) = ax2 + bx + c, untuk a, b, c tertentu?

• Banyak fungsi kerapatan peluang yang dapat dinyatakan dalam kurva berbentuk lonceng (Gaussian).

Skewness dari data

•

Sebaran bersifat simetrik (setangkup) atau tak

simetrik (skewed).

Sebaran kumulatif

• Berdasarkan Tabel 2.2, kita dapat membuat sebaran

frekuensi kumulatif dari umur batere, spt pada Tabel 2.3 dan estimasi F(x).

Batas kelas

Frekuensi kumulatif relatif

< 1.45 0.000

< 1.95 0.050

< 2.45 0.075

< 2.95 0.175

< 3.45 0.550

< 3.95 0.800

< 4.45 0.925

< 4.95 1.000 _* * *

* * * * 0.250 0.500 0.750 1.000

1.45 2.45 3.45 4.45

* Frekuensi kumulatif relatif Umur batere F(x) Kuartil pertama ~3.05

2.5 Sebaran

Peluang

Peluang gabungan diskrit

•

Jika dimensi ruang cuplikan lebih dari satu,

misalnya hasil pengukuran dua besaran P dan V

yng dinyatakan sbg (p, v), kita sebut sebaran

peluangnya sebagai sebaran peluang gabungan.

•

Def.2.8: Fungsif(x,y) adalah fungsi peluang

gabungan dari dua peubah diskrit X dan Y jika

1. f(x,y) ≥ 0 untuk seluruh (x,y) 2. ∑_x ∑_y f(x,y) = 1

3. P[(X,Y)∈A] = ∑∑_A f(x,y)

Contoh 2.8

• Soal: Suatu kotak berisi tiga refil (tinta isian) berwarna biru, dua refil merah, dan 3 refil hijau. Akan diambil dua refil secara acak dari kotak tsb. Jika X menyatakan jumlah refil biru, dan Y

jumlah refil merah, tentukan: (1) fungsi peluang gabungan

f(x,y), dan (2) P[(X,Y)∈A], dimana A adalah daerah {(x,y)|x + y≤1}.

• Jawab: pasangan (x,y) yang dapat muncul adalah (0,0), (0,1), (1,0), (1,1), (0,2), dan (2,0). Tinjau f(0,1) yang menyatakan

peluang terpilihnya refil merah dan hijau (karena refil biro nol). Jumlah total kombinasi terpilihnya dua refil dari delapan buah refil yang ada di dalam kotak adalah C(8,2) =

8!/(6!)(2!)=8⋅7/2=28. Cacah kombinasi terpilihnya satu dari dua refil berwarna merah dan satu dari tiga refil hijau adalah

C(2,1)⋅C(3,1) = 2⋅(3!/2!) = 6. Dengan demikian, f(0,1) = 6/28 =3/14. Dengan cara yang sama, nilai f(x,y) untuk seluruh

…

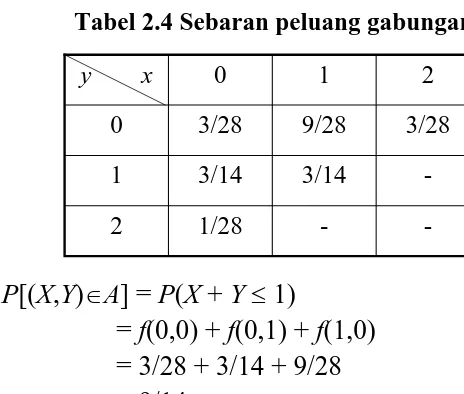
y x 0 1 2

0 3/28 9/28 3/28

1 3/14 3/14

-2 1/28 -

-2). P[(X,Y)

∈

A] = P(X + Y

≤

1)

= f(0,0) + f(0,1) + f(1,0)

= 3/28 + 3/14 + 9/28

= 9/14

Peluang gabungan kontinyu

• Def.2.9: Suatu fungsif(x,y) adalah fungsi kerapatan gabungan dari peubah acak kontinyu X dan Y jika

1. f(x,y) ≥0 untuk semua (x, y) 2. ∫∫_-∞∞ f(x,y) dxdy = 1

3. P[(X,Y)∈A] = ∫∫_Af(x,y) dx dy

• Contoh 2.9: Tinjau fungsi rapat peluang berikut

f(x,y) = x(1+3y2)/4; 0<x<2, 0<y<1

= 0, lainnya

1. Periksa kondisi 2 pada Def.2.9

2. Tentukan P[(X,Y)∈A] dimana A adalah daerah {(x,y)|

Sebaran peluang marjinal

• Jika f(x,y) adalah sebaran gabungan dari

peubah acak X dan Y, maka sebaran peluang

untuk masing-masing peubah acak X dan Y

(sebaran marjinal) adalah:

Diskrit:

g(x) =

∑

_y

f(x,y)

h(y) =

∑

_x

f(x,y)

…

•

Fungsig(x) dan h(y) disebut sebagai sebaran marjinal

dari X dan Y. Bahwa masing-masing benar berupa

fungsi sebaran dapa diperiksa berdasarkan Def.2.4.

dan Def.2.6. Sbg contoh, untuk kasus kontinyu:

∫

-∞∞

g(x) dx =

∫

-∞∞

∫

-∞∞

f(x,y) dy dx = 1

dan

P(a<X<b) =

P(a<X<b, -

∞

<Y<

∞

)

=

∫

_ab

∫

-∞∞

f(x,y) dy dx

Sebaran bersyarat diskrit

• Kembali ke definisi peluang bersyarat:

P(B|A) = P(A∩B)/P(A), P(A)>0

Jika A dan B adalah peristiwa yang dimana X=x dan Y=y,

P(Y=y|X=x) = P(X=x,Y=y)/P(X=x)

= f(x,y)/g(x) ; g(x) >0 untuk peubah acak diskrit X dan Y.

• Dapat ditunjukkan bahwa fungsif(x,y)/g(x) memenuhi syarat sebagai sebaran peluang dan akan dituliskan sebagai f(y|x), yakni:

f(y|x) = f(x,y)/g(x), g(x)>0

dan disebut sebagai sebaran bersyarat dari peubah acak diskrit Y, diberikan X=x.

• Dengan cara sama, sebaran bersyaratf(x|y) dari peubah acak X jika diberikan Y=y dapat dituliskan sebagai

Sebaran bersyarat kontinyu

•

Perdefinisi, sebaran rapat peluang bersyarat dari

peubah acak kontinyu X, jika diberikan Y=y adalah

f(x|y) = f(x,y)/h(y), h(y)>0

sedangkan sebaran rapat peluang bersyarat untuk

peubah acak kontinyu Y, diberikan X=x, adalah

f(y|x) = f(x,y)/g(x), g(x)>0

•

Peluang dari peubah acak kontinyuiX yang

terletak antara a dan b, jika diketahui Y=y, dapat

dihitung sbb:

Contoh 2.10

• Soal: Mengacu ke contoh 2.8 tentang pengambilan refil tinta, tentukan f(x|1) dan P(X=0|Y=1).

• Jawab: f(x|1) = f(x,1)/h(1), tentukan tlbh dulu h(1)

h(1) = ∑_x=01 f(x,1) = (3/14)+(3/14)+0 = 3/7

Karena itu f(x|1) = (7/3) f(x,1), untuk x=0, 1, 2. Karena itu

f(0|1) = (7/3) f(0,1) = (7/3)(3/14) = ½ f(1|1) = (7/3) f(1,1) = (7/3)(3/14) = ½ f(2|1) = (7/3) f(2,1) = (7/3) (0) = 0

dan sebaran bersyarat untuk X, diberikan Y=1 adalah

x

0

1

2

f(x|1)

½ ½ 0

Contoh 2.11

• Soal: Fungsi kerapatan gabungan dari peubah acak X dan Y

dinyatakan sebagai

f(x,y) = 8xy; 0<x<1, 0<y<x

= 0; selain itu

Tentukan g(x), h(y), f(y|x), dan P(Y<1/8|X=1/2)

• Jawab: Berdasarkan definisi, kita peroleh hasil-hasil berikut ini:

g(x)= ∫_-∞∞ f(x,y) dy = ∫₀x 8xy dy = 4xy2|x_y=0 = 4x3 ; 0<x<1

h(y)= ∫_-∞∞ f(x,y) dx = ∫₀y 8xy dx = 4x2y|y_x=0 = 4y3 ; 0<y<x

Selanjutnya

f(y|x) = f(x,y)/g(x) = 8xy/4x3 = 2y/x2 ; 0<y<x

Kebebasan Statistik

• Contoh 2.12: Tinjau kasus fungsi kerapatan bersama pada

Contoh 2.9. Tentukan g(x), h(y), f(x|y), dan P(1/4<X<1/2|Y=1/3)

• Jawab: Berdasarkan definisi kita peroleh

g(x)= ∫_-∞∞ f(x,y) dy = ∫₀x x(1+3y2)/4 dy = x/2; 0<x<2

h(y)= ∫_-∞∞ f(x,y) dx = ∫₀y x(1+3y2)/4 dx = (1+3y2)/2 ; 0<y<1 Akibatnya

f(x|y) = f(x,y)/h(y)

= {x(1+3y2)/4}/{(1+3y2)/2} = x/2 ; 0<x<2

dan P(1/4<X<1/2|Y=1/3) = ∫_1/41/2 (x/2)|_y=1/3 dx = 3/64

• Contoh ini memperlihatkan peluang bersyaratf(x|y) tidak

bergantung pada y. Untuk kasus demikian, dapat ditunjukkan bahwa

…

• Bukti:substitusikan f(x,y) = f(x|y)h(y) ke sebaran marjinal dari X, yakni

g(x)= ∫_-∞∞ f(x,y) dy= ∫_-∞∞ f(x|y)h(y) dy

Karena f(x|y) tdk bergatung y, maka peluang bersyarat ini bisa dikeluarkan dari integral. Akibatnya

g(x)= f(x|y) ∫_-∞∞ h(y) dy = f(x|y)⋅1 = f(x|y) Oleh karena itu

g(x) = f(x|y) dan

f(x,y) = g(x)⋅h(y)

Def. Kebebasan Statistik

• Def.2.10: AndaikanX dan Y dua peubah acak, baik diskret maupun kontinyu, dengan sebaran peluang gabungan f(x,y) dan sebaran marjinal g(x) dan h(y). Peubah acak X dan Y disebut bebas secara statistik, jika dan hanya jika,

f(x,y) = g(x)⋅h(y)

untuk semua nilai (x,y)

• Peubah acak kontinyu pada contoh 2.12 adalah bebas secara

statistik

• Peubah acak kontinyu pada contoh 2.11 tidak bebas statistik

• Berdasarkan contoh 2.8:

f(0,1) = 3/14

g(0) = ∑2_y=0 f(0,y) = 3/28 + 3/14 + 1/28 = 5/14 h(1) = ∑2_x=0 f(x,1) = 3/14 +3/14 + 0 = 3/7

Generalisasi ke n-buah peubah acak

• Hasil-hasil yang diperoleh dari 2-buah peubah acak dapat

di-generalisasi ke n-buah peubah acak. Tinjau fungsi peluang

bersama f(x₁, x₂, …, x_n) dari peubah acak X₁, X₂, …, X_n.

• Sebaran marjinal untuk X₁ diberikan oleh

diskrit: g(x₁) = ∑_x2 …∑_xn f(x₁, x₂, …, x_n)

kontinyu: g(x₁) = ∫_-∞∞… _-∞∞ f(x₁, x₂, …, x_n)dx₂…dx_n • Sebaran marjinal gabungan φ(x₁, x₂)

diskrit: φ(x₁, x₂) = ∑_x3 …∑_xn f(x₁, x₂, …, x_n)

kontinyu: φ(x₁, x₂) = ∫_-∞∞… _-∞∞ f(x₁, x₂, …, x_n)dx₃…dx_n

• Sebaran gabungan bersyarat X₁, X₂, X₃ diberikan X₄= x₄, X₅=

x₅, …, X_n= x_n adalah

Generalisasi kebebasan statistik

• Def.2.11: AndaikanX₁, X₂, …, X_n adalah n-buah peubah acak, diskrit atau kontinyu, dengan sebaran peluang bersama f(x₁, x₂, …, x_n) dan sebaran marjinal f₁(x₁), f₂(x₂), …, f_n(x_n). Peubah acak X₁, X₂, …, X_n disebut saling bebas secara statistik jika dan hanya jika

f(x₁, x₂, …, x_n) = f₁(x₁)⋅f₂(x₂) ⋅ … ⋅ f_n(x_n)

• Contoh 2.13: Andaikan X₁, X₂, dan X₃ adalah tiga peubah acak yang saling bebas secara statistik dan andaikan masing-masing memiliki fungsi rapat peluang: f(x) = e-x _{, x>0}

= 0 , selain itu Tentukan P(X₁<2, 1<X₂<3, X₃>2)

• Jawab:Fungsi rapat peluang bersama dari X₁, X₂, dan X₃ adalah f(x₁, x₂, x₃) = f(x₁) f(x₂) f(x₃) = e-x1 _e-x2 _e-x3

= exp(-x₁ - x₂ - x₃), x₁>0, x₂>0, x₃>0

Latihan

• Peluang marjinal: 23 dan 24

• Peluang bersyarat: 27 dan 28

• Kebebasan statistik: 29, 30

2.6 Nilai

Harap

dari

Peubah

Konsep dan Definisi

• Def.2.12: AndaikanX suatu peubah acak dengan sebaran

peluang f(x). Nilai harap dari X adalah

E(X) = ∑_x x⋅f(x) ; untuk X diskrit = ∫_-∞∞ x⋅f(x)dx ; untuk X kontinyu

• Jika dua buah koin dilantunkan 16 kali dan X menyatakan jumlah

munculnya sisi H per-lantunan, maka X dpt bernilai 0, 1, atau 2. Jika eksperimen ini menghasilkan 4 lantunan tanpa H, 7 lantunan dengan 1H, dan 5 lantunan dengan 2H, maka rata-rata jumlah H perlantunan dari dua koin adalah:

(0⋅4 + 1⋅7 + 2⋅5)/16 = 1.06

• Nilai rata-rata dari peubah acak yang demikian disebut sebagai

Contoh 2.14

• Soal: Hitung nilai harap dari jumlah Kimiawan dalam seleksi suatu Komite yang terdiri dari tiga orang,

berdasarkan 4 kandidat Kimiawan dan 3 kandidat Biologiwan

• Jawab: Jika X menyatakan banyaknya Kimiawan dalam Komite, maka sebaran peluang dari X akan diberikan oleh

f(x) = C(4, x)⋅C(3, 3-x)/C(7,3); x=0, 1, 2, 3

---{kombinasi x dari 4 Kimiawan} * ---{kombinasi (3-x) dari 3 angg. komite}

yakni f(0)=1/35, f(1)=12/35, f(2)=18/25, dan f(3)=4/35. Oleh karena itu:

Contoh …

•

Soal: Andaikan X peubah acak yang menyatakan

waktu hidup lampu tabung dalam jam. Fungsi

kerapatan peluangnya dinyatakan sebagai:

f(x) =

20.000/x

3

, x>100

= 0

, selain itu

Tentukan nilai harapan hidup dari tabung jenis ini.

•

Jawab: Berdasarkan Def.2.12, maka

E(X) =

∫

∞₁₀₀

x

⋅

(20.000/x

3

)dx

=

∫

∞₁₀₀

(20.000/x

2

)dx =

= 20.000 (-x

-1

)|

∞

Nilai harap g(X)

•

Tinjau fungsi g(X) dari peubah acak X. Sbg

contoh untuk X diskrit dengan sebaran peluang

f(x), dimana x=-1, 0, 1, 2 dan g(X)=X

2

, maka

P[g(X)=0] = P(X=0) = f(0)

P[g(X)=1] = P(X=-1)+P(X=1) = f(-1)+f(1)

P[g(X)=4] = P(X=2) = f(2)

Perdefinisi 2.12,

E[g(X)] =

∑

_g(x)

g(x)P[g(X)=g(x)]

= 0

⋅

P[g(X)=0] + 1

⋅

P[g(X)=1]+4

⋅

P[g(X)=4]

= 0

⋅

f(0) + 1

⋅

[f(1)+f(-1)] +4

⋅

f(2)

=

∑

_x

g(x)

⋅

f(x)

• Teorema 2.1: Andaikan X suatu peubah acak dengan sebaran peluang f(x). Nilai harap dari fungsi g(X) adalah

E[g(X)] = ∑_x g(x)⋅f(x) ; jika X diskrit

= ∫_-∞∞ g(x)⋅f(x)dx ; jika X kontinyu

Nilai harap dari g(X) …

• Contoh 2.17: Andaikan X adalah peubah acak dengan sebaran

peluang berikut

x | 0 1 2 3

---f(x)| 1/3 ½ 0 1/6 Tentukan nilai harap dari Y = (X-1)2

• Jawab: Berdasarkan Teorema 2.1, nilai harap dari Y adalah

E[(X-1)2] = ∑₀3 (x-1)2 f(x)

= (-1)2⋅f(0) + (0)2⋅f(1) + (1)2⋅f(2) + (2)2⋅f(3)

• Def.2.13: Andaikan X dan Y peubah acak dengan sebaran peluang bersama f(x,y). Nilai harap dari fungsi g(X,Y ) adalah

E[g(X,Y)] = ∑_x,y g(x,y)⋅f(x,y) ; jika X dan Y diskrit = ∫_-∞∞∫_-∞∞ g(x,y)⋅f(x,y)dxdy ; jika X dan Y kontinyu

Nilai harap dari g(X,Y)

• Jawab: Perdefinisi 2.13, kita dapat menyatakan E(XY) = ∑2

x=0 ∑ 2y=0 xy⋅f(x,y)

= 0⋅0⋅f(0,0) + 0⋅1⋅f(0,1) + 0⋅2⋅f(0,2) + 1⋅0⋅f(1,0) + 1⋅1⋅f(1,1) + 2⋅0⋅f(2,0) = 0 + 0 + 0 + 0 + f(1,1) + 0 = f(1,1)

y x 0 1 2

0 3/28 9/28 3/28

1 3/14 3/14

-2 1/28 -

2.7 Hukum

N

ilai

Teorema

• Teorema 2.2: Jikaa dan b konstanta, maka

E(aX + b) = aE(X) + b

• Corollary 1: Dengan membuat a=0, maka

E(b) = b

• Corollary 2: Dengan membuat b=0, maka

Teorema

• Teorema 2.3: Nilai harap dari jumlah atau perbedaan dari dua atau lebih fungsi dari peubah acak X adalah jumlah atau perbedaan dari nilai harap fungsinya. Yakni

E[g(X) ± h(X)] = E[g(X)] ± E[h(X)]

• Contoh 2.21: Dalam contoh 2.17, kita dapat menuliskan E[(X-1)2_{] = E(X}2 _{– 2X +1) = E(X}2_{) -2E(X) + E(1)} Dari Corollary 1, E(1) = 1, Sehingga

E(X) = 0⋅(1/3) + 1⋅(1/2) + 2⋅(0) + 3⋅(1/6) = 1

E(X2_{) = 0}⋅_{(1/3) + 1}⋅_{(1/2) + 4}⋅_{(0) + 9}⋅_{(1/6) = (1/2) + 1.5 = 2} Dengan demikian

E[(X-1)2_{] = 2- 2}⋅_{1 + 1 = 1}

x | 0 1 2 3

Teorema

• Teorema 2.4: Nilai harap dari jumlah atau perbedaan dari dua atau lebih fungsi dari peubah acak X dan Y adalah

jumlah atau perbedaan dari nilai harap fungsinya. Yakni

E[g(X,Y) ± h(X,Y)] = E[g(X,Y)] ± E[h(X,Y)]

• Corollary: Dengan membuat g(X,Y) = X dan h(X,Y) = Y diperoleh

E[X ± Y] = E[X] ± E[Y]

• Teorema 2.5: Andaikan X dan Y dua peubah acak yang saling bebas. Maka

Contoh 2.23

• Andaikan X dan Y dua peubah acak yang saling bebas dengan

sebaran peluang

f(x,y) = x(1+3y2)/4 ; 0<x<2, 0<y<1

= 0 ; selain itu

Periksa berlakunya Teorema 2.5 untuk kasus ini.

( )

(

)

(

)

(

)

₆5

3 3 1 2 12 3 1 4 3 1 1 0 2 1 0 2 0 2 3 1 0 2 0 2 2 = + = + = + =

∫∫

∫

∫

= = dy y y dy y y x dxdy y y x XY E x x

( )

(

)

(

)

(

)

3 4 3 3 1 2 12 3 1 4 3 1 1 0 2 1 0 2 0 2 3 1 0 2 0 2 2 = + = + = + =

∫∫

∫

∫

= = dy y dy y x dxdy y x X E x x

( )

(

)

(

)

(

)

₈5

2 3 1 8 3 1 4 3 1 1 0 2 1 0 2 0 2 2 1 0 2 0 2 = + = + = + =

∫∫

∫

∫

= = dy y y dy y y x dxdy y xy Y E x x

2.8 Ekspektasi Khusus

Momen ke-k

• Jika g(X) = Xk, Teorema 2.1 akan menghasilkan nilai yang disebut sebagai momen ke-k dari titik asal dari peubah acak X, yang dinyatakan sebagai μ’_k. Karena itu

( )

( )

( )

∫

∑

∞ ∞ − = = = kontinyu X dx x f x diskrit X x f x X E k x k k k ; ; ' μ

• Jika k=0, kita dapatkan E(1) = 1 karena

μ’₀= E(1) = ∑_x f(x) = 1 ; X diskrit

= ∫∞_-∞ f(x) dx =1 ; X kontinyu

• Jika k=1, kita dapatkan μ’₁=E(X), yaitu nilai harap peubah acak X. Momen pertama juga disebut mean dari peubah acak μ, jadi

Momen ke-k thd mean, variansi

• Jika g(X) = (X-μ)k_{, Teorema 2.1 menghasilkan momen}

ke-k terhadap mean dari peubah acake-k X, yang dilambangke-kan

sebagai μ_k. Dengan demikian:

(

)

[

]

(

) ( )

(

) ( )

∫

∑

∞ ∞ − − = − = − = kontinyu X dx x f x diskrit X x f x X E k x k k k ; ; μ μ μ μ

• Momen kedua terhadap mean, μ₂, memberikan ukuran

keragaman (variability) hasil pengamatan terhadap mean. μ₂ disebut juga sebagai variansi dari peubah acak X,

dinyatakan sebagai σ2.

σ2 ₌ μ

2 = E[(X-μ)2]

Variansi

• Teorema 2.6: Variansi dari peubah acak X diberikan oleh

σ2 _{= E(X}2_{) -} μ2

• Bukti:

σ2 _{= E[(X-}μ₎2_{] = E(X}2 _{- 2}μ_X+μ2₎

= E(X2) - 2μE(X) + E(μ2) = E(X2_{) - 2}μ⋅μ ₊ μ2

Contoh 2.24

•

Soal: Hitung variansi dari X, dimana X adalah

banyaknya Kimiawan dalam komite yang terdiri

dari 3 orang dan dipilih dari 4 Kimiawan dan 3

Biologiwan

•

Jawab: Dalam contoh 2.14 sudah didapatkan

μ

=

12/7. Selanjutnya

E(X

2

) = 0

2

⋅

(1/35) + 1

2

⋅

(12/35) + 2

2

⋅

(18/35)

+ 3

2

⋅

(4/35) = 24/7

Oleh karena itu

Contoh 2.25

• Soal: Tentukan mean dan variansi dari peubah acak X, dimana

X memiliki fungsi kerapatan

f(x) = 2(x-1), 1<x<2

= 0, selain itu

• Jawab:

( )

( )

53

2

1

1

2

−

=

=

=

E

X

∫

x

x

dx

μ

( )

( )

176

2

1 2 2

1

2

−

=

=

∫

x

x

dx

X

E

Kovariansi

•

Jika g(X,Y) = (X-

μ

_X

)(Y-

μ

_Y

), dimana

μ

_X

=E(X) dan

μ

Y

= E(Y), Def. 2.13 akan menghasilkan nilai harap

yang disebut kovariansi dari X dan Y, yng

dilambangkan sebagai

σ

_XY

atau cov(X,Y).

(

)(

)

[

]

(

)(

) ( )

(

x

)(

y

) ( )

f

x

y

dx

dy

X

dan

Y

kontinyu

Sifat-sifat Kovariansi

•

Kovariansi positif:

– tingginya nilai X berasosiasi dengan tingginya nilai Y, dan

– rendahnya nilai X berasosiasi dengan rendahnya nilai Y

•

Kovariansi negatif:

– tingginya nilai X berasosiasi dengan rendahnya nilai Y, atau sebaliknya

•

Jika X dan Y saling bebas secara statistik, maka

kovariansi akan bernilai nol. Hal sebaliknya tidak

berlaku, kovariansi nol tidak berarti X dan Y

Kovariansi ..

•

Teorema 2.7 Kovariansi dari dua buah peubah

acak X dan Y dengan mean masing-masing

μ

_X

dan

μ

Y

adalah

σ

XY

= E(XY) -

μ

X

⋅μ

Y

•

Bukti:

σ

XY

= E[(X -

μ

X

)(Y -

μ

Y

)]

= E(XY-

μ

_X

Y-

μ

_Y

X+

μ

_X

μ

_Y

)

= E(XY)-

μ

_X

E(Y)-

μ

_Y

E(X) +E(

μ

_X

μ

_Y

)

= E(XY) -

μ

_X

μ

_Y

-

μ

_Y

μ

_X

+

μ

_X

μ

_Y

Contoh 2.26

• Tinjau sebaran peluang bersama pada contoh 2.8. dan perhitungan 2.19 yang menghasilkan E(XY) = 3/14.

y x 0 1 2

0 3/28 9/28 3/28

1 3/14 3/14

-2 1/28 -

-g(x) 10/28 15/28 3/28

μX = E(X) = ∑2x=0 ∑ 2y=0 xf(x,y)

= ∑2_x=0 xg(x)

= 0(10/28)+1(15/28)+2(3/28) =21/28=3/4

Sedangkan μ_Y = E(Y) = ∑2

x=0 ∑ 2y=0 yf(x,y)= ∑2y=0yh(y)

= 0(15/28)+1(12/28)+2(1/28) = 14/28 = ½ Akibatnya

σXY = E(XY) - μX μY = 3/14 – (3/4)(1/2)

= -9/56

h(y)

15/28

12/28

2.9 Sifat-Sifat

Sifat-sifat variansi …

• Teorema 2.8: Andaikan X suatu peubah acak dengan sebaran peluang f(X). Variansi dari fungsi g(X) adalah

σ2

g(X) = E[{g(X) - μg(X)}2]

• Teorema 2.9: JikaX suatu peubah acak dan b konstanta, maka

σ2

X+b = σ2X = σ2

• Teorema 2.9: JikaX suatu peubah acak dan a konstanta, maka

σ2

Sifat-sifat variansi …

• Teorema 2.11: Jika X dan Y peubah acak dengan sebaran peluang gabungan f(x,y), maka

σ2

aX+bY = a2σ2X + b2σ2Y + 2abσXY

• Corollary 1: Jika X dan Y peubah acak yang saling bebas, maka

σ

2

aX+bY

=

a2σ2X + b2σ2Y

• Corollary 2: Jika X dan Y peubah acak yang saling bebas, maka

σ

2

Contoh 2.8

•

Soal: Jika X dan Y peubah acak dengan variansi

σ

2_X

=

2,

σ

2_Y

= 4 dan kovariansi

σ

_XY

= -2, tentukan variansi

dari peubah acak Z = 3X - 4Y + 8

•

Jawab:

σ

2

Z

=

σ

23X - 4Y + 8

=

σ

2_3X-4Y

; T.2.9

= 9

σ

2_X

+ 16

σ

2_Y

- 24

σ

_XY

; T.2.11

= 9

⋅

2 + 16

⋅

4 - 24

⋅

(-2)

Teorema Chebyshev dan Bukti

• Teorema Chebyshev: Peluang sebarang peubah acak X jatuh dalam rentang k kali simpangan baku dari mean sekurang-kurangnya adalah (1 - 1/k2). Yakni

P(μ-kσ<X< μ+kσ) ≥ 1 – 1/k2

(

)

[

]

(

) ( )

(

) ( )

(

) ( )

(

) ( )

(

) ( )

∫

(

) ( )

∫

∫

∫

∫

∫

∞ + − ∞ − ∞ + + − − ∞ − ∞ ∞ − − + − ≥ − + − + − = − = − = σ μ σ μ σ μ σ μ σ μ σ μ μ μ μ μ μ μ μ σ k k k k k k dx x f x dx x f x dx x f x dx x f x dx x f x dx x f x X E 2 2 2 2 2 2 2 2

• Karena integral kedua bernilai tak negatif. Selanjutnya, karena |x - μ| ≥ kσ berarti x ≥ μ+kσ atau x≤ μ-kσ, diperoleh

…

( )

∫

( )

∫

₊∞ − ∞ − + ≥ σ μ σ μ σ σ σ k k dx x f k dx x f

k2 2 2 2

2

( )

∫

( )

∫

₊∞ − ∞ − ≤ + σ μ σ μ k k k dx x f dx x

f 1₂

Akibatnya

Dan bahwa

(

)

( )

2

1 1 k dx x f k X k P k k − ≥ = + < < − +

∫

− σ μ σ μ

σ

μ

σ

μ

Oleh karena itu

Konsekuensi Teorema Chebyshev

• Untuk k=2, teorema ini menyatakan bahwa peubah acak X memiliki peluang sedikitnya 1-(1/2)2 = ¾ untuk masuk

dalam rentang dua kali simpangan baku dari mean.

μ σ

2σ

f(x)

∫

( )

+

−

σ μ

σ μ

k

k

dx

x

f

Contoh 2.30

•

Soal: Suatu peubah acak X memiliki mean

μ

=8,

variansi

σ

2

=9 dan (fungsi) sebaran peluang

yang tak diketahui. Tentukan: (1) P(-4<X<20)

dan (2) P(|X-8|

≥

6).

•

Jawab: simpangan baku

σ

=

√

9 = 3,

μ

=8

1. P(-4<X<20) = P[8-(4)(3)<X<8+(4)(3)]

= P[μ - (4)(σ)<X< μ + (4)(σ)]

≥ 15/16 ; (1-1/k2_)=1-1/16

2. P(|X-8|>6) = 1-P(|X-8|≤6)

= 1 – P(-6<X-8<6)

= 1 - P[μ -(2)(σ)<X<μ +(2)(σ)]