LECTURE NOTES
LOGIKA MATEMATIKA
Disusun Oleh :
UNIVERSITAS GUNADARMA
DAFTAR ISI
BAB I HIMPUNAN DAN OPERASI BINER...2
1.1. OPERASI PADA HIMPUNAN...4
1.2. PERHITUNGAN ANGGOTA HIMPUNAN...6
1.3. ALJABAR HIMPUNAN...7
BAB II RELASI...9
2.1. PERKALIAN CARTESIAN DAN RELASI...9
2.2. PENYAJIAN RELASI...11
2.3. RELASI INVERS...11
2.4. SIFAT RELASI...13
2.5. RELASI EKIVALEN...14
2.6. RELASI PENGURUTAN SEBGAIAN...15
BAB III FUNGSI...17
3.1. FUNGSI SATU-SATU DAN FUNGSI PADA...18
3.2. INVERS DARI FUNGSI...19
Pertemuan 1
BAB I HIMPUNAN DAN OPERASI BINER
Sebuah himpunan adalah kumpulan obyek atau simbol yang memiliki sifat yang sama. Anggota himpunan disebut elemen.
Contoh 1.1.
D himpunan nama hari dalam satu minggu.
M himpunan mahasiswa jurusan teknik informatika di Universitas Gunadarma.
N himpunan bilangan asli.
Sebuah himpunan dapat dinyatakan dalam bentuk daftar anggota (bentuk pendaftaran) atau dengan menyebutkan sifat yang dimiliki oleh semua anggota (bentuk pencirian).
Contoh 1.2.
D = { Senin, Selasa, Rabu, Kamis, Jumat, Sabtu, Minggu } = { x x nama hari dalam satu minggu }
Himpunan P disebut himpunan bagian (subset) dari himpunan Q, jika setiap anggota P merupakan anggota Q. Hubungan antara P dan Q tersebut dapat ditulis
sebagai P Q. Dengan cara lain, hubungan antara P dan Q tersebut dapat ditulis
sebagai Q P dan dibaca Q superset dari P atau P terdapat di dalam Q .
Contoh 1.3.
merupakan himpunan bagian dari himpunan M dan ditulis sebagai P M.
Dapat pula ditulis sebagai M P dan dibaca M superset dari P .
Dua himpunan dikatakan saling lepas (disjoint) jika mereka tidak memiliki anggota bersama.
Contoh 1.4.
Himpunan mahasiswa S1 Universitas Gunadarma dan himpunan dosen S1 Universitas Gunadarma merupakan himpunan yang saling lepas.
Himpunan kosong adalah himpunan yang tidak memiliki anggota dan
dinyatakan sebagai { } atau .
Contoh 1.5.
A = { x x bilangan asli dan x < 1 } = .
Dalam rangka menyelidiki hubungan antara beberapa himpunan, seringkali dibutuhkan pendefinisian sebuah himpunan yang disebut himpunan semesta. Himpunan-himpunan lain yang dibicarakan merupakan himpunan bagian dari himpunan semesta tersebut. Himpunan semesta biasanya dinyatakan sebagai himpunan S atau U .
Contoh 1.6.
Himpunan bilangan riil R merupakan semesta dari himpunan bilangan asli N
dan himpunan bilangan bulat Z .
Dua buah himpunan dikatakan sama jika keduanya memiliki anggota yang benar-benar sama.
Contoh 1.7.
Diagram Venn biasa digunakan untuk menggambarkan himpunan dan hubungan antar himpunan. Anggota dari setiap himpunan ditempatkan dalam sebuah bentuk tertutup, biasanya lingkaran. Himpunan semesta didefinisikan harus
Gabungan (union) himpunan A dan himpunan B, ditulis sebagai A B, adalah sebuah himpunan yang anggotanya merupakan anggota A atau anggota B atau anggota keduanya.
A B = { x x A atau x B }
S = { k k Z , 1 k 12 }
A = { x x Z , 1 < x < 10 }.
B = { y y Z , y kelipatan 3 dan 3 y 12 }.
Gambarkan diagram Venn yang memperlihatkan hubungan ketiga himpunan
tersebut dan hitung banyaknya anggota A B, A B, A’, B’, A’ B’ .
Jawab : ... diserahkan kepada pembaca ...
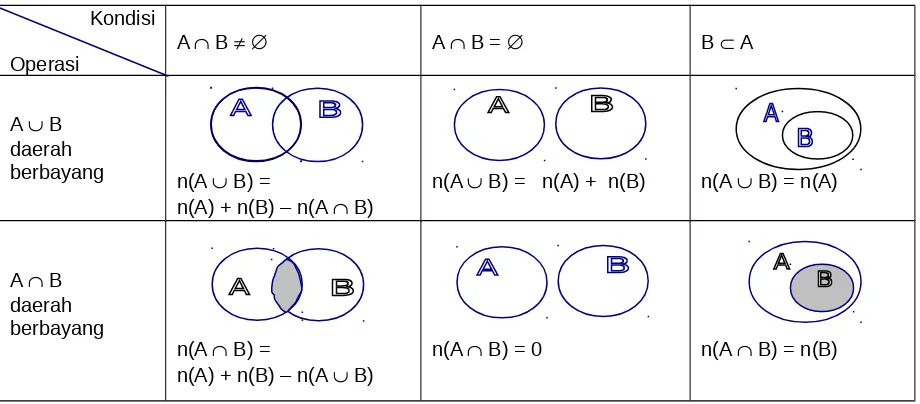
Gambar di bawah ini menunjukkan beberapa keadaan yang mungkin terjadi.
Kondisi
Selain ketiga operasi tersebut di atas, pada himpunan berlaku pula operasi selisih dan operasi selisih simetri.
anggota gabungan himpunan A dan B, tetapi bukan merupakan anggota irisan himpunan A dan B.
A B = ( A B ) – ( A B ) atau
A B = ( A – B ) ( B - A ).
1.2. PERHITUNGAN ANGGOTA HIMPUNAN
Banyaknya anggota himpunan D (kardinalitas D) dinyatakan sebagai n(D)
atau D.
Contoh 1.10.
Dari contoh sebelumnya, n(D ) = 7, n(N ) tak hingga.
Contoh 1.11.
Sebuah survei dilakukan terhadap 30 siswa SD dan diperoleh data berikut : B himpunan siswa yang memiliki sepeda, D himpunan siswa yang memiliki
anjing. n(B)=23 , n(D)=10, n(B D) = 6.
Tentukan :
a). banyaknya anak yang memiliki sepeda dan anjing.
b). banyaknya anak yang tidak memiliki sepeda maupun anjing.
c). banyaknya anak yang memiliki salah satu sepeda atau anjing, tapi tidak keduanya.
Jawab : ... diserahkan kepada pembaca ...
Soal Latihan 1.1.
1. Sajikan himpunan A = { x x + 2 < 10, x Z+ } dalam bentuk pendaftaran.
2. Tunjukkan bahwa jika A B dan B C , maka A C.
3. Tunjukkan bahwa himpunan A dan himpunan B merupakan himpunan bagian
dari A B.
4. Tunjukkan bahwa (A B) merupakan himpunan bagian dari himpunan A dan
5. Tunjukkan bahwa jika A dan B adalah himpunan, maka (A – B) (A B).
Pertemuan 2
Contoh 1.13.
Jika P, Q dan R adalah himpunan,
tunjukkan bahwa P’ (Q R)’ (P’ Q’ ) = P’ Q’
Jawab : ...diserahkan kepada pembaca....
Soal Latihan 1.2.
1. Buktikan bahwa (A B) (A B’ ) = A.
2. Buktikan bahwa, jika A B = S, maka A’ B. (S = semesta).
Pertemuan 3
BAB II RELASI
Anggota sebuah himpunan dapat dihubungkan dengan anggota himpunan lain atau dengan anggota himpunan yang sama. Hubungan tersebut dinamakan relasi.
Contoh 2.1.
Misalkan M = { Ami, Budi, Candra, Dita } dan N = { 1, 2, 3 }. Misalkan pula, Ami berusia 1 tahun, Budi berusia 3 tahun, Candra berusia 2 tahun dan Dita berusia 1 tahun, maka kita dapat menuliskan sebuah himpunan P = {(Ami, 1), (Budi, 3), (Candra, 2), (Dita, 1)} dimana P merupakan himpunan pasangan terurut yang menggambarkan hubungan antara himpunan M dengan himpunan N. Himpunan P merupakan relasi antara himpunan M dengan
himpunan N dan dapat ditulis sebagai P = { (x,y) x berusia y, dimana xM
dan yN }.
2.1. PERKALIAN CARTESIAN DAN RELASI
Misalkan A dan B adalah sembarang himpunan yang tidak kosong. Perkalian Cartesian A x B adalah himpunan semua pasangan terurut (x,y) dimana
xA dan yB.
A x B = { (x,y) | untuk setiap xA dan yB }
Contoh 2.2.
Misalkan C = { 2, 3, 4 } dan D = { x, y }.
Banyaknya anggota himpunan hasil perkalian cartesian A x B sama dengan hasil kali antara banyaknya anggota A dengan banyaknya anggota B .
n(A x B ) = n (A ) x n(B ) .
Sebuah relasi R yang memasangkan anggota himpunan A kepada anggota himpunan B merupakan sebuah himpunan bagian dari perkalian cartesian A x B,
ditulis R : A B .
2.2. PENYAJIAN RELASI
Sebuah relasi dapat disajikan dalam beberapa bentuk, yaitu : himpunan pasangan terurut dalam bentuk pendaftaran (tabulasi), himpunan pasangan terurut dalam bentuk pencirian, diagram panah, diagram koordinat atau grafik relasi, matriks relasi, bentuk graf berarah (digraf)
Contoh 2.5.
Diketahui C = { 2, 3, 4 }, D = { x, y } dan sebuah relasi yang ditulis dalam bentuk pendaftaran R1 = {(2,y) , (3,x) , (4,x), (4,y) }. Relasi tersebut dapat disajikan dalam bentuk lain, misalnya :
Bentuk diagram panah Bentuk diagram koordinat Bentuk Matriks
2.3. RELASI INVERS
Setiap relasi R dari himpunan A kepada himpunan B memiliki invers yang dinamakan R-1 dari himpunan B kepada himpunan A, yang ditulis sebagai
R-1 = { ( y , x ) ( x , y ) R }
Dengan kata lain, relasi invers R-1 dari R mengandung pasangan-pasangan
terurut yang bila dibalikkan akan terkandung dalam relasi R .
Misalkan W = {a, b, c}, relasi R = { (a,b) , (a,c) , (c,c) , (c,b) } merupakan relasi pada W . Invers dari relasi R adalah relasi
R-1 = { (b,a) , (c,a) , (c,c) , (b,c) }
Soal Latihan 2.1.
1. Diketahui G = { 5, 7, 11 }. Tentukan G x G dan n(G x G ).
2. Diketahui himpunan A = {a, b} dan himpunan B = { 9 }. Tentukan semua relasi
R : A B yang dapat didefinisikan dan hitung jumlahnya.
3. Diketahui himpunan C = {x, y}. Tentukan semua relasi R : C C yang dapat didefinisikan dan hitung jumlahnya.
4. Misalkan D = {1, 3, 5, 9}. Pada himpunan tersebut didefinisikan relasi
a. R 1 = { (x,y) x y }
b. R 2 = { (x,y) x + 2 y }
c. R 3 = { (x,y) x.y 50 }
Sajikan relasi-relasi tersebut dalam bentuk himpunan pasangan terurut. Tentukan invers dari setiap relasi tersebut.
5. Nyatakan invers dari tiap relasi berikut :
a. R = { (x,y) x habis dibagi oleh y, x, y Z }
b. R = { (x,y) x y, x, y Z }
Pertemuan 4
2.4. SIFAT RELASI
Misalkan R sebuah relasi yang didefinisikan pada himpunan A. Relasi R
dikatakan bersifat refleksif jika untuk setiap a A berlaku (a,a) R.
Contoh 2.8.
Diketahui A = { 1, 2, 3 }. Pada A didefinisikan relasi R1 = { (1,1), (1,2), (2,2),
(2,3) , (3,3) , (3,2) }. Relasi R1 tersebut bersifat refleksif.
Contoh 2.9.
Diketahui B = {2,4,5}. Pada B didefinisikan relasi R2={(x,y)x kelipatan y,
x,yB }. Maka R2 = {(2,2), (4,4), (5,5), (4,2)}. Relasi R2 tersebut bersifat
refleksif.
Contoh 2.10.
Diketahui B = {2,4,5}. Pada B didefinisikan relasi R3 = {(x,y)x + y <10, x,yA}. Maka R3={(2,2), (2,4), (2,5), (4,2), (4,4), (4,5), (5,2), (5,4)}. Relasi R3 tersebut
tidak bersifat refleksif.
Relasi R bersifat simetris jika untuk setiap (a,b) R berlaku (b,a) R.
Contoh 2.11.
Diketahui A = { 1, 2, 3 }. Pada A didefinisikan relasi R4 = { (1,1) , (1,2) ,
(2,2) , (2,1) , (3,3) }. Relasi R4 tersebut bersifat simetris.
Contoh 2.12.
Diketahui B = { 2, 4, 5 }. Pada B didefinisikan relasi R2 = { (x,y) x kelipatan
y , x,y B } = { (2,2) , (4,4) , (5,5) , (4,2) }. Relasi R2 tersebut tidak bersifat
Relasi R bersifat transitif, jika untuk setiap (a,b)R dan (b,c)R berlaku (a,c)R.
Contoh 2.13.
Diketahui A = { 1, 2, 3 }.
Pada A didefinisikan relasi R4 = { (1,1) , (1,2) , (2,2) , (2,1) , (3,3) } Relasi R4 tersebut bersifat transitif.
Contoh 2.14.
Relasi R1 = { (1,1) , (1,2) , (2,2) , (2,3) , (3,3) , (3,2) } yang didefinisikan pada
himpunan A = {1, 2, 3 } tidak bersifat transitif, karena terdapat (1,2) R1 dan
(2,3) R1, tetapi (1,3) R1 .
Relasi R dikatakan bersifat antisimetris jika untuk setiap (a,b) R dan (b,a) R
berlaku a = b.
Contoh 2.15.
Pada himpunan B = { 2, 4, 5 } didefinisikan relasi R2 = { (x,y) x kelipatan y ,
x,y B }. Dengan demikian R2 = {(2,2),(4,4),(5,5),(4,2)}. Relasi R2 tersebut
bersifat antisimetris.
Contoh 2.16.
Diketahui A = { 1, 2, 3 }.
Pada A didefinisikan relasi R5 = { (1,1) , (1,2) , (2,2) , (2,1) , (3,3) }
Relasi R5 tersebut tidak bersifat antisimetris karena terdapat (1,2)R5 dan
(2,1) R5, tetapi 1 2.
2.5. RELASI EKIVALEN
Contoh 2.17.
Diketahui A = { 1, 2, 3 }.
Pada A didefinisikan relasi R5 = { (1,1) , (1,2) , (2,2) , (2,1) , (3,3) }
Relasi R5 tersebut bersifat refleksif, simetris dan transitif. Oleh karena itu
relasi R5 merupakan relasi ekivalen.
Contoh 2.18.
Diketahui B = { 2, 4, 5 }.
Pada B didefinisikan relasi R2 = { (x,y) x kelipatan y , x,y B }.
R2 = { (2,2) , (4,4) , (5,5) , (4,2) }
Relasi R2 tersebut tidak bersifat simetris, oleh karena itu relasi tersebut
bukan relasi ekivalen.
2.6. RELASI PENGURUTAN SEBGAIAN
Relasi R disebut sebagai sebuah relasi pengurutan sebagian (partial ordering), jika relasi tersebut bersifat refleksif, transitif dan antisimetris.
Contoh 2.19.
Diketahui A = { 1, 2, 3 }.
Pada A didefinisikan relasi R5 = { (1,1) , (1,2) , (2,2) , (2,1) , (3,3) } Relasi R5 tersebut bersifat refleksif dan transitif, tetapi tidak bersifat antisimetris. Oleh karena itu relasi tersebut bukan merupakan relasi
pengurutan sebagian.
Contoh 2.20.
Diketahui B = { 2, 4, 5 }.
Pada B didefinisikan relasi R2 = { (x,y) x kelipatan y , x,y B }.
R2 = { (2,2) , (4,4) , (5,5) , (4,2) }
Relasi R2 tersebut bersifat refleksif, antisimetris dan transitif. Oleh karena itu
Soal Latihan 2.2.
1. Diketahui D = { x x garis lurus }
Pada D didefinisikan relasi R = { (x,y) x sejajar y, x D , y D }
Relasi R tersebut bersifat ... 2. Diketahui P = { x x subset dari himpunan A }
Pada P didefinisikan relasi R = { (x,y) x y , x P , y P }
Relasi R tersebut bersifat ... 3. Diketahui D = { x x garis lurus }
Pada D didefinisikan relasi R = { (x,y) x tegak lurus y, x D , y D }
Relasi R tersebut bersifat ... 4. Relasi-relasi berikut didefinisikan pada himpunan B = { 2, 4, 5 }.
a. R = { (2,2) , (4,4) , (5,5) }
b. R = { (2,4) , (4,5) , (2,5) , (5,2) , (2,2) } c. R = { (5,4) }
d. R = { (x,y) x habis membagi y , x,y B }.
Tentukan sifat yang dimiliki oleh masing-masing relasi tersebut.
5. Relasi-relasi berikut didefinisikan pada himpunan Z (himpunan bilangan bulat). a. R = { (2,2) , (4,4) , (5,5) }
b. R = { (2,4) , (4,5) , (2,5) , (2,2) } c. R = { (5,4) }
d. R = { (x,y) x habis membagi y }.
e. R = { (x,y) x y }.
Tentukan sifat yang dimiliki oleh masing-masing relasi tersebut. 6. Diketahui D = { x x garis lurus }. Pada D didefinisikan relasi
a. R = { (x,y) x sejajar y, x D , y D }
b. R = { (x,y) x tegak lurus y, x D , y D }
Pertemuan 5
BAB III FUNGSI
Misalkan A dan B adalah himpunan yang tidak kosong. Sebuah relasi f
dari A pada B disebut fungsi jika untuk setiap x A terdapat satu dan hanya
satu y B dimana (x ,y ) f .
Contoh 3.1.
Relasi R1 didefinisikan pada himpunan A={3,4,5} sebagai R1 = {(3,4),(4,4),
(5,3)}. Relasi R1 tersebut merupakan sebuah fungsi.
Relasi R2 didefinisikan pada himpunan A={3,4,5} sebagai R2 = {(3,4),(3,5),
(4,4), (5,3)}. Relasi R2 tersebut bukan sebuah fungsi.
Relasi R3 didefinisikan pada himpunan A={3,4,5} sebagai R3 = {(3,4),(3,5),
(5,3)}. Relasi R3 tersebut bukan sebuah fungsi.
Jika f merupakan fungsi yang memasangkan kepada setiap anggota A satu
dan hanya satu anggota B , atau ditulis f : A B, maka A disebut sebagai domain dan B disebut sebagai co-domain. Jika f(x) = y , maka y disebut image dari x di bawah f dan x disebut preimage dari y .
Contoh 3.2.
Dari contoh 1, fungsi R1 = {(3,4),(4,4), (5,3)}. Himpunan A = {3, 4, 5}
merupakan domain dan co-domain dari fungsi R1 .
Contoh 3.3.
Misalkan f sebuah fungsi dari himpunan A pada himpunan B. Fungsi f disebut fungsi satu-satu (one-to-one) atau injectif jika semua preimage adalah unik.
Dengan kata lain, jika a b maka f(a) f(b) . Fungsi f disebut fungsi pada (onto) atau surjectif jika setiap y pada B memiliki preimage. Dengan kata lain, untuk setiap y dalam B terdapat sebuah x dalam A demikian hingga f(x) = y . Fungsi f disebut bijectif, jika f merupakan fungsi satu-satu dan pada .
Contoh 3.4.
1. Fungsi pada contoh 3.3 di atas bukan merupakan fungsi satu-satu dan bukan merupakan fungsi pada. Dengan demikian, fungsi tersebut bukan merupakan fungsi bijektif.
Jika terdapat bijeksi antara himpunan A dan himpunan B, maka banyaknya anggota kedua himpunan tersebut harus sama. Dengan kata lain, kedua himpunan tersebut harus memiliki kardinalitas yang sama.
3.2. INVERS DARI FUNGSI
Misalkan f sebuah fungsi dari himpunan A pada himpunan B. Invers dari fungsi
f adalah relasi f -1 : B A dimana f -1(B) = { x | f (x) = y , xA, yB }.
Contoh 3.7.
Fungsi f dari contoh soal 3.5. di atas bukan fungsi invers, karena f-1 bukan
fungsi.
3.3. KOMPOSISI FUNGSI
Misalkan f : B C dan g : A B adalah fungsi. Komposisi f dengan g ,
ditulis fog adalah fungsi dari A kepada C yang didefinisikan sebagai fog(x) = f(g(x)). Contoh 3.8.
1. Di antara relasi-relasi berikut, relasi manakah yang merupakan fungsi ?
2. Fungsi-fungsi berikut didefinisikan pada himpunan bilangan riil R. Tentukan fungsi yang merupakan fungsi satu-satu, fungsi pada atau fungsi bijektif.
d. f(x) = | x |
3. Fungsi-fungsi berikut didefinisikan pada himpunan bilangan riil R. Tentukan invers dari setiap fungsi tersebut dan tentukan fungsi yang merupakan fungsi invers. a. f(x) = x
b. f(x) = x2
c. f(x) = x3
d. f(x) = | x |
4. Diketahui A = { 1, 2, 3 }. Tentukan semua fungsi invers yang dapat didefinisikan untuk memetakan A pada A.
5. Diketahui f(x) = 2 x . Tentukan