Matematika 24

(1)

M A T E M A T I K A

PROGRAM STUDI IPA

SMA/MA

DEPARTEMEN PENDIDIKAN NASIONAL

PANDUAN MATERI

UJIAN NASIONAL

(2)

KATA PENGANTAR

Dalam rangka sosialisasi kebijakan dan persiapan penyelenggaraan Ujian Nasional dan Ujian Sekolah/Madrasah Tahun Pelajaran 2004/2005, Pusat Penilaian Pendidikan Balitbang Depdiknas menyiapkan panduan materi untuk setiap mata pelajaran yang diujikan pada Ujian Nasional dan Ujian Sekolah. Panduan tersebut mencakup:

1. Gambaran Umum Format dan Bentuk Ujian

2. Standar Kompetensi Lulusan (SKL) dan Ruang Lingkup Materi 3. Contoh Spesifikasi Soal

4. Pedoman Penskoran

Panduan ini dimaksudkan sebagai pedoman bagi sekolah/madrasah dalam mempersiapkan penyelenggaraan Ujian Nasional dan Ujian Sekolah, serta sebagai informasi dan acuan bagi peserta didik, guru, dan pihak-pihak terkait dalam menghadapi Ujian Nasional dan Ujian Sekolah/Madrasah.

Semoga panduan ini digunakan sebagai acuan oleh semua pihak yang terkait dalam penyelenggaraan Ujian Nasional dan Ujian Sekolah Tahun Pelajaran 2004/2005.

Jakarta, Januari 2005

Kepala Pusat Penilaian Pendidikan,

Balitbang Depdiknas

(3)

DAFTAR ISI

Halaman

Kata Pengantar ... i

Daftar Isi ... ii

Gambaran Umum... 1

Standar Kompetensi Lulusan ... 2

Ruang Lingkup dan Ringkasan Materi ... 4

• Standar Kompetensi Lulusan 1 ... 4

(4)

• Pada ujian nasional tahun pelajaran 2004/2005, bentuk tes Matematika tingkat SMA/MA berupa tes tertulis dengan bentuk soal pilihan ganda, sebanyak 30 soal dengan alokasi waktu 120 menit.

• Acuan yang digunakan dalam menyusun tes ujian nasional adalah kurikulum 1994 beserta suplemennya, dan standar kompetensi lulusan.

• Materi yang diujikan untuk mengukur kompetensi tersebut meliputi: eksponen, logaritma, persamaan eksponen, persamaan logaritma, persamaan kuadrat, pertidaksamaan kuadrat, sistem persamaan liniear, matriks, program liniear, vektor, notasi sigma, barisan dan deret bilangan, fungsi komposisi, fungsi invers, suku banyak, dan teorema sisa, lingkaran ellips, parabola, hiperbola, transformasi, bangun ruang, ukuran pemusatan, ukuran penyebaran, peluang, fungsi trigonometri, persamaan dan pertidaksamaan trigonometri, logika matematika, limit, diferensial, dan integral.

(5)

Standar Kompetensi Lulusan

Standar Kompetensi Lulusan (SKL) Ruang Lingkup Materi

1. Siswa mampu melakukan operasi hitung aljabar, menyelesaikan persamaan dan pertidaksamaan, serta menggunakannya dalam kehidupan sehari-hari.

• Bentuk pangkat dan akar • Eksponen dan logaritma • Persamaan kuadrat • Pertidaksamaan kuadrat

• Sistem persamaan linear dan kuadrat • Program linear

• Matriks • Vektor • Suku banyak

2. Siswa mampu menyatakan dan mengkaji hubungan antara dua himpunan yang dapat dirumuskan sebagai fungsi atau barisan bilangan, serta menggunakannya dalam kehidupan sehari-hari.

• Fungsi linear dan fungsi kuadrat • Fungsi komposisi dan fungsi invers • Barisan dan deret

3. Siswa mampu memahami sifat dan konsep kedudukan titik, garis, dan bidang dalam ruang, dan mampu menghitung unsur-unsur yang terkait dengan sudut, garis dan bidang dalam ruang, serta menggunakannya untuk menyelesaikan masalah.

• Ruang dimensi tiga

4. Siswa mampu mengolah, menyajikan, menafsirkan data, dan menggunakan kaidah pencacahan untuk menentukan nilai peluang kejadian, serta menggunakannya dalam kehidupan sehari-hari.

• Statistika • Peluang

5. Siswa mampu memahami konsep dan mampu menghitung unsur-unsur yang terkait dengan segitiga, khususnya sudut dan identitas trigonometri, serta menggunakannya untuk menyelesaikan masalah.

• Trigonometri

6. Siswa mampu memahami dasar-dasar logika dan mampu menarik kesimpulan dari serangkaian premis yang diberikan.

(6)

7. Siswa mampu memahami konsep irisan kerucut dan sifat-sifatnya, efek transformasi serta mampu menggunakannya untuk menyelesaikan masalah.

• Irisan kerucut • Transformasi

8. Siswa mampu memahami konsep dan mampu menghitung limit fungsi di suatu titik, turunan, dan integral.

(7)

RUANG LINGKUP DAN RINGKASAN MATERI

Ruang Lingkup

• Bentuk pangkat dan akar

• Eksponen dan logaritma

• Persamaan kuadrat

• Pertidaksamaan kuadrat

• Sistem persamaan linear dan kuadrat

• Program linear

• Matriks

• Vektor

• Suku banyak

Ringkasan Materi

I. 1. Eksponen, Logaritma, persamaan eksponen, persamaan logaritma.

A. Sifat-sifat eksponen

1. ap× aq= ap+q 5. p

b a      

= p p b a

2. ap : aq= ap−q 6. a0= 1 3.

q p a 

   

 ₌_ap.q_7._a-p₌ p a

1

4.

( )

a.b p = ap.bp 8. qap = q p

a

STANDAR KOMPETENSI LULUSAN 1

(8)

B. Sifat-sifat logaritma

1. alogb + alogc = alogbc 2. alogb − alogc =

c b log a

3. alogbn= n alogb

4. alogb × blogc = alogc

5. alogb =

a log c

b log c

C. Bentuk persamaan eksponen

x

4. Persamaan eksponen yang dapat dikembalikan ke persamaan kuadrat.

D. Pertidaksamaan eksponen

1. Untuk 0<a<1

a. Jika af

( )

x ≥ ag

( )

x maka f

( )

x ≤ g

( )

x

dengan syarat : f

( )

x >0 dan g

( )

x >0

3. Persamaan logaritma yang dapat dikembalikan ke persamaan kuadrat.

F. Pertidaksamaan logaritma

1. Untuk 0<a<1

a. Jika alog f(x) ≥ alogg(x) maka f

( )

x ≤ g

( )

x

Contoh:

1. Nilai x yang memenuhi persamaan 4x+3 = 48x+5 adalah …. a.

5 9

− c.

5 2

e. 5

9

b. 5 2

− d.

5 4

Pembahasan :

4x+3= 48x+5

( )

₂ 3

2 x+ =

( )

4

5 3 2

+ x

2x + 6 =

4 15 3x+

5x = −9 x =

5 9

−

Kunci : A Contoh:

2. Himpunan penyelesaian 2log(x2 −3x+2) < 2log(10−x), x∈Radalah …. a. {x|−2< x<1 atau 2<x<4}

b. {x|x<1 atau x>2} c. {x|−2< x<4}

d. {x|x>10} e. {}

(10)

Pembahasan : syarat : )

x x

log( 2 3 2

2 ₋ ₊ _< 2_log(₁₀₋_x₎ _⊗ _x2 ₋₃_x₊₂_>₀ x2 −3x+2<10−x

(

x−2

)

10 < x

1 2< <

− x atau 2<x<4

Kunci : A

3. Nilai x yang memenuhi 3x2−3x+4< 9x−1 adalah …. a. 1<x<2 c. −3<x<2 e. −1<x<2

b. 2< x<3 d. −2<x<3

Pembahasan :

4 3 2

3x − x+ < 9x−1 4

3 2

3x − x+ < 32

(

x−1

)

2 2 4 3

2₋ _x₊ _< _x₋ x

0 6 5 2₋ _x₊ _< x

(

x−2

)(

x−3

)

<0 3

2< x<

Kunci : B

4. Jika x₁ dan x₂ adalah akar-akar persamaan : 33 2 0 2

3 _ ₋ ₊ ₌

  



 _log_x _. _log_x _,

maka x₁

.

x₂ = ….

a. 2 c. 8 e. 27

b. 3 d. 24

-2 4

1 2

(11)

Pembahasan : 33 2 0 2

3 _ ₋ ₊ ₌

  



 _log_x _. _log_x

0 1 3

2

3 _₌

  



 ₋

   



 _log_x₋ _log_x

2

3 ₌

x

log atau 3logx=1 x=9 atau x=3

x₁ . x₂ = 9 . 3 = 27

Kunci : E

I. 2. Persamaan dan Pertidaksamaan kuadrat.

A. Persamaan Kuadrat

1. Bentuk Umum : ax2 +bx+c=0, ,a,b dan c∈R dan a≠0

2. Menentukan akar-akar persamaan kuadrat dengan cara a. memfaktorkan

b. melengkapi kuadrat sempurna

c. menggunakan rumus ABC :

a ac b

b x _.

2 4 2

2 1

− ±

− =

3. Jenis-jenis akar persamaan kuadrat :

0 2₊_bx₊_c₌

ax mempunyai : akar real berlainan jika D>0

akar real sama jika D=0

akar tidak real jika D<0

D adalah diskriminan ax2 +bx+c=0, D=b2−4ac

4. Rumus jumlah dan hasil kali akar-akar persamaan kuadrat : Akar-akar persamaan ax2 +bx+c=0adalah x1 dan x2.

1

x + x₂ = a b

− dan x₁

.

x₂ = a c

5. Menyusun persamaan kuadrat yang diketahui akar-akarnya dengan cara : a. perkalian faktor :

(

x−x₁

)

(

x−x₂

)

= 0

b. menggunakan rumus jumlah dan hasil kali akar-akar tersebut :

(

)

0

2

2 1 2

1+ + =

− x x x x .x

x

(12)

B. Pertidaksamaan Kuadrat

1. Bentuk Umum : ax2+bx+c<0, bisa juga menggunakan tanda >, ≤ atau ≥ , a,b, dan c∈R, a≠0

2. Menyelesaikan pertidaksamaan kuadrat dengan menggunakan garis bilangan atau grafik fungsi kuadrat.

3. Pemakaian diskriminan persamaan kuadrat .

Menentukan koefisien persamaan kuadrat yang akarnya memenuhi sifat tertentu.

misal : akar real, akar tidak real, akar berkebalikan, dan sebagainya.

1. Jika x₁ dan x₂ akar-akar persamaan x2 + px+1=0, maka persamaan kuadrat yang akar-akarnya

2 1

2 2

x

x + dan x1 + x2 adalah …. a. x2−2p2x+3=0 d. x2 −3px+ p2 =0 b. x2+2px+3p2 =0 e. x2 + p2x+ p=0 c. x2+3px+2p2 =0

Pembahasan :

Misal akar-akar persamaan kuadrat baru adalah α dan β.

α =

2 1

2 2

x

x + =

(

)

2 1

2 x x

x x +

(

x−

( )

−p

)

=0

(

x+2p

)(

x+ p

)

=0

0 2 2 3

2₊ _px₊ _p ₌

x

Kunci : C

2. Jika x₁ dan x₂ adalah akar-akar persamaan kuadrat x2 +x− p=0, p konstanta positif, maka + =

1 2 2 1

x x x x

….

a.

p 1 2−

− c.

p 1

2− e.

p 1 2+

b. 1 −2

p d. p

(13)

Pembahasan : yang memenuhi adalah ….

a. m≤−4atau m≥8 c. m≤−4atau m≥10 e. −8≤m≤4 b. m≤−8atau m≥4 d. −4≤m≤8

Pembahasan :

Persamaan kuadrat mempunyai akar-akar nyata jika D≥0 0

Pembahasan :

(14)

I. 3. Sistem Persamaan Linear.

Bentuk Umum :

A. Sistem Persamaan Linear 2 peubah



B. Sistem Persamaan Linear 3 peubah



C. Penyelesaian Sistem Persamaan Linear

Dengan cara :

1. Substitusi 2. Eliminasi 3. Determinan 4. Matriks

1. Himpunan penyelesaian : 

Pembahasan :

1

(15)

2. Himpunan penyelesaian sistem persamaan :

Pembahasan :

5+ 4 =13

Program linear adalah suatu metode untuk mencari nilai optimum suatu bentuk linear (bentuk atau fungsi obyektif atau fungsi tujuan) pada daerah himpunan penyelesaian suatu sistem pertidaksamaan linear.

Nilai optimum tersebut dapat ditentukan dengan cara :

(16)

1. Nilai minimum fungsi objektif

(

5x+10y

)

pada himpunan penyelesaian sistem pertidaksamaan yang grafik himpunan penyelesaiannya disajikan pada daerah terasir gambar di bawah adalah…

a. 400

b. 320

c. 240

d. 200

e 160

Pembahasan :

Persamaan garis yang melalui (16, 0) dan (32, 0) 2x+y=32……. ( garis g₁)

Persamaan garis yang melalui (36, 0) dan (0, 24) 2x+3y=72……( garis g₂)

Persamaan garis yang melalui (48, 0) dan (0, 16) 48x+3y= ……..( garis g₃)

0 16 36

16

48 24

32

X Y

0 16 36

16

48 24

32

Y

g₁ g2 g3

A

B

Hp

(17)

A adalah titik potong garisg₁dang₂ B adalah titik potong garisg₂ dang₃ 2x + y = 32 2x + 3 y = 72

2x + 3 y = 72 x + 3 y = 48 −2 y = −40 x = 24

y =20

2x+y=32 x+3y=48

2x=12 3y=24

6 =

x y=8

Koordinat titik A (6, 20) Koordinat titik B (24, 8) Koordinat titik sudut pada daerah penyelesaian

(0, 32), (6, 20), (24, 8), dan (48, 0) Nilai optimum :

Bentuk obyektif : 5x + 10y

Pada titik (0, 32) 5.0 + 10.32 = 320 (6, 20) 5.6 + 10.20 = 230

(24, 8) 5.24 + 10.8 = 200 Nilai minimum (48, 0) 5.48 + 10.0 = 240

∴

Nilai minimum = 200

Kunci : D

2. Untuk menambah penghasilan, seorang ibu setiap harinya memproduksi dua jenis kue untuk dijual. Setiap kue jenis I modalnya Rp 200,00 dengan keuntungan 40%, sedangkan setiap kue jenis II modalnya Rp 300,00 dengan keuntungan 30%. Jika modal yang tersedia setiap harinya adalah Rp 100.000,00 dan paling banyak hanya dapat memproduksi 400 kue, maka keuntungan terbesar yang dapat dicapai ibu tersebut dari modalnya adalah ….

a. 30% c. 34% e. 40%

b. 32% d. 36%

Pembahasan :

Misal banyaknya kue jenis I = x buah dan kue jenis II = y buah

200x+300y≤100000

Sistem pertidaksamaan linear : x+ y≤400

x≥0

0

≥

y

Laba kue I = 40% = 100

40

× 200 = 80

Laba kue II = 30% = 100

30

(18)

Daerah himpunan penyelesaian :

Garis 10002x+3y=

Titik potong dengan sumbu X adalah(500, 0) dan sumbu Y adalah (0, 3 1000

) Garis x + y = 400

Titik potong dengan sumbu X adalah(400, 0) dan sumbu Y adalah (0, 400) Titik potong :

10002x+3y= × 1

x+y =400 × 2

10002x+3y=

800 2

2x+ y=

y=200

x=200 (200, 200) Bentuk obyektif : 80x + 90y

Koordinat titik-titik sudut dan nilai optimum bentuk obyektif (0, 0) 800.0 + 90.0 = 0

(400, 0) 80.400 + 90.0 = 32000

(200, 200) 80. 200 + 90.200 = 34000 maksimum (0,

3 1000

) 80.0 + 90. 3 1000

= 30000

Laba maksimum Rp 34.000,0 = 100% 34% 100000

34000

= ×

Kunci : C

3. Nilai maksimum fungsi sasaran z = 6x + 8y dari sistem pertidaksamaan : 604x+2y≤

48 4 2x+ y≤

0 ≥

x , y≥0 adalah ….

a. 120 c. 116 e. 112

b. 118 d. 114

Pembahasan :

Daerah himpunan penyelesaian :

garis 4x+2y =60

Titik potong dengan sumbu X adalah (15, 0) dan sumbu Yadalah(0, 30) garis 2x+4y=48

Titik potong dengan sumbu X adalah(24, 0) dan sumbu Y adalah(0, 12) 400

1000 3

400 500 0

(200, 200)

X Y

(19)

Titik potong garis

Matriks adalah susunan bilangan berbentuk persegi panjang yang diatur dalam baris dan kolom.

Misal : Matriks A = _

1. Transpose Matriks _

(20)

6. Invers Matriks _

I , I adalah matriks identitas

8. A . A-1=A-1. A =I

Matriks C yang memenuhi ABC = I dengan I matriks identitas adalah ….

a. _

Pembahasan :

ABC = I

(21)

2. Diketahui matriks A = _

3. Diketahui hasil kali matriks _

(22)

Pembahasan :

1. Vektor adalah besaran yang mempunyai panjang (besar) dan arah.

2. Jika suatu titik A(a₁, a₂, a₃) dalam ruang (juga pada bidang) dan O titik pangkal,

maka OA=a adalah vektor posisi dari titik A dan dapat ditulis



3. Vektor dapat dijumlahkan dengan aturan jajar genjang atau aturan segitiga.

(23)

(24)

Jawab:

(25)

Pembahasan :

Pembahasan:

4

Bentuk Umum Suku banyak :

2

Suku banyak sering dinyatakan dengan f

( )

x

(26)

Teorema Sisa

a = 0

1. Jika suku banyak P(x) = 2x4+ ax3– 3x2+ 5x + b dibagi oleh 

  

 _x2₋₁

memberi sisa

(

6x+5

)

maka a . b = ….

a. –6 c. 1 e. 8

b. –3 d. 6

Pembahasan :

Sisa = S = f(x) = 6x + 5

Pembagi 

  



_x2₋₁ ₌

(

_x₊₁

)

(27)

b = 6 a = 1

a . b = 1 . 6 = 6

Kunci : D

2. Diketahui

(

x+1

)

salah satu faktor dari suku banyak :

( )

x

Pembahasan :

( )

−1

f = 2 + 2 + p + 1 – 2 = 0 p = –3

( )

x

f = 2x4– 2x3+ 3x2 – x – 2

∴

faktor yang lain adalah

(

x−2

)

Kunci : A

-1 2 -2 -3 -1 -2

-2 4 -1 2

2 2 -4 1 -2 0

4 0 2

(28)

Ruang Lingkup

•

Fungsi linear dan fungsi kuadrat

•

Fungsi komposisi dan fungsi invers

•

Barisan dan deret

Ringkasan Materi

II. 1. Notasi Sigma, Barisan Bilangan, dan Deret

A. Notasi Sigma

Notasi sigma atau ∑ digunakan untuk menyatakan operasi penjumlahan

bilangan berurutan. Sifat-sifat Notasi ∑ : 1. ∑

=

n

m i

i = ∑

=

n

m p

p

2. ∑

=

n

m i

i

k

.

= ∑

=

n

m i

i

k , k = konstanta

3. ∑−

=

1 a

m i

i + ∑

=

n

a i

i

k

.

= ∑

=

n

m i

i k

.

4. ∑+

(

)

+

= −

a n

a m i

a

i = ∑−

(

)

−

= +

a n

a m i

a i

5. ∑

=

n

m i

ai ± ∑

=

n

m i

bi = ∑

(

)

= ±

n

m i

bi ai

Siswa mampu menyatakan dan mengkaji hubungan antara dua himpunan yang dapat dirumuskan sebagai fungsi atau barisan bilangan, serta menggunakannya dalam kehidupan sehari-hari.

(29)

B. Barisan dan Deret Aritmetika ⊗ Barisan Aritmetika

U₁,U₂,U₃,… ,U _n ,

a a+b, a+2b,…, a+

(

n−1

)

b

⊗ Deret Aritmetika

U1 +U2 + U3 +… + U _n

a +(a+ b) + (a + 2b) + … + (a + (n –1) b)

n ₊

2 = Jumlah n suku pertama U = _n S_n −S_n_-₁

C. Barisan dan Deret Geometri

⊗ Barisan Geometri

,

1

U U₂,U₃,… ,U _n a,ar,ar2 … , arn−1

⊗ Deret Geometri

U1 +U2 + U3 +… + U _n

a+ar+ar2 + … +arn−1

keterangan :

U1 = a = suku pertama r =

1 2

U U

= rasio

U = _n arn−1 = suku ke–n

S = _n ,

n r

n r a

1 1

−    



 ₋

1

>

r

S = _n ,

n r

n r a

−    

  −

1 1

0<r<1

(30)

D. Deret Geometri tak hingga

Suatu deret geometri mempunyai jumlah sampai tak hingga jika −1<r <1,

0 ≠ r

r a S

− = ∞

1

= ∞

S Jumlah sampai tak hingga a= suku pertama

r = rasio

1. Nilai dari ∑

=

100

1

2 k

k + ∑

(

+

)

=

100

1

2 3 k

k = ….

a. 25450 c. 25700 e. 50750 b. 25520 d. 50500

Pembahasan : ∑

=

100

1

2 k

k + ∑

(

+

)

=

100

1

2 3 k

k =

(

)

∑ + +

=

100 1

2 3 2 k

k

k = ∑

(

+

)

=

100 1

2 5 k

k = 7+12+17+ … + 502

selanjutnya penjumlahan di atas dapat dicari dengan menggunakan rumus jumlah n suku pertama deret aritmetika.

7+12+17+ … + 502 = …

a = 7 b = 5 U_n =502 a+

(

n−1

)

b=502

7+

(

n−1

)

5=502

7+5n−5=502

5n=500

n=100 (n dapat ditentukan dari indeks atas 100 ) 1

∑

=

k _n n

(

a U_n

)

2 1

S = +

S₁₀₀ =50

(

7+502

)

= 25450 Kunci : A

(31)

2. Suku kedua suatu barisan geometri adalah 2 dan suku kelima adalah 27 16

. Suku ketujuh adalah ….

a.

3. Jumlah n suku pertama deret aritmetika adalah _n n n 2 5 2

S = + . Beda dari deret aritmetika tersebut adalah ….

(32)

beda = b = 2 2 1 3 2 1 5 U

-U₂ ₁ = − =

Kunci : C

4. Empat bilangan positif membentuk barisan aritmetika. Jika perkalian bilangan pertama dan keempat adalah 46 dan perkalian bilangan kedua dan ketiga adalah 144, maka jumlah keempat bilangan tersebut adalah ….

a. 40 c. 98 e. 190

b. 50 d. 100

Pembahasan :

a2 +3ab=46

a2+21a−46=0

(

a+23

)(

a−2

)

=0

a=2

∴

ke-4 bilangan tersebut 2, 9, 16, 23

Jumlah ke-4 bilangan tersebut = 2+9+16+23 = 50 Kunci : B

5. Pertambahan penduduk suatu kota tiap tahun mengikuti aturan barisan geometri. Pada tahun 1996 pertambahannya sebanyak 6 orang, tahun 1998 sebanyak 54 orang. Pertambahan penduduk pada tahun 2001 adalah ….

a. 324 orang c. 648 orang e. 4.374 orang b. 486 orang d. 1.458 orang

Pembahasan :

U₁=6

U₃ =54

6 54 2

1 U

3 U

= =

a ar

9 2 ₌

r r =3

U₆ =ar5 =6

⋅

35 =1.458 orang

(33)

6. Jumlah deret geometri tak hingga adalah 7, sedangkan jumlah suku-suku yang bernomor genap adalah 3. Suku pertama deret tersebut adalah ….

a. 4 7

c. 7

4

e. 4

1

b. 4 3

d. 2

1

Pembahasan :

Misal deret tersebut a,ar,ar2,ar3,ar4,ar5 … , ,arn−1

S_∞ =7 

  

  − =₃ ₁ _r2 ar

7

1−r =

a

₍

₎

   

  − =

− 3 1 2

1

7 r r r

a=7

(

1−r

)

7r−7r2 =3−3r2

S_∞genap =3 4r2 −7r+3=0

3

2 1

= −r

ar

₍

₎₍

₎

0 1 3

4r− r− =

, r

4 3

= r =1

4 3

=

r

4 7 4 1 7 4 3 1

7 = =

     −

= .

a

(34)

II. 2. Fungsi kuadrat, Fungsi Komposisi dan Fungsi Invers.

A. Fungsi Kuadrat

1. Bentuk Umum : f

( )

x =ax2 +bx+c, a,b dan c∈R dan a≠0

2. Grafik fungsi kuadrat disebut parabola, dengan persamaan : c

bx ax

y= 2 + +

3. Nilai maksimum atau nilai minimum y =ax2+bx+c adalah

a D y

4

− =

untuk

a b x

2

− =

4. Persamaan fungsi kuadrat yang grafiknya :

a. mempunyai titik balik maksimum/minimum

( )

p,q adalah y = f

( )

x =α

(

x− p

)

1. Komposisi fungsi adalah pemetaan dua fungsi (lebih) secara berturutan. 2. Notasi Komposisi Fungsi :

A ∈

x , y∈B, dan z∈C y

) x (

f = , g(y)= z dan h(x)= z

( )

(

f x

) (

g f

)( )

x g

) x (

h = = o

go f

( )

x = komposisi fungsi f dilanjutkan dengan fungsi g. 3. Sifat Komposisi Fungsi :

f g g

f o ≠ o

f f I I

f o = o = , I adalah fungsi identitas

(

f og

)

oh= f o

(

goh

)

C. Fungsi Invers

A ∈

x dan By∈

( )

x y

f = , f−1

( )

y =x

1

−

f adalah fungsi invers dari f.

Fungsi f mempunyai fungsi invers jika f korespondensi satu-satu. Sifat Fungsi Invers :

1. f o f−1 = f−1o f =I

2.

(

go f

)

−1 = f −1 og−1

x y z

h

A B C

f g

x y

f -1

A B

(35)

1. Suatu fungsi kuadrat mempunyai nilai minimum 2− untuk x=3 dan untuk

0 =

x nilai fungsi itu 16. Fungsi kuadrat itu adalah ....

0 =16

f f

( )

0 =α

(

0−3

)

2−2=16

18 9α=

α=2

∴

Fungsi kuadrat f

( ) (

x =2 x−3

)

2−2 f

( )

x =2x2−12x+16

Kunci : D

2. Nilai maksimum dari fungsi f

( )

x =−2x2+

(

k+5

)

x+1−2k adalah 5. Nilai k yang positif adalah .…

a. 1 c. 7 e. 9

b. 5 d. 8

Pembahasan :

Nilai maksimum adalah

a ac b

a D y

4 4 2

4

   

  ₋ − = − =

( )

x x

(

k

)

x k

f =−2 2+ +5 +1−2

(36)

(37)

Pembahasan :

(38)

6. Fungsi f :R→R didefinisikan sebagai

( )

Pembahasan :

(39)

Ruang Lingkup

•

Ruang dimensi tiga

Ringkasan Materi

Dimensi Tiga. A. Irisan :

Irisan bidang α dengan bangun ruang adalah bidang datar yang dibatasi oleh garis potong-garis potong bidang α dengan sisi-sisi bangun ruang tersebut. Irisan bidang dapat digambarkan dengan cara :

1. Menggunakan sumbu Afinitas

2. Menggunakan diagonal bidang irisan B. Garis tegak lurus bidang

Garis g tegak lurus pada bidang α, jika garis g tegak lurus pada dua garis yang berpotongan yang terletak pada bidang α.

C. Jarak

1. Jarak antara dua titik

Jarak titik A dan titik B = panjang ruas

A B garis AB

2. Jarak antara titik dan garis

Jarak titik A dan garis g = panjang ruas garis AB (AB tegak lurus g)

Siswa mampu memahami sifat dan konsep kedudukan titik, garis, dan bidang dalam ruang, dan mampu menghitung unsur-unsur yang terkait dengan sudut, garis dan bidang dalam ruang, serta menggunakannya untuk menyelesaikan masalah.

STANDAR KOMPETENSI LULUSAN 3

α

l

g

h

g

h

(40)

3. Jarak antara titik dan bidang

Jarak titik A dan bidang α = panjang ruas garis AB (AB tegak lurus bidang α)

4. Jarak antara dua garis sejajar

Garis g sejajar h.

Jarak garis g dan h= panjang ruas garis AB (AB tegak lurus g dan h)

5. Jarak antara dua garis bersilangan

Garis g bersilangan dengan garis h.

Jarak garis g dan h= panjang ruas garis AB. (AB tegak lurus garis g dan garis h)

6. Jarak antara garis dan bidang yang sejajar

Garis g sejajar dengan bidang α.

Jarak antara garis g dan bidang α= panjang ruas garis AB.

(AB tegak lurus garis g dan bidang α)

7. Jarak antara dua bidang yang sejajar

Bidang α sejajar dengan bidang β.

Jarak bidang α dan bidang β= panjang ruas garis AB.

(AB tegak lurus bidang α dan bidang β) α

A

B

α

β

A

B

g

h

g

h

α

B A

g

h

g

h

α

g

A

B

(41)

D. Proyeksi

1. Proyeksi titik pada garis

Titik B adalah proyeksi titik A pada garis g. (AB tegak lurus g)

2. Proyeksi titik pada bidang

Titik B adalah proyeksi titik A pada bidang

α. (AB tegak lurus bidang α)

3. Proyeksi garis pada bidang 1. Garis g menembus bidang α

Garis BA menembus bidang α di titik A. Titik B′ adalah proyeksi titik B pada bidang α. Proyeksi garis BA pada bidang α = ruas garis AB′.

2. Garis g sejajar bidang α

Titik A dan B pada garis g.

Titik A′ dan B′ berturut-turut proyeksi titik A dan B pada bidang α.

Proyeksi garis g pada bidang α = ruas garis A′ B′

E. Sudut

1. Sudut antara dua garis yang bersilangan

Garis g dan h bersilangan.

∠(g, h) = ∠(g', h) = ∠(g, h')

= ∠(g', h') α

A

B

α B

B

A

B

gg

g

α A B

B A

g

h g g

h

g' g

(42)

2. Sudut antara garis dan bidang

Garis BA menembus bidang α di titik A. Titik B′ adalah proyeksi titik B pada bidang α, garis AB′ proyeksi AB pada bidang α.

∠(BA, bidang α) = ∠(BA, AB′)

3. Sudut antara dua bidang.

(α, β) garis potong bidang α dengan bidang β. AB tegak lurus (α, β)

BC tegak lurus (α, β)

Sudut antara bidang α dan bidang β adalah :

∠(AB, BC) = ∠ABC

1. Panjang rusuk kubus ABCD. EFGH adalah 6 cm. Jika S adalah titik potong EG dan FH, maka jarak DH ke AS adalah ….

a. 2 3cm c. 3 2cm e. 6 cm

b. 4 cm d. 2 6cm

Pembahasan :

HS tegak lurus DH HS tegak lurus AS

Jadi HS = jarak DH ke AS

HF = 62 +62 = 72 =6 2cm

HS =

2 1

HF = 2 1

.6 2 = 3 2cm

Kunci : C

α B

B

A

A B

C D

E _F

G H

S

Latihan dan Pembahasan

β

α

(α, β)

A

C

(43)

2. Pada kubus ABCD. EFGH, jika θ adalah sudut antara bidang ACF dan ACGE, maka sin θ= ….

a. 2 1

c. 2

2 1

e. 6

2 1

b. 3 3 1

d. 3

2 1

Pembahasan :

AC adalah garis potong bidang ACF dan ACGE FM tegak lurus AC

MN tegak lurus AC

Sudut antara bidang ACF dan ACGE adalah ∠ FMN.

∆ FMN siku-siku di N

Misal : AB =a cm FH =a 2 cm

NF = 2

2 1

a cm

Perhatikan : ∆ FBM BF =a cm, MB = 2

2 1

a cm

MF =

2

2 ₂

2 1

   

 

+ a

a = 2

2 3

a = 6 2 1

a

3 3 1 6 2 1

2 2 1

MF NF

θ

FMN= = = =

∠

a a sin

sin

Kunci : B

3. Pada kubus ABCD. EFGH dengan panjang rusuk 6 cm, jarak titik B ke diagonal ruang AG adalah ….

a. 63 cm c. 3 3 cm e. 3 cm b. 62 cm d. 2 3 cm

A B

C D

E F

G H

N

θ

(44)

Pembahasan :

AE // CG

∠(CG, AFH) = ∠(AE, AFH)

AP = proyeksi AE ke AFH

∠(AE, AFH) = ∠(AE, AP) = ∠EAP atau ∠EAN.

tan ∠EAN = 2

2 1 6

2 3 AN EN

=

Kunci : D

A B

C D

E _F

G H

N

(45)

Ruang Lingkup

•

Statistika

•

Peluang

Ringkasan Materi

III. 1. Statistika.

Rumus ukuran pemusatan (rata-rata, modus, median, dan kuartil) dan ukuran penyebaran (simpangan kuartil, simpangan rata-rata, ragam antar varians, dan simpangan baku)

A. Untuk data tunggal :

Dari data : x₁, x₂, x₃, …, x_n

1. Rata-rata = Mean =

∑

=

= +

+

= n

i i x n n

x x

x

x n

1 2

1 .... 1

2. Modus adalah ukuran yang paling banyak muncul.

3. Median adalah ukuran yang membagi data terurut menjadi 2 bagian sama banyak.

4. Kuartil adalah ukuran yang membagi data terurut menjadi 4 bagian sama banyak.

Kuartil terdiri atas Q1, Q2, dan Q3. Q2 = median 5. Jangkauan = ukuran terbesar – ukuran terkecil. 6. Jangkauan antar kuartil = Q3 – Q1

7. Jangkauan semi interkuartil = Simpangan kuartil

= Simpangan kuartil = Qd =

(

Q₃ -Q₁

)

2

1

Siswa mampu mengolah, menyajikan, menafsirkan data, dan menggunakan kaidah pencacahan untuk menentukan nilai peluang kejadian, serta menggunakannya dalam kehidupan sehari-hari.

(46)

8. Simpangan rata-rata =

∑

B. Untuk data kelompok :

1. Mean = rata-rata = rataan = x

S = Selisih frekuensi kelas modus dengan kelas sebelumnya

2

S = Selisih frekuensi kelas modus dengan kelas sesudahnya i = interval

kelas modus = kelas dengan frekuensi terbesar 3. Kuartil

(47)

6. Simpangan baku =

(

)

2

Kelas Median pada frekuensi kumulatif untuk (

∑

f = 20)

2. Modus dari histogram di samping adalah ….

a. 47,5

Latihan dan Pembahasan

(48)

Pembahasan :

frekuensi terbesar = 12 Modus = _

  

 

+ + =

2 1

1

S S

S b

o t

M .i

b

t = 44,5 = 44,5 + 

    

+6 4

4 . 5

1

S = 12 – 8 = 4 = 46,5

2

S = 12 – 6 = 6 i = 5

Kunci : B

3. Histogram pada gambar menunjukkan nilai test matematika di suatu kelas. Nilai rata-rata = ….

a. 69 b. 69,5 c. 70 d. 70,5 e. 71

Pembahasan :

Nilai rata-rata =

50 3500

= ∑

∑

⋅

f x f

= 70

∑ =f 50 ∑ fx=3500

Kunci:C III. 2. Peluang

A. Kaidah Pencacahan

Jika suatu kejadian dapat terjadi dalam p cara berlainan dan kejadian berikutnya dapat terjadi dalam q cara berlainan, maka kedua kejadian tersebut dapat terjadi dalam (p ×q) cara.

4 2 12

0

f

14 18

Nilai

57 62 67 72 77

( f ) Frekuensi ( x )

Titik tengah

f . x

2 4 18 14 12

(49)

Faktorial :

n! = 1 × 2 × 3 × … ×n 0 ! = 1

1 ! = 1 B. Permutasi

Banyak permutasi (susunan berurutan) k unsur dari n unsur adalah

( )

₍

₎

,

! ! P

, P

k n

n n

k

n _k

− =

= k ≤n

Permutasi dengan beberapa unsur sama

Banyak susunan dari n unsur dengan p unsur sama, q unsur sama, dst, … adalah …

... q p

n

× × ! !

!

C. Kombinasi

Banyak kombinasi (susunan) k unsur dari n unsur adalah

( )

₍

₎

,

! !

! C

, C

k n k

n n

k

n _k

− =

= k ≤n

D. Teorema Binomial Newton

(x+y)n= C(n,0)xn+ C(n,1)xn−1y+ C(n,2)xn−2y2+….. + C(n,n)yn.

E. Peluang suatu kejadian

Peluang suatu kejadian A = P(A) = n k

atau

P(A) = (S) (A) n n

k = hasil kejadian A

n = seluruh hasil yang mungkin terjadi n(A) = banyak anggota himpunan A

n(S) = banyak anggota himpunan ruang sampel F. Kisaran Nilai Peluang

1 P(A)

0≤ ≤

G. Frekuensi Harapan Kejadian A = F_h(A) (A)F_h = P(A) × N

P(A) = peluang kejadian A N = banyak percobaan

(50)

H. Peluang Kejadian Majemuk

1. Peluang gabungan dua kejadian B)

P(AU = P(A)+P(B)−P(AIB)

2. Peluang gabungan dua kejadian yang saling lepas B)P(AU = P(A) + P(B)

3. Peluang kejadian yang saling bebas stokastik B)

P(AI = P(A) × P(B)

4. Peluang kejadian bersyarat (peluang kejadian A setelah B terjadi) B)

| P(A =

P(B) B) P(AI

atau P(AIB)=P(A|B)×P(B)

\

1. Dari kota A ke kota B dilayani oleh 4 bus dan dari B ke C oleh 3 bus. Seseorang berangkat dari kota A ke C melalui B kemudian kembali lagi ke A juga melalui B. Jika saat kembali dari C ke A ia tidak mau menggunakan bus yang sama, banyak cara perjalanan orang tersebut adalah …

a. 12 c. 72 e. 144

b. 36 d. 96

Pembahasan :

Banyak cara perjalanan orang tersebut adalah 4×3×2×3 = 72

Kunci : C

2. Suatu kelas terdiri dari 40 orang. Peluang seorang siswa lulus tes matematika adalah 0,4. Peluang seorang siswa lulus tes fisika adalah 0,2. Banyak siswa yang lulus tes matematika atau fisika adalah ….

a. 6 orang c. 14 orang e. 32 orang b. 7 orang d. 24 orang

Pembahasan :

10 4 4 0 =

= ,

) m ( p

10 2 2 0 =

= ,

) f ( p

m dan f kejadian saling lepas,

10 6 10

2 10

4

= + = +

=P(m) P( f ) )

f m (

P U

A B C

(51)

Banyak siswa yang lulus = 40 24 10

6 _× ₌

orang

Kunci : D

3. Dua buah dadu dilempar undi bersama-sama. Peluang muncul jumlah mata dadu 9 atau 10 adalah ….

a. 36

5

c. 36

8

e. 36

11

b. 36

7

d. 36

9

Pembahasan :

Misal : A kejadian muncul jumlah mata dadu 9 B kejadian muncul jumlah mata dadu 10 A =

{

(3,6),(4,5),(5,4),(6,3)

}

→

36 4 P(A)=

B =

{

(4,6),(5,5),(6,4)

}

→

36 3 P(B)= A dan B kejadian saling lepas, P(AUB)= P(A) + P(B) =

36 7 36

3 36

4

=

+

Kunci : B

4. Sebuah dompet berisi uang logam, 5 keping lima ratusan rupiah dan 2 keping ratusan rupiah. Dompet yang lain berisi uang logam 1 keping lima ratusan rupiah dan 3 keping ratusan rupiah. Jika sebuah uang logam diambil secara acak dari salah satu dompet, peluang untuk mendapatkan uang logam ratusan rupiah adalah ….

a. 56

5

c. 28

8

e. 56

30

b. 28

6

d. 56

29

Pembahasan :

Misal : A kejadian terambilnya uang ratusan rupiah di dompet pertama B kejadian terambilnya uang ratusan rupiah di dompet kedua A dan B kejadian saling bebas,

P(AIB) = P(A) . P(B) =

7 2

. 4 3

(52)

Ruang Lingkup

•

Trigonometri

Ringkasan Materi

V.1.Rumus-rumus segitiga dalam trigonometri A. Hubungan antara sin a, cos a, dan tan a

1. sin2a+cos2a =1 2.

a cos

a sin a

tan =

B. Pada setiap segitiga berlaku :

1. Aturan sinus :

C sin B sin A sin

c b

a

=

2. Aturan kosinus : 2 2 2

2 ₌_b ₊_c ₋

a bc cosA 2

2 2

2 ₌_a ₊_c ₋

b ac cosB 2

2 2

2 ₌_a ₊_b ₋

c ab cosC 3. Luas segitiga ABC

= 2 1

sin c

b⋅ ⋅ A

= 2 1

sin c

a⋅ ⋅ B

= 2 1

sin b a⋅ ⋅ C

Siswa mampu memahami konsep dan mampu menghitung unsur-unsur yang terkait dengan segitiga, khususnya sudut dan identitas trigonometri, serta menggunakannya untuk menyelesaikan masalah.

A B

C

a b

c

(53)

V.2. Rumus-rumus Trigonometri Rumus trigonometri untuk 1. Jumlah dan selisih dua sudut

cos (a ± b)= cos a cos b m sin a sinb

2. Sudut rangkap

a

3. Perkalian sinus dan kosinus

2 cos a cos b = cos (a + b) + cos (a − b) 2 sin a sin b = cos (a − b)− cos (a + b) 2 sin a cos b = sin (a + b) + sin (a − b) 2 cos a sin b = sin (a + b)− sin (a − b) 4. Penjumlahan dan pengurangan sinus dan kosinus

(

a b

)

cos

(

a b

)

V.3. Grafik fungsi trigonometri

1. f(x) = a cos (kx + b) = a cos k 

(54)

c. geser grafik ke kiri sejauh k b

jika k b

positif,

geser grafik ke kanan sejauh k b

jika k b

negatif

d. periode grafik adalah k

π

2

V.4. Persamaan dan pertidaksamaan trigonometri

⊗ Persamaan trigonometri

1. Persamaan dasar trigonometri a. sin x= sin a, x = a + k.2 π

x = ( π−a ) + k.2 π b. cos x = cos a, x = ± a + k.2 π c. tan x= tan a, x = a + k.π

2. Persamaan yang dapat diselesaikan dengan cara memfaktorkan Misal : sin 2x + cos x = 0

2 sin x cos x + cos x = 0

cos x (2 sin x + 1) = 0 …. dan seterusnya.

3. Persamaan yang dapat dikembalikan ke persamaan kuadrat Misal : 2 cos2 x − sinx − 1=0

(

1

)

1 0 2 − sin2 x − sinx − =

0 1

2 sin2x + sinx − = …. dan seterusnya. 4. Persamaan berbentuk a cos x + b sin x =C,

dapat diselesaikan dengan a2 + b2 ≥ C2

⊗ Pertidaksamaan trigonometri

Pertidaksamaan trigonometri dapat diselesaikan dengan 1. Menggambar grafiknya

2. Menggunakan garis bilangan

1. Nilai sinus sudut terkecil dari segitiga yang sisinya 5 cm, 6 cm, dan 21cm adalah .…

a. 21 5 1

c. 5

5 1

e. 5

3 1

b. 21 6 1

d. 5

(55)

2. Diketahui A adalah sudut lancip dan

(56)

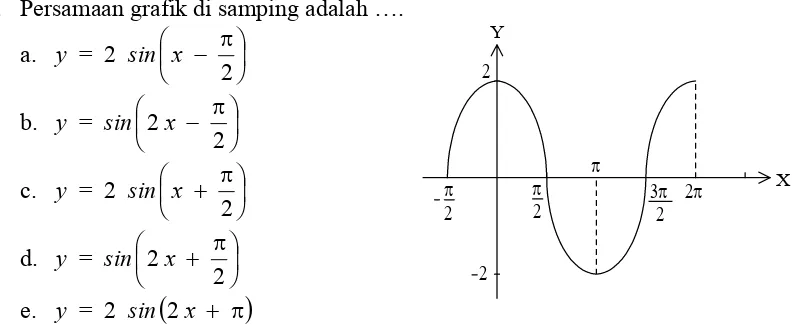
3. Persamaan grafik di samping adalah ….

Grafik pada gambar tersebut dapat diperoleh dengan cara menggeser grafik y = sin x sejauh

2

π

(57)

4. Himpunan penyelesaian sin

(

x+200

)

+ sin

(

x−700

)

cos 450 ≤ 1

(

)

2

2 1 250 ≤

−

x sin

x−250 =450 atau 135 0

x=700 atau 160 0

Yang diminta :

(

)

2 0 2

1

250 − ≤

−

x sin

Yang memenuhi adalah daerah I dan III

∴

{

0 0 0 0

}

360 160

atau 70 0

| ≤ x ≤ ≤ x ≤

x

Kunci : A

I II III

3600 1600

(58)

Ruang Lingkup

•

Logika matematika

Ringkasan Materi

VI.1. Pernyataan kalimat terbuka serta ingkarannya

Pernyataan adalah suatu kalimat yang mempunyai nilai benar saja atau salah saja,

tetapi tidak sekaligus benar dan salah. Contoh : 7 adalah bilangan ganjil (benar)

Malang adalah ibu kota Jawa Timur (salah). Pernyataan dinotasikan dengan huruf p, q, r, s, …

Kalimat terbuka adalah kalimat yang masih memuat peubah/variabel dan belum

dapat ditentukan nilai benar atau salah.

Jika peubah/variabel diganti dengan konstanta maka menjadi suatu pernyataan. Contoh : 3 +x = 8,

Jika x diganti dengan 5 maka kalimat terbuka menjadi pernyataan yang benar.

Ingkaran adalah pernyataan baru dengan nilai kebenaran berlawanan dengan nilai pernyataan semula, dinotasikan dengan ″~″

Contoh : Pernyataan p : 6 > 2 (B) maka ~ p : 6 ≤ 2 (S)

p: 4 + 1 = 5 (B) maka ∼p: 4 + 1 ≠ 5 (S)

Siswa mampu memahami dasar-dasar logika dan mampu menarik kesimpulan dari serangkaian premis yang diberikan.

(59)

VI.2. Operasi logika (konjungsi, disjungsi, implikasi, biimplikasi).

A. Konjungsi

Konjungsi dari pernyataan p dan q ditulis p∧q.

Dua pernyataan p dan q (p ∧ q) bernilai benar, hanya jika komponen p dan q bernilai benar.

Tabel kebenaran dari p∧q

p q p∧q

B B B B S S S B S S S S

B. Disjungsi

Disjungsi dari pernyataan p atau q dinotasikan dengan p∨q

Disjungsi dua pernyataan p atau q bernilai salah, hanya jika komponen-komponennya bernilai salah.

Tabel kebenaran dari p∨q

p q p∨q

B B B B S B S B B S S S

C. Implikasi

Implikasi dari pernyataan p dan q dinotasikan dengan lambang ″p→q″ Implikasi p→q bernilai salah, hanya jika p benar dan q salah

Tabel kebenaran implikasi p→q

p q p→q

B B B B S S S B B S S B

(60)

D. Biimplikasi

Biimplikasi dari pernyataan p dan q dinotasikan dengan lambang ″p↔q″.

Biimplikasi dua pernyataan benar, hanya jika p dan q mempunyai nilai kebenaran yang sama

Tabel kebenaran biimplikasi p↔q

p q p↔q

B B B B S S S B S S S B

VI.3. Pernyataan Majemuk

A. Pernyataan Majemuk yang ekuivalen

Dua pernyataan majemuk dikatakan ekuivalen, jika kedua pernyataan majemuk tersebut mempunyai nilai kebenaran yang sama.

Contoh :

1. Tunjukkan bahwa : p→q≡ ~ p∨q

Jawab :

p q ∼p ∼p∨q p→q

B B S B B

B S S S S

S B B B B

S S B B B

sama terbukti 2. Tunjukkan bahwa : p∧∼q≡∼(q∨∼p)

Jawab :

p q ∼p ∼q p∧∼q q∨∼p ∼(q∨∼p)

B B S S S B S

B S S B B S B

S B B S S B S

S S B B S B S

(61)

B. Negasi Pernyataan Majemuk

•Negasi Konjungsi dan Disjungsi

∼(p∧q)≡∼p∨∼q

Hukum De Morgan

∼(p∨q) ≡∼p∧∼q

Dapat ditunjukan pada tabel berikut :

p q ∼p ∼q p ∧ q ∼(p ∧ q) ∼p ∨∼q

B B S S B S S

B S S B S B B

S B B S S B B

S S B B S B B

sama

p q ∼p ∼q p ∨ q ∼(p ∨ q) ∼p∧∼q

B B S S B S S

B S S B B S S

S B B S B S S

S S B B S B B

sama

p q ∼p ∼q p→q ∼(p→q) p∧∼q

B B S S B S S

B S S B S B B

S B B S B S S

S S B B B S S

sama Contoh:

Tentukan Negasi dari :

1. Jika 932 = maka 6 + 2 > 7 Jawab : ~(p→q)≡p∧∼q

(62)

2. Jika Mandor tidak datang maka semua kuli senang

Jawab :

Negasinya adalah : Mandor tidak datang dan ada kuli yang tidak

senang.

VI.4. Konvers, Invers, dan Kontraposisi

Dari implikasi p →q dapat dibentuk implikasi lain yaitu : q→p, yang disebut konvers dari p→q

∼p→∼q , disebut invers dari p→q

∼q→∼p , disebut kontraposisi dari p→q

Hubungan tersebut dapat ditunjukan dalam tabel berikut :

P q ∼p ∼q p→q q→p ∼p→∼q ∼q →∼p

B B S S B B B B

B S S B S B B S

S B B S B S S B

S S B B B B B B

sama sama

Contoh: Tentukan konvers, invers, dan kontroposisi dari implikasi Jika harga BBM naik, maka semua harga barang naik. Jawab: Konversnya ialah

Jika semua harga barang naik, maka harga BBM naik. Inversnya adalah

Jika harga BBM tidak naik, maka ada harga barang yang tidak naik Kontraposisinya adalah

Jika ada harga barang yang tidak naik maka harga BBM tidak naik.

VI.5. Penarikan Kesimpulan

1. Prinsip Modus Ponens

Premis 1 : p q benar

Premis 2 : p benar

Konklusi : ∴ q benar

Contoh: Jika 3x= 12 maka x= 4 benar 3x= 12 benar ∴x = 4 benar

2. Prinsip Modus Tollens

(63)

Contoh :

Jika segitiga ABC sama kaki, maka ∠Α=∠ B benar ∠ A ≠∠ B benar

∴Segitiga ABC bukan segitiga sama kaki benar

3. Prinsip Silogisma

Premis 1 : p q benar Premis 2 : q r benar

Konklusi ∴ p r benar

Contoh: Selidikilah sah tidaknya argumentasi berikut :

p ∼q

p

∴ ∼q

Jawab: Untuk menyelidikinya dibuat tabel kebenaran dari {(p→∼q)∧p} →∼q

Cara 1.

p q ∼q p→∼q (p→∼q)∧p [(p→∼q)∧p]→∼q

B B S S S B

B S B B B B

S B S B S B

S S B B S B

→ nilai selalu benar jadi argumentasi sah

Cara 2.

p q ∼q p→∼q

B B S S B S B B S B S B S S B B Pada baris ke-2

Premis 1 → benar Premis 2 → benar Konklusi → benar

→ argumentasi sah Contoh:

1. Invers dari pernyataan (p∧∼q)→p adalah ….

Jawab :

p→q inversnya adalah ∼p →∼q

(64)

2. Ingkaran pernyataan “Beberapa peserta UAN membawa kalkulator “ adalah … Jawab :

“Semua peserta UAN tidak membawa kalkulator“

1. Diketahui p dan q adalah suatu pernyataan dari penarikan kesimpulan berikut 1. p→ q 2. p→ q 3. p→ q

∼q p→ r p

∴∼p ∴q→ r ∴q Argumentasi yang sah adalah ….

a. hanya 1 c hanya 2 dan 3 e. 1, 2, dan 3. b. hanya 1 dan 2 d. hanya 1 dan 3

Jawab: 1.

p q ∼p ∼q p→q

B B S S B B S S B S S B B S B S S B B B 2.

p q r p→q p→r q→r

B B B B B B

B B S B S S

B S B S B B

B S S S S B

S B B B B B

S B S B B S

S S B B B B

S S S B B B

3.

p q p→q

B B B B S S S B B S S B

Kunci : D

Tidak sah sah

sah

(65)

Ruang Lingkup

•

Irisan kerucut

•

Transformasi

Ringkasan Materi

VII.1. Irisan Kerucut

A. Lingkaran

1. Persamaan lingkaran

a. Persamaan lingkaran yang berpusat di O(0, 0) dengan jari-jari r adalah

2 2 2 _y _r

x + =

b. Persamaan lingkaran yang berpusat di (a, b) dengan jari-jari r adalah

(

x−a

) (

2 + y−b

)

2 =r

c. Bentuk umum persamaan lingkaran adalah x2 +y2 +Ax+By+C=0,

pusatnya 

  



₋ ₋

B 2 1 A, 2 1

dan B C

2 1 A

2 1 R

2 2

−      − +    

 − =

2. Jari-jari lingkaran

Lingkaran menyinggung sumbu X maka R = b

Lingkaran menyinggung sumbu Y maka R = a

Lingkaran menyinggung garis Ax + By + C = 0, maka R = Aa+Bb+C

R

M (a, b) R

M (a, b)

x y

X Y

M (a,

b)

R y + C

= 0

Siswa mampu memahami konsep irisan kerucut dan sifat-sifatnya, efek transformasi serta mampu menggunakannya untuk menyelesaikan masalah.