Kalkulus I

BAB

I

SISTET{

BILANGAN

RIIL

l.l

Sistem

Bilangan

Riil

Semesta pembicaraan dalam

matakuliah Kalkulus

ini

adalah

Himpunan bilangan

riil.

Himpunan

Bilangan

Riil

merupakan sekumpulan

bilangan Rasional

dan

lrrasional.

Secara lengkap dapat

dilihat

dari bagan

berikut:

R:

Himpunan

Bilangan

Riil

,Y:

Himp.

Bil.

Asli

Gb.

l.

I

Diagram Venn

Himpunan

Bilangan

Riil

,V:

Hirnpunan

Bilangan

Asli

Z:

Hirnpunan Bilangan Bulat

C:

Hirnpunan Bilangan

Rasional

1r:

Himpunan Bilangan

Irrasional

R:

Hirnpunan Bilangan

Riil

.1,2,3,...

'.

...,

_-3,-2,-1,0,

1,2-3,...'

_a

:qeO,rt=1,u.beZ,b=A

' b'

.r€Q,,{T,\11.o,..

't

-

6*t

ir

;2i

I

]

Sifat-sifat dalam

hirnpunan bilangan

riil

rnernainkan peranan yang sangat

penting

dalam

Kalkulus,

oleh

karena

itu

dalam sub

bab

ini

akan dibahas _beberapa

sifat

dari

_himpunan

bilangan

riil

dan permasalahan yang menyangkut bilangan

riil

itu

sendiri,

misalnya

nilai

rnutlak^persalnaan dan pertaksamaan aljabar.

Sifat-sifat Bilangan

Riil

.

a.

Sifat Medan

Jika

a

v,

z

adalah

anggota

biiangan

Riil,

rnaka

i.

x *

y

:

y

+

x

dan-ry

:.),r (

hukum

komutatif)

ii-

x

*

(y+':)

:

(x-ll

+;

dan

-r(y:):(xy)z

(hukum asosiatig

iii.

x(jt--1

:.r.1l

.

-r:(hukum

distributif)

ir,'.

{}nsur

ldentitias.

Terdapat

bilangan

Riil

yang

berlainan

0

dan

1 sehinesa

x

+ 0

:,r

_{dan -r-.} 1

:;r.

\'.

Unsur

Invers.

Setiap

bilangan

x

mempunyai invers penjurnianan

;

--r

sehingga

x

- Lr):

0 dan

mempunyai

in'ers

perkatian: -r-r sehingga

x1x-t1:i.

b.

Sifat

Ururan

i-

Trikotomi.

Jika -r

dan;,bilangan,

inaka pasti

beriaku

salah satu

x

<

y

atau -x

:

v a'iau -r -r,

-H

\

a ii.

Transitif.

n <

_{_1'} tlun _1,

<

-- :+.r

<:

iii.

Penambahin.

,r<;r

<> .r+ 3

11tl_

-ir,.

Perkalian. Jil*a

;

biiangan

positif, -t<y<+-r:<3,:,

jika

:

bilanga::

negatif,

Jr

<

,,

<:>

x:>F.

'1.

a4

l

Garis

bilangan

: Interval

dan

himpunan

Hirnpunan

Bilangan

Riil

(

n

)

secara

konkrit

dapat dinyatakan

dalarn

suatu garis bilangan.

koordinat

"t'

7i

-3-2-lOt234

Gb

1.2 Garis bilangan

Riil

Bilangan

Riil

_{-vang bersesuaian dengan}

titik

pada garis

bilangan disebut

koordinat

dari

titik

tersebut.

Bagian yang

lebiir

kecil

dari

garis bilangan dikenal

sebagai

interval

(

selang

).

Benkut

beberapa

inten'al

,cara penulisannva dalarn bentuk

himpunan,

dan

grafiknva

dalarn

oaris bilangan.

[a.h1={.1

"a-r<Ai ffi

interval

rutup

{-(a

_-b1

=

i.ti

o.

.t

.

Ai

a

b

inren,al

_buka

R

J'

tl.\t, (

-Lu,D)

-

t-tlo.

-,,

.

,i

a

b

inten/al

setengah

bul:a

(kanan)

ln'h)*{'l"..'<6}#inten,aisctengl'lrbuka(kiri)

{a,.,t)=

{-r1,.>.2}

\-r,a)=

{x

i .r

< a}

(-ar,

o:):

,P

inten'al

tak terbatas

inten'al

tak

terbaus

'rL-$

4*

c

t

I

i i

-l

Pertai-i2 rT:e.ei

Sa.-

-,,

a-,-:

:,-.;

pennasalahan

pokok

disini

adalah bagairnana

mencari

.;.,*si

i

i.,:-i

-

=j-::

'.-.7:--:.

t

dari

pertaksamaan aliabar- Solusi pertaksamaan

aliabar

-::=lolerr

::

=:

-l-,E-

=-.'.rsi persamaan

terlebih

dahultr- Pada

umutnnva

solusi

pertaksamaz:.

:r-*

-::. :t.:t?:a

nilai

(

bilangan

riil

)

atau

mungkin berupa

suatu

iatcn'al

{:.i.''5

Se:.,-=:..: :.'--r?:ii-

kembali

masalah suku ttarryak atau

polinom-S:r:":'oar'. '.;. 1a----L-

-

::-

:--:-ian sebagai :

P'.;

=

-,

-::-

---,t

-...+cr,,x"

dengan ath

Ql,a2,

.-.,

a,, e

R-Jer:uk

urr,::

*-,abar adalah :

.j. .: :

=''-

(l'1)

::rgan

l-.: : : -, :z:

-,.rf

: suku banyak.

(

tanda

<

dapat

diganti

oleh

:

>- >,

<

).

li:=punel

s-

r;

:,-:.='---,1

-r vang lnemenuhi

pertaksarnaan

(1.1)

disebut

dengan

IIim

p u na n

P+;*':tr;:

rgr E;

i pertaksatnaan.

'-;-..i. nrci::-.--:-=,

]-

.:-

--:-- :ertaksamaan adalah sebasai

berikut

:

-

Suat

!-

'i::-;i

-

. r-r

:-i

nol

atau

A(x)

-(l(-r)

< 0

B(,r)

1f(.r)

I

3enru;:

-,r:

-I

fakrar.:;-

'-'-:

,--- :,:;

dan

Qft)

menjadi

faktor

linier

dan atau

faktor

kuadrat

-: _{-J:_:- _ - --_:}

u3lill:: _-|'r

-.

:.

Tentuia:

---{

:--,.=:

:embuat

nol )

dari

rnasing-inasing

laktor linier

<ian ata.r

.<Ua,lraf

----

:"1;1-;:

".am

gariS

bilanf*p.

*.4*

j ilunal.:-:;-

--'-,

-

---rk

menentukan

tanda'(

+

atau

- )

interv'al paCa

gar,.

Tentukan Himpunan Penyelesaian

dari

'

?

I

=

-'

+l

Contoh

1.1

Jarvab

:

)

l--r-12

0 -I

?- "l - x

.T .T

-2

,

x:o

titik

pemecah:

x:l

,

aka

Hp =

(-

-,-Z]u

(O,r]

Contoh

1.2

Teniukan

Hirnpunan penyelesaian

dari

2 + 3.r

<

5-r- + 1 <

Jarvab

:

Pertaksamaan dapat dipecah m.,1ia'Ji di':a

bagian

2+3x

<

5x+l

3x-5x<1-2

-2x<-1

x>1i2

Hpr

:

(1i2

,4)

dan

5x+l<16

l6

-5x

<

l-5

x<3

Hp.:

(-.o,3)

Sehingga Himpunan penvelesa'an untuk

penaksamaan

tersebut

meniadi

Hp

=

Hp,

a

HP:=

(1i 2,co)

n(-co,3)

=

(l/?-3)

I

1.3

Pertaksamaan dengan

Nilai

lllutlak

Nilai

rnuttak

didefinisikan

sebagai bilangan yang

bernilai non negatit.

Secara

'eometr.s

nilai

mutlak dari

x

(

notasi

ixl

)

merupakan

jarak

antara

x

terhadap

titik

0

rada

gar-s

biiangan. Secara formal definisi

nilai

mutlak adalah :

r

r

[-r-

,-rZ0

l_Tl ₌ <

rr l--r

,-r<o

(1i

*

_it'

i'ti

-

=;

:

danlnl=i#''.0

--

_:.1

-r>i:aka

.

lrl

3a e -aS-r3aa x2-a

clunxSct

ex2

<a=

;

Iti

>a e xla

ctau

-r3-a

<9x2>ct=

:

."-,;

!

-:

+ _i-v

i

(

ketaksamaan segitiga )

.22

_:.

j. =, jf <y

i

sl

{-:,r"th

Ii

.:;:iukan

Himpunan penl'elesaian

dari

i:

+:l

>

t

|

-rl

Jz+z*:

lelgan

menggunakan

sifat

yatrg ke 2 bagian 2-

kita

dapatkan

s5

;-'

;'

1

atau

2+:

<

-l

,I .\'

-: tak lain

merupakan

dua

pertaksamaan

yang akan

dicari :r::r'eiesaiannya.

5

)r-+5-r

r'+-i

p

2+1.-l>0<>

--' - ">0 <f '- ->0 <-)-r<-5atuu-r'>A

i lr'ri-r' ir'-l-i i

.l+a+l<0 <= --''" "<0

<>

-" "<0

<.r

-

<-r<0

irJ-r3

:<eingga Himpunan pen-r'elesaian

dari

pertaksarnaan tersebut

adalah

:

r

;n:,,;h

1.4 -:imlian

Hirnpunan pen-1'elesian

dari

_lZ.r

-:i

<

_l.r + 3l

Jrxafi

:

3erdasarkan

sifat

nilai

tnutlak

vans ke-4- ttraka

(2-r-3)2

<(-r+3;:

=

(2x-3)t-(;r+3't:<0

<+

[(2x

-3)+(-r

+

3)][(2x

-3)

-

(;r+3)]

<

0

c+

3x(-r

-

6) < O

titik

pemecah: 0 dan 6

Hp:

[0,6]

o

6

Contoh

1.5

Tentukan Himpunan penyclesaian

dari

3 _I

r

_i

-

_i

.r-11

<

5

Jawab

:

Hilangkan

tanda

nilai

mutlak dari

pertaksamaan tersebut dengan meggunakan

definisi nilai

mutlali

(

persamaan _{1.2 )}

Ix-;r20

lr

l={

dan

l.r-

I

l.-

'r

,

x<o

\

, Ir-1,

.r-120

'

L-(r-l),r-1<0

[.r-

I

,

x2l

=1

l.-

(r-

l),-r<1

dan

1. Jadi,

terjadi

perubahan tanda

niiai

mutlak

di

0

x<0

0<;r

<l

-r> I

I I I : I I, a\\'al_I I I I : I I I i : : I I I I ;

s{bstitusi

ke pertaksarnaan

ixl:-'

lx-1i:-(x-

1)

3(-r)-(-("-l))<5

-

3-r +,.r

-

l <5

-

2r<6

r)-

3

Hp,

=(-op)

nl-3,co)

= [_3,0)

lxFx

lx-1F-(x-1)

3x

-

(-(x

-

1))

<5

3x+r-l<5

4xS6

3

1(-7

Hp,

_{L I}

=10j)n (-..,

_{L ) f '. t -)'}

'I

L

:

[0,])

;{ .,.? . V.e,-lxi--x

lx-11:*-t

-i---3-r-(-r-1)<5

3-r-r+1<5

^ /-Y1r2.

x<2

Hpr=l7,.n1n

(-.r:.1,

_ rr al

perhatikan

_{bahwa Himpunan} penyelesaiaq masing-masing selang

harus selalu

diiriskan

dengan ketentuan berlaliunya selang. Karena proses oenyelesaian pertaksarnaan

terjadi

aias

tiga

kasus terpisah

,

nraka

Himpunan

penyelesaiannya adalah gabungan

ketiga Hp

tersebut.

Jadi,

Hp

= Hprw

Hpzv

Hh

=

[-3,0)u[0,1)u[1,2]

=

[-3,2]

.

1.4

Kuadrat

dan

Akar Kuadrat

Setiap bilangan

positif

mernpunyai dua akar kuadrat-

Misalnya,

dua

akar kuadrat

dari

4

adalah 2

dan-2

; dua akar kuadrat

dari

16 adalah

4

dan

4.

Untuk c

2

0,

larnbang

J7,

discbut

akar

kuadrat utama dari

a,

yang rnenunjulikan

akar

kuadrat

tak

negatif

dari a.

Jadi

Ja

=2

dan

G10f

=.fi00

=

10.

Tidak

benarmenuliskan

.',6:13.

Jadi , penting untuk diingat bahwa

,

J?

=l

-r

l.

Soal

Latihan I

Tentukan Himpunan

Penyelesaian dari pertaksamaan

berikut

:

1.

:r2

-

3t+

>

-4

2.

4x-7 <3x+5

3

-2 <1-5x<3

2x-5

I

1

-<'1 t.^i!

x-/.

v+5

s -' -

<0

2::-1

6

6

"

-5+-r<0

x

23

'l-/-r x-4

-13

v-x+1

-r-2

9.

5lxi-2ix-3i<3

10

l2r

-

7lr

3

ll.l-r-21 .31.t+ii

12.

lxl

-

lx-

tl

<

5

1

13.2(.r-l)'-l-r-tl st

^ r.-l

-)- L.\t

-l

<4

l+x

I 14.

t5.

.:i' ilt!-16.

1l

l"-al

lr+7'i

I

1

-,n

aw

l"-3i

i:r+4i

l-ri- I

"

-<0

lxi-z

l

BAB

II

FUNGSI

2.1 Fungsi dan

Grafik

Definisi 2.1

Misaikan

A.B

c

R-

Fungsi

.f

:A-->

Badalah mengaitkan (memadankan) setiap ;r e

I

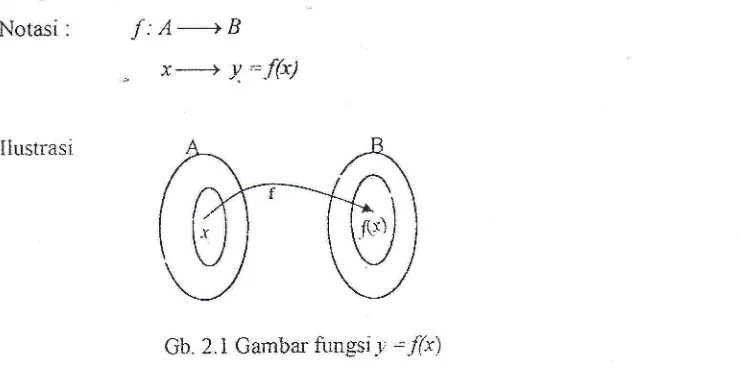
dengan tepat satuy € .&.

Notasi

.

f:A---+B

,.

x----)

Y.:-f(x)

Ilustrasi

Gb. 2.

i

Gambar fi.ingsi-Y

:/Ix)

Domain

i

daerah asal

danf(x)

adalahD,

:

l,,vairu

{r

e

R _{I ./'(-r) e} R} - Sedangkan

daerahniiai

/ Range dari fungsi./', Cinotasikan dengan

fty,

_1'aitu

{/(.r)e

Rl.re

Dr\sB

. [image:10.612.112.489.214.401.2]

Selanjutnya

hirnpunan

titik

di

bidang,{(x,.1')iv:f (-r),-reD"y,}'e

R.,-}disebut

grafik

furrgsi_f

Contch

2.1

Misalkan

f(x)

:

s:

+ 2x + 5 tnaka'

. (i):

12+2.1 + 5

:8,

f(-2)

_A-2)2

+2.(-2)-

5

:5

. dan

f(h+l)

:

(h+1)2 + 2(h+1)

- i

:

h2

-

4 h

*

8

.

Daeral'L asal

darif(x),

adalah

4:

R (hirnpunan bilangan

riil),

karena untuk setiapx€

R,

-f(x)terdefinisi-

'+,

.

Daerah

nilai

dari

f(x)

adalah

Il:14, a ).

karena.f(x)

: ,t *

2-t

- j

=

(r-

l)2 +

/,

maka

nilai

rninirnurn dari-/[-rl ada]ah 4.

suatu

aturail

yang

Contoh

2.2

Tentukan D.ldan

{1

dari

.f(9

:

t

*

..G

Jawab

:

1),

:

{.r'e

1? _|

l+Ji

e

R} = {-'-

e

It

i -. >

0l

= [0,cr:) 1?, ₌

{1"

Ji

lx

e[O.co)]

:

[l.co)

Jenis-jenis fungsi

.

.

1.

Fungsi Polinorn (suku banyak)

:,/

(-t _{) =} o ₀ + a

g

+ a ₂

t2

* - -.+Q,r,"

2.

Ftrngsi Rasional

:

.f(x)

=

#

O"n* an

p(x)

dan q(x)mentpakan firngsi polinom , dan

q(l

!(i.

I

s'G)

I

3.

Ftrngs' banval- aturan .

-/(t):

j

I

Ig'(")

[

^o

r-x<-]

Contolt .

-[(x)=l-t'

'

-lS-t

<3

|

-r+2:

-r>3

4.

Fungsi Genap dan Fungsi Garljil

.

.f(x)

disebut

filrgsi

genap

blla.f(x)

:.fGxl I

gafik

fungsi genap sitnet'is terhadap _{sur:rbuy ]}

.

.f(x)

disebut fungsi

ganjil

bi\a./(x)

: --fki

I

grafik

fi.ur-esi

ganjil

simetris

terhadap

titik

asal koordinat

l

5.

Fungsi Trigonornetri

.

.f(g

:

sin

x :

_.f(x)

:

csc

x

.

./(!)

:

cos

x

:

_.f(x)

:

.s'ec.r

.

_./(x)

:

tan

x

:

Jk)

:

cot x

6.

Fungsi

periodik

_..i

7.

Fungsi

Nilai

lt4utlak

[.r,

-r>o

/(x)

:l:

l:

{

[--r,

.r<0

8.

Fungsi Bilangan Bulat Terbesar

./(r)

=

ll .r

ll

yaitu bilangan bulat terbesar yang lebih kecil atau sama dengan x Notasi

lain: [r]

[image:12.612.89.540.62.708.2]

Contoh

2.3

ll5,9ll:5

Grafik

Fungsi Sederhana :

I.

Fungsi

Linier

:

,f(x)

:

ax*

b

Contoh

2.4

Grafik

fungsi

_-f

(-tj

_{-- 2x}

+3

adaiah :

Fungsi Kuad;at

:

tr(;r)

₌

oxt

+ bx + c

Contoh

2.5 Gralik

fiugsi ,f(..)

=

-r:

adalah :

ll-2,611:

-3

,li-0.91i

:

-l

)

-.4_!a

Il

IJ

3.

Ftrngsi

Tigonometri

:

./(-r):

sin-r ,

-/(-.):

cos-t

Contoh

?.5 Grafik fungsi _{.it(-r) = {-rl dan -/(-r)} =ll -r

li

adalah

4

3

2

I

^{

-l

r5 ts:

zl-

O--.o

rl.<

trrrJd

rrr.

-2-1 | : 2 3 r

.--.4-I

'{r

_{v =}

i'

_i

I

-3 *2

Dilihat

dari

bennrk

grafikny4

rnaka

fiurgsi

.i(.r)

= ii,ti1

riikenal

_juga sebagai fungsitangga.

Illenggambar

Grafik

Fungsi dengan Pergeseran

iika

diketairtri grafik fi.rngsi

y :

_J(.r),

naka

.

Grafik

)

:

_{J(.r-h) +} /r diperolelr dengan cara

mengqcer

graf,rk

y

:.1k1

sqault

ft satuan

*"

katrun

ilpu1,

Posirti'danllsanran

k" o'ot

iikak

Po''ti'/

kiri '

negatif

hcn+ult'

ttez;tif

[image:13.612.66.506.60.792.2]

Contoh

2.7

,t

Contoh

2-8 Gambai{<an grafik

nPgsi

Jawab

:

[1-rt

.f(r)'=lr+,

,r<I

.x2l

2. 2 Operasi Fungsi

A.

OPersi aliabar

Definisi

2.2

Misalkan fungsi./fx/

dn

g(x) mernpr-rnyai daerah asal

Dldan

Dn ' tnaka

.

(f!g)(x)

:f(x)

x

elx)

dan

D

₌

D!*r

- p'

r.'D"

.

(fg)(x)

:J@-g(x)

dan

D

-- Dtz

=

D,

r'' De

'

(flg)k)

:f(x)

i

g(x)'e6)+0

dan

Dr

r

:D-{'t

e

R!

gt-r)+0}

B.

Funesi

Kornposisi

.-Definisi

2.3

Komposisi dari fungsi.f/xi dengafr?ft,

didefinisikan

sebagai :

(-f"gXx)="f(g(x))'

Gb. 2.3 diagram ftrngs!

/"

g

Sifat-sifat

funesi

komoosisi :

l.

J'o g

vg o.f

2.

Dr"r=

{.r

e4

ig(.r)

e

Dr}

3.

R.r.,

:

{r,' e

R, lrt

=

f(t)-

t

e

ft"}

Contoh

2-9

Diketahui .f(x) =

E

aon

8(x)

=

xt -1

Tentukan

(ika

ada)

a)

.f

_"

g

dan D _s"r

'

Rr',

b)

g"f

danDr"t'Rr"r

Jawab

.

a)

Syarat agar

.fo

g

ada

adalah

tl"

rt

fi,

+

6'

D,

=

[0..c)

R,

:

[0.'c)

Dr=

R

n*

=[-

t,"o)

Disini didapat

Ilrr-,D,'

=

[-1,-)n[O'-)=

[0,"o)+

4

rnaka

_./'o

g

terdefinisi-(./'"

gX.t)

=.1'(S(")

=

.l'(x'

-l)

=

{?J

D,"e

=ft

e

1), l

s(x)

. Drl

t

=[.=Rl,,:

-re[o'*)]

#

:

{.

.

1l I x'?

-l

>

0]=

[r

e

/? |

(x-l)(x+11

>

0]

R,-"*

=

17,

e

llr l

y

=

.ftr),

I

e

/l*l=

tu =

o _I

v--

S''

>

-t|:

[0'*)-6':.

i,

b)Syarat agr

gol

terdefinisiadalah:

/lrn

Dsi@

Karena

R, fiDr=[0'co)nff:[O'ca) +@

'naka

g"'f

terdefinisi-(s

"./Xx)

₌

s(f(x))=

s(G)

=

(G)'

-1

=

r-tr'

Dr.r

:

\r

e

D,lf(x)

e

Dr\

={xe[0,*)l*._^t

= [0,co).

R*.,

:{} .

RrP

= g(.1), t

e

Ry}

:

trt

>-

-lly

₌

lt

-

i,l

> 01 =

[-l.co).

Contoh

2-10

Diketahui -/(-r) =

cos'r

dan

g(-r) =

JiL

Teiitukan (

jika

ada

)

g o

f

,Dr",

Jawab:

Syarat agar

g".f

adaadalah: R.,.

n

Dr*A

D.r

:R

,

Rr

=

[-1,1]

,

D,

=LZ,a)

KaretraR'nD*:[-i'l]n[2'a)=Q'tnakag"'l't.idakterdefirlisi-',fc:.

:

:

i

I I

,t

il

i

l1

Soal t-atihan

2

l.

Diketahui

:

./(x)

=ly'

'"-

1

. Hitung :

[z-r

,.r

<

3

a. .f( -4)

b.

f(0)

c..1(t2+:1

Nyatakan

fingsi

berikut tidak dalam nilai mutlak (

a

f(x):lxl+l3x+11

b.

(x):3+l2x-51

c.(x):3ix-2i-lx+ll

Tennrkan domain dan range dari :

./(-r)-Jzr+3

D;

i

s(r)

=

4x-l

c. /i\-rl:

t

.f

(r)

=

tl't

-

+

-r-+l

o{ vl:

-L\ \",/

-t

Tentukan .t''G +

|t)-

./

(x)

, h

*

A dari frrngsi berikut .

.f&1

:2x

- 1 b..f(x)

Ix

l*F{

[-x

,x)0

,x<0

3. f. 5-h. i. a. b.

:

.\

.l

G): L

-t rl

g(u):i2ii*31

:a

h( tt\

- -.'6?5 - r"

cos(-r +

I)

f(-r)=---\'2-r'-3r+i

== z-Y - _T

d.

4

a

a-

f(x):x2

+

I

b.

f(x):tt*

1

c..f(*):/+Jx

d.

./(t): G

6. Gambarkan

grafik

fungsi berikut :

a

(x):*'-

I

b.

,f(r)

:(x*2)2

c. .f(x)

= (x

-

Z\2

-

t

d.(x):

lx

-2

l+

2

I

c

, 'r<o

e.g(-r)=1-.t.0<.r<2

L-..*6,x>2

{x

+2,x

<

-1

f.

/("):

i

1

x:, x)-1

'-11

g

rr,)

=

llip

h.

./(.'):

_lis-'i,

i.s(r)=,*iitii

7. Tentukan (-f " g

)

(x1 dan (

g

" .f') (xS bila terdefinisi

dari

:

a.

_-f

(xj:

.ft

-

'

;

gf'')

:

3

.\

c.

f(x)=

j;

,

g(x):x2

-r+1

d

/(-r)

-

!.f- ;

g(-r):l-r-l

1

e.

/'(-r) =

J- :

_,

g(-r)

:

Jx

-\

:1

tii..

t.

.f(x)=4x-x2

; -e(x):l+.[

i

I

i

I

I s-t

,-r-< o

9.Hirung

(f.g) (x).bita-/(t)=1-t ,0<x(E i

8(-r)=

t3

L.t;

,-r>8

8. Tenttrkan domain dan Range dari soal nomor 7 diatas'

1 0. Carilah/1"r1, bila :

t

-f(x+1)=x2+3x+5

ir

b.

/(3r)

=

-n--x-+l

2

'

c.

_9(-t)

=

2x

-

I

dan

(gol)(-x)

:

-t-d. g(:)

=

Jr

+ 5. dan

(gof)(x)

= 3 i -x i

e.

g(xi:.vG'+5

;

(.fog)G):

l'rf,-'

.T

1t\rr2,

I-

_8',(-r

j

₌

-r-

_'

t./og/\-tl

: ar

-r u

11. Tuliskan

f(x)

sebagai komposisi dari dua fun-esi :

a. .f

(x)=

sin

Jl

+

t

t'. ./(x)

=

./i;i;

12.

Tuliskan

p(x)=fogJF;

sebagai kornposisi dari

tiga

frrngsi dengan dua cara

berbecia. _,.

13. Andaikan

.f(x)

-

-x

-

j

- Buktikan

bahlaf(f(f(x))):x'

dengan '!

=

=..1'

r+1 -

,

14. _{.{nrlaikan ./'(.r)} =

-+

Tenrukan dan sederhanakan tiap harga

r--

1

"/t\,

/ r

)

a.

.fl

-

|

u

fflf*lt

c.

ll

\.r.,

-

\./(.t)J

t

;,f

;l 'g

-!

*

rl

'?

BAB

ITT

LIMIT

DAN KEKO\TTNT]AN

3.1

Limit

Fungsi

di

Satu

Titik

3.1.1

Pcngertian

limit

secara

intuisi

"l - .,- - 6

Pandang srratu fungsi

"f(-.)

-

j---::---:.

Fungsi

ini

tidak terdefinisi

dix:

3.

Tetapi

-f-J

kita masiir dapat ;r:enanyakan "berapa

rulu.f(x),jika.r

mendekati 3 ?" Dengan bantuan kalkulator akan diperoleh nilai-nilai berikut :

7r

r

--T

-o

I t-t, = f

- 1

Dari nilai

di

atas reriihat bairrva./i.r7 akan mendekati

nilai

5

jika

.r dibuat mendekati 3.

tetapi x _{= 3.} Secar* matematis dapat dirulis,

7t

,. J -X O

nm-__

-

).

l+i _{X_3}

-ladi secara inriusi kita puny,a :

Deiinisi

3.1

lim/(x)

=

t

berartijika.x

dekat ke

.,

fuli

berlainan dengan

c- makaf/;;

dekat

ke L.

L;

5.ii1

2t

Contoh

3.1

l,E3x+5:8

J

"z

_-3-r

-2

_.

r,_(2-r+lXx-2)

=

lim2r+

t = 5

Contoh

3.2 lirnl---

=

lim

'

x+2 X _-2 r+? X _-2 xs2

conroh

vvrr'v"

3.3

v'*

li,, Fe-

''-r

=

ti,n

-Fe-f+

=

li'r.,.9:?qi1

=

liry,.,1i+3:6

Jr-3

i;;

J-r

-3

Jx

+3 r+e

x-9

r+e

3.1.2

Pengertian

timit

secara

formal

Misaikan

fungsi

l,

:.f(x)terdefinisi

pada selang I yang memuat c, kecuali'mungldn

di

c sendiri.

Jtka

-1ft)

dapat dibuat sebarang dekat dengan

I

dengan

cara

mengambii

x

yang

cukup dekat dengan

c tetapi

ir*c,

lnaka

ini

dapat

ditulis ,

" jika

-r rnendekati

c.

makaf(x,1 rnendekati

I.

f(r)

lnfonnasi yang dapat diperoleh dari

bentuli

[1/(xl

=

Ladalahf(xt

dekat ke

t

jika

-r dekat ke

c, tetapi

x

=

c.

Atauf(-r) dapal dibuat sebarang dekat

kel

dengan cara

nengalnbil

x

cukup dekat ke c, , tetapi

x =

c.

Jika untuk

istilah

_{dekat digunakan ukuran -iarali}

nilai

mutiak,

inaka dapat dikatakan if

$)-Ll

dapat dibuat sebarang kecil dengan

mengambii x-ci

yang cukup kecil,

tetapi .r

=

c.

Secara matetnatis.

jika

bilangan yang.&ecll dinyatakan dengan e (baca epsilon)

dan

5

(baca delta), rnaka disirnpulkan bahrva

,f@:i:i

dapat dibuar

kecil

dari sebarang

e >0 dengan

rnelgarnbil

:.r-ci ),ang

lebih

kecil

dari

5

>0

dan

x

+

c. .{khirnva

kita

sampai pada

Definisi

3.2

\4isalf(x)

terdefinisi pada selang buka I yang uremuat c, kecuali c iru sendiri.

Limit

fungsi/di

c'adalalrr(ditulisltg/(-r)=L)jika

Ve>0,3t>0 )

0<{r-ci<d-=1./(-r)-I-t,<e

-Contoh

3.4

Buktikan dengan definisi

limit

bahwa

it11t3* + 5) -- 1

I

Analisis Pendahuluan : Andaikan e bilangan positif sebarang. Hams didapat srtaftt

6

> 0

sehingga 0 <l

r-2

_l<

d

+

|

(3.r+5)-l

I

1

<

a

Unruk

i(3-r+5)

.lll

<€

€

l3-r-6

lca

<r3l

-r- 2l<

e

f

<+

i-r-21.;

Bukti

formal:

Arnbil

e>0

sebarang.

Pilitr

5

=:,**u ***

0

<i:r-21<dberlaliu

l(3-r + 5)

-1

1 _1=13-:

-

6

l=3lx- 2l<3.!=t

J

Jadi

Va>

0:d^>

03untuk

0

<lr-21<d=rl(3x+5)-lll<e

atau

[.1ot:-t+5)=11

terbukti-3.2

Limit

Sepihak

Cara .r menqju c bisa dari arah kanan (dari arah bilangan 1'ang lebih besar

dari c)

atau

dari

kiri

(

dari

arah biiangan

)'ang lebih

kecil

dari c).

Jika

-r

menuju

c dari

arali

kanan

diperoleh

lirnit

kanan.

notasi

lim.l'(-r;,

_-iika

x

menu-iu

c dari arali

kiri

diperoleh

limit

kiri-notasi

lirl

i (r)

Definisi

3.3

a)

limitkiri: lirq/(.r)

=

L Jika

V

a>0,=d>0

> 0<c--...

<

d

=i"f(r)

-L\<

e

b)

limitkanan:

lirn/(x)

=[-1ika

V.q>0,]d>0

r

0<-r--c<6

=l.r'(-r)-l-i<e

Fungsi _-r-

:

_{_fk)} dikatakan memp'.rnyai

limit

di c

atau

lim,/(-r)

ada _iika

iimit

kiri

:

limit

kana;r

dan

nilainya

sama dengan

lirnit

kiri

atau kanan terselut, sebaliknva fungsi

y :

f(x)

dikatalan tidak mempunyai

lirnit

di c: Hal

ini

dinriis dalaln t.or-&ru

berikut

:

,'-2t

Contoh

3.5

.lawab

a

3.3

Sifat-sifat

limit:

\{isal

lirn/(r)=1,

.T--+rt

I

tirn

[./'(x)

+s(:)]

x--+a

2

rirn

[/'("r)

-

e(")]

N--+cr

datt

tirn

g(x)

-t--+Q

=

L+G

=

L-G

=

G.

Malia:

Diketahui

Tentukan

lim

_r'+O'

/(-r)

:

lirn ./'(x)

=

lin

-r2 =

0,

lim,f(-r):

lim

r

=

0,

/(.-r)

=

[-.'

,

x<0

{.r,

O<x<l

I

[2 +.;r'

,

.r

)

I

dan

lin.f

(x)

jika

ada.

x+0' r+0'

karena

]ir;r

-/t-t)=

lirn

f(*)

,maka'ftg,/(x)

ada dan

Jim f1x)

=

0

.

lim./'(x)

=

lim

x

: l,

lim'/(x)

=

lim

2+.r3

₌ J"

J+l- x+l- r+l' r+l*

karena

lirn /i.v)

;r

lirn

/(r)

_, maka

t_g/(.r)

tidali ada.

Contoh 3.6 Pandarrg grafik berikut :

rnaka

irm.f(.r)

_{= 6}

dan lim

,f(*):5

tetapi lirn

/(.r)

=

t.

r+&- r+ i

-!+

3. lg

it'"

[./{-')si.')]

=

x--+a

LG

,hila

G

*

O

t

i

5.

,flitn/1x)

='{Z

urtuk

L>

obilangenaP

1x-+a

Prinsip

Apit

Jika /(-r)<g(x)<&(,r)untuk

setiap

x

di

sekitar

c, dan

ft11./(x):f

rnaka

limg(x)=

L

Limit

Fungsi

Trigonometri

l.

lirn _r+0

shx

=

l

-t

2.

limcosx

= 1

3. lim

tmx

₌ I l+O .T

2

Contoh

3.7

,,*

_r+o -r' + 3-r = 1;n-t(-t + 3)

-Sin _f- x+0 Sin -f

.I

Contoh

3.8

Hitung

liln(.r-l)'?sin-J-r+l _,r-l

Jawab

:

Perhatikan ketaksarnaan berikut,

limft(:r):

L,

lirn(-r + 3)/lir:r sln

'r

-

311 -- 3

r+0 r+Lr _{_I}

.

/(.r)

lllil-=

,*,

g(':r) 3.4

Limif

Tak

Hingga dan

Limit

di

Tak Hingga

N'lisal

lim./(x)

=

I

*

0

dan

limg(x)

=

0

maka

";;

(ii)

(iii)

(iv)

-l <sin-f

'.

<

I e

-(-"-l)'S

(.r-l)?sip--J--<(-t-l)=

(.'

-

l)

(.t

-

l)

Karena

$(-t.r-1)')

= 0

=

lim(-r-l)r.

maka

lj.T(t-l\2sin-1-

= 6"

+@

_,

jika

I

>

0 dan

g(x)

-->

0

dan ar4!t atas ( dari arah nilai g(-r)

positill

:i.--"o

,

jika

I

:'

f/ dan

S6)

-->

0

dan ar'fii'bawah

(

dari aratr

nilaig(r7

negarif) +

co

_{, -jika}

I

<

0 dan

g(x)

--+ (/ dari aralr bawah

/)

'i

Secara geolnefris gpafik./ akan melonjak secara tiba-tiba bila -r mendekati

a,

garis _-r

:

a

yarrg

scpcrti

ini

disebut asirntot regak dari

grafik

fungsil

contoh3.9:

ti,n

11*,1

:-f@,karena

lim

x2+l=2>0

dan (x-l)-+0darinilai

s-+l*

X-l

s-+l*

positifjika

x menuju

I

dari kanan ( dari bilangan yang

lebh

besar

dari

1)

Sebaliknya -lika

nilai

{lurgsi.;i!

rnendekati suatu nilai tertentu

jika

-r

rnenuju

-f

co

atau -

oo

,

maka

dikatakan

J(9

rnempunyai

limit

di

tak

hingga.

Secara geometris grafrk

.f(x)

ak*t

mendekati garis

y

:

konstdnjika.r

membssar tanoa batas

(

menuju tali hingga) atau mengecil tanpa batas (menu-iu minus tak hingga). Garis yang seperti

ini

disebut asimtot datar dari

grafik

fl.r)

Brla

J(.r.t

rnerupalian

ftrngsi

rasional,

misal

/(-t)

=

#

dengan

p(x)

dan q(x)

tlrerupakan

polirlorn malia unruk

_{rnenvelesaikan}

tg./(-r)

dilatulian

dengan

_mernbagi

pembilang,

p(x)

dan penyebut, q(-r) dengan.r pangliat tertinggi yang rerjadi.

Contoh

3.lo

li:n

-

'tt

=

li,n

l,/-t

=

:0.

'+-.rJ+_r+l

,**l*+_+

,rt

-r-'

ccnroh

3.1I

l-,*

-"f.1-1

=

!i,,,

@--zx€+r)

,r-

_.1

;:;-

_{1_p _ 2}

Xrf

_{+ 2)}

I

J-r(l

+:;

- l:'-' r.'-\ - 1 - rrr.. ---_-;- - i.

'*-..,f(l

₊

-:

₎

1j -t-'

3.5

Kekontinuan

Fungsi

Frurgsi./(.r7 dikatakan

kontinu

pada suatu titik _r

:

a jika

:

1

_./( a

)

ada atat

tfu)

eR.

l.

lirn

/'(.r)

ada.

t'akni

:

x-+o

i"

lirn

_{./'1.r) = .1'@)}

x--+a

x

-i*

Bila

paling kurang saftr dari tiga s-r,arat diatas tidak

dipenuhi

rnatia./(,r/ dikatakan

tidak

kontinu

atau

diskontinu di

x

:

a

dan

x

:

a

disebut

titik

diskontinu.

Secara geomerris-kekontintran

dpri

_{ftlngsi -f(.r1} terliltat

dari

grafiknya vang rnulus dan

ddak

ada

loncaran

pada

lim

/(-r)

=

lim_

/(.r)

yang

tidak

konrinu.

LO

sedang garnbar 3.1(c) garnbar

3.1(a) dan

(b)

terlilrat contoh

ftrngsi

rnernperlihatkar contoli fungsi yang kontinu.

.f (x)

./lx)

tidak kontinu

dia

karena

lim/(x)

tidak ada

tlat

"f(x) tidak kontinu

dia

karena

|g/tr)

*

"f(a)

./{-r7 kontinu di a

karena

fim.f(x)

= ./-(a|.

Fungsif(x)

dikatakan

kontinu

nada

intervat

b

( a"b

i

bilaJkl

_kontinu pada setiap

titi!:

di

dalam interval tersebut. Sedangkan./1-rl dikatakan

kontinu

nada

interval tutup

I

_{aU 1}

bila:.,

l.

f(r)

kontinu

pada ( a,b

)

2.f(rtkontinu

karan

di.r

-

a

[

,,,r,

_.f(.r-)

=

/(".,.l

\.r*)a

-

j

3.f(x,tkontinu

kiridi

t

:

bf

tirn

./'(.r):

f(6)'J

\-t-+6-

)

BiIa _,f(.x) kondntt

urtuk

setiap nilai

x e

R rnaka dikatakan.(.r/ konrinu ( dirnana-rnana _). Teorema 3.2

l.

Fungsi Polinorn kontinu dimana-lnana

2.

Fungsi Rasional konrinu pada Dornainnva

-3.

Misalkan

_.f

(x)

=:!x

, nruka

a)

./(x)

kontinu

di

setiap

ritik

.r e R _.iika fuan1if

b)

JH

konrinu di setiap ,t >

0,

den-ean .r e R

jika

_n genap.

27

!

conroh

3. i 2

Selidiki

apakal frrngsi

g(x)

=

+

korttitru di x-- 2

l

_\-L

.larvab

:

Karena

g(2)

tidak ada,

maliag(x)

tidak kontinu di

x:

2

per6atikan

,

_{pada conrch}

3.l2 ini

titik-r

:

2 discbut

titik

diskontinu yang terhapuskan atau biasa disebut

titik

removable

disconlinuity.

Artinya

titik

x

:

2

dapat rnenjadi

titik

kontinu -jika fr.rngsig(x/ didefinisikan kembali- Seperti

'antoh

3.13 berikut.

itt-s

Y=1

Contoh 3.13

Selidiki

apakah fungsi

8(x)

=

{

t-2

)

^

- -

kontinu

di-r:2'

t

12'x=2

rarvab

.

s(2):t2.$=

₌

fglSS#I19

=tt

Karena

g(2)

adadan

limg(x)

:

S(2),

maka g/-rl kontinu

di

2.

r+l

Contoh

3.1a

_.f

g)=

.

-t-2

,

: ,

-l,r

t

=.

tidak

kontinrrdi-r

:

l.

dan

x:2.

.r:

-3x+2

(:-t)(-t-2)

Titik

x

:

2 disebut

titik

rernovable

discontinuitv,

tapi

x

:1

tidak rernovable

(

disebut

infinite

discontinuity).

Contoh 3.15 Tenfirkan konstanta c dan kagar fungsi berikut

kontinu

cii R

f

.t+2c,x<-2

I

./(-r)

=

j3c.r+

k,

-2<.x

< I

[

3.t

-2k.x>l

Jarvalr

:

_{Agar- ./f:r/}

koltilu

di

R

malia periksa kekontittuatt

i(,

di

-l

dal

1 .

(l)

agar.fk) kontinu di -2,

maka,lirn

/(.r)

:

-f(-2)

dan,l:r1

-f(-r)

:,f(-2)

Itq /ft)

=-f(-2)

a-2+1c=4c+k

e

8c-lf

=2

.(i)

lim

/(,,-)

=

J'?2)

o

-6c+k

=4c+k

(

trivial

)

(ii)

aewJ/x)kontinu

<ii

I,

mai<a

lirn.f(.r)

=

.f(l)

dan

lin.i

i.r;

=

.f(11

]11

./(-tl

=

./(l)

<+

3c+

k

:3c

+

k

(

frivial

)

a

lim

_./

(r)

:

_./'(1)

e

3

-

2k = 3c +

l;

."1*

r'+l'

<+

3c+3I-

:3

...

(ii)

Limit

qq

fPU

tinuan

Fungsi Komposisi

Teorema

33

( Teorerna Lirnit Komposisi )

Jika lirng(.r\

=

L

datt.f(fl kontinu di

l.

rnaka

lg.f(S(x))

:

./'lirng(-r)

:

./'(f

₎ Teorema

3.4

( Teorema kekontinuan frrngsi kornposisi )

Jtka g(x) kontinu di

a.fft)

kontinu di

gtui.

maka fi-urgsi

(/

_"

g)(.t)

kontinu di a.

tsukti

: lllf

_"

gXx)

=

lg1,f(s(x))

:

/limg(x),

karena.f kontinu di g(a)

=

f

k@D

, karena g kontinu

dia

= (.f "

eX;)

Hal

ini

nenunjukkan bahwa

(./

_"

SX..)

konrinu di a.

Contoh 3.16 Tennrlian dimana fungsi berikul kontinu

.

I (.r)

=.orf':!!f:I1

L..'*3x-A)

-

-rt-3-r+l

Jarvab

:

Misalkan

/(.r)

= (g _" h)(.r)dengan /i(.r )

=

.r, +

1-

dan

g/.r7:cosr

Karena

/z(r/

fungsi

rasional.

rnalia

/ii.v

kontinu

di

R

kecuali

di

-4

dan

l.

Soal

l,atihan

3

..1.1. Diketairui _"f

(x)

:/

fr'

Lr'-.f

(x\

a. Hitung

lim

x-+l-b.

Selidiki

apakah

lim

r-+l

+1,

xSl

-:+2,x>l

dan

lim./(')

x--+l'

f

(x)

ada

jika

limit

ini

ada tenrukan nilainya.

Z.

Diketahui

e6)

:

lx

* 2l-

3r,

hitung ( bila ada

)

:

L

lim

g(x)

'b. lim

s(x)

x--+z

x__+2'

c.

lim

s(x)

x--+2

3

Dikerahu

i

_.f

(x)-

i'-:l

_, hitung

(

bita ada _,) :

x-

)

a.

lim

-f(')

b.

lim

./(-.)

c.

iim.f(,)

.r-+2-

-r--r2+

x--+2

(,

Z*-a,

_{-x <}

-3

4

Diketahui ,f(r)

:]o*+2b,-3<.r

<3,

_tentukan

nilai

a

_dan

b agar

lim

,f(:r)

_dan

I a-5-t,.r>3

'r-+-3

lim.f(.r)

ada.

.r-+ _-l

-;

Diketahu

i

_.f

(x)=

{;r;I:

_1,

setidiki kekonrinuan tungsi

.f(x1

dtx:

-l

| ,*1,.v<l

6-

Agarflrngsi

J-(x)=

lax+b,l<

x

<2,

kontinu pada R, rnakaberapaliaha

+

2b2

l.

sx.x

> z

la::'+bx-4

_z

)

/.

Ienru,--ana

oanbagarfungsl

.l{x)=j x_2'

^

\',

kontinudi.r =2

| 2-4x.

x>2

8. Tentukan nilai a, b d,an

c

agil fungsi berikut kontinu di

x

:

l.

lo'2-.r-t

i .r-l

f

t.rl=

j

b

[

-.{+c

:

-r>

I

;-t=l

;.r-

<

I

*

9. Tentukan

nilai

ir agar membuat fungsi berikut kontinu :

flx-z

,

x(

I

a.J(r)=to.r, ,

x>l

I

*.t' .

xs2

b-

/("r)=l^

i.2.r+/r

.

x>2

ftt-l

;o<x<k

c.

/'(x)=J

6

t ;

;x>K

10. Canlah

titit

Oistontinu dari fungsi

)^

-r-

+

lx

a. _.l

(t

)

=

--'-;

.T+J

x-2

1,.

./(-r):;;;

lxl-/

1

l.

Tentukan dirnana

l(r/

kontinu ,

r_l

a. .! \^)

4

-

rlr'

-9

b.

,f(x)

:

'!4x

-

x''

B.

Hitrurg

li'nit

berik-ut (

bila

ada

)

:

3+-x

I

lim-..+

3--t

_T--+J

3

J. llm -.

-x--+?+

x' -

4

3.

lini(x-

li .r ll)

I

J.

lirn xsin

I

I+€ _{_T}

-;..1i61J'.-i

-Jil

,,,r,ll

x

ii

-5

r+5 -f-5

.T

lirn

"

r--+:c I +

-r:-6.

lim

-r-+-:c

7.

lirn

-T-+€

,3

i _--Y

B.

lirn

l\--r- --) -:' r 'r ?

-

3r -r 'r'l

9.

Iim

--_T-+..

I +

x'

.3

'l'

10.

lirn -";

-r-+z i

-

-rJ

! i-i-'5

_

c.

/(.r)

=

..2-4

-.3-8

n

L1

\.i- + I

.T -l

.r-

+ -r

C. Diberikan grafik suatu

fungsi/seperti

gambar berikut '

Cari

limit

yang ditunjukkan atau

nilai

firngsi, alau nyatakan bahwa

lirnit

tidak ada"

a

lirn

/(x)

c..it-1)

e../(1)

g.

t$

/(x)

D.

1. Skctsa grafik dari

(z

| -r',jika.r<0

.f

(x):1

.t

,O < -r < I

It

+..'

,-iika -r 2 I

Kemudian cari

a. lirrr./(-t)

c.

ltun

/(.t)

c.

lirn

/(-r)

r+O-b/(1)

d.

lirn

/(x)

r+l-2. Sketsa grafik

dari ./(-r)

=

r

-litll,kemudia-n

cari :

a.f(O)

b.

lrr4/(-r)

b.,(-3)

d.

hm

/(x)

t

lirn./(x)

h. litq./(x)

d.

li4-/(-t)

?3,

BAB

IV

TURTIIIAN

4.1 Konsep

Turunan

4.1.1

Turunan di

Satu

Titik

Definisi

4.1 Msalkan

fi-rngsi

/

terdefinisi pada selang 1 _]'ang memuat

c.

Turunan pertama

fungsi/di titik

c,

ditulis

_-f

'(c)

didefinisikan sebagai

f'(c)

=tt*'f(x) -

/(c)

:+r+c _{I -} C

bila

limit

ini

ada-Arti

geornetris: Perhatikan gambar benkut

):

Q{x.fky

\{isal

diberikan grafik

fungsiy

:f(x)

dengan P (

cJk)

I

_terierak

padaktnaf(x).

Rila

_Q

6,f(x))

rnerupakal

titik

sebarang pada

kuwa.fl.rl

maka gradien

tali

busur

po

dapat dinyatakan dengan :

.f

(x)-.f

{c)

iilPO :

-

.{-c

Jika

r ?

c,

rnaka

tali

busur

PQ

akan

beru[i!

<-,*-dengan kerniringan

menjadi garis

singgr-rng

di

ntik

P

3-l

Jadi,

arti

geometris

dari

-/'(c)

adalah kemiringan garis singgung

kurva/di

titik

(c,f(c)).

Selanjutnya, akan dilihat

arti

fisis dari

turunan-Misalkan sebuah benda bergerak sepanjang garis koordinat,

Jk)

f(c+h)

,n

t/

_

f

(c'+

h\-

f

(c) Dari sini kita dapatlra.. ,

rota

h

Jlka

tt

)

0.

rnalia

didapat

V:nf9+f9,

yang

biasa

disebut dengan kecepatan sesaat di c.

Bila -t=c+/,. maka akan diperoleh

p

₌

t* /(r) -/(ct =

_-f'(c) rec _t _-c

iadi. iirri

fisis dari

.f

'(c)adaiahiajtr

po"rrbahan

niiai

fungsiy'.r7 terhadap peuhahx.

Notasi lain unruk turunan pertama fungsiy'tii c adalah

, 49,UP,-r"(s).

clr

dr

Contoh

4.1

Diketairui

./(.r)

=f

,,"nnkan .f'(3)

-r

11

Jarab

:

r,(3)=*{*#=Hl==i,*#*='.$+=

-;

4.1.2

Turunan

Sepihak

Definisi

4.2

(i)

Tumrian

kiri

dan

filngsi

.f

di titik

c, ditulis .f-'(c'),

didefinisikan sebagai :

f-(c):

lim

'f$)-'f(c)

l_c _-f-C

(ii)

Tunnan

kanan

dari fungsi./]di

titik

c-

dituiis -f-'(c),

didefinisikan sebagai :

.f.(r)

:

1irn

f6)

-J(4

bila

limit

ini ada

Fungsi

/

dikatakan mempunSnai turunan

(

diferensiabel

)

di c

atarr,

J''@)

ad,a

jikaf'(c)

₌

f*'(c\.

dan

-f'(c):

f-'(c)=

-f*'(c),

sebaliknya

y'

dikatakan

tidal:

mempunyai ftrrunandi

c-lrt-x+3.x<I

Contoh

4.2

Diketahui

f(x):

i

[I+2rlx .x2l

a)

Selidiki

apakahJft) diferensiabet di

x:t

b)

JikaYa

tentukan .f '(1)

..

,f

(*)- f

tt;

lllll-= lllTl

.r'--r+3-(l

r

z./i)

Jawab:

a)

f-(r)

=

_r+l-

.X-l r+l- _X-l

!ir,

'tt

--*

=

l;,r.,I(1:

1

:+l- -1 _{- |} r+l- -f'- 1

r(i)=l11r*#=l*

t+2J;-qr+zJi)

b)

-r-l

"

z"'T

-

z

z

ti,r,

_--.

tF

-!

=

t

:

lYr

..'-

I =

r+r- (./-y

-

lXri

.- +

l)

,

Jadi,/diferensiabel di

x:1.

./-(t)

=

i(t)

= 1

.

rnaka

.f'(1)

=

t.

o

Keterdiferensialandan

kekontinuan

Teorema

4.1

Jika/diferensiabel di

c,

malia/

kontinu di c.

Bukti :

Yang perlu ditunjukkan adalah baltrva

!*./(.r)

:

_.f (c) .

Perhatikan bahrva, _-f

(x)

= ./'(c) +

'i

(x)

-

_'f (c).(-r

-. )

-{ ;1 c

.r-c

Maka rrm./(.r)

:

l:l[rr.,

.

rs:y,.,

-.,j

:

lirn/(c),,,,n'f('t)

-

-/'rt).lim(.r

-c)

= ,,",. ,'(";;

'r - c r+c

=-f(c)-

(terbukti

)

i',

i

keterdiferelsialan.

Sifat tersebut

tidali

berlaku sebaliknya.

Artinya,

Jika/kontinu

<ii

c,

maka

tidak

benarbahrva/

diferensiabel

di

c.

Hal

ini,

dirunjukkan oleh

contoh berikut.

Contoh4.3 Tunjukkanbahwa/fx/:

ix

I kontinudix:0tetapitidalidiferensiabel

dix

:

(/

Jarvab:

[-r -

-r>0

'/(x)

:r

r"r

v

l:

J

[-r,

-r<0

(i)

Akan ditunjukkan

bahwa/

kontinu di

x:0

.

_.f(0)

:

0

.

karena

lim f(-r) =iirrt(--*)

=

0

dan

iirn .f

(-ri

=

hqr

:0

r'u*u

,'tir,rr:

,'-

-

'*o'

r+o

.

Jadi

lirl./(.r/

_..rit

:

_-f(O

)

Iadi.f(x)

:

-r I kontinu di

x

:

()

(ii)

Selanjutnl'a

selidiki apakah

.ftr)

diferensiabel

di x:0

atau

.i(c)

=

-t(0)

?

r(-r)-/(o)

,. lrl-lo, ,.

-.\-. f(0)=lim't'

'

'

=lllTlr_-._--.----j=ltm---l

r+0- _{t - 0} r+0- _-{ r+G- -1

..

fi.r)

- /tOi ,.

I .r

I

_' n

. f(0)=limJ'

-

-111n:-'

r"i:lim'.-1.

r+0- _{-f - 0} :+iJ- .f :+0-

-1-Karena

-

1 ₌

l(0)

= ./:(0)

=l

:makal(9

:

-x ddak diferensiabel di

x-L,.

Contoh 4.4 Tenrukan konstanta a dan

b

agw fungsi berikut diferensiabel di

x:

1.

l.r'+6

-

x<I

/(.r)

=

1

i

ar.

-r>)

Jarvab

:

Agar fungsi./l,r-i diferensiabel di

x:1.

ma}ra.f(x) harus kontinu di

-r:l

dan

.f (t) =

/-(t)

.i

(i)

Svarat agar.l' kontinu

di

I

adalah

iY(l

)

= lim

./(-r )

:

lirn .l'(-r).

Maka

a=

lim

x'

+b-=

iim

ax

e o=tu'l':

u

a

b =

a-7

3{;

!

(ii) -r(r)

=

ly

a*#

:

ly*#

=

l*

&55

=ti*'t'-l=lim.r+l=2

_r+l-

-1 _-l

r+l-.f,o)

=

l11r

4*#

:.lgp

T+

=

oltl.'j

= o

nsar

l(t)

=i(i) a

a:2.

Sehingga agar/diferenpiabel di

x:1,

maka

c

:

2

dan

b

:

1" 4.2

Aturan

Pencarian

Turunan

.

Fungsi

Turunan

Pertama

Definisi

4.3 Misalkan

f(x)terdefinisi

pada selangl. Fungsi turunan pertama du1-f,

ditulis

/

'(-.),

didefinisikan sebagai

f

'(:):

,

f(t)-

f

(x)

, v.r

e I

fer _{t_X}

atau-iika

h:t-x

f

,(r)=

r'

_i+0

f(x+h)-f(x).v-rer

h

bila lirnitnya ada.

Nrotasi

iain

adalah

.

t'-X,ry,D,y,D,f(x),

benruk

4ait"nut

sebagai notasi

Leibniz.

Dengan

rnenggunakan

definisi

diatas

dapat

diturunkan

aturan untuk

mrncari

turunan

sebagai berikut :

1. Jkalk)

:

k,

rnalia

.f'(x)

= g.

ak

)

-_,

2.

r-{":-r>0-reR

cir

3

d(/(,r)+g(x))

=./-

(x)+F

(.r)

dta

4

a(lt'')s(''))

=

/'(.'j

g(.r)+./1-x)

g'(x).=.

ax

.

,1('(')rq,

,)

"r

'(-.)

g(.*)

-,f

(-r) g '(-r)

,s. \ r\^'/

dengan

girt

*().

clr

g 2

,f

Contoh

4.5

Tentukan ftrngsi ftlrunan pertama dari

./(x)

=

-t

*

t

-t:+l

l.(-r2 +

l)-

2-r(-r'+3)

-r-2 + I

-6.r-

2.rr

-.tr

-6.t+

I

Jarvab:

"l'(.r)=-,

r-.-

=--=-1-r -r

I)2

(-t: +

l)2

(-t2 + l)2

4.3

Turunan

Fungsi Sinus dan Cosinus

Turunan dari firngsi sinus dapat diperoleh dari definisi 4.3,

yaitu:

.f(-r):

sin-r

-+ -/'(-r)

=

cosr

./(t):

msx

-+.f'("t):

-sinx

Buldi

:

\dsal./(rl

:

sirzt lv{aka,

^ (r+-r\.{r-r\

I-x

/\r) :

lllryI#=

mry'"(

t

J

=

irjlcos(sr,,*"]=)

-

2-" t ,

₎

=

cosr.l:

coSx.

Dengan cara vaug sama didapatkan

D.

ko.u1

:

- siar.

Untuk

tunxran

fungsi trrigonornetri yang

lain

dapat diperoleh dengpn menerapkan

runlrs

perhitungan turunari' :

t_.. .. _\

,

d(tan

.*)

'd(""'

''

"or.*J

₂

l. _{- 5gu} .r

dr-Contoh

4.6

Tentukan

./'(x)

dari ./(-r)

=

-r2sinr

Jawab

:

.f'(x)

=

2xsinx+

x'cosx

=

x(2sin'r

+

xcosr)'

Contoh

4.7

l'entukan

/'(x)

dari ./(-r)

= tanx

-

sec-r

Jawab

:

-f'(r):

secz

r

-

secr tan

r

_{= secr(secr}

-

tan -r )

4.4 Aturan

Rantai

Andaikan

y

=

f

(u)danu

:

SG) menentukan firngsi kornposisi

)'=

(f

" g)(-xi-

Jika

gdifrensiabeldixdan/diferensiabel diu:g(x).rnaka

-f

"gdiferensiabel

di-t

dan

(.f

'

g)'(:t)

:

/'(g(r))g'(x)

dv

dv du

vakru-

--:-

=-=--dr

du dx

Jika

_-r"

:-f(u

) ,u

:

g(v*) dan v

:

h(x)

m{<a

, != ***

Metoda penunrnan di atas dikenal dengan

aturan

rantai-Contoh

4.8

Tenfakan

frd^*

-1,= S'ino(x3 + 5)

Jawab:

Misal

r,=-t3+5

maka

4=3tt

u

:

Sittr.'

maka

t/'

= aorr' = cos(x3 + 5)

dr

.J- .

.y

: tt{

rnaka

{

:4ut

='lSil3(-r'+5)

c{u

Sehingga

+

=

+

+.!-

=,2-r2,sini1-r3 + 5

rCos('ri

.i

5)

.

dx dtt d| ta

Contoh

4.9

Tentukan

./'(x:)

iip,

4tf(-.'))

=

r'+

l

LLI

Jarvatr

t

o

(/'(-r?)):.r'+l

€

fl(n'?).2.r=,r:-i

dr t'J

\^

l''

- -'

:..;-_

<r /'(-tt)

=

'\'

+ I

39

4.5

Turunan

Tingkat

Tinggi

Turunan kedua

dari

firngsi

f(x)

didapatkan dengan rnenumnkan sekali lagi turunan pertama,

./'(r)

"

Demikian seterusn.va untuk turunan

ke-n

didapatkan dari penurunan turunan ke-(z-l _).

Turunan

pertama

-/'(-r)

=#

Turunan

kedua

_-{"

(x)

=

#

Tunrnan

ketiga

f''

(r)

:

#

Turunan

ke-n

_.,f

''(-t)

:#

=

D:)'=

v(')(-r)

4.6 Turunan

Fungsi

Implisit

Jika huburgan antara

y

dan

x

dapat diruliskan dalarn bennrk

y

:

f(-r)

_{, maka}

f,urgsi

ini

disebut

dengan

fungsi

elaplisit

yaitu

antara

peubah

bebas

dan

tak bebasnya dituliskan dalam ruas yan-s berbeda. Bila

tidak

dernikian maka

dikatakanJ

fungsi

implisit

dari x.

Untuk menentukan

y'

dari bentuk

irnpiisit

digrinakan at'.ran rzurtai dan

anggapl' fungsidari-r.

Secara ringkas dapat dirulis sebagai

berikut

:

lr'{isalkan

t'(x,y)

:

G(x,y)

_, mernuat-v -- y(x)

$ 8ur:rlian ;:i:r-anmnrai

.td^

'-17;1_r. r.)) =

a(G1..-,.y))

tlr

rlr

U

1''=

/(-r.-r')

.b

Contoh

4.10

Tenhrkan

J,'daribentuk

inrpfsit -

,Sin(.w')=.r'

+ i

Cos(xY)(Y*xY'):2x

.,

,-

2-i-JCos(-r-Y)

r _

*Co."1_g,y

Contoh

4.11 Tentukan

]r

dari -rt-1,

=

2)'-

*)''

Jar*ab

,

4tx'1,y=!12r,-.r.)':

)

dx

dx

ZxY + x2 _{Y' =} 2Y' _-

]'t

-

2-r-ry''

,

y'+2xy

(x?

+Lry-2)y'=

-(y'

*2r,r;)

=

Y'=-i;t;i:;.

4.7

Garis

Singung

dan Garis

Normai

Persanraan earis singguqg frrngsi

y :

J(r)

di

titik

1.ro,l'n.l dengan kemiringan nr adalah

!-!o:m()c-xo).

Garis yang tegak lurus dengan

gris

singgung disebut decgan garis normal. Persamaan qaris _{normal di}

titik

(xo,yd adalair :

I

t_!o=__(x_-ro).

_m

Contoh

4.12 Tenrukan persamhan garis singgung dan garis nonnal ftlngsi

-),

:

-r-i

-

2.t2 +

6

di

titrk

(2,4).

Ja*'ab

2

y':3xz -

4x

-+

_{.r/(2,4) =} 3.22

-

4.2 ₌

I

.

lersainaan garis singgung adalah

:

,t'-

-l

:

4(-t

-

2) <+ _{-t' =} 4-r

-

4

.

Persamaan garisnonnal

adalah:

.J,-4

=-11.r-l)e .y-1=-;t-l

19

(+),-

-;r

+;-.+L

4.8 Diferensiai Can

Hampiran

4.8.1 Diferensial

.i

.l

4l

PQ

zCalahtali busur dengan gradien

,,

₌

*

.

IrI'adalahgaris singgun 91'

:

.f(x)

di

p

dengan

gradien

m=f'{x)

.

untuk

_suatu

nilai ax

yang

sangat

kecil,

gradien

tali

busur

dan

gradien

garis

singgung

di P

hampir

saina.

-ladi

Ar.'

!

=

fl(t-),

Ar

=/'(.r)Ar.

Ar

Definisi

4.4

llka

y

:f(x)

diferensiabel di

r,

rnaka

.

Diferensial dari x , dinvatakan dengan

dr.

adalali

dr

=

&x

.

Diferensial

dari.t

, dinvatakan denganrf.',

adalah

aly:

f'(x)dr

Dari

definisi

ini

kita

dapatkan trahrva

fr=./''{r).

r-ang

berarti

./'(.r)

bennakna

ganda. 1'akni sebagai turunan dari-r'

,.nru*O.r

dan hasil bagi diferensial r., terhadap

diferensial.r

( hasil bagi dari n)'terhadap

dr)

.

4.8.2

Hampiran

dengan

diferensiel

,v./k)

_\-y

Misalkan

y :

-f(x)

diferensiabel

di

interval

I

yang memuat

-r

dan

:--\r-

Jika

'x

ditambah A-r, makay bertarnbah sepadan dengan Ayyang dapat diharnpiri oleh r/.r'.

Jadi.

/(r+

Ar)

x./(:)+ $'= f (-t)+/'(r)At

Contoh

4.13

Harnpiri 3J28

Jawab

:

Pandang

/('r)=-tl

*'f(27)

:27!'

="!27

:3

.f,(x)=f,-i

-

.f'(zr=+er)-t

=Jtr'l-1

:l-3-J

I(arena _.f(-r +

Ar)

₌

/(r)

+

/'('t)Ax

' rnaka

'"

_{.f (2s\ = .f}

(27\+

f'(27){78'27)

atau

V28=3+lrtl =3+-

'

Soal

latihan

4

A

Untuk nomor 1 sarnpai dengan

lo,

tentukan

fi

a*r,

L

2. 4. 5. 6.

-12

t'--^o 2x

tl

)-

-r

.

xo

1

Y:x(x-+l

)

-u =

(ro

*

rrxrt

*z-ri *

r) I

3-t'

+ 9

2x

-1

!-- .r!--l

2^

.r -l_T+)

.r +lx-J

7-I-sin-r

8.

y:

cos -t

cos -r

9.y=

x

I0.

n.

tan -x

v-srn

r

-

cos.r

r/x-l

{-r+l

Unnrk nomor i

I

sampai 13, tentulian

nilai a

daa b agar fungsi berikut diferensiabel

di

nilai yang diberikan.

[r,E*;o<x<l

1i'

/(-r)_={

.,z_6.r

;.r->!

;-r:1

,--r = 2

(t

t-!-l

;x<3

_.

t3. /(..-)=i-'

:x:J

[2ar+b

;-r2

3

14. Tentukan persamaan garis singgung dan garis normal dan fungsi berikut

di

titik

yang diberikan

a.))

:

rt

-

2*di

( o.o )

b.

y

:

ton

r

di

t:r/o

n

.i

'---'44

.ls

15. Tentukan fungsi turunan pertarna

dari

a.

1,

=

(2x-

3)to

b.

-1,

=

sin3x

c.

-)'

:

co{4r'z

-

4

/-x+l\2

d.

'

v=l-l

[*-1l

e.

y:

sinx

tan

tf

+ t

1

('2

* t)2

l5.Hitung

/'(3)

bila

f

(*)

=

[.

"-,

J

l7.Hitung g'(ll2)

bila g(r)

=cosnt

sin2

tt

z \'. . 1 1

18.Tenruka"

{fod (-

t)

Uita

f

(*)

=;-

1

dan

g(x):

x'

-

4x

lg.Tentukan

peisamaan garis singgung dan

normal

kurva

_-u

:

(t2

*

t)t(-ro

*

t)2

Ol

titit

dengan absis

x:

l.

B.

(Untuk

soal 1 s/d 4) Tentukan turunan kedua

dari

1.

-i,=sin(2x-l)

2.

y,

=(zr-3)4

-)[

1 1r__

x+

t

4-)'

=

"ot2

(ot)

5-

Tentukannilaic

dari

f"(c)=0

bila

-f-(x)=t3*3-tl -45x-6

..L

45

7.

Dua

buah partikel

bergerak sepanjang

garis

koordinat.

Pada saat

uaktu

r

jarak

berarah

dari

titik

pusat diberikan

dengan

s1

dan

s:.

Bilamana

kedua partikel

mempunyai

kecepatan sama

bila

:

a.

st

:

4

t

-3

t2

danst

:

t2

-2 t

3)?,

?

b.

.tl

:

3

i

- 3

t-

.

l8r

-

5dan

s2

: -[ -

9t-

-

]2

t 8.

Tentukan

turunan pertama

(

V'

₎ clari bentuk

implisit

22

a"

x-

-y-

:1

b.2xy*-3x-2y:l

./\

c.-),+

srn(;r1J

=

I

d.x3-

3-r2-t,+v2

=o

e.lan('xy.)

-2y:0

g..Diketahui kurva

yang dinyatakan secara

implisit

,

tt

-

xy

*

;

-

3 _:v

:1C.

Tcntukan

a.

Turunan

pertama

dix:2

b.

Persarnaan garis singgung dan normal

dir:2

10. Gunakan

diferensiai

untuk memperkirakan

^ Io;

,- I-u

a.

{o,1,

D.

{ru,i

[image:45.612.71.503.82.636.2]

1 1.

Periksa

apakah

fungsi

berikut

difbrensiabel

di

titik

yang diberikan dan sar,b*rk.in

grafiknya

(

I .rr,.rsl

a.

f(-r-)

=

{

:-r:

I

[2.r

-

3 ,.r

>

i

. i.tt+x,.r<o

b. f(x)=i

'

:x:0

lsin.r+

l.x

> 0

/T

12.

Tentukan

:(.r:g(-r:

₎₎

c/-t'

46

-3,

g'(5)

=

2-

Tentukan

"

[i],',

g'(3)

=

5- Tentukan

'[*),',

I

,l(5)

=

6,

g(5)

=

o

[r],,r,

\g/

3)

=2

_,

.f'(3)

-

-6

,

Andaikan

./(5)

=

a.(.fg)'(s)

Jika

/(3):4,

g(

14.

15.

a.

(f

+g)'(3)

b.

(,fgx3)

f'(4r-BAB V

PENGGUNAAN

TURUI{AN

5.1

Untuk

Menggambar

Grafik

Fungsi

Infonnasi yang dibutuhkan untuk rnenggambar grafil< fungsi adalah

A.Titik

potong dengan sumbu

r

dan strmbu.l'

B.$simtot

fungsi

Definisi

5.1 Asimtot fungsi adalah garis lurus yang didekati grafik

fungsinya.

Ada Tiga asimiot frrngsi, yakni

o

asimtci iegak

Garis

x:

c disebut asimtot tegak grafik fungsi 1'

:

.f(x) stka

$'f(')

=

+*

.

asirntot datar

Garisy:6

disebut asimtot datar grafik frrngsi

t'

:-f(x;

jika

lim

/(x)

:

6

.

asimtot rniring

Ggarisy

:

ux

t

f

disebut asimtot rniring

jika

./'/ -.\

1in1

lY

/

-

a

dan 1;n

/'(x)

-

ar

= b

r+ff; jf r+l-r'

Perlu dicatat, bahrva

grafik

fun-ssi tidak akan mempunyai astmtot datar sekali-eus

miring.

Dapat dilihat, _{_iika}

a

=

(1, rnaka grafik filngsi tersebut

tidak

punya asimtot

datar, tetapi ia punya asimtot rniring.

Contoh

5.1 Tentukan sernua asitntot

dari

_./(-r1

-

(r

+

l):

.t

Jawab

:

(i)

asirntot tegak .

x

:

O,karena

1;*

(t1lf

=

-t

u*r,

datar

:

r+o

-t

(ii)

asirntot lniring

/

datar'

.

x:+2-t+l--r?

6=

lim

f(t)-ax:ltm

r+a!o'_ - H1€

=

rim

2t+1=2

r+lF _X

Jadi asimtot miring :

y

:

x

-

2,

asimtot datar tidali ada.

C.

Kemonotonan Fungsi

Definisi

5.2 Grafik

i,ngsif(x)

dikatakan

.

monotcn

naik

pada interval I

jika

unn*

rr

(

rz

=+,f(*,)

.

f(*r),

V:,,-tr

€

/

.

@noton

turun

pada interval I

jika

untuk .r,

<.rr+/(x,)

t./(rr)

_, V -r,,.r, e .f .

Fungsi naik atau turun disebut

fiinasi

monoton.

X2

^1

(b) monoton

(a)

Garnbar

5.i

fungsi [image:48.612.109.524.71.711.2] [image:48.612.176.465.72.140.2]

Garnbar 5.1(a) rnerupakan

grafik fiugsi

yang

lnonoton mrun

pada selang

i

dan gambar 5.1 (b) merupakan

grafik

fungsi yang monoton

naik

pada selang

I.

Dari gambar (a) tertihat bahwa sudut yang dibenturk anta.m garis singgung dan surnbu -r

positif

adalah sudut

tumpul,

atau dengan

kata

iain

gradient

(kerniringan.r earis singgung

bemilai

negatif.

Dari

garnbar

(b)

terlilrat

bah*'a

sudut yang dibentuk

,i9

Teorema 5.1 Andaikanrfdiferensiabel di selang I, ntaka

i.

Fungsif(x)

nonoton naik pada I

jika

_,f'(-r)> 0 V -r e 1

it.

Fungsi.f(.rr,l monoton turun pada I

jika

/'(-r)<

0

Vr

e

/

Contoh

5.2 Tenftrkan selang kemonotonan dari

.f(-r)

-

(-r +

l)l

x

(-r+l): -r2+2-r+l ^

I

Jarvab.f(x)

=-=-r+''+-'r.'t,/\\,/

-r'(:r)=

l--1.-:

-rt

tt;'

x'

-

('r-lX-x+l)