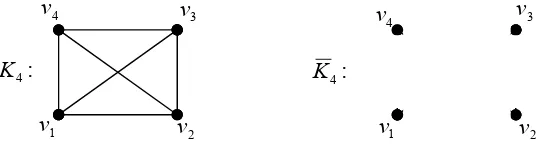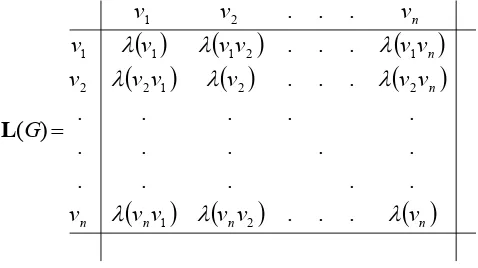PELABELAN-k TOTAL TAK TERATUR SISI DAN NILAI KETAKTERATURAN TOTAL SISI
DARI GRAF LINTANG
oleh
DWI HANDAYANI M 0102019
SKRIPSI
ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SEBELAS MARET
SKRIPSI
PELABELAN-k TOTAL TAK TERATUR SISI DAN NILAI KETAKTERATURAN TOTAL SISI
DARI GRAF LINTANG
yang disiapkan dan disusun oleh DWI HANDAYANI
M 0102019
dibimbing oleh Pembimbing I,
Dra. Mania Roswitha, M.Si NIP. 130 285 863
Pembimbing II,
Drs. Bambang Harjito, M.App.Sc. NIP. 131 947 765
telah dipertahankan di depan Dewan Penguji pada hari Rabu, tanggal 2 Mei 2007 dan dinyatakan telah memenuhi syarat.
Anggota Tim Penguji
1.Drs. Tri Atmojo K, M.Sc., Ph.D. 2.Dra. Diari Indriati, M.Si
3.Winita Sulandari, M.Si
Tanda Tangan 1.
2. 3.
Surakarta, Mei 2007
Disahkan oleh
Fakultas Matematika dan Ilmu Pengetahuan Alam Dekan,
Drs. Marsusi, M.S.
Ketua Jurusan Matematika,
iii ABSTRAK
Dwi Handayani, 2007. PELABELAN-k TOTAL TAK TERATUR SISI DAN NILAI KETAKTERATURAN TOTAL SISI DARI GRAF LINTANG. Fakultas Matematika dan Ilmu Pengetahuan Alam. Universitas Sebelas Maret.
Pelabelan-k total tak teratur sisi dari graf G(V,E) dengan himpunan titik tak kosong V dan himpunan sisi E adalah pelabelan λ:V ∪E→{1,2,...,k}, sedemikian sehingga bobot setiap sisi berbeda. Bobot sebuah sisi uv dengan pelabelan λ adalah jumlah dari label sisi uv dan label semua titik yang incident dengan uv,
) ( ) ( ) ( )
(uv u uv v
wt =λ +λ +λ .
Nilai ketakteraturan total sisi dari graf G yang dinotasikan dengan tes(G), adalah bilangan bulat positif terkecil k sehingga G memiliki pelabelan-k total tak teratur sisi.
Skripsi ini mengkaji ulang secara teoritis hasil dari Nurdin dkk. (2005) mengenai nilai ketakteraturan total sisi graf lintang sLn, untuk suatu bilangan bulat positif s≥1 dan n≥2. Graf lintang Ln adalah join dari graf K2 dan Kn yang dinotasikan dengan K2 +Kn, dengan Kn adalah komplemen dari graf lengkap dengan n titik.
Berdasarkan pembahasan, dapat disimpulkan bahwa pelabelan total tak teratur sisi dapat diberikan pada graf lintang sLn dan nilai ketakteraturan total sisinya dapat ditentukan, yaitu
( )
= + 3 2 2ns sL
ABSTRACT
Dwi Handayani, 2007. ON EDGE IRREGULAR TOTAL k-LABELING AND TOTAL EDGE IRREGULARITY STRENGTH OF LINTANG GRAPH. Faculty of Mathematics and Natural Sciences. Sebelas Maret University.
An edge irregular total k-labeling of a graph G
(
V,E)
with a non empty set V of vertices and a set E of edges, is a labeling λ:V ∪E →{1,2,...,k}, such that the weights calculated at every edges are distinct. The weight of an edge uv, under a total labeling λ, is the sum of label of an edge uv and all labels of vertices that incident with uv,) ( ) ( ) ( )
(uv u uv v
wt =λ +λ +λ .
The total edge irregularity strength of a graph G, denoted by tes
( )
G , is the minimum k for which the graph G has an edge irregular total k-labeling.This final assignment studies the result of Nurdin et al. (2005) on total edge irregularity strength of lintang graph sLn, for any positive integers s≥1 and
2 ≥
n . A lintang graph Ln is a join of K2 and Kn , denoted by K2+Kn, where n
K is the complement of complete graph on n vertices.
Based on the discussion, we conclude that an edge irregular total labeling can be given on a lintang graph sLn and the total edge irregularity can be determined, that is
( )
= + 3 2 2ns sL
v MOTO
Proses yang kita alami sebenarnya lebih penting dari hasil yang sudah jadi.
(Spirit)
Cara pikir yang positif akan selalu menyelesaikan masalah yang sudah dianggap tidak
mungkin untuk diatasi.
(Spirit)
Orang yang tak berani mencoba memang tak akan pernah gagal, namun pada saat yang sama
mereka tidak akan pernah menang!
PERSEMBAHAN
Karya ini kupersembakan untuk
á My lovely Mom... I love R always miss u á Bapak, kakak dan adik-adikku tersayang
vii
KATA PENGANTAR
Segala puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa, atas segala berkat dan rahmat yang telah dilimpahkanNya sehingga penulis dapat menyelesaikan dan menyusun skripsi ini.
Di dalam penulisan skripsi ini, penulis tidak lepas dari segala kesulitan dan keterbatasan yang akhirnya dapat penulis atasi berkat bantuan dari berbagai pihak. Oleh karena itu, sudah sepantasnya pada kesempatan ini penulis mengucapkan terima kasih kepada
1. Dra. Mania Roswitha, M.Si. dan Drs. Bambang Harjito, M. App. Sc., sebagai pembimbing I dan pembimbing II yang telah memberikan petunjuk dalam penyusunan skripsi ini,
2. seluruh staf dosen di Jurusan Matematika,
3. rekan-rekan Matematika, khususnya angkatan 2002 FMIPA UNS atas dukungannya,
4. segenap pihak yang telah membantu sehingga skripsi ini dapat selesai. Akhirnya penulis berharap semoga skripsi ini bermanfaat bagi pembaca.
Surakarta, April 2007
DAFTAR ISI
Halaman
HALAMAN JUDUL ... i
HALAMAN PENGESAHAN ... ii
ABSTRAK ... iii
ABSTRACT... iv
MOTO... v
PERSEMBAHAN... vi
KATA PENGANTAR ... vii
DAFTAR ISI... viii
DAFTAR GAMBAR ... ix
DAFTAR NOTASI DAN SIMBOL ... x
BAB I. PENDAHULUAN... 1
1.1. Latar Belakang Masalah... 1
1.2. Perumusan Masalah ... 2
1.3. Batasan Masalah ... 2
1.4. Tujuan Penulisan... 2
1.5. Manfaat Penulisan... 2
BAB II. LANDASAN TEORI ... 3
2.1. Tinjauan Pustaka ... 3
2.1.1. Graf ... 3
2.1.2. Pelabelan Graf... 8
2.2. Kerangka Pemikiran... 12
BAB III. METODE PENELITIAN ... 13
BAB IV. PEMBAHASAN... 14
4.1. Batas Nilai Ketakteraturan Total Sisi Sembarang Graf ... 14
4.2. Nilai Ketakteraturan Total Sisi Graf Lintang sLn ... 18
BAB V. PENUTUP ... 30
5.1. Kesimpulan ... 30
ix
DAFTAR GAMBAR
Halaman
Gambar 2.1 : Graf G... 3
Gambar 2.2 : Graf dengan loop dan sisi rangkap... 4
Gambar 2.3 : Cycle 3 C dan C4 ... 4
Gambar 2.4 : Graf lengkap... 5
Gambar 2.5 : Graf dan komplemennya... 5
Gambar 2.6 : Dua graf yang isomorfik
(
G1 ≅G2)
... 6Gambar 2.7 : Gabungan dari graf 2K3 dan 3K2... 6
Gambar 2.8 : Join dari graf K3 dan K2... 7
Gambar 2.9 : Graf 3L9... 7
Gambar 2.10 : Graf berbobot ... 8
Gambar 2.11 : Pelabelan total pada C3... 9
Gambar 2.12 : Pelabelan-3 total tak teratur sisi pada C5... 10
Gambar 4.1 : Pelabelan total tak teratur sisi ... 15
Gambar 4.2 : Pelabelan total tak teratur sisi yang optimal ... 16
Gambar 4.3 : Graf sLn... 18
DAFTAR NOTASI DAN SIMBOL
G : Suatu graf
G : Komplemen suatu graf
G(V, E) : Graf G dengan himpunan titik tak kosong V dan himpunan sisi E V : Himpunan titik dari graf G(V, E)
E : Himpunan sisi dari graf G(V, E) |V| : Order (banyak titik) dari graf G(V, E) |E| : Size (banyak sisi) dari graf G(V, E)
λ : Suatu pemetaan yang membawa elemen-elemen graf ke bilangan-bilangan bulat positif atau non negatif
i
u : Titik u ke-i
j
v : Titik v ke-j
i
w : Titik w ke-i
i
x : Titik x ke-i j
i
v : Titik v ke-i dari kopi graf ke-j ei : Sisi e ke-i
j iv u
e= : Sisi e yang incident dengan titik ui dan vj 2
1 G
G ∪ : Gabungan dari graf G1 dan G2
2 1 G
G + : Join dari graf G1 dan G2 nG : Gabungan dari n graf G
n
sL : s kopi graf lintang dengan s≥1 dan n≥2 s : Banyaknya kopi graf lintang
n : Banyaknya titik dari graf Kn n
K : Graf lengkap dengan n titik
n
K : Komplemen graf lengkap dengan n titik
n
xi )
(ui
wt : Bobot titik ui
( )
uivjwt : Bobot sisi yang incident dengan titik ui dan vj
k : Bilangan bulat positif terkecil dari label terbesar dari semua pelabelan
( )
Gtes : Nilai ketakteraturan total sisi graf G
L(G) : Matriks L yang menyajikan label titik dan sisi dari graf G Lj(G) : Matriks L yang menyajikan label titik dan sisi kopi ke-j dari
graf G
x : Ceiling dari x (bilangan bulat terkecil yang lebih besar atau sama dengan x)
x : Floor dari x (bilangan bulat terbesar yang lebih kecil atau sama dengan x)≅ : Isomorfik
BAB I PENDAHULUAN
1.1.Latar Belakang Masalah
Teori graf merupakan salah satu cabang ilmu matematika yang memiliki banyak terapan, misalnya penyelesaian masalah penentuan jarak terpendek, matching, game, puzzle dan pelabelan (labeling). Menurut Wallis (2001), pelabelan suatu graf adalah pemetaan yang membawa elemen-elemen graf ke bilangan-bilangan bulat positif atau non negatif. Pada umumnya domain dari pemetaan ini adalah himpunan titik (pelabelan titik atau vertex labelings), himpunan sisi (pelabelan sisi atau edge labelings) atau himpunan semua titik dan sisi (pelabelan total atau total labelings).
Wallis (2001) menyatakan bahwa bobot (weight) dari elemen graf adalah jumlah dari semua label yang berhubungan dengan elemen graf tersebut. Bobot sebuah sisi uv dengan pelabelan λ adalah
) ( ) ( ) ( )
(uv u uv v
wt =λ +λ +λ .
Bača et al. (2003) menyatakan bahwa pelabelan-k total tak teratur sisi pada graf G(V,E), dengan himpunan titik tak kosong V dan himpunan sisi E, adalah pelabelan λ:V ∪E →{1,2,...,k} sedemikian sehingga untuk setiap dua sisi yang berbeda, e=uivj dan f =ukvl, berlaku
) ( ) (e wt f
wt ≠ .
Bača et al. (2003) menyatakan bahwa nilai ketakteraturan total sisi dari graf G yang dinotasikan dengan tes(G), adalah bilangan bulat positif terkecil k sehingga G memiliki pelabelan-k total tak teratur sisi. Bača et al. (2003) memberikan batas bawah dan batas atas nilai ketakteraturan total sisi untuk sembarang graf G(V, E), yaitu
( )
G E tesE
≤ ≤
+
3 2
.
2
1
≥
s dan n≥2, berdasarkan batas bawah yang diberikan oleh Bača et al.
(2003). Dalam skripsi ini akan dikaji ulang secara teoritis hasil dari Nurdin dkk. (2005) mengenai nilai ketakteraturan total sisi graf lintang.
1.1.Perumusan Masalah
Berdasarkan latar belakang masalah, dapat dirumuskan permasalahan sebagai berikut.
1. Bagaimana memberikan pelabelan-k total tak teratur sisi padagraf lintang?
2. Bagaimana menentukan nilai ketakteraturan total sisi dari graf lintang?
1.2.Batasan Masalah
Batasan-batasan masalah dalam penulisan skripsi ini adalah 1. graf berhingga, sederhana dan tidak berarah,
2. pelabelannya adalah pelabelan-k total tak teratur sisi.
1.3.Tujuan Penulisan
Tujuan dari penulisan skripsi ini adalah dapat memberikan pelabelan pada suatu graf. Secara khusus tujuannya adalah
1. dapat memberikan pelabelan-k total tak teratur sisi padagraf lintang,
2. dapat menentukan nilai ketakteraturan total sisi dari graf lintang.
1.4.Manfaat Penulisan
Manfaat yang diperoleh dari penulisan skripsi ini adalah
1. memperdalam pengetahuan tentang pelabelan, khususnya pelabelan-k total tak
teratur sisipada graf lintang,
BAB II
LANDASAN TEORI
2.1. Tinjauan Pustaka
Bagian ini berisi tentang tinjauan pustaka yang memuat beberapa teori yang
digunakan dalam penulisan skripsi ini, antara lain pengertian tentang graf dan
pelabelan, khususnya pelabelan total tak teratur sisi.
2.1.1. Graf
Definisi 2.1. (Johnsonbaugh, 2001)Suatu graf G (graf tidak berarah) terdiri dari himpunan titik tak kosong V dan himpunan sisi E sedemikian sehingga setiap sisi
E
e∈ dihubungkan oleh sebuah pasangan tak berurutan dari titik. Sebuah sisi e yang menghubungkan titik v dan w dapat dituliskan sebagai e=vw atau e=wv.
Jumlah titik dari graf G disebut order yang dinotasikan dengan |V|, sedangkan
jumlah sisi dari graf G disebut size yang dinotasikan dengan |E|. Gambar 2.1
menunjukkan sebuah graf dengan himpunan titik V dan himpunan sisi E, yaitu
{
v1,v2,v3,v4}
V = dan E =
{
v1v2,v1v4,v2v3,v2v4,v3v4}
. Dengan demikian, ordergraf G adalah |V | = 4 dan size graf G adalah |E| = 5.
Gambar 2.1. Graf G
Definisi 2.2. (Chartrand, 1986) Dua titik u dan v dikatakan adjacent jika uv∈E(G). Jika e=uv∈E(G), maka u dan v masing-masing dikatakan incident
dengan e.
3
v
1
v
4
v
2
4
Pada Gambar 2.1 dapat dilihat bahwa titik v1 adjacent dengan titik v2 dan v4,
tetapi tidak adjacent dengan titik v3. Pada Gambar 2.1 dapat dilihat juga bahwa
sisi v2v3 incident dengan titik v2 dan v3, sisi v2v4 incident dengan titik v2 dan v4,
tetapi sisi v1v2 tidak incident dengan titik v3 maupun titik v4.
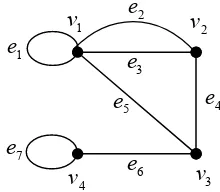
Definisi 2.3. (Johnsonbaugh, 2001) Suatu graf tanpa loop dan sisi rangkap
(paralel edge) disebut graf sederhana (simple graph).
Gambar 2.2. Graf dengan loop dan sisi rangkap
Sebuah loop merupakan sebuah sisi yang terhubung pada suatu titik yang
sama. Sisi rangkap adalah dua sisi atau lebih yang menghubungkan pasangan titik
yang sama.
Graf G pada Gambar 2.1 merupakan graf sederhana, sedangkan graf pada
Gambar 2.2 bukan graf sederhana karena mengandung loop dan sisi rangkap. Sisi
e2 dan e3 merupakan sisi rangkap karena menghubungkan dua titik yang sama
yaitu v1 dan v2.Sedangkan sisi e1 dan e7 merupakan loop karena masing-masing
terhubung pada titik v1 dan v4 itu sendiri.
Definisi 2.4. (Chartrand and Oellermann, 1993) Cycle merupakan barisan
titik-titik u0,u1,...,un, dengan n≥3, u0 =un dan u1,u2,...,un adalah titik-titik yang
berbeda.
Gambar 2.3. Graf 3
C dan C4 1
v e2
2 v
3 v 4
v 1 e
3 e
4 e 5
e
6 e 7
e
2 v
2 v 4
v
1 v
3 v
3
C : C4:
1 v
5
Suatu cycle dengan panjang n atau mempunyai sejumlah n titik disebut Cn
atau n-cycle. Gambar 2.3 merupakan contoh cycle dengan n=3 dan n=4.
Definisi 2.5. (Fletcher et al., 1991)Graf lengkap (complete graph) dengan n titik
yang dinotasikan dengan K , adalah graf sederhana yang setiap titiknya n
adjacent.
Gambar 2.4 merupakan contoh lima graf lengkap. Terlihat bahwa setiap titik
pada masing-masing graf tersebut adjacent.
K1 K2 K3 K4 K5
Gambar 2.4. Graf lengkap
Definisi 2.6. (Chartrand and Oellermann, 1993) Komplemen graf G yang
dinotasikan dengan G , adalah graf dengan V(G) = V(G) dan uv merupakan sisi
dari G jika dan hanya jika sisi tersebut bukan sisi dari G.
Gambar 2.5. Graf dan komplemennya
Gambar 2.5 menunjukkan graf lengkap dan komplemennya. Sisi-sisi dari graf
lengkap K4 tidak dimiliki oleh komplemen dari graf lengkap tersebut.
2 v 4
v
1 v
3 v
4
K : K4:
2 v
3 v 4
v
6
Definisi 2.7. (Chartrand, 1986) Dua buah graf G1 dan G2 dikatakan isomorfik
(
G1 ≅G2)
jika terdapat pemetaan satu-satu φ:V( )
G1 →V( )
G2 , sedemikiansehingga dua titik v dan vi j adjacent dalam graf G1 jika dan hanya jika titik
( )
viφ dan φ
( )
vj adjacent dalam graf G2.Graf G1 dan G2 pada Gambar 2.6 merupakan contoh dua buah graf yang
isomorfik. Pemetaannya adalah φ:V
( )
G1 →V( )
G2 , dengan( )
uiφ =vi, (i=1,2,3,4).
Gambar 2.6. Dua graf yang isomorfik
(
G1 ≅G2)
Definisi 2.8. (Chartrand and Oellermann, 1993) Gabungan dari dua graf G1 dan
G2 yang dinotasikan dengan G1∪G2, adalah graf yang mempunyai
(
G1 G2)
V( )
G1 V( )
G2V ∪ = ∪ dan E
(
G1∪G2)
=E( )
G1 ∪E( )
G2 .Jika G1 ≅G2 ≅G, maka dinotasikan dengan 2G untuk G1∪G2. Pada
umumnya, jika G1,G2,...,Gn adalah n graf yang isomorfik dengan G, maka
dinotasikan dengan nG untuk G1∪G2∪...∪Gn. Dengan kata lain, nG adalah n
kopi graf G, yaitu gabungan dari n graf G. Gambar 2.7 menunjukkan graf
2 3 3 2K ∪ K .
Gambar 2.7. Gabungan dari graf 2K3 dan 3K2 2
3 3
2K ∪ K :
G1 : G2 :
1
u u2
3 u 4
u
1 v
3 v
2 v
7
Definisi 2.9. (Chartrand and Oellermann, 1993) Join dari dua graf G1 dan G2
yang dinotasikan dengan G1+G2, adalah graf yang terdiri dari perpaduan
2 1 G
G ∪ dan semua sisi uv, dengan u∈V
( )
G1 dan v∈V( )
G2 .Graf K3 + K2 ditunjukkan oleh Gambar 2.8. Setiap titik dari masing-masing
graf saling dihubungkan oleh sebuah sisi baru sehingga kedua graf terhubung.
Gambar 2.8. Join dari graf K3 dan K2
Definisi 2.10. (Nurdin dkk., 2005) Graf lintang yang dinotasikan dengan L , n
adalah join dari graf K2 dan Kn , atau graf K2 +Kn.
1 9 v
1 4
v
1 1
v
1 2
v
1 3
v
1 5
v
1 6
v
1 7
v
1 8
v
2 9 v
2 4
v
2 1
v
2 2
v
2 3
v
2 5
v
2 6
v
2 7
v
2 8
v
3 9
v
3 4
v
3 1
v
3 2
v
3 3
v
3 5 v
3 6 v
3 7
v
3 8
v
1
v v2 v3 v4 v5 v6
Gambar 2.9. Graf 3L9
Gambar 2.9 menunjukkan tiga kopi graf L9 yang dinotasikan dengan 3L9,yaitu
gabungan dari tiga graf lintang L9. Suatu graf lintang sLn mempunyai s(n + 2) titik
dan 2ns sisi dengan himpunan titik
( )
sL {v 2 ,v |1 i n,1 j 2s}V j
j
i
n = ≤ ≤ ≤ ≤
dan himpunan sisi
( )
sL {v v 2 |1 i n,1 j 2s}E
j
i j
n = ≤ ≤ ≤ ≤
. K2 :
K3 :
8
Titik
2 j
i
v merupakan anggota dari V
( )
Kn dan titik vj merupakan anggota dari( )
K2V .
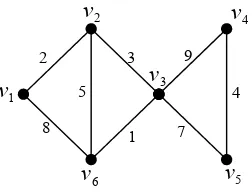
Definisi 2.11. (Bondy and Murty, 1976) Graf berbobot adalah graf yang setiap
sisinya diberi sebuah bilangan yang disebut bobot.
Gambar 2.10. Graf berbobot
Gambar 2.10 adalah contoh dari graf berbobot. Gambar tersebut menunjukkan
bahwa bobot masing-masing sisinya, dinotasikan dengan wt(vivj), adalah
2 ) (v1v2 =
wt , 8wt(v1v6)= , 3wt(v2v3)= , 5wt(v2v6)= , 1wt(v3v6)= ,
9 ) (v3v4 =
wt , 7wt(v3v5)= dan 4wt(v4v5)= .
2.1.2. Pelabelan Graf
Definisi 2.12. (Wallis, 2001) Pelabelan suatu graf adalah suatu pemetaan yang
membawa elemen-elemen graf ke bilangan-bilangan bulat positif atau non
negatif. Pada umumnya domain dari pemetaan ini adalah himpunan semua titik
dan sisi (pelabelan seperti ini disebut pelabelan total), himpunan titik saja
(pelabelan titik), atau himpunan sisi saja (pelabelan sisi). Bobot (weight) dari
elemen graf adalah jumlah dari semua label yang berhubungan dengan elemen
graf tersebut. Bobot dari titik v dengan pelabelan λ adalah
∑
∈
+ =
E uv
uv v
v
wt( ) λ( ) λ( ),
dan bobot dari sisi uv adalah
) ( ) ( ) ( )
(uv u uv v
wt =λ +λ +λ .
1 v
2 v
3 v
4 v
5 v 6
v 2
8 5
3
1 7
9
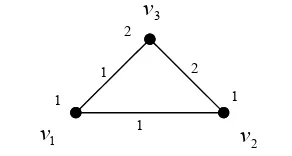
Gambar 2.11. Pelabelan total pada C3
Gambar 2.11 merupakan contoh graf yang titik dan sisinya diberi label
bilangan bulat positif sehingga disebut pelabelan total. Pelabelan setiap titik pada
C3 yaitu
1 ) (v1 =
λ , λ(v2)=1 dan λ(v3)=2,
sedangkan pelabelan sisi-sisinya yaitu
1 ) (v1v2 =
λ , λ(v2v3)=2 dan λ(v3v1)=1.
Bobot titik vi atau )wt(vi dari graf tersebut adalah
3 1 1 1 )
(v1 = + + =
wt , wt(v2)=1+1+2=4, wt(v3)=2+2+1=5,
sedangkan bobot sisi vivj atau wt(vivj) adalah
3 1 1 1 )
(v1v2 = + + =
wt , 5wt(v2v3)=1+2+2= , 4wt(v3v1)=2+1+1= .
Definisi 2.13. (Bača et al., 2003) Suatu graf G = (V, E) dengan himpunan titik tak
kosong V dan himpunan sisi E yang mempunyai pelabelan λ:V ∪E→{1,2,...,k}
disebut pelabelan-k total tak teratur sisi jika untuk sembarang dua sisi e=u1v1
dan f =u2v2 yang berbeda di G berlaku
) ( ) (e wt f
wt ≠ ,
dengan wt(e)=λ(u1)+λ(e)+λ(v1) dan wt(f)=λ(u2)+λ(f)+λ(v2).
Gambar 2.11 menunjukkan pelabelan total tak teratur sisi karena dengan
pelabelan tersebut terlihat bahwa bobot setiap sisi berbeda, yaitu
≠ ) (v1v2
wt wt(v1v3)≠ wt(v2v3). Selanjutnya ditunjukkan pelabelan total tak
teratur sisi graf C5 seperti pada Gambar 2.12. 2
1
v v2
3 v
2
1 1
10
Gambar 2.12. Pelabelan-3 total tak teratur sisi pada C5
Pelabelan setiap titik pada C5 yaitu
1 ) (v1 =
λ , λ(v2)=1, λ(v3)=2, λ(v4)=2 dan λ(v5)=2,
sedangkan label setiap sisinya yaitu
1 ) (v1v2 =
λ , λ(v2v3)=1, λ(v3v4)=3, λ(v4v5)=2 dan λ(v5v1)=2.
Bobot setiap sisi pada Gambar 2.12 dapat ditentukan dengan menjumlahkan label
sisi dengan label titik yang incident dengan sisi tersebut. Bobot setiap sisi graf C5
tersebut yaitu
3 1 1 1 )
(v1v2 = + + =
wt , 6wt(v4v5)=2+2+2= ,
4 2 1 1 )
(v2v3 = + + =
wt , 5wt(v5v1)=2+2+1= .
7 2 3 2 )
(v3v4 = + + =
wt ,
Berdasarkan pelabelan yang diberikan seperti pada Gambar 2.12 terlihat
bahwa bobot setiap sisi berbeda, yaitu wt(v1v2)≠ wt(v2v3)≠ wt(v3v4)≠ wt(v4v1).
Inilah yang disebut pelabelan total tak teratur sisi.
Menurut Bača et al. (2003), pelabelan pada suatu graf G dapat disajikan dalam
suatu bentuk matriks L(G) seperti berikut.
L(G)
( )
(
)
(
)
(
)
( )
(
)
(
n) (
n)
( )
nn
n n n
v v
v v v v
v v v
v v v
v v v
v v
v
v v
v
λ λ
λ
λ λ
λ
λ λ
λ
. . .
. . .
. .
. .
. .
.
. .
. .
.
. . .
. . .
. . .
2 1
2 2
1 2 2
1 2
1 1
1
2 1
=
1 v 5 v
4 v
3 v
2 v
2
2 2
1 1
1 1 3 2
11
Karena v1v2 =v2v1, v1vn=vnv1, v2vn =vnv2 dan seterusnya, maka matriks L(G)
merupakan matriks simetris.
Diagonal matriks tersebut merupakan label titik, sedangkan label sisinya
adalah label selain diagonal yang tidak nol. Angka nol (0) menunjukkan bahwa
dua titik tidak adjacent. Bobot setiap sisi dapat ditentukan dengan menjumlahkan
label sisi dan label titik yang incident dengan sisi tersebut, yaitu label yang berada
dalam satu kolom dan satu baris dengan label sisi tersebut.
Sebagai contoh, pelabelan graf C5 pada Gambar 2.12 disajikan dalam bentuk
matriks L(C5) berikut:
L(C5)
2 2 0 0 2
2 2 3 0 0
0 3 2 1 0
0 0 1 1 1
2 0 0 1 1
5 4 3 2 1
5 4 3 2 1
v v v v v
v v v v v
=
Bobot setiap sisi graf C5 dapat ditentukan dari matriks L(C5), yaitu
(
v1v2)
=1+1+1=3wt , wt
(
v4v5)
=2+2+2=6,(
v3v4)
=3+2+2=7wt , wt
(
v1v5)
=2+1+2=5.(
v2v3)
=1+1+2=4wt ,
Definisi 2.14. (Bača et al., 2003) Nilai ketakteraturan total sisi graf G yang
dinotasikan dengan tes(G), adalah bilangan bulat positif terkecil k sehingga G
memiliki pelabelan-k total tak teratur sisi.
Pelabelan graf C5 pada Gambar 2.12 merupakan pelabelan-3 total tak teratur
12
2.2. Kerangka Pemikiran
Berdasarkan pada tinjauan pustaka, disusun suatu kerangka pemikiran sebagai
berikut. Suatu graf G yang diberi label bilangan bulat positif pada setiap titik dan
sisinya sedemikian sehingga bobot pada setiap sisi berbeda, merupakan pelabelan
total tak teratur sisi. Bobot dari sebuah sisi e dalam graf G merupakan jumlah dari
label sisi e dan label semua titik yang incident dengan sisi tersebut. Setelah
dilakukan pelabelan, maka dapat ditentukan nilai ketakteraturan total sisi dari graf
G yang dinotasikan dengan tes(G), yaitu bilangan bulat positif terkecil k sehingga
G memiliki pelabelan-k total tak teratur sisi.
Selanjutnya akan dikaji ulang bagaimana memberikan pelabelan total tak
teratur sisi pada graf lintang sLn untuk suatu bilangan bulat positif s≥1 dan
2 ≥
n , yang mempunyai himpunan titik V
( )
sL {v 2 ,vj |1 i n,1 j 2s}j
i
n = ≤ ≤ ≤ ≤
dan himpunan sisi E
( )
sL {v v 2 |1 i n,1 j 2s}j
i j
n = ≤ ≤ ≤ ≤
. Setelah semua titikdan
sisi diberi label dan bobot setiap sisi dari sLnberbeda, maka dapat ditentukan nilai
BAB III
METODE PENELITIAN
Metode yang digunakan dalam penulisan skripsi ini adalah studi literatur,
dengan cara mengkaji ulang hasil dari Nurdin dkk. (2005) dan mengumpulkan
referensi yang dapat mendukung pembahasan.
Nilai ketakteraturan total sisi sembarang graf secara umum memiliki batas
sebagai berikut
( )
G E tesE
≤ ≤
+
3 2
.
Berdasarkan batas bawah tersebut, Nurdin dkk. (2005) memberikan nilai
ketakteraturan total sisi graf lintang sLn sebagai berikut
( )
= + 3 2 2ns sL
tes n ,
dengan s≥1 dan n≥2.
Oleh karena itu, untuk mencapai tujuan penulisan, diambil langkah-langkah
sebagai berikut.
1. Menyajikan konsep dan pengertian tentang graf secara umum dan pelabelan,
khususnya pelabelan-k total tak teratur sisi.
2. Membuktikan teorema tentang batas nilai ketakteraturan total sisi sembarang
graf.
3. Mengkaji ulang penentuan nilai ketakteraturan total sisi graf lintang sLn
berdasarkan batas bawah nilai ketakteraturan total sisi sembarang graf.
4. Memberikan penyajian secara umum pelabelan-k total tak teratur sisi pada
graf lintang sL ,n sehingga dapat ditentukan nilai ketakteraturan total sisinya.
5. Memberikan contoh pelabelan-k total tak teratur sisi pada suatu graf lintang
n
14
BAB IV
PEMBAHASAN
Bab ini membahas tentang nilai ketakteraturan total sisi graf lintang sLn,
untuk suatu bilangan bulat positif s≥1 dan n≥2. Dimisalkan graf sLn
mempunyai himpunan titik
( )
sL {v 2 ,v |1 i n,1 j 2s}V j
j
i
n = ≤ ≤ ≤ ≤
dan himpunan sisi
( )
sL {v v 2 |1 i n,1 j 2s}E
j
i j
n = ≤ ≤ ≤ ≤
.
Menurut Nurdin dkk. (2005), nilai ketakteraturan total sisi graf sLn adalah
+
3 2 2ns
.
Sebelumnya dibahas juga tentang batas nilai ketakteraturan total sisi untuk sembarang graf yang diberikan oleh Bača et al. (2003).
4.1. Batas Nilai Ketakteraturan Total Sisi Sembarang Graf
Suatu graf yang diberi pelabelan total tak teratur sisi dapat ditentukan nilai ketakteraturan total sisinya. Nilai ketakteraturan total sisi dari suatu graf G
mempunyai batas atas dan batas bawah seperti yang dituliskan dalam Teorema 4.1.
Teorema 4.1. (Bača et al., 2003) Misal G=
(
V,E)
suatu graf dengan himpunan titik tak kosong V dan himpunan sisi E, maka( )
G E tesE
≤ ≤
+
3 2
.
15
berbeda dari G. Hal ini menunjukkan bahwa pelabelan tersebut adalah pelabelan total tak teratur sisi dengan label terbesar E , sehingga batas atas nilai
ketakteraturan total sisi yang dinotasikan dengan tes
( )
G , adalah E .Untuk batas bawah, dimisalkan λ adalah pelabelan total tak teratur sisi yang optimal dari G. Bobot terbesar sisi e dari G, yaitu wt
( )
e ≥ E +2. Bobot tersebutmerupakan jumlah dari tiga label, sehingga terdapat satu sisi atau titik yang diberi
label paling sedikit 3
2
+
E
. Oleh karena itu, dapat disimpulkan bahwa batas
bawah tes
( )
G adalah
+
3 2
E
. ■
Menurut Teorema 4.1, nilai ketakteraturan total sisi dari suatu graf G yang
dinotasikan dengan tes
( )
G , tidak kurang dari
+
3 2
E
dan tidak melebihi jumlah
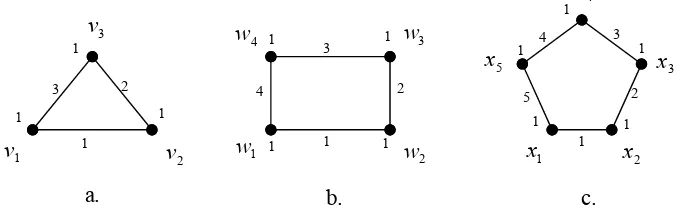
sisinya. Sebagai ilustrasi dari pembuktian Teorema 4.1, diberikan contoh pelabelan untuk menentukan batas atas seperti yang ditunjukkan oleh Gambar 4.1.
Gambar 4.1. Pelabelan total tak teratur sisi
Ketiga graf pada Gambar 4.1 diberi label 1 pada setiap titiknya dan sisi-sisinya diberi label secara terurut 1, 2, ..., E . Gambar 4.1.a menunjukkan graf C3 dengan
bobot setiap sisinya adalah 3 ) (v1v2 =
wt , wt(v2v3)=4 dan wt(v1v3)=5. Gambar 4.1.b menunjukkan graf C4 dengan bobot setiap sisinya adalah
a. b. c.
1
v v2 w1 x1
3
v
2
w
3
w
4
w
5
x
4
x
3
x
2
x
1 1 1
1 1
1
1 1
1 1
1 1
1 1
1
2 2
2
3
3
3 4
16
3 ) (w1w2 =
wt , wt(w2w3)=4, wt(w3w4)=5 dan wt(w1w4)=6. Gambar 4.1.c menunjukkan graf C5 dengan bobot setiap sisinya adalah
3 ) (x1x2 =
wt , wt(x2x3)=4, wt(x3x4)=5, wt(x4x5)=6 dan wt(x1x5)=7. Terlihat bahwa bobot setiap sisi dari masing-masing graf berbeda. Hal ini menunjukkan bahwa ketiga pelabelan tersebut merupakan pelabelan total tak teratur sisi. Nilai ketakteraturan total sisi masing-masing graf tersebut merupakan jumlah sisinya, yaitu
( )
C3 =3tes , tes
( )
C4 =4 dan tes( )
C5 =5.Pelabelan yang lebih besar daripada pelabelan seperti pada Gambar 4.1 tidak mungkin dilakukan. Oleh karena itu, nilai ketakteraturan total sisi dari suatu graf tidak mungkin lebih dari jumlah sisinya, E .
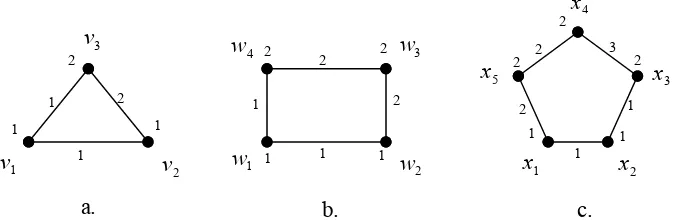
Selanjutnya diberikan contoh pelabelan optimal dari graf yang sama untuk menentukan batas bawah seperti yang ditunjukkan oleh Gambar 4.2.
Gambar 4.2. Pelabelan total tak teratur sisi yang optimal
Ketiga graf pada Gambar 4.2 merupakan graf yang diberi pelabelan optimal. Gambar 4.2.a menunjukkan graf C3 dengan bobot setiap sisinya adalah
3 ) (v1v2 =
wt , wt(v2v3)=5 dan wt(v1v3)=4.
Bobot sisi terbesarnya adalah wt(v2v3)=5≥ E +2=5. Oleh karena itu, label
terbesar dari graf C3 tersebut paling sedikit 2
3 2
=
E +
. Pada Gambar 4.2.a
menunjukkan bahwa label terbesarnya adalah 2, sehingga diperoleh
b. c. a.
1
v v2
3
v
2
1 1
1 2 1
1
w
2
w
3
w
4
w 2 2
1 1 1
2 2
1
1
x
5
x
4
x
3
x
2
x
2
2 2
1 1
1 1 3 2
17
( )
23 2 2
C3 =
+ ≥
= E
tes .
Gambar 4.2.b menunjukkan graf C4 dengan bobot setiap sisinya adalah
3 ) (w1w2 =
wt , 5wt(w2w3)= , 6wt(w3w4)= dan wt(w1w4)=4.
Bobot sisi terbesarnya adalah wt(w3w4)=6≥ E +2=6. Oleh karena itu, label
terbesar dari graf C4 tersebut paling sedikit 2
3 2
=
E +
. Pada Gambar 4.2.b
menunjukkan bahwa label terbesarnya adalah 2, sehingga diperoleh
( )
23 2 2
C4 =
+ ≥
= E
tes .
Gambar 4.2.c menunjukkan graf C5 dengan bobot setiap sisinya adalah
3 ) (x1x2 =
wt , wt(x2x3)=4, wt(x3x4)=7, wt(x4x5)=6 dan wt(x1x5)=5.
Bobot sisi terbesarnya adalah wt(x3x4)=7≥ E +2=7. Oleh karena itu, label
terbesar dari graf C5 tersebut paling sedikit 3
3 2
=
E +
. Pada Gambar 4.2.c
menunjukkan bahwa label terbesarnya adalah 3, sehingga diperoleh
( )
33 2 3
C5 =
+ ≥
= E
tes .
Pelabelan yang lebih kecil daripada pelabelan seperti pada Gambar 4.2 tidak mungkin dilakukan. Oleh karena itu, nilai ketakteraturan total sisi dari suatu graf
tidak mungkin kurang dari
+
3 2
E
.
Selanjutnya akan dibahas tentang nilai ketakteraturan total sisi graf lintang sLn
18
4.2. Nilai Ketakteraturan Total Sisi s Kopi Graf Lintang
n
sL
Suatu graf lintang sLn, untuk suatu bilangan bulat positif s≥1 dan n≥2,
tepat mempunyai nilai ketakteraturan total sisi sebesar
+ 3
2
2ns seperti yang
dituliskan dalam Teorema 4.2. Sebagai ilustrasi, diberikan graf sLn pada Gambar 4.3.
1 1
v
1 2
v
1 3
v
1
n
v
2
v
1
v
2 1
v
2 2
v
2 3
v
2
n
v
4
v
3
v
s
v1
s v2
s
v3
s n
v
s v2
1 2s− v
Gambar 4.3. Graf sLn
Teorema 4.2. (Nurdin dkk., 2005) Untuk suatu bilangan bulat positif s≥1 dan
2
≥
n berlaku
( )
= + 3 2 2ns sL
tes n .
Bukti. Dimisalkan
( )
sL {v 2 ,v |1 i n,1 j 2s}V j
j i
n = ≤ ≤ ≤ ≤
dan
( )
sL {v v 2 |1 i n,1 j 2s}E
j i j
n = ≤ ≤ ≤ ≤
.
Karena jumlah sisinya, yaitu E =2ns, maka berdasarkan batas bawah dari Teorema 4.1 diperoleh
( )
≥ + 3 2 2ns sL
19
Selanjutnya dibuktikan kebalikan dari pertidaksamaan tersebut, yaitu
( )
≤ + 3 2 2ns sL
tes n .
Dimisalkan + = 3 2 2nj
Mj , untuk j=1,2,...,s dan dikonstruksikan
pelabelan-s
M total tak teratur sisi λ dari graf sLn. Label titik dikonstruksikan sebagai
( )
= 2 j j M vλ untuk j = 1, 2, ..., 2s
dan
(
)
(
)
(
)
− − − = − = − − = − − + − + + − = , 1 2 ..., , 1 , 0 dengan , untuk , 2 ..., , 2 , 1 untuk , 2 1 2 1 2 1 2 1 1 1 2 2 M n n k k n i k M M n i i M n n M M v j j j i λsedangkan label sisi sebagai
( )
− − + + − = 2 2 2 1 2 2 j i j j ij q v v
j n v
v λ λ
λ
untuk i=1,2,...,n dan j=1,2,...,2s dengan
. genap jika , ganjil jika , + = j i n j i q
Label terbesar dari pelabelan tersebut dapat ditentukan. Sebelumnya akan ditunjukkan urutan nilai yang digunakan sebagai label sisi. Diambil sembarang j
dan j' di
{
}
s 2 ..., , 2 ,
1 dengan j< j', maka untuk setiap i=1,2,...,n berlaku
≤ 2 ' ' 2 j i j j i
jv v v
v λ
λ
dan sembarang i dan i' di
{
1,2,...,n}
dengan i<i', maka untuk setiaps
j=1,2,...,2 berlaku
. 2 2 ' ≤ j i j j i
jv v v
v λ
20
Oleh karena itu, untuk sisi
2 j i jv
v dengan i=1,2,...,n dan j=1,2,...,2s, label terbesar diperoleh pada i = n dan j = 2s, yaitu
. 3 2 2 3 2 2 2 3 2 2 3 3 2 2 2 2 2 3 2 2 2 2 ) ( ) 1 ( 2 2 + ≤ + − + = + − + = + − + + + − = ns ns ns ns ns ns n n s n v v j i j λ
Titik vj dengan j=1,2,...,2s, label terbesar diperoleh pada j=2s, yaitu
( )
= = + 3 2 2 2 ns Mv s s
λ
dan untuk titik
2 j i
v dengan i=1,2,...,n dan j=1,2,...,2s, label terbesar diperoleh pada i = n dan j = 2s, yaitu
. 3 2 2 0 2 2 2 2 + = = − = ns M M
v s s
s n
λ
Jadi label terbesar pada pelabelan tersebut adalah
+ 3 2 2ns .
Selanjutnya ditunjukkan bahwa bobot setiap sisi berbeda. Bobot setiap sisi graf
n
sL adalah
( )
2 1 2 2 2 2 2 + + − = + + = q j n v v v v v v wt j i j i j j j ij λ λ λ
dengan i∈
{
1,2,...,n}
, j∈{
1,2,...,2s}
dan . genap jika , ganjil jika , + = j i n j i qOleh karena itu, untuk i,i'∈
{
1,2,...,n}
dan j, j'∈{
1,2,...,2s}
dengan j≠ j'21
1. Jika j dan j' keduanya ganjil, maka
2 1
2 2
2 + +
− = i j n v v wt j i j dan 2 1 2 ' 2 ' 2 ' ' ' + + − = i j n v v wt j i j . Andaikan = 2 ' 2 ' ' j i j j i
jv wt v v
v
wt , maka
' 2
' 2 2
2n j i n j +i
= +
atau
. 2 ' 2 2 ' i i j j
n = −
−
Karena i,i'∈
{
1,2,...,n}
, maka i' −i ≤n−1. Akibatnya2 1 2 1 2 1 2 1 2 '
2 = − <
− ≤ − n n n j j
. (4.2)
Karena j, j'∈
{
1,2,...,2s}
dengan j≠ j', maka1 2
'
2 ≤ −
−
j j s
. (4.3)
Diberikan beberapa contoh untuk s≥1 adalah sebagai berikut.
Jika s=1, maka j=1,2. Untuk j≠ j' diperoleh
0 2 2 ' = −
j j
.
Pertidaksamaan (4.3) menunjukkan kebenaran bahwa
0 1 2
'
2 ≤ − =
−
j j s
, sedangkan pertidaksamaan (4.2)
menunjukkan kemungkinan lain bahwa
− 2 ' 2 j j
dapat kurang dari
2 1
22
Jika s=2, maka j=1,2,3,4. Untuk j≠ j' diperoleh
1 2 2 ' ≤ −
j j
.
Pertidaksamaan (4.3) menunjukkan kebenaran bahwa
1 1 2
'
2 ≤ − =
− s j j
, sedangkan pertidaksamaan (4.2) menunjukkan
bahwa − 2 ' 2 j j
hanya kurang dari
2 1
.
Jika s=3, maka j=1,2,3,4,5,6. Untuk j≠ j' diperoleh
2 2 2 ' ≤ −
j j
.
Pertidaksamaan (4.3) menunjukkan kebenaran bahwa
2 1 2
'
2 ≤ − =
− s j j
, sedangkan pertidaksamaan (4.2) menunjukkan
bahwa − 2 ' 2 j j
hanya kurang dari
2 1
.
Berdasarkan contoh yang diberikan, maka pertidaksamaan (4.2) kontradiksi dengan pertidaksamaan (4.3). Sehingga untuk sembarang i, '
i ,
j dan '
j diperoleh ≠ 2 ' 2 ' ' j i j j i
jv wt v v
v
wt .
2. Jika salah satu dari j dan j' adalah ganjil, dimisalkan j ganjil dan j ' genap, maka
2 1
2 2
2 + +
23 Andaikan = 2 ' 2 ' ' j i j j i
jv wt v v
v
wt , maka
' 2
' 2 2
2nj+i= nj+n+i atau n j j =i −i
− − ' 2 1 2 ' 2 2 .
Karena i,i'∈
{
1,2,...,n}
, maka i' −i ≤n−1. Akibatnya1 2 1 2 ' 2
2 ≤ −
− −
j j n
n atau 1 2 1 1 2 1 2 2 '
2 = − <
− ≤ − n n n j j
. (4.4)
Karena j, j'∈
{
1,2,...,2s}
dengan j≠ j', maka1 2
'
2 ≤ −
− s j j
. (4.5)
Seperti pertidaksamaan (4.2) dan (4.3) pada Kasus I, demikian juga pertidaksamaan (4.4) kontradiksi dengan pertidaksamaan (4.5). Sehingga untuk sembarang i, '
i , j dan '
j diperoleh ≠ 2 ' 2 ' ' j i j j i
jv wt v v
v
wt .
3. Jika j dan j' keduanya genap, maka
2 1
2 2
2 + + +
− = i n j n v v wt j i j dan 2 1 2 ' 2 ' 2 ' ' ' + + + − = i n j n v v wt j i j . Andaikan = 2 ' 2 ' ' j i j j i
jv wt v v
v
wt , maka
' 2
' 2 2
2nj+i= nj+i atau . 2
' 2
2n j j =i'−i
24
Karena i,i'∈
{
1,2,...,n}
, maka i' −i ≤n−1. Akibatnya2 1 2
1 2 1 2
1 2
'
2 = − <
− ≤ −
n n
n j j
. (4.6)
Karena j, j'∈
{
1,2,...,2s}
dengan j≠ j', maka1 2
'
2 ≤ −
−
j j s
. (4.7)
Seperti pertidaksamaan (4.2) dan (4.3) pada Kasus I, demikian juga pertidaksamaan (4.6) kontradiksi dengan pertidaksamaan (4.7). Sehingga untuk sembarang i, '
i , j dan '
j diperoleh
≠
2 ' 2
' '
j i j j
i
jv wt v v
v
wt .
Jadi terbukti bahwa bobot setiap sisi berbeda.
Karena bobot setiap sisi berbeda dan label terbesar yang digunakan adalah
+
3 2 2ns
, maka diperoleh nilai ketakteraturan total sisi graf sLn adalah
( )
≤ + 3 2 2ns sL
tes n . (4.8)
Berdasarkan pertidaksamaan (4.1) dan (4.8), terbukti bahwa untuk suatu bilangan bulat positif s≥1 dan n≥2 diperoleh nilai ketakteraturan total sisi graf
n
sL adalah
( )
= + 3 2 2ns sL
tes n . (4.9)
■
25
L1
( )
sLn =26
L2
( )
sLn =
( )
[
( )
( )
]
[
( )
( )
]
[
( )
( )
]
( )
( )
[
]
( )
[
( )
( )
]
( )
( )
[
]
( )
[
( )
( )
]
( )
( )
[
]
( )
[
( )
( )
]
( )
( )
[
]
[
( )
( )
]
[
( )
( )
]
( )
n n n27
Lj
( )
sLn =
(
)
[
(
)
( )
]
[
(
)
( )
]
[
(
)
( )
]
(
)
( )
[
]
( )
[
( )
( )
]
(
)
( )
[
]
( )
[
( )
( )
]
(
)
( )
[
]
( )
[
( )
( )
]
( )
( )
[
]
[
( )
( )
]
[
( )
( )
]
( )
j n j n jn28
[image:39.612.137.547.157.402.2]Berikut diberikan contoh graf lintang 3L9, dengan gambar graf seperti pada
Gambar 4.4. 3 1 v 3 2 v 13 3 3 v 3 4 v 3 5 v 13 18 17 16 15 3 6 v 14 3 8 v 3 7 v 15 15 15 15 17 18 18 18 18 3 9 v 15 18 14 14 15 16 17 18 19 13 14 5 v
13 v6 19
1 1 v 1 2 v 4 2 1 3 1 3 v 1 4 v 1 2 1 5 v 1 6 5 4 3 1 6 v 5 2 1 8 v 6 1 7 v 2 3 3 3 3 5 6 6 6 6 1 9 v 7 3 6 1 v
1 v2 7
2 1 v 2 2 v 10 8 7 9 2 3 v 2 4 v 7 8 2 5 v 7 12 11 10 9 2 6 v 11 8 2 8 v 12 2 7 v 8 9 9 9 9 11 12 12 12 12 2 9 v 13 9 12 3 v
7 v4 13
Gambar 4.4. Pelabelan-19 total tak teratur sisi graf 3L9
Pelabelan setiap titik dan sisi dari graf 3L9 tersebut diperoleh dari matriks Lj(sLn),
yaitu sebagai berikut:
L1(3L9) =
0 124 135 145 156 166 176 186 196 206 7
29
L2(3L9) =
(
)
(
)
30 31 32 33 34 35 36 37 3813 12 12 12 12 12 12 11 11 10 0 29 12 13 0 0 0 0 0 0 0 0 9 28 12 0 12 0 0 0 0 0 0 0 9 27 12 0 0 11 0 0 0 0 0 0 9 26 12 0 0 0 10 0 0 0 0 0 9 25 12 0 0 0 0 9 0 0 0 0 9 24 12 0 0 0 0 0 8 0 0 0 9 23 11 0 0 0 0 0 0 8 0 0 8 22 11 0 0 0 0 0 0 0 7 0 8 21 10 0 0 0 0 0 0 0 0 7 7 0 9 9 9 9 9 9 8 8 7 7 2 / 4 4 2 9 2 8 2 7 2 6 2 5 2 4 2 3 2 2 2 1 3 2 / 3 4 2 9 2 8 2 7 2 6 2 5 2 4 2 3 2 2 2 1 3 j i j i v v wt v v v v v v v v v v v v v wt v v v v v v v v v v v
L3(3L9) =
(
)
(
)
48 49 50 51 52 53 54 55 5619 18 18 18 18 18 18 17 17 16 0 47 18 19 0 0 0 0 0 0 0 0 15 46 18 0 18 0 0 0 0 0 0 0 15 45 18 0 0 17 0 0 0 0 0 0 15 44 18 0 0 0 16 0 0 0 0 0 15 43 18 0 0 0 0 15 0 0 0 0 15 42 18 0 0 0 0 0 14 0 0 0 15 41 17 0 0 0 0 0 0 14 0 0 14 40 17 0 0 0 0 0 0 0 13 0 14 39 16 0 0 0 0 0 0 0 0 13 13 0 15 15 15 15 15 15 14 14 13 13 2 / 6 6 3 9 3 8 3 7 3 6 3 5 3 4 3 3 3 2 3 1 5 2 / 5 6 3 9 3 8 3 7 3 6 3 5 3 4 3 3 3 2 3 1 5 j i j i v v wt v v v v v v v v v v v v v wt v v v v v v v v v v v
Dari pelabelan yang disajikan dalam matriks L1(3L9), L2(3L9) dan L3(3L9),
terlihat bahwa bobot setiap sisi berbeda dan label terbesarnya adalah 19. Oleh karena itu, pelabelan pada graf 3L9 merupakan pelabelan-19 total tak teratur sisi
dengan nilai ketakteraturan total sisinya adalah tes
( )
3L9 =19. Jika tes( )
3L9dihitung dengan persamaan (4.9), maka diperoleh hasil yang sama, yaitu
( )
193 2 3 . 9 . 2
3 9 =
30
BAB V
PENUTUP
5.1 Kesimpulan
Berdasarkan pembahasan yang telah dilakukan maka dapat disimpulkan
sebagai berikut.
1. Pelabelan-k total tak teratur sisi dapat diberikan pada graf lintang sLn, untuk
suatu bilangan bulat positif s≥1 dan n≥2, dengan aturan pelabelan tertentu.
2. Nilai ketakteraturan total sisi dari graf lintang sLn, untuk suatu bilangan bulat
positif s≥1 dan n≥2, dapat ditentukan. Berdasarkan pembahasan Teorema
4.2, diperoleh nilai ketakteraturan total sisi graf lintang sLn adalah
( )
= + 32 2ns sL
DAFTAR PUSTAKA
Bača, M., S. Jendrol, M. Miller and J. Ryan. On Irregular Total Labelings. Discrete Mathematics. Accepted for publication March 2003.
Bondy, J. A. and U. S. R. Murty. (1976). Graph Theory with Applications.
Elsevier Science Publishing Company Inc, New York.
Chartrand, Gary and O. R. Oellermann. (1993). Applied and Algorithmic
graph Theory. McGraw-Hill Inc, New York.
Chartrand, Gary. (1986). Introductory Graph Theory. Dover Publications Inc,
New York.
Deo, Narshingh. (1980). Graph Theory with Applications to Engineering and
Computer Science. Prentice-Hall of India, New Delhi.
Fletcher, P., H. Hoyle and C. W. Patty. (1991). Foundation of Discrete
Mathematics. PWS Kent Publishing Company, Boston.
Johnsonbaugh, R.(2001). Discrete Mathematics. Fifth Edition. Prentice Hall,
New Jersey.
Nurdin, E. T. Baskoro dan A. N. M. Salman. (2005). Nilai Ketakteraturan
Total Sisi dari Graf Lintang. Seminar Nasional MIPA, Depok.