Pemrograman Bilangan Bulat (Integer Programming)

LOGO

Pemrograman Bilangan Bulat

(Integer Programming)

Amelia Kurniawati ST., MT.

2

Outline

Konsep

Bilangan

Bulat

Metode

pemecahan

bilangan bulat

• Pengantar

pemrograman bilangan bulat

• Contoh model

pemrograman

• Metode branch

GOAL

Memahami permasalahan dan solusi

variabel integer

_{Memahami metode Branch and Bound}

LOGO

Konsep Bilangan Bulat

LOGO

①

Pengantar Pemrograman

6

Pemrograman Bilangan Bulat

Pemrograman bilangan bulat (integer

programming) mensyaratkan bahwa

beberapa variabel keputusan harus mempunyai nilai yang bulat (bukan pecahan)

Disini, pembahasan hanya ditujukan

untuk masalah pemrograman linier

bilangan bulat (integer linear

Jenis Pemrograman Linier

Bilangan Bulat

Pemrograman linier bilangan bulat

murni (pure integer linear

programming, PILP)

Pemrograman linier bilangan bulat

campuran (mixed integer linear

programming, MILP)

Pemrograman linier bilangan bulat

biner (binary integer linear

8

Pembatas Either-Or

18

LP format:

 

0,1



i

y

Fungsi dengan N Nilai yang Mungkin



x x xn



d d dN

f ₁, ₂,, _{ 1} atau ₂ atau atau





_





N

i

i i

n d y

x x

x f

1 2

1, ,,

Perumusan ILP:

1

1







N

i

i

y

 

i N y_{i } 0,1 , _1,2,,

10

Contoh Kasus:

18 atau 12

atau 6

2

3x_{1 } x_{2 }

3 2

1 2

1 2 6 12 18

3x _ x _ y _ y _ y

Perumusan ILP:

1

3 2

1  y  y  y

 

0,1 , _1,2,3

 i

y_i

Representasi Biner untuk Variabel Bilangan Bulat

u

x

_



0

_dimana

₂

₂

_1





N

N

_u

Representasi biner:







N

i

i i

_y

x

0

2

 

i

N

y

_i

_

0

,

1

,

_

1

,

2

,



,

Batas-batas untuk variabel x:

12

Contoh Kasus:

5

1



x

Representasi biner:

5

4

2

_{1 2}

0



y



y



y

 

0

,

1

,

_

0

,

1

,

2



i

y

_i

30

3

2

x

₁

_

x

₂

_



2

4

 

3

2

4

8



30

2

y

₀

_

y

₁

_

y

₂

_

w

₀

_

w

₁

_

w

₂

_

₃

_

u untuk x₁ = 5  22  5  23

u untuk x₂ = 10  23  10  24

 

0

,

1

,

_

0

,

1

,

2

,

3



i

w

_i

LOGO

②

Beberapa Contoh Model

14

Beberapa Contoh Model-model

Pemrograman Bilangan Bulat

Fixed charge problem Knapsack problem

Set covering problem

 Set Partitioning Problem

Traveling salesman problem

Fixed Charge Problem

(1)

Misalkan terdapat n jenis produk p_j = harga satuan produk j

K_j = biaya tetap untuk memproduksi produk j (independen terhadap jumlah produksi) c_j = biaya variabel untuk memproduksi

produk j (proporsional terhadap jumlah produksi)

b_i = kapasitas sumber i (i = 1, …m)

16

Fixed Charge Problem

(2)

Permasalahan :

Menentukan produk mana yang perlu diproduksi dan jumlah produksinya masing-masing agar diperoleh profit (selisih penjualan dengan biaya tetap dan variabel) total yang maksimum dengan memperhatikan kondisi:

 ketersediaan kapasitas

 jika suatu produk diputuskan untuk tidak diproduk maka jumlah produksinya nol.

Variabel keputusan :

x_j = jumlah produk j yang diproduksi

y_j = keputusan untuk memproduksi atau tidak produk j;

y_j = 1 jika produk j diproduksi

Fixed Charge Problem

(3)

dengan pembatas-pembatas:

18

Knapsack Problem

(1)

Misalkan terdapat n item.

w_j = berat item j v_j = nilai item j

W = kapasitas muatan (berat) dari kantong Permasalahan :

Menentukan jumlah item yang perlu dimasukkan ke dalam kantong agar diperoleh nilai total yang

maksimum dengan memperhatikan kondisi kapasitas muatan (berat) dari kantong

Variabel keputusan :

Knapsack Problem

(2)







n

j

j j

x

v

Z

1

Maksimasi

dengan pembatas-pembatas:

W

x

w

n

j

j j





1

bulat

bilangan

dan

0



j

20

Set Covering Problem

(1)

Jalan C

Jalan D Jalan B Jalan A

Jalan E

Jalan F

Ja

la

n

G Jala

n

K

Ja

la

n

J

Ja

la

n

I

Ja

la

n

H

1 2

6 7

4

8 5 3

Set Covering Problem

(2)

Misalkan terdapat n lokasi pendirian pos dan m jalan.

c_j = biaya mendirikan pos di lokasi j a_ij = konstanta biner (0-1)

a_ij = 1 jika jalan i dilayani oleh pos yang berlokasi di j a_ij = 0 jika sebaliknya

Pertanyaan:

Menentukan lokasi pendirian pos dimana tiap jalan dapat

dilayani minimal oleh satu pos sehingga diperoleh biaya total pendirian yang minimum

Variabel keputusan

x_j = variabel biner (0-1) yang menentukan keputusan untuk mendirikan pos di lokasi j (x_j = 1 jika pos

22

Set covering problem

(3)







n

j

j j

x

c

Z

1

Minimasi

dengan pembatas-pembatas:

m

i

x

a

n

j

j

ij

1

,

1

,...,

1









 

j

n

Set Partitioning Problem







n

j

j j

x

c

Z

1

Minimasi

dengan pembatas-pembatas:

m

i

x

a

n

j

j

ij

1

,

1

,...,

1









 

j

n

x

_j

_

0

,

1

,

_

1

,...,

Tiap jalan

tepat dilayani

24

Traveling Salesman Problem

(1)

1

2

3

4 5

5

6

3 4

3 8

2 6

1 7

Traveling Salesman Problem

(2)

Misalkan terdapat n titik.

c_ij = jarak antara titik i ke titik j (c_ij =  untuk i = j) Permasalahan

Menentukan rute salesman yang berangkat dari suatu titik dan mengunjungi setiap titik yang lain paling

banyak sekali, serta kembali ke titik asal agar diperoleh jarak total yang minimum

Variabel keputusan

X_ij = keputusan untuk melintasi atau tidak busur (i, j) x_ij = 1 jika busur (i, j) dilintasi

26

Traveling Salesman Problem

(3)

 

dengan pembatas-pembatas:

n

Traveling Salesman Problem

(4)

1

2

3

4 5

Subtour

28

Traveling Salesman Problem

(5)

1

2

3

4 5

Tour

Job Scheduling Problem

(1)

Misalkan

 terdapat n job dengan operasi-tunggal

 terdapat satu mesin tunggal

p_j = waktu pengerjaan job j w_j = bobot kepentingan job j

Permasalahan:

30

Job Scheduling Problem

(2)

Variabel keputusan:

B_j = saat awal pengerjaan job j C_j = saat akhir pengerjaan job j

y_ij = keputusan apakah job i mendahului job i y_ij = 1 jika job i mendahului job j

y_ij = 0 jika sebaliknya

0

3 1 4 5 2

p₃ p₁ p₄ p₅ p₂

Job Scheduling Problem

(3)

dengan pembatas-pembatas:

n

Disjunctive constraint

LOGO

32

Metode Pemecahan

Metode pemecahan kasus pemrograman bilangan bulat:

Cutting method

 Cutting Plane

Search method

LOGO

Metode Cutting Plane

Algoritma

Cutting Plane

Dikembangkan oleh R.E. Gomory

Algoritma

 Fractional algorithm untuk masalah

pemrograman bilangan bulat murni (PILP)

 Mixed algorithm untuk masalah pemrograman

36

Ilustrasi Suatu Masalah

ILP

Maximasi Z = 7x₁ + 9x₂

dengan pembatas-pembatas: –x₁ + 3x₂  6

7x₁ + x₂  35

Daerah layak

x₂

38 Solusi Optimal Kontinyu

(dengan mengabaikan kondisi integralitas) x₂

x₁





63

3 , 4 )

,

( 1₂

2 1 2

1



 Z

Ide Dasar dari

Cutting Plane

Mengubah convex set dari daerah

ruang pemecahan (solution space)

sehingga titik ekstrem menjadi bilangan bulat

Perubahan dibuat tanpa men-slicing

off daerah layak dari masalah awal.

Perubahan dilakukan dengan

penambahan beberapa secondary

40

Penambahan pembatas sekunder

x₂

x₁ secondary constraint

 

55

3 , 4 )

, ( _{1 2}



 Z

Fractional Algorithm

(1)

 Digunakan untuk memecahkan masalah pemrograman linier bilangan bulat murni

(PILP).

 Mensyaratkan bahwa semua koefisien

teknologi dan konstanta ruas kanan adalah bilangan bulat.

 _{Pada awalnya, masalah PILP dipecahkan} sebagai LP reguler, yaitu dengan

mengabaikan kondisi integralitas.

2 13 3

1

2

1  x 

42

Fractional Algorithm

(2)

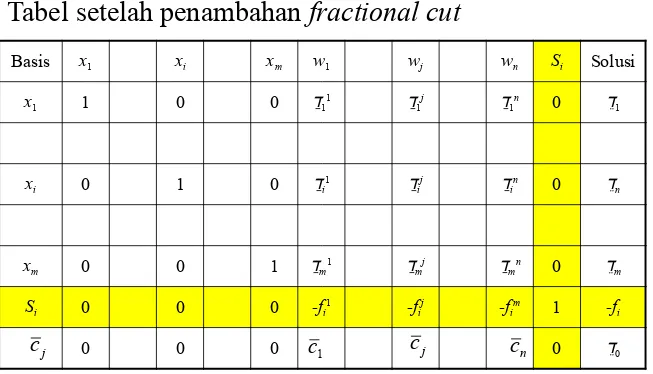
Basis x₁ x_i x_m w₁ w_j w_n Solusi

x₁ 1 0 0 ₁1 _

1j 1n 1

x_i 0 1 0 _i1 _

ij in n

x_{m 0 0 1} _m1 _

mj mn m

0 0 0 ₀

j

c _c1 cj c_n

Fractional Algorithm

(3)

Variabel x_i (i = 1, …, m) menunjukkan variabel basis

Variabel w_j (j = 1, …, n) menunjukkan variabel non basis

Misalkan persamaan ke-i dimana variabel x_i diasumsikan bernilai bilangan bulat

bulat bilangan

bukan

, _i

1

 







 

n

j

j j i i

i w

x

44

Fractional Algorithm

(4)

Misal:

_

_i

_

 

_

_i

_

f

_i

 

ij j

i j

i 



 f



dimana

N = [a] adalah bilangan bulat terbesar sehingga N  a

Fractional Algorithm

(5)

Dari baris sumber diperoleh:

 

_

 



 

 

 

n

j

j j i i

i n

j

i ij

i f w x w

f

1 1

 

Agar semua x_i dan w_j adalah bilangan bulat,

maka ruas kanan dari persamaan harus bilangan bulat

46

Fractional Algorithm

(6)

Untuk f_ij  0 dan w_j  0 untuk semua i dan j maka

0

1







n

j

j ij

w

f

Akibatnya

i n

j

j ij

i

f

w

f

f

_

_

_

Fractional Algorithm

(7)

1

1









n

j

j ij

i

f

w

f

Karena f_i < 1 maka

Karena ruas kiri harus bilangan bulat, maka syarat perlu untuk memenuhi integralitas adalah:

0

1









n

j

j ij

i

f

w

48

Fractional Algorithm

(8)

Pertidaksamaan terakhir dapat dijadikan sebagai pembatas dalam bentuk:

i n

j

j ij

i

f

w

f

S

_

_

_

1

Fractional Algorithm

(9)

Basis x₁ x_i x_m w₁ w_j w_n S_i Solusi

x₁ 1 0 0 ₁1 _

1j 1n 0 1

x_i 0 1 0 _i1 _

ij in 0 n

x_m 0 0 1 _m1 _

mj mn 0 m

S_i 0 0 0 -f_i1 _-f

ij -fim 1 -fi

0 0 0 0 ₀

j

c _c1 cj c_n

50

Fractional Algorithm

(10)

Dengan penambahan fractional cut,

tabel terakhir menjadi tidak layak walaupun optimal sehingga metode

dual simplex diterapkan untuk meniadakan ketidaklayakan.

Algoritma berhenti jika solusi optimal

Fractional Algorithm

(11)

i n

j

j

ij

w

f

f

_



1

k n

j

j

kj

w

f

f

_



1

Cut (1) dikatakan lebih kuat dari cut (2) jika

f_i  f_k dan f_ij  f_kj untuk semua j dengan strict inequality

52

Fractional Algorithm

(12)

Aturan :

 

i i

f

max































 n

j

ij i i

f

f

Ilustrasi Penerapan

Fractional Algorithm

(1)

Maximasi Z = 7x₁ + 9x₂

dengan pembatas-pembatas: –x₁ + 3x₂  6

7x₁ + x₂  35

54

Ilustrasi Penerapan

Fractional Algorithm

(2)

Basis x₁ x₂ x₃ x₄ Solusi

x₂ 0 1 7/22 1/22 3 1/

2

x₁ 1 0 -1/22 3/22 4 1/ 2

Ilustrasi Penerapan

Fractional Algorithm

(3)

2

Fractional cut:

56

Ilustrasi Penerapan

Fractional Algorithm

(4)

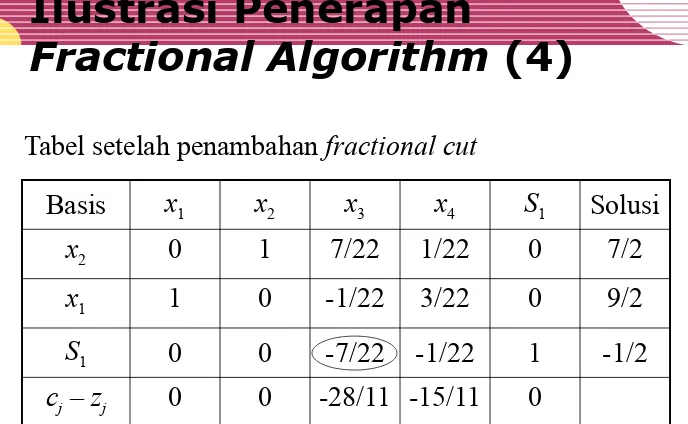
Basis x₁ x₂ x₃ x₄ S₁ Solusi

x₂ 0 1 7/22 1/22 0 7/2

x₁ 1 0 -1/22 3/22 0 9/2

S_{1 0 0 -7/22 -1/22 1 -1/2} c_j – z_j 0 0 -28/11 -15/11 0

Ilustrasi Penerapan

Fractional Algorithm

(5)

Basis x₁ x₂ x₃ x₄ S₁ Solusi

x₂ 0 1 0 0 1 3

x₁ 1 0 0 1/7 -1/7 4 4/

7

x_{3 0 0 1 1/7 -22/7} 1 4/ 7

c_j – z_j 0 0 0 -1 -8 Z = 59

58

Ilustrasi Penerapan

Fractional Algorithm

(6)

7

Fractional cut:

Ilustrasi Penerapan

Fractional Algorithm

(7)

Basis x₁ x₂ x₃ x₄ S₁ S₂ Solusi

x₂ 0 1 0 0 1 0 3

x₁ 1 0 0 1/7 -1/7 0 4 4/

7

x₃ 0 0 1 1/7 -22/7 0 1 4_/ 7

S_{2 0 0 0 -1/7 -6/7 1 -4/7}

c_j – z_j 0 0 0 -1 -8 0

60

Ilustrasi Penerapan

Fractional Algorithm

(8)

Basis x₁ x₂ x₃ x₄ S₁ S₂ Solusi

x₂ 0 1 0 0 1 0 3

x₁ 1 0 0 0 -1 1 4

x₃ 0 0 1 0 -4 1 1

x_{4 0 0 0 1 6 -7 4}

c_j – z_j 0 0 0 -2 -7 0 Z = 55

2

Ilustrasi

Fractional Cut

secara grafis (1)









62

Ilustrasi

Fractional Cut

secara grafis (2)

x₂

x₁

3

2 

7

Ilustrasi

Fractional Cut

secara grafis (3)









64

Ilustrasi

Fractional Cut

secara grafis (4)

x₂

x₁

3

2 

x

7

2 1  x 

Mixed Algorithm

(1)

Digunakan untuk memecahkan

masalah pemrograman linier bilangan

bulat campuran (MILP)

Pada awalnya, masalah MILP

dipecahkan sebagai LP reguler, yaitu

66

Mixed Algorithm

(3)

Maximasi Z = 7x₁ + 9x₂

dengan pembatas-pembatas: –x₁ + 3x₂  6

7x₁ + x₂  35

x₁ ≥ 0 dan bilangan bulat

Mixed Algorithm

(3)

Misal x_k adalah variabel bilangan bulat dari masalah MILP.

Persamaan-x_k dalam solusi kontinyu optimal:

 

_

68

Mixed Algorithm

(4)

Untuk x_k adalah bilangan bulat, maka

 

atau

_

 

_

1



_{k k k}

k

x

x

_

_

harus dipenuhi

k n

j

k j

k

w



f



1



Dari baris sumber, kondisi ini ekivalen dengan

1

1









k n

j

k j

k

w

f



(1)

Mixed Algorithm

(5)

Misal

J+ = himpunan subscripts j untuk _

kj  0

J- = himpunan subscripts j untuk _

kj < 0

Dari (1) dan (2) diperoleh

k n

J j

k j

k

w



f



_ 



k n

J j

k j k k

k

_w

_f

f

f













1

(1)

70

Mixed Algorithm

(6)

Karena (1) dan (2), tidak dapat terjadi secara simultan, maka (3) dan (4) dapat digabungkan menjadi satu

pembatas dalam bentuk

Ilustrasi Penerapan

Mixed Algorithm

(1)

Maximasi Z = 7x₁ + 9x₂

dengan pembatas-pembatas: –x₁ + 3x₂  6

7x₁ + x₂  35

x₁ ≥ 0 dan bilangan bulat

72

Ilustrasi Penerapan

Mixed Algorithm

(2)

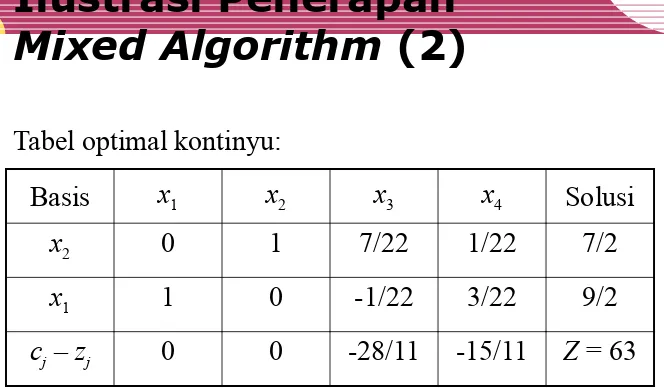
Basis x₁ x₂ x₃ x₄ Solusi

x₂ 0 1 7/22 1/22 7/2

x₁ 1 0 -1/22 3/22 9/2

Ilustrasi Penerapan

Mixed Algorithm

(3)

74

Basis x₁ x₂ x₃ x₄ S₁ Solusi

x₂ 0 1 7/22 1/22 0 7/2

x₁ 1 0 -1/22 3/22 0 9/2

S_{1 0 0 -1/22 -3/22 1 -1/2} c_j – z_j 0 0 -28/11 -15/11 0

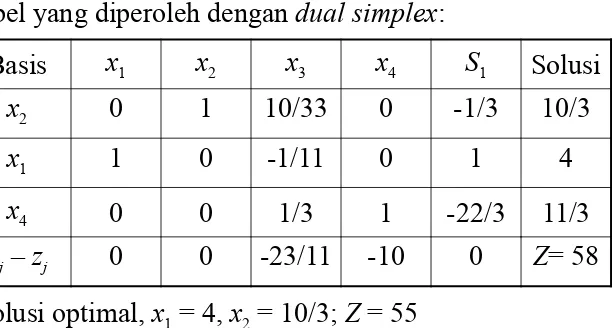
Basis x₁ x₂ x₃ x₄ S₁ Solusi

x₂ 0 1 10/33 0 -1/3 10/3

x₁ 1 0 -1/11 0 1 4

x_{4 0 0 1/3 1 -22/3 11/3} c_j – z_j 0 0 -23/11 -10 0 Z= 58 Tabel yang diperoleh dengan dual simplex:

LOGO

Metode

Branch and Bound

Algoritma

Branch-and-Bound

(1)

Metode yang paling banyak digunakan

dalam praktek untuk memecahkan

masalah pemrograman bilangan bulat baik murni maupun campuran.

Digunakan sebagian besar software

komersial

Pada dasarnya merupakan prosedur

enumerasi yang efisien untuk

78

Algoritma

Branch-and-Bound

(2)



Algoritma BB untuk ILP

(PILP & MILP)

Algoritma BB untuk ILP (1)

Misalkan diberikan suatu masalah pemrograman bilangan bulat sebagai berikut:

Maksimasi Z = cx dengan pembatas

Ax = b x  0

x_j bilangan bulat untuk j  I

80

Algoritma BB untuk ILP (2)

 _{Langkah pertama adalah memecahkan masalah} ILP sebagai LP dengan mengabaikan pembatas bilangan bulat (bounding)

 _{Misalkan masalah LP dinyatakan sebagai LP-1} yang mempunyai nilai optimal dari fungsi

tujuan Z₁.

PL-1

Maksimasi Z = cx

dengan pembatas

Ax = b

x  0

Algoritma BB untuk ILP (3)

 Asumsikan bahwa solusi optimal dari LP-1 mengandung beberapa variabel bilangan bulat yang mempunyai nilai pecahan.

 Oleh karena itu, solusi optimal bilangan bulat untuk ILP belum diperoleh dan Z₁

menjadi batas atas (upper bound) dari nilai maksimum Z untuk ILP.

 Langkah berikutnya adalah mempartisi daerah layak dari LP-1 dengan

82

Algoritma BB untuk ILP (4)

 Misalkan variabel x_j dipilih untuk

dicabangkan dengan nilai pecahan _j dalam

LP-1.

 Misalkan dibuat dua masalah pemrograman linier baru, LP-2 dan LP-3 dengan

Algoritma BB untuk ILP (5)

Maksimasi Z = cx

dengan pembatas

Ax = b

x_j  []

x  0

Maksimasi Z = cx

dengan pembatas

Ax = b

x_j  []+1

x  0

84

Algoritma BB untuk ILP (6)

LP-1

LP-2 _LP-2

Solusi pecahan

Z₁

Solusi pecahan

Z₂

] [ _j

j

x _

_

_{xj [j ]1}

Solusi pecahan

Algoritma BB untuk ILP (7)

Memecahkan (bounding) LP-2 dan LP-3

Asumsikan solusi LP-2 dan LP-3 masih pecahan

Langkah berikutnya adalah memilih node

86

Algoritma BB untuk ILP (8)

 Setelah masalah LP dipilih untuk

dicabangkan lebih lanjut, langkahnya selanjutnya adalah

 memilih variabel bilangan bulat dengan nilai pecahan yang akan dicabangkan untuk membentuk dua masalah LP baru (proses branching)

 memecahkan masalah LP yang baru (proses bounding)

 Jika solusi bilangan bulat diperoleh dari

suatu masalah LP maka nilai Z-nya menjadi batas bawah (lower bound) dari nilai

Algoritma BB untuk ILP (9)

Proses branching dan bounding

berlanjut hingga semua node dalam

kondisi fathomed.

Fathoming suatu node (masalah LP):

 Solusi optimal LP merupakan bilangan bulat

 Masalah LP adalah tak layak

 Nilai optimal Z dari masalah LP tidak lebih baik

88

Algoritma BB untuk ILP (10)

LP-1

LP-2 LP-3

Solusi pecahan

Z₀ = Z₁

Solusi pecahan

Z₂

] [ _j

j

x _{ } x_{j }[_j]_1

Solusi pecahan

Z₅

LP-3 LP-4

Tidak layak Solusi bulat

Z₄

] [ _i

i

Algoritma BB untuk ILP (11)

LP-1

LP-2

LP-3 LP-4

LP-5

LP-6 LP-7

Solusi pecahan

Z₀ = Z₁

Solusi pecahan

Z₂

Tidak layak Solusi bulat

Z₄

Solusi pecahan

Z₆ < Z₄

] [ _j

j

x _{ } x_{j }[_j]_1

] [ _i

i

x _{ } x_{i }[_i]_1 _{xk [k]} x_{k }[_k ]_1 Solusi pecahan

Z₅

Solusi pecahan

90

Algoritma BB untuk ILP (12)

Esensi dari algoritma BB

Ilustrasi Penerapan Algoritma BB (1)

Maximasi Z = 2x₁ + 3x₂

dengan pembatas-pembatas:

5x₁ + 7x₂  35

4x₁ + 9x₂  36

92

LP-1

178

176 2

17 12 1

14

2 ,

3



 

Z

LP-1

LP-2 LP-3

94

LP-1

LP-2 LP-3

178

LP-1

LP-2 LP-3

178

96

LP-1

LP-2 LP-3

178

LP-1

LP-2 LP-3

178

LP-4 LP-5 4

Fathomed karena perbedaan nilai Z dengan lower bound < 1 dan semua koefisien fungsi tujuan adalah bulat

Solusi bilangan bulat optimal

x₁ = 4, x₂ = 2

98

LP-1

178

176 2

17 12 1

14

2 ,

3



 

Z

x x

LP-1

LP-2 LP-3

100

LP-1

LP-2 LP-3

178

Tidak layak

LP-1

LP-2 LP-3

178

Tidak layak

102

LP-1

LP-2 LP-3

178

Tidak layak

3

LP-6 LP-7

LP-1

LP-2 LP-3

178

Tidak layak

3

LP-6 LP-7

104

LP-1

LP-2 LP-3

178

Tidak layak

3

LP-6 LP-7

LP-1

LP-2 LP-3

178

Tidak layak

3

LP-6 LP-7

13

106

LP-1

LP-2 LP-3

178

Tidak layak

3

LP-6 LP-7

13

LP-1

LP-2 LP-3

178

Tidak layak

3

LP-6 LP-7

13

LP-8 LP-9 4

108

Aturan Pencabangan (1)

Aturan-aturan pencabangan variabel

adalah sebagai berikut:

 Pilih variabel bilangan bulat yang mempunyai

nilai pecahan terbesar dalam solusi LP.

 Pilih variabel bilangan bulat yang mempunyai

prioritas paling tinggi.

 Menunjukkan keputusan yang terpenting dalam

model

 Mempunyai koefisien profit/biaya paling besar  Mempunyai nilai yang kritis yang didasarkan

pengalaman pengguna

 Aturan pemilihan bebas, misal, pilih variabel

Aturan Pencabangan (2)

Aturan penentuan masalah LP yang

hendak dicabangkan:

 Nilai optimal dari fungsi tujuan

 LIFO (Last-In First-Out), yaitu masalah LP

110

Algoritma BB untuk BILP

Maximasi Z = 9x₁ + 5x₂ + 6x₃ + 4x₄

dengan pembatas-pembatas:

6x₁ + 3x₂ + 5x3 + 2x4  10 x₃ + x₄  1

-x1 + x3 +  0 -x2 + x4  0

LP-1

) ; , , ,

112

LP-1

LP-2 LP-3

) ; , , ,

(x₁ x₂ x₃ x₄ Z



65 ,1,0,1;16 12



0

1 

x

1

1 

x



0,1,0,1;9





₅1



54 5

4 _{,0, ;16}

LP-1

LP-2 LP-3

) ; , , ,

(x₁ x₂ x₃ x₄ Z



65 ,1,0,1;16 12



0

1 

x

1

1 

x



0,1,0,1;9





₅1



54 5

4 _{,0, ;16}

114

LP-1

LP-2 LP-3

) ; , , ,

(x₁ x₂ x₃ x₄ Z



65 ,1,0,1;16 12



0

1 

x

1

1 

x



0,1,0,1;9





₅1



54 5

4 _{,0, ;16}

, 1

LP-4 _LP-5 0

2 

x x_{2 }1



1,0, 54 ,0;13 54



LP-1

LP-2 LP-3

) ; , , ,

(x₁ x₂ x₃ x₄ Z



65 ,1,0,1;16 12



0

1 

x

1

1 

x



0,1,0,1;9





₅1



54 5

4 _{,0, ;16}

, 1

LP-4 _LP-5 0

2 

x x_{2 }1



1,0, 54 ,0;13 54





1,1,0, ₂1 ;16



LP-6 _LP-7 0

3 

x x₃ 1



1,1,0, 1₂ ;16



116

LP-1

LP-2 LP-3

)

LP-4 _LP-5 0

2 

x x_{2 }1



1,0, 54 ,0;13 54





1,1,0, ₂1 ;16



LP-6 _LP-7 0

3 

x x₃ 1



1,1,0, 1₂ ;16



Tidak layak

LP-8 _LP-9



1,1,0,0;14



0

4 

x x₄ 1

117

LP-1

LP-2 LP-3

)

LP-4 _LP-5 0

2 

x x_{2 }1



1,0, 54 ,0;13 54





1,1,0, ₂1 ;16



LP-6 _LP-7 0

3 

x x₃ 1



1,1,0, 1₂ ;16



Tidak layak

LP-8 _LP-9



1,1,0,0;14



0

4 

x x₄ 1

118

LP-1

LP-2 LP-3

)

LP-4 _LP-5 0

2 

x x_{2 }1



1,0, 54 ,0;13 54





1,1,0, ₂1 ;16



LP-6 _LP-7 0

3 

x x₃ 1



1,1,0, 1₂ ;16



Tidak layak

LP-8 _LP-9



1,1,0,0;14



0

4 

x x₄ 1

LOGO

Thank you!

ADD YOUR COMPANY SLOGAN