commit to user
MODEL EPIDEMI CONTINUOUS TIME MARKOV CHAIN
(CTMC) SUSCEPTIBLE INFECTED RECOVERED (SIR)
oleh
DETA NURVITASARI M0108036
SKRIPSI
ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SEBELAS MARET
SURAKARTA
commit to user
commit to user
ABSTRAK
Deta Nurvitasari, 2012. MODEL EPIDEMICONTINUOUS TIME MARKOV
CHAIN (CTMC) SUSCEPTIBLE INFECTED RECOVERED (SIR).
Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sebelas Maret.
Model epidemiCTMC SIRmerupakan salah satu model yang menggambar-kan penyebaran penyakit dengan karakteristik, setiap individu sembuh memiliki kekebalan tubuh. Model tersebut menggambarkan transisi individu dari kelom-pok susceptible keinfected dan dari kelompokinfected kerecovered dalam waktu kontinu. Pada penyebaran penyakit, parameter yang sangat berperan adalah β
dan γ yang nilainya tidak diketahui secara pasti tetapi dapat diestimasi meng-gunakan metode maksimum likelihood.
Tujuan dari penelitian ini adalah menurunkan ulang model CTMC SIR
dengan terlebih dahulu menentukan asumsi, probabilitas transisi, dan matriks probabilitas transisi. Selanjutnya, mengestimasi parameterβdanγdengan meng-gunakan metode maksimumlikelihood dan menetukan probabilitas berakhir epi-demi. Berdasarkan hasil estimasi, diperoleh suatu model yang dapat diterap-kan pada penyakit smallpox di Nigeria. Model yang diperoleh dapat disimulasi-kan dengan pengambilan nilai awal jumlah individu terinfeksi I(0) yang ber-beda. Sehingga, berdasarkan hasil simulasi diperoleh bahwa pemberian nilaiI(0) yang berbeda dapat berpengaruh terhadap periode infeksi dan jumlah maksimum individu terinfeksi.
commit to user
ABSTRACT
Deta Nurvitasari, 2012. MODEL OF CONTINUOUS TIME MARKOV CHAIN (CTMC) SUSCEPTIBLE INFECTED RECOVERED (SIR) EPIDEMIC. Faculty of Mathematics and Natural Sciences, Sebelas Maret University.
Model of CTMC SIR epidemic is one of model that describe the spread of the disease with the charactheristics that individuals who have recovered immune. In the model of CTMC SIR, there are a transition from susceptible to infected and infected to recovered in a continuous time interval. There are parameters that influence the spread of the disease, i.e infection rate and rate of recovery. The value of the parameters are not known exactly, but it can be estimated using the method of maximum likelihood estimation.
The aims of the research are to reformed of CTMC SIR model by deter-mined the assumptions, the transition probability, and the transition matrix of CTMC SIR model. Furthemore, the parameters in the model i.eβ and γ will be estimated using maximum likelihood estimation and determine probability of the end of epidemic. Based on the estimation results, to illustrate an application of the model is taken to refer the case smallpox in Nigeria. The model can be simu-lated by taking some of the number of individuals infected at the time to zero,
I(0). Based on the graph simulation that the initial valuesI(0) can influence the infection period and the maximum number of individuals infected.
Key words: CTMC, likelihood, SIR
commit to user
MOTO
Karena sesungguhnya sesudah kesulitan itu ada kemudahan.
Sesungguhnya sesudah kesulitan itu ada kemudahan.
(Q.S. Al - Insyirah : 5-6)
commit to user
PERSEMBAHAN
Karya ini kupersembahkan untuk
Ayah, Ibu, dan Prima Bayu Sulistyo.
commit to user
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Allah SWT, yang telah melimpahk-an rahmat dmelimpahk-an karunia-Nya, sehingga penulis dapat menyelesaikmelimpahk-an skripsi ini. Penyusunan skripsi ini tidak lepas dari bantuan beberapa pihak, oleh karena itu penulis ingin mengucapkan terima kasih kepada
1. Bapak Dr. Sutanto, DEA. selaku Dosen Pembimbing I dan Ibu Sri Kuntari, M.Si. selaku Dosen Pembimbing II yang telah memberikan bimbingan dan dukungan dalam penulisan skripsi ini,
2. Ibu Dra. Respatiwulan, M.Si. yang telah memberikan saran dan masukan dalam proses skripsi ini,
3. Ibu Dra. Purnami Widyaningsih, M.App.Sc. yang telah memberikan ma-sukan dalam proses skripsi ini,
4. semua pihak yang turut membantu dalam penulisan skripsi ini.
commit to user
Daftar Isi
ABSTRAK . . . iii
ABSTRACT . . . iv
MOTO . . . v
PERSEMBAHAN . . . vi
KATA PENGANTAR . . . vii
DAFTAR ISI . . . . ix
DAFTAR GAMBAR . . . x
I PENDAHULUAN 1 1.1 Latar Belakang Masalah . . . 1
1.2 Perumusan Masalah . . . 3
1.3 Tujuan . . . 3
1.4 Manfaat . . . 3
II LANDASAN TEORI 4 2.1 Tinjauan Pustaka . . . 4
2.1.1 Model Susceptible Infected Recovered (SIR) . . . 4
2.1.2 Model SIR Deterministik . . . 5
2.1.3 Proses Stokastik . . . 6
2.1.4 Proses Markov . . . 7
2.1.5 Metode Estimasi MaksimumLikelihood . . . 7
2.1.6 Embedded Continuous Time Markov Chain . . . 8
2.2 Kerangka Pemikiran . . . 9
III METODE PENELITIAN 10
commit to user
IV PEMBAHASAN 11
4.1 Model CTMC SIR . . . 11
4.2 Estimasi Parameter . . . 15
4.3 Probabilitas Berakhir Epidemi . . . 18
4.4 Penerapan Kasus . . . 19
V PENUTUP 22 5.1 Kesimpulan . . . 22
5.2 Saran . . . 23
commit to user
Daftar Gambar
2.1 Skema Model SIR . . . 5 4.1 Pola Penyebaran Jumlah Individu Terinfeksi untuk I(0) =
1,-I(0) = 2, dan I(0) = 5 . . . 20 4.2 Pola Penyebaran Jumlah Individu Terinfeksi untuk I(0) =
1,-I(0) = 2, dan I(0) = 5 berdasarkan Probabilitas Berakhir Epidemi 21
commit to user
Bab I
PENDAHULUAN
1.1
Latar Belakang Masalah
Kesehatan merupakan faktor terpenting dalam kehidupan manusia. Per-ubahan cuaca, dan pola hidup serta kondisi lingkungan yang kurang sehat dalam suatu populasi merupakan beberapa faktor yang dapat menyebabkan timbulnya penyakit, baik secara langsung maupun tidak langsung. Penyakit menular yang disebabkan oleh jamur, bakteri maupun virus sudah menjadi masalah umum di berbagai belahan dunia.
Penularan suatu penyakit dari satu individu ke individu lain dapat melalui kontak langsung, saluran napas maupun saluran cerna. Epidemi adalah suatu penyakit menular yang berjangkit dalam masyarakat yang jumlah penderitanya meningkat pada waktu dan daerah tertentu. Di Indonesia, epidemi diartikan sebagai wabah, yaitu penyakit menular yang dengan cepat berjangkit di daerah yang luas dan menimbulkan banyak korban. Epidemi tidak hanya menimbul-kan tingginya angka kematian tetapi juga dapat mengakibatmenimbul-kan kerugian finan-sial yang besar. Sehingga, perlu dilakukan pengendalian terhadap penyebaran penyakit. Salah satu langkah awal dalam usaha pengendalian tersebut adalah mempelajari pola penyebaran penyakit.
Model matematika merupakan salah satu alat yang dapat digunakan dalam menyelesaikan permasalahan yang berkaitan dengan kehidupan manusia. Salah satu penerapannya, yaitu analisis pola penyebaran suatu penyakit. Untuk menge-tahui proses penyebaran penyakit, dikenal beberapa model penyebaran penyakit (epidemi), baik ditinjau secara deterministik maupun probabilistik.
commit to user
satu model epidemi adalah model SIR. Menurut Brauer et al. [4], model SIR
merupakan suatu model matematika yang menggambarkan penyebaran epidemi, dengan setiap individu yang telah sembuh dari infeksi mempunyai sistem ke-kebalan tubuh. Pada model SIR, populasi terbagi dalam tiga kelompok, yaitu
susceptible (S), infected (I),dan recovered (R). Kelompok S terdiri dari individu sehat yang belum terinfeksi penyakit tetapi rentan terhadap infeksi, kelompokI
terdiri dari individu yang terinfeksi penyakit, dan kelompok R terdiri dari indi-vidu yang mempunyai sistem kekebalan tubuh karena telah sembuh dari infeksi penyakit. Dalam kondisi awal, total jumlah popolasi merupakan penjumlahan da-ri nilai awal dada-ri jumlah individu rentan penyakit, jumlah individu teda-rinfeksi, dan jumlah individu sembuh sehingga dapat dituliskan sebagaiN =S(0)+I(0)+R(0). ModelSIR dapat ditinjau secara deterministik maupun probabilistik. Pola penyebaran epidemi yang ditinjau secara probabilistik terbagi menjadi tiga mo-del, yaituDTMC (discrete time markov chain),CTMC (continuous time markov chain), dan SDE (stochastic differential equation).
ModelDTMC merupakan suatu model penyebaran penyakit dalam selang waktu diskrit, t= 0,1,2, ...T. Model tersebut menggambarkan perpindahan indi-vidu dari kelompokSkeI dan dari kelompokI keRyang diambil secara random dalam suatu populasi.
Model CTMC merupakan suatu model penyebaran penyakit dalam selang waktu kontinu,t = [0, T). Model tersebut menggambarkan perpindahan individu dari kelompok S ke I dan dari kelompok I ke R yang diambil secara random dalam suatu populasi.
Model SDE merupakan suatu model penyebaran penyakit dalam selang waktu kontinu, t = [0, T). Model tersebut menggambarkan perubahan jumlah individu pada kelompok S, I, dan R yang diambil secara random dalam suatu populasi.
Menurut Parzen [11], perubahan jumlah individu terinfeksi berkaitan erat dengan probabilitas suatu kejadian. Dengan demikian, penyebaran epidemi suatu penyakit merupakan suatu kejadian random yang bergantung pada waktu dan
commit to user
berkaitan dengan probabilitas, atau dapat disebut sebagai suatu proses stokastik. Suatu epidemi diharapkan berhenti sebelum menginfeksi seluruh individu dalam suatu populasi karena berakibat dapat menimbulkan kerugian yang cukup besar. Suatu epidemi dikatakan berhenti apabila tidak ada lagi individu yang terinfeksi. Pada penelitian ini, penulis ingin mengetahui pola penyebaran penyakit tertentu yang ditinjau secara probabilistik. Model yang digunakan adalah model
continuous time markov chain (CTMC) susceptible infecected recovered (SIR). Model tersebut mengkaji mengenai perubahan variabel random diskrit, yaitu jumlah individu yang rentan terhadap infeksi (S) dan jumlah individu terinfeksi
(I) dalam selang waktu kontinu.
1.2
Perumusan Masalah
Berdasarkan latar belakang masalah, diperoleh perumusan masalah 1. bagaimana menurunkan ulang model epidemi CTMC SIR ?
2. bagaimana menerapkan dan mensimulasikan model CTMC SIRpada suatu kasus epidemi dengan pengambilan I(0) yang berbeda?
1.3
Tujuan
Tujuan penelitian ini adalah
1. dapat menurunkan ulang model epidemi CTMC SIR,
2. dapat menerapkan dan mensimulasikan model pada suatu kasus epidemi dengan pengambilan I(0) yang berbeda.
1.4
Manfaat
commit to user
Bab II
LANDASAN TEORI
2.1
Tinjauan Pustaka
Salah satu penelitian yang telah membahas mengenai model epidemi yang ditinjau secara probabilistik, yaitu The SIS and SIR stochastic epidemic models revisited oleh Altalejo [1]. Dalam penelitian ini, akan dibahas mengenai pe-nurunan ulang model epidemiSIRditinjau secara probabilistik dengan mengguna-kan CTMC (continuous time markov chain) yang merujuk dari Brauer et al.
[4]. Selanjutnya, model tersebut diterapkan dalam suatu kasus epidemi dan disimulasikan pada beberapa nilaiI(0) yang berbeda. Untuk menurunkan ulang model CTMC SIR, diuraikan terlebih dahulu beberapa hal yang mendasarinya.
2.1.1
Model
Susceptible Infected Recovered (SIR)
ModelSIRmerupakan suatu model yang menggambarkan pola penyebaran suatu penyakit dari satu individu ke indivu yang lain. Menurut Braueret al. [4], pada model SIR individu yang sembuh dari infeksi memiliki kekebalan tubuh. Total populasi dari model epidemi SIR terbagi menjadi tiga kelompok, yaitu kelompoksusceptible (S),infected (I), danrecovered (R). KelompokSmerupakan kelompok individu sehat dan belum terinfeksi penyakit tetapi rentan terinfeksi, kelompokI merupakan kelompok individu terinfeksi, dan kelompokRmerupakan kelompok individu yang telah sembuh dari infeksi.
Pada modelSIR, penyebaran penyakit terjadi apabila terdapat perpindahan individu dari kelompokSkeIdengan laju penularan sebesarβdan dari kelompok
I keR dengan laju kesembuhan sebesarγ, yang ditunjukkan oleh Gambar (2.1). Setiap individu susceptible akan menjadi terinfeksi apabila berinteraksi dengan individu infected dengan laju penularan sebesar β, sedangkan nilai parameter γ
commit to user
Gambar 2.1. Skema Model SIR
menunjukkan besarnya laju kesembuhan pada kelompok infected.
2.1.2
Model
SIR
Deterministik
ModelSIRdeterministik merupakan salah satu model epidemi yang diguna-kan untuk mengetahui pola penyebaran suatu penyakit. Asumsi dari model SIR
deterministik sebagai berikut
1. populasi tertutup (konstan) dan dalam jumlah yang besar,
2. populasi bercampur homogen sehingga setiap individu mempunyai karak-teristik yang sama,
3. tidak memperhatikan faktor kelahiran dan kematian, 4. hanya satu penyakit yang menyebar dalam populasi.
Menurut Hethcote [7], jumlah individu pada kelompok S, I, dan R pada waktu t masing - masing dinyatakan sebagai S(t), I(t), dan R(t). Karena di-asumsikan bahwa populasi konstan sehingga S(t) +I(t) +R(t) = N, dengan N
merupakan total populasi. Besarnya laju penularan dan laju kesembuhan masing-masing dinyatakan dengan β, dan γ. Apabila setiap individu infected, dengan kemungkinan I
N berinteraksi dengan individu susceptible dengan laju penularan
sebesar β, akan berakibat jumlah individu susceptible berkurang sebesar βIS N.
Pengurangan sebesar βIS
N pada kelompoksusceptible mengakibatkan
commit to user
Brauer et al. [4], model SIR deterministik dinyatakan sebagai
dS
Pada persamaan (2.1), dS dt ,
dI dt, dan
dR
dt masing - masing menunjukkan perubahan
jumlah individu pada kelompok susceptible,infected, dan recovered.
2.1.3
Proses Stokastik
Menurut Taylor dan Karlin [12], proses stokastik merupakan sekumpulan variabel random {Xl(y)/l ϵ L, y ϵ Y} dengan L himpunan indeks dan Y ruang sampel. Himpunan indeks L sering dinyatakan sebagai himpunan waktu. Him-punan L dikatakan kontinu apabila L berada pada interval [0, L]. Sedangkan, himpunan L dikatakan diskrit apabilaL berada pada 0,1,2, ..., L.
Menurut Nguyen [9], proses stokastik merupakan kumpulan variabel ran-dom yang dinotasikan dengan Xl atau X(l), dengan l merupakan indeks yang menjelaskan waktu. Proses stokastik terbagi dalam empat kategori yang berbeda tergantung l atau Xl, yaitu
1. discrete processes : l dan Xl diskrit, sebagai contoh discrete time markov chain (DTMC),
2. continuous time discrete state processes : (Xl) diskrit tetapi l kontinu pada interval bilangan real R, sebagai contoh
(a) poisson process
(b) continuous time markov chain (CTMC)
(c) queuing processes
3. continuous processes : l dan Xl kontinu,
commit to user
2.1.4
Proses
Markov
Menurut Taylor dan Karlin [12] serta Parzen [11], proses stokastik denganl
diskrit{X(l), l= 0,1,2, ...}maupun proses stokastik denganl kontinu{X(l), l ≥
0} dapat dikatakan sebagai proses Markov, apabila diberikan suatu nilai Xl, maka nilai X(m) dengan m > l tidak bergantung pada nilai X(u) dengan u < l. Sehingga, probabilitas bersyarat dari X(ln) dengan syarat X(l1), . . . , X(ln−1)
hanya bergantung pada nilaiX(ln−1). Jika diberikan suatu nilai tertentux1, . . . , xn,
maka probabilitas bersyarat tersebut adalah
P[X(ln)≤xn|X(l1) =x1, . . . , X(ln−1) = xn−1] =P[X(ln)≤xn|X(ln−1) = xn−1]
Suatu nilai tertentu x dikatakan sebagai suatu state dari proses stokastik
{Xl,l ϵ L}jika terdapatl dalamL. Sehingga, probabilitasP[x−h < Xt< x+h] bernilai positif untuk setiap h > 0. Selanjutnya, himpunan nilai yang mungkin dalam suatu proses stokastik dinamakan ruang state. Suatu ruang state disebut diskrit jika terdiri dari state yang memuat bilangan berhingga (finite) ataupun
state yang memuat bilangan countable yang tak berhingga (infinite). Suatu proses Markov yang mempunyai ruang state diskrit dinamakan rantai Markov (Markov chain).
2.1.5
Metode Estimasi Maksimum
Likelihood
Menurut Brauer et al. [4], parameter - parameter pada model CTMC SIR
dapat diestimasi dengan menggunakan metode maksimum likelihood. Bain dan Engelhardt [3], memaparkan definisi dari fungsi likelihood sebagai berikut.
Definisi 2.1.1. StatistikW =w(X1, X2, . . . , Xn) digunakan untuk mengevaluasi
nilai dari τ(θ) disebut sebagai estimator dari τ(θ) yang dinotasikan dengan τ(θb) dan suatu observasi dari statistikw=w(x1, x2, . . . , xn) merupakan nilai estimasi
dari τ(θ).
commit to user
x1, x2, . . . , xn, yaitu f(x1, x2, . . . , xn). Untuk suatu nilai tertentu x1, x2, . . . , xn,
fungsi likelihood adalah fungsi dari θ yang dinotasikan dengan L(θ). Apabila dimisalkanX1, X2, . . . , Xn merupakan suatu sampel random dari f(xn, θ), maka
L(θ) = f(x1;θ)f(x2;θ). . . f(xn;θ).
Definisi 2.1.3. Misalkan L(θ) = f(x1, . . . , xn;θ),dengan θ ϵΩ merupakan fungsi
kepadatan probabilitas bersama dariX1, . . . , Xn. Jika diberikan suatu himpunan
observasi (x1, . . . , xn), nilai θbpada Ω dengan L(θ) maksimum disebut estimasi
maksimumlikelihood dariθ. Sehinggaθbmerupakan estimator dari θ, dan berlaku
f(x1, . . . , xn;θb) = max
θϵΩ f(x1, . . . , xn;θ).
Pada Definisi 2.1.3,L(θ) mencapai maksimum apabila
d
dθL(θ) = 0. (2.2)
Selanjutnya, jika nilaiθ padaL(θ) maksimum, maka nilailoglikelihood dari L(θ) juga maksimum. Sehingga diperoleh
d
dθ lnL(θ) = 0.
2.1.6
Embedded Continuous Time Markov Chain
Menurut Nielsen [10], apabila proses transisi terjadi dari state i menuju
state j dengan j ̸=i, maka probabilitasnya sebesar
Vij(h) =P r[X(h) = j\X(h)̸=i, X(0) =i] = Pij(h)
1−Pii(h)
(2.3)
denganVij merupakan probabilitas transisi pada embedded markov chain.
Menurut Brauer et al. [4]embedded markov chain dapat digunakan dalam proses berakhirnya epidemi. Dalam hal ini, diperlukan perhitungan probabilitas transisi dari state (s, i), dengan s = 0,1, . . . , N dan i = 0,1, . . . , N −s. Pada proses berakhirnya suatu epidemi,embedded markov chain hanya mementingkan probabilitas transisi.
commit to user
2.2
Kerangka Pemikiran
Berdasarkan tinjauan pustaka, dapat disusun suatu kerangka pemikiran un-tuk menyelesaikan permasalahan dalam penelitian ini. Pada penyebaran epidemi dalam suatu populasi, setiap individu mempunyai kekebalan tubuh sehingga indi-vidu yang telah sembuh tidak dapat terinfeksi kembali dan digambarkan melalui model SIR.
Apabila ditinjau secara probabilistik, penyebaran epidemi diartikan sebagai suatu proses stokastik yang dapat digambarkan dalam suatu model, yaitu model epidemi CTMC SIR. Pada model tersebut variabel random yang dikaji adalah variabel random jumlah individu yang rentan terhadap infeksi penyakitS(t) dan jumlah individu terinfeksi I(t) dalam selang waktu kontinu t= [0, T].
Penurunan ulang model CTMC SIR dilakukan dengan menentukan besar-nya probabilitas transisi terlebih dahulu. Terdapat parameter laju penularan dan laju kesembuhan yang berpengaruh secara signifikan terhadap penyebaran penyakit. Nilai dari kedua parameter tersebut tidak diketahui secara pasti tetapi dapat diestimasi. Pada penelitian ini, metode estimasi parameter yang digunakan adalah metode estimasi maksimum likelihood.
Suatu epidemi dikatakan berakhir jika tidak ada individu yang terinfeksi. Dengan kata lain, jumlah individu terinfeksi pada waktu t adalah nol. Selanjut-nya, melalui hasil simulasi dapat digambarkan pola penyebaran suatu penyakit.
commit to user
Bab III
METODE PENELITIAN
Metode yang digunakan dalam penelitian ini adalah studi literatur, yaitu dengan cara mempelajari materi dari berbagai referensi antara lain buku - buku, artikel ilmiah, dan jurnal - jurnal yang sesuai dengan tujuan penelitian. Adapun langkah - langkah yang ditempuh dalam mencapai tujuan penelitian adalah
1. menurunkan ulang model CTMC SIR yang terdiri dari (a) menentukan asumsi model CTMC SIR,
(b) menentukan probabilitas transisi individususceptible (S)dan individu
infected (I),
(c) menentukan matriks probabilitas transisi pada individususceptible (S)
dan individuinfected (I).
2. mengestimasi nilai parameter yang berpengaruh terhadap penyebaran suatu penyakit dengan menggunakan metode maksimum likelihood,
3. menentukan probabilitas berakhir epidemi denganembedded markov chain, 4. menerapkan model pada suatu kasus epidemi dengan simulasi untuk nilai
I(0) yang berbeda,
5. memberikan interpretasi terhadap hasil simulasi.
commit to user
Bab IV
PEMBAHASAN
4.1
Model
CTMC SIR
Pada bagian ini penurunan ulang dari model Continuous Time Markov Chain (CTMC) SIR mengacu pada Brauer et al. [4]. Menurut Brauer et al. [4], model CTMC SIR merupakan suatu fungsi probabilitas jumlah individu yang rentan terhadap infeksi dan jumlah individu terinfeksi pada waktu ke t. Hal ini dikarenakan terdapat dua variabel random independen, {S(t), I(t)} dan dapat dinyatakan sebagai R(t) =N −S(t)−I(t). Sehingga, proses epidemiSIR dapat dipandang bivariat. Misalkan S(t) dan I(t) masing - masing merupakan jumlah individu yang rentan terhadap infeksi dan jumlah individu terinfeksi pada waktu
t, maka fungsi probabilitas bersama diberikan
p(s,i) =P rob[S(t) =s, I(t) = i]
dengant= [0, T],s= 1,2, ..., N, dani= 1,2, ..., N. Selain itu,SdanI dipandang sebagai variabel random yang masing - masing dinyatakan dalam suatu sampel randoms dan i.
Perpindahan dari individu rentan ke individu terinfeksi disebut transisi. Dalam penelitian ini, dimungkinkan hanya ada satu individu yang bertransisi pada selang waktu yang sangat kecil. Sehingga, pada setiap waktu dalam interval
t= [0, T], terjadi perubahan jumlah individuS,I, danR yang dapat dinyatakan dalam suatu probabilitas.
commit to user
waktu tertentu adalah
p(s+k,i+j),(s,i)(∆t) = P rob{(∆S,∆I) = (k, j)|S(t), I(t)) = (s, i)} (4.1)
Menurut Trapman [13], asumsi yang digunakan dalam penurunan model epidemi
CTMC SIR adalah
1. penyakit menyebar pada suatu populasi yang tertutup sehingga tidak ada individu yang migrasi (masuk dan keluar) dari populasi tersebut,
2. pada kondisi awal terdapatN−mjumlahsusceptibledanmjumlahinfected, 3. populasi bercampur homogen,
4. model tidak memperhatikan faktor kelahiran dan kematian sehingga transisi pada kelompok S, I, dan R hanya melibatkan laju penularan dan laju kesembuhan,
5. setiap individu merupakan kelompok recovered jika periode infeksi pada kelompok infected berakhir,
6. hanya terdapat satu individu yang bertransisi dari s kes+k dan dari i ke
i+j pada selang waktu yang sangat kecil,
7. hanya terdapat satu penyakit yang menyebar dalam populasi tersebut. Berdasarkan asumsi ke enam, transisi terjadi pada selang waktu yang sangat kecil sehingga dimungkinkan hanya terdapat satu individu yang bertransisi, yaitu dari state (s, i) ke state (s − 1, i+ 1), dari state (s, i) ke (s, i− 1), dan dari
state (s, i) ke (s, i). Pada saat individu bertransisi dari (s, i) ke (s−1, i+ 1) berarti jumlah individu sehat (S) berkurang satu, sedangkan jumlah individu terinfeksi (I) bertambah satu. Dengan demikian, terjadi transisi satu individu dari kelompok S ke kelompok I yang berakibat terjadi infeksi baru (penularan penyakit dari individu I ke individu S) melalui suatu interaksi.
Jikaβ menyatakan besarnya laju penularan, I(t) menyatakan jumlah indi-vidu terinfeksi pada waktu t, S(t) menyatakan jumlah individu rentan terhadap
commit to user
infeksi pada waktu t, dan N menyatakan total populasi. Menurut Hethcote [6]
βI(t)
N merupakan rata-rata jumlah penularan setiap individu susceptible dengan
individu infected tiap satuan waktu. Sehingga, menurut Brauer et al. [4], besar-nya probabilitas transisi daristate (s, i) kestate (s−1, i+ 1) dalam selang waktu ∆t adalah
βis
N∆t+o(∆t) (4.2)
dengan o(∆t) menunjukkan suatu nilai probabilitas yang sangat kecil dan tidak dapat dinyatakan dengan pasti.
Pada saat jumlah individu bertransisi dari (s, i) ke (s, i−1), berarti jumlah individu terinfeksi berkurang satu. Hal ini disebabkan adanya perpindahan satu individu dari kelompok I ke kelompok R dengan laju kesembuhan sebesar γ. Sehingga, besarnya probabilitas transisi dari state (s, i) ke state (s, i−1) dalam selang waktu ∆t adalah
γi∆t+o(∆t). (4.3) Selain itu, saat jumlah individu bertransisi dari state (s, i) ke state (s, i), berarti tidak ada penambahan maupun pengurangan jumlah individu sehat dan individu terinfeksi. Dengan kata lain, tidak ada perpindahan satu individu dari kelompok S dan kelompok I. Sehingga, besarnya probabilitas transisi dari state
(s, i) ke (s, i) adalah
1− (
βis N +γi
)
∆t+o(∆t). (4.4) Pada selang waktu yang sangat kecil, dimungkinkan hanya terdapat satu individu yang bertransisi. Dari suatustate kestate lainnya, kemungkinan jumlah individu yang bertransisi lebih dari atau sama dengan dua individu (>2) sangat-lah kecil. Oleh sebab itu, besarnya probabilitas transisi dengan jumsangat-lah individu yang bertransisi lebih dari sama dengan dua dalam selang waktu ∆t adalah
commit to user
Persamaan (4.2), (4.3), (4.4), dan (4.5) dapat dituliskan ulang dalam suatu sistem persamaan probabilitas transisi yang dinyatakan sebagai
p(s+k,i+j),(s,i)(∆t) =
Persamaan (4.6) dapat dinyatakan dalam suatu matriks probabilitas transisi yang memuat besarnya probabilitas perpindahan individu daristate (s, i) menuju
state (s+k, i+j). Matriks tersebut dimulai dari (k, j) = (0,0) dan berakhir pada (k, j) = (−N, N). Jika P(∆t) merupakan matriks probabilitas transisi pada selang waktu ∆t, berdasarkan persamaan (4.6) dapat dituliskan sebagai berikut
PHDtL=
Jika dimisalkan bahwa matriksP(∆t) dengan ukuran N2xN2 memuat
par-tisi yang menunjukkan transisi individu dari kelompok S, I, dan R dengan
commit to user
Sehingga, matriks P(∆t) dapat dituliskan sebagai
P(∆t) =
Parameter pada model CTMC SIR dapat diestimasi dengan mengguna-kan metode maksimum likelihood. Dalam suatu rantai markov, fungsi likelihood
merupakan hasil kali dari semua probabilitas yang mungkin. Pada modelCTMC SIR dalam penelitian ini, terdapat tiga transisi yang mungkin, yaitu dari state
(s, i) ke (s−1, i+ 1), state (s, i) ke (s, i−1), dan state (s, i) ke (s, i) sehingga fungsi likelihood diberikan dalam persamaan (4.7)
L=∏
Menurut Clancy dan O’Neill [5], fungsi likelihood pada model epidemi di-pengaruhi oleh fungsi kedatangan. Menurut Kypraios [8], suatu epidemi meru-pakan proses poisson dengan waktu antar kedatangan berdistribusi eksponensial sehingga dapat dinyatakan sebagai
commit to user
Dalam hal ini, fungsi log-likelihood dapat dinyatakan sebagai ln(L(β, γ)) =
Persamaan maksimum likelihood dapat diperoleh dengan memaksimumkan fungsi log-likelihood. Dalam hal ini, memaksimumkan fungsilog-likelihood terjadi ketika turunan parsial fungsi tersebut terhadap suatu parameter sama dengan nol. Parameter-parameter pada model CTMC SIR adalah β dan γ. Fungsi
loglikelihood untuk parameter β dikatakan maksimum apabila
∂ln(L(β, γ))
Dari persamaan (4.8) diperoleh 1
Fungsiloglikelihood untuk parameterγ dikatakan maksimum apabila
∂ln(L(β, γ)
∂γ ) = 0
sehingga diperoleh
commit to user Dari persamaan (4.10) diperoleh
γ = T −β
Dengan mensubstitusi persamaan (4.11) pada persamaan (4.9) akan di-peroleh estimasi dari β yang dinyatakan
2β
Sehingga diperoleh estimasi laju penularan (β) yang dinyatakan pada persamaan (4.12)
commit to user
persamaan (4.11) akan diperoleh estimasi untuk parameter γ yang dinyatakan
γ =
Sehingga diperoleh estimasi laju kesembuhan (γ) yang dinyatakan pada persa-maan (4.13)
b
γ = T
3∫0T I(t)dt. (4.13)
4.3
Probabilitas Berakhir Epidemi
Menurut Brauer et al. [4], pada model epidemi SIR stokastik terdapat suatu distribusi yang berkaitan dengan berakhirnya epidemi. Suatu epidemi di-katakan berakhir apabila tidak ada individu yang terinfeksi atau nilai I(t) = 0. Probabilitas berakhirnya epidemi merujuk pada persamaan (2.3). Dalam hal ini, probabilitas transisi yang berkaitan dengan berakhirnya suatu epidemi adalahβis
N
dan γi yang masing - masing menyatakan transisi dari (s, i) ke (s−1, i+ 1) dan (s, i) ke (s, i−1). Sehingga besarnya probabilitas berakhirnya epidemi dinyatakan sebagai
Persamaan (4.14) dan (4.15) masing- masing menunjukkan probabilitas ke-sembuhan dari individu infected dan probabilitas terinfeksi (penularan) pada in-dividu susceptible.
commit to user
4.4
Penerapan Kasus
Menurut Hethcote [7], smallpox merupakan salah satu contoh penyakit dengan tipe penyebarannya adalah SIR. Smallpox merupakan suatu penyakit yang ditularkan dari satu individu ke individu lain melalui perantara virus. Pada penerapan kasus dalam penelitian ini, data yang digunakan adalah datasmallpox
di Nigeria yang merujuk pada Andersson [2]. Pada kasus tersebut, diketahui total jumlah populasi sebesar N = 120 dan periode terinfeksi T = 83. Besarnya laju penularan dan laju kesembuhan diestimasi menggunakan metode maksimum like-lihood karena nilai dari kedua parameter tersebut tidak diketahui dengan pasti.
Hasil estimasi masing - masing parameter tersebut sebesar βb= 0,158 dan
b
γ = 0,129. Berdasarkan persamaan (4.6), model penyebaran smallpox dinyata-kan sebagai
Selanjutnya, hasil simulasi model menggunakan program yang merujuk pada Bra-uer et al. [4], dengan algoritma sebagai berikut
1. memasukkan nilai laju penularan, laju kesembuhan, jumlah total populasi, lama periode infeksi, dan jumlah awal individu terinfeksi,
2. memasukkan nilai awal dari jumlah individu terinfeksi dan variabel waktu, 3. membangkitkan data random berdistribusi uniform (0,1),
4. mencari besarnya probabilitas jumlah individu terinfeksi terhadap jumlah individu yang bertransisi,
commit to user
6. mendefinisikan proses iterasi, yaitu membandingkan besarnya probabilitas transisi dari S ke I dan dari I ke R yang berpengaruh terhadap jumlah individu terinfeksi. Sehingga, diperoleh grafik perubahan jumlah individu terinfeksi dalam selang waktu t.
Hasil simulasi model epidemi tersebut dapt ditunjukkan pada Gambar (4.1).
0
10
20
30
40
50
60
70
0
1
2
3
4
5
6
7
8
Hari
Jumlah Individu Terinfeksi
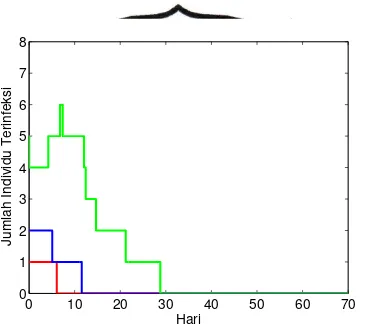
Gambar 4.1. Pola Penyebaran Jumlah Individu Terinfeksi untukI(0) = 1,I(0) = 2, dan I(0) = 5
Berdasarkan Gambar (4.1) terlihat bahwa terdapat tiga pola penyebar-an ypenyebar-ang ditunjukkpenyebar-an oleh garis berwarna merah, biru dpenyebar-an hijau. Garis merah menunjukkan pola penyebaran saat I(0) = 1, garis biru menunjukkan pola pe-nyebaran saat I(0) = 2, dan garis hijau menunjukkan pola penyebaran saat
I(0) = 5. Sehingga, diperoleh jumlah maksimum individu terinfeksi berturut -turut adalah satu, dua, dan enam. Selain itu, diperoleh lamanya periode infeksi
commit to user
berturut - turut adalah lima, sebelas, dan dua puluh delapan.
Selanjutnya, dengan menggunakan probabilitas berakhir epidemi pada per-samaan (4.15) diperoleh simulasi terhadap individu terinfeksi yang ditunjukkan dengan Gambar (4.2). Keterangan pada Gambar (4.2) merujuk pada Gambar
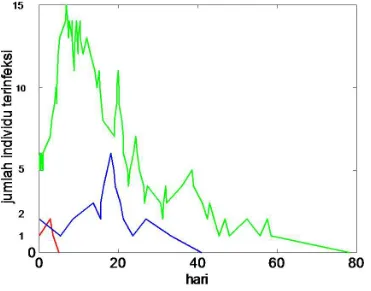
Gambar 4.2. Pola Penyebaran Jumlah Individu Terinfeksi untukI(0) = 1,I(0) = 2, dan I(0) = 5 berdasarkan Probabilitas Berakhir Epidemi
(4.1) dengan jumlah maksimum individu terinfeksi berturut - turut adalah dua, enam, dan lima belas. Selain itu, lama periode infeksi berturut - turut adalah lima, empat puluh, dan delapan puluh.
commit to user
Bab V
PENUTUP
5.1
Kesimpulan
Dari hasil pembahasan diperoleh kesimpulan sebagai berikut 1. Model CTMC SIR dinyatakan sebagai
p(s+k,i+j),(s,i)(∆t) =
2. Dengan metode estimasi maksimum likelihood diperoleh hasil estimasi ter-hadap parameter yang berpengaruh pada penyebaran penyakit, yaitu
(a) estimasi terhadap parameter laju penularan sebesar
b
(b) estimasi terhadap parameter laju kesembuhan sebesar
b
γ = T 3∫0T I(t)dt.
3. Berdasarkan grafik hasil simulasi pola penyebaran penyakit smallpox, di-peroleh bahwa pemberian nilai awal jumlah individu terinfeksi (I(0)) dapat mempengaruhi lamanya periode infeksi dan jumlah maksimum individu ter-infeksi.
commit to user
5.2
Saran
Pada penelitian ini hanya membahas mengenai model epidemiCTMC SIR
commit to user
Daftar Pustaka
[1] Altalejo, J.,The SIS and SIR Stochastic Epidemic Models Revisited, Faculty of Mathematics, University Complutense of Madrid, Spain, 2011.
[2] Andersson, H. and Tom Britton, Stochastic Epidemic Model and Their Sta-tistical Analysis, Group Financial Risk Control, Swedbank, Sweden, 2000. [3] Bain, L. J. and M. Engelhardt,Introduction to Probability and Mathematical
Statistics, 2 ed., Duxbury Press Belmont California, 1992.
[4] Brauer, F., P. Driessche, and J. Wu, Mathematical Epidemiology, Springer, Februari 2008.
[5] Clancy, D. and Philip D. O’Neill,Bayesian Estimation of The Basic Repro-duction Number in Stochastic Epidemic Models, Department of Mathema-tical Sciences, University of Liverpool, University of Nothingham, United Kingdom, 2008.
[6] Hetchote, H. W., The Mathematics of Infectious Disease, Journal of Siam Review 42 (2000), no. 4, 599–653.
[7] Hethcote, H. W., The Basic Epidemiology Models: Models, Expressions for
R0 Parameter Estimation, and Applications, Journal of Master Review 9
(2005), 1–61.
[8] Kypraios, T.,A Note Maximum Likelihood Estimation of The Initial Number of Susceptible in the General Stochastic Epidemic Model, Journal of Statistics and Probability Letters 19 (2009), no. 18, 1972–1976.
commit to user
[9] Nguyen, V. M.,Mathematical Modeling and Simulation, 2010.
[10] Nielsen, S. F., Continuous Time Homogeneous Markov Chains, University of Copenhagen, Department of Mathematical Sciences, 2009.
[11] Parzen, E.,Stochastic Processes, Holden-Day,Inc. United States of America, 1962.
[12] Taylor, H. M. and S. Karlin,An Introduction to Stochastic Modeling, received ed., Academic Press, United States of America, 1994.