REVITALISASI DAN SOSIALISASI DIRI UNTUK BERPERAN AKTIF DALAM PENINGKATAN KUALITAS PENELITIAN PENDIDIKAN MATEMATIKA DI INDONESIA

Seminar Nasional

Mahasiswa S3 Matematika

REVITALISASI D A N SOSIALISASI DIRI

U N T U K B E R P E R A N A K T I F D A L A M

PENINGKATAN KUALITAS PENELITIAN &

PENDIDIKAN MATEMATIKA DI INDONESIA

Editor :

Muslim Ansori

Ismail Djakaria

PROSIDING

SEMINAR NASIONAL

MAHASISWA S3 MATEMATIKA INDONESIA 2008

EDITOR:

Muslim Ansori

Ismail Djakaria

Dhoriva Urwatul Wutsqa

Agus Maman Abadi

M. Andy Rudhito

Umu Sa’adah

Karyati

Hasih Pratiwi

PENERBIT:

JURUSAN MATEMATIKA FMIPA UGM

ALAMAT:

Sekip Utara Unit III Yogyakarta

Puji syukur kami panjatkan kehadirat Allah SWT atas terselenggarakannya Seminar

Nasional Mahasiswa S3 Matematika Indonesia pada tanggal 31 Mei 2008 di Jurusan Matematika FMIPA UGM Yogyakarta. Kegiatan ini merupakan kegiatan ilmiah rutin yang

diadakan oleh Forum Komunikasi Mahasiswa S3 Matematika Indonesia sejak tahun 2005. Seminar Nasional ini diselenggarakan dengan tujuan (1) memberikan wawasan dan

berbagi informasi diantara mahasiswa matematika/statistika dan pendidikan matematika, atau peminat matematika tentang hasil penelitian yang telah atau sedang dilakukan; (2)

mendorong terciptanya kerjasama keilmuan antara mahasiswa S3 matematika/satistika dan pendidikan matematika, atau antara mahasiswa S3 matematika/statistika/pendidikan

matematika dengan para pakar matematika/statis-tika/pendidikan matematika lainnya di Indonesia; dan (3) membentuk korps keilmuan untuk pengembangan profesi ke depan dan menjalin silaturahmi antara sesama mahasiswa dan alumni S3

matematika/statistika/pendidikan matematika se-Indonesia.

Peserta yang berpartisipasi dalam kegiatan ini berjumlah 90 orang yang berasal dari

berbagai institusi/instansi, yaitu ITB, UNY, UPI, UT, UNMER Malang, UNMUL, UNNES, UM, IPB, UNIMED, USD, ITS, UNSOED, UNTAD, IAIN Antasari Banjarsari, UNISBA,

Universitas Widya Dharma Klaten, UNESA, SMA Sang Timur Yogyakarta, UBAYA, Universitas Veteran Bangun Nusantara Sukoharjo, UNIKA Parahyangan, UNTAD,

Universitas Mahasaraswati, UI, UII, UNPAD, STAIN Purwokerto, UNHALU, UNSRAT, Universitas PGRI Palembang, UNCEN, UNPAD, STKIP YASIKA Majalengka, UNEJ,

STKIP PGRI Pontianak, UIN Syarif Hidayatullah, UNPATI, STT Garut, UNILA, Universitas Negeri Gorontalo, SMKN 2 Ygyakarta, BATAN, UBINUS, Universitas Muhammadiyah Bengkulu, UNAND, SKIP Siliwangi Bandung, Sekolah Tinggi Sandi Negara, dan UGM. Di

antara peserta ini, yang membawakan makalah berjumlah 50 orang. Pembicara utama pada

fasilitas dan dukungan dananya. Ucapan terima kasih juga kami sampaikan kepada Forum Komunikasi Mahasiswa S3 Matematika Indonesia atas dukungan dan publikasinya. Terakhir,

terima kasih juga kami sampaikan kepada rekan-rekan Panitia dan staf Jurusan Matematika FMIPA UGM atas dukungan dan kerjasamanya sehingga Seminar Nasional ini dapat

terselenggara dengan lancar.

Yogyakarta, Mei 2008

Yang terhormat Dekan Fakultas MIPA,

Yang terhormat Direktur Ketenagaan Ditjen Dikti Depdiknas, Yang terhormat Staf Pengajar S3 Matematika FMIPA UGM, Yang terhormat Hadirin Peserta Seminar Nasional,

Assalamu ‘alaikum Warahmatullaahi Wabarakaatuh,

Selamat pagi dan salam sejahtera bagi kita semua.

Pertama-tama marilah kita memanjatkan puji dan syukur kehadirat Tuhan Yang Maha Kuasa karena atas perkenan-Nya kita dapat berkumpul pada acara seminar yang penting ini, yaitu

Seminar Nasional Mahasiswa S3 Matematika se-Indonesia. Kami menyambut baik acara

yang diprakarsai dan diselenggarakan oleh mahasiswa S3 Matematika karena dapat mendorong terciptanya kerjasama keilmuan antara mahasiswa S3 Matematika/Satistika dan Pendidikan Matematika, atau antara mahasiswa S3 Matematika/Statistika/Pendidikan Matematika dengan para pakar Matematika/Statistika/Pendidikan Matematika lainnya di Indonesia.

Pada kesempatan ini, kami mengucapkan selamat mengikuti rangkaian Seminar Nasional Mahasiswa S3 Matematika se-Indonesia yang sangat penting ini. Semoga upaya yang kita laksanakan ini dapat menghasilkan sumbangan yang berharga dan menjadi bekal bagi kita semua dalam mencapai masyarakat Indonesia yang andal, cerdas, mempunyai komitmen moral dan semangat pengabdian.

Lebih jauh lagi, kami mengharapkan Seminar Nasional ini dapat memberikan wawasan dan berbagi informasi diantara mahasiswa Matematika/Statistika dan Pendidikan Matematika, atau Peminat Matematika tentang hasil penelitian yang telah atau sedang dilakukan.

Demikian sambutan ini kami sampaikan, atas perhatian seluruh peserta Seminar Nasional, kami ucapkan terimakasih dan semoga Tuhan Yang Maha Kuasa memberkahi seluruh upaya bersama yang terus kita lakukan ini.

Wassalamu‘alaikum Warahmatullaahi Wabarakaatuh.

Yogyakarta, 31 Mei 2008

Makalah Bidang Aljabar

The Sufficient Conditions forR[x,



] to be a GCD-ring (Santi Irawati) ………

1

Lapangan yang Memenuhi Sifat Unit 1-Stable Range

(Indriati Nurul Hidayah) ………..………..

10

Aljabar Max-Plus Interval (M. Andy Rudhito,Sri Wahyuni,Ari Suparwamto,

F.Susilo,SJ) ………...

14

Matriks Atas Aljabar Max-Plus Interval (M. Andy Rudhito,Sri Wahyuni,

Ari parwamto,F.Susilo,SJ) ……….………

23

Syarat Perlu dan Cukup Ideal Prime Terkait (Sufficient and Nessecary Condition of

The Associated Prime) (Suprapto,Sri Wahyuni,Indah Emilia Wijayanti,Irawati) ……

33

Makalah Bidang Analisis

Operator Integral Fraksional dan Ketaksamaan Olsen di Ruang Morrey Tak Homogen yang Diperumum (Idha Sihwaningrum,Hendra Gunawan,

dan Wono Setya Budhi) ……….………

40

Barisan Fibonacci Ditinjau dari Teori Bilangan (Sangadji) ………...……….

48

Fungsi Riemann Zeta (Sangadji) ……….

53

Konvergensi Metode Newton dan Metode Turun Tercuram dalam Menyelesaikan

Sistem Persamaan Non-Linear (Lusia Krismiyati Budiasih) ……….………

60

Representation Of SM-Operators on Classical Sequenceslp, 1 <p<(Muslim Ansori,

Soeparna Darmawijaya,Supama) ………

68

Representasi Operator-SMmodpada Ruang Barisanlp, 1 <p<(Muslim Ansori,

Soeparna Darmawijaya,Supama) ………

78

Makalah Bidang Pendidikan Matematika

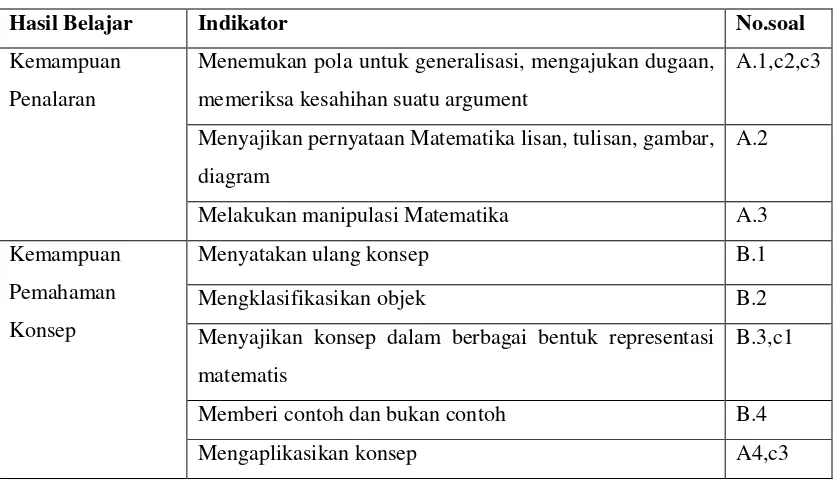
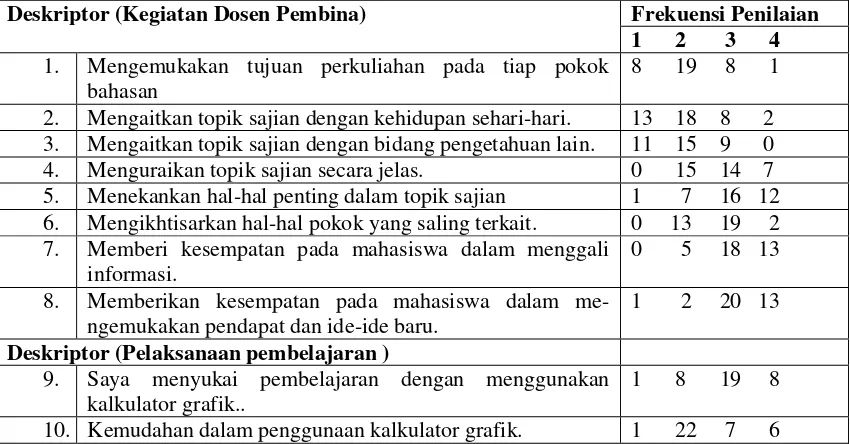
Kemampuan Pemahaman Konsep dan Penalaran Matematika Melalui Penggunaan Kalkulator Grafik pada Mahasiswa Jurusan Matematika Universitas Negeri Malang

(Indriati Nurul Hidayah,Santi Irawati,Ipung Yuwono) ……….……….

92

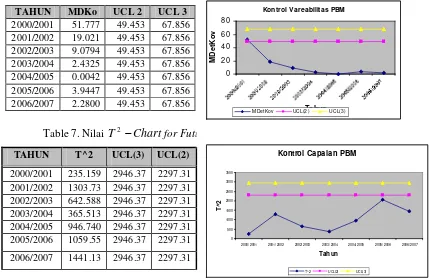
Kontrol Proses Pembelajaran pada Mata Pelajaran yang Di-Ebtanas/Uan-Kan TP 2000/2001-2006/2007 pada SMPN 6 Medan (Menggunakan Pendekatan Analisis

Multivariat) (Hasratuddin) ………

103

Pemahaman Matematis dan Penggunaan Komputer dalam Pembelajaran Matematika

Kriswianti Nugrahaningsih) ………

137

Peningkatan Motivasi Belajar Dan Pemahaman Keruangan Siswa Melalui Pembelajaran Geometri Berbantuan Program Komputer (MG. Erni Harmiati dan

Agustin Rahayu) ………

148

Meningkatkan Daya Matematika Siswa Melalui Paikem Berbantuan Teknologi

Multimedia (Yonandi) ……….

159

Meningkatkan Kualitas Pembelajaran Matematika Di Sekolah Melalui Penelitian

Tindakan Kelas (Zaenuri Mastur dan Nurkaromah Dwidayati) ………..

174

Merancang Tugas untuk Mendorong Berpikir Kreatif Siswa dalam Belajar Matematika

(Tatag Yuli Eko Siswono) ………

188

Proses Berfikir Mahasiswa dalam Mengkonstruksi Konsep Grup

(Herry Agus Susanto) ……….

201

Adversity Quotient: Kajian Kemungkinan Penginterasiannya dalam Pembalajaran

Matematika (Sudarman) ………

209

Visualisasi Geometris dalam Pemahaman Masalah Matematika (I Wayan Ponter) ……

219

Explicit Values In Statistics Education: A case of Informatics Engineering Students

(Bambang Suharjo) ………

230

Matematika Melalui Perkuliahan Berbasis Masalah (Djamilah Bondan Widjajanti) ……

240

Karakteristik Proses Kognitif dalam Pemecahan Masalah Matematika (Wilmintjie

Mataheru) ………..………..

251

Penalaran Visuospatial dalam Mengkonstruk Bentuk Bangun Geometri

(Ronaldo Kho) ………..………

263

Proses Berpikir Anak Tunanetra dalam Menyelesaikan Permasalahan Matematika

(Susanto) ………..……….

268

Analisis Kontrol Proses Pembelajaran melalui Data Ujian Nasional di SMA PGRI

Ciranjang Cianjur (Rudy Kurniawan) ……….

281

Metakognisi dalam Pemecahan Masalah Matematika Kontekstual

(Mustamin Anggo) ………

296

ImplementasiLesson Studypada Matakuliah Analisis Real I (Manuharawati) ………….

310

Implementasi Pendekatan PMRI dalam Pembelajaran Materi Pecahan di Sekolah

Generator Frame Wavelet Ketat dari Kelas Box Spline Multivariate (Mahmud Yunus,

JannyLindiarni,Hendra Gunawan) ……….

334

Generalized Regression dalam Pendugaan Area Kecil (Anang Kurnia,Khairil A.

Notodiputro,Asep Saefuddin, danI Wayan Mangku) ………

346

Chain Ladder Method as a Gold Standard to Estimate Loss Reserves (Aceng K.

Mutaqin,Dumaria R. Tampubolon,Sutawanir Darwis) ……….

356

Optimalisasi Respon Ganda pada Metode Respon Permukaan (Response Surface) dengan Pendekatan FungsiDesirability(Hari Sakti Wibowo,I Made Sumertajaya,

Hari Wijayanto) ……….

365

Sifat Penaksir Simulated MLE pada Respon Multinomial (Jaka Nugraha) …………..

376

Estimasi Model Probit pada Respons Biner Multivariat Menggunakan MLE dan

GEE (Jaka Nugraha) ……….

386

Analisis Komponen Utama Temporar (Ismail Djakaria) ……….

399

PendekatanDynamic Linear ModelatauState Space Modelpada Pendugaan Area

Kecil (Small Area Estimation) (Kusman Sadik dan Khairil Anwar Notodiputro) …….

411

Pengembangan Algoritma EM untuk Data Tidak Lengkap (Incomplete Data) pada

Model Log-Linear (Kusman Sadik) ………...

422

CRUISE sebagai Metode Berstruktur Pohon (Tree-Structured) pada Data

Non-Biner (Kusman Sadik) ………...

433

ModelProportional Hazards CoxdenganMissing Covariates(Nurkaromah

Dwidayati,Sri Haryatmi,Subanar) ……….

447

Aplikasi Mixture Distribution dalam Pemodelan Resiko Aktuaria (Adhitya Ronnie

Effendie) ………

459

Analisis Komponen Utama Probabilistik pada DataMissing(Ismail Djakaria) ……..

464

Malakah Bidang Terapan

Bilangan Ramsey untuk Graf BintangS6dan Graf Bipartit LengkapK2,N,N=2,3,4

(Isnaini Rosyida) ……….

476

H-supermagic labelings ofccopies of some graphs (Tita Khalis Maryati,A.N.M.

Jurusan Matematika FMIPA Universitas Negeri Malang (UM)

Abstract

.

Let R be a commutative ring. An element c  R is called a greatest common divisor(GCD for short) ofaandbin R if (i).cRaR,bRand (ii). For anydR

ifdRaR,bRthendRcR. If each pair of elements ofRhas a GCD inR, thenR

is called aGCD-ring. A GCD-domain is an integral domain which is a GCD-ring. Gilmer proved that if D is a GCD-domain with quotient field K, then its polynomial ring D[x] is also a GCD-domain. Based on this idea, it will be investigated the sufficient conditions for a non-commutative skew polynomial ringR[x,] ={a a xa x2 ...a_nxn

2 1

0 

a

iR}, withAut(R) satisfies

xb=(b)xfor anybRwhereRis an order in a simple Artinian ringQ, to be a GCD-ring.

Keywords:greatest common divisor, order, skew polynomial ring.

In what follows all of the rings are assumed to be commutative with nonzero identity 1. An elementuRis aunitif there existsvRsuch thatuv= 1. An elementxRis azero divisor

if there exists a nonzero elementxRsuch that either rx= 0 orxr= 0. A nonzero elementa

in a ring R is said to beregular if a is not a zero divisor. A nonzero ring R is anintegral

domain if R has no zero divisor [H: 1989]. An element c in a non commutative ring R is

called a rightgreatest common divisor(GCD for short) ofaandbinRif (i)cRaR,bRand

(ii) for any d R if dR aR,bR then dR cR. A ringR is a GCD ringif it is an integral

domain which any two elements of R have a GCD. IfR is a commutative GCD domain, it will be investigated the sufficient condition for a non-commutative skew polynomial ring

R[x,] = {a a xa x ...anxn

2 2 1

0 

a

i R}, with Aut(R) satisfies xb = (b)x for

anyb Rwhere Ris an order in a simple Artinian ringQ, to be a GCD-ring. We will start

with the following easy lemmas.

Lemma 1.If u is a unit of a ring R with



Aut(R), then



(u) is a unit of R.

Proof.Sinceuis a unit of a ringR, there existsvRsuch thatuv= 1. Therefore, we get

Lemma 2.GCD {



(a),



(b)}=



(GCD {a,b}).

Proof.Letc= GCD{a,b}. We will show that



(c) = GCD{



(a),



(b)}.

SincecR



aR,bR, thena=ceandb=cf, for somee, fR.

It implies



(a) =



(ce) =



(c)



(e)



(c)Rand



(b) =



(c)



(f)



(c)R.

We get



(a)R,



(b)R





(c)R. LetdRsuch that



(a)R,



(b)R



dR.

We will show that



( )c R  dR. Since



(a)R



dRand



Aut(R), there existsgR

such thata=



1

( )

d



1

( )

g

 1

( )

d R





. It meansaR



1

( )

d R

. Dengan cara serupa,

diperolehbR



1

( )

d R

. Sincec= GCD{a,b},cR



1

( )

d R

. Then,c=



1

( )

d



1

( )

t

=

1

( )

dt





for sometR. We get



(c) =dtdRand hence



( )c R dR.

By combination of Lemma 1 and Lemma 2, we have

Corollary 3.If GCD{a, b}=uU(R),the set of unit elements of R, thenGCD {



(a),



(b)} =



(u)U(R).

LetR[x] be a polynomial ring overRin an indeterminatex. If



is an automorphism

ofR, we have a skew polynomial ringR[x,



] =





a

x

a

i



R



i

i withxb=



(b)x. A

polynomial f(x) =



 n i

i ix a 0

inR[x,



] is calledright primitive polynomialif the GCD of

0

,

1

,

2

, ...,

n

a a a

a

is a unit inR[H:1989]. A finitely generated right idealIofRisprimitive

ifIis contained in no proper principal right ideal ofR. Equivalently, a right idealIof R is a

primitive right ideal ifI=Af =



 n i

iR a 0

, for some right primitive polynomial f(x) =



 n i

i ix a 0

inR[x,



].

Lemma 4.Let R be aGCDdomain and I is a finitely generated right ideal of R. Then, I is

Proof.Assume thatIis primitive. LetI= 0 n i i a R 



. SinceIis primitive, then GCD

{

a a a

0

,

1

,

2

, ...,

a

n} =cfor some unitcR. It means,

a

i



c

.



i andc=

a

i



i for some

,

i i

R

  

. Therefore,I=

0 n i i a R 



= 0 n i i

c R







R=cR=

0

n i i i

a



R 



 0 n i i a R 



=I. So,I=R.

Theorem 5.If f(x),g(x)are right primitive polynomials in R[x,



],then the product f(x)g(x)

is also a right primitive polynomial in R[x,



].

Proof.Letf(x) =



 n i i ix a 0

andg(x) =



 m j j j

x

b

0

with right GCD{

a

1

,

a

2

,

...,

a

n}=uU(R) and

right GCD {

b

1

,

b

2

,

...,

b

m}=vU(R). Then we obtainAf =



 n i iR a 0

and Ag=



 m j j

R

b

0 .

Sincef(x)g(x) =



  m n k k kx c 0 with



  

 n m

k j k i

j i i

k a b

c

0

) (



. By rearrangement the terms of the

coefficients off(x)g(x), we have

fg

A =



  m n k kR c 0 =



 m j j

R

b

a

0

0 +



 m j j

R

b

a

0

1



(

)

+ … +



 m j

j n

n

b

R

a

0

)

(



=



 m j j

R

b

a

0

0 +



 m j j

R

b

a

0

1



(

)

+ … +



 m j

j n

n

b

R

a

0

)

(



= a0Ag + a1



(Ag) + … +

(

g

)

n n

A

a



=



 n i g i i A a 0 ) (



LetdRAfg. We will show thatdis a unit ofR. Based on Lemma 4, we get

(

)

i

g

A



=Rfor

any 0in. Thus, dRAfg 

(

g

)

i

i

A

a



=

a

iRimpliesdRuR=R. We obtaindis a unit

inR. It means that Afg is a primitive ideal ofRand hencef(x)g(x) is a right primitive

Corollary 6.If R is a commutative GCD domain and I and J are primitive ideals of R, then IJ is a primitive ideal of R.

A nonzero polynomialf(x) inR[x] isirreducibleiff(x) is not a unit and in every factorizationf(x) =g(x)h(x), eitherg(x) orh(x) is a unit inR[x]. A nonzero polynomialf(x) in

R[x] isprimeiff(x)R[x] is a prime right ideal ofR[x], that is, the conditionf(x)R[x]

g(x)R[x]h(x)R[x] impliesf(x)R[x]g(x)R[x] orf(x)R[x]h(x)R[x].

Lemma 7. Let R is a commutative GCD domain. If f(x) is an irreducible polynomial in

R[x;], then f(x)R[x;]is a maximal element of any principal right ideal of R[x;].

Proof. If f(x)R[x;]  g(x)R[x;], then either f(x)R[x;]  g(x)R[x;] or f(x)R[x;] =

g(x)R[x;]. It means, that f(x)R[x;] is a maximal element of any principal right ideal of

R[x;].

Theorem 8. Let R is a commutative GCD domain. If f(x) is an irreducible polynomial in

R[x;], then f(x) is prime, that is, f(x)R[x;]is a prime right ideal of R[x;].

Proof.

We will show that if f(x) is an irreducible polynomial inR[x;], thenf(x)R[x;] is a maximal

right ideal ofR[x;] and therefore a prime right ideal ofR[x;].

Iff(x)R[x;] g(x)R[x;], then either f(x)R[x;]g(x)R[x;] orf(x)R[x;] = g(x)R[x;]. It

means that f(x)R[x;] is a maximal element of any principal right ideal of R[x;]. Now,

suppose that f(x)R[x;]  I where I is a right ideal of R[x;]. Then, there exists g(x)I

-f(x)R[x;] such that f(x)R[x;]  f(x)R[x;] + g(x)R[x;] I. Let f(x) = a xi i and g(x) =

 j j

b x

. Since R is GCD domain, there exists a regular element c  R such that c = GCD

{a bi, j}. Let

a

i



c



i and bjc



j for some

 

i, j R. Therefore, f(x)R[x;] 

(a xi i)R[x;] + ( j j

b x

)R[x;] = (c x



i i)R[x;] + ( j j

c



x

)R[x;] = (

c x

r)R[x;] 

cR[x;]. The maximality off(x) impliescis a unit inR. Hence,I=Rwhich meansf(x)R[x;]

Theorem 9. Let R is a commutative GCD domain. Then any non-constant primitive polynomial in R[x,



] can be expressed as a finite product of irreducible polynomials in

R[x,



].

Proof.Letf(x) be a non-constant primitive polynomial inR[x,



]. If degf= 1, it is clear that

f(x) is irreducible. Assume degf > 1. Iffis irreducible, then it is proved. Now we assume

thatfis not irreducible, sayf(x) =g(x)h(x) for someg(x),h(x)R[x,



] where 0 < degg,

degh< degf. Letg(x) =

0 n i i i a x 



, h(x) =

0 m j j i b x 



, and thenf(x) =

0 n m k k k c x  



where , 0

( )

n m i

k i j

i j k k

c

a



b



  





. Ifgis not primitive, thenI= Ag=



a R

i  cRR, for some

regular elementcR. Then, for anyiwe get

a

i=

cr

i, for some

r

iR. It implies Af =

k

c R



= i

( )

i j

a



b R



= i

( )

i j

c



r



b R

 cRR, a contradiction. Similarly, ifhis not primitive we will get a contradiction. Therefore,gand hmust be primitive polynomials. By

hypothesis induction,gand hare products of finite irreducible polynomials inR[x;] and so

isf.

Corollary 10.Let R is a commutativeGCDdomain.Then any non-constant primitive

polynomial in R[x,



]can be expressed as a product of prime polynomials in R[x,



].

Proof.Use Theorem 9 and Theorem 8.

Theorem 11.Let R is a commutativeGCDdomain.Then for any primitive irreducible

polynomials f(x),g(x)in R[x,



]such that f(x).g(x) =h(x).f(x),for some h(x)in R[x,



],then

h(x)is primitive irreducible polynomial.

Proof.By using Theorem 5, iff(x),g(x) are primitive polynomials inR[x,



] then f(x).g(x)

also a primitive polynomial inR[x,



] or Afg is a primitive ideal ofR ……...(#).

It implies thath(x) must be primitive since otherwise, ifh(x) =

0 m j j j

d x





then

A

h=



d R

j

 cRRfor some regular elementcR. If f(x) =

0 n i i i a x 

0 m j j j

d x

















0

n i i i

a x

















= 0

( )

n m

j j i

j i

i j

d



a x





 



and then Afg= Ahf=

0

( )

n m j j i i j

d



a R



 





j

d R



 cRRwhich contradicts (#). Now, suppose thath(x) is not irreducible

polynomial. Then either,h(x) is a unit orh(x) is decomposable. Ifh(x) is a unit, thenf(x).g(x)

=h(x).f(x) implieshAf= Ahf = Afg and then Af =

1 h Ahf =

1

h



a

i



i

( )

b R

j =

1

( )

i

i j

a



b h R





= i

( )

i j

a



b R



= Afg since

1

h is also a unit inR. From Af= Afg, we

getf(x) =f(x).g(x) org(x) = 1, a contradiction. Next, ifh(x) is decomposable then by Theorem

9 there exist irreducible polynomials

d

1(x),

d

2(x) , …,

d

n(x) inR[x,



] such that h(x) =

1

d

(x)

d

2(x) …

d

n(x). Therefore,

f(x).g(x) =

d

1(x)

d

2(x)…

d

n(x)f(x)

d

1(x)R[x,



] …………... (##)

Since

d

1(x) R[x,



] is a prime right ideal of R[x,



] by Theorem 8 and f(x), g(x) are

primitive irreducible polynomials, then f(x), g(x) 

d

1(x) R[x,



] which implies f(x)g(x) 

f(x)R[x,



]g(x) 

d

1(x) R[x,



]. This contradicts (##). So, h(x) should be an irreducible

polynomial inR[x,



].

Corollary 12.Let R is a commutativeGCDdomain.Then any non-unit primitive polynomial

f(x)in R[x,



]can be factorized as f(x) = 1 1 ( )

p x 2

2 ( )

p x … n( )

n

p x where

p x

i

( )

are

primes and

 

i

0

.

Theorem 13.Let R is a commutativeGCDdomain.Then for any primitive irreducible

polynomials f(x),g(x)in R[x,



],there exists a primitive polynomial h(x)in R[x,



]such that

h(x)is a rightGCDof f(x)and g(x).

Proof.Letf(x) = 1 1 ( )

p x 2

2 ( )

p x … n( )

n

p x andg(x) = 1 1 ( )

p x 2

2 ( )

p  x … n( )

n

p  x with

( )

i

p x

are primes and

  

i

,

i

0

. If we chooseh(x) =

1 1 ( )

p x 2

2 ( )

p  x … n( )

n

p x with



i=

For a ringR, we denote byU(R) the set of all units ofRand by

C

R(0) the set of all

regular elements of R. Let Cbe a multiplicatively closed subset of a ring R. We say thatR satisfies the right Ore condition with respect to Cor thatCis called aright Ore set of Rif, for

anyaRandcC, there existbR anddCsuch that ad=cb. If C

C

R(0), then it is

called aregular right Ore set of R. Similarly, we can define a (regular)left Ore setofR. IfC

is a (regular) right and left Ore set ofR, then it is simply called (regular)Ore setofR. LetC

be a regular right Ore set of a ringR. An overringTofRis called theright quotient ring of R

with respect to Cif (i) cU(T) for anycCand (ii) for anyqT, there existaRandc

Csuch thatq=ac1. We denote the ringTby

R

C. We note that for a multiplicative subsetC

ofRwithC

C

R(0), the right quotient ring

R

C ofRwith respect toCexists if and only ifC

is a regular right Ore set ofR([MMU]: 1997).

A subringRof a ringQis called aright order in QifQis the right quotient ring ofR

with respect to

C

R(0), and sometimes we denote the ringQbyQ(R). In particular,Ris a right

order inQif and only if

C

R(0) is a right Ore set ofR. Similarly, we can define aleft order in

Qand a ring which is both a right and left order inQis called anorder in Q.

LetRbe an order in a simple Artinian ringQ. If



Aut(R), then we can extend to

be an automorphism onQby



(ab1) =



(a)



(c)-1fora,bRandbis a regular element of

R. A rightR-submoduleIofQis called aright R-idealifaR



I



bR, for some unitsa,bin

Q. A left R-ideal of Q is defined similarly and an R-ideal of Q, we mean a right R-ideal

which is also a left R-ideal. For A and B any subsets of a simple Artinian ring Q, we set

(A:B)l= {qR

qA

B

} and (A:B)r= {qR

Aq



B

}. For any rightR-ideal IofQ, we set

v

I

= (R:(R:I)l)r. IfI=

I

v, then we callIaright

v

–(I)-idealofQ. Aleft

v

–(I)-idealJofQis

defined similarly,J=vJ= (R:(R:J)r)l. AnR-idealAis said to be a

v

–(I)-idealif

A

v=A=vA.

Ris aright

v

-Bezout ringif there exists a regular element cQ, such that

I

v=cR for any

Theorem 14.Let R be an order in a simple Artinian ring Q. If R is commutativeGCD

domain,then any nonzero polynomial f(x)in Q[x,



]is uniquely expressible as f(x) =

a

f x

1

( )

,where aQ and

f x

1

( )

is a primitive polynomial in Q[x,



].

Proof.Letf(x) =

0

n i i i

a x 



,

a

iQ. There exist

b

i,dR,d0 such that

a

i =

1

i

b d . Since

Ris GCD domain, we haveb= GCD {

b

i} for somebR. Then,f(x) =

1 i i

b d x





=

1

( )

i i

b



d x





= a

f x

1

( )

, wherea= 1

bd Qand

f x

1

( )

=

i i x



is a a primitive

polynomial inQ[x,



]. Now, if a

f x

1

( )

=b

f

2

(

x

)

witha,bQand

f x

1

( )

,

f

2

(

x

)

are

primitive polynomials inR[x,



] thenaR=a(Af1)v = (Aaf1)v= (Abf2)v=b (Af2)v=bR. It

meansaandbdiffers by units inRand so

f

1and

f

2 differs by units inR.

Theorem 15.Let R be an order in a simple Artinian ring Q. If R is aGCDdomain and a right invariant ring, then R[x,



]is a rightGCD domain,that is, for any non-constant

polynomials f(x),g(x)in R[x,



],there exists h(x)in R[x,



]such that h(x)is a rightGCDof

f(x)and g(x).

Proof.Letf(x) andg(x) are any non-constant polynomials inR[x,



]. By Theorem 14, we

writef(x) = a

f x

1

( )

andg(x) =b

f x

2

( )

, for somea,bQand

f x

1

( )

,

f

2

(

x

)

are primitive

polynomials inR[x,



]. SinceRis GCD domain and by Theorem 13, there existcinRand a

primitive polynomialh(x) inR[x,



] such thatc= GCD {a,b} andh(x) = right GCD {f(x),

g(x)}. We show thatch(x) is GCD off(x) andg(x).

c= GCD {a,b}  cRaR  a=c

a

1, for some

a

1R.

h(x) = right GCD {f(x), g(x)} h(x)R[x,



]

f x

1

( )

R[x,



]

f x

1

( )

=h(x)r(x), for

somer(x)R[x,



].

Since We getf(x) = a

f x

1

( )

= (c

a

1)h(x)r(x)cR[x,



]h(x)r(x)ch(x)R[x,



]. Now, let

t(x)R[x,



]f(x)R[x,



],g(x)R[x,



]. We will show thatt(x)R[x,



]ch(x)R[x,



].

Lett(x) = d

t x

₁

( )

for somedRand primitive polynomial

t x

₁

( )

inR[x,



].

k(x) =e

k x

1

( )

for someeRand primitive polynomial

k x

1

( )

inR[x,



]. Therefore,

a

f x

1

( )

=f(x) =t(x)k(x) = [d

t x

1

( )

] [e

k x

1

( )

] =d

e

0

t x

1

( )

k x

1

( )

.

This meansdRaRand

t x

₁

( )

R[x,



]

f x

1

( )

R[x,



]. Similarly, we getdRbRand

1

( )

t x

R[x,



]

f x

₂

( )

R[x,



]. Sincec= GCD {a,b} andh(x) = right GCD {f(x), g(x)}, then

we obtaint(x)R[x,



]= d

t x

₁

( )

R[x,



]ch(x)R[x,



].

References:

[G] Gilmer R., Multiplicative Ideal Theory, Queen’s Papers in Pure and Applied Mathematics,90Queen’s University, 1992.

[H] Hungerford, T.W.Algebra, Springer-Verlag, New York, 1989 (Fifth printing).

dosen jurusan Matematika Universitas Negeri Malang

Abstrak

Untuk sebarang gelanggang R, pernyataan-pernyataan berikut ini ekuivalen (1)Jika a b x, , R memenuhi ax b 1 maka ada suatu u U R ( ) sehingga

( )

a bu U R  . (2) Jika a b, R memenuhi aR bR R maka ada suatu

( )

u U R sedemikian hingga a bu U R  ( ).(3

)Jika

a a

1

,

2

,...,

a

n



R

memenuhi

a R a R

1



2

 

...

a R

n



R

maka ada suatu

1

, ,...,

2 n

( )

u u

u



U R

sehingga

a u

1 1



a u

2 2

 

...

a u

n n



1

. Gelanggang R

memenuhi sifat unit 1-stable range jika salah satu kondisi pada pernyataan di atas memenuhi dalam R. Dalam tulisan ini akan dibahas bahwa lapangan F dengan sifat tertentu memenuhi sifat unit 1-stable range. Kemudian diberikan contohnya pada lapangan bilangan kompleks dan terakhir akan diberikan bahwa Himpunan matriks atas lapangan F dengan sifat tertentu juga memenuhi sifat unit 1-stable range.

Kata kunci

:Gelanggang yang memenuhi sifat unit 1-stable range, lapangan, matriks atas lapangan F.

Abstract

For any ring R, these statements are equivalent: (1) if a b x, , Rsatisfies

1

ax b  then there exists u U R ( )such that a bu U R  ( )(2). if

,

a bRsatisfies aR bR Rthen there exists u U R ( )such that

( )

a bu U R  (3). if

a a

₁

,

₂

,...,

a

n



R

satisfies then there exist

1

, ,...,

2 n

( )

u u

u



U R

such that

a u

_{1 1}



a u

_{2 2}

 

...

a u

n n



1

. Ring R satisfies 1-stable

range unit property if one of three conditions of those statements are satisfied in R. In this study, it will be discussed that a field F with special properties satisfies 1-stable range unit property. Moreover, it will be provided the examples of a complex field and a matrix ring over a field F with special properties that satisfy 1-stable range unit property.

Key words:

Ring R satisfies 1-stable range , field, matrix ring over a field F

Dalam tulisan ini akan dibahas tentang definisi gelanggang yang memenuhi sifat unit 1-stable range, keberlakuan sifat unit 1-stable range pada lapangan, contohnya dan sifat

Pendefinisian gelanggang yang memenuhi sifat unit 1-stable range berdasarkan pada teorema yang dikemukakan oleh Goodearl pada tahun 1988. Berikut ini akan dibahas definisi

tentang gelanggang yang memenuhi sifat unit 1-stable range. Pendefinisiannya berdasarkan pada teorema yang dikemukakan oleh Goodearl.

Teorema 1 :Diketahui gelanggang R. Pernyataan-pernyataan berikut ini ekuivalen:

1. Jika a b x, , R memenuhi ax b 1 maka ada suatu u U R ( ) sehingga

( )

a bu U R 

2. Jika a b, R memenuhi aR bR R maka ada suatu u U R ( )sedemikian

hingga a bu U R  ( ).

3. Jika

a a

1

,

2

,...,

a

n



R

memenuhi

a R a R

1



2

 

...

a R

n



R

maka ada suatu

1

, ,...,

2 n

( )

u u

u



U R

sehingga

a u

1 1



a u

2 2

 

...

a u

n n



1

Definisi 2 (Goodearl,1988): Gelanggang R dikatakan memenuhi sifat unit 1- stable range

jika salah satu kondisi pada teorema 1 memenuhi dalam R.

Contoh gelanggang yang memenuhi sifat unit 1-stable range adalah gelanggang

bilangan rasional dan contoh gelanggang yang tidak memenuhi sifat unit 1-stable range adalah gelanggang bilangan bulat modulo 2.

Dalam hubungan dengan gelanggang bagian , jika

S

gelanggang bagian

R

dengan

R

adalah gelanggang yang memenuhi sifat unit 1-stable range maka

S

belum

tentu memenuhi sifat unit 1-stable range, seperti pada gelanggang bilangan bulat

Z

sebagai gelanggang bagian dari gelanggang bilangan rasional yang memenuhi sifat

unit 1-stable range, tapi

Z

tidak memenuhi sifat unit 1-stable range .

Teorema 3 (Goodearl, 1988): Diketahui gelanggang R. Jika untuk setiap x y, Rada

( )

u U R sehingga x u U R  ( ) dan

y u



1



U R

( )

makaR memenuhi sifat unit

1-stable range.

Teorema 4 (Chen,1998) Jika R gelanggang maka pernyataan berikut ini ekuivalen:

1. R memenuhi sifat unit 1-stable range

2. Untuk sebarang x y, R ada u U R ( ) sedemikian hingga1x y u(  ) U R( )

3. Jika ax b 1dalam R maka ada v U R ( ) sedemikian hingga x vb U R  ( )

LapanganFmerupakan gelanggang komutatif dengan elemen identitas yang setiap unsurnya mempunyai invers. Dalam hubungannya dengan sifat unit 1-stable range, didapat

teorema sebagai berikut:

Teorema 5:Jika F lapangan dengan 2a0 untuk setiap aF , maka F memenuhi sifat unit 1-stable range.

Bukti:Akan dibuktikan aF bF  F jika a0 atau b0

Akan dibuktikan

aF



bF



F

untuk a,bF dan a0 atau b0. Ambil

bF

aF

bf

af

1



2





. Jelas bahwa

af

1



bf

2



F

.

Akan dibuktikan

F



aF



bF

untuk a,bF dan a0 atau b0 . Ambil sebarang

F

f  akan dibuktikan

f



af

1



bf

2.

Jika a0 atau b0 maka 2 1 



fb

f

atau 1 1





fa

f

. Jika a0 dan b0 maka



1



1

(

)









a

f

a

b

f

. Jadi f aF bF.

Terbukti bahwa aFbF F jika a0 atau b0.

Perlu ditunjukkan bahwa ada uU(F) F{0} sedemikian hingga abuU(F).

Sedangkan abuU(F) jika dan hanya jika abuF dan abu 0. Pilih

1

Matriks atas gelanggang R yang dilambangkan dengan

M

n

(

R

)

merupakan salah

satu contoh gelanggang. Sudah banyak buku-buku atau artikel-artikel yang menyatakan

keterkaitan sifat antara gelanggang R dengan matriks atas gelanggang R. Salah satunya

adalah yang berkaitan dengan elemen identitas, yaitu jika gelanggang R mempunyai elemen

identitas terhadap perkalian maka

M

_n

(

R

)

juga mempunyai elemen identitas terhadap

perkalian. Namun tidak demikian halnya dengan sifat komutatif, jika gelanggang R bersifat

komutatif maka

M

n

(

R

)

belum tentu bersifat komutatif..

Teorema berikut ini akan menjelaskan keterkaitan antara gelanggang R dengan

gelanggang matriks atas gelanggangRdalam hal sifat unit 1-stable range, yaitu

Teorema 6 (Chen,1998) Jika gelanggang R memenuhi unit 1-stable range maka demikian

juga

M R

n

( )

untuk sebarang n1.

Dari teorema yang dikemukakan oleh Chen tersebut, didapat teorema akibat sebagai berikut:

Teorema Akibat: Jika F lapangan dengan 2a0, untuk setiap aF, maka

M

n

(

F

)

memenuhi sifat unit 1-stable range.

Bukti: Menurut teorema 5, jika F lapangan dengan 2a0, untuk setiap aF , makaF

memenuhi sifat unit 1-stable range. Akibatnya dengan menggunakan teorema 6 maka

)

(

F

M

n juga memenuhi sifat unit 1-stable range.

DAFTAR PUSTAKA

Adkins, W.a. & Weintreub, S.H. 1992,Algebra: An Approach via Module Theory, Springer-Verlag, New York.

Brown, William C.,1992,Matrices over Commutative Rings,Marcel-Dekker, New York.

Goodearl, K.R.; Menal,P.,1988, .Stable Range One for Rings with Many Units, J.Pure Appl. Algebra, 54,261-287

Mahasiswa S3 Matematika FMIPA UGM,

Staff Pengajar Jurusan PMIPA FKIP USD Paingan Maguwoharjo Yogyakarta

rudhito@staff.usd.ac.id

Sri Wahyuni

Jurusan Matematika FMIPA UGM. Sekip Utara, Yogyakarta

swahyuni@ugm.ac.id , swahyuni@indosat.net.id

Ari Suparwanto

Jurusan Matematika FMIPA UGM. Sekip Utara, Yogyakarta ari_suparwanto@yahoo.com

F. Susilo, S.J.

Jurusan Matematika FST USD. Paingan Maguwoharjo Yogyakarta

fsusilo@staff.usd.ac.id

Abstrak

Makalah ini membahas suatu aljabar himpunan semua interval dalam aljabar max-plus yang dilengkapi dengan operasi maximum dan penjumlahan. Aljabar ini merupakan perluasan aljabar max-plus dan dapat menjadi dasar pembahasan aljabar max-plus bilangan kabur melalui Teorema Dekomposisi dalam himpunan kabur.

Dapat ditunjukkan bahwa himpunan semua interval dalam aljabar max-plus yang dilengkapi dengan operasi maximum dan penjumlahan merupakan semiring idempoten komutatif. Semiring idempoten komutatif ini disebut aljabar max-plus interval. Gabungan himpunan semua interval dan himpunan semua interval tak sejati dalam aljabar max-plus yang dilengkapi dengan operasi maximum dan penjumlahan merupakan semifield. Semifield ini disebut aljabar max-plus interval tergeneralisasi.

Kata-kata kunci:

semiring , idempoten, aljabar max-plus, interval.

1. Pendahuluan

Aljabar max-plus (himpunan R {}, dengan R adalah himpunan semua bilangan

real, yang dilengkapi dengan operasi maximum dan penjumlahan) telah digunakan untuk

memodelkan dan menganalisis jaringan, seperti penjadwalan proyek, sistem produksi, jaringan antrian, dan sebagainya. Pemodelan dan analisa suatu jaringan dengan pendekatan

ini dapat memberikan hasil analitis dan lebih mudah pada komputasinya, seperti dalam Bacelli, et al. (2001), Rudhito, A. (2004), Krivulin, N.K. (2001). Pemodelan tersebut

kebanyakan masih berupa model deterministik, di mana waktu aktifitas pada jaringan berupa bilangan real. Pada kenyataanya, oleh karena beberapa faktor, misalkan operator mesin,

seperti dalam Bacelli,et al. (2001) dan B. Heidergott, B., et. al. (2005). Peubah acak dalam model stokastik diasumsikan mengikuti suatu distribusi peluang tertentu. Distribusi ini

biasanya disusun berdasarkan data-data yang diperoleh setelah jaringan dioperasikan untuk jangka waktu tertentu.

Dalam masalah pemodelan dan analisa suatu jaringan di mana waktu aktifitasnya

belum diketahui, misalkan karena masih pada tahap perancangan, data-data mengenai waktu aktifitas belum diketahui secara pasti maupun distribusinya. Waktu aktifitas ini dapat

diperkirakan berdasarkan pengalaman maupun pendapat dari para ahli maupun operator jaringan tersebut. Untuk itu waktu aktifitas jaringan dimodelkan dalam suatu bilangan kabur

(fuzzy number). Akhir-akhir ini telah berkembang pemodelan jaringan yang melibatkan bilangan kabur. Untuk masalah penjadwalan yang melibatkan bilangan kabur dapat dilihat

pada Chanas, S., Zielinski, P. (2001). Sedangkan untuk masalah model jaringan antrian yang melibatkan bilangan kabur dapat dilihat pada Lüthi, J., Haring, G. (1997).

Pemodelan dan analisa suatu sistem jaringan yang melibatkan bilangan kabur, sejauh penulis ketahui, belum ada yang menggunakan pendekatan aljabar max-plus. Operasi-operasi

pada bilangan kabur dapat dilakukan menggunakan Teorema Dekomposisi dalam himpunan

kabur, yaitu melalui potongan-potongan--nya yang berupa interval-interval (Susilo, F.

2006). Untuk itu makalah ini akan membahas suatu aljabar dengan elemen-elemennya

berupa interval dengan operasi maximum dan penjumlahan yang didefinisikan di dalamnya. Aljabar ini merupakan perluasan aljabar max-plus dan dapat menjadi dasar pembahasan

aljabar max-plus bilangan kabur melalui Teorema Dekomposisi dalam himpunan kabur.

2. Aljabar Max-Plus

Dalam bagian ini dibahas konsep dasar aljabar max-plus. Pembahasan selengkapnya dapat dilihat pada Baccelli et.al (1992), Rudhito A (2003) dan Schutter (1996).

Suatusemiring(S, ,) adalah suatu himpunan tak kosong S yang dilengkapi dengan

dua operasi binerdan, yang memenuhi aksioma berikut:

i) (S,) adalah semigrup komutatif dengan elemen netral0,yaitua,b,cS:

(ab)c = a(bc) , ab = ba, a 0 =a.

(ab)c = a(bc) , a1 = 1a = a,

iii) Elemen netral0merupakan elemen penyerap terhadap operasi,yaituaS:

a0= 0a = 0.

iv) Operasidistributif terhadap, yaitua,b,cS:

(ab)c = (ac)(bc) , a(bc) = (ab)(ac) .

Semiring (S, , ) dikatakan idempoten jika operasi  bersifat idempoten, yaitu a  S :

aa=a, dan dikatakankomutatifjika operasibersifat komutatif. Suatu semiring komutatif

(S, , ) disebut semifield jika setiap elemen tak netralnya mempunyai invers terhadap

operasi . Jika (S, + ) merupakan semigrup komutatif idempoten maka relasi “



” yang

didefinisikan padaSdengan x



yx+y=ymerupakan urutan parsial padaS. Operasi

dandikatakankonsisten terhadap urutan “” dalamS bhb jikax  y, makax +z  y +z

danxz  yz ,x,y,zS. Dapat ditunjukkan bahwa dalam semiring idempoten (S,+,

) operasi + dan konsistenterhadap urutan



dalamS.Semiring (S,,) dengan elemen

netral0dikatakantidak memuat pembagi nol bhb jika xy=0 maka x=0atauy=0,x,

yS.

DiberikanR:=R{} denganRadalah himpunan semua bilangan real dan: =.

PadaRdidefinisikan operasi berikut:

a,bR,ab:= max(a, b) dan ab: =ab.

Dapat ditunjukkan bahwa (R, , ) merupakan semiring idempoten komutatif dengan

elemen netral  =  dan elemen satuan e = 0. Lebih lanjut (R , , ) merupakan

semifield, yaitu bahwa (R,,) merupakan semiring komutatif di mana untuk setiapa 

terdapat a sehingga berlaku a (a) = 0. Kemudian (R, ,) disebut denganaljabar

max-plus, yang selanjutnya cukup dituliskan denganRmax.

Dalam hal urutan pengoperasian (jika tanda kurang tidak dituliskan), operasi 

mempunyai prioritas yang lebih tinggi dari pada operasi . Karena (Rmax , ) merupakan

semigrup komutatif idempoten, maka relasi “m” yang didefinisikan padaRmaxdenganx m

yxy=ymerupakanurutan parsialpadaRmax. Lebih lanjut relasi ini merupakanurutan

konsistenterhadap urutan m, yaitua,b,cRmax, jikaa mb, makaac mbc, dan

ac m bc. Aljabar max-pusRmaxtidak memuat pembagi nolyaitux, yRberlaku:

jikaxy= makax= atauy=.

3. Aljabar Max-Plus Interval

Berikut dibahas aljabar max-plus interval yang merupakan perluasan aljabar max-plus

dan akan digunakan sebagai dasar pembahasan aljabar max-plus bilangan kabur melalui Teorema Dekomposisi. Ide pembahasan didasarkan pada analisis idempoten interval dalam Litvinov, G.L., Sobolevskii, A.N. (2001)

Definisi 1

MisalkanSadalah himpunan terurut parsial dengan relasi . Suatuinterval(tertutup) dalam

Sadalah himpunan bagianSyang berbentuk x = [

x

,

x

] = {xS

x

 x 

x

}, dengan

x

,

x

S berturut-turut disebutbatas bawahdanbatas atasinterval [

x

,

x

].

Misalkan x dan y adalah interval dalamS. Perhatikan bahwa interval xy jika dan

hanya jika y

x



x



y

. Secara khusus x = y jika dan hanya jika

x

=ydan

x

=

y

. Sebuah interval dengan x dengan

x

=

x

merepresentasi suatu elemen dalamS.

Contoh 1

Telah diketahui bahwaRmaxmerupakan himpunan terurut parsial dengan relasi



m. Interval

dalamRmaxberbentuk x = [

x

,

x

] = {x Rmax

x



m x



m

x

}. Bilanganx Rmaxdapat

dinyatakan dengan menggunakan intervalx= [x,x]. Interval dalamRmaxmisalnya [2, 3], [4,

1], [0, 0] = 0 dan [,] =.

Definisi 2

Diberikan (S, +,) adalah suatu semiring idempoten dan tidak memuat pembagi nol, dengan

elemen netral0. Didefinisikan

I(S) = { x = [

x

,

x

]

x

,

x

S,0 

x



x

}{[0,0]}. PadaI(S) didefinisikan operasi  dan



dengan:

Teorema 1

(I(S), ,



) merupakan semiring idempoten dengan elemen netral 0I = [0, 0] dan elemen

satuan 1I=[1,1]. Bukti:

Terlebih dahulu akan ditunjukkan bahwa I(S) tertutup terhadap operasi  dan



seperti yang didefinisikan pada Definisi 2 di atas. Ambil sembarang x, yI(S). Jika salah

satu dari x, y sama dengan [0,0], maka x  y adalah interval itu sendiri dan x



y=[0,0] , sedangkan jika keduanya sama dengan [0,0], maka x  y dan x



y keduanya sama dengan

[0,0]. Jika x, y keduanya[0,0], maka

x

,

x

Sdan0 

x



x

, y,

y

S

dan0  y 

y

. Karena0 

x

, maka0 

x

dan

x

0, juga karena 0  y, maka 0 y

dan y0. Karena 0 + ( x + y) = x + y, maka0  x + y, dan karena

x

0dan y0

maka x + y 0. Hal ini berarti 0  x + y. Karena

x



x

, y S dan S semiring idempoten, maka operasi + konsisten terhadap urutan



, maka

x

+ y

x

+ y. Karena

y 

y

,

x

S danSkonsisten terhadap + maka

x

+ y 

x

+

y

. Oleh karena itu

x

+ y 

x

+

y

. Jadi 0  x + y

x

+

y

, yang berarti x y I(S). Dengan cara yang sama seperti pada operasi  di atas dapat ditunjukkan bahwa 0  x  y. Karena

x

0dan y

0sertaStidak memuat pembagi nol, maka x  y0. Hal ini berarti0  x  y. Dengan cara yang sama seperti pada operasi  di atas dapat ditunjukkan bahwa

x

 y 

x



y

. Jadi0 

x

 y 

x



y

, yang berarti x



yI(S).

Selanjutnya karena operasi-operasi  dan



pada (I(S),) didefinisikan komponen

demi komponen dariS,maka sifat-sifat pada (I(S), ,



) mengikuti seluruh sifat-sifat pada

(S, +,) yang merupakan semiring idempoten, dengan elemen netral0dan elemen satuan1.

Dengan demikian terbukti bahwa (I(S), ,



) merupakan semiring idempoten komutatif dengan elemen netral 0I=[0,0] dan elemen satuan 1I= [1,1]. ■

Teorema 2

Untuk operasi  dan



yang didefinisikan pada (I(S) berlaku

x



y=[ x + y,

x

+

y

] = inf{zI(S)zx + y} dan x



y=[

x

 y,

x



y

] = inf{zI(S)zxy},

x, yI(S), di mana x + y = {tSt=x+y,xx ,yy} dan

Bukti:

Akan dibuktikan untuk operasi . Untuk operasi



dapat dilakukan dengan cara yang

sama. Andaikan zI(S) sedemikian hingga x + yz. Karena x + y x + yz dan

x

+

y

x + yz , maka z  x+ ydan

x

+

y

 z. Karena x+ y

x

+

y

, maka [x+ y,

x

+

y

]z. Ambil sembarangtx + y dan misalkanxx danyy sedemikian hinggat=x

+y. Menurut definisi interval di atas, berlaku x  x 

x

dan y y 

y

. Karena operasi + konsisten terhadap urutan , maka x + y x + y  x +

y

, sehingga x + y  [x+y,

x

+

y

]. Jadi x



y=inf { zSzx + y} = [x + y,

x

+

y

]. ■

Dengan kata lain Teorema di atas mengatakan bahwa [ x +y,

x

+

y

] adalah interval

terkecil yang memuat himpunan x + y. Lebih khususnya batas-batas x



y termuat dalam x +

y. Demikan juga untuk x



y.

Karena (I(S), ) merupakan semigrup komutatif, maka relasi “



I” yang

didefinisikan pada I(S) dengan x



I y x  y = y x  y dan x 

y

merupakan

urutan parsial padaI(S).

Contoh 2

Telah diketahui (R,, ) merupakan semiring idempoten dan tidak memuat pembagi nol,

dengan elemen netral. Didefinisikan

I(R)= { x = [x,

x

] x,

x

R, 



m x



m

x

}{[,]}.

PadaI()didefinisikan operasi  dan  dengan:

x  y = [ x y,

x



y

] dan x  y = [xy,

x



y

] ,x, yI(R).

Misalnya [1, 1]  [1, 3] = [1, 3] dan [1, 1]  [1, 3] = [0, 4].

Menurut Teorema 2 di atas (I(R),,) merupakan semiring idempoten dengan elemen

netral  = [, ] dan elemen satuan 0 = [0, 0]. Lebih lanjut karena (R, , ) merupakan

semiring idempoten komutatif, maka (I(R),,) merupakan semiring idempoten

komutatif. Selanjutnya (I(R),,) disebut dengan aljabar max-plus intervalyang cukup

Semiring idempoten komutatif (I(R),,) bukan merupakan semifield, karena tidak

setiap elemen tak netralnya mempunyai invers. Elemen satuan, yaitu 0 = [0, 0] berupa bilangan real. Elemen tak netral yang mempunyai invers hanya elemen yang berupa bilangan

real x = [x, x], dengan x  0. Sementara untuk x = [x,

x

] dengan 



m x



m

x

tidak

mempunyai invers. Perhatikan untuk  x = [

x

, x], didapat bahwa x  (x) = [x

(

x

),

x

 x] , yang berupa interval dengan panjang 2

x

2x.

Karena (I(R),) merupakan semigrup komutatif idempoten, maka relasi “



Im” yang

didefinisikan pada I(R)max dengan x



Im y  x  y = y merupakan urutan parsial pada

I(R)max. Perhatikan bahwa x  y = y  x



_m y dan

x



_m

y

. Relasi “



Im” ini bukan

merupakan urutan total, karena terdapat x = [1, 3] dan y = [0, 1] dengan xy = [1, 3]

 [0, 1] = [0, 3] , sehingga xyy dan xyx.

Berikut didefinisikan pengertian interval taksejati (improper interval) yang akan

berperan sebagai invers terhadap . Hal ini diharapkan akan mempermudah dalam

pengoperasian interval.

Definisi 3

MisalkanSadalah himpunan terurut parsial dengan relasi . Suatuinterval tak sejati dalam

S adalah suatu bentuk [

x

,

x

] , dengan

x

,

x

 Sdan

x



x

. Suatu interval tak sejati [

x

,

x

] dalamS kadang akan cukup dituliskan dengan x*, di mana x*= [

x

,

x

].

Interval x = [

x

,

x

]I(S) disebut denganinterval sejati.

Definisi 4

Diberikan (S, +,) adalah suatu semiring idempoten dan tidak memuat pembagi nol, dengan

elemen netral0. Didefinisikan

I(S) = { x = [

x

,

x

]

x

,

x

S,0 

x



x

} dan I(S)*= I(S)I(S).

Teorema 4

Bukti:

Dengan operasi yang serupa dengan operasi padaI(S), jelas bahwa (I(S)*, ,



) merupakan semiring komutatif , dengan elemen netral 0 = [0, 0] dan elemen satuan 1 = [1, 1]. Untuk

setiap [

x

,

x

][0, 0], karena (S, +,) adalah suatu semifield, maka terdapat

x

1

,

x

1_

S,

sehingga

x

+ (

x

1

) =1dan

x

+ (

x

1

) =1. Dengan demikan untuk setiap [

x

,

x

][0,0]

(I(S)* , terdapat [

x

1

,

x

1

] sehingga [

x

,

x

]



[

x

1

,

x

1

] = [1, 1]. Jadi (I(S)*, ,



)

merupakan semifield. ■

Untuk setiap interval x = [

x

,

x

] anggota semifield interval I(S)*, [

x

, 

x

] disebut

lawan(oppsite)dari x dan dilambangkan denganopp(x). Dengan demikian diperoleh bahwa

x  opp(x) = [0,0].

Akibat 5

AljabarI(R)*max= (I(R)*,,) merupakan semifield.

Bukti:

Telah diketahui (R, , ) merupakan semifield, sehingga (I(R)*,,) merupakan

semifield. Untuk setiap [

x

,

x

][0, 0]I(R)*max, terdapat [

x

, 

x

]I(R)*max sehingga

[

x

,

x

]  [

x

,

x

] = [0,0]. ■

Semifield I(R)*maxseperti di atas disebut aljabar max-plus interval tergeneralisasi.

Dengan demikian untuk interval a, bI(R)*max, persamaan aljabar max-plus interval a  x

= b mempunyai penyelesaian interval x = b  opp(a). Hal ini karena berlaku bahwa a  (b

 opp(a)) = (a  opp(a))  b = 0  b.

Contoh 3

Persamaan interval max-plus [1, 2] [

x

,

x

] = [3, 5] mempunyai penyelesaian interval x

= [3, 5]  opp([1, 2]) = [3, 5]  [1, 2] = [2, 3]. Perhatikan bahwa [2, 3] memenuhi

persamaan interval di atas, yaitu bahwa [1, 2] [2, 3] = [3, 5].

4. Penutup

menyatakan waktu aktifitas antar titik pada jaringan tersebut. Pemodelan waktu aktifitas jaringan dengan menggunakan bilangan kabur dengan pendekatan aljabar max-plus akan

terkait dengan matriks yang unsur-unsurnya berupa bilangan kabur. Lebih lanjut dapat dibahas matriks atas aljabar max-plus interval, di mana operasi-operasinya merupakan perluasan dari operasi-operasi pada aljabar max-plus interval.

Daftar Pustaka

Bacelli, F.,et al. 2001.Synchronization and Linearity. New York: John Wiley & Sons.

Boom, T.J.J.,et al.2003. , Identification of stochastic max-plus-linear systems. Proceedings of the 2003 European Control Conference (ECC'03),Cambridge, UK, 6 pp., Sept. 2003. Paper 104.

B. Heidergott, B.,et. al.(2005). Max Plus at Work. Princeton: Princeton University Press.

Chanas, S., Zielinski, P. 2001. Critical path analysis in the network with fuzzy activity times.

Fuzzy Sets and Systems.122 (2001) 195–204.

Litvinov, G.L., Sobolevskii, A.N. 2001. Idempotent Interval Anaysis and Optimization Problems.Reliab. Comput.,7, 353 – 377 (2001); arXiv: math.SC/010180.

Lüthi, J., Haring, G. 1997. Fuzzy Queueing Network Models of Computing Systems.

Proceedings of the 13th UK Performance Engineering Workshop, Ilkley, UK, Edinburgh University Press, July 1997.

Rudhito, Andy. 2003.Sistem Linear Max-Plus Waktu-Invariant. Tesis: Program Pascasarjana Universitas Gadjah Mada. Yogyakarta.

Schutter, B. De., 1996, Max-Algebraic System Theory for Discrete Event Systems, PhD thesis Departement of Electrical Enginering Katholieke Universiteit Leuven, Leuven.

Mahasiswa S3 Matematika FMIPA UGM,

Staff Pengajar Jurusan PMIPA FKIP USD Paingan Maguwoharjo Yogyakarta

rudhito@staff.usd.ac.id

Sri Wahyuni

Jurusan Matematika FMIPA UGM. Sekip Utara, Yogyakarta

swahyuni@ugm.ac.id , swahyuni@indosat.net.id

Ari Suparwanto

Jurusan Matematika FMIPA UGM. Sekip Utara, Yogyakarta ari_suparw