Bab 3 SISTEM PERSAMAAN LINEAR

(1)

Bab 3

SISTEM PERSAMAAN

LINEAR

Sejauh ini, hanya diperlakukan sistem persamaan linear yang terdiri dari persamaan yang banyaknya sama dengan variabel, dan hanya mempunyai matriks koefisien tak singular. Tepatnya, ini adalah sistem yang selalu mempunyai suatu penyelesaian tunggal. Pada bab ini akan dipelajari permasalahan dalam menyelesaikan suatu sistem linier m persamaan dalam n variabel. Kasus tidak tertutup untuk sistem persegi panjang, m ¹ n, dengan matriks koefisien singular. Ide utama yang didasarkan pada algoritma eliminasi Gauss untuk sistem tak singular dapat secara langsung menyesuaikan diri dalam kasus tersebut. Secara sistematis digunakan operasi baris elementer untuk memanipulasi matriks koefisien ke bentuk reduksi tertentu yang berbentuk segitiga atas.

Pada bagian akhir bab ini diberikan beberapa aplikasi dari sistem linear seperti pada sirkuit elektrik sederhana, jaringan lalu lintas, persamaan kimia, dan model ekonomi untuk pertukaran barang.

3.1 Konsep Dasar

Suatu persamaan linear dalam n variabel, misalkan x1, x2, …, xn, adalah suatu persamaan yang dapat dinyatakan dalam bentuk

a1x1 + a2x2 + …+ anxn = b

dengan a

1

, a

2

, …, a

n

, dan b adalah konstanta.

Secara geometris, misalkan x dan y berturut-turut merupakan nilai x

1

dan

x

2

maka persamaan linear 2x + 3y = 6 menyatakan garis yang melalui titik (3, 0)

dan (0, 2). Sejalan dengan itu, untuk x, y, z berturut-turut merupakan nilai x

1

, x

2

,

dan x

3

maka persamaan linear 2x + 3y + 4z = 12 menyatakan garis yang melalui

titik (6, 0, 0), (0, 4, 0), (0, 0, 3).

Suatu sistem dari m persamaan linear dalam n variabel x1, x2, …, xn, atas suatu field F, disebut sistem persamaan linear (SPL), adalah keluarga dari persamaan-persamaan linear berikut ini:

a11x1 + a12x2 + …+ a1nxn = b1

a21x1 + a22x2 + …+ a2nxn = b2

!

(2)

Sistem persamaan tersebut dapat dituliskan secara singkat dalam bentuk: i n j j ijx b a =

å

=1 , untuk i = 1, 2, …, m.

Berdasarkan kesamaan dua matriks, sistem tersebut dapat dituliskan dalam bentuk persamaan matriks tunggal, yaitu

ú ú ú ú û ù ê ê ê ê ë é = ú ú ú ú û ù ê ê ê ê ë é + + + + + + + + + m n mn m m n n n n b b b x a x a x a x a x a x a x a x a x a ! ! 2 1 2 2 1 1 2 2 22 1 21 1 2 12 1 11 ... ... ...

dan ekuivalen dengan

ú ú ú ú û ù ê ê ê ê ë é = ú ú ú ú û ù ê ê ê ê ë é ú ú ú ú û ù ê ê ê ê ë é m n mn m m n n b b b x x x a a a a a a a a a ! ! " ! ! ! " " 2 1 2 1 2 1 2 22 21 1 12 11 .

Relasi matriks di atas dapat dituliskan dalam bentuk yang singkat menjadi AX = B,

dengan A adalah matriks koefisien (matrix of coefficients), X adalah matriks variabel (matrix of variables), dan B adalah matriks konstanta (matrix of constants). Seringkali diperlukan untuk mengeluarkan matriks variabel X dan akan menuliskan matriks diperbesar (augmented matrix) dari sistem seperti

[

]

ú ú ú ú û ù ê ê ê ê ë é = m mn m m n n b a a a b a a a b a a a B A ! " " " " ! ! 2 1 2 2 22 21 1 1 12 11 .

Persamaan matriks dengan manfaat lain yang ekuivalen dengan SPL di atas yaitu

ú ú ú ú û ù ê ê ê ê ë é = ú ú ú ú û ù ê ê ê ê ë é + + ú ú ú ú û ù ê ê ê ê ë é + ú ú ú ú û ù ê ê ê ê ë é n nn n n n n n b b b a a a x a a a x a a a x ! ! " ! ! 2 1 2 1 2 22 12 2 1 21 11 1 . CONTOH 3.1.1 Sistem x + y + z = 1 x – y + z = 0 ekuivalen dengan persamaan matriks

ú û ù ê ë é = ú ú ú û ù ê ê ê ë é ú û ù ê ë é - 0 1 1 1 1 1 1 1 z y x

dan juga dengan persamaan

ú û ù ê ë é = ú û ù ê ë é + ú û ù ê ë é -+ ú û ù ê ë é 0 1 1 1 1 1 1 1 z y x .

(3)

DEFINISI 3.1.1 Himpunan penyelesaian dari suatu SPL adalah himpunan semua vektor yang memenuhi setiap persamaan. Dengan kata lain, himpunan tersebut adalah irisan dari himpunan penyelesaian setiap persamaan.

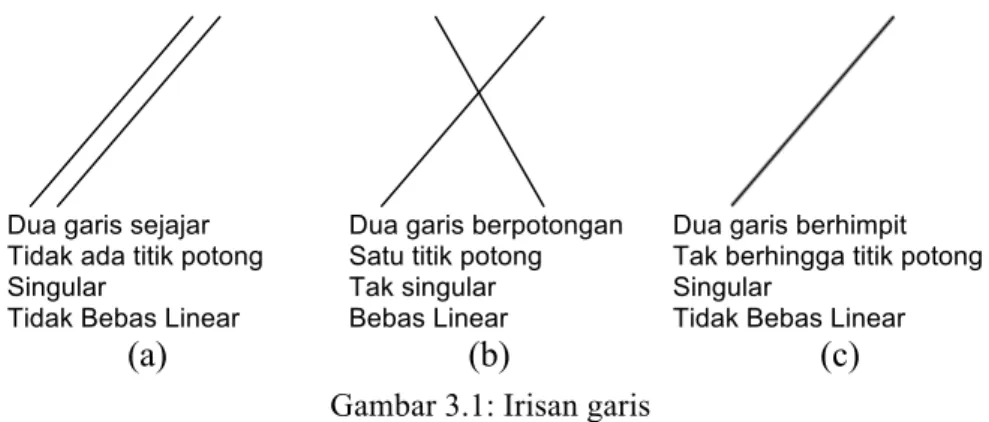
Secara geometris, menyelesaikan suatu SPL dalam dua atau tiga variabel adalah ekuivalen dengan menentukan apakah keluarga garis atau bidang mempunyai titik potong ataukah tidak. Untuk SPL dalam dalam dua variabel x dan y, penyelesaian yang mungkin dapat diilustrasikan seperti pada Gambar 3.1.

Gambar 3.1: Irisan garis

Gambar bagian (a) di atas mempunyai arti bahwa sistem tidak mempunyai penyelesaian, sedangkan untuk gambar bagian (b) sistem mempunyai tepat satu penyelesaian yaitu pada perpotongannya, dan gambar bagian (c) sistem mempunyai tak berhingga banyak penyelesaian.

Untuk ruang dimensi 3, suatu persamaan linear tunggal ax + by + cz = d mendefinisikan suatu bidang P. Penyelesaian untuk sistem tiga persamaan linear dalam tiga variabel adalah irisan dari tiga bidang, yaitu P1 Ç P2 Ç P3. Seperti pada sistem dalam

dua variabel, tiga bidang beririsan dalam suatu titik tunggal terjadi jika hanya jika matriks koefisien adalah tak singular. Kasus penyelesaian tak berhingga banyak terjadi ketika tiga bidang beririsan pada suatu garis. Di sisi lain, bidang-bidang yang beririsan pada garis-garis sejajar, tidak mempunyai titik potong yang sama, dan ini merupakan kasus dari suatu sistem yang tidak mempunyai penyelesaian. Lebih jauh lagi, tidak ada kemungkinan lain yang terjadi, secara jelas tidak dapat dipunyai tiga bidang yang mempunyai secara tepat dua titik dalam irisannya. Kemungkinan penyelesaian dalam bentuk geometris diilustrasikan pada Gambar 3.2.

Gambar 3.2: Irisan bidang

DEFINISI 3.1.2 Diambil suatu baris tak nol dari suatu matriks. Masukan tak nol pertama dari baris tersebut dinamakan poros (pivot) untuk baris tersebut.

Dua garis sejajar Tidak ada titik potong Singular

Tidak Bebas Linear

(a)

Dua garis berpotongan Satu titik potong Tak singular Bebas Linear

(b)

Dua garis berhimpit Tak berhingga titik potong Singular

Tidak Bebas Linear

(4)

DEFINISI 3.1.3 Pada matriks yang diperbesar dari sistem linear AX = B yang mempunyai bentuk eselon baris (tereduksi), variabel-variabel yang berkorespondensi dengan kolom-kolom yang memuat poros disebut variabel-variabel utama (basic variables), sedangkan variabel-variabel yang berkorespondensi dengan kolom-kolom yang tidak memuat poros disebut variabel-variabel bebas (free variables).

Secara umum, jika matriks koefisien m´n dari suatu sistem m persamaan linear dalam n variabel mempunyai peringkat r, maka terdapat m – r baris nol dalam bentuk eselon baris, dan m – r persamaan tersebut harus mempunyai nol pada ruas kanan agar sistem mempunyai suatu penyelesaian. Lebih lanjut, terdapat sejumlah r variabel utama dan n – r variabel bebas dan juga penyelesaian umum yang tergantung pada n – r parameter.

Meringkas pembahasan di atas, diketahui bahwa terdapat tiga kemungkinan untuk penyelesaian suatu sistem linear.

TEOREMA 3.1.1 Suatu sistem AX = B dari m persamaan linear dalam n variabel

mempunyai, salah satu dari: (i) tepat satu penyelesaian tunggal, (ii) tidak ada penyelesaian, (iii) penyelesaian tak berhingga banyak.

Dalam Aljabar Linear, kita tidak hanya tertarik untuk menemukan satu penyelesaian dari sistem persamaan linear.

DEFINISI 3.1.4 (Konsistensi) Sistem persamaan linear dikatakan konsisten (consistent) jika mempunyai paling sedikit satu penyelesaian, dan dikatakan tidak konsisten (inconsistent) jika tidak mempunyai penyelesaian.

CONTOH 3.1.1 Selesaikan persamaan 2x + 3y = 6.

Penyelesaian. Persamaan 2x + 3y = 6 ekuivalen dengan

y

x

₌

₃

_-

₂3

dengan y adalah sebarang. Jadi terdapat penyelesaian tak berhingga banyaknya. CONTOH 3.1.2 Selesaikan sistem

x + y + z = 1 x – y + z = 0.

Penyelesaian. Jika persamaan pertama dikurangi persamaan kedua maka akan diperoleh 2y = 1 atau 2 1

=

y

. Akibatnya diperoleh x = y – z = ₂1 – z

dengan z adalah sebarang. Jadi terdapat penyelesaian tak berhingga banyaknya. CONTOH 3.1.3 Tentukan suatu polinomial berbentuk

y = a0 + a1x + a2x2 + a3x3

yang melalui titik-titik (–3, –2), (–1, 2), (1, 5), dan (2, 1).

Penyelesaian. Dengan mensubstitusikan nilai x dan y dari setiap titik ke bentuk polinomial, akan diperoleh empat persamaan sebagai berikut:

a0 – 3a1 + 9a2 – 27a3 = –2

(5)

a0 + a1 + a2 + a3 = 5

a0 + 2a1 + 4a2 + 8a3 = 1.

Sistem tersebut mempunyai penyelesaian tunggal yaitu

a0 = ₂₀93, a1 = ₁₂₀221, a2 =

-

₂₀23, a3 =

-

₁₂₀41 .

Jadi polinomial yang diminta adalah

3 12041 2 2023 120221 20 93

_x

y

=

+

-

.

Perlu dicatat bahwa suatu sistem linear atas field tak hingga tidak pernah mempunyai penyelesaian yang banyaknya berhingga selain 0 atau 1. Jadi, suatu sistem linear yang mempunyai lebih dari satu penyelesaian secara otomatis mempunyai tak berhingga banyak penyelesaian. Hasil ini tidak diaplikasikan untuk sistem tak linear seperti suatu persamaan kuadratik real ax2 + bx + c = 0 yang dapat mempunyai sebanyak 2, 1, atau 0 penyelesaian real.

3.2 Eksistensi Penyelesaian

Sekarang akan dijawab pertanyaan yang ditentukan ketika suatu sistem persamaan linear adalah konsisten.

LEMMA 3.2.1 Diberikan A Î Mm´n(F) dalam bentuk eselon baris, dan diambil

X Î Mn´1(F) sebagai matriks variabel. Sistem homogen AX = 0m´1, selanjutnya cukup

ditulis AX = 0, dari m persamaan dengan n variabel mempunyai (i) suatu penyelesaian tunggal jika m = n, (ii) penyelesaian tak hingga banyak jika m < n.

Bukti. Jika m = n, maka A adalah suatu matriks segitiga persegi dengan elemen-elemen diagonalnya tidak sama dengan 0. Karena itu

AX = 0 Þ X = A–1_{0 = 0}

yang berarti hanya terdapat penyelesaian tunggal X = 0 atau x1 = x2 = … = xm = 0, yang disebut penyelesaian trivial.

Jika m < n, maka terdapat n – m variabel bebas. Dengan mengambil nilai variabel-variabel tersebut adalah elemen-elemen di field, diperoleh penyelesaian ganda. Jadi jika field mempunyai elemen tak berhingga banyak, diperoleh penyelesaian tak berhingga banyak, dan jika field mempunyai k elemen, diperoleh sebanyak kn–m penyelesaian. Diperhatikan bahwa dalam kasus ini dipunyai penyelesaian trivial, dan juga penyelesaian lain yang disebut penyelesaian tak trivial.n

Yang perlu dicatat dari lemma di atas yaitu bahwa sistem persamaan linear homogen selalu konsisten karena pasti mempunyai suatu penyelesaian trivial.

Dipunyai bahwa jika A adalah matriks persegi tak singular maka A ekuivalen baris dengan suatu matriks eselon baris yang tidak memuat suatu baris nol. Tetapi jika A adalah singular maka A ekuivalen baris dengan suatu matriks eselon baris yang memuat suatu baris nol. Selanjutnya berdasarkan Lemma 3.2.1 diperoleh akibat di bawah ini. AKIBAT 3.2.1 Diberikan A Î Mn(F) dan sistem homogen AX = 0.

(1) Jika A tidak singular, maka sistem hanya mempunyai penyelesaian trivial. (2) Jika A adalah singular, maka sistem mempunyai penyelesaian tak trivial.

CONTOH 3.2.1 Sistem homogen berikut hanya mempunyai penyelesaian trivial.

x – y = 0 x + y = 0.

(6)

CONTOH 3.2.2 Sistem homogen

x – y + z = 0 x + y + z = 0

mempunyai penyelesaian trivial x = y = z = 0. Selain itu juga mempunyai penyelesaian lengkap x = –z dan y = 0 untuk sebarang z. Secara khusus, diambil z = 1 maka suatu penyelesaian tak trivialnya yaitu x = –1, y = 0, dan z = 1.

CONTOH 3.2.3 Diberikan sistem AX = 0 dengan

ú ú ú û ù ê ê ê ë é = 7 4 3 1 0 1 3 2 1 A .

Matriks A adalah singular dan mempunyai bentuk eselon baris tereduksi

ú ú ú û ù ê ê ê ë é 0 0 0 1 1 0 1 0 1 .

Jadi sistem mempunyai suatu penyelesaian tak trivial yaitu x = –1, y = –1, z = –1.

TEOREMA 3.2.1 (Teorema Kronecker-Capelli) Diambil A Î Mm´n(F), Y Î

Mm´1(F) sebagai matriks konstanta dan X Î Mn´1(F) sebagai matriks variabel. Sistem

persamaan AX = Y adalah konsisten jika hanya jika rk(A) = rk([A|Y]).

Bukti. Diambil kolom-kolom dari [A|Y] yang dinotasikan dengan Ki, 1 £ i £ n. Diamati bahwa [A|Y] Î Mm´(n+1)(F) dan kolom ke (n + 1) dari [A|Y] adalah

å

= + = ú ú ú ú û ù ê ê ê ê ë é + + + + + + + + + = = n i i i nn n n n n n n n n x K a x a x a x a x a x a x a x a x a x AX K 1 2 2 1 1 2 22 2 21 1 1 12 2 11 1 1 ... ... ... ! . Dengan membentuk 1 1 1 + = + -

å

® n n j j j n x K K

K pada [A|Y] = [A|AX], diperoleh [A|0]. Jadi

rk([A|Y]) = rk([A|0]) = rk(A).

Sekarang diandaikan bahwa r = rk(A) = rk([A|Y]). Ini berarti bahwa menjumlahkan suatu kolom tambahan ke A tidak merubah peringkat, dan karena itu, dengan serangkaian operasi kolom diperoleh [A|Y] ekuivalen dengan [A|0]. Diperhatikan bahwa tidak ada operasi tersebut yang merupakan suatu permutasi dari kolom-kolom, karena n kolom pertama dari [A|Y] dan [A|0] adalah sama. Ini berarti bahwa Y dapat diperoleh dari kolom-kolom Ki, 1 £ i £ n, dari A. Selanjutnya

å

= = n i i iK x Y 1 . Jadi penyelesaiannya adalah

ú ú ú ú û ù ê ê ê ê ë é = n x x x X ! 2 1 .n

(7)

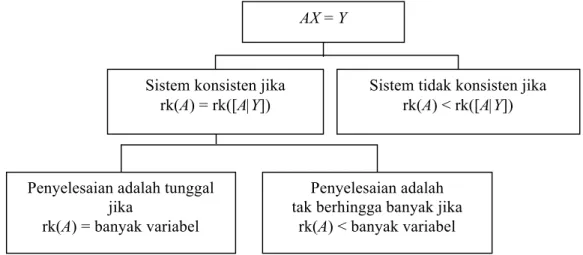
Secara ringkas, berikut ini disajikan skema ketunggalan dan eksistensi penyelesaian untuk suatu sistem linear.

Gambar 3.3: Skema ketunggalan dan eksistensi penyelesaian SPL

CONTOH 3.2.4 Tunjukkan apakah sistem AX = Y berikut ini adalah konsisten.

ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é ú ú ú û ù ê ê ê ë é 2 , 279 2 , 177 8 , 106 1 12 144 1 8 64 1 5 25 3 2 1 x x x .

Penyelesaian. Dibentuk matriks yang diperbesar dari sistem, yaitu

[

]

ú ú ú û ù ê ê ê ë é = 2 , 279 1 12 144 2 , 177 1 8 64 8 , 106 1 5 25 Y A .

Pada Contoh 2.2.1 diperoleh bahwa det(A) = –48 ¹ 0, karena itu rk([A|Y]) = 3 dan juga rk(A) = 3. Karena rk(A) = rk([A|Y]) maka sistem tersebut adalah konsisten.

Diberikan dua sistem persamaan linear homogen dalam n variabel yang mempunyai matriks koefisien A dan B. Jika setiap baris dari B adalah kombinasi linear dari baris-baris A (yaitu jumlahan dari kelipatan baris-baris A) dan setiap baris A adalah kombinasi linear dari baris-baris B, maka ini mudah dibuktikan bahwa dua sistem mempunyai penyelesaian yang sama. Sebaliknya adalah benar tetapi tidak mudah untuk dibuktikan. Sejalan dengan itu jika A dan B mempunyai bentuk eselon baris tereduksi yang sama, maka kedua sistem mempunyai penyelesaian yang sama dan sebaliknya juga benar.

Hal tersebut juga sejalan dalam kasus dua sistem yang tidak homogen, dengan syarat bahwa dalam pernyataan yang sebaliknya diperlukan kondisi tambahan bahwa kedua sistem adalah konsisten.

Lebih lanjut, untuk sistem linear konsisten yang berhubungan dengan dua atau lebih persamaan diperlukan sekali suatu metode yang sistematis agar dapat ditemukan semua penyelesaiannya. Penyelesaian sistem linear homogen maupun tak homogen yang konsisten dapat dicari dengan bermacam-macam cara. Berikut ini akan dibahas cara menyelesaikan sistem linear dengan menggunakan invers, aturan Cramer, eliminasi Gauss-Jordan, dan dekomposisi LU.

AX = Y

Sistem konsisten jika

rk(A) = rk([A|Y]) Sistem tidak konsisten jika rk(A) < rk([A|Y])

Penyelesaian adalah tunggal jika

rk(A) = banyak variabel

Penyelesaian adalah tak berhingga banyak jika

(8)

3.3 Menyelesaikan SPL Menggunakan Invers

Suatu sistem persamaan linier AX = Y dapat diselesaikan dengan menggunakan invers matriks dan aturan Cramer jika A merupakan matriks persegi tak singular.

TEOREMA 3.3.1 Jika A adalah tak singular, maka sistem AX = Y mempunyai

penyelesaian tunggal X = A-1Y. Bukti. Diandaikan bahwa A-1 ada.

1. (Ketunggalan) Diandaikan bahwa AX = Y, maka

( )

A-1AX = A-1Y Û InX = A-1Y Û X = A-1Y. 2. (Eksistensi) Diambil X = A-1Y, maka

( ) ( )

A Y AA Y I Y A

AX = -1 = -1 = n .n

CONTOH 3.3.1 Selesaikan sistem di bawah ini dengan menggunakan invers.

x + y + z = 6 2x + 3y + 4z = 20 4x + 2y + 3z = 17.

Penyelesaian. Dicari invers dari matriks koefisien sebagai berikut: [A|I3] = ú ú ú û ù ê ê ê ë é 1 0 0 0 1 0 0 0 1 3 2 4 4 3 2 1 1 1

®

-1 3 1 2 42b b b b ú ú ú û ù ê ê ê ë é -- 4 0 1 0 1 2 0 0 1 1 2 0 2 1 0 1 1 1

®

+ 1 3 2b b ú ú ú û ù ê ê ê ë é -1 2 8 0 1 2 0 0 1 3 0 0 2 1 0 1 1 1

®

3 3 1_b ú ú ú û ù ê ê ê ë é -3 1 3 2 3 8 0 1 2 0 0 1 1 0 0 2 1 0 1 1 1

®

-3 1 3 2 2 b b b b ú ú ú û ù ê ê ê ë é -3 1 3 2 3 8 3 2 3 1 3 10 3 1 3 2 3 11 1 0 0 0 1 0 0 1 1

®

1-b2 b ú ú ú û ù ê ê ê ë é -3 1 3 2 3 8 3 2 3 1 3 10 3 1 3 1 3 1 1 0 0 0 1 0 0 0 1 = [I3|A–1]. Diperoleh ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é ú ú ú û ù ê ê ê ë é -= ú ú ú û ù ê ê ê ë é 3 2 1 17 20 6 3 1 3 2 3 8 3 2 3 1 3 10 3 1 3 1 3 1 z y x .

3.4 Aturan Cramer

TEOREMA 3.4.1 (Aturan Cramer untuk 2 persamaan dalam 2 variabel)

Sistem

ax + by = e cx + dy = f

mempunyai penyelesaian tunggal jika D = ad – bc ¹ 0, yaitu x = D Dx _{dan y =} D Dy _, dengan Dx = d f b e dan Dy = f c e a .

(9)

Bukti. Diambil A =

_ú

û

ù

ê

ë

é

d

c

b

a

dan diandaikan D ¹ 0, maka

ú

û

ù

ê

ë

é

-D

=

-a

c

b

d

A

1 1 .

Berdasarkan Teorema 3.3.1 diperoleh bahwa sistem mempunyai penyelesaian tunggal

ú

û

ù

ê

ë

é

y

x

=

_ú

û

ù

ê

ë

é

-f

e

A

1 =

_ú

û

ù

ê

ë

é

ú

û

ù

ê

ë

é

-D

f

e

a

c

b

d

1

=

_ú

û

ù

ê

ë

é

+

-D

ce

af

bf

de

1

=

_ú

û

ù

ê

ë

é

D

y x

1

=

_ú

û

ù

ê

ë

é

D

y x . Karena itu x =

D

₁ dan y =

D

₂ .n

AKIBAT 3.4.1 Sistem homogen

ax + by = 0 cx + dy = 0

hanya mempunyai penyelesaian trivial jika D = ad – bc ¹ 0. CONTOH 3.4.1 Sistem

7x + 8y = 100 2x – 9y = 10 mempunyai penyelesaian tunggal x =

D Dx _{dan y =} D Dy _dengan D = 7(–9) – 2.8 = –79, Dx = 9 10 8 100 - = –980, Dy = 2 10 100 7 = –130. Jadi x = 79 980_{dan y =} 79 130_.

Secara umum, untuk sistem AX = Y dalam n persamaan dan n variabel x1, x2, …,

xn, dinotasikan D_x_i (i = 1,2, …n) adalah determinan untuk matriks yang diperoleh dari A dengan mengganti kolom ke-i, yang berkorespondensi dengan variabel xi, dengan kolom konstanta. Penyelesaian dari sistem adalah tunggal yang dirumuskan oleh

D D = xi

i

x , untuk i = 1, 2, …, n, dengan D adalah determinan dari matriks A.

CONTOH 3.4.2 Akan diselesaikan sistem pada Contoh 3.3.1 dengan menggunakan aturan Cramer. Pertama kali dihitung dulu determinan dari A yaitu det(A) = D = 3. Selanjutnya dari rumus Cramer di atas, diperoleh

3 3 2 17 4 3 20 1 1 6 = = Dx , 6 3 17 4 4 20 2 1 6 1 = = Dy , dan 9 17 2 4 20 3 2 6 1 1 = = Dz .

Karena itu penyelesaian untuk sistem yaitu 1 3 3 = = x , 2 3 6 = = y , 3 3 9 = = z .

(10)

3.5 Reduksi Baris

Jika matriks yang diperbesar dari SPL dibawa ke bentuk eselon baris (tereduksi) dengan serangkaian operasi baris elementer, maka penyelesaian dari sistem dapat diperoleh dari pengamatan.

CONTOH 3.5.1 Diberikan matriks yang diperbesar dari sistem dan sudah dibawa ke bentuk eselon baris tereduksi yaitu

ú ú ú û ù ê ê ê ë é -1 1 0 0 2 0 1 0 5 0 0 1 .

Jika variabel-variabel sistem adalah x1, x2, dan x3 untuk kolom 1, 2, dan 3 secara

berurutan, maka penyelesaian untuk sistem di atas yaitu x1 = 5, x2 = –2, dan x3 = 1.

CONTOH 3.5.2 Diberikan matriks yang diperbesar dari sistem mempunyai bentuk eselon baris tereduksi yaitu

ú ú ú û ù ê ê ê ë é -2 3 1 0 0 6 2 0 1 0 1 4 0 0 1 .

Dimisalkan variabel-variabel sistem adalah x1, x2, x3, dan x4 untuk kolom 1, 2, 3 dan 4

secara berurutan. Sistem persamaan yang berkorespondensi yaitu x1 + 4x4 = –1

x2 + 2x4 = 6

x3 + 3x4 = 2.

Karena kolom 1, 2, dan 3 memuat poros berarti variabel x1, x2, dan x3 sebagai variabel

utamanya, sedangkan x4 sebagai variabel bebasnya.

Selanjutnya dengan menyelesaikan sistem untuk variabel utama diperoleh x1 = –1 – 4x4

x2 = 6 – 2x4

x3 = 2 – 3x4.

Diambil nilai tertentu untuk x4, misalkan k, diperoleh penyelesaian sistem yaitu

x1 = –1 – 4k, x2 = 6 – 2k, dan x3 = 2 – 3k.

CONTOH 3.5.3 Diberikan matriks yang diperbesar dari sistem berbentuk eselon baris tereduksi yaitu

ú ú ú û ù ê ê ê ë é 1 0 0 0 0 2 1 0 0 0 0 1 .

Karena sistem memuat persamaan dengan bentuk 0x1 + 0x2 + 0x3 = 1 yang tidak pernah

mempunyai penyelesaian, maka sistem tersebut tidak konsisten.

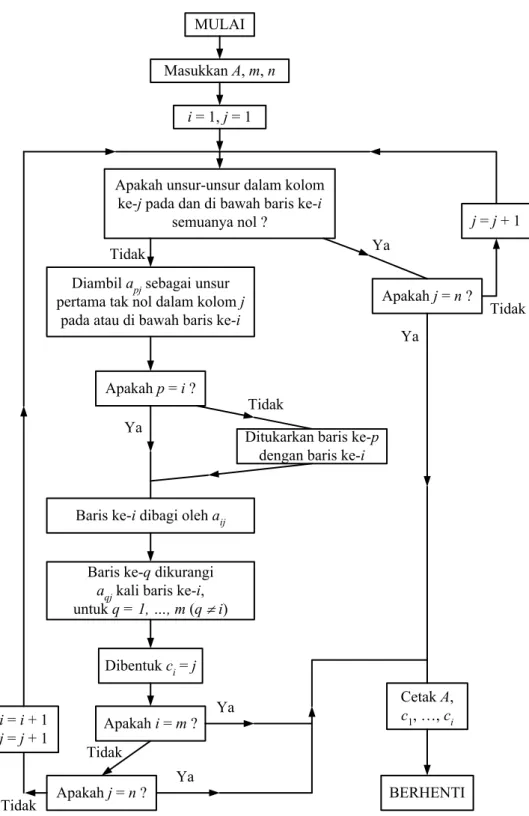
Secara umum, SPL dengan m persamaan dalam n variabel dapat diselesaikan dengan eliminasi Gauss (Jordan). Prosedur untuk menghasilkan bentuk eselon baris dinamakan eliminasi Gauss, sedangkan prosedur untuk menghasilkan bentuk eselon baris tereduksi dinamakan eliminasi Gauss-Jordan.

(11)

MULAI Masukkan A, m, n

i = 1, j = 1

Apakah unsur-unsur dalam kolom ke-j pada dan di bawah baris ke-i

semuanya nol ?

Apakah j = n ?

j = j + 1

Diambil a_pj sebagai unsur

pertama tak nol dalam kolom j pada atau di bawah baris ke-i

Apakah p = i ?

Ditukarkan baris ke-p dengan baris ke-i

Baris ke-i dibagi oleh a_ij

Baris ke-q dikurangi

a_qj kali baris ke-i,

untuk q = 1, …, m (q ¹ i) Dibentuk c_i = j Apakah i = m ? Apakah j = n ? Cetak A, c₁, …, c_i BERHENTI i = i + 1 j = j + 1 Ya Ya Ya Ya Ya Tidak Tidak Tidak Tidak Tidak

(12)

Berikut ini diberikan langkah-langkah eliminasi Gauss. Langkah 1: Tentukan kolom tak nol paling kiri.

Langkah 2: Jika unsur yang paling atas/ puncak dari kolom yang ditentukan dalam langkah pertama sama dengan nol, maka tukarkan baris atas dengan baris lain sehingga unsur puncak dari kolom tersebut adalah tidak nol.

Langkah 3: Jika unsur yang sekarang berada di puncak dari kolom yang ditentukan dalam langkah pertama tidak sama dengan nol, katakan a ¹ 0, maka baris pertama dikalikan dengan _a1_{agar diperoleh 1 utama.}

Langkah 4: Tambahkan kelipatan yang tepat dari baris teratas ke baris-baris di bawahnya sehingga semua unsur di bawah 1 utama sama dengan nol.

Langkah 5: Tutup baris paling atas dari matriks tersebut dan lakukan mulai langkah pertama lagi untuk matriks bagian yang tersisa.

CONTOH 3.5.4 Diberikan matriks

ú ú ú û ù ê ê ê ë é -1 15 6 5 4 2 28 12 6 10 4 2 12 7 0 2 0 0 .

Matriks tersebut dapat dibawa ke bentuk eselon baris dengan langkah : 1. Kolom tak nol paling kiri yaitu

2 2 0

2. Karena unsur puncak kolom tersebut adalah 0 maka baris pertama ditukar dengan baris kedua menjadi

ú ú ú û ù ê ê ê ë é -1 15 6 5 4 2 12 7 0 2 0 0 28 12 6 10 4 2 .

3. Karena unsur puncak dari kolom pertama sama dengan 2, maka baris pertama dibagi dua sehingga menjadi

ú ú ú û ù ê ê ê ë é -1 15 6 5 4 2 12 7 0 2 0 0 14 6 3 5 2 1

4. Unsur di bawah 1 utama pada kolom pertama dibuat sama dengan nol dengan cara baris ketiga dikurangi dua kali baris pertama, sehingga menjadi

ú ú ú û ù ê ê ê ë é -29 17 0 5 0 0 12 7 0 2 0 0 14 6 3 5 2 1

5. Dilakukan lagi seperti langkah pertama dan seterusnya dengan menutup baris pertama: ú ú ú û ù ê ê ê ë é -29 17 0 5 0 0 12 7 0 2 0 0 14 6 3 5 2 1

®

- ₂ 2 1_b ú ú ú û ù ê ê ê ë é -29 17 0 5 0 0 6 0 1 0 0 14 6 3 5 2 1 2 7 b

®

3-5b2

(13)

ú ú ú û ù ê ê ê ë é -1 0 0 0 0 6 0 1 0 0 14 6 3 5 2 1 2 12 7

®

2b3 ú ú ú û ù ê ê ê ë é -2 1 0 0 0 0 6 0 1 0 0 14 6 3 5 2 1 2 7 _.

Matriks yang terakhir sudah berbentuk eselon baris.

Selanjutnya untuk mendapatkan bentuk eselon baris tereduksi (eliminasi Gauss-Jordan) dari bentuk eselon baris, ditambahkan langkah berikut.

Langkah 6: Dimulai dari baris tak nol terakhir dan dikerjakan ke atas, ditambahkan kelipatan yang sesuai dari baris tak nol tersebut ke baris di atasnya untuk mendapatkan nilai nol di atas 1 utama.

CONTOH 3.5.5 Berikut ini dilanjutkan proses dari matriks eselon baris pada Contoh 3.5.4 untuk memperoleh bentuk eselon baris tereduksi:

ú ú ú û ù ê ê ê ë é -2 1 0 0 0 0 6 0 1 0 0 14 6 3 5 2 1 2 7

®

+₂7 3 2 b b ú ú ú û ù ê ê ê ë é -2 1 0 0 0 0 1 0 0 1 0 0 14 6 3 5 2 1

®

- 3 1 6b b ú ú ú û ù ê ê ê ë é -2 1 0 0 0 0 1 0 0 1 0 0 2 0 3 5 2 1

®

+ 2 1 5b b ú ú ú û ù ê ê ê ë é 2 1 0 0 0 0 1 0 0 1 0 0 7 0 3 0 2 1 . Matriks yang terakhir sudah berbentuk eselon barisan tereduksi.

CONTOH 3.5.6 Selesaikanlah sistem berikut dengan eliminasi Gauss-Jordan

x1 + 3x2 – 2x3 + 2x5 = 0

2x1 + 6x2 – 5x3 – 2x4 + 4x5 – 3x6 = –1

5x3 + 10x4 + 15x6 = 5

2x1 + 6x2 + 8x4 + 4x5 + 18x6 = 6.

Penyelesaian. Matriks yang diperbesar dari sistem tersebut adalah

ú ú ú ú û ù ê ê ê ê ë é -6 18 4 8 0 6 2 5 15 0 10 5 0 0 1 3 4 2 5 6 2 0 0 2 0 2 3 1 .

Selanjutnya dengan menggunakan eliminasi Gauss-Jordan, bentuk matriks yang diperbesar tersebut dibawa ke bentuk eselon baris tereduksi sebagai berikut:

ú ú ú ú û ù ê ê ê ê ë é -6 18 4 8 0 6 2 5 15 0 10 5 0 0 1 3 4 2 5 6 2 0 0 2 0 2 3 1

®

-1 4 1 2 2 2 b b b b ú ú ú ú û ù ê ê ê ê ë é -6 18 0 8 4 0 0 5 15 0 10 5 0 0 1 3 0 2 1 0 0 0 0 2 0 2 3 1

®

-b2 ú ú ú ú û ù ê ê ê ê ë é -6 18 0 8 4 0 0 5 15 0 10 5 0 0 1 3 0 2 1 0 0 0 0 2 0 2 3 1

®

-2 4 2 3 4 5 b b b b ú ú ú ú û ù ê ê ê ê ë é -2 6 0 0 0 0 0 0 0 0 0 0 0 0 1 3 0 2 1 0 0 0 0 2 0 2 3 1

®

«4 3 b b

(14)

ú ú ú ú û ù ê ê ê ê ë é -0 0 0 0 0 0 0 2 6 0 0 0 0 0 1 3 0 2 1 0 0 0 0 2 0 2 3 1

®

6 3 1_b ú ú ú ú û ù ê ê ê ê ë é -0 0 0 0 0 0 0 1 0 0 0 0 0 1 3 0 2 1 0 0 0 0 2 0 2 3 1 3 1

®

- ₂ 2 3b b ú ú ú ú û ù ê ê ê ê ë é -0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 2 1 0 0 0 0 2 0 2 3 1 3 1

®

+ ₂ 1 2b b ú ú ú ú û ù ê ê ê ê ë é 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 2 1 0 0 0 0 2 4 0 3 1 3 1

Matriks yang terakhir sudah berbentuk eselon baris tereduksi. Diperoleh sistem persamaan yang berkorespondensi yaitu

x1 + 3x2 + 4x4 + 2x5 = 0

x3 + 2x4 = 0

x6 = ₃1.

dan diselesaikan dalam variabel utama, diperoleh

x1 = –3x2 – 4x4 – 2x5

x3 = –2x4

x6 = ₃1.

Selanjutnya dengan mengambil nilai sebarang x2 = r, x4 = s dan x5 = t maka diperoleh

penyelesaian untuk sistem dengan rumus

x1 = –3r – 4s – 2t, x3 = –2s, dan x6 = ₃1.

Seringkali lebih disukai untuk menyelesaikan SPL dengan eliminasi Gauss. Apabila eliminasi ini dikerjakan maka untuk menentukan penyelesaian akhir dari sistem persamaan linear yang berkorespondensi digunakan teknik yang dinamakan substitusi balik (back-substitution) yaitu

1. Diselesaikan persamaan untuk variabel utama.

2. Dimulai dari persamaan paling bawah dan dikerjakan ke atas secara berurutan disubstitusikan setiap persamaan ke persamaan di atasnya.

3. Diambil sebarang nilai untuk variabel bebas, jika ada.

CONTOH 3.5.7 Pada Contoh 3.5.6 diperoleh matriks eselon baris yaitu

ú ú ú ú û ù ê ê ê ê ë é -0 0 0 0 0 0 0 1 0 0 0 0 0 1 3 0 2 1 0 0 0 0 2 0 2 3 1 3 1 .

Sistem persamaan yang berkorespondensi yaitu

x1 + 3x2 – 2x3 + 2x5 = 0

x3 + 2x4 + 3x6 = 1

x6 = ₃1.

Sistem diselesaikan dengan subsitusi balik sebagai berikut.

Pertama kali dinyatakan dulu persamaan di atas dalam variabel utama yaitu

(1) x1 = –3x2 + 2x3 – 2x5

(2) x3 = –2x4 – 3x6

(15)

Dengan mensubstitusikan nilai x6 dari persamaan (3) ke persamaan (2), diperoleh

x3 = –2x4 – 3(₃1) = –2x4 – 1.

Kemudian nilai x3 disubstitusikan ke persamaan (1), diperoleh

x1 = –3x2 + 2(–2x4 – 1) – 2x5 = –3x2 – 4x4 – 2x5 – 2.

Jika diambil sebarang nilai x2 = a, x4 = b dan x5 = c maka diperoleh penyelesaian akhir

untuk sistem yaitu

x1 = –3a – 4b – 2c – 2, x3 = –2b – 1, dan x6 = ₃1.

DEFINISI 3.5.1 Dalam eliminasi Gauss (Jordan), kelipatan (bilangan) dari suatu baris dikurangkan dari baris lainnya untuk memperoleh masukan nol disebut pengali (multiplier). Sebagai contoh, suatu operasi b3 – 2b1 memberikan suatu pengali m31 = 2.

3.6 Penyelesaian Sistematis dari SPL

Diberikan suatu sistem m persamaan linear dalam n variabel x1, x2, …, xn yang mempunyai matriks yang diperbesar M dan ekuivalen baris dengan matriks N yang mempunyai bentuk eselon baris tereduksi melalui eliminasi Gauss-Jordan. Berdasarkan hal tersebut maka M dan N berukuran m´(n+1). Diandaikan bahwa N mempunyai r baris tak nol dan bahwa 1 utama pada baris i terdapat pada kolom ci, untuk 1 £ i £ r, maka

1 £ c1 < c2 < …< cr £ n + 1.

Diandaikan juga bahwa kolom sisanya adalah kolom cr+1, …, cn+1 dengan 1 £ cr+1 < cr+2 < …< cn £ n + 1.

Kasus 1: cr = n + 1. Sistem adalah tidak konsisten. Untuk baris tak nol terakhir dari N yaitu (0, 0, …, 1) dengan persamaan yang berkorepondensi adalah

0x1 + 0x2 + … + 0xn = 1

tidak mempunyai penyelesaian. Akibatnya SPL tidak mempunyai penyelesaian.

Kasus 2: cr £ n. Sistem persamaan yang berkorespondensi dengan baris tak nol dari B adalah konsisten. Perlu dicatat bahwa r £ n.

Jika r = n, maka c1 = 1, c2 = 2, …, cn = n dan

ú ú ú ú ú ú ú ú ú û ù ê ê ê ê ê ê ê ê ê ë é = 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 2 1 ! " " ! ! " " ! ! n d d d N .

Dalam hal ini terdapat penyelesaian tunggal yaitu x1 = d1, x2 = d2, …, xn = dn.

Jika r < n, maka akan terdapat lebih dari satu penyelesaian. Untuk semua penyelesaian yang diperoleh dengan mengambil variabel

1 c x , …, r c x sebagai variabel tak bebas dan menggunakan r persamaan yang berkorespondensi dengan baris tak nol di N untuk menyatakan variabel tersebut dalam suku-suku dari variabel bebas sisanya yaitu

1 + r c x , …, n c

x , maka dapat diambil nilai sebarang:

1 c x = n n r r c c c c n b x b x b₁_, ₊₁- ₁_, ₊₁ ₊₁ -!- ₁_,

!

r c

x

= n n r r c rc c c r n r

b

x

b

x

b

_, ₁ _, _, 1 1

-

--

₊ ₊ +

!

.

(16)

Secara khusus, dengan mengambil

x

_c_r₊₁

=

...

=

x

_c_n_-₁

=

x

_c_n

=

0

, atau secara berurutan diambil 1, akan dihasilkan minimal dua penyelesaian untuk sistem.

CONTOH 3.6.1 Selesaikanlah sistem

x + y = 0 x – y = 1 4x + 2y = 1.

Penyelesaian. Matriks yang diperbesar dari sistem dan matriks reduksi barisnya, secara berturut-turut, yaitu

ú ú ú û ù ê ê ê ë é -= 1 2 4 1 1 1 0 1 1 M , ú ú ú û ù ê ê ê ë é -= 0 0 0 1 0 0 1 2 1 2 1 N .

Dari situ diperoleh penyelesaian tunggal _x₌1₂_dan 2 1

-=

y .

(Dalam hal ini n = 2, r = 2, c1 = 1, c2 = 2; cr = c2 = 2 < 3 = n + 1; r = n.)

2x1 + 2x2 – 2x3 = 5

7x1 + 7x2 + x3 = 10

5x1 + 5x2 – 3x3 = 5.

ú ú ú û ù ê ê ê ë é -= 5 1 5 5 10 1 7 7 5 2 2 2 M , ú ú ú û ù ê ê ê ë é = 1 0 0 0 0 1 0 0 0 0 1 1 N .

Dari situ diperoleh bahwa ternyata SPL tidak konsisten.

(Dalam hal ini n = 3, r = 3, c1 = 1, c2 = 3 dan juga cr = c3 = 4 = n + 1.)

x1 – x2 + x3 = 1

x1 + x2 – x3 = 2.

ú û ù ê ë é -= 2 1 1 1 1 1 1 1 M , ú ú û ù ê ê ë é -= 2 12 3 1 1 0 0 0 1 N .

Diperoleh penyelesaian lengkap yaitu x1 = ₂3, x2 = ₂1 + x3 dengan x3 adalah sebarang.

(Dalam hal ini n = 3, r = 2, c1 = 1, c2 = 2; cr = c2 = 2 < 4 = n + 1; r < n.)

6x3 + 2x4 – 4x5 – 8x6 = 8

3x3 + x4 – 2x5 – 4x6 = 4

2x1 – 3x2 + x3 + 4x4 – 7x5 + x6 = 2

6x1 – 9x2 + 11x4 – 19x5 + 3x6 = 1.

(17)

ú ú ú ú û ù ê ê ê ê ë é -= 1 3 19 11 0 9 6 2 1 7 4 1 3 2 4 4 2 1 3 0 0 8 8 4 2 6 0 0 M , ú ú ú ú ú û ù ê ê ê ê ê ë é -= 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 4 1 3 5 3 2 3 1 24 1 6 19 6 11 2 3 N .

Penyelesaian lengkap SPL, dengan x2, x4, x5 adalah sebarang, yaitu

x1 = ₂₄1 +3₂x₂ -11₆ x₄ +19₆ x₅,

x3 = ₃5-₃1x₄ +₃2x₅,

x6 = 1₄.

(Dalam hal ini n = 6, r = 3, c1 = 1, c2 = 3, c3 = 6; cr = c3 = 6 < 7 = n + 1; r < n.)

CONTOH 3.6.5 Tentukanlah bilangan rasional t agar sistem berikut ini konsisten dan selanjutnya selesaikan sistem untuk nilai t tersebut.

x + y = 2 x – y = 0 3x – y = t.

ú ú ú û ù ê ê ê ë é -= t M 1 3 0 1 1 2 1 1 , ú ú ú û ù ê ê ê ë é -= 2 0 0 1 1 0 2 1 1 t N .

Karena itu, jika t – 2 ¹ 0 atau t ¹ 2 maka sistem adalah tidak konsisten. Jika t = 2 maka sistem adalah konsisten dan

ú ú ú û ù ê ê ê ë é = 0 0 0 1 1 0 2 1 1 N ®

ú

û

ù

ê

ë

é

0

1

0

1

0

1

, sehingga diperoleh penyelesaian untuk sistem yaitu x = 1 dan y = 1.

CONTOH 3.6.6 Tentukanlah bilangan rasional a dan b dari sistem di bawah ini agar (i) tidak mempunyai penyelesaian, (ii) penyelesaiannya tunggal, (iii) penyelesaiannya tak berhingga banyak.

x – 2y + 3z = 4 2x – 3y + az = 5 3x – 4y + 5z = b.

Penyelesaian. Dilakukan reduksi baris pada matriks yang diperbesar dari sistem:

ú ú ú û ù ê ê ê ë é -b a 5 4 3 5 3 2 4 3 2 1

®

-1 3 1 2 32b b b b ú ú ú û ù ê ê ê ë é -12 4 2 0 3 6 1 0 4 3 2 1 b a

®

- ₂ 3 2b b ú ú ú û ù ê ê ê ë é -6 2 8 0 0 3 6 1 0 4 3 2 1 b a a

Kasus 1. Jika 8 – 2a ¹ 0 atau a ¹ 4 maka matriks dapat direduksi ke bentuk

ú ú ú û ù ê ê ê ë é + -2-68 1 0 0 0 1 0 0 0 1 a b v u

dan diperoleh penyelesaian tunggal yaitu x = u, y = v, dan ₂ 6₈ + -

-= b_a

(18)

Kasus 2. Jika a = 4, maka diperoleh matriks ú ú ú û ù ê ê ê ë é -6 0 0 0 3 2 1 0 4 3 2 1 b .

Jika b – 6 ¹ 0 atau b ¹ 6 maka sistem tidak mempunyai penyelesaian. Sebaliknya jika b = 6 maka diperoleh penyelesaian lengkap yaitu x = z – 2 dan y = 2z –3 untuk sebarang z.

Berikut ini adalah prinsip yang umum untuk sistem AX = Y.

Suatu sistem linear adalah tidak konsisten jika bentuk eselon baris A memuat suatu baris nol dan ruas kanan dari persamaan yang berkorespondensi tidak sama dengan nol. Jika bentuk eselon baris dari matriks A tidak memuat suatu baris nol, maka sistem selalu konsisten, dengan mengabaikan ruas kanan.

Jika setiap kolom pada bentuk eselon baris dari matriks koefisien memuat 1 utama dari suatu baris, maka sistem linear tidak akan pernah mempunyai lebih dari satu penyelesaian.

Di sisi lain, jika suatu kolom tidak memuat 1 utama untuk suatu baris, maka variabelnya dapat berupa himpunan sebarang dan akibatnya jika terdapat suatu penyelesaian, maka penyelesaian tersebut tak berhingga banyaknya.

Cara lain menyatakan prinsip kedua yaitu apakah suatu sistem linear dapat mempunyai lebih dari satu penyelesaian atau tidak, tergantung pada apakah bentuk eselon baris dari matriks koefisien mempunyai kolom yang lebih banyak daripada baris tak nol. (Catat bahwa bentuk eselon baris tidak mungkin mempunyai kolom yang lebih sedikit dari baris tak nol. (Kenapa?))

Secara khusus, jika matriks koefisien asli mempunyai kolom lebih banyak dari baris, maka sistem tidak hanya mempunyai satu penyelesaian. Aplikasinya adalah Lemma 3.2.1 yang sudah dibicarakan lebih dulu.

3.7 Dekomposisi-LU

Sekarang diandaikan bahwa diperlukan untuk menyelesaikan AX = Y secara berulang, untuk suatu matriks A berukuran n´n tetapi untuk ruas kanan Y berganda. Dalam hal ini dapat dimanfaatkan faktorisasi (hasil kali matriks elementer). Asumsinya yaitu bahwa A dapat direduksi ke bentuk eselon baris tanpa menukarkan baris. Alasan untuk asumsi tersebut yaitu bahwa pengembangannya lebih sederhana.

Jadi dipunyai matriks elementer E1, E2, …, Ek, yang menyatakan jumlahan suatu kelipatan sembarang baris i ke sembarang baris j, dengan i > j, sehingga EkEk–1 …E1A =

U, suatu matriks ekuivalen baris dalam bentuk eselon baris. Karena E ada untuk setiap _i-1 1 ≤ i ≤ k, maka A=E₁-1E₂-1...E_k-1U. Berdasarkan aksi dari setiap matriks, dapat dilihat bahwa setiap matriks tersebut adalah segitiga bawah, dan karena itu E juga segitiga _i-1 bawah. Pada kenyataannya, matriks Ei dan E adalah segitiga bawah satuan (unit lower _i-1

(19)

triangular), yang berarti bahwa semua masukan diagonal utamanya adalah 1. Diketahui bahwa hasil kali matriks-matriks segitiga bawah satuan adalah segitiga bawah satuan, sehingga diketahui juga bahwa E₁-1E₂-1...E_k-1 adalah segitiga bawah satuan. Diambil L yang menotasikan hasil kali tersebut, dipunyai A = LU, hasil kali dari suatu matriks segitiga bawah dengan matriks segitiga atas. Faktorisasi dari A tersebut dikenal sebagai dekomposisi LU (LU-decomposition) dari A.

Gambar 3.5: Dekomposisi LU dari matriks n´n

Selanjutnya, menyelesaikan AX = Y adalah ekuivalen dengan menyelesaikan LUX = Y. Kenapa ini penting? Dapat diselesaikan LUX = Y dengan menyelesaikan serangkaian sistem segitiga. Pertama kali diselesaikan LZ = Y menggunakan substitusi maju, atau seringkali disebut eliminasi maju. Diselesaikan sistem persamaan yang berkorespondensi dengan proses awal Y menggunakan operasi baris elementer yang sama dengan yang digunakan untuk mereduksi A ke bentuk eselon baris. Sekarang diselesaikan UX = Z dengan substitusi balik untuk memperoleh penyelesaian vektor X.

Sudah dilihat bahwa U adalah bentuk eselon baris dari A yang dihasilkan oleh eliminasi Gauss, tetapi bagaimana menghitung L dalam prakteknya? Diketahui bahwa L adalah segitiga bawah satuan, jadi masukan diagonal dan superdiagonal diketahui. Mulai dari kiri ke kanan, dicatat informasi yang dibangun selama eliminasi, mulai kolom 1. Untuk setiap i = 2, …, n, diambil

11 1 1

a a

m_i = i . Selanjutnya baris i, 2 ≤ i ≤ n, dikurangi dengan mi1 kali baris 1 untuk menghapus masukan (i,1). Dinotasikan A(2) =

( )

a_ij(2) sebagai matriks yang diperoleh dengan menghapus semua masukan kolom 1 di bawah poros. (Ingat, bahwa asumsinya adalah tidak ada penukaran baris). Selanjutnya untuk setiap i = 3, …, n, diambil ) 2 ( 22 ) 2 ( 2 2 a a

m_i = i , dan baris i dikurangi dengan mi2 kali baris 2. Ini akan menghapus semua masukan kolom 2 di bawah poros. Dilanjutkan cara tersebut, dan diakhiri sampai dengan

ú ú ú ú û ù ê ê ê ê ë é = ) ( ) 2 ( 2 ) 2 ( 22 1 12 11 0 0 0 n nn n n a a a a a a U ! ! " " " " " ! ! ! ! , untuk memperoleh ú ú ú ú ú ú û ù ê ê ê ê ê ê ë é = - 1 0 0 0 1 0 0 1 0 0 0 1 1 , 2 1 32 31 21 n n n n m m m m m m L ! ! " # # # # ! ! ! ! ! .

(20)

CONTOH 3.7.1 Tentukan dekomposisi LU dari matriks ú ú ú û ù ê ê ê ë é = 3 2 4 4 3 2 1 1 1 A .

Penyelesaian. Pertama kali, faktorisasi dari matriks A dimisalkan oleh

LU u u u u u u m m m A = ú ú ú û ù ê ê ê ë é ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é = 33 23 22 13 12 11 32 31 21 0 0 0 1 0 1 0 0 1 3 2 4 4 3 2 1 1 1 . Dicari matriks U dengan menerapkan eliminasi Gauss pada matriks A:

U A b b b b b b = ú ú ú û ù ê ê ê ë é ú ú ú û ù ê ê ê ë é -ú ú ú û ù ê ê ê ë é =

®

- -

®

-3 0 0 2 1 0 1 1 1 1 2 0 2 1 0 1 1 1 3 2 4 4 3 2 1 1 1 ₄2 , ₍ ₂ ₎ 2 3 1 3 1 2 .

Selanjutnya diperhatikan langkah-langkah eliminasi Gauss di atas untuk menentukan unsur-unsur m21, m31, dan m32 pada matriks L, yaitu :

(i) unsur m21 berkorespondensi dengan a21 = 2 yang pengali pembuat nolnya adalah 2

(b2 ® b2 – 2b1), karena itu m21 = 2,

(ii) unsur m31 berkorespondensi dengan a31 = 4 yang pengali pembuat nolnya adalah 4

(b3 ® b3 – 4b1), karena itu m31 = 4, dan

(iii) unsur m32 berkorespondensi dengan –2 yang pengali pembuat nolnya adalah –2 (b3

® b3 – (–2b2)), karena itu m32 = –2.

Jadi, dekomposisi LU untuk matriks A yaitu

ú ú ú û ù ê ê ê ë é ú ú ú û ù ê ê ê ë é -= ú ú ú û ù ê ê ê ë é 3 0 0 2 1 0 1 1 1 1 2 4 0 1 2 0 0 1 3 2 4 4 3 2 1 1 1 .

Secara ringkas, langkah-langkah untuk mendapatkan penyelesaian dari SPL dengan menggunakan metode dekomposisi LU adalah sebagai berikut :

1. Dibentuk sistem AX = Y. 2. Ditentukan A = LU.

3. Diselesaikan persamaan LZ = Y dengan Z = [z1 z2 … zn]T. 4. Diselesaikan persamaan UX = Z.

CONTOH 3.7.2 Selesaikan SPL berikut dengan metode dekomposisi LU

x1 + x2 + x3 = 6

2x1 + 3x2 + 4x3 = 20

4x1 + 2x2 + 3x3 = 17

Penyelesaian.

Langkah 1. Dibentuk sistem AX = Y sebagai berikut

ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é ú ú ú û ù ê ê ê ë é 17 20 6 3 2 4 4 3 2 1 1 1 3 2 1 x x x . Langkah 2. Ditentukan A = LU (ini sudah diperoleh di Contoh 3.7.1).

(21)

ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é ú ú ú û ù ê ê ê ë é - 17 20 6 1 2 4 0 1 2 0 0 1 3 2 1 z z z ® ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é + -+ 17 20 6 2 4 2 3 2 1 2 1 1 z z z z z z . Diperoleh z1 = 6, z2 = 20 – 2.6 = 8, dan z3 = 17 – 4.6 + 2.8 = 9.

Langkah 4. Dibentuk persamaan UX = Z dan diselesaikan sebagai berikut

ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é ú ú ú û ù ê ê ê ë é 9 8 6 3 0 0 2 1 0 1 1 1 3 2 1 x x x ® ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é + + + 9 8 6 3 2 3 3 2 3 2 1 x x x x x x . Dari persamaan yang terakhir diperoleh penyelesaian sistem yaitu

x3 = 3, x2 = 8 – 2.3 = 2, dan x1 = 6 – 2 – 3 = 1.

3.8 Aplikasi Sistem Persamaan Linear

3.8.1 Sirkuit elektrik (electric circuits)

Satu aplikasi penting aljabar linear untuk elektronika adalah menganalisa sirkuit elektrik. Sasarannya yaitu menghitung arus yang mengalir dalam setiap cabang sirkuit atau menghitung tegangan di setiap titik sirkuit. Terdapat dua analisa, yaitu analisa simpul (loop analysis) untuk menemukan arus secara langsung, dan analisa titik (nodal analysis) untuk menemukan tegangan secara langsung.

Dalam aplikasi ini diperlukan konsep-konsep dari elektronika: 1. Istilah dan simbol sirkuit elektrik:

• Simbol untuk sumber tegangan (yang menyebabkan arus elektrik mengalir dalam sirkuit).

• Simbol untuk resistor (alat penghambat aliran arus elektrik). • Simbol untuk kabel (diasumsikan tidak mempunyai hambatan). 2. Titik utama dan cabang:

• Simbol untuk suatu titik utama (principal node), yaitu suatu titik dengan 3 atau lebih kabel bertemu.

• Cabang: suatu lintasan (path) dalam sirkuit yang mempunyai suatu titik pada setiap ujung dan memuat minimal satu sumber tegangan atau resistor tetapi titik memuat titik lainnya.

3. Hukum Arus Kirchoff: jumlah arus yang mengalir ke suatu titik sama dengan jumlah arus yang mengalir keluar dari titik.

4. Persamaan Hukum Ohm: V = IR, dengan V adalah beda tegangan antara dua ujung resistor yang diukur dalam volt, I adalah arus yang melalui resistor diukur dalam ampere, dan R adalah resistansi resistor diukur dalam ohm.

5. Hukum Tegangan Kirchoff: di sekitar suatu lintasan tertutup (closed path) dalam suatu sirkuit elektrik, jumlah kenaikan tegangan melalui sumber tegangan sama dengan jumlah penurunan tegangan yang melalui resistor.

Analisa arus simpul sirkuit elektrik

Dalam metode ini, dibentuk dan diselesaikan suatu sistem persamaan dalam variabel-variabel arus simpul. Arus dalam berbagai cabang sirkuit mudah ditentukan dari arus simpul.

Langkah-langkah dalam metode arus simpul:

(22)

2. Dipilih m arus simpul yang saling bebas, namakan I1, I2, …, Im, dan dituliskan pada diagram sirkuit

3. Diaplikasikan Hukum Tegangan Kirchoff untuk setiap simpul. Hasilnya adalah sistem m persamaan linear dalam m variabel arus simpul berbentuk:

ï ï î ï ï í ì = + + + = + + + = + + + m m mm m m m m m m V I R I R I R V I R I R I R V I R I R I R ... ... ... 2 2 1 1 2 2 2 22 1 21 1 1 2 12 1 11 !

dengan R11, R12, …, Rmm dan V1, V2, …, Vm adalah konstanta.

4. Selesaikan sistem persamaan untuk m arus simpul I1, I2, …, Im menggunakan metode yang sudah dipelajari.

5. Susun kembali arus-arus cabang dari arus simpul.

CONTOH 3.8.1 Tentukan arus yang mengalir dalam setiap cabang sirkuit elektrik di bawah ini.

Penyelesaian.

Langkah 1. Ditentukan banyaknya arus simpul yang diperlukan, yaitu 3.

Langkah 2. Dipilih arus simpul seperti yang ditunjukkan pada gambar di bawah ini.

Langkah 3. Dinyatakan Hukum Tegangan Kirchoff untuk setiap simpul. Hasilnya adalah sistem persamaan berikut:

ï î ï í ì = + -+ -= -+ + -= -+ -+ 0 55 ) ( 1 ) ( 50 0 ) ( 1 30 ) ( 25 10 ) ( 50 ) ( 25 1 3 2 3 1 3 3 2 2 1 2 3 1 2 1 1 I I I I I I I I I I I I I I I . Setelah disederhanakan menjadi:

ï î ï í ì = + -= -+ -= -0 106 1 50 0 1 56 25 10 50 25 76 2 2 1 3 2 1 3 2 1 I I I I I I I I I .

Langkah 4. Diselesaikan sistem persamaan menggunakan metode yang sudah dipelajari untuk memperoleh arus (semua diukur dalam ampere):

(23)

Bab 3 Sistem Persamaan Linear 73

Langkah 5. Disusun kembali arus cabang dari arus simpul yang memberikan hasil seperti yang ditunjukkan pada gambar berikut.

CONTOH 3.8.2 Tentukan arus yang mengalir dalam setiap cabang sirkuit di bawah ini.

Penyelesaian.

Langkah 1. Banyaknya arus simpul yang diperlukan adalah 3.

Langkah 2. Dipilih arus simpul seperti yang ditunjukkan pada gambar berikut ini.

Langkah 3. Dinyatakan Hukum Tegangan Kirchoff untuk setiap simpul. Hasilnya adalah sistem persamaan berikut:

ï î ï í ì -= + + + -= + + + + + -= + + + 2000 2000 ) ( 5 35 25 1000 2000 ) ( 5 40 ) ( 20 15 1000 1000 30 ) ( 20 10 2 3 3 3 3 2 2 1 2 2 1 2 1 1 I I I I I I I I I I I I I I

Sistem disederhanakan menjadi:

ï î ï í ì = + + = + + = + + 0 65 5 0 1000 5 80 20 0 0 20 60 3 2 1 3 2 1 3 2 1 I I I I I I I I I

(24)

Langkah 4. Diselesaikan sistem persamaan menggunakan metode yang sudah dipelajari untuk memperoleh arus (semua diukur dalam ampere):

I1 = –4,57; I2 = 13,7 dan I3 = –1,05

Langkah 5. Disusun kembali arus cabang dari arus simpul yang memberikan hasil seperti yang ditunjukkan pada gambar di bawah ini.

Analisa tegangan titik dari sirkuit elektrik

Dalam metode ini dibentuk dan diselesaikan suatu sistem persamaan dengan variabelnya adalah tegangan pada titik utama sirkuit.

Langkah-langkah dalam metode analisis titik:

1. Dihitung banyaknya titik utama dalam sirkuit, misalkan n.

2. Ditetapkan titik N1, N2, …, Nn dan dinyatakan pada diagram sirkuit. Tegangan pada titik tersebut berturut-turut dinamakan V1, V2, …, Vn.

3. Dipilih satu titik untuk menjadi titik acuan dan disyaratkan tegangannya 0.

4. Untuk setiap titik kecuali titik acuan, dinyatakan Hukum Arus Kirchoff dalam bentuk jumlahan aljabar dari arus yang mengalir keluar dari suatu titik sama dengan nol.

Diperhatikan gambar-gambar di bawah ini.

(a) (b) (c) (d)

Sebagai contoh, untuk titik N pada gambar (a) di atas akan dihasilkan persamaan:

Ia + Ib + Ic = 0.

Arus dalam setiap cabang dinyatakan dalam suku-suku tegangan titik pada setiap akhir cabang menggunakan hukum Ohm (I = V/R). Sebagai contoh, untuk gambar (b) arus yang mengalir ke bawah dari titik N1 tergantung pada beda

tegangan V1 – V3 dan hambatan dalam cabang.

Dalam kasus gambar (c), beda tegangan yang melewati hambatan adalah V1 – V2 kurang dari tegangan yang melewati sumber tegangan. Jadi arus yang

mengalir ke bawah adalah seperti yang ditunjukkan.

Dalam kasus gambar (d), beda tegangan yang melewati hambatan harus 100 volt lebih besar dari pada V1 – V2. Jadi arus yang mengalir adalah seperti

(25)

Hasil, setelah disederhanakan, adalah suatu sistem m persamaan linear dalam m variabel tegangan titik (dengan m = n – 1):

ï ï î ï ï í ì = + + + = + + + = + + + m m mm m m m m m m I V G V G V G I V G V G V G I V G V G V G ... ... ... 2 2 1 1 2 2 2 22 1 21 1 1 2 12 1 11 !

dengan G11, G12, …, Gmm dan I1, I2, …, Im adalah konstanta.

5. Diselesaikan sistem persamaan untuk m titik tegangan V1, V2, …, Vn.

CONTOH 3.8.3 Gunakan analisa titik untuk menemukan tegangan dari setiap titik pada sirkuit di bawah ini.

Penyelesaian.

Langkah 1. Dicatat bahwa ”pasangan titik” pada bagian bawah sebenarnya adalah 1 titik. Jadi banyaknya titik utama sirkuit adalah 3.

Langkah 2. Ditetapkan titik utama pada diagram sirkuit.

Langkah 3. Dipilih titik N2 sebagai titik acuan dan disyaratkan tegangannya nol.

Langkah 4. Diaplikasikan Hukum Arus Kirchoff untuk setiap titik.

Dimisalkan V1 adalah tegangan pada titik N1, dan V3 adalah tegangan

pada titik N3, serta diingat bahwa V2 = 0. Diperoleh sistem persamaan:

ï î ï í ì = + + -= -+ -+ 0 20 10 10 0 10 5 100 30 3 3 1 3 3 1 1 1 V V V V V V V V .

Persamaan pertama dihasilkan dari Hukum Arus Kirchoff yang diaplikasikan pada titik N1 dan persamaan kedua dihasilkan dari Hukum

Arus Kirchoff pada titik N3. Dikumpulkan suku-suku tersebut menjadi:

ï ï î ïï í ì = ÷ ø ö ç è æ ₊ ₊ + ÷ ø ö ç è æ -= ÷ ø ö ç è æ -÷ ø ö ç è æ ₊ ₊ 0 20 1 10 1 10 1 10 1 20 10 1 10 1 5 1 30 1 3 1 3 1 V V V V .

(26)

CONTOH 3.8.4 Gunakan analisa titik untuk menemukan tegangan dari setiap titik pada sirkuit di bawah ini.

Penyelesaian.

Langkah 1. Ditentukan banyaknya titik utama yaitu 4. Langkah 2. Ditetapkan titik utama pada diagram sirkuit.

Langkah 4. Diaplikasikan Hukum Arus Kirchoff untuk setiap titik. Dimisalkan V1

tegangan pada titik N1, V3 tegangan pada titik N3, V4 tegangan pada titik

N4, dan diingat bahwa V2 = 0. Hasilnya adalah sistem persamaan berikut:

ï ï ï î ïï ï í ì = + + -+ + -= + -+ -+ -= + -+ -+ 0 60 300 100 120 20 20 0 100 120 20 30 250 0 30 250 90 200 15 4 3 4 4 3 4 4 3 4 3 1 3 3 1 1 1 V V V V V V V V V V V V V V V V .

Persamaan pertama, kedua, dan ketiga dihasilkan dari Hukum Arus Kirchoff yang diaplikasikan berturut-turut pada titik N1, N3, dan N4.

Suku-suku persamaan tersebut dikumpulkan menjadi:

ï ï ï î ï ï ï í ì -= ÷ ø ö ç è æ ₊ ₊ ₊ + ÷ ø ö ç è æ ₊ -= ÷ ø ö ç è æ ₊ -÷ ø ö ç è æ ₊ ₊ + -= -÷ ø ö ç è æ ₊ ₊ 60 300 100 120 60 1 100 1 20 1 20 1 100 1 20 1 100 120 30 250 100 1 20 1 100 1 20 1 30 1 30 1 30 250 90 200 30 1 30 1 90 1 15 1 4 3 4 3 1 3 1 V V V V V V V .

(27)

CONTOH 3.8.5 Gunakan analisa titik untuk menemukan tegangan setiap titik pada sirkuit di bawah ini.

Penyelesaian.

Langkah 1. Ditentukan banyaknya titik utama yaitu 4. Langkah 2. Ditetapkan titik utama pada diagram sirkuit.

Langkah 4. Diaplikasikan Hukum Arus Kirchoff untuk setiap titik. Dimisalkan V1

tegangan pada titik N1, V2 tegangan pada titik N2, V3 tegangan pada titik

N3, dan diingat bahwa V4 = 0. Hasilnya adalah sistem persamaan berikut:

ï ï ï î ïï ï í ì = -+ -+ -= + + -+ + -= -+ -+ -0 60 2000 5 2000 15 0 40 40 1000 20 1000 0 15 40 1000 20 1000 3 3 1 3 2 1 2 1 2 3 1 2 1 2 1 V V V V V V V V V V V V V V V .

Persamaan pertama, kedua, dan ketiga dihasilkan dari Hukum Arus Kirchoff yang diaplikasikan berturut-turut pada titik 1, 2, dan 3. Dikumpulkan suku-suku tersebut menjadi:

ï ï ï î ï ï ï í ì + = ÷ ø ö ç è æ ₊ ₊ + -= ÷ ø ö ç è æ ₊ ₊ + ÷ ø ö ç è æ ₊ -+ = -÷ ø ö ç è æ ₊ -÷ ø ö ç è æ ₊ ₊ 60 2000 5 2000 60 1 5 1 15 1 15 1 40 1000 20 1000 40 1 40 1 20 1 40 1 20 1 40 1000 20 1000 15 1 40 1 20 1 15 1 40 1 20 1 3 1 2 1 3 2 1 V V V V V V V .

Langkah 5. Diselesaikan sistem di atas untuk memperoleh:

(28)

Bab 3 Sistem Persamaan Linear 78 F _E D 600 400 400 1600 w v u z t

3.8.2 Jaringan lalu lintas (traffic network)

Jaringan di bawah ini menggambarkan arus lalu lintas yang melalui suatu kompleks jalan tertentu. (Banyaknya arus dinyatakan oleh rata-rata arus ke dalam dan ke luar jaringan pada saat puncak kesibukan lalu lintas)

Dengan Hukum Arus Kirchoff, dihasilkan sistem sebagai berikut: 800 = x + v (A) u + x = y + 400 (B) y = z + 600 (C) 1600 + z = t + 400 (D) t = u + w (E) u + w = 1000 (F). Matriks yang diperbesar dari sistem adalah

ú ú ú ú ú ú ú ú û ù ê ê ê ê ê ê ê ê ë é -1000 0 1 1 0 0 0 0 0 1 1 0 1 0 0 0 1200 1 0 0 0 1 0 0 600 0 0 0 0 1 1 0 400 0 0 0 1 0 1 1 800 0 0 1 0 0 0 1 .

yang ekuivalen baris dengan

ú ú ú ú ú ú ú ú û ù ê ê ê ê ê ê ê ê ë é -0 0 0 0 0 0 0 0 1000 0 1 1 0 0 0 0 1000 1 0 1 1 0 0 0 200 0 0 1 1 1 0 0 400 0 0 1 1 0 1 0 800 0 0 1 0 0 0 1 .

Lebih lanjut penyelesaiannya yaitu

x = w – 200 y = t – 600 z = t – 1200 u = t – w v = 1000 – w.

Sebagai contoh, jika w = 300 dan t = 1300 (kendaraan per jam), maka x = 100, y = 700, z = 100, u = 1000, dan v = 700.

(29)

Sekarang diandaikan bahwa jalan dari A ke B dan dari B ke C harus ditutup (misalnya untuk perbaikan), berarti x = 0 dan y = 0. Bagaimana kemungkinan lalu lintasnya?

Untuk menjawab pertanyaan ini, ditetapkan x = y = 0 dalam penyelesaian di atas, diperoleh w = 200, t = 600, z = –600, u = 400, dan v = 800. Tentu saja, nilai negatif untuk z adalah tidak normal. Dihindari arus negatif, sehingga harus dibalik arah jalan yang menghubungkan C dan D, dan diubah menjadi z = 600.

3.8.3 Persamaan-persamaan kimia

Aplikasi sistem linear untuk kimia adalah keseimbangan suatu persamaan kimia. Alasan pemikiran ini adalah hukum kekekalan massa yang dinyatakan sebagai berikut:

”Massa tidak diciptakan atau dimusnahkan dalam reaksi kimia yang manapun. Oleh karena itu penyeimbangan persamaan memerlukan jumlah atom yang sama

pada kedua sisi dari suatu reaksi kimia. Massa dari semua komponen reaktan (unsur yang memasuki suatu reaksi) harus sama dengan massa dari produk

(unsur yang dihasilkan oleh reaksi).” Sebagai contoh, diberikan persamaan kimia sebagai berikut

C2H6 + O2 ® CO2 + H2O.

Menyeimbangkan reaksi kimia tersebut sama artinya dengan mencari nilai x, y, z, dan t sehingga banyaknya atom dari setiap unsur adalah sama pada kedua sisi persamaan:

xC2H6 + yO2 ® zCO2 + tH2O.

Diperoleh sistem persamaan linear:

2x = z 6x = 2t 2y = 2z + t. Penyelesaian umum dari sistem di atas adalah

y = 7₂x z = 2x t = 3x.

Dipilih x = 2 dan diperoleh y = 7, z = 4, t = 6. Persamaan yang seimbang adalah: 2C2H6 + 7O2 ® 4CO2 + 6H2O.

3.8.4 Model ekonomi untuk pertukaran barang

Dalam rangka memahami dan mampu menggerakkan ekonomi suatu negara atau suatu daerah, orang harus sampai pada suatu model tertentu berdasarkan berbagai sektor ekonomi. Model Leontief adalah suatu usaha dalam arah ini. Didasarkan pada asumsi bahwa setiap industri dalam ekonomi mempunyai dua jenis permintaan: permintaan eksternal (dari luar sistem) dan permintaan internal (permintaan pada satu industri oleh yang lainnya tetapi dalam sistem yang sama), model Leontief menggambarkan ekonomi sebagai sistem persamaan linier. Model Leontief ditemukan oleh Profesor Wassily Leontief yang mengembangkan suatu model ekonomi yang menyangkut ekonomi Amerika Serikat dengan membaginya ke dalam 500 sektor ekonomi. (Pada tanggal 18 Oktober 1973, Profesor Leontief mendapatkan penghargaan Nobel dalam ekonomi.)

(30)

Model Leontief Tertutup

Dipertimbangkan suatu ekonomi yang terdiri dari n industri (sektor) yang saling tergantung S1, S2, …, Sn. Ini berarti bahwa setiap industri memakai beberapa barang yang diproduksi oleh industri lain, termasuk dari dirinya sendiri. Suatu ekonomi dikatakan tertutup jika terpenuhi dari kebutuhannya sendiri, berarti tidak ada barang yang keluar atau masuk sistem. Diambil mij adalah banyaknya unit yang diproduksi oleh industri Si dan dipakai untuk memproduksi satu unit dari industri Sj. Jika pj adalah tingkat produksi dari industri Sj, maka mijpj menyatakan banyaknya unit yang diproduksi oleh industri Si dan dipakai oleh industri Sj. Jadi jumlah total unit yang diproduksi oleh industri Si adalah

p1mi1 + p2mi2 + … + pnmin.

Untuk menyeimbangkan ekonomi, total produksi dari setiap industri harus sama dengan total pemakaian. Diperoleh sistem linear:

m11p1 + m12p2 + … + m1npn = p1 m21p1 + m22p2 + … + m2npn = p2

!

mn1p1 + mn2p2 + … + mnnpn = pn. Jika diambil ú ú ú ú û ù ê ê ê ê ë é = nn n n n n m m m m m m m m m A ! " " " " ! ! 2 1 2 22 21 1 12 11

maka sistem dapat dituliskan sebagai AP = P, dengan

ú ú ú ú û ù ê ê ê ê ë é = n p p p P ! 2 1 ,

dan A disebut matriks masukan-keluaran (input-output matrix).

Selanjutnya dilihat vektor kolom P yang memenuhi AP = P dan unsur-unsurnya tak negatif.

CONTOH 3.8.6 Diandaikan bahwa ekonomi suatu daerah tertentu tergantung pada tiga industri: pelayanan, elektrisitas, dan produksi minyak. Berdasarkan pengawasan operasi terhadap tiga industri tersebut atas periode satu tahun diperoleh pengamatan sebagai berikut:

1. Untuk memproduksi 1 unit pelayanan, industri pelayanan harus memakai 0,3 unit dari produknya sendiri, 0,3 unit elektrisitas dan 0,3 unit minyak untuk menjalankan operasinya.

2. Untuk memproduksi 1 unit elektrisitas, pabrik pembangkit daya harus membeli 0,4 unit pelayanan, 0,1 unit dari produksinya sendiri, dan 0,5 unit minyak.

3. Terakhir, perusahaan yang memproduksi minyak memerlukan 0,3 unit pelayanan, 0,6 unit elektrisitas dan 0,2 unit dari produksinya sendiri untuk memproduksi 1 unit minyak.

Tentukan tingkat produksi dari setiap industri tersebut dalam rangka memenuhi permintaan internal dan eksternal dengan asumsi bahwa model di atas adalah tertutup. Penyelesaian.

Diambil variabel-variabel sebagai berikut: