BAB II
LANDASAN TEORI
Antrian adalah suatu kejadian yang biasa dijumpai dalam kehidupan sehari–hari. Seperti menunggu di depan loket untuk mendapatkan tiket kereta api atau tiket bioskop, pada pintu jalan tol, pada bank, pada kasir supermarket, dan situasi–situasi yang lain merupakan kejadian yang sering ditemui. Studi tentang antrian bukan merupakan hal yang baru.
Antrian disebabkan oleh kebutuhan akan layanan melebihi kemampuan (kapasitas) pelayanan atau fasilitas layanan, sehingga pengguna fasilitas yang tiba tidak bisa segera mendapat layanan disebabkan kesibukan layanan. Pada banyak hal, tambahan fasilitas pelayanan dapat diberikan untuk mengurangi antrian atau untuk mencegah timbulnya antrian. Akan tetapi biaya karena memberikan pelayanan tambahan, akan menimbulkan pengurangan keuntungan mungkin sampai di bawah tingkat yang dapat diterima. Sebaliknya, sering timbulnya antrian yang panjang akan mengakibatkan hilangnya pelanggan / nasabah[1].
2.1. Sejarah Teori Antrian
Antrian yang sangat panjang dan terlalu lama untuk memperoleh giliran pelayanan sangatlah menjengkelkan. Rata – rata lamanya waktu menunggu (waiting time) sangat tergantung kepada rata – rata tingkat kecepatan pelayanan (rate of services). Teori tentang antrian diketemukan dan dikembangkan oleh A.K. Erlang, seorang insinyur dari Denmark yang bekerja pada perusahaan telepon di Kopenhagen pada tahun 1910. Erlang melakukan eksperimen tentang
fluktuasi permintaan fasilitas telepon yang berhubungan dengan automatic dialing equipment, yaitu peralatan penyambungan telepon secara otomatis. Dalam waktu – waktu yang sibuk operator sangat kewalahan untuk melayani para penelepon secepatnya, sehingga para penelepon harus antri menunggu giliran, mungkin cukup lama.
Persoalan aslinya Erlang hanya memperlakukan perhitungan keterlambatan (delay) dari seorang operator, kemudian pada tahun 1917 penelitian dilanjutkan untuk menghitung kesibukan beberapa operator. Dalam periode ini Erlang menerbitkan bukunya yang terkenal berjudul Solution of some problems in the theory of probabilities of significance in Automatic Telephone Exhange. Baru setelah perang dunia kedua, hasil penelitian Erlang diperluas penggunaannya antara lain dalam teori antrian[1].
2.2. Komponen Proses Antrian
Proses antrian yang terjadi sangat sederhana atau sangat kompleks. Komponen dasar proses antrian adalah kedatangan dan pelayanan. Komponen ini dapat terlihat pada Gambar 2.1.
Dari Gambar 2.1 dapat dilihat komponen antrian ,yaitu ;
1. Sumber Kedatangan
Setiap masalah antrian melibatkan kedatangan ,misalnya orang , mobil atau panggilan telepon untuk dilayani. Unsur ini sering disebut proses input. Proses input meliputi sumber kedatangan (calling population) dan cara terjadinya kedatangan yang umumnya proses random.
2. Fasilitas Pelayanan
Pelayanan dapat terdiri dari satu atau lebih pelayan atau satu atau lebih fasilitas pelayanan. Contohnya pada sebuah check out counter dari suatu supermarket terkadang hanya ada seorang pelayan, tetapi bisa juga diisi seorang kasir dengan pembantunya untuk memasukkan barang barang ke kantong plastik. Sebuah bank dapat memperkerjakan satu atau banyak teller. Disamping itu ,perlu diketahui cara pelayanan dirampungkan ,yang kadang-kadang merupakan proses acak.
3. Antrian
Inti dari analisis antrian adalah antri itu sendiri. Timbulnya antrian terutama tergantung dari sifat kedatangan dan proses pelayanan. Penentu antrian yang lain adalah adalah disiplin antrian[2].
Disiplin antrian adalah aturan yang menjelaskan cara melayani pengantri, misalnya datang lebih awal dilayani lebih awal dikenal dengan singkatam FCFS (First Come First Serve) atau datang terakhir dilayani terlebih dahulu (Last come First Serve), berdasarkan prioritas, berdasarkan abjad, berdasarkan janji, dan lain lain. Jika tak ada antrian berarti terdapat pelayan yang menganggur atau kelebihan
fasilitas pelayanan. Disiplin antrian adalah aturan yang menjelaskan cara melayani pengantri. Ada 5 bentuk disiplin pelayanan yang biasa digunakan, yaitu :
1. First Come First Served (FCFS) atau First In First Out (FIFO) artinya lebih dulu datang (sampai), lebih dulu dilayani (keluar), misalnya antrian pada loket karcis kereta api.
2. Last Come First Served (LCFS) atau Last In FirstOut (LIFO) artinya, yang tiba terakhir yang lebih dulu keluar. Misalnya, sistem antrian dalam elevator pada lantai yang sama.
3. Service In Random Order (SIRO) artinya, panggilan didasarkan pada pe-luang secara random, tidak soal siapa yang lebih dulu tiba.
4. Priority Service (PS) artinya, prioritas pelayanan kepada pelanggan yang mempunyai proritas lebih tinggi dibandingkan dengan pelanggan yang mempunyai prioritas lebih rendah, meskipun yang terakhir ini kemungkinan sudah terlebih dahulu dalam garis tunggu.
5. RR (Round Robin) artinya pelayanan diberikan pada jangka waktu tertentu saja. Contoh sistem parallel jobs pada sistem komputer.
2.3. Struktur Dasar Proses Antrian
Proses antrian pada umumnya dikelompokkan ke dalam empat struktur dasar menurut sifat – sifat dan pelayanan ,yaitu ;
1. Satu Saluran Satu Tahap
Satu saluran satu tahap ( single channel single phase) adalah model antrian yang sangat sederhana dimana terdapat satu sisi masuk dan satu sisi keluar seperti
pada Gambar 2.2. Contoh model antrian ini misalnya : pembelian tiket atau karcis pada salah satu loket penjualan tiket bioskop.
Gambar 2.2 Satu Saluran Satu Tahap 2. Banyak Saluran Satu Tahap
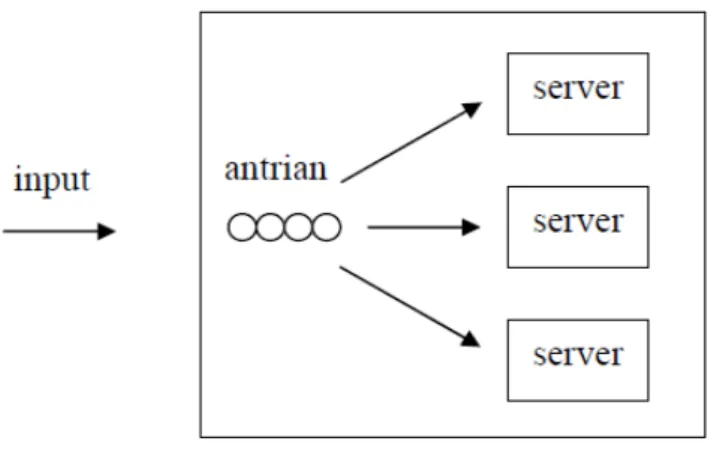
Banyak saluran satu tahap (multi channel single phase) adalah model antrian yang mempunyai banyak barisan serta hanya satu pelayanan seperti pada Gambar 2.3. Contoh model antrian ini misalnya pelayanan potong rambut dimana terdapat lebih satu tukang potong rambut.
Gambar 2.3 Banyak Saluran Satu Tahap 3. Satu Saluran Banyak Tahap
Satu saluran banyak tahap (single channel multi phase) adalah model antrian yang mempunyai satu barisan pelayanan seperti pada Gambar 2.4. Contoh model
antrian ini adalah dalam urutan suatu pekerjaan, mengurus izin usaha melalui beberapa orang pejabat pemerintah.
Gambar 2.4 Satu saluran banyak tahap 4. Banyak Saluran Banyak Tahap
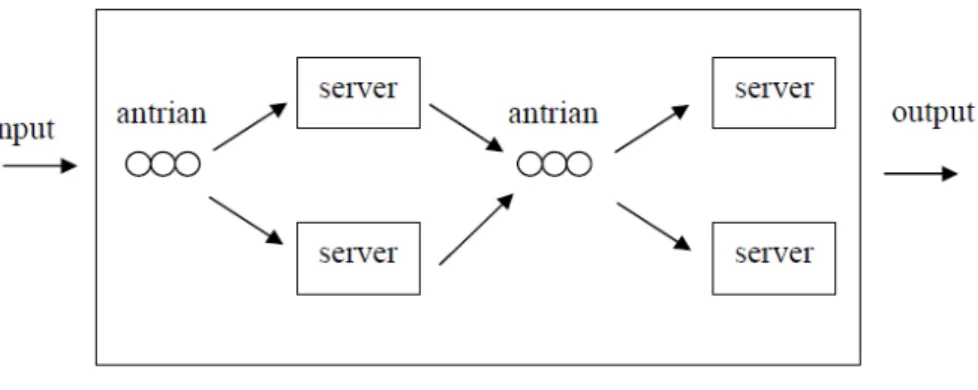
Banyak saluran banyak tahap (multi channel multi phase) adalah antrian yang mempunyai banyak barisan dan banyak pelayanan seperti pada Gambar 2.5. Contoh model ini adalah pelayanan kepada pasien rumah sakit. Beberapa perawat akan mendatangi pasien secara teratur dan memberikan pelayanan secara kontinu (sebagai urutan suatu pekerjaan).
Gambar 2.5 Banyak Saluran Banyak Tahap
Banyaknya saluran dalam proses antrian adalah jumlah pelayanan paralel yang tersedia. Sedangkan banyaknya tahap menunjukkan jumlah pelayanan
berurutan yang harus dilalui. Setiap kedatangan kategori yang disajikan diatas merupakan kategori dasar.
2.4. Karakteristik Antrian[3]
Dari beberapa masalah teori dalam antrian, perlu dibuat beberapa dasar asumsi tentang aspek – aspek khusus di sistem antrian. Dalam model dasar teori antrian, asumsi-asumsi yang dibuat adalah :
a. Sumber Populasi
Pengantri yang datang ke suatu sistem dapat berasal dari suatu populasi yang terbatas atau tidak terbatas. Bila jumlah pekerjaan tidak mempunyai batas diperbolehkan menunggu dalam suatu antrian, maka ini disebut sebagai antrian tidak terbatas sebaliknya antrian mempunyai batas disebut antrian yang terbatas.
b. Pola Kedatangan
Cara yang umum dipakai untuk menggambarkan pola kedatangan adalah dengan menggunakan waktu antar kedatangan yang didefenisikan sebagai interval antara kedatangan yang berurutan. Bila kedatangan berubah-ubah secara stokastik, dibutuhkan pendefenisian fungsi probabilitas antar waktu kedatangan. Untuk membahas pola kedatangan, digunakan notasi sebagai berikut :
tk adalah rata – rata waktu antar kedatangan
λ adalah tingkat kedatangan
Besaran – besaran tersebut dihubungkan oleh Persamaan 2.1 berikut:
Untuk menjelaskan pola kedatangan, sering kali distribusi dinyatakan dalam probabilitas yang waktu antar kedatangannya lebih besar dari waktu yang diberikan . Dengan mendefenisikan Ao(t) sebagai distribusi kedatangan, maka Ao adalah probabilitas yang waktu antar kedatangannya lebih besar dari t.
𝐴𝑜(𝑡) = 1− 𝐹(𝑡) ... (2.2)
c. Pola Kedatangan Poisson
Kedatangan biasanya dikatakan terjadi secara acak. Artinya kedatangan dapat terjadi setiap saat dan hanya dipengaruhi oleh kendala bahwa tingkat kedatangan memiliki suatu nilai tertentu. Dengan kata lain, diasumsikan bahwa waktu kedatangan berikutnya tidak bergantung pada kedatangan sebelumnya dan terdistribusi dalam interval Δt. Jika λ merupakan laju jumlah kedatangan rata- rata persatuan waktu, maka probabilitas kedatangan dalam Δt adalah λΔt. Fungsi kerapatan probabilitas waktu antar kedatangan diberikan oleh :
𝑓(𝑡) = 𝜆𝑒−𝜆𝑡 ( 𝑡> 0). ... (2.3)
Dan distribusi kedatangan adalah
𝐴𝑜(𝑡) =𝑒−𝜆𝑡𝑎. ... (2.4)
Notasi λ merupakan kedatangan rata-rata persatuan waktu. Jumlah kedatangan sebenarnya dalam periode waktu t merupakan variabel yang acak.
d. Distribusi Eksponensial
Dengan mendefenisikan F(t) = y maka dengan menggunakan Persamaan 2.4 yang dihitung dengan integral diperoleh fungsi kumulatif yang diberikan oleh 𝑦= ∫𝑡 𝜆𝑒−𝜆𝑡
0 =𝑦 = 1− 𝑒−𝜆𝑡𝑎 ... (2.5)
Yang bila dibalik atau di inversikan akan menghasilkan seperti berikut :
Karena y menunjukkan distribusi kumulatif, dimana untuk nilai 1- y berada di antara 0 dan 1. Dalam rentang nilai ini logaritma berharga negatif. Tanda negatif dalam rumus diatas akan menghasilkan nilai positif.
Dengan menggunakan rumus logaritma natural dan menggantikan nilai y dengan sederet bilangan acak yang terdistribusi serba sama antar 0 dan 1, akan menghasilkan keluaran berupa sederetan bilangan acak yang terdistribusi secara eksponensial. Jika nilai – nilai untuk 1 – y juga berada di antara 0 dan 1, sehingga dimungkinkan untuk menggunakan rumus yang lebih sederhana ;
𝑡𝑎 = −𝑙𝑛𝜆 (𝑦) = −𝑡𝑘𝑙𝑛 (𝑦). ... (2.7)
Dengan tk adalah nilai rata- rata waktu antar kedatangan yang muncul sebagai pengganti dalam rumus untuk menghasilkan bilangan acak yang terdistribusi secara eksponensial.
e. Kepanjangan Antrian
Dalam teori antrian umumnya dimulai dengan sumsi sumber kedatangan dan panjang antrian adalah tidak terbatas, meski asumsi ini sering kali tidak realistis. f. Disiplin Antrian
Istilah disiplin antrian menyatakan metode atau suatu set aturan yang digunakan untuk menentukan urutan pekerjaan yang akan dilayani, dalam antrian diasumsikan pekerjaan akan dilayani menurut “First Come First Serve”, yaitu menurut urutan yang sama sebagaimana mereka datang dalam antrian.
g. Pola Pelayanan
Waktu pelayanan dalam proses antrian dapat juga sesuai dengan salah satu bentuk distribusi probabilitas. Asumsi yang biasa digunakan bagi distribusi waktu
pelayanan adalah distribusi eksponensial negatif. Rumus umum fungsi kepadatan probabilitas eksponensial negative adalah ;
𝐸(𝑡) = 𝜇𝑒−µ𝑡𝑐 ... (2.8)
Dimana :
tc = waktu pelayanan
E(t) = probabilitas kepadatan yang berhubungan dengan t µ = tingkat pelayanan rata-rata
i/µ = waktu pelayanan rata- rata
Fungsi distribusi kumulatif diperoleh dari distribusi eksponensial yang dihitung dengan integral sebagai berikut :
𝐹(𝑡) =∫0𝑡µ𝑒−µ𝑡𝑐𝑑𝑡= 1− 𝑒−µ𝑡𝑐 ... (2.9) Dengan cara yang sama seperti beda waktu antar kedatangan (ta) pada persamaan 2.9, didapatkan rumus yang lebih sederhana sebagi berikut :
𝑡𝑐 = −𝑙𝑛𝜇 (𝑦) = −𝑡𝑝𝑙𝑛 (𝑦). ... (2.10)
Dengan tp adalah rata-rata waktu pelayanan yang muncul sebagai pengali dalam rumus untuk menghasilkan bilangan acak yang terdistribusi secara eksponensial. h. Keluar
Bila seorang individu telah selesai dilayani, maka akan keluar dari sistem. Sesudah keluar ia akan bergabung pada satu diantara populasi.
2.5. Notasi Sistem Antrian[4]
Dalam suatu sistem antrian digunakan sebuah notasi untuk mengetahui ciri dari suatu antrian. Notasi merupakan kombinasi proses kedatangan dengan pelayanan. Pada umumnya notasi antrian ini dikenal sebagai notasi Kendall, yaitu:
A / S / m / B / K / SD
dimana simbol A/S/m/B/K/SD ini merupakan unsur – unsur dasar dari model sistem antrian. Penjelasan dari simbol – simbol ini adalah sebagai berikut:
A = Distribusi kedatangan (Arrival Distribution) S = Distribusi waktu pelayanan atau keberangkatan
(Service Time Departure)
m = Jumlah server / pelayan dalam paralel (dimana c = 1,2,3,…,
∞
) B = Jumlah buffer (sistem kapasitas)K = Besar populasi
SD = Tertib layanan (service discipline)
Notasi standar ini dapat diganti dengan kode – kode yang sebenarnya dari distribusi – distribusi yang terjadi dan bentuk – bentuk lainnya, seperti:
M = Distribusi kedatangan atau keberangkatan dari proses Poisson. Dapat juga menggunakan distribusi eksponensial D = Konstanta atau deterministic interarrival atau service time
(waktu pelayanan)
k = Jumlah pelayanan dalam bentuk paralel atau seri N = Jumlah maksimum paket dalam sistem
Ek = Distribusi Erlang atau Gamma untuk waktu antar kedatangan atau
waktu pelayanan dengan parameter d
G = Distribusi umum dari service time atau keberangkatan (departure) GI = Distribusi umum yang independen dari proses kedatangan.
GD = General Discipline (disiplin umum) dalam antrian NPD = Non-Preemptive Discipline
PRD = Preemptive Discipline
Contoh penerapan dari kode – kode ini adalah sebagai berikut: (M/M/k):(GD/
∞
/∞
)Kode di atas berarti:
M = Distribusi Poisson atau Eksponensial untuk waktu antar kedatangan
M = Distribusi yang sama untuk waktu pelayanan k = Jumlah server
GD = General Discipline
∞
= Paket yang masuk dan sumber yang tak terhingga2.6. Antrian M/M/1/N
Model antrian M/M/1/N merupakan variasi dari model antrian pelayanan saluran tunggal M/M/1, dimana panjang antrian atau kapasitas tunggu dibatasi maksimum N individu . Jumlah maksimum ini meliputi individu yang menunggu dan yang sedang dilayani. Bila individu mencapai N atau lebih, individu yang datang berikutnya akan ditolak atau meninggalkan antrian[3].
Jenis model ini sering merupakan perkiraan logis untuk memecahkan persoalan antrian dalam sektor industri jasa. Sebagai contoh adalah rumah makan dengan kapasitas parkir yang terbatas. Bila pelanggan tiba dan tidak mendapatkan tempat parkir, maka pelanggan tersebut pasti langsung pergi ke tempat lain . Kecuali batas jumlah dalam sistem, asumsi yang mendasari model ini, sama dengan yang mendasari model M/M/1.
Adapun sifat dari sistem antrian M/M/1/N adalah sebagai berikut; a. Sumber kedatangan terdistribusi Poisson ( Markov)
b. Distribusi service time; eksponensial negative (Markov) c. Hanya ada satu server
d. Disiplin antrian : FIFO
e. Kapasitas terbatas untuk N pelanggan dalam sistem[8]
Adapun pemodelan dari sistem antrian dengan server tunggal yakni seperti yang ditunjukkan pada Gambar 2.6 dibawah ini :
Kedatangan
Paket
Buffer
Server
Keberangkatan
Paket
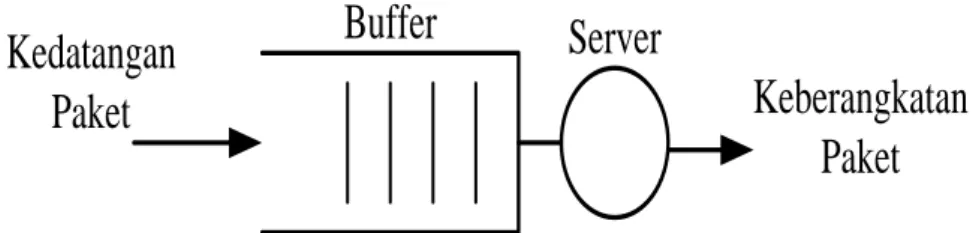
Gambar 2.6 Model Antrian Pelayanan Tunggal
Pada Gambar 2.6 dapat dilihat sebuah model antrian pelayanan tunggal (single server). Paket – paket tiba secara acak, kemudian paket antri di dalam buffer sebelum dilayani oleh server. Setelah selesai dilayani, maka paket meninggalkan sistem antrian[4].
Pada umumnya untuk memecahkan masalah antrian yang sederhana formula-formula yang digunakan berdasarkan pada asumsi λ < µ, yaitu tingkat pelayanan harus lebih besar daripada kedatangan paket/pelanggan, dengan demikian semua pengantri akan dapat dilayani jika tidak maka antrian akan semakin panjang sehingga tidak ada solusi keseimbangan.Pada sistem antrian
Rumus-rumus dasar model antrian M/M/1/N adalah sebagai berikut[9]: 1. Rata – rata jumlah paket di dalam sistem
𝐿𝑠 = 𝑁���= 1−𝜌𝜌− (𝑁+1).𝜌 𝑁+1
1−𝜌𝑁+1 ... (2.12)
2. Rata-rata jumlah pelanggan di tempat antri
𝐿𝑞= 𝑁���– (1− 𝑃𝑜) . ... (2.13)
Dimana 𝑃𝑜jika nilai ρ ≠ 0 terlebih dahulu dicari dengan rumus :
𝑃𝑜= 1−𝜌1−𝜌𝐾+1 ... (2.14)
3. Rata- rata waktu tunggu didalam sistem 𝑊 =𝐿𝑠
𝜆 ... (2.15)
4. Rata – rata waktu tunggu pada antrian 𝑊𝑞 =𝐿𝑞
𝜆 ... (2.16)
2.7. Diagram Transisi Kondisi
Untuk memperoleh formulasi suatu sistem antrian dibutuhkan suatu diagram transisi kondisi ( state transition diagram). Diagram transisi kondisi ini mewakili suatu proses yang disebut birth-death process.
Jika dianggap bahwa sebuah ‘state’ adalah ukuran suatu populasi maka ia bisa bertambah pada suatu waktu (birth) dengan satu anggota atau pada suatu waktu anggota dari populasi tersebut bisa berkurang satu (death). Dalam suatu sistem yang sesungguhnya sebuah ‘state’ bisa berupa Jumlah paket di dalam sebuah proses, jumlah panggilan baru di dalam sentral telepon atau jumlah job di
dalam komputer, dan lain-lain. Diagram transisi kondisi sistem antrian M/M/1/N adalah seperti Gambar 3.2 dibawah ini[7] :
Gambar 2.7 Diagram Transisi Kondisi Sistem Antrian M/M/1/N
2.8. Pembangkit Nilai Acak
Pembangkit Nilai Acak adalah suatu algoritma yang digunakan untuk menghasilkan urutan-urutan dari angka angka sebagai hasil dari perhitungan dengan komputer yang diketahui distribusinya sehingga angka-angka tersebut muncul secara acak dan digunakan terus menerus. Nilai-nilai acak uyang dihasilkan akan digunakan sebagai masukan bagi sistem antrian.
2.8.1 Penyelesaian R.N.G
Pada Congruential Pseudo Random Number Generator dapat dijelaskan untuk masing-masing formula/ rumus sebagai berikut :
1. Additive / Arithmatic RNG Bentuk rumusnya :
𝑍𝑖 = ( 𝑎 .𝑍𝑖−1 + 𝑐 ) 𝑚𝑜𝑑.𝑚. ... (2.17)
Dengan catatan :
Zi-1 = merupakan hasil akhir
Z0 = merupakan angka pertama yang bebas tertentu m = angka modulo
Bagi Additive RNG ini diperlukan perhatian syarat-syaratnya sebagi berikut : a. Konstanta a harus lebih besar dari √m. Dan biasanya dinyatakan dengan syarat:
m/100 < a < m - √m.
b. Konstanta c harus berangka ganjil apabila m bernilai pangkat dua. Tidak boleh nilai berkelipatan dari m.
c. Modulo m harus bilangan prima atau bilangan tidak terbagikan, sehingga memudahkan dan memperlancar perhitungan-perhitungan didalam komputer. d. Untuk Zo harus merupakan angka integer dan juga ganjil dan cukup besar.
2.8.2 Multiplicate RNG
Bentuk rumus dari multiplicate RNG adalah :
𝑍 𝑖+1= ( 𝑎 .𝑍𝑖+𝑐 )𝑚𝑜𝑑𝑚 . ... (2.18)
Dengan catatan:
Zi = Angka random nomor semula Zi + 1 = angka random nomor yang baru a > 1 ; c = 0; m > 1
Syarat-syarat lainnya adalah sama dengan Additive RNG. Dalam perumusan multiplicate ini terdapat tiga variabel yang menentukan untuk nilai-nilai Random Number yang dapat diperoleh seterusnya dengan tidak ada pengulangan pada angka-angkanya. Dan untuk pemilihan nilai-nilai yang terbaik dijabarkan sebagai berikut :
a. Pemilihan nilai : m (modulo) merupakan satu angka integer yang cukup besar dan merupakan satu kata (word) dari yang dipakai pada komputer. Sebagai contoh :
1) Dalam komputer IBM 360/370 sistem sebuah kata adalah 32 bits panjangnya, berarti angka integer yang terbesar dalam satu kata komputer (computer words) adalah :
232−1 - 1 = 231 – 1 = 2147488647
Maka nilai m harus lebih satu integer, atau : m = 232−1 + 1 = 2147.483.648
2) Untuk mesin komputer sistem 1130 / 1800 IBM yang dikenal dengan 16 Bit words maka untuk memilih m adalah :
m = 216−1 = 32.768
3) Pada microcomputer dengan 8 bit akan digunakan : m = 28−1 = 128
4) Nilai m ini adalah merupakan pembagi dari nilai ( a x Z1) yang mengikuti operasi modulo.
Hal ini akan menjadikan mesin komputer hanya dapat tertinggi dengan integer m -1 dan apabila produk-produknya lebih besar dari nilai-nilai ini akan mengakibatkan overflow atau hang.
b. Pemilihan konstanta multiplier a harus tepat.
1) Pemilihan nilai a harus bilangan prima terhadap m. a juga harus bilangan ganjil .Pemilihan yang terbaik adalah dengan rumus
a = 2𝑏/2± 3 yang lebih mendekat pada ketepatan.
2) Untuk sistem IBM 1130/1800 dengan 16 bit akan diperoleh a = 216/2 ± 3 = 28 + 3 = 259
3) Untuk mikrokomputer dengan 8 bit ,maka akan diperoleh : a = 28 ± 3 = 24 + 3
= 16 + 3 = 19
c. Pemilihan untuk Zo, yang dikenal dengan : SEED = Zo mengharuskan bilangan prima terhadap m. Dengan demikian untuk Zo adalah setiap angka angka yang ganjil.
d. Bilangan c yang dipilih harus bukan merupakan kelipatan dari m dan juga harus bilangan ganjil.
2.9. Faktor –Faktor Sistem Antrian[4]
Dalam suatu sistem antrian terdapat faktor – faktor yang harus diperhatikan agar suatu fasilitas pelayanan dapat melayani paket yang berdatangan, yaitu bentuk kedatangan paket, bentuk fasilitas pelayanan, kapasitas fasilitas pelayanan untuk menampung paket, utilisasi sistem, dan disiplin antrian yang mengatur pelayanan kepada paket.
2.9.1 Bentuk Kedatangan
Bentuk kedatangan paket diperhitungkan melalui waktu antarkedatangan, yaitu waktu antara dua paket yang berurutan pada suatu fasilitas pelayanan. Bentuk ini dapat bergantung pada jumlah paket yang berada dalam sistem ataupun tidak bergantung pada keadaan sistem tersebut. Asumsinya adalah kedatangan paket mengikuti suatu proses dengan distribusi probabilitas tertentu.Distribusi probabilitas yang sering digunakan adalah distribusi Poisson, dimana kedatangan paket bersifat bebas, tidak terpengaruh oleh kedatangan sebelum ataupun sesudahnya. Asumsi distribusi Poisson menunjukkan bahwa kedatangan paket sifatnya acak dan mempunyai rata – rata laju kedatangan sebesar lamda (λ).
Proses kedatangan paket – paket yang mengikuti distribusi Poisson dapat dilihat pada Gambar 2.8.
Waktu
t t + ∆t
∆t
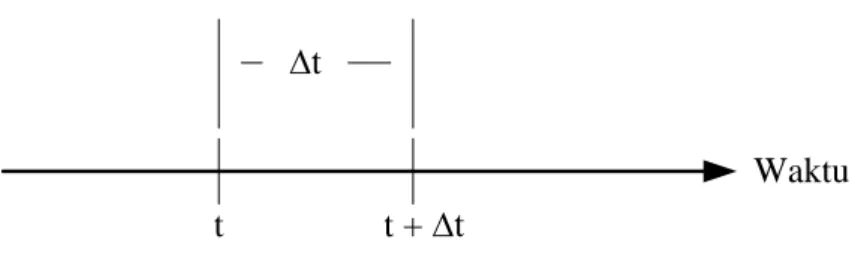
Gambar 2.8 Interval Waktu Antar Kedatangan Paket pada Proses Poisson Pada Gambar 3.3 dapat dilihat bahwa sebuah interval waktu yang kecil ∆t (∆t
→ 0), antara waktu t dan t + ∆t. Jika terdapat interval waktu terbatas yang
panjangnya T, seperti dilihat pada Gambar 2.9.
Waktu
∆t ∆t ∆t ∆t
T
Gambar 2.9 Distribusi Poisson dengan Interval Waktu T
Maka pada interval waktu T, dapat diketahui probabilitas kedatangan p(k) dari k kedatangan yaitu:
𝑝(𝑘) =(𝜆𝑇)𝑘𝑘 !𝑒−𝜆𝑇...(2.19)
dimana :
p(k) = probabilitas dari k kedatangan
λ = Laju kedatangan paket (paket/detik)
k = 0, 1, 2…
Poisson sering digunakan sebagai model untuk kedatangan paket yang acak ke dalam sistem antrian. Pada analisa ini, perlu untuk menghasilkan suatu urutan waktu kedatangan paket 0 = 𝑡0 ≤ 𝑡1 ≤ 𝑡2 ≤ ⋯dimana kejadian ke i terjadi pada saat ti (i = 1, 2,…) dan distribusi dari waktu kejadian {ti} mengikuti pola tertentu. 𝑁(𝑡) = max(𝑖 ∶ 𝑡𝑖 ≤ 𝑡 ) adalah jumlah kejadian yang terjadi pada saat atau sebelum t untuk t ≥ 0 . Sebuah proses {𝑁(𝑡),𝑡 ≥ 0} dikatakan proses Poisson jika:
1. Paket yang tiba sebanyak satu paket, pada suatu waktu.
2. N(t + s) – N(t) adalah jumlah kedatangan pada interval waktu (t, t + s), adalah independen dari { 𝑁 (𝑢), 0 ≤ 𝑢 ≤ 𝑡}
3. Distribusi dari N(t + s) – N(t) independen dari t untuk t,s
≥
0 2.9.2 Bentuk PelayananPelayanan dapat dilakukan dengan satu atau lebih fasilitas pelayanan, yang masing – masing dapat mempunyai satu atau lebih saluran atau tempat pelayanan yang disebut dengan server. Apabila terdapat lebih dari satu fasilitas pelayanan maka paket dapat menerima pelayanan melalui suatu urutan fase tertentu. Pada suatu fasilitas pelayanan, paket akan masuk dalam suatu tempat pelayanan dan menerima pelayanan secara tuntas dari server. Bila tidak disebutkan secara khusus, pada bentuk pelayanan ini, maka dianggap bahwa satu server, dapat melayani secara tuntas satu paket. Bentuk pelayanan dapat konstan dari waktu ke
waktu. Rata – rata laju pelayanan (mean server rate) diberi simbol µ (miu), merupakan jumlah paket yang dapat dilayani dalam satuan waktu. Sedangkan rata – rata waktu yang dipergunakan untuk melayani setiap paket diberi simbol 1�𝜇, merupakan rata – rata waktu yang dibutuhkan untuk suatu pelayanan.
2.9.3 Kapasitas Sistem
Kapasitas sistem adalah jumlah maksimum paket, mencakup yang sedang dilayani dan yang berada dalam antrian, yang dapat ditampung oleh fasilitas pelayanan pada saat yang sama. Sebuah sistem yang tidak membatasi jumlah paket di dalam fasilitas pelayanannya dikatakan memiliki kapasitas tak terhingga, sedangkan suatu sistem yang membatasi jumlah paket yang ada di dalam fasilitas pelayanannya dikatakan memiliki kapasitas yang terbatas.
2.9.4 Utilisasi Sistem
Utilisasi sistem adalah perbandingan antar kedatangan acak paket – paket dengan laju λ, terhadap laju pemrosesan paket µ, maka antrian akan mulai terbangun. Untuk sebuah buffer antrian yang terbatas, antrian akan menemukan
keadaan titik maksimumnya yaitu λ melampaui µ dan terus menerus bertambah.
Jika buffer penuh, semua paket lain yang tiba akan diblok.
Jika buffer diasumsikan tidak terbatas, maka sistem menjadi tidak stabil yaitu λ → µ . Untuk menjamin sistem menjadi stabil pada antrian dengan pelayanan tunggal maka dapat dilihat bahwa λ < µ . Terutama sekali maka akan didapat parameter ρ, yaitu:
dimana:
ρ = Utilisasi Sistem
λ = Laju Kedatangan Paket (paket/detik)
µ = Laju Pelayanan Paket (paket/detik)
Parameter ρ ini sering disebut juga dengan utilisasi link atau intensitas trafik. Untuk antrian dengan pelayanan tunggal, jika nilai ρ mendekati atau melampaui satu, maka akan dijumpai keadaan kongesti, yang menyebabkan waktu tunggu dalam antrian akan meningkat, dan paket – paket lain yang tiba akan diblok.
2.10. Simulasi Antrian
Simulasi merupakan salah satu cara untuk memecahkan berbagai persoalan yang dihadapi di dunia nyata. Simulasi dapat diartikan sebagai suatu sistem yang digunakan untuk memecahkan atau menguraikan persoalan-persoalan dalam kehidupan nyata yang penuh dengan ketidakpastian dengan tidak atau menggunakan model atau metode tertentu dan lebih ditekankan pada pemakaian komputer untuk mendapatkan solusinya[5].
1. Alasan Menggunakan Simulasi
Metode simulasi digunakan secara luas dalam analisi permasalahan. Survey yang dilakukan pada tahun 1978 oleh Institut Manajemen (TIMS) dan Riset operasi ( ORSA) di Amerika menginformasikan bahwa simulasi menduduki ranking tiga setelah analisis ekonomi dan analisis statistik. Informasi tersebut menyatakan bahwa simulasi merupakan alat atau metode yang dapat digunakan untuk memecahkan masalah dan memberikan keputusan[6].
2. Keuntungan Simulasi
Ada berbagai keuntungan yang bisa diperoleh dengan memanfaatkan simulasi, yaitu sebagai berikut :
a. Menghemat Waktu (CompressTime)
Kemampuan menghemat waktu ini dapat dilihat dari pekerjaan yang dikerjakan tahunan tetapi kemudian dapat disimulasikan hanya dalam beberapa menit, bahkan dalam beberapa kasus hanya dalam hitungan detik.
b. Dapat Mengembangkan Waktu (Expand Time)
Simulasi dapat digunakan untuk menunjukkan perubahan struktur dari suatu Sistem Nyata (Real System) yang sebenarnya tidak dapat diteliti pada waktu yang seharusnya (Real Time). Dengan demikian simulasi dapat membantu mengubah Real System hanya dengan memasukkan sedikit data.
c. Dapat Mengontrol Sumber-Sumber yang Bervariasi (Control Sources of Variation)
Kemampuan Pengawasan dalam simulasi ini tampak terutama apabila analisis statistik digunakan untuk meninjau hubungan antara variable bebas (independent) dengan variable terkait yang merupakan faktor faktor yang akan dibentuk dalam percobaan. Hal ini dalam kehidupan sehari-hari merupakan suatu kegiatan yang harus dipelajari dan ditangani dan tidak dapat diperoleh dengan cepat.
d. Mengkoreksi Kesalahan-Kesalahan Perhitungan (Error in Measurement) Dalam prakteknya, pada suatu kegiatan ataupun percobaan dapat saja muncul ketidak-benaran dalam mencatat hasil-hasilnya. Sebaliknya dalam simulasi komputer jarang ditemukan kesalahan perhitungan terutama bila
angka-angka diambil dari komputer secara teratur dan bebas. Komputer mempunyai kemampuan untuk melakukan penghitungan dengan akurat.
e. Dapat Dihentikan dan Dijalankan Kembali (Stop Simulation and Restart) Simulasi komputer dapat dihentikan untuk kepentingan peninjauan ataupun pencatatan semua keadaan yang relevan tanpa berakibat buruk terhadap program simulasi tersebut. Dalam dunia nyata, percobaan tidak dapat dihentikan begitu saja. Dalam simulasi komputer, setelah dilakukan penghentian maka kemudian dapat dengan cepat dijalankan kembali (restart).
f. Mudah Diperbanyak (Easy to Replicate)
Dengan simulasi komputer percobaan dapat dilakukan setiap saat dan dapat diulang-ulang. Pengulangan dilakukan terutama untuk mengubah berbagai komponen dan variabelnya, seperti dengan perubahan pada parameternya,perubahan pada kondisi operasinya , dengan memperbanyak output. 3. Tahap dari Simulasi
Diperlukan tahap-tahap yang sederhana tetapi sitematis agar penyususnan program simulasi dapat berjalan dengan baik. Tahap-tahap simulasi adalah:
a. Menggunakan atau tidak menggunakan Simulasi.
Apabila diputuskan untuk tidak mempergunakan sistem simulasi maka perlu memberikan cara model atau metode lain yang dapat dipergunakan untuk memecahkan persoalan tersebut. Namun apabila keputusan adalah menggunakan sistem simulasi maka dapat lansung menuju langkah langkah berikutnya.
b. Pemodelan Formulasi
Disini dilakukan pemodelan untuk menentukan formulasi yang akan digunakan, yaitu dengan menggunakan fungsi matematis, yang dalam penyusunan modelnya
harus memperhatikan variabel yang menentukan fungsi tersebut dan ada atau tidaknya konstanta yang harus dimasukkan.
c. Persiapan Pengambilan Data
Dalam mengumpulkan data harus diperhatikan aturan yang berlaku atau yang diwajibkan yaitu menguraikan data yang sudah dikumpulkan dalam bentuk statistik untuk membuat program simulasi, menggunakan teori analisis untuk menguraikan data yang telah dikumpulkan, meninjau apakah mempergunakan analisis regresi atau analisis yang lainnya serta meninjau juga computer time untuk simulasi ini sehingga dapat dibuat rencana dengan alokasi waktu yang tepat.
d. Penulisan Program
Dalam penulisan program seseorang sudah memasuki liku-liku ketentuan dalam penggunaan komputer dan meninjau serta memperhatikan bahasa komputer yang dipergunakan dalam simulasi.
e. Verifikasi
Langkah verifikasi merupakan langkah untuk mengetahui apakah program benar dan sesuai dengan simulasi yang dikehendaki. Kemudian melakukan debugging terhadap program yang dimasukkan ke dalam komputer, melaksanakan perbaikan pada program simulasi yang sudah dimasukkan kedalam komputer, perbaikan atas program atau berupa pengeditan atas program. Apabila sudah tepat dan dapat beroperasi dengan benar maka akan dilanjutkan dengan langkah berikutnya.
f. Validasi
Langkah validasi ini juga merupakan langkah untuk mengawasi atau mengecek apakah model yang sudah diprogramkan itu asli, sudah sesuai dan benar. Kemudian mengecek model yang sudah diprogramkan apakah dapat
berjalan dengan baik. Apabila belum memenuhi kebutuhan yang sebenarnya, maka dilakukan peninjauan kembali pada formulasi model untuk diubah dan diperbaiki. Apabila sudah memenuhi kebutuhan maka dapat dilanjutkan ke langkah berikutnya.
g. Desain Eksprimen
Langkah eksprimen ini dilakukan untuk menguji desain dengan menggunakan teori Experimental Design. Bagaimana mendapatkan data input untuk dapat melaksanakan percobaan ini dengan baik. Perlu juga untuk mencari nilai efektif dari percobaan ini yang dikenal sebagai MOE ( Measure Of Effectiveness). Bila diperlukan langkah ini merupakan langkah tambahan untuk melakukan percobaan guna mendapatkan ketepatan simulasi. Apabila tidak dibutuhkan percobaan, baik secara fisik maupun kimiawi, maka kita dapat langsung mengerjakan langkah berikutnya.
h. Perencanaan yang Taktis
Langkah ini merupakan bentuk studi kelayakan dari Experimental Design yakni untuk melihat bagaimana percobaan dapat dikerjakan melalui perencanaan yang terarah. Perencanaan juga dilakukan untuk menentukan berapa lama percobaan dapat dilakukan sehingga kita dapat mengetahui dengan tepat kapan kita akan memulai dan mengakhiri percobaan itu. Langkah ini juga digunakan untuk merencanakan prosedur pelaksanaan percobaan guna memudahkan pelaksanaannya.
i. Percobaan Dilaksanakan
Langkah ini merupakan pelaksanaan dari percobaan yang sudah didesain. Dalam melaksanakan percobaan kita dapat mempergunakan berbagai peralatan
penelitian atau lainnya. Percobaan dapat dilakukan dengan menggunakan teknik penelitian kimia dan fisika dengan teori yang sudah diketahui dan dikuasai. Kemudian melakukan interpretasi terhadap hasil percobaan tersebut dengan tetap memungkinkan untuk dikoreksi bila perlu dan membuat laporan yang terperinci mengenai percobaan yang telah dilaksanakan.
j. Model Terpakai
Langkah ini merupakan langkah untuk menjawab pertanyaan apakah model yang sudah didesain itu dapat memberikan hasil yang benar dan memadai sesuai yang diharapkan. Apabila output sudah memadai dan sesuai dengan yang diharapkan , maka kita akan langsung ke langkah terakhir , yaitu dokumentasi.
k.Dokumentasi
Langkah yang terakhir ini merupakan langkah yang menyatakan bahwa model simulasi telah dapat diterima dan sesuai dengan yang diharapkan. Dapat dilakukan berbagai dokumentasi, merekam program-programnya, dan prin-out hasil outputnya serta memberikan label pada media penyimpannya serta menyelesaikan kebutuhan dokumentasi lainnya dan membuat laporan akhir dari pekerjaan simulasi ini[5]
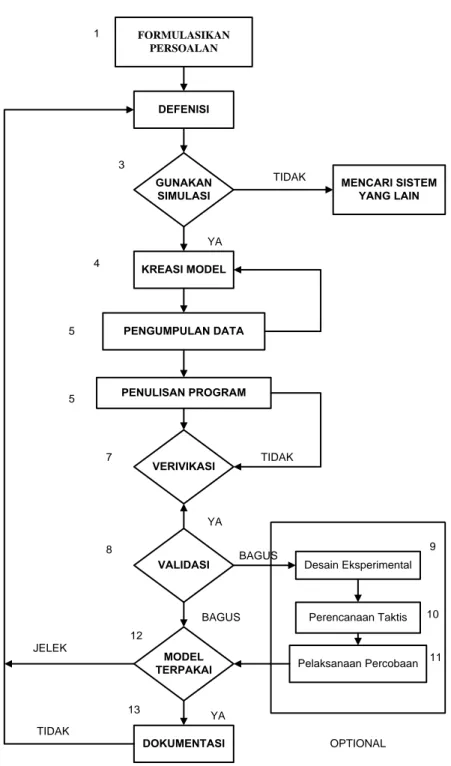
4. Flow Chart Tahap Simulasi
Flowchart dari tahap simulasi diperlihatkan pada Gambar 2.10.
FORMULASIKAN PERSOALAN DEFENISI GUNAKAN SIMULASI KREASI MODEL PENGUMPULAN DATA PENULISAN PROGRAM VERIVIKASI VALIDASI MODEL TERPAKAI DOKUMENTASI MENCARI SISTEM YANG LAIN Desain Eksperimental Perencanaan Taktis Pelaksanaan Percobaan 1 TIDAK YA TIDAK YA BAGUS YA JELEK TIDAK OPTIONAL BAGUS 3 4 5 5 7 8 12 13 9 10 11