KUANTISASI ENERGI PADA RANGKAIAN RLC SKRIPSI Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Fisika

KUANTISASI ENERGI PADA RANGKAIAN RLC

SKRIPSI

Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Fisika

Disusun Oleh:

BAMBANG SETYAWAN NIM : 033214003

PROGRAM STUDI FISIKA JURUSAN FISIKA

FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS SANATA DHARMA

QUANTIZATION OF RLC _{CIRCUIT ENERGY}

A THESIS

Presented as Partial Fulfillment of the Requirements To Obtain the Sarjana Science Degree

in Physic Study Program

by:

HALAMAN PERSEMBAHAN

K arya ini kupersembahkan kepada D ia J uru S elamatku, sehingga kupercaya

kepada semua anugerahN ya yang senantiasa membimbingku dalam menghadapi

berbagai rintangan hidup

K epada B apak, I bu, adik, dan saudara- saudaraku terkasih yang terus ada

disampingku, yang terus bersabar menunggu sampai tiba waktunya aku

menyelesaikan studi

K epada teman- teman seperjuangan, kakak angkatan, adik angkatan yang selalu

membantu tanpa pamrih dalam kuliah

K epada sahabat- sahabat yang aku kasihi, karena merekalah ada canda dan tawa,

HALAMAN MOTTO

“S iapa yang mempunyai selera untuk membaca buku- buku yang baik,

niscaya ia sanggup menanggung kesepian di suatu tempat dengan

tentram”(M ahatma Gandhi)

PERNYATAN KEASLIAN KARYA

Saya menyatakan sesungguhnya bahwa skripsi yang telah saya tulis ini tidak memuat karya orang lain, kecuali yang telah disebutkan dalam daftar pustaka sebagaimana layaknya karya ilmiah.

Yogyakarta, 17 September 2008 Penulis,

ABSTRAK

KUANTISASI ENERGI PADA RANGKAIAN RLC

Telah dilakukan kuantisasi energi pada rangkaian RLC dengan menggunakan pengkuantuman secara aljabar. Jika digunakan asumsi bahwa muatan Q sebagai koordinat q, I sebagai momentum p, dan A sebagai

m

2 1

, maka energi total rangkaian RLC mirip dengan energi osilator harmonik. Energi pada rangkaian RLC dapat dituliskan menjadi E_δ =hω

(

δ +1

)

dengan

L

, 3 , 2 , 1

=

ABSTRACT

QUANTIZATION OF RLC CIRCUIT ENERGY

Quantization of energy RLC circuit using the algebraic quantization have been performed. If use assumption that the charge Q as coordinate q, I as the momentum p, and A as the

m

2 1

KATA PENGANTAR

Puji syukur kepada Tuhan karena telah memberikan rahmatNya dan karena peran sertaNya dalam membantu pembuatan skripsi ini. Berkat Dialah alam semesta dan segala isinya diciptakan, sehingga kita dapat mempelajari gejala- gejala alam yang luar biasa melalui ilmu fisika.

Banyak pihak telah membantu saya dalam menyelesaikan karya ini. Oleh karena itu dengan rendah hati saya mengucapkan banyak terima kasih kepada

1. Bapak Drs. Drs. Vet Asan Damanik, M.Si sebagai dosen pembimbing tugas akhir yang dengan sabar membimbing saya dalam menyelesaikan skripsi ini.

2. Bapak, Ibu, Adik, yang telah berkorban sedemikian banyak dan yang telah memberi dukungan kepada saya.

3. Dekan fakultas Sains danTeknologi Rm. Gregorius Heliarko SJ, beserta

staf.

4. Dosen program studi fisika Ibu Ir. Sri Agustini Sulandari, M.Si, Bapak Dr.

Edi Santosa, M.Si, Bapak Prasetyadi, S.Si, M.Si, Ibu Dwi Nugrahaeni Rositawati, S.Si, M.Si, Bapak Prof. Dr. Liek Wilardjo, Bapak Drs. BA. Tjipto Sujitno, M.T, APU, dan semua dosen yang telah membantu saya dalam menyelesaikan studi S1.

7. Teman- teman dari fisika baik kakak angkatan dan adik angkatan seperti

Mbak Ayu, Mbak Yuni, Mbak Ratna, Mas Ridwan, Mas Adit, Mas Basil, Manggar, Sujad, Ade, Siska, dan teman- teman lainnya yang tidak dapat saya sebutkan satu persatu.

8. Ibu dan Bapak Kost yang telah menjaga saya selama berada di Yogya. 9. Teman- teman kost Danang, Yansen, dan Willy.

Saya menyadari bahwa skripsi ini masih banyak kekurangan, oleh karena itu kritik dan saran yang membangun sangat berguna bagi perkembangan skripsi ini.

Yogyakarta, 16 September 2008 Penulis,

DAFTAR ISI

HALAMAN JUDUL………. i

HALAMAN PERSETUJUAN……….. ii

HALAMAN PENGESAHAN……… iii

HALAMAN PERSEMBAHAN……… iv

HALAMAN MOTTO……… v

HALAMAN PERNYATAAN KEASLIAN KARYA………... vi

ABSTRAK……….. vii

ABSTRACT……… viii

KATA PENGANTAR……… ix

DAFTAR ISI……….. xii

BAB I PENDAHULUAN 1.1 Latar Belakang………. 1

1.2 Perumusan Masalah………. 3

1.3 Batasan Masalah……….. 3

1.4 Tujuan Penelitian………. 3

1.5 Kegunaan Penelitian……… 4

BAB II DASAR TEORI

2.1 Hamiltonian Osilator harmonik……… 6

2.2 Persamaan Nilai Eigen………. 7

2.3 Operator Kreasi dan Operator Annihilasi... 12

2.4 Persamaan Differensial Orde Dua……… 15

BAB III METODE PENELITIAN 3.1 Studi dan Elaborasi Persamaan Differensial Orde Dua... 18

3.2 Perumusan Energi pada Kapasitor yang Terangkai pada Rangkaian RLC ……….. 18

3.3 Kuantisasi Energi pada Rangkaian RLC……… 18

BAB IV KUANTISASI ENERGI RANGKAIAN RLC 4.1 Energi Rangkaian RLC……….. 19

4.2 Kuantisasi Energi Rangkaian RLC……… 19

4.3 Implikasi Kuantisasi Energi Rangkain RLC... 24

BAB V PENUTUP 5.1 Kesimpulan……… 25

5.2 Saran………. 25

BAB I PENDAHULUAN

1.1 Latar Belakang Masalah

Fisika merupakan ilmu yang mengalami perkembangan yang sangat pesat dibandingkan dengan ilmu lain. Perkembangan ilmu fisika dapat dilihat dari beberapa bidang seperti astronomi, fisika kuantum, energi dan beberapa bidang fisika terapan. Banyak gejala fisis yang diamati dari eksperimen, yang tidak dapat dijelaskan oleh fisika klasik. Sebagai contoh, energi elektron, energi radiasi benda hitam, efek fotolistrik, hamburan Compton, spektrum garis dari atom, dan lain- lain yang menunjukkan bahwa energi terkuantisasi.

Kuantisasi energi dalam fisika merupakan suatu yang sangat penting terkait dengan fenomena-fenomena fisis yang teramati dalam eksperimen. Dalam fisika dikenal kuantisasi kanonik yang dikaitkan dengan teori medan gelombang dalam bentuk harmonik dengan melakukan generalisasi formalisme Hamiltonian. Generalisasi formalisme Hamiltonian adalah suatu transisi dari teori medan klasik ke teori medan terkuantisasi yang dilakukan dengan cara mengganti Poisson bracket klasik menjadi Poisson bracket kuantum (Silaban, 1977). Jika suatu medan suatu sistem fisis terkuantisasi, maka secara otomatis energi sistem fisis itu juga terkuantisasi.

Cara yang lain untuk mengkuantisasi energi adalah cara aljabar dengan mendefinisikan operator kreasi dan operator annihilasi. Sebagai contoh, energi

V m p

H ˆ

2 ˆ ˆ ₌ 2 ₊

dengan pˆ operator momentum, mmassa partikel, dan Vˆ operator energi potensial

2 2_ˆ

2 1

ˆ _{m x}

V = ω ,

menghasilkan energi terkuantisasi

, 2 1

      +

= ω δ

δ h

E δ =1,2,3,L

dengan

π

2

h

=

h , h adalah tetapan Planck, dan ω frekuensi sudut.

Dalam fisika dikenal rangkaian seri RLC yang terdiri dari tahanan ( R ), kumparan ( L ), dan kapasitor ( C ). Kapasitor dapat menyimpan muatan listrik (Q). Muatan listrik yang tersimpan dalam kapasitor diberikan oleh

CV

Q=

dengan V adalah beda potensial listrik. Energi yang tersimpan dalam kapasitor tersebut dikenakan oleh

2

2 1

CQ

E= .

Energi yang tersimpan di dalam kapasitor mirip dengan energi potensial osilator harmonik

2 2

1

x m

1.2 Perumusan Masalah

Berdasarkan latar belakang masalah yang telah diuraikan sebelumnya bahwa energi potensial dari kapasitor keping sejajar yang terangkai seri dengan L

dan R mirip dengan energi potensial osilator harmonik. Oleh sebab itu, permasalahan dalam penelitian ini adalah bagaimana mengkuantisasi energi yang tersimpan pada rangkaian RLC.

1.3 Batasan Masalah

Masalah yang diteliti dibatasi pada

1. Rangkaian RLC yang tersusun secara seri pada rangkaian pengosongan

dan rangkaian pengisian.

2. Masalah kuantisasi energi rangkaian RLC menggunakan pengkuantuman

secara aljabar.

1.4 Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk

1. Mengkuantisasi energi dalam rangkaian RLC secara aljabar.

1.5 Kegunaan Penelitian

Penelitian ini berguna untuk

1. Menjelaskan kuantisasi energi rangkaian RLC.

2. Mengembangkan ilmu pengetahuan khususnya mengenai konsep

kuantisasi energi pada rangkaian RLC seri.

1.6 Sistematika Penelitian Bab I pendahuluan

Dalam bab ini dijelaskan mengenai latar belakang masalah, batasan masalah, metode penelitian, tujuan penelitian, kegunaan penelitian, dan sistematika penelitian.

Bab II

Dalam bab ini akan dijelaskan teori kuantisasi secara aljabar, persamaan nilai eigen, operator kreasi dan annihilasi, dan perumusan persamaan diferensial rangkaian RLC beserta penyelesaiannya.

Bab III

Bab IV

Bab IV menjabarkan kuantisasi energi rangkaian RLC menggunakan metode kuantisasi pada osilator harmonik secara aljabar.

Bab V

BAB II DASAR TEORI

2.1 Hamiltonian Osilator Harmonik

Secara umum osilator harmonik diibaratkan sebagai sebuah massa m yang ditempatkan pada sebuah pegas dengan konstanta k dan kemudian ditarik dengan jarak tertentu dari posisi setimbangnya kemudian dilepas. Persamaan geraknya mengikuti hukum Hooke (Griffihs,1995)

₂

2

dt x d m kx

F =− = (2.1)

dan solusi dari persamaan (2.1) menjadi

) cos( )

sin( )

(t A t B t

x = ω + ω (2.2)

dimana

m k

≡

ω (2.3)

adalah frekuensi osilasi. Energi potensial osilator harmonik (V) dapat diperoleh dari relasi

dx dV

F =− (2.4)

atau

. 2_ˆ2

2 1 ) (

ˆ _{x m x}

V = ω . (2.7)

Energi suatu sistem fisis diwakilkan oleh sebuah operator yang disebut

Hamiltonian

( )

Hˆ . Operator Hamiltonian diberikan oleh

Hˆ =Tˆ+Vˆ (2.8) dengan Tˆ operator tenaga kinetik dan Vˆ operator tenaga potensial. Jika osilator

harmonik dengan tenaga potensial Vˆ diberikan oleh persamaan (2.7), maka

Hamiltonian menjadi

2 2_ˆ

2 1 ˆ

ˆ _{T m x}

H = + ω , (2.9)

dengan

m p T

2 ˆ

ˆ₌ 2 _(2.10)

2.2 Persamaan Nilai Eigen

Operator yang berkorespondensi untuk menunjukkan suatu momentum linear diberikan oleh (Liboff, 1980)

∇ − = ih

pˆ . (2.11)

Jika ditinjau hanya ke arah x saja, maka operator momentum pˆ menjadi

x i p_x

∂ ∂ −

= h

ˆ . (2.12)

n x

n p

x

i ψ = ψ

∂ ∂

− h . (2.13)

dengan ψ_n fungsi eigen dan pˆ nilai eigen yang tidak lain adalah momrntum ke _x arah x.

Operator yang berkorespondensi terhadap energi adalah Hamiltonian Hˆ .

Untuk partikel tunggal bermassa m berada dalam medan potensial V(x),

persamaan Hamiltonian diberikan oleh

) ( 2

) ( 2

ˆ

ˆ 2

2 2

x V m x

V m p

H = + =−h ∇ + (2.14)

Persamaan nilai eigen untuk Hˆ menjadi

) ( )

(

ˆ _{x E x}

Hψ_n = ψ_n (2.15)

atau

n

n E

Hˆψ = ψ . (2.16) Hamiltonian untuk partikel bebas

(

V =0

)

menjadi

2

2 2

2 2

ˆ

ˆ _{= =− ∇}

m m

p

H h (2.17)

Jika gerak partikel ditinjau ke satu arah saja ( misalnya ke arah sumbu x ), maka persamaan Schrodinger yang tak bergantung waktu menjadi

n

n E

x

m∂ ψ = ψ

∂ − 2 2₂

2

maka persamaan (2.18) menjadi 0 2 2 2 = + n n dx d ψ ξ ψ (2.20)

Penyelesaian persamaan (2.20) adalah

x i x i

n Ae Be

ξ ξ

ψ _{= +} − _(2.21)

Dengan A dan B adalah tetapan integrasi yang dapat ditentukan dari syarat batas.

Persamaan (2.21) adalah fungsi eigen dari Hˆ yang berkorespondensi untuk energi

nilai eigen (Liboff, 1980)

m k E 2 2 2 h

= . (2.22)

Persamaan Schrodinger tak bergantung waktu diberikan oleh

n n n E x m dx d

m ω ψ ψ

ψ _{+ =}

− 2 2

2 2 2 2 1 2

h _(2.23)

Persamaan energi osilator harmonik dalam bentuk Hamiltonian dapat memperoleh persamaan Schrodinger tak bergantung waktu seperti persamaan (2.23)

(Purwanto, 2006). Dengan memenuhi variabel z m x

ω

h

= , membuat persamaan (2.23) menjadi n n n E x m dz d ψ ψ ω ψ ω + =

− 2 2

2 2 ˆ 2 1 2 1

h (2.24)

atau

(

2

)

0

ω λ

h E

2

= . (2.26)

Untuk memperoleh solusi persamaan (2.25) diberikan nilai 2

)

( z

n u z e

η

ψ _{= =} − _{, sehingga diperoleh}

(

)

2

2 2 2 2 2 4 2 z z e z dz e

d η _η

η

η −

−

+ −

= . (2.27)

Sehingga persamaan ( 2.25) menjadi

(

−2η+4η2_z2

)

_e−ηz2 +

(

λ−_z2

)

_e−ηz2 =0 _(2.28)

Sebagai contoh, persamaan (2.28) terpenuhi jika diberikan , 1. 2 1

=

= λ

η Fungsi

2 /

2

) (z e z

u = − merupakan solusi pada persamaan (2.25) dengan λ =1 (Purwanto,2006)

(

1 2

)

0

2 2 = − + n n z dz d ψ ψ

. (2.29)

Dengan mengambil bentuk umum sembarang yang merupakan perkalian dengan

2 /

2

) (_{z e} z

f = − ,

) ( 2 / 2 z f e z n − =

ψ (2.30)

dan mensubstitusikan ke persamaan (2.30) dengan persamaan (2.29) diperoleh persamaan baru dalam f(z)

( )

∑

= + + +L ∞ = 2 2 1 0 0 z a z a a z a z f r r

r (2.32)

Dengan mensubstitusikan persamaan (2.32) ke persamaan (2.31) diperoleh persamaan baru

(

)(

)

{

(

)

}

[

]

k

k

k

k k k a k z

a

∑

∞ = + − − − + + = 0

2 2 1 2 1

0 λ . (2.33)

Persamaan (2.33) terpenuhi oleh semua z jika koefisien _zk =0

(

2

)(

1

)

{

2

(

1

)

}

0

2 + + − − =

+ k k a k λ

a_{k k} . (2.34)

Persamaan (2.34) menunjukkan bahwa pemecahannya akan berbentuk deret takhingga, yakni berhenti pada k=δ

δ

λ−1=2 , δ =0,1,2,3,4,L . (2.35) Dari persamaan (2.35) dan persamaan (2.26) diperoleh energi dari osilator harmonik

ω δ

δ h

     + = 2 1

E , (2.36)

dan sketsa dari energi osilator harmonik diperlihatkan seperti pada Gambar 2.1.

Gambar 2.1 Sketsa aras- aras tenaga pada osilator harmonik

1 E

2 E

x

V ₂ 2

1 )

(x m x

2.3 Operator Kreasi dan Operator Annihilasi

Melalui pedoman persamaan Schrodinger, dan melihat kembali osilator harmonik secara aljabar diperoleh operator-operator

p i x a p i x a ˆ ˆ ˆ ˆ ˆ ˆ ρ γ ρ γ − = + = +

− _(2.37)

atau

(

)

(

m x ip

)

m a p i x m m a ˆ ˆ 2 1 ˆ ˆ ˆ 2 1 ˆ 2 1 2 1 −       = +       = + − ω ω ω ω h h (2.38) dengan ω ρ ω γ m m h h 2 1 , 2 =

= (2.39)

Persamaan ( 2.38) mempunyai hubungan komutator dasar

[ ]

xˆ,pˆ =ih (2.40) Hubungan komutator dasar menunjukkan bahwa

[

]

− + + − + − + = = a a a a a a ˆ ˆ 1 ˆ ˆ 1 ˆ , ˆ (2.41)

Dengan menambahkan aˆ dengan ₊ aˆ dan dengan mengurangkan ₋ aˆ dengan ₊ aˆ ₋

Persoalan untuk menemukan nilai eigen dari Hˆ telah diubah bentuk untuk

menemukan nilai eigen dari operator

− +

≡a a

Nˆ ˆ ˆ (2.44)

Perhitungan komutator dari Nˆ dengan aˆ dan ₋ aˆ yaitu (Cohen-Tannoudji,1977) ₊

[ ]

[

]

[

] [

]

[ ]

+

[

+ − +

]

+

[

− +

] [

+ +

]

− + − − − + − − + − − + = + = = − = + = = a a a a a a a a a a a N a a a a a a a a a a a N ˆ ˆ ˆ , ˆ ˆ ˆ ˆ ˆ , ˆ ˆ ˆ , ˆ ˆ ˆ ˆ , ˆ ˆ , ˆ ˆ ˆ , ˆ ˆ ˆ , ˆ (2.45) dan

[ ]

[ ]

+ + − − = − = a a N a a N ˆ ˆ , ˆ ˆ ˆ , ˆ (2.46)

Fungsi ψ_n menjadi fungsi eigen dari Nˆ yang berkorespondensi dengan nilai eigen n sehingga diperoleh (Liboff, 1980)

n

n n

Nˆψ = ψ . (2.47) Hubungan antara aˆ₋ψ_n dengan Nˆ diberikan oleh

(

)

(

)

( )

n

(

)

n

(

)

n n n n n n a n n a N a a N a a a a a a a a a a N ψ ψ ψ ψ ψ ψ ψ ψ − − − − − + − − + − − − + − − = − = − = − = − = = ˆ 1 1 ˆ 1 ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ ˆ ˆ ˆ (2.48)

Fungsi aˆ₋ψ_nadalah fungsi eigen dari Nˆ , yang berkorespondensi dengan nilai

eigen n−1

1

ˆ_{− n} = _n−

a ψ ψ (2.49)

dan

2 1

ˆ_{− n−} = _n−

a ψ ψ . (2.50)

Dengan cara yang sama seperti persamaan (2.47) , maka operasi dalam bentuk

n

a

Nˆˆ₊ψ menghasilkan

(

)

n

n n a

a

Nˆˆ₊ψ = +1 ˆ₊ψ (2.51) Persamaan (2.51) mengindikasikan bahwa aˆ₊ψ_nadalah fungsi eigen dari Nˆ , yang

berkorespondensi dengan nilai eigen n+1

1

ˆ_{+ n} = _n+

a ψ ψ (2.52)

dan

2 1

ˆ_{+ n+} = _n+

aψ ψ (2.53)

Operator aˆ disebut sebagai operator kreasi. ₊

Jika operator annihilasi aˆ dan operator kreasi ₋ aˆ dikenakan pada suatu keadaan ₊

δ maka menghasilkan (Cohen-Tannoudji,1977) 1 1 ˆ₊ δ = δ + δ +

a (2.54)

dan

1 ˆ₋δ = δ δ −

2.4 Persamaan Differensial Orde Dua

Persamaan differensial orde dua mempunyai bentuk

0

0 1

2 2

2 + +a y=

dx dy a dx

y d

a (2.56)

dan

) (

2 0

2 1 2 2

x F y a a dx dy a a dx

y d

= +

+ (2.57)

dimana a₂,a₁,a₀ merupakan konstanta. Persamaan (2.56) merupakan persamaan

differensial orde dua homogen, sedangkan persamaan (2.57) merupakan persamaan differensial orde dua takhomogen.

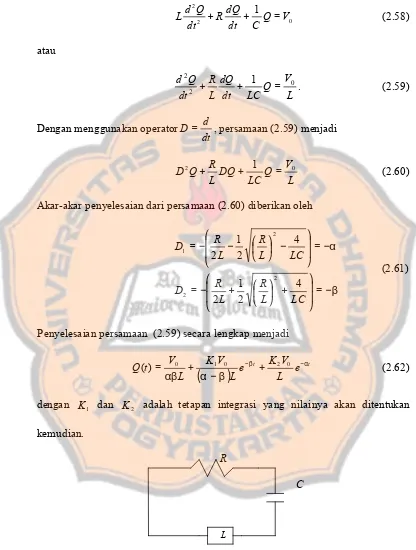
Suatu rangkaian RLC terdiri dari kapasitor, resistor, dan induktor yang

disusun seri kemudian dihubungkan dengan sumber tegangan baterai sebesar V₀,

seperti Gambar 2.2

R

0

V C

L

Gambar 2.2 Rangkaian RLC _{dengan sumber}

0 2 2 ₁ V Q C dt dQ R dt Q d

L + + = (2.58)

atau L V Q LC dt dQ L R dt Q d 0 2 2 1 = +

+ . (2.59)

Dengan menggunakan operator

dt d

D= , persamaan (2.59) menjadi

L V Q LC DQ L R Q

D2 + + 1 = 0

(2.60)

Akar-akar penyelesaian dari persamaan (2.60) diberikan oleh

β α − =         +       + − = − =         −       − − = LC L R L R D LC L R L R D 4 2 1 2 4 2 1 2 2 2 2 1 (2.61)

Penyelesaian persamaan (2.59) secara lengkap menjadi

(

)

t e t

L V K e L V K L V t

Q β α

β α αβ − − ₊ − +

= 0 1 0 2 0

)

( (2.62)

dengan K₁ dan K₂ adalah tetapan integrasi yang nilainya akan ditentukan

kemudian.

R

Jika tanpa sumber tegangan, maka persamaan differensial orde dua rangkaian

RLC pada Gambar 2.3 menjadi

0 1

2 2

= +

+ Q

C dt dQ R dt

Q d

L (2.63)

Dengan menggunakan operator

dt d

D= , persamaan (2.63) menjadi

0 1

2 + + _Q=

LC DQ L R Q

D . (2.64)

Karena mempunyai akar-akar penyelesaian yang sama seperti pada persamaan (2.61), maka penyelesaian secara lengkap persamaan (2.64) menjadi

t t

e K e K t

Q( )= ₃ −α + ₄ −β . (2.65) dengan K₃ dan K₄adalah tetapan integrasi yang nilainya akan ditentukan

BAB III

METODE PENELITIAN

Penelitian dilakukan dengan studi pustaka terhadap teori osilator harmonik dan penyelesaian persamaan differensial orde dua untuk rangkaian RLC yang disusun secara seri. Langkah- langkah yang ditempuh sebagai berikut.

3.1 Studi dan Elaborasi Persamaan Differensial Orde Dua Rangkaian RLC Persamaan differensial orde dua pada rangkaian RLC tersebut diselesaikan

persamaan umum untuk nilai Q

( )

t . Dari persamaan umum yang diperoleh,

kemudian dicari persamaan khusus dengan memasukkan syarat batas.

3.2 Perumusan Energi pada Kapasitor yang Terangkai pada Rangkaian RLC Dengan mengunakan hubungan yang ada dalam persamaan osilator harmonik, dijabarkan kembali energi pada kapasitor yang terangkai pada rangkaian RLC.

3.3 Kuantisasi Energi pada Rangkaian RLC

Kuantisasi energi pada rangkaian RLC dilakukan dengan mengubah

energiErmenjadi operator, dengan memperhatikan persyaratan matematis dan fisis

BAB IV

KUANTISASI ENERGI RANGKAIAN RLC

4.1 Energi Rangkaian RLC

Dari persamaan (2.69), dan dengan menggunakan syarat batas

0

) 0 (t q

Q = = dan Q(t=∞)=0 dimana K₁ =0 dan K₂=q₀ diperoleh persamaan baru

t

e Q t

Q( )= ₀ −β . (4.1)

Persamaan (4.1) menunjukkan bahwa muatan yang tersimpan di kapasitor adalah muatan yang berasal dari proses pengosongan. Hal tersebut terjadi karena rangkaian tidak diberi sumber tegangan.

Sedangkan dari persamaan (2.68), dengan menggunakan syarat batas Q(t=0)=0 dan Q'(t=0)=0diperoleh persamaan baru

(

)(

)

t L e t

V e

L V t

Q β α

αβ α β

α β α

β α

αβ + − − + + −

− +

= 0

2

0 1

)

( (4.2)

Persamaan (4.2) menunjukkan bahwa muatan yang tersimpan di kapasitor adalah muatan yang berasal dari proses pengisian. Peristiwa tersebut terjadi karena rangkaian diberi sumber tegangan

Melalui persamaan (4.1) dapat diperoleh besarnya arus yang dimiliki pada rangkaian RLC, yaitu sebesar

_{Q e} t

dt t dQ

(

)(

)

t e t L V e t t dQ

I β α

αβ α α β α β α β α β − − + − − + − − = = 0 2 1 ) ( (4.4)

Energi potensial yang dimiliki oleh muatan yang disimpan di kapasitor yang terhubung pada rangkaian RLC sebesar

2

2 1

CQ

V = (4.5)

Sedangkan energi kinetik yang dimiliki pada rangkaian RLC yaitu sebesar

            ₋ + = = C L i R I IR T ω

ω 1 . (4.6)

Dari persamaan (4.5) dan persamaan (4.6) diperoleh energi total dari rangkaian

RLC 2 2 1 1 CQ C L i R I V T H

E_{tot }+

           ₋ + = + = = ω

ω . (4.7)

4.2 Kuantisasi Energi Rangkaian RLC

Persamaan (4.7) mirip dengan persamaan energi osilator harmonik dengan operator Hamiltonian 2 2 2 ˆ 2 1 2 ˆ q m m p

H = + ω

dengan pˆ menyatakan momentum dan qˆ sebagai koordinat, dan dengan

Jika mengunakan hubungan antara persamaan (4.8) dengan persamaan energi osilator harmonik dengan operator Hamiltonian, maka diperoleh

I pˆ2 = dan A m = 2 1 yang menghasilkan I

pˆ = (4.9)

dan 2 2 2 2 1 ˆ 2 1 CQ q

mω =

yang menghasilkan

Q

qˆ= (4.10)

Metode pengkuantuman osilator harmonik secara aljabar dengan

menggunakan operator annihilasi aˆ dan operator kreasi ₋ aˆ didefinisikan sebagai ₊

(

)

(

m q ip

)

m a p i q m m a ˆ ˆ 2 1 ˆ ˆ ˆ 2 1 ˆ 2 1 2 1 −       = +       = + − ω ω ω ω h h

Jika pasangan momentum (persamaan (4.9)) dan koordinat (persamaan (4.10)) disubstitusikan ke dalam operator annihilasi dan operator kreasi, maka untuk rangkaian pengosongan muatan, operator annihilasi menjadi

(

m Q e i I

)

m

a  t +

     = −

− _ω ω 0 β

2 1

2 1 ˆ

sedangkan operator kreasi menjadi

(

m Q e i I

)

m

a _ t −

     = −

+ _ω ω 0 β

2 1

2 1 ˆ

h (4.12)

Untuk rangkaian pengisian muatan, operator annihilasi menjadi

(

)

(

)(

)

(

)

_     +     + + − + − +       = − −

− i I

L e V e L V m m a t t αβ α β α β α β α αβ ω ω α β 2 0 0 2 1 2 1 ˆ

h (4.13)

sedangkan operator kreasi menjadi

(

)

(

)(

)

(

)

_     −     + + − + − +       = − −

+ i I

L e V e L V m m a t t αβ α β α β α β α αβ ω ω α β 2 0 0 2 1 2 1 ˆ

h (4.14)

Penjumlahan persamaan(4.11) dengan persamaan (4.12) menghasilkan

t

e Q m a

a₊ + ₋ = ω ₀ −β

2 2 ˆ ˆ

h (4.15)

Pengurangan persamaan (4.11) dengan persamaan (4.12) menghasilkan

ω m I i a a h 2 2 ˆ

ˆ₊− ₋ = (4.16)

Penjumlahan persamaan (4.13) dan persamaan (4.14) menghasilkan

(

)

(

)(

)

(

)

_   + + − + − + = + − − − + L e V e L V m a a t t αβ α β α β α β α αβ ω β α 2 0 0 2 2 ˆ ˆ

h (4.17)

Pengurangan persamaan (4.13) dan persamaan (4.14) menghasilkan

ω

I i a

Mengingat sifat- sifat operator kreasi aˆ dan operator annihilasi ₊ aˆ seperti pada ₋

persamaan (2.58) dan persamaan (2.59) maka energi rangkaian RLC untuk suatu

keadaan δ dapat diperoleh dengan menggunakan operator energi rangkaian

RLC Eˆ pada keadaan δ yang diberikan oleh

δ δ ω δ δ δ ω δ ω δ       + = − +       _{+ + −} =       ₊ = _{+ −} 2 1 1 1 1 1 2 1 2 1 ˆ ˆ ˆ h h

h a a

E

(4.20)

Sehingga energi rangkaian RLC pada keadaan δ diberikan oleh

      + = 2 1 δ ω δ h

E ; δ =0,1,2,3,_L (4.21) Jadi energi rangkaian RLC terkuantisasi sebagaimana terlihat pada persamaan (4.20). Kuantisasi energi rangkaian RLC dapat dilakukan karena terdapat hubungan korespondensi koordinat q dan momentum p sebagaimana

4.3 Implikasi Kuantisasi Energi Rangkaian RLC

Anggapan bahwa ada kesetaraan atau kemiripan antara energi rangkaian

BAB V PENUTUP

5.1 Kesimpulan

Pengkuantuman rangkaian RLC dapat dilakukan karena arus rangkaian yaitu Idan muatan yang dimiliki kapasitor Q memenuhi hubungan antara

koordinat qdan momentum psebagaimana yang terdapat pada osilator harmonik

yaitu

dt dp q=− dan

dt dq

p = .

Arus pada rangkaian I dan muatan pada kapasitor Q merupakan kombinasi

linear dari operator kreasi aˆ dan operator annihilasi ₊ aˆ sebagaimana yang ₋

dipakai dalam osilator harmonik.

5.2 Saran

DAFTAR PUSTAKA

Liboff, R.L, 1980, Introductory Quantum Mechanics, Cornell University, USA Cohen-Tannoudji, C., Diu, B.,dan Laloe, F.,1977, Quantum Mechanics, Vol.I,

John Wiley& Sons, New York, USA

Silaban, P., 1977, Teori Grup dalam Fisika, Angkasa, Bandung Purwanto, A., 2006, Fisika Kuantum, Gava Media, Yogyakarta