PEMODELAN MATEMATIS PENYEBARAN COVID-19 YANG MELIBATKAN PENURUNAN KEKEBALAN TUBUH
DAN PENYELESAIAN NUMERISNYA MENGGUNAKAN METODE RUNGE-KUTTA ORDE EMPAT
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Ferdinandus Steven Millicent NIM: 183114009
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
2022
i
PEMODELAN MATEMATIS PENYEBARAN COVID-19 YANG MELIBATKAN PENURUNAN KEKEBALAN TUBUH
DAN PENYELESAIAN NUMERISNYA MENGGUNAKAN METODE RUNGE-KUTTA ORDE EMPAT
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Ferdinandus Steven Millicent NIM: 183114009
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
2022
ii
MATHEMATICAL MODELING OF THE SPREAD OF COVID-19 THAT INVOLVING DECREASED IMMUNITY
AND ITS NUMERICAL SOLUTIONS USING THE FOURTH ORDER RUNGE-KUTTA METHOD
THESIS
Presented as Partial Fulfillment of the
Requirements to Obtain the Degree of Sarjana Matematika Mathematics Study Program
Written By:
Ferdinandus Steven Millicent Student Number: 183114009
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
2022
HALAMAN PERSETUJUAN
SKRIPSI
PEMODELAN MATE MATIS PENYEBARAN COVID-19 YANG MEL IBA TKAN PENURUNAN KEKEBALAN TUBUH
DAN PENYELESAIANNUMERISNYA MENGGUNAKAN METODE RUNGE-KUTTAORDE EMPAT
Dr. Lusia Krismiyati Budiasih Tanggal: 17 Januari 2022
iii
HALAMANPENGESAHAN
SKRIPSI
PEMODELAN MATEMATIS PENYEBARAN COVID-19 YANG MELIBATKAN PENURUNAN KEKEBALAN TUBUH
DAN PENYELESAIANNUMERISNYAMENGGUNAKAN METODE RUNGE-KUTTAORDE EMPAT
NamaLengK~I\
Ketua Sekretaris Anggota
; ' -
Di~~Is~ap~aanditulis oleh:
4'" •
~lJ;cllnandus_Steven Millicent
. .;;a. '--'"". •.
7_.r_'NIM:~183(lLl009 .
J. ¥ .
Yogyakarta,27Januari2022 Fakultas Sains dan Teknologi
Universitas Sanata Dhanna Dekall,
-(Prof. If. Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D.)
iv
v
HALAMAN PERSEMBAHAN
“The only way to do great work is to love what you do. If you haven’t found it yet, keep looking. Don’t settle”
– Steve Jobs –
Skripsi ini saya persembahkan untuk kedua orang tua tercinta yang telah mendukung, anggota keluarga tersayang, dan Universitas Sanata Dharma
vi
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 17 Januari 2022 Penulis
Ferdinandus Steven Millicent
vii
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:
Nama : Ferdinandus Steven Millicent NIM : 183114009
Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:
PEMODELAN MATEMATIS PENYEBARAN COVID-19 YANG MELIBATKAN PENURUNAN KEKEBALAN TUBUH
DAN PENYELESAIAN NUMERISNYA MENGGUNAKAN METODE RUNGE-KUTTA ORDE EMPAT
beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.
Demikian pernyataan ini saya buat dengan sebenarnya.
Dibuat di Yogyakarta
Pada tanggal 17 Januari 2022 Yang menyatakan,
Ferdinandus Steven Millicent
viii ABSTRAK
Skripsi ini membahas tentang pemodelan matematis penyebaran COVID- 19 yang melibatkan penurunan kekebalan tubuh dan penyelesaian numerisnya menggunakan metode Runge-Kutta orde empat. Model matematis yang dibangun adalah model 𝑆𝐸𝐼𝐴𝐼𝑆𝑍𝑍0, dimana 𝑆 adalah kelompok individu yang memiliki risiko terinfeksi, 𝐸 adalah kelompok individu yang terpapar dan sedang dalam masa inkubasi, 𝐼𝐴 adalah kelompok individu terinfeksi tanpa gejala, 𝐼𝑆 adalah kelompok individu terinfeksi dengan gejala, 𝑍 adalah kelompok individu sembuh, dan 𝑍0 adalah kelompok individu sembuh yang kembali menjadi individu yang memiliki risiko terinfeksi akibat turunnya kekebalan tubuh. Model matematis tersebut disajikan dalam sistem persamaan diferensial biasa nonlinear. Skripsi ini juga membahas analisis titik kesetimbangan dan kestabilan titik kesetimbangan dari model yang telah dibentuk. Selanjutnya, model diselesaikan secara numeris dengan metode Runge-Kutta orde empat. Dapat diamati bahwa penyelesaian akan menuju titik kesetimbangan yang diperoleh. Selain itu, analisis pengaruh adanya penurunan kekebalan tubuh dan vaksinasi juga dilakukan. Hasil analisis menunjukkan bahwa semakin tinggi probabilitas penurunan kekebalan tubuh dari individu sembuh, maka semakin banyak jumlah individu terinfeksi dengan gejala, semakin sedikit jumlah individu sembuh, dan semakin banyak jumlah individu sembuh yang kembali memiliki risiko terinfeksi akibat turunnya kekebalan tubuh. Semakin tinggi laju vaksinasi, maka semakin sedikit jumlah individu terinfeksi tanpa gejala, semakin sedikit jumlah individu terinfeksi dengan gejala, dan semakin banyak jumlah individu sembuh.
Kata kunci: pemodelan COVID-19, sistem persamaan diferensial biasa, metode Runge-Kutta orde empat.
ix ABSTRACT
This thesis discusses the mathematical modeling of the spread of COVID- 19 that involving decreased immunity and its numerical solution using the fourth order Runge-Kutta method. The mathematical model that was built is the 𝑆𝐸𝐼𝐴𝐼𝑆𝑍𝑍0 model, where 𝑆 is a group of individuals who have a risk of being infected, 𝐸 is a group of individuals who are exposed and in the incubation period, 𝐼𝐴 is a group of infected individuals without symptoms, 𝐼𝑆 is a group of infected individuals with symptoms, 𝑍 is the group of recovered individuals, and 𝑍0 is the group of recovered individuals who return to being individuals who have a risk of infection due to decreased immunity. The mathematical model is presented as a system of nonlinear ordinary differential equations. This thesis also discusses the analysis of the equilibrium point and the stability of the equilibrium point of the model that has been formed. Furthermore, the model was solved numerically by the fourth-order Runge-Kutta method. It can be observed that the solution will go to the equilibrium points obtained. Moreover, analysis of the effect of decreased immunity and vaccination was also carried out.The results of the analysis show that the higher the probability of decreased immunity of recovered individuals, then the greater the number of infected individuals with symptoms, the fewer the number of recovered individuals, and the greater the number of recovered individuals who again have the risk of being infected due to decreased immunity. The higher the vaccination rate, then the fewer the number of infected individuals without symptoms, the fewer the number of infected individuals with symptoms, and the greater the number of recovered individuals.
Keywords: modeling COVID-19, system of ordinary differential equations, fourth order Runge-Kutta method.
x
KATA PENGANTAR
Puji dan syukur penulis haturkan ke hadiran Tuhan Yang Maha Esa, karena berkat dan rahmat-Nya penulis dapat menyusun dan menyelesaikan penyusunan skripsi yang berjudul “Pemodelan Matematis Penyebaran COVID-19 yang Melibatkan Penurunan Kekebalan Tubuh dan Penyelesaian Numerisnya Menggunakan Metode Runge-Kutta Orde Empat” dengan baik dan lancar. Skripsi ini disusun dalam rangka memenuhi persyaratan akhir mencapai gelar Sarjana Matematika pada Fakultas Sains dan Teknologi, Universitas Sanata Dharma Yogyakarta.
Dalam penyusunan skripsi ini, banyak pihak yang telah membantu dan mendukung penulis dalam penyusunan skripsi ini, baik secara langsung maupun tidak langsung. Oleh karena itu, dengan hati yang tulus penulis ingin menyampaikan rasa syukur dan terima kasih yang sebesar-besarnya kepada:
1. Ibu Dr. Lusia Krismiyati Budiasih selaku dosen pembimbing yang dengan sabar dan semangat dalam mengarahkan, membimbing, dan memberikan saran dalam penyusunan skripsi.
2. Bapak Prof. Ir. Sudi Mungkasi, S.Si, M.Math.Sc., Ph.D. selaku Dekan Fakultas Sains dan Tekonologi, Universitas Sanata Dharma Yogyakarta.
3. Bapak Hartono, Ph.D. selaku Ketua Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma Yogyakarta.
4. Ibu Any Herawati, S.Si., M.Si. selaku Dosen Pembimbing Akademik.
5. Romo Prof. Dr. Frans Susilo, SJ., Bapak Ig. Aris Dwiatmoko, M.Sc., Bapak Dr. rer. nat. Herry P. Suryawan, M.Si., dan Bapak Ricky Aditya, M.Sc.
selaku dosen-dosen Program Studi Matematika yang telah memberikan banyak ilmu pengetahuan serta pengalamannya kepada penulis selama belajar di Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma Yogyakarta.
6. Kedua orang tua penulis yang mendukung dan menyemangati penulis dalam penyusunan karya tulis ilmiah ini dan selalu mendoakan penulis dalam berproses.
xi
7. Kedua kakak penulis yang telah membantu penulis memilih buku referensi yang digunakan dalam penyusunan karya tulis ilmiah ini.
8. Tassya sebagai sahabat seperjuangan selama masa perkuliahan.
9. Ovie sebagai teman seperjuangan satu dosen pembimbing.
10. Teman-teman program studi matematika angkatan 2018 yang telah mendukung dan memberi masukan selama proses belajar.
11. Seluruh pihak yang tidak dapat disebutkan satu-persatu, yang telah membantu penulis.
Penulis menyadari masih terdapat banyak kekurangan dan kelemahan dalam penyusunan skripsi ini, sehingga masih perlu dikaji dan dikembangkan secara lebih lanjut. Penulis berharap semoga skripsi yang telah disusun ini dapat bermanfaaat bagi pembaca.
Yogyakarta, 17 Januari 2022 Penulis,
Ferdinandus Steven Millicent
xii DAFTAR ISI
HALAMAN JUDUL ...i
HALAMAN JUDUL DALAM BAHASA INGGRIS ...ii
HALAMAN PERSETUJUAN...iii
HALAMAN PENGESAHAN ...iv
HALAMAN PERSEMBAHAN ...v
PERNYATAAN KEASLIAN KARYA ...vi
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI ...vii
ABSTRAK ...viii
ABSTRACT...ix
KATA PENGANTAR ...x
DAFTAR ISI...xii
DAFTAR GAMBAR ...xiv
DAFTAR LAMPIRAN...xv
BAB I PENDAHULUAN ...1
A. Latar Belakang ...1
B. Rumusan Masalah ...3
C. Batasan Masalah ...3
D. Tujuan Penulisan...3
E. Manfaat Penulisan...4
F. Metode Penelitian ...5
G. Sistematika Penulisan ...5
BAB II PEMODELAN MATEMATIS DAN SISTEM PERSAMAAN DIFERENSIAL ...7
A. Pemodelan Matematis ...7
B. Persamaan Diferensial...10
C. Matriks Jacobian ...17
D. Nilai Eigen dan Vektor Eigen ...18
E. Persamaan Karakteristik ...19
F. Polinomial Karakteristik ...19
xiii
G. Kriteria Routh-Hurwitz ...20
H. Titik Kesetimbangan ...21
I. Kestabilan Titik Kesetimbangan ...23
J. Bilangan Reproduksi Dasar ...26
K. Matriks Generasi Berikutnya ...27
L. Metode Runge-Kutta Orde Empat ...29
BAB III MODEL MATEMATIS PENYEBARAN COVID-19 YANG MELIBATKAN PENURUNAN KEKEBALAN TUBUH ...33
A. Asumsi-Asumsi yang Digunakan ...33
B. Penyusunan Model ...36
C. Analisis Titik Kesetimbangan ...47
D. Analisis Kestabilan Titik Kesetimbangan ...52
E. Bilangan Reproduksi Dasar ...67
BAB IV PENYELESAIAN MODEL DENGAN METODE RUNGE-KUTTA ORDE EMPAT ...74
A. Skema Penyelesaian Model dengan Metode Runge-Kutta ...74
B. Penyelesaian Model ...77
C. Analisis Pengaruh Adanya Penurunan Kekebalan Tubuh ...88
D. Penyelesaian Model dengan Adanya Laju Vaksinasi ...91
E. Analisis Pengaruh Adanya Vaksinasi ...100
BAB V PENUTUP ...104
A. Kesimpulan ...104
B. Saran...105
DAFTAR PUSTAKA ...106
LAMPIRAN...108
xiv
DAFTAR GAMBAR
Gambar 2.10.1. Illustrasi untuk 𝑅0 = 3 ...26
Gambar 3.2.1 Diagram Model Penyebaran COVID-19...37
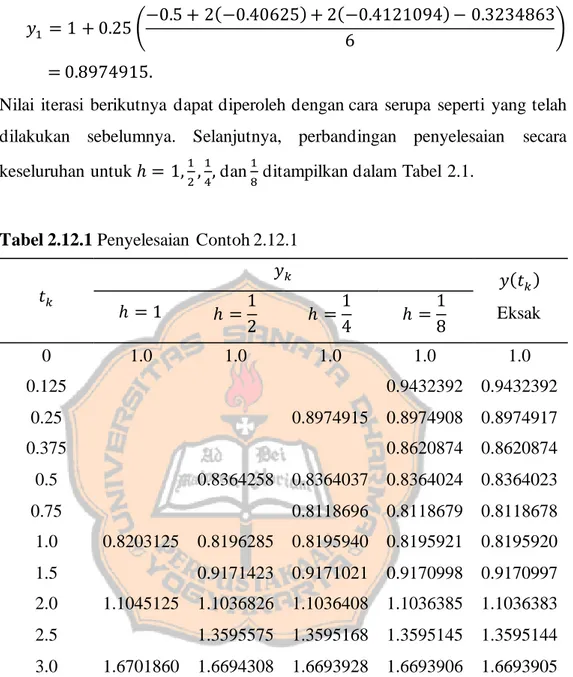
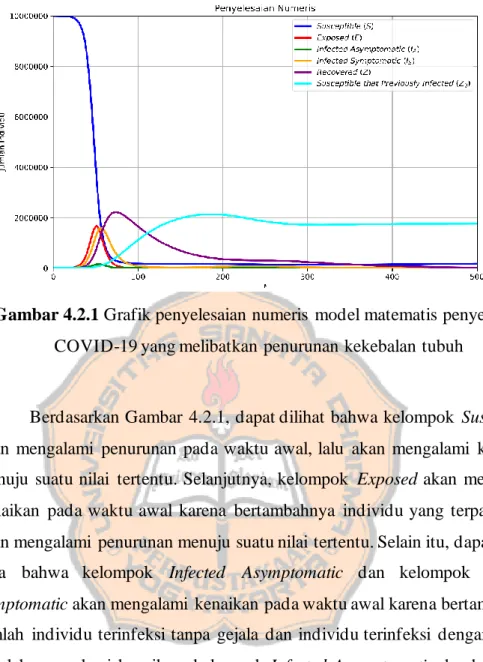
Gambar 4.2.1 Grafik penyelesaian numeris mod el...81
Gambar 4.2.2 Grafik-1 penyelesaian numeris kelompok 𝑆 ...83
Gambar 4.2.3 Grafik-2 penyelesaian numeris kelompok 𝑆 ...83
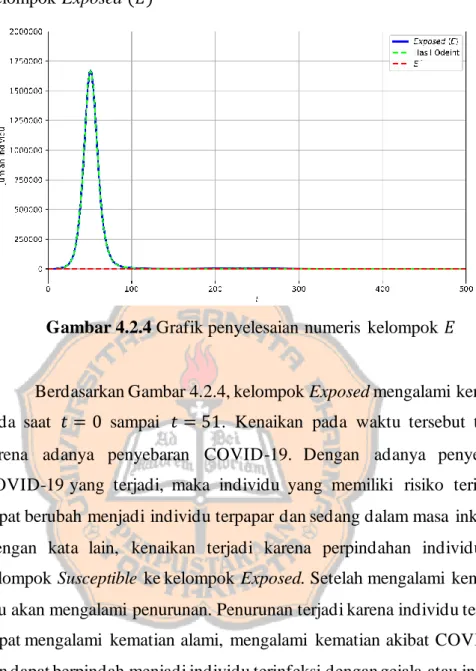
Gambar 4.2.4 Grafik penyelesaian numeris kelompok 𝐸 ...84
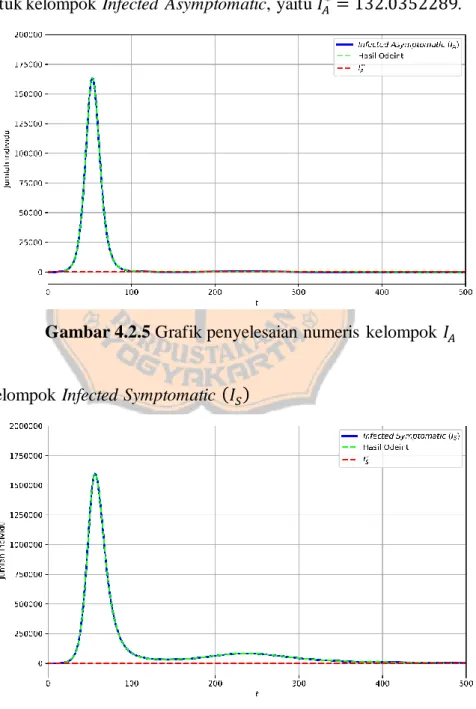
Gambar 4.2.5 Grafik penyelesaian numeris kelompok 𝐼𝐴...85
Gambar 4.2.6 Grafik penyelesaian numeris kelompok 𝐼𝑆 ...85
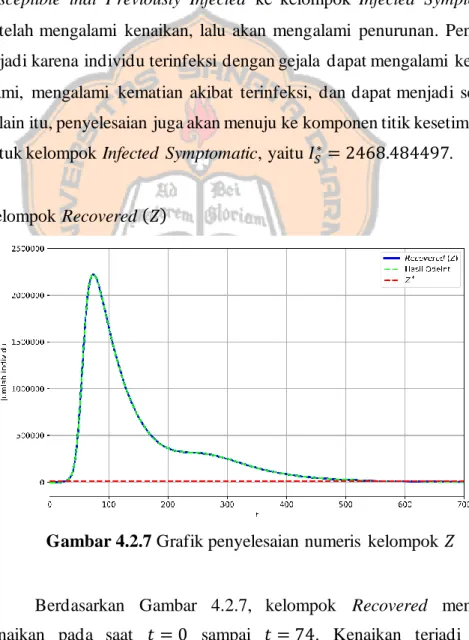
Gambar 4.2.7 Grafik penyelesaian numeris kelompok 𝑍 ...86
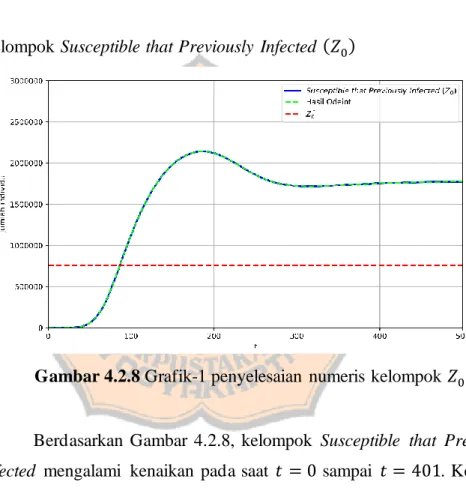
Gambar 4.2.8 Grafik-1 penyelesaian numeris kelompok 𝑍0 ...87
Gambar 4.2.9 Grafik-2 penyelesaian numeris kelompok 𝑍0 ...88
Gambar 4.3.1 Pengaruh parameter 𝜉 terhadap kelompok 𝐼𝑆 ...89
Gambar 4.3.2 Pengaruh parameter 𝜉 terhadap kelompok 𝑍 ...90
Gambar 4.3.3 Pengaruh parameter 𝜉 terhadap kelompok 𝑍0 ...90
Gambar 4.4.1 Grafik penyelesaian numeris model untuk 𝑅0 < 1 ...94
Gambar 4.4.2 Grafik-1 penyelesaian numeris kelompok 𝑆 untuk 𝑅0 < 1 ...95
Gambar 4.4.3 Grafik-2 penyelesaian numeris kelompok 𝑆 untuk 𝑅0 < 1 ...96
Gambar 4.4.4 Grafik penyelesaian numeris kelompok 𝐸 untuk 𝑅0 < 1...96
Gambar 4.4.5 Grafik penyelesaian numeris kelompok 𝐼𝐴 untuk 𝑅0 < 1 ...97
Gambar 4.4.6 Grafik penyelesaian numeris kelompok 𝐼𝑆 untuk 𝑅0 < 1...98
Gambar 4.4.7 Grafik-1 penyelesaian numeris kelompok 𝑍 untuk 𝑅0 < 1...98
Gambar 4.4.8 Grafik-2 penyelesaian numeris kelompok 𝑍 untuk 𝑅0 < 1...99
Gambar 4.4.9 Grafik penyelesaian numeris kelompok 𝑍0 untuk 𝑅0 < 1 ...99
Gambar 4.5.1 Pengaruh parameter 𝜎 terhadap kelompok 𝑆 ...100
Gambar 4.5.2 Pengaruh parameter 𝜎 terhadap kelompok 𝐼𝐴 ...101
Gambar 4.5.3 Pengaruh parameter 𝜎 terhadap kelompok 𝐼𝑆...102
Gambar 4.5.4 Pengaruh parameter 𝜎 terhadap kelompok 𝑍 ...102
xv
DAFTAR LAMPIRAN
LAMPIRAN
A. Program Maple untuk Menentukan Titik Kesetimbangan Endemik ...108
B. Titik Kesetimbangan Endemik...108
C. Program Bab IV Subbab B ...120
D. Program Bab IV Subbab C ...124
E. Program Bab IV Subbab D ...127
F. Program Bab IV Subbab E...130
1 BAB I PENDAHULUAN
A. Latar Belakang
Perkembangan teknologi dan informasi memudahkan manusia untuk melakukan penyelesaian terhadap permasalahan-permasalahan kompleks yang terjadi dalam kehidupan sehari-hari. Sebelum melakukan penyelesaian tersebut, diperlukan suatu model yang merupakan representasi dari permasalahan tersebut. Model yang biasa digunakan untuk menyelesaikan permasalahan kompleks dalam kehidupan sehari-hari adalah model matematis.
Pemodelan matematis merupakan salah satu cara untuk merepresentasikan persoalan-persoalan atau permasalahan-permasalahan kompleks ke dalam bentuk model matematika. Model matematis merupakan abstraksi, penyederhanaan, dan konstruksi matematika terkait bagian dari kenyataan dan dibentuk untuk suatu tujuan. Dengan demikian, model matematis harus dapat merepresentasikan situasi dari permasalahan yang diteliti. Model matematis memiliki peranan yang penting dalam menganalisa suatu fenomena epidemik dalam bidang kesehatan dengan mengetahui tingkat penyebaran virus pada penyakit menular (Muntoyimah et al., 2018). Model matematis dapat berupa sistem persamaan atau pertidaksamaan.
Coronavirus disease 2019 atau COVID-19 adalah penyakit yang disebabkan oleh Severe Acute Respiratory Syndrome Coronavirus 2 (SARS- CoV-2). COVID-19 dapat ditularkan dari manusia ke manusia lain melalui droplet yang keluar saat batuk atau bersin. Penyebaran COVID-19 yang terjadi telah memberikan banyak dampak secara sosial dan ekonomi. Tanda dan gejala umum infeksi COVID-19 antara lain gejala gangguan pernapasan akut seperti demam, batuk dan sesak napas. Masa inkubasi COVID-19 rata-rata mencapai 5-6 hari dengan masa inkubasi terpanjang selama 14 hari. Pada kasus COVID- 19 yang berat dapat menyebabkan pneumonia, sindrom pernapasan akut, gagal ginjal, dan bahkan kematian (Kemenkes, 2020).
COVID-19 ditemukan pertama kali di Wuhan, China pada Desember 2019, yang menyebabkan kematian sebesar 12.784 penderita, dan telah menyebar ke beberapa negara (Shankar, A. dkk, 2020). COVID-19 dilaporkan terjadi di Indonesia pertama kali pada tanggal 2 Maret 2020 sejumlah dua kasus.
Kasus meningkat dan menyebar dengan cepat di seluruh wilayah Indonesia.
Sampai dengan tanggal 9 Juli 2020, Kementerian Kesehatan melaporkan 70.736 kasus konfirmasi COVID-19 dengan 3.417 kasus meninggal (Kemenkes, 2020).
Pada tanggal 11 Maret 2020, World Health Organization (WHO) sudah menetapkan COVID-19 sebagai pandemi (Kemenkes, 2020). Selama pembuatan dan pengembangan vaksin yang efektif untuk mengatasi penyebaran COVID-19 masih berjalan, dunia harus mempersiapkan diri untuk hidup berdampingan dengan COVID-19. Dalam hal ini, perlu dibentuk suatu model matematis mengenai penyebaran COVID-19 untuk mengetahui dan menganalisis bagaimana penyebaran COVID-19 terjadi.
Permasalahan berbagai bidang pada dunia nyata dapat diselesaikan dengan membuat model matematis dan mencari penyelesaiannya. Salah satu metode untuk memperoleh penyelesaian dari model matematis secara numeris adalah metode Runge-Kutta. Metode Runge-Kutta adalah metode yang dapat digunakan untuk menyelesaikan persamaan diferensial dengan nilai awal yang diketahui. Metode Runge-Kutta dapat memberikan hasil ketelitian yang cukup tinggi dan tidak memerlukan turunan dari fungsi. Selain itu, metode Runge- Kutta orde empat memiliki tingkat ketelitian yang lebih baik dibandingkan dengan metode Runge-Kutta orde satu, dua, ataupun orde tiga. Metode Runge- Kutta orde empat merupakan salah satu metode numeris yang populer, memiliki ketelitian yang baik, dan mudah untuk dilakukan.
Dalam skripsi ini akan dibahas tentang model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh. Model matematis yang akan disusun juga mempertimbangkan adanya parameter laju vaksinasi.
Skripsi ini juga akan membahas penyelesaian numeris dari model matematis tersebut. Penyelesaian ditentukan untuk mengamati perilaku dinamis dan pendekatan yang dilakukan secara numeris dari model matematis tersebut.
Selain itu, juga akan dilakukan analisis pengaruh adanya penurunan kekebalan tubuh dan vaksinasi dari model matematis yang telah disusun. Dalam skripsi ini, metode yang digunakan untuk menyelesaikan model adalah metode Runge- Kutta orde empat.
B. Rumusan Masalah
Rumusan masalah yang akan dibicarakan pada skripsi ini adalah:
1. Bagaimana menyusun model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh?
2. Bagaimana penyelesaian model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh menggunakan metode Runge-Kutta orde empat?
3. Bagaimana pengaruh adanya penurunan kekebalan tubuh terhadap beberapa kelompok individu dalam model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh menggunakan metode Runge-Kutta orde empat?
4. Bagaimana pengaruh adanya vaksinasi terhadap beberapa kelompok individu dalam model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh menggunakan metode Runge-Kutta orde empat?
C. Batasan Masalah
Batasan masalah dalam skripsi ini adalah:
1. Penyebaran COVID-19 yang dibahas adalah penyebaran COVID-19 yang terjadi antar manusia.
2. Penyelesaian numeris dilakukan dengan metode Runge-Kutta orde empat dan menggunakan program Python.
D. Tujuan Penulisan
Berdasarkan rumusan masalah di atas, tujuan dari penulisan skripsi ini adalah:
1. Mengetahui model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh.
2. Mengetahui penyelesaian model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh menggunakan metode Runge-Kutta orde empat.
3. Mengetahui pengaruh adanya penurunan kekebalan tubuh terhadap beberapa kelompok individu dalam model matematis penyebaran COVID- 19 yang melibatkan penurunan kekebalan tubuh menggunakan metode Runge-Kutta orde empat..
4. Mengetahui pengaruh adanya vaksinasi terhadap beberapa kelompok individu dalam model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh menggunakan metode Runge-Kutta orde empat..
E. Manfaat Penulisan
Manfaat dari penulisan skripsi ini adalah:
1. Memperoleh model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh.
2. Mendapatkan penyelesaian model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh menggunakan metode Runge-Kutta orde empat.
3. Memperoleh hasil analisis pengaruh adanya penurunan kekebalan tubuh terhadap beberapa kelompok individu dalam model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh menggunakan metode Runge-Kutta orde empat.
4. Mendapatkan hasil analisis pengaruh adanya vaksinasi terhadap beberapa kelompok individu dalam model matematis penyebaran COVID-19 yang melibatkan penurunan kekebalan tubuh menggunakan metode Runge-Kutta orde empat.
F. Metode Penelitian
Metode penelitian yang digunakan dalam penulisan skripsi ini adalah metode studi pustaka, yaitu dengan membaca dan mempelajari buku-buku dan jurnal-jurnal yang berkaitan dengan pemodelan matematis, metode Runge- Kutta orde empat serta penyelesaiannya menggunakan program Pyhton, dan COVID-19.
G. Sistematika Penulisan
Sistematika penulisan yang digunakan dalam skripsi ini adalah sebagai berikut:
BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penelitian G. Sistematika Penulisan
BAB II SISTEM PERSAMAAN DIFERENSIAL A. Pemodelan Matematis
B. Persamaan Diferensial C. Matriks Jacobian
D. Nilai Eigen dan Vektor Eigen E. Persamaan Karakteristik F. Polinomial Karakteristik G. Kriteria Routh-Hurwitz H. Titik Kesetimbangan
I. Kestabilan Titik Kesetimbangan J. Bilangan Reproduksi Dasar K. Matriks Generasi Berikutnya L. Metode Runge-Kutta Orde Empat
BAB III MODEL MATEMATIS PENYEBARAN COVID-19 YANG MELIBATKAN PENURUNAN KEKEBALAN TUBUH
A. Asumsi-Asumsi yang Digunakan B. Penyusunan Model
C. Analisis Titik Kesetimbangan
D. Analisis Kestabilan Titik Kesetimbangan E. Bilangan Reproduksi Dasar
BAB IV PENYELESAIAN NUMERIS DENGAN METODE RUNGE- KUTTA ORDE EMPAT
A. Skema Penyelesaian Model dengan Menggunakan Metode Runge-Kutta Orde Empat
B. Penyelesaian Model
C. Analisis Pengaruh Adanya Penurunan Kekebalan Tubuh D. Penyelesaian Model dengan Adanya Laju Vaksinasi E. Analisis Pengaruh Adanya Vaksinasi
BAB V PENUTUP A. Kesimpulan B. Saran
DAFTAR PUSTAKA LAMPIRAN
7 BAB II
PEMODELAN MATEMATIS DAN SISTEM PERSAMAAN DIFERENSIAL
Dalam bab ini akan dibahas mengenai landasan teori yang menjadi dasar dari skripsi ini. Landasan teori yang digunakan dalam skripsi ini adalah pemodelan matematis, persamaan diferensial, matriks Jacobian, nilai eigen dan vektor eigen, persamaan karakteristik, polinomial karakteristik, kriteria Routh-Hurwitz, titik kesetimbangan, kestabilan titik kesetimbangan, bilangan reproduksi dasar, matriks generasi berikutnya , dan metode Runge-Kutta orde empat.
A. Pemodelan Matematis
Pada bagian ini akan dijelaskan pemodelan matematis dan langkah- langkah dalam penyusunan model matematis yang baik. Referensi yang digunakan diambil dari buku A First Course in Mathematical Modeling, fifth edition (Giodarno, et al., 2014).
Pemodelan matematis merupakan salah satu cara untuk menggambarkan permasalahan kompleks ke dalam bentuk matematika. Model matematis merupakan penyederhanaan dan konstruksi matematika terkait bagian dari kenyataan atau fenomena dunia nyata yang dirancang untuk suatu tujuan tertentu. Model matematis dapat berupa persamaan atau pertidaksamaan.
Model matematis yang dibentuk harus mampu menjelaskan permasalahan yang sedang diamati.
Model matematis yang baik dapat disusun melalui beberapa langkah.
Langkah-langkah dalam penyusunan model matematis tersebut adalah:
1. Mengidentifikasi Masalah
Langkah pertama dalam menyusun model matematis adalah mengidentifikasi masalah. Biasanya langkah awal ini adalah langkah yang sulit karena dalam situasi kehidupan nyata, bentuk permasalahan matematika yang harus dipecahkan dari masalah yang ingin diidentif ikasi tidak diberikan secara langsung. Oleh karena itu, pada langkah ini harus
dilakukan proses pemilahan data yang akan digunakan dan mengidentifikasi beberapa aspek tertentu yang akan dipelajari sesuai dengan masalah yang dipilih. Selain itu, dalam mengidentifikasi masalah perlu ditetapkan pertanyaan dan tujuan apa yang ingin dijawab. Pertanyaan ini merupakan suatu hal yang penting karena menjadi sebuah acuan dalam membangun model matematis.
2. Membuat Asumsi
Langkah selanjutnya adalah membuat asumsi. Pada langkah ini, faktor-faktor apa saja yang mempengaruhi masalah harus ditentukan. Akan tetapi, dalam penyusunan model matematis, tidak semua faktor tersebut dapat digunakan karena akan mempengaruhi kompleksitas model matematika dari masalah yang diidentifikasi. Dalam hal ini, model matematis dari masalah tersebut dapat disederhanakan dengan mengurangi jumlah faktor yang akan dipertimbangkan dalam penyusunan model. Selain itu, hubungan antara variabel harus ditentukan. Dengan mengasumsikan hubungan yang relatif sederhana dapat mengurangi kompleksitas masalah.
Dengan demikian, asumsi dibagi menjadi dua bagian:
a. Klasifikasi Variabel
Hal-hal yang mempengaruhi masalah dan telah diidentifikasi pada langkah pertama disebut sebagai variabel. Variabel dapat diklasifikasikan menjadi variabel terikat atau variabel bebas. Dalam hal ini, variabel yang dijelaskan dalam model adalah variabel terikat, dan variabel yang tersisa adalah variabel bebas.
b. Menentukan Keterkaitan antara Variabel
Sebelum menentukan keterkaitan antara variabel, umumnya dibuat beberapa penyederhanaan tambahan. Masalah yang ingin diidentifikasi mungkin sangat kompleks sehingga kita tidak dapat melihat hubungan antara variabel-variabel yang ada. Oleh karena itu, perlu untuk mempelajari submodel, yang mempelajari satu atau lebih variabel bebas secara terpisah dan pada akhirnya menghubungkan submodel tersebut secara bersama-sama. Selain itu, dengan mempelajari
berbagai teknik, seperti proporsionalitas, akan membantu dalam menentukan keterkaitan antara variabel.
3. Menyelesaikan atau Menginterpretasikan Model
Langkah ketiga adalah menyelesaikan atau menginterpretasikan model. Yang dilakukan pada langkah ini adalah mengumpulkan semua submodel untuk melihat informasi apa yang dapat diambil dari model yang dibentuk. Model dapat terdiri dari persamaan atau pertidaksamaan matematis yang kemudian harus diselesaikan. Pada saat menyelesaikan model tersebut, ada kemungkinan dimana kurangnya informasi yang menyebabkan tidak dapat menyelesaikan model tersebut. Selain itu, ada kejadian dimana kita mungkin berakhir dengan model yang begitu kompleks sehingga kita tidak dapat menyelesaikannya. Untuk mengatasi hal tersebut dapat dilakukan dengan kembali ke langkah dua, yaitu dengan membuat asumsi tambahan untuk menyederhanakan model.
4. Verifikasi Model
Langkah berikutnya adalah verifikasi model. Sebelum model dapat digunakan, harus dilakukan verifikasi atau pengujian terlebih dahulu.
Dalam hal ini, pengujian dapat dilakukan dengan menjawab tiga pertanyaan berikut:
a. Apakah model dapat menjawab masalah yang diidentifikasi pada langkah pertama?
b. Apakah model dapat digunakan secara praktis, yang artinya bisa atau tidaknya dikumpulkan data-data yang diperlukan untuk menyelesaikan model?
c. Apakah model tersebut masuk akal?
5. Implementasi Model
Langkah selanjutnya adalah implementasi model. Model yang diverifikasi dapat kita implementasikan sesuai dengan data yang kita miliki.
Model yang dibangun ini diharapkan dapat bermanfaat dan dipahami dengan mudah oleh siapapun.
6. Mempertahankan Model
Langkah terakhir dalam penyusunan model matematis adalah mempertahankan model. Langkah ini mengingatkan bahwa model yang telah dibuat diturunkan atau didasarkan pada identifikasi masalah pada langkah pertama dan asumsi pada langkah kedua. Oleh karena itu, model harus tetap dipertahankan berdasarkan kedua hal tersebut.
B. Persamaan Diferensial
Pada subbab ini akan dibahas mengenai persamaan diferensial, persamaan diferensial biasa, persamaan diferensial parsial, orde dari persamaan diferensial, persamaan diferensial biasa linear, persamaaan diferensial biasa nonlinear, sistem persamaan diferensial biasa linear orde pertama, dan sistem persamaan diferensial biasa nonlinear.
1. Persamaan Diferensial
Pada bagian ini akan dibahas mengenai pengertian persamaan diferensial beserta contohnya.
Definisi 2.2.1
Persamaan diferensial adalah persamaan yang melibatkan turunan dari satu atau lebih variabel terikat terhadap satu atau lebih variabel bebas dengan variabel terikat tersebut (Ross, 1989). Dengan kata lain, persamaan diferensial adalah persamaan yang melibatkan hubungan fungsi dengan turunan-turunannya.
Contoh 2.2.1
Berikut ini adalah beberapa contoh dari persamaan diferensial:
𝑑2𝑦
𝑑𝑥2+ 𝑥𝑦 (𝑑𝑦 𝑑𝑥)
2
= 0 𝑑4𝑥
𝑑𝑡4 + 5𝑑2𝑥
𝑑𝑡2 + 3𝑥 = sin 𝑡 𝑑𝑢
𝑑𝑧 + 𝑧2𝑢 = 𝑧𝑒𝑧
𝜕𝑣
𝜕𝑠 +𝜕𝑣
𝜕𝑡 = 𝑣
(2.2.1) (2.2.2) (2.2.3) (2.2.4)
𝜕2𝑠
𝜕𝑥2+ 𝜕2𝑠
𝜕𝑦2+𝜕2𝑠
𝜕𝑧2 = 0
𝜕4𝑤
𝜕𝑥2𝜕𝑦2+𝜕2𝑤
𝜕𝑥2 +𝜕2𝑤
𝜕𝑦2 + 𝑤 = 0
2. Persamaan Diferensial Biasa
Pada bagian ini akan dijelaskan mengenai pengertian persamaan diferensial biasa dan contohnya.
Definisi 2.2.2
Persamaan diferensial biasa (PDB) adalah persamaan diferensial yang melibatkan turunan biasa dari satu atau lebih variabel terikat terhadap satu variabel bebas (Ross, 1989).
Contoh 2.2.2
Persamaan (2.2.1), (2.2.2), dan (2.2.3) adalah persamaan diferensial biasa. Pada persamaan (2.2.1), variabel 𝑥 adalah variabel bebas dan variabel 𝑦 adalah variabel terikatnya. Pada persamaan (2.2.2), variabel bebasnya adalah 𝑡 dan variabel terikatnya adalah 𝑥. Pada persamaan (2.2.3), variabel bebasnya adalah 𝑧 dan variabel terikatnya adalah 𝑢
3. Persamaan Diferensial Parsial
Pada bagian ini akan dibahas mengenai pengertian persamaan diferensial parsial beserta contohnya.
Definisi 2.2.3
Persamaan diferensial parsial (PDP) adalah persamaan diferensial yang memuat turunan parsial dari satu atau lebih variabel terikat terhadap lebih dari satu variabel bebas(Ross, 1989).
Contoh 2.2.3
Persamaan (2.2.4), (2.2.5), dan (2.2.6) adalah persamaan diferensial parsial. Pada persamaan (2.2.4), variabel 𝑠 dan 𝑡 adalah variabel bebas dan variabel 𝑣 adalah variabel terikatnya. Pada persamaan (2.2.5), variabel bebasnya adalah 𝑥, 𝑦, dan 𝑧, sedangkan variabel terikatnya adalah (2.2.5)
(2.2.6)
𝑠. Pada persamaan (2.2.6), variabel bebasnya adalah 𝑥 dan 𝑦, sedangkan variabel terikatnya adalah 𝑤.
4. Orde dari Persamaan Diferensial
Pada bagian ini akan dijelaskan mengenai pengertian orde dari persamaan diferensial dan contohnya.
Definisi 2.2.4
Orde dari persamaan diferensial adalah derajat atau tingkat turunan tertinggi yang terlibat dalam persamaan diferensial (Ross, 1989).
Contoh 2.2.4
Persamaan (2.2.1) adalah persamaan diferensial biasa orde dua karena tingkat turunan tertingginya adalah dua. Persamaan (2.2.2) adalah persamaan diferensial biasa orde empat karena tingkat turunan tertingginya adalah empat. Persamaan (2.2.3) adalah persamaan diferensial biasa orde satu karena tingkat turunan tertingginya adalah satu. Selanjutnya, persamaan (2.2.4) adalah persamaan diferensial parsial orde satu karena tingkat turunan tertingginya adalah satu. Persamaan (2.2.5) adalah persamaan diferensial parsial orde dua karena tingkat turunan tertingginya adalah dua. Terakhir, persamaan (2.2.6) adalah persamaan diferensial parsial orde empat karena tingkat turunan tertingginya adalah empat.
5. Persamaan Diferensial Biasa Linear Orde ke-𝒏
Pada bagian ini akan dibahas mengenai persamaan diferensial biasa linear orde ke-𝑛 beserta contohnya.
Definisi 2.2.5
Suatu persamaan diferensial biasa linear orde ke-𝑛, dimana variabel 𝑦 adalah variabel terikat dan variabel 𝑥 adalah variabel bebas, adalah suatu persamaan yang dapat dinyatakan dalam bentuk:
𝑎0(𝑥)𝑑𝑛𝑦
𝑑𝑥𝑛+ 𝑎1(𝑥)𝑑𝑛−1𝑦
𝑑𝑥𝑛−1+ ⋯ + 𝑎𝑛−1(𝑥)𝑑𝑦
𝑑𝑥 + 𝑎𝑛(𝑥)𝑦 = 𝑏(𝑥) dengan 𝑎0(𝑥) ≠ 0 (Ross, 1989). Perhatikan bahwa
a. Variabel terikat 𝑦 dan turunannya hanya terjadi pada pangkat pertama.
b. Tidak ada perkalian antara 𝑦 dan turunannya.
Contoh 2.2.5
Berikut ini adalah contoh persamaan diferensial biasa linear:
𝑑2𝑦
𝑑𝑥2+ 5𝑑𝑦
𝑑𝑥+ 6𝑦 = 0 𝑑4𝑦
𝑑𝑥4+ 𝑥2𝑑3𝑦
𝑑𝑥3+ 𝑥3𝑑𝑦
𝑑𝑥 = 𝑥𝑒𝑥
Pada persamaan (2.2.7) dan (2.2.8), variabel 𝑦 adalah variabel bebas.
Perhatikan bahwa 𝑦 dan turunannya hanya terjadi pada pangkat pertama dan tidak ada perkalian antara 𝑦 dan turunannya.
6. Persamaan Diferensial Biasa Nonlinear
Pada bagian ini akan dibahas mengenai persamaan diferensial biasa nonlinear beserta contohnya.
Definisi 2.2.6
Persamaan diferensial biasa yang tidak linear disebut Persamaan diferensial biasa nonlinear (Ross, 1989).
Contoh 2.2.6
Berikut ini adalah contoh persamaan diferensial biasa nonlinear:
𝑑2𝑦
𝑑𝑥2+ 5𝑑𝑦
𝑑𝑥+ 6𝑦2= 0 𝑑2𝑦
𝑑𝑥2+ 5 (𝑑𝑦 𝑑𝑥)
3
+ 6𝑦 = 0 𝑑2𝑦
𝑑𝑥2+ 5𝑦𝑑𝑦
𝑑𝑥+ 6𝑦 = 0
Persamaan (2.2.9) adalah PDB nonlinear karena variabel terikat 𝑦 muncul dalam pangkat dua, yakni 𝑦2. Persamaan (2.2.10) adalah PDB nonlinear karena terdapat bentuk 5 (𝑑𝑦
𝑑𝑥)3, yang artinya terdapat pangkat tiga dari turunan pertamanya. Persamaan (2.2.11) juga merupakan PDB nonlinear (2.2.7) (2.2.8)
(2.2.9) (2.2.10) (2.2.11)
karena terdapat bentuk 5𝑦𝑑𝑦
𝑑𝑥, yang artinya terdapat perkalian antara variabel terikat dan turunan pertamanya.
7. Persamaan Diferensial Biasa Linear Orde Pertama
Pada bagian ini akan dibahas mengenai persamaan diferensial biasa linear orde pertama dan contohnya.
Definisi 2.2.6
Persamaan diferensial biasa linear orde pertama dengan variabel terikat 𝑦 dan variabel bebas 𝑥 adalah persamaan yang secara umum berbentuk
𝑑𝑦
𝑑𝑥+ 𝑃(𝑥)𝑦 = 𝑄(𝑥)
dengan 𝑃 dan 𝑄 adalah fungsi terhadap 𝑥 atau konstanta yang diberikan (Ross, 1989).
Contoh 2.2.6
Perhatikan persamaan berikut:
𝑥𝑑𝑦
𝑑𝑥+ (𝑥 + 1)𝑦 = 𝑥4 (4 + 𝑥2)𝑑𝑦
𝑑𝑥+ 2𝑥𝑦 = 4𝑥 𝑑𝑦
𝑑𝑥+2
𝑥𝑦 = sin 3𝑥 𝑥2
Persamaan (2.2.13), (2.2.14), dan (2.2.15) adalah persamaan diferensial biasa linear orde pertama. Persamaan (2.2.13) dapat diubah ke dalam bentuk (2.2.12) dengan mengalikan kedua ruas dengan 1
𝑥, sehingga bentuknya menjadi seperti persamaan (2.2.12) dengan 𝑃(𝑥) = (𝑥+1)
𝑥 dan 𝑄(𝑥) = 𝑥3. Persamaan (2.2.14) juga dapat diubah ke dalam bentuk (2.2.12) dengan mengalikan kedua ruas dengan 1
4+𝑡2, sehingga bentuknya menjadi seperti persamaan (2.2.12) dimana 𝑃(𝑥) = 2𝑥
4+𝑥2 dan 𝑄(𝑥) = 4𝑥
4+𝑥2. (2.2.12)
(2.2.13) (2.2.14) (2.2.15)
Persamaan (2.2.15) memiliki bentuk yang sama seperti persamaan (2.2.12) dengan 𝑃(𝑥) =2
𝑥 dan 𝑄(𝑥) =sin 3𝑥
𝑥2 .
8. Persamaan Diferensial Biasa Nonlinear Orde Pertama
Pada bagian ini akan dibahas mengenai persamaan diferensial biasa nonlinear orde pertama beserta contohnya.
Definisi 2.2.7
Persamaan diferensial biasa orde pertama yang tidak linear atau tidak dapat ditulis atau dibentuk dalam bentuk persamaan (2.2.12) disebut persamaan diferensial biasa nonlinear orde pertama (Ross, 1989).
Contoh 2.2.7
Perhatikan persamaan berikut:
𝑑𝑦
𝑑𝑥 = 𝑥𝑦3 𝑑𝑦
𝑑𝑥+ 𝑃(𝑥)𝑦 + 𝑄(𝑥)𝑦4= 𝑅(𝑥)
Persamaan (2.2.16) adalah persamaan diferensial biasa nonlinear orde pertama dengan variabel terikatnya adalah variabel 𝑦 dan variabel bebasnya adalah variabel 𝑥. Penyebab persamaan (2.2.16) merupakan persamaan diferensial biasa nonlinear orde pertama adalah variabel 𝑦 yang memuat pangkat tiga, yaitu 𝑦3. Persamaan (2.2.17) adalah persamaan diferensial biasa nonlinear orde pertama dengan variabel terikatnya adalah variabel 𝑦 dan variabel bebasnya adalah variabel 𝑥. Penyebab persamaan (2.2.17) merupakan persamaan diferensial biasa nonlinear orde pertama adalah variabel 𝑦 yang memuat pangkat empat, yaitu 𝑦4.
9. Sistem Persamaan Diferensial Biasa Linear Orde Pertama
Pada bagian ini akan dibahas mengenai sistem persamaan diferensial biasa linear orde pertama dan contohnya.
(2.2.17) (2.2.16)
Definisi 2.2.8
Secara umum, bentuk dari sistem persamaan diferensial biasa linear orde pertama adalah
𝑥1′ = 𝑎11(𝑡)𝑥1+ 𝑎12(𝑡)𝑥2+ ⋯ + 𝑎1𝑛(𝑡)𝑥𝑛+ 𝑓1(𝑡), 𝑥2′ = 𝑎21(𝑡)𝑥1+ 𝑎22(𝑡)𝑥2+ ⋯ + 𝑎1𝑛(𝑡)𝑥𝑛+ 𝑓2(𝑡),
⋮
𝑥𝑛′ = 𝑎𝑛1(𝑡)𝑥1+ 𝑎𝑛2(𝑡)𝑥2 + ⋯ + 𝑎𝑛𝑛(𝑡)𝑥𝑛 + 𝑓𝑛(𝑡)
dengan fungsi-fungsi yang diberikan (Boyce, 2012). Sistem persamaan (2.2.18) juga dapat disederhanakan menjadi bentuk:
𝐱′ = 𝐀(𝑡)𝐱 + 𝐟(𝑡)
dengan 𝐱′ adalah vektor dengan elemen 𝑥1′, 𝑥2′, … , 𝑥𝑛′, 𝐀(t) adalah matriks 𝑛 × 𝑛 dengan elemen 𝑎11(𝑡), 𝑎12(𝑡), … , 𝑎𝑛𝑛(𝑡) , 𝐱 adalah vektor dengan elemen 𝑥1, 𝑥2, … , 𝑥𝑛, dan 𝐟 adalah vektor dengan elemen 𝑓1(𝑡), 𝑓2(𝑡), … , 𝑓𝑛(𝑡).
Contoh 2.2.8
Perhatikan contoh sistem persamaan berikut:
𝑥1′ = −2𝑥1+ 𝑥2, 𝑥2′ = 𝑥1− 2𝑥2
𝑥1′ = 𝑥2, 𝑥2′ = −𝑥1−1
8𝑥2
Sistem persamaan (2.2.19) dan (2.2.20) adalah sistem persamaan diferensial biasa linear orde pertama. Pada persamaan (2.2.19) dan (2.2.20), variabel 𝑥1 dan 𝑥2 adalah variabel terikat.
10. Sistem Persamaan Diferensial Biasa Nonlinear Orde Pertama
Pada bagian ini akan dibahas mengenai sistem persamaan diferensial biasa nonlinear orde pertama beserta contohnya.
(2.2.18)
(2.2.19)
(2.2.20)
Definisi 2.2.9
Sistem persamaan diferensial biasa orde pertama yang tidak linear adalah sistem persamaan diferensial biasa nonlinear orde pertama (Boyce, 2012).
Contoh 2.2.9
Perhatikan contoh sistem persamaan berikut:
𝑥1′ = 𝑥2(−2𝑥1+ 𝑥2), 𝑥2′ = 𝑥1(𝑥1− 2𝑥2)
Sistem persamaan (2.2.21) adalah sistem persamaan diferensial biasa linear orde pertama, dimana variabel 𝑥1 dan 𝑥2 adalah variabel terikat. Sistem persamaan tersebut merupakan sistem persamaan diferensial biasa linear orde pertama karena melibatkan perkalian 𝑥1 dan 𝑥2.
C. Matriks Jacobian
Pada bagian ini akan dibahas mengenai matriks Jacobian beserta contohnya.
Definisi 2.3.1 Diberikan
𝐟(𝐱) = (𝑓1(𝑥1, 𝑥2, … , 𝑥𝑛), 𝑓2(𝑥1, 𝑥2, … , 𝑥𝑛), … , 𝑓𝑛(𝑥1, 𝑥2, … , 𝑥𝑛)) dengan 𝑛 variabel bebas 𝑥1, 𝑥2, … , 𝑥𝑛. Matriks
𝐽(𝐟(𝐱)) =
(
𝜕𝑓1
𝜕𝑥1(𝐱) 𝜕𝑓1
𝜕𝑥2(𝐱) ⋯ 𝜕𝑓1
𝜕𝑥𝑛(𝐱)
𝜕𝑓2
𝜕𝑥1(𝐱) 𝜕𝑓2
𝜕𝑥2(𝐱) ⋯ 𝜕𝑓2
𝜕𝑥𝑛(𝐱)
⋮ ⋮ ⋱ ⋮
𝜕𝑓𝑛
𝜕𝑥1(𝐱) 𝜕𝑓𝑛
𝜕𝑥2(𝐱) ⋯ 𝜕𝑓𝑛
𝜕𝑥𝑛 (𝐱) ) disebut matriks Jacobian dari 𝐟 di titik 𝐱 (Perko, 2001).
Contoh 2.3.1
Diketahui fungsi
𝐟(𝐱) = [𝑓1(𝑥1, 𝑥2)
𝑓2(𝑥1, 𝑥2)] = [ 𝑥1− 𝑥22
−𝑥2+ 𝑥1𝑥2] Perhatikan bahwa
(2.2.21)
(2.3.1)
𝜕𝑓1
𝜕𝑥1 = 1, 𝜕𝑓1
𝜕𝑥2= −2𝑥2,
𝜕𝑓2
𝜕𝑥1= 𝑥2, 𝜕𝑓2
𝜕𝑥2= −1 + 𝑥1.
Dengan demikian, berdasarkan bentuk matriks (2.3.1), matriks Jacobian dari 𝑓 di titik 𝐱 = (1, −1)𝑇 adalah
𝐽(𝐟(𝐱)) = (
𝜕𝑓1
𝜕𝑥1(1, −1) 𝜕𝑓1
𝜕𝑥2(1, −1)
𝜕𝑓2
𝜕𝑥1(1, −1) 𝜕𝑓2
𝜕𝑥2(1, −1) ) atau
𝐽(𝐟(𝐱)) = ( 1 2
−1 0)
D. Nilai Eigen dan Vektor Eigen
Pada bagian ini akan dijelaskan mengenai nilai eigen dan vektor eigen beserta contohnya.
Definisi 2.4.1
Jika 𝐴 adalah matriks 𝑛 × 𝑛, maka vektor taknol 𝐱 di ℝ𝑛 disebut vektor eigen dari 𝐴 bila 𝐴𝐱 adalah perkalian skalar dari 𝐱 sedemikian hingga
𝐴𝐱 = 𝜆𝒙
untuk beberapa skalar 𝜆. Skalar 𝜆 disebut nilai eigen dari 𝐴 dan 𝐱 dikatakan sebagai vektor eigen yang bersesuaian atau berkaitan dengan 𝜆 (Anton and Rorres, 2013).
Contoh 2.4.1
Diketahui matriks 𝐴 berukuran 2 × 2, yaitu 𝐴 = [5 −6
2 −2]. Maka vektor 𝐱 = [2
1] merupakan vektor eigen dari matriks 𝐴 karena 𝐴𝐱 = [5 −6
2 −2] [2 1] = [4
2] = 2 [2
1] = 2𝐱
Dapat diamati bahwa 𝐱 adalah vektor eigen yang bersesuaian dengan nilai eigen 𝜆 = 2.
E. Persamaan Karakteristik
Pada bagian ini akan dibahas mengenai persamaan karakteristik beserta contohnya.
Teorema 2.5.1
Jika 𝐴 adalah matriks berukuran 𝑛 × 𝑛, maka 𝜆 adalah nilai eigen dari matriks 𝐴 jika dan hanya jika memenuhi persamaan
det(𝜆𝐼 − 𝐴) = 0
Persamaan (2.5.1) merupakan persamaan polinomial dalam 𝜆 dan disebut persamaan karakteristik dari matriks 𝐴 (Anton and Rorres, 2013).
Contoh 2.5.1
Diberikan matriks 𝐴 berukuran 2 × 2, yaitu 𝐴 = [ 5 7
−2 −4].
Berdasarkan persamaan (2.5.1), diperoleh bahwa nilai eigen dari 𝐴 adalah penyelesaian dari persamaan det(𝜆𝐼 − 𝐴) = 0, yang dapat ditulis sebagai berikut:
|𝜆 − 5 7
−2 𝜆 + 4| = 0 atau
(𝜆 − 5)(𝜆 + 4) − (−2)(7) = 0 atau
𝜆2− 𝜆 − 6 = 0 atau
(𝜆 + 2)(𝜆 − 3) = 0
Jadi, 𝐴 mempunyai dua nilai eigen yaitu 𝜆1= −2 dan 𝜆2= 3.
F. Polinomial Karakteristik
Pada bagian ini akan dijelaskan mengenai polinomial karakteristik dan contohnya.
Definisi 2.6.1
Jika 𝐴 adalah matriks berukuran 𝑛 × 𝑛, maka persamaan (2.5.1) dapat dijabarkan dan persamaan karakteristik dari 𝐴 akan berbentuk:
𝜆𝑛+ 𝑐1𝜆𝑛−1+ ⋯ + 𝜆𝑐𝑛−1+ 𝑐𝑛 = 0
(2.5.1)
Persamaan polinomial
𝑃(𝜆) = 𝜆𝑛+ 𝑐1𝜆𝑛−1+ ⋯ + 𝜆𝑐𝑛−1 + 𝑐𝑛 disebut polinomial karakteristik dari 𝐴 (Anton and Rorres, 2013).
Contoh 2.6.1
Perhatikan bahwa pada Contoh 2.5.1, persamaan karakteristiknya adalah
𝜆2− 𝜆 − 6 = 0 Sehingga polinomial karakteristiknya adalah
𝑃(𝜆) = 𝜆2− 𝜆 − 6
Dapat dilihat bahwa persamaan (2.6.1) adalah polinomial karakteristik pangkat dua.
G. Kriteria Routh-Hurwitz
Pada bagian ini akan dibahas mengenai kriteria Routh-Hurwitz.
Referensi yang digunakan diambil dari buku An Introduction to Mathematical Biology (Allen, 2007).
Nilai eigen dapat diperoleh dengan menghitung nilai 𝜆 yang memenuhi persamaan det(𝜆𝐼 − 𝐴) = 0. Namun, permasalahan yang sering timbul adalah nilai akar-akar persamaan karakteristik yang sulit untuk didapatkan. Akibatnya, nilai akar-akar tersebut tidak diketahui. Dalam menentukan kestabilan, diperlukan suatu hal yang dapat menjamin bahwa nilai dari akar-akar persamaan karakteristik bernilai negatif atau tidak. Salah satu cara yang dapat dilakukan untuk menjamin bahwa nilai akar-akar persamaan karakteristik negatif atau tidak adalah dengan menggunakan kriteria Routh-Hurwitz.
Teorema 2.7.1
Diberikan polinomial karakteristik dalam bentuk polinomial pangkat 𝑛 berikut:
𝑃(𝜆) = 𝜆𝑛 + 𝑎1𝜆𝑛−1+ 𝑎2𝜆𝑛−2+ ⋯ + 𝜆𝑎𝑛−1+ 𝑎𝑛
dengan 𝑎𝑖 adalah bilangan real, untuk 𝑖 = 1, 2, … , 𝑛. Didefinisikan 𝑛 matriks Hurwitz dengan menggunakan koefisien 𝑎𝑖 dari polinomial karakteristik 𝑃(𝜆):
𝐻1 = [𝑎1],
(2.6.1)
𝐻2 = [𝑎1 1 𝑎3 𝑎2], 𝐻3= [
𝑎1 1 0
𝑎3 𝑎2 𝑎1 𝑎5 𝑎4 𝑎3
],
⋮
𝐻𝑛 = [
𝑎1 1 0 0 ⋯ 0
𝑎3 𝑎2 𝑎1 1 ⋯ 0 𝑎5 𝑎4 𝑎3 𝑎2 ⋯ 0 𝑎7 𝑎6 𝑎5 𝑎4 ⋯ 0
⋮ ⋮ ⋮ ⋮ ⋱ ⋮
0 0 0 0 ⋯ 𝑎𝑛]
,
dimana 𝑎𝑗= 0 jika 𝑗 > 𝑛. Semua akar dari polinomal karakteristik 𝑃(𝜆) adalah negatif atau memiliki bagian real negatif jika dan hanya jika determinan dari semua matriks Hurwitz adalah positif, yakni
det(𝐻𝑗) > 0, 𝑗 = 1, 2, 3, … , 𝑛.
Untuk 𝑛 = 2, sesuai dengan kriteria Routh-Hurwitz, maka haruslah 𝑎1 > 0 dan det(𝐻2) = 𝑎1𝑎2> 0 atau 𝑎1> 0 dan 𝑎2> 0. Untuk polinomial karakteristik berderajat 𝑛 = 3, 4 dan 5, kriteria Routh-Hurwitz yang harus terpenuhi adalah sebagai berikut:
a. Untuk 𝑛 = 3, haruslah 𝑎1 > 0, 𝑎2> 0, 𝑎3 > 0, dan 𝑎1𝑎2 > 𝑎3
b. Untuk 𝑛 = 4, haruslah 𝑎𝑖 > 0 untuk 𝑖 = 1, 2, 3 dan 4, serta memenuhi:
𝑎1𝑎2𝑎3 > 𝑎32+ 𝑎12𝑎4
c. Untuk 𝑛 = 5, haruslah 𝑎𝑖 > 0 untuk 𝑖 = 1, 2, 3, 4 dan 5, serta memenuhi:
𝑎1𝑎2𝑎3 > 𝑎32+ 𝑎12𝑎4 dan
(𝑎1𝑎4− 𝑎5)(𝑎1𝑎2𝑎3 − 𝑎32− 𝑎12𝑎4) > 𝑎5(𝑎1𝑎2− 𝑎3)2+ 𝑎1𝑎52
H. Titik Kesetimbangan
Pada bagian ini akan dibahas mengenai titik kesetimbangan beserta contohnya.
Titik kesetimbangan merupakan solusi dari suatu sistem persamaan diferensial yang tidak mengalami perubahan terhadap waktu. Dalam sistem
epidemiologi terdapat dua jenis titik kesetimbangan, yaitu titik kesetimbangan bebas penyakit (disease-free equilibrium) dan titik kesetimbangan endemik (endemic equilibrium). Titik kesetimbangan bebas penyakit adalah titik dimana penyakit tidak mungkin menyebar pada suatu populasi karena jumlah individu yang terinfeksi penyakit sama dengan nol. Hal ini berarti menandakan keadaan dimana setiap individu dalam suatu populasi bebas dari virus, artinya tidak ada individu yang terinfeksi penyakit lagi. Titik kesetimbangan endemik adalah titik dimana penyakit pasti dapat menyebar pada suatu populasi. Hal ini juga berarti bahwa keadaan dimana penyakit tidak dapat hilang secara total, tetapi masih ada pada suatu populasi.
Berikut ini adalah definisi mengenai titik kesetimbangan.
Definisi 2.8.1
Diberikan suatu sistem persamaaan diferensial 𝑥̇ = 𝑓(𝑥)
dimana 𝑓: 𝐸 ⊂ ℝ𝑛 → ℝ𝑛. Titik 𝑥0∈ ℝ𝑛 disebut titik kesetimbangan dari sistem persamaan (2.8.1) jika 𝑓(𝑥0) = 0 (Perko, 2001).
Contoh 2.8.1
Tentukan titik kesetimbangan dari sistem persamaan diferensial yang diberikan sebagai berikut:
𝑓(𝑥) = ( 𝑥1+ 2
4 − (𝑥1𝑥2+ 𝑥12) ) Penyelesaian:
Berdasarkan Definisi 2.8.1, titik kesetimbangan dari sistem persamaan (2.8.2) adalah 𝑥0 jika 𝑓(𝑥0) = 0. Sehingga untuk mendapatkan titik kesetimbangan, sistem persamaan (2.8.2) ditulis menjadi
𝑥1+ 2 = 0 4 − (𝑥1𝑥2+ 𝑥12) = 0 Dari persamaan (2.8.3) didapatkan
𝑥1+ 2 = 0 atau
𝑥1= −2
(2.8.1)
(2.8.2)
(2.8.3) (2.8.4)
Subtitusi 𝑥1 = −2 ke persamaan (2.8.4), diperoleh 4 − ((−2)𝑥2+ (−2)2) = 0 atau
4 − (4 − 2𝑥2) = 0 atau
2𝑥2= 0 atau
𝑥2 = 0
Diperoleh 𝑥1 dan 𝑥2 yang memenuhi 𝑓(𝑥0) = 𝑓(𝑥1, 𝑥2) = 0, yaitu 𝑥1 = −2
dan
𝑥2 = 0 Jadi, titik kesetimbangannya adalah
𝑥0 = (𝑥1, 𝑥2) = (−2, 0).
I. Kestabilan Titik Kesetimbangan
Pada bagian ini akan dijelaskan mengenai kestabilan titik kesetimbangan dan contohnya. Kestabilan titik kesetimbangan pada sistem persamaan nonlinear dapat ditentukan berdasarkan tanda nilai eigen dari matriks Jacobian.
Definisi 2.9.1 (Olsder and Woude, 2003)
Diberikan sistem persamaan diferensial orde satu 𝑥̇ = 𝑓(𝑥), serta solusi dari sistem persamaan tersebut pada saat 𝑡 yang dinotasikan dengan 𝑥(𝑡, 𝑥0), dengan kondisi awal 𝑥(0) = 𝑥0.
a. Vektor 𝑥̅ yang memenuhi 𝑓(𝑥̅) = 0 disebut titik kesetimbangan.
b. Titik kesetimbangan 𝑥̅ dikatakan stabil jika untuk setiap 𝜀 > 0 terdapat 𝛿 >
0 sedemikian hingga, jika ‖𝑥0− 𝑥̅‖ < 𝛿, maka ‖𝑥(𝑡, 𝑥0) − 𝑥̅‖ < 𝜀 untuk setiap 𝑡 ≥ 0.
c. Titik kesetimbangan 𝑥̅ dikatakan stabil asimtotik jika titik kesetimbangannya stabil dan terdapat 𝛿1 > 0 sedemikian hingga
𝑡→∞lim‖𝑥(𝑡, 𝑥0) − 𝑥̅‖ = 0 apabila ‖𝑥0− 𝑥̅‖ < 𝛿1.
d. Titik kesetimbangan 𝑥̅ dikatakan tidak stabil jika titik kesetimbangan tidak memenuhi (b).
Pada definisi tersebut, ‖ ‖ menotasikan norm atau panjang di ℝ𝑛.
Teorema 2.9.1 (Olsder and Woude, 2003)
Diberikan sistem persamaan 𝑥̇ = 𝐴𝑥, dengan 𝐴 adalah matriks berukuran 𝑛 × 𝑛 yang memiliki nilai eigen berbeda 𝜆1, 𝜆2, … , 𝜆𝑘 (𝑘 ≤ 𝑛).
a. TItik kesetimbangan 𝑥̅ stabil asimtotik jika dan hanya jika ℜ𝑒(𝜆𝑖) < 0 untuk 𝑖 = 1, 2, … , 𝑘.
b. Titik kesetimbangan 𝑥̅ stabil jika ℜ𝑒(𝜆𝑖) ≤ 0 untuk 𝑖 = 1, 2, … , 𝑘.
c. Titik kesetimbangan 𝑥̅ tidak stabil jika terdapat setidaknya satu ℜ𝑒(𝜆𝑖) > 0 untuk 𝑖 = 1, 2, … , 𝑘.
Teorema 2.9.2 (Allen, 2007)
Diberikan sistem persamaan diferensial nonlinear orde satu 𝑥̇ = 𝑓(𝑥) dengan titik kesetimbangan 𝑥̅.
a. Misalkan persamaan karakteristik dari matriks Jacobian 𝐽(𝑓(𝑥̅)) adalah 𝜆𝑛+ 𝑎1𝜆𝑛−1+ 𝑎2𝜆𝑛−2 + ⋯ + 𝑎𝑛−1𝜆 + 𝑎𝑛 = 0
Jika persamaan karakteristik (2.9.1) memenuhi kriteria Routh-Hurwitz pada Teorema 2.7.1, yakni determinan dari semua matriks Hurwitz adalah positif, maka titik kesetimbangan 𝑥̅ stabil asimtotik lokal.
b. Jika terdapat determinan matriks Hurwitz yang bernilai negatif, maka titik kesetimbangan 𝑥̅ tidak stabil.
Teorema 2.9.3 (Hale and Kocak, 1991)
Diberikan titik kesetimbangan 𝑥̅ dari sistem persamaan diferensial nonlinear orde satu 𝑥̇ = 𝑓(𝑥).
(2.9.1)
a. Jika semua bagian real nilai eigen dari matriks Jacobian 𝐽(𝑓(𝑥̅)) bernilai negatif, maka titik kesetimbangan 𝑥̅ stabil asimtotik lokal.
b. Jika terdapat satu nilai eigen dari matriks Jacobian 𝐽(𝑓(𝑥̅)) yang bernilai positif, maka titik kesetimbangan 𝑥̅ tidak stabil.
Contoh 2.10.1
Tentukan jenis kestabilan titik kesetimbangan (0,0) dari sistem persamaan diferensial nonlinear berikut:
𝑑𝑥1
𝑑𝑡 = 4𝑥1+ 2𝑥2+ 2𝑥12− 3𝑥22 𝑑𝑥2
𝑑𝑡 = 4𝑥1− 3𝑥2+ 7𝑥1𝑥2 Penyelesaian:
Matriks Jacobian dari sistem persamaan (2.9.2) di titik 𝐱 = (0,0) adalah
𝐽(𝑓(𝐱)) = (
𝜕𝑓1
𝜕𝑥1(𝐱) 𝜕𝑓1
𝜕𝑥2(𝐱)
𝜕𝑓2
𝜕𝑥1(𝐱) 𝜕𝑓2
𝜕𝑥2(𝐱) ) atau
𝐽(𝑓(𝐱)) = (4 + 4(0) 2 − 6(0) 4 + 7(0) −3 + 7(0)) atau
𝐽(𝑓(𝐱)) = (4 2 4 −3)
Sehingga persamaan karakteristik dari matriks 𝐽(𝑓(𝐱)) adalah det (𝜆𝐼 − 𝐽(𝑓(𝐱))) = 0
atau
|𝜆 − 4 −2
−4 𝜆 + 3| = 0 atau
(𝜆 − 4)(𝜆 + 3) − (−2)(−4) = 0 atau
(2.9.2)
𝜆2 − 𝜆 − 20 = 0 atau
(𝜆 − 5)(𝜆 + 4) = 0
Sehingga didapatkan dua nilai eigen yang berbeda, yaitu 𝜆1= 5 dan 𝜆2= −4.
Karena terdapat nilai eigen yang bagian realnya positif, yakni 𝜆1= 5, maka titik (0,0) tidak stabil.
J. Bilangan Reproduksi Dasar
Pada bagian ini akan dibahas mengenai bilangan reproduksi dasar beserta contohnya.
Bilangan reproduksi dasar, yang dinotasikan dengan 𝑅0, adalah jumlah infeksi baru yang dihasilkan oleh adanya satu individu terinfeksi dalam suatu populasi. Jika 𝑅0 < 1, maka rata-rata individu yang terinfeksi menghasilkan kurang dari satu individu baru yang terinfeksi selama periode infeksinya, infeksi tidak dapat berkembang. Sebaliknya, jika 𝑅0 > 1, maka setiap individu terinfeksi rata-rata menghasilkan lebih dari satu infeksi baru, dan penyakit tersebut dapat menyebar dalam suatu populasi.
Contoh 2.10.1
Sebagai contoh, jika nilai 𝑅0 = 3, maka hal ini berarti bahwa satu individu terinfeksi dalam suatu populasi dapat menghasilkan tiga individu terinfeksi baru. Illustrasi untuk contoh ini diberikan pada Gambar 2.10.1.
Gambar 2.10.1. Illustrasi untuk 𝑅0 = 3 (Ndii, 2018)