i
MENINGKATKAN KEMAMPUAN PEMECAHAN MASALAH MATEMATIKA PADA POKOK BAHASAN PENERAPAN BENTUK ALJABAR DENGAN SUB POKOK BAHASAN MEMBUAT MODEL PERSAMAAN DAN PERTIDAKSAMAAN LINEAR SATU VARIABEL
MELALUIRECIPROCAL TEACHING MODEL
DI SMPN 4 DEPOK SLEMAN
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika
Disusun oleh: Lusia Yuliani
051414034
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
i
MENINGKATKAN KEMAMPUAN PEMECAHAN MASALAH MATEMATIKA PADA POKOK BAHASAN PENERAPAN BENTUK ALJABAR DENGAN SUB POKOK BAHASAN MEMBUAT MODEL PERSAMAAN DAN PERTIDAKSAMAAN LINEAR SATU VARIABEL
MELALUIRECIPROCAL TEACHING MODEL
DI SMPN 4 DEPOK SLEMAN
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika
Disusun oleh: Lusia Yuliani
051414034
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
iv
HALAMAN PERSEMBAHAN
“Segala perkara dapat ku tanggung dalam Dia
Yang memberi kekuatan kepadaku”
Filipi 4:13
Karya ini kupersembahkan untuk:
Bapak, Ibu, kakak, dan adikku tercinta
Sahabat-sahabat terbaik yang pernah aku miliki
Untuk semua orang yang telah hadir dalam hidupku
v
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sungguh-sungguh bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 9 September 2011 Penulis
vi
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:
Nama : Lusia Yuliani
Nomor Mahasiswa : 051414034
Demi pengembangan ilmu pengetahuan, saya memberikan kepada perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:
“MENINGKATKAN KEMAMPUAN PEMECAHAN MASALAH
MATEMATIKA PADA POKOK BAHASAN PENERAPAN BENTUK ALJABAR DENGAN SUB POKOK BAHASAN MEMBUAT MODEL PERSAMAAN DAN PERTIDAKSAMAAN LINEAR SATU VARIABEL MELALUIRECIPROCAL TEACHING MODELDI SMPN 4 DEPOK SLEMAN” Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, untuk mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu ijin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.
Demikian ini pernyataan yang saya buat dengan sebenarnya.
Dibuat di Yogyakarta
Pada tanggal: 9 September 2011 Yang menyatakan
vii ABSTRAK
Lusia Yuliani, 051414034. 2011. Meningkatkan Kemampuan Pemecahan Masalah Matematika Pada Pokok Bahasan Penerapan Bentuk Aljabar dengan Sub pokok Bahasan Membuat Model Persamaan dan Pertidaksamaan Linear Satu Variabel MelaluiReciprocal Teaching ModelDi SMPN 4 Depok Sleman. Skripsi. Program Studi Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma Yogyakarta
Penelitian ini bertujuan untuk mengetahui apakah kemampuan siswa dalam memecahkan masalah matematika pada pokok bahasan penerapan bentuk aljabar dengan sub pokok bahasan membuat model persamaan dan pertidaksamaan linear satu variabel mengalami peningkatan dengan menggunakan Reciprocal Teaching Model untuk siswa kelas VII SMP. Selain itu, penelitian ini juga bertujuan untuk melihat minat siswa terhadap pembelajaran dengan menggunakanReciprocal Teaching Model.
Jenis penelitian ini adalah kombinasi dari penelitian kuantitatif dan penelitian kualitatif dengan desain penelitian pra-eksperimental. Subjeknya adalah siswa kelas VII SMPN 4 Depok Sleman dengan materi persamaan dan pertidaksamaan linear satu variabel. Pelaksanaan penelitian ini dilakukan dalam 3 pertemuan dengan instrumen penelitian dan pembelajaran : 1) pre-tes dan pos-tes, 2) lembar kerja siswa, 3) pertanyaan wawancara.
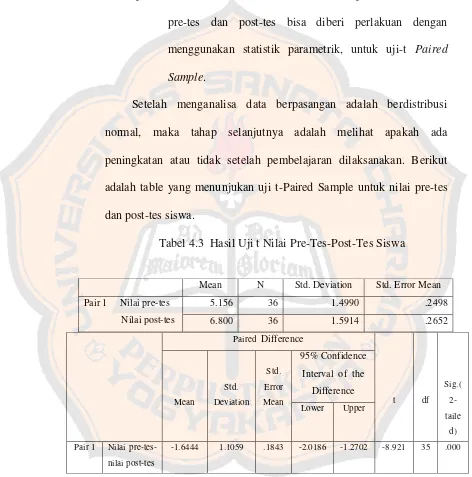
Setelah dilakukan penelitian, dari data pretes dan posttes di mana rata -rata nilai pre-tes = 5,156 dan -rata – rata nilai post-tes = 6,800 yang dianalisis
menggunakanUji Paired Sample t-Tesdidapatkan angka signifikansi 0.00 < 0.05, yang berarti terdapat peningkatan nilai pre-tes – post-tes siswa setelah mengikuti
viii ABSTRACT
Lusia Yuliani. 051414034. 2011. Improving Mathematics Problem Solving Ability on the Topic of Application of Algebraic Expressions, with the Sub Topic of Constructing the Models of Linear Equations and Inequations in One Variable, through Reciprocal Teaching Model, in SMPN 4 Depok Sleman. Thesis. Mathematics Education Study Program. Faculty of Teacher Training and Education. Sanata Dharma University, Yogyakarta.
This research aimed to determine whether the ability of the Junior High School students of grade VII in solving mathematical problems dealing with the application of algebraic expressions increased through reciprocal teaching model. In addition, this research also aimed to see the students’interest toward the use of the reciprocal teaching model.
The type of research was a combination of quantitative research and qualitative research with pre-experimental research design. The subjects were the students of grade VII of SMPN 4 Depok Sleman with linear equations and inequations in one variable as the learning material. The implementation of this research was conducted in three meetings with research instrumens : 1) pre-test and post-test, 2) student worksheets, 3) interview questions.
ix
KATA PENGANTAR
Puji syukur kehadirat Allah Bapa di surga yang telah melimpahkan kasih dan karunianya sehingga penulis dapat menyelesaikan skripsi dengan judul
”Meningkatkan Kemampuan Pemecahan Masalah Matematika Pada Pokok Bahasan Penerapan Bentuk Aljabar dengan Sub pokok Bahasan Membuat Model Persamaan dan Pertidaksamaan Linear Satu Variabel Melalui Reciprocal Teaching Model Di SMPN 4 Depok Sleman”.
Penulis ingin mengucapkan terimakasih kepada semua pihak yang telah membantu penulis dalam menyelesaikan skripsi ini dalam bentuk apapun, kepada: 1. Bapak Rohandi M.Ed., Ph.D. selaku Dekan Fakultas Keguruan dan Ilmu
Pendidikan Universitas Sanata Dharma Yogyakarta.
2. Bapak Drs. A. Atmadi, M.Si. selaku Ketua Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam Universitas Sanata Dharma Yogyakarta.
3. Bapak Dr. M. Andy Rudhito, S.Pd. selaku Ketua Prodi Pendidikan Matematika dan dosen penguji atas masukan dan kritik yang bermanfaat untuk penyempurnaan skripsi ini.
4. Bapak Prof. Dr. St. Suwarsono selaku dosen pembimbing yang selalu memberikan bimbingan, dorongan, semangat, saran dan kritik serta kesabaran membimbing penulis dalam penyusunan skripsi ini.
x
6. Segenap dosen JPMIPA, khususnya dosen-dosen Program Studi Pendidikan Matematika, Universitas Sanata Dharma Yogyakarta yang telah mendidik dan membagi pengetahuan dan pengalaman yang bermanfaat kepada penulis.
7. Staf Sekretariat JPMIPA atas bantuan dan keramahan dalam melayani penulis. 8. Bpk. Y. Sukamto, S.Pd selaku kepala sekolah SMPN 4 Depok dan guru mata
pelajaran matematika di SMPN 4 Depok.
9. Budiyono dan Valentina Suprihatinah selaku orang tua yang selalu memberikan dukungan selama proses penyelesaiaan skripsi ini..
10. Kakak dan adik tercinta, Ari dan Trino yang telah mendukung penulis dalam menyelesaikan skripsi ini.
11. Para sahabatku Fera, Eva, Indah, Made, Adi dan Paul yang telah memberikan dukungannya selama kuliah maupun dalam pengerjaan skripsi ini.
12. Yohanes Handoko Purnomo yang tak henti memberikan cinta, doa, semangat dan dukungan kepada penulis selama ini.
13. Cicilia, Rita, Krisna dan semua teman-teman kost, terima kasih atas dukungan, semangat serta perhatian yang diberikan kepada penulis.
Penulis menyadari masih banyak kekurangan dan kesalahan dalam skripsi ini. Oleh karena itu penulis mengharapkan kritik dan saran demi penyempurnaan skripsi ini. Akhir kata semoga skripsi ini bermanfaat bagi pembaca.
Yogyakarta, 9 September 2011
xi DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN ... iii
PERSEMBAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ... vi
ABSTRAK ... vii
ABSTRACT ... viii
KATA PENGANTAR ... ix
DAFTAR ISI ... xi
DAFTAR TABEL ... xiv
DAFTAR LAMPIRAN ... xv
BAB I PENDAHULUAN ... 1
A..Latar Belakang Masalah ... 1
B. Identifikasi Masalah ... 5
C. Perrumusan Masalah ... 6
D. Tujuan Penelitian ... 6
E. Penjelasan Istilah ... 6
xii
BAB II LANDASAN TEORI ... 11
A. Proses Belajar Mengajar Matematika ... 11
B. Pemecahan Masalah ... 14
C. PendekatanReciprocal Teaching ... 16
D. Langkah - Langkah PelaksanaanReciprocal Teachingyang Akan Dilaksanaakan Peneliti ... 20
E. Materi Bentuk Aljabar yang Dijadikan Objek Penelitian ... 21
F. Kerangka Berpikir ... 27
G. Hipotesis ... 28
BAB III METODE PENELITIAN ... 29
A. Jenis Penelitian ... 29
B. Popolasi dan Sampel Penelitian ... 29
C. Treatmen ... 30
D. Instrumen Penelitian ... 31
E. Validitas ... 34
F. Analisis Data ... 35
BAB IV PELAKSANAAN, HASIL, DAN PEMBAHASAN HASIL PENELITIAN ... 41
A. Deskripsi Pelaksanaan Penelitian ... 41
B. Data dan Analisis Hasil Penelitian ... 62
xiii
D. Keterbatasan Penelitian ... 73
BAB V PENUTUP ... 75
A. Kesimpulan Hasil Penelitian ... 75
B. Temuan Lain (Kesan–Kesan) ... 75
C. Saran ... 76
xiv
DAFTAR TABEL
Tabel 3.1 Tabel Kisi - Kisi Tes ... 33
Tabel 3.2 Tabel Pedoman Pemberian Skor ... 35
Tabel 3.3 Pengambilan keputusan berdasarkan nilai thitungdengan ttabel ... 36
Tabel 3.4 Pengambilan keputusan berdasarkan angka signifikansi(α) ... 37
Tabel 3.5 Kormogorov-Smirnov Zhitungdengan Kolmogorov-Smirnov Ztabel ... 37
Tabel 3.6 Pengambilan Keputusan dengan Absolut (Dtabel) ... 38
Tabel 3.7 Pengambilan Keputusan dengan Angka signifikansi (α) ... 38
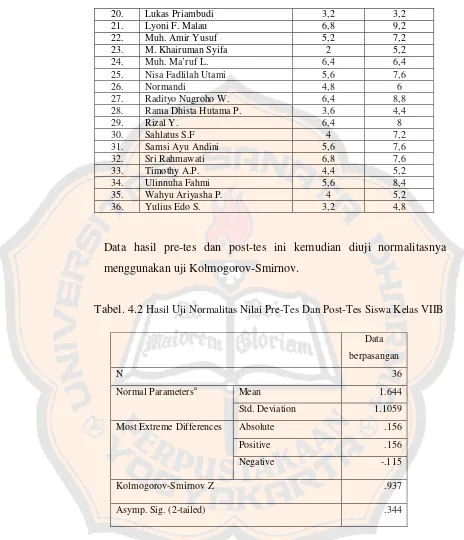
Tabel 4.1 Daftar Nilai Pre-tes dan Post-tes Siswa ... 59
Tabel. 4.2 Hasil Uji Normalitas Nilai Pre-Tes Dan Post-Tes Siswa Kelas VIIB ...60
xv
DAFTAR LAMPIRAN
LAMPIRAN 1 Rencana Pelaksanaan Pembelajaran (RPP) LAMPIRAN 2 Soal Latihan Kelompok dan Kunci Jawaban LAMPIRAN 3 Soal Pretes, Soal Postes, dan Kunci Jawaban LAMPIRAN 4 Contoh Hasil Pretes dan Postes Siswa LAMPIRAN 5 Hasil Jawaban Tiap Kelompok LAMPIRAN 6 Pertanyaan Wawancara
1 BAB I PENDAHULUAN
A. Latar Belakang Masalah
Pendidikan merupakan hal yang sangat penting bagi kehidupan manusia. Pendidikan sangat mempengaruhi setiap aspek kehidupan manusia. Pendidikan ditujukan kepada manusia agar manusia dapat mengembangkan potensi – potensi dasar menjadi nyata dan lebih baik. Banyak faktor yang
berpengaruh dalam pendidikan, faktor guru dan metode pengajarannya merupakan faktor yang sangat penting. Kepribadian, sikap, pengetahuan, dan bagaimana cara guru mengajar turut menentukan hasil belajar yang dicapai siswa. Hal ini sangat berpengaruh khususnya dalam pembelajaran matematika. Menurut pengalaman selama ini, pelajaran matematika cukup sulit untuk dipahami oleh banyak siswa. Terlebih karena selama ini matematika sering dianggap sebagai momok yang menakutkan bagi siswa, baik dari segi materi maupun guru. Padahal matematika sendiri mendapatkan waktu yang lebih banyak dalam penyampaiannya dibandingkan dengan pelajaran yang lain, tetapi siswa tetap tidak menaruh perhatian penuh pada matematika. Siswa cenderung malas untuk mengerjakan soal – soal karena menganggap bahwa
Guru menyampaikan materi secara cepat dan tergolong terburu –buru,
sehingga siswa malas dan tidak tertarik untuk memperhatikan. Guru harus bisa menyajikan pelajaran matematika semenarik mungkin agar siswa tertarik untuk belajar matematika. Terutama pada saat guru memberikan soal dan membimbing siswa dalam pemecahan masalahnya, sehingga siswa mudah memahami soal dan mampu menyelesaikannya dengan baik. Pemilihan metode pembelajaran yang tepat akan sangat membantu guru dalam penyampaian materi. Sehingga siswa dapat memahami dengan baik setiap materi yang disampaikan dan akhirnya akan tercipta proses belajar mengajar yang optimal. Maka dari itu diperlukan guru yang kreatif, menyenangkan dan profesional supaya mampu menciptakan suasana belajar mengajar yang kondusif, menyenangkan dan menggairahkan siswa untuk belajar matematika dan tertantang untuk menyelesaikan setiap soal yang diberikan guru.
cenderung langsung menuliskan jawaban tanpa menyertakan langkah bagaimana mereka mendapatkan jawaban tersebut yang belum tentu benar.
Masalah kemampuan siswa dalam menyelesaikan permasalahan matematika selain kerena kemampuan siswa dalam memahami soal tersebut juga peran serta guru yang selalu aktif dalam membimbing anak didiknya. Guru dan siswa selalu berinteraksi bila terdapat kesulitan dalam memecahkan masalah matematika. Guru juga harus mengetahui kemampuan siswanya, bila memberikan soal harus mengetahui bobotnya. Bila bobot soal tidak melebihi kemampuan siswa, maka siswa akan terbiasa dengan soal-soal matematika dan kemampuan siswa dalam menyelesaikan permasalahan matematika sedikit demi sedikit akan semakin meningkat.
Gambaran permasalahan diatas, memperlihatkan bahwa proses pembelajaran matematika harus diperbaiki, dan dapat diawali dengan penggunaanreciprocal teaching model, guna meningkatkan pemahaman siswa dan kemampuan siswa dalam menyelesaikan soal cerita. Siswa dilibatkan secara aktif dalam pembelajaran, dan mendorong pembelajaran mandiri yang berpusat pada siswa dan guru hanya sebagai fasilitator. Selama ini kenyataan di lapangan menunjukan bahwa pembelajaran matematika cenderung hanya disampaikan dengan cara langsung yaitu diberikan sejumlah rumus, lalu siswa mengerjakan sejumlah soal dengan menggunakan rumus-rumus tersebut.
kembali pengetahuan yang telah diperolehnya kepada teman - temannya, kemudian memprediksi pertanyaan selanjutnya dari persoalan yang disodorkan kepada siswa. Metodenya sendiri dilakukan pertama secara klasikal kemudian siswa diminta untuk mempraktekkannya dalam kelompok. Manfaatnya adalah dapat meningkatkan antusiasme siswa dalam pembelajaran karena siswa dituntut untuk aktif berdiskusi dan menjelaskan hasil pekerjaannya dengan baik sehingga penguasaan konsep suatu pokok bahasan matematika dapat dicapai. Diharapkan dengan pendekatan ini siswa dapat dengan mudah memahami soal cerita yang diberikan dan memahami konsep matematika yang ada dalam soal tersebut, setelah siswa melihat beberapa contoh soal yang digunakan dalam menyelesaikan soal-soal cerita tersebut, mengulanginya dan memprediksi kemungkinan soal yang lebih sulit yang akan diberikan guru diwaktu-waktu selanjutnya.
Reciprocal teaching model merupakan salah satu model pembelajaran yang dilaksanakan agar tujuan pembelajaran tercapai dengan cepat melalui proses belajar mandiri dan siswa mampu menyajikan di depan kelas. Harapannya adalah agar tujuan pembelajaran tersebut tercapai dan kemampuan siswa dalam belajar mandiri dapat ditingkatkan.
saat belajar. Sehingga pada pelaksanaanya reciprocal teaching model tidak lepas dari pembelajaraan kooperatif, dimana dalam pembelajaran kooperatif siswa juga belajar dalam kelompok. Tetapi perbedaannya adalah bahwa yang ditekankan pada reciprocal teaching model ini adalah pendekatan dialogis dalam pembelajaraan baik antara guru dengan siswa ataupun siswa dengan siswa. Guru dituntut untuk memiliki kemampuan dialog yang baik serta teliti dan peka dalam mengamati.
Atas dasar latar belakang sebagaimana yang telah diuraikan di atas, maka penulis merasa tertarik untuk mengadakan penelitian tentang cara meningkatkan kemampuan pemecahan masalah matematika melalui reciprocal teaching model.
B. Identifikasi Masalah
Identifikasi masalah yang diambil berdasarkan latar belakang yaitu terkait mengenai hubungan penggunaan reciprocal teaching model dalam meningkatkan kemampuan pemecahan masalah matematika siswa pada pokok bahasan penerapan bentuk aljabar yaitu dengan subpokok bahasan membuat model matematika pada persamaan dan pertidaksamaan linear satu variabel serta penyelesaiannya pada siswa kelas VII SMPN 4 Depok Sleman.
C. Perumusan Masalah
Berdasarkan latar belakang dan identifikasi masalah di atas, maka dapat dikemukakan rumusan permasalahan penelitian : “ Apakah pembelajaran matematika dengan menggunakan model pembelajaran resiprokal dalam pokok bahasan penerapan bentuk aljabar pada materi persamaan dan pertidaksamaan linear satu variabel dapat meningkatkan
prestasi belajar siswa dalam memecahkan masalah? “
D. Tujuan Penelitian
Tujuan penelitian adalah untuk mengetahui apakah kemampuan siswa dalam memecahkan masalah matematika pada pokok bahasan penerapan bentuk aljabar mengalami peningkatan dengan menggunakan reciprocal teaching model untuk siswa kelas VII SMP. Selain itu, penelitian ini juga bertujuan untuk melihat minat siswa terhadap pembelajaran dengan menggunakanreciprocal teaching model.
E. Penjelasan Istilah
Agar penelitian ini sesuai dengan tujuan yang diharapkan dan untuk menghindarkan kesalahpahaman, maka perlu diberikan penjelasan menyangkut beberapa istilah penting yaitu sebagai berikut :
a. Kemampuan Pemecahan Masalah
matematika untuk melakukan tindakan dalam mengidentifikasi berbagai faktor yang akan berpengaruh terhadap hasil belajar yang akan dicapai. Kemampuan pemecahan masalah ini dibatasi dalam empat langkah, yaitu:
1) Memahami masalah
Mengerti kondisi permasalahan yang dikemukakan yaitu dapat menemukan hubungan informasi-informasi tersembunyi yang ditambahkan dalam soal, yang terdiri atas bilangan-bilangan yang ada dalam soal tersebut dan menghilangkan data-data berupa bilangan yang tidak berkaitan dengan soal tetapi ada dalam teks soal.
2) Membuat kalimat matematika
Menulis kembali soal ke dalam bentuk lain yaitu ke dalam bentuk kalimat matematika atau model matematika seperti table, pola persamaan, dan lain-lain.
3) Menyelesaikan kalimat matematika
Artinya mencari bilangan mana yang membuat kalimat itu menjadi benar. Mungkin siswa pernah menemukan masalah yang serupa dengan masalah yang diberikan, sehingga dapat menerapkannya untuk menyelesaikan soal tersebut.
b. Penerapan Bentuk Aljabar
Penerapan bentuk aljabar merupakan aplikasi atau penerapan perhitungan aljabar pada aktivitas kehidupan sehari-hari yang sering ditampilkan pada soal berbentuk soal cerita.
c. Reciprocal Teaching Model
Merupakan salah satu model pembelajaran yang memiliki manfaat agar tujuan pembelajaran tercapai melalui kegiatan belajar mandiri dan peserta didik mampu menjelaskan temuan-temuannya kepada pihak lain. Reciprocal Teaching Model yang terdiri atas empat strategi pemahaman mandiri, yaitu
• menyimpulkan bahan ajar,
• menyusun pertanyaan dan menyelesaikannya,
• menjelaskan kembali pengetahuan yang telah diperolehnya kepada teman - temannya,
• memprediksi soal selanjutnya dari soal yang semula disodorkan kepada siswa.
Dari kegiatan ini diharapkan dapat meningkatkan kemampuan siswa dalam belajar mandiri.
d. Tingkat kemampuan pemecahan masalah matematika siswa dalam penelitian ini diukur dari hasil prestasi belajar siswa baik pre-tes maupun pos-tes dalam materi penerapan bentuk aljabar.
Membuat Model Persamaan dan Pertidaksamaan Linear Satu Variabel MelaluiReciprocal Teaching Model
Jadi judul di atas merupakan suatu upaya untuk meningkatan kemampuan siswa dalam menyelesaikan perhitungan aljabar yang berkaitan dengan kehidupan sehari-hari yang sering tampil dalam soal setelah dilakukannya kegiatan pembelajaran mandiri Reciprocal Teaching Model.
F. Manfaat Penelitian 1. Manfaat Teoritis
Secara umum hasilpenelitian ini diharapkan secara teoritis dapat memberikan sumbangan kepada pembelajaran matematika utamanya kepada peningkatan kemampuan memecahkan masalah matematika dengan menggunakanreciprocal teaching model. Mengingatreciprocal teaching model ini sangat penting dalam pengajaran matematika dan peranannya cukup besar bagi siswa dalam bidang matematika. Oleh karena itu guru mempunyai keyakinan untuk menerapkannya dalam pembelajaran matematika.
2. Manfaat Praktis
11 BAB II
LANDASAN TEORI
A. Proses Belajar Mengajar Matematika
Pengertian proses belajar mengajar matematika dapat diketahui dengan menguraikan istilah proses, belajar, mengajar dan matematika. Proses diartikan sebagai suatu interaksi semua komponen atau unsur yang terdapat dalam belajar mengajar yang satu sama lain saling berhubungan (interdependent) dalam ikatan untuk mencapai tujuan (Usman, 2000:5).
Kegiatan belajar merupakan hal penting yang paling pokok dalam keseluruhan proses pendidikan. Hal ini mengandung arti bahwa berhasil tidaknya pencapaian tujuan pendidikan banyak bergantung kepada bagaimana proses belajar mengajar yang dialami oleh siswa.
Slameto (1988:2) menyatakan bahwa belajar adalah suatu proses usaha yang dilakukan individu untuk memperoleh suatu perubahan tingkah laku yang baru secara keseluruhan, sebagai hasil pengalaman individu itu sendiri dalam interaksi dengan lingkungannya.
seseorang untuk memperoleh suatu perubahan tingkah laku yang baru secara keseluruhan, sebagai hasil pengalamannya sendiri dalam interaksi dengan lingkungannya.
Sudjana (2000: 28) menyatakan bahwa belajar adalah suatu proses yang ditandai dengan adanya perubahan pada diri seseorang. Perubahan sebagai hasil proses belajar dapat ditunjukkan dalam berbagai bentuk seperti perubahan pemahaman, pengetahuan, sikap dan tingkah lakunya, daya penerimaan dan lain-lain aspek yang ada pada individu siswa.
Dari uraian di atas, kata kunci dari defenisi belajar adalah perubahan tingkah laku. Perubahan yang disadari sehingga mengakibatkan bertambahnya pengetahuan, keterampilan, nilai dan sikap yang diperoleh dari interaksi individu dengan lingkungannya.
Mengajar merupakan usaha guru untuk menciptakan kondisi-kondisi atau mengatur lingkungan sedemikian rupa, sehingga terjadi interaksi antara murid dengan lingkungan, termasuk guru, alat pelajaran, dan sebagainya yang disebut proses belajar, sehingga tercapai tujuan pelajaran yang telah ditentukan. Adapun definisi lain di negara-negara yang sudah maju mengatakan bahwa mengajar adalah bimbingan kepada siswa dalam proses belajar. Definisi ini menunjukkan bahwa yang aktif adalah siswa, yang mengalami proses belajar. Sedangkan guru hanya membimbing, menunjukkan jalan dengan memperhitungkan kepribadian siswa. Kesempatan untuk berbuat dan aktif berpikir lebih banyak diberikan kepada siswa (Slameto,1995: 30).
menyampaikan pengetahuan kepada siswa didik atau murid sekolah. Rooijakers (199: 1) mendefinisikan mengajar sebagai penyampaian pengetahuan kepada siswa dan harus terjadi suatu proses yaitu proses belajar.
Jadi, mengajar tidak hanya menyampaikan bahan pelajaran, tetapi yang lebih penting adalah memberikan bantuan dan bimbingan kepada siswa dalam aktivitas belajarnya.
Matematika berasal dari bahasa latin ”manhenern” atau ”mathema”
yang berarti belajar atau hal yang harus dipelajari, sedangkan dalam bahasa
Belanda disebut ”wiskunde” atau ilmu pasti yang berkaitan dengan penalaran.
Matematika merupakan pelajaran yang memerlukan pemusatan pemikiran untuk mengingat dan mengenal kembali semua aturan-aturan yang ada yang harus dipenuhi untuk menguasai materi yang dipelajari (Hamzah, 2000:60).
Menurut Hudoyo (1988: 3) bahwa matematika itu berkenaan dengan ide-ide (gagasan-gagasan), struktur-struktur dan hubungan-hubungan yang diatur secara logik sehingga matematika itu berkaitan dengan konsep-konsep abstrak. Karena matematika berkenaan dengan ide-ide abstrak yang diberi simbol-simbol itu tersusun secara hirarkis dan penalarannya deduktif, maka konsep-konsep matematika harus dipahami lebih dahulu sebelum manipulasi simbol-simbol itu.
terjadinya proses belajar matematika tersebut. Karena kehirarkisan matematika, Hudoyo (1988: 4) menyatakan bahwa belajar matematika yang terputus-putus akan mengganggu terjadinya proses belajar. Ini berarti bahwa belajar matematika akan terjadi dengan lancar bila belajar itu sendiri dilakukan secara kontinu.
Dari uraian di atas, dapat disimpulkan bahwa proses belajar mengajar matematika adalah proses belajar mengajar yang melibatkan guru dan siswa, perubahan tingkah laku siswa diarahkan pada pemahaman konsep matematika yang mengantarkan siswa berpikir secara sistematis, dan guru dalam mengajar harus pandai mencari pendekatan pembelajaran yang tepat sehingga dapat membantu siswa dalam aktivitas belajarnya.
B. Pemecahan Masalah
adanya rasa tertarik untuk menghadapi tantangan dan tumbuhnya kemauan untuk menyelesaikan tantangan tersebut, merupakan modal utama dalam pemecahan masalah.
Berbicara pemecahan masalah tidak bisa dilepaskan dari tokoh utamanya yaitu George Polya. Menurut Polya, dalam pemecahan suatu masalah terdapat empat langkah yang harus dilakukan yaitu :
1. Memahami masalah
Siswa memahami masalah yang diberikan, termasuk mengerti kondisi permasalahan yang dikemukakan, yaitu dapat menemukan hubungan informasi-informasi tersembunyi yang disebutkan dalam soal, yang terdiri atas bilangan-bilangan dan informasi-informasi lain yang ada dalam soal tersebut.
2. Merencanakan pemecahannya
Dalam tahap ini siswa merencanakan strategi untuk menyelesaikan soal itu, termasuk menulis kembali soal ke dalam bentuk lain yaitu ke dalam bentuk kalimat matematika atau model matematika seperti table, pola persamaan, dan lain-lain.
3. Menyelesaikan masalah sesuai rencana langkah kedua
4. Memeriksa kembali penyelesaian yang diperoleh (looking back).
Dalam tahap ini siswa memeriksa kembali penyelesaian yang sudah dibuat termasuk mengkritisi hasil penyelesaian soal untuk melihat kelemahan dari solusi yang didapatkan (seperti: ketidak konsistenan atau ambiguitas atau langkah yang tidak benar).
C. PendekatanReciprocal Teaching
Palincsar (1986) mendeskripsikan konsep pembelajaran resiprokal: Reciprocal teaching refers to an instructional activity that takes place in the form of a dialogue between teachers and students regarding segments of text. The dialogue is structured by the use of four strategies: summarizing, question generating, clarifying, and predicting. The teacher and students take turns assuming the role of teacher in leading this dialogue.
Menurut Palincsar dan Brown seperti yang dikutip oleh Slavin (1997) bahwa strategi reciprocal teaching adalah pendekatan konstruktivis yang didasarkan pada prinsip-prinsip membuat pertanyaan, mengajarkan keterampilan metakognitif melalui pengajaran, dan pemodelan oleh guru untuk meningkatkan keterampilan membaca pada siswa yang berkemampuan rendah.
Peranan (tugas) guru dalam Reciprocal Teaching menurut Palinscar dan Brown (1984) adalah sebagai berikut :
1. Pada tahap awal pembelajaran , guru bertanggung jawab memimpin tanya jawab dan melaksanakan keempat strategi Reciprocal Teaching yaitu merangkum, menyusun pertanyaan, menjelaskan kembali dan memprediksi.
2. Guru menerangkan bagaimana cara merangkum, menyusun pertanyaan, menjelaskan kembali dan memprediksi setelah membaca.
3. Selama membimbing siswa melakukan latihan mengunakan empat strategi Reciprocal Teaching, guru meminta siswa berkelompok dalam menyelesaikan tugas..
4. Selanjutnya siswa belajar untuk memimpin tanya jawab dengan atau tanpa adanya guru, dan berperan sebagai guru.
Reciprocal teaching adalah prosedur pengajaran atau pendekatan yang dirancang untuk mengajarkan kepada siswa tentang strategi-strategi kognitif serta untuk membantu siswa memahami bacaan dengan baik. Model reciprocal teaching mengutamakan peran aktif siswa dalam pembelajaran untuk membangun proses berfikir siswa sehingga siswa dapat lebih berfikir kreatif . Hal itu sejalan dengan prinsip dasar konstruktivisme menurut Supomo (Nuryani, 2003:22) prinsip konstruktivisme adalah sebagai berikut :
1. Menyediakan pengalaman belajar belajar dengan mengkaitkan pengetahuan yang telah dimiliki siswa sedemikian rupa sehingga belajar melalui proses pembentukan pengetahuan
2. Menyediakan berbagai alternatif pengalaman belajar, tidak semua mengerjakan tugas yang sama, misalnya suatu masalah dapat diselesaikan dengan berbagai cara.
3. Mengintergrasikan pembelajaran dengan situasi yang realistik dan relevan dengan melibatkan pengalaman konkrit misalnya untuk memahami suatu konsep matematika melalui kegiatan kehidupan sehari-hari.
4. Mengintergrasikan pembelajaran pembelajaran sehingga memungkinkan terjadinya interaksi dan kerjasama seseorang dengan orang lain atau dengan lingkungannya, misalnya interaksi dan kerjasama antara siswa, guru dan siswa.
6. Melibatkan siswa secara emosional dan sosial sehingga pembelajaran menjadi menarik dan siswa rajin belajar.
Proses pembelajaran merupakan suatu proses aktif siswa yang sedang belajar untuk membangun pengetahuannya sendiri dan guru hanya berperan sebagai fasilitator untuk menyediakan suasana belajar yang mendukung proses konstruksi pengetahuan siswa. Berdasarkan pandangan konstruktivisme untuk lebih mengoptimalkan model pembelajaran resiprokal, kelas dibagi menjadi beberapa kelompok. Menurut Michael (Rahma.2004,26) kelompok belajar adalah merupakan cara yang memadai , mendukung konstruksi pengetahuan individu dengan berbagai cara dari setiap anggota kelompok tersebut .Djamaroh (2002:147) mengatakan bahwa proses kelompok adalah usaha untuk mengelompokan siswa kedalam beberapa kelompok dengan berbagai pertimbangan individual sehingga terciptanya kelas yang bergairah dalam belajar. Sehingga diharapkan belajar kelompok dapat meningkatkan pengetahuan siswa dan menjadikan belajar itu menjadi sesuatu yang menyenangkan dan dengan diterapkannya pembelajaran resiprokal dengan cara pembagian kelompok diharapkan mempunyai pengaruh yang besar terhadap tingkat kemampuan berpikir kreatif siswa
pendekatan pembelajaran yang menerapkan empat strategi pemahaman mandiri, yaitu menyimpulkan bahan ajar, menyusun pertanyaan dan menyelesaikannya, menjelaskan kembali pengetahuan yang telah diperolehnya, kemudian memprediksikan (menyusun) pertanyaan selanjutnya atau soal selanjutnya dari soal yang semula disodorkan kepada siswa .
D. Langkah - Langkah Pelaksanaan Reciprocal Teaching yang Akan Dilaksanaakan Peneliti
Berdasarkan pada uraian di atas langkah – langkah pelaksanaan reciprocal teaching yang akan dilaksanakan peneliti pada penelitian ini adalah sebagai berikut :
1. Peneliti mempersiapkan bahan ajar yang akan digunakan pada setiap pertemuan. Bahan ajar tersebut meliputi soal pretes, postes dan soal –soal latihan. Soal–soal latihan yang digunakan berupa soal cerita.
2. Pada pertemuan pertama peneliti memperagakan peran sebagai guru kepada para siswa. Peneliti memberikan soal kepada siswa kemudian membimbing siswa untuk merangkum atau memahami isi soal, membentuk model matematika dari soal dan menyelesaikannya. Kemudian meminta siswa untuk membuat soal baru yang bisa diselesaikan, dan peneliti meminta salah satu siswa untuk menuliskan soal serta jawaban yang telah dibuat (dengan maksud untuk melatih siswa menjelaskan kembali pengetahuan yang di dapat ).
soal yang diberikan, dan membuat satu soal baru yang nanti akan dipresentasikan bersama dengan hasil penyelesaian soal yang diberikan oleh peneliti.
4. Selanjutnya setiap wakil dari kelompok harus mempresentasikan hasil diskusi kelompok serta soal yang telah mereka buat.
E. Materi Bentuk Aljabar yang Dijadikan Objek Penelitian
Aljabar digunakan untuk menyelesaikan suatu permasalahan baik aritmatika, biologi, kimia, fisika, ekonomi, dan sebagainya. Permasalahan tersebut terlebih dahulu ditulis dalam bentuk aljabar.
a) Persamaan Linear Satu Variabel
Suatu kalimat yang dapat ditentukan benar atau salah adalah kalimat yang nilai kebenarannya dapat dipastikan. Kalimat seperti ini disebut pernyataan. Contoh pernyataan: Jumlah dari dua dan tiga adalah lima. Contoh kalimat salah: Limabelas habis dibagi tujuh.
Kalimat terbuka adalah kalimat yang belum diketahui nilai kebenarannya. Perhatikan kalimat berikut ini:
…+5=12
Kalimat terbuka Variabel Konstanta
(i) x+ 4 = 9 x 4 dan 9
(ii) 2y–x= 7 y dan x 2 dan 7
(iii) 2z + 1 = 23 z 2,1,dan 23
Bentuk(i) dan(iii) merupakan bentuk persamaan linear satu variabel dan bentuk (ii) merupakan bentuk persamaan linear dua variabel. Persamaan adalah kalimat terbuka yang dihubungkan oleh tanda sama dengan (=) dan persamaan linear satu variabel adalah kalimat terbuka yang dihubungkan oleh tanda sama dengan (=) dan hanya mempunyai satu variabel dan variabel tersebut berpangkat satu. Untuk menentukan penyelesaian dan himpunan penyelesaian persamaan linear satu variabel ada dua cara, yaitu dengan:
1. Metode coba-coba
Metode ini tidak terlalu efektif untuk digunakan karena menjadi sangat tidak jelas penyelesaiannya. Kecuali jika diberikan himpunan semestanya untuk mencari jawaban. Contoh : selesaikan persamaan berikut ini 3x – 1 = 14, jika x adalah anggota himpunan A = {3,4,5,6}!
Jadi penyelesaian 3x–1 = 14, adalah 5. 2. Mencari persamaan-persamaan yang ekuivalen
Contoh: Selesaikan persamaan berikut ini 3x–1 = 14, Jawab:
3x–1 = 14 kedua ruas ditambahkan 1⇔3x–1 + 1 = 14 + 1
⇔ 3x= 15
3x= 15 kedua ruas dikalikan 1/3 ⇔ 1/3(3x) = 1/3(15)
⇔ x= 5 Jadi , nilaixyang diminta adalah 5.
Materi penerapan bentuk aljabar yaitu menyelesaikan permasalahan sehari-hari yang berkaitan dengan persamaan linear satu variabel yang disajikan dalam bentuk soal cerita. Langkah pertama yang harus ditempuh dalam menyelesaikan soal cerita adalah membuat model matematika dari soal tersebut. Dalam pemodelan matematika, data dalam soal diterjemahkan ke dalam bentuk persamaan.
Langkah-langkah penyelesaian soal cerita adalah sebagai berikut: 1) Menentukan sebuah huruf sebagai peubah
2) Membentuk persamaan
3) Menyelesaikan persamaan itu
Contoh soal :
Berat Ika 3 kg lebihnya dari berat badan Rina. Jika berat Rina x kg, dan berat badan Ika 12kg. Berapakah berat badan Rina?
Berat Rina =x Berat Ika = 12
Berat Ika = 3 +x
⇔ 12 = 3 +x
⇔ 12–3 = 3–3 + x
⇔ 9 =x Jadi berat badan Rina adalah 9 kg b) Pertidaksamaan Linear Satu Variabel
Pertidaksamaan adalah suatu kalimat terbuka yang menggunakan lambang “<”, “>”, “ ≤”, dan “≥”. Pertidaksamaan linear satu variabel adalah suatu kalimat terbuka yang hanya memuat satu variabel dan variabel tersebut berderajat satu, yang dihubungkan oleh lambang “<”, “>”, “ ≤”, dan “≥”.
Contoh:y+ 3≤7 , z–2≥4
Sifat–sifat pertidaksamaan adalah:
1. Jika pada suatu pertidaksamaan kedua ruasnya ditambah atau dikurangi dengan bilangan yang sama, maka akan diperoleh pertidaksamaan baru yang ekuivalen dengan pertidaksamaan semula. Contoh:
Tentukan himpunan penyelesaian 3x – 7 > 2x + 2 jika x merupakan anggota {1,2,3,…,15} !
{
}
2. Jika kedua ruas suatu pertidaksamaan dikalikan dengan bilangan positif, maka akan diperoleh pertidaksamaan baru yang ekuivalen dengan pertidaksamaan semula.
Contoh : Tentukan himpunan penyelesaian dari 4x−5≤x+22, jika variable x merupakan anggota {0,1,2,…} !
Jawab:
3. Jika kedua ruas pertidaksamaan dikalikan dengan bilangan negatif yang sama maka diperoleh pertidaksamaan baru yang ekuivalen dengan pertidaksamaan semula, jika tanda pertidaksamaan dibalik.
Contoh:
Materi penerapan bentuk aljabar yaitu menyelesaikan permasalahan sehari-hari yang berkaitan dengan pertidaksamaan linear satu variabel yang disajikan dalam bentuk soal cerita. Langkah pertama yang harus ditempuh dalam menyelesaikan soal cerita adalah membuat model matematika dari soal tersebut. Dalam pemodelan matematika, data dalam soal diterjemahkan ke dalam bentuk pertidaksamaan.
Langkah-langkah penyelesaian soal cerita adalah sebagai berikut: 1) Menentukan sebuah huruf sebagai peubah
2) Membentuk pertidaksamaan
3) Menyelesaikan pertidaksamaan itu
Contoh:
setinggi-tingginya Rp.15.000,00. Tentukan batas maksimal uang saku Kiki dan adiknya!
Jawab:
Misalkan uang saku Kiki adalah x maka uang saku adiknya adalah
(
x−2.000)
. Sehingga:Uang saku Kiki + uang saku adik≤15.000
(
)
adiknya adalah Rp. 6.500,00F. Kerangka Berfikir
Berdasarkan landasan teori yang telah dikemukakan di atas, maka dapat disimpulkan kerangka berpikir dalam penelitian ini, adalah bahwa prestasi belajar siswa dalam mata pelajaran matematika dipengaruhi oleh kemampuan dan keaktifan siswa selama proses belajar mengajar berlangsung. Diantara faktor yang mempengaruhi prestasi belajar matematika adalah faktor model pembelajaran, suatu strategi atau cara belajar mengajar merupakan penunjang dari tujuan pembelajaran. Semakin baik guru menguasai dan menggunakan stateginya maka semakin efektif pencapaian tujuan belajar.
kenyataanya, harapan itu belum sepenuhnya dapat terwujudkan. Salah satu pendekatan pembelajaran yang menyenangkan dan dapat mengaktifkan siswa adalah reciprocal teaching diharapkan dengan pendekatan tersebut siswa dapat mengatasi kesulitan belajarnya, dan agar prestasi yang didapat siswa akan mengalami peningkatan.
G. Hipotesis
29 BAB III
METODE PENELITIAN
A. Jenis Penelitian
Pada penelitian ini, penelitian yang digunakan adalah penelitian pra-eksperimental yaitu peneliti melakukan penelitian tanpa menggunakan kelompok kontrol. Penelitian ini adalah kombinasi penelitian kuantitatif dan kualitatif. Penelitian diadakan dari tanggal 11 November 2009 sampai dengan 23 November 2009 di SMP Negeri 4 Depok.
B. Populasi dan Sampel Penelitian 1. Populasi
Populasi adalah keseluruhan subyek penelitian (Suharsimi Arikunto1989 :102). Populasi dalam penelitian ini adalah seluruh siswa kelas VII SMP Negeri 4 Depok Tahun ajaran 2009-2010. Besarnya sebanyak 108 siswa. Latar belakang kehidupan sosial ekonomi siswa di sekolah ini cukup beragam, begitupun dengan latar belakang kemampuan akademik siswa, mulai dari yang kemampuan akademiknya tinggi, sedang sampai dengan rendah.
2. Sampel
sama untuk ditetapkan sebagai sampel. Kemudian dipilih secara random, dan akhirnya terpilihlah kelas VIIB dengan jumlah siswa 36 sebagai sampelnya. Alasan sampel dipilih secara random karena siswa di sekolah ini tidak dgolongkan berdasarkan kemampuan akademiknya.
C. Treatment
Dalam penelitian ini, peneliti akan mengajar sendiri dalam kelas yang menjadi sampel penelitian untuk memperoleh data yang diinginkan. Peneliti mengajar dengan menggunakan reciprocal teaching model pada pokok bahasan penerapan bentuk aljabar. Sebelumnya siswa telah mendapat pengajaran tentang materi tersebut. Sebelum proses pembelajaran oleh peneliti dimulai siswa terlebih dahulu diberikan soal pre-tes. Kemudian peneliti menjelaskan pada siswa cara belajar dengan menggunakan reciprocal teaching model. Kemudian siswa dibagi dalam kelompok dan masing – masing kelompok terdiri dari 4 siswa. Siswa
mempraktekkan model pembelajaran resiprokal tersebut dalam kelompok untuk menyelesaikan beberapa soal. Kemudian hasil diskusi mereka, dipresentasikan di depan kelas. Peneliti kemudian memberikan kesimpulan akhir, dan siswa diberikan soal post-tes. Langkah – langkahnya sebagai
berikut :
soal latihan. Soal–soal latihan yang digunakan berupa soal cerita.
2. Pada pertemuan pertama peneliti memperagakan peran sebagai guru kepada para siswa. Peneliti memberikan soal kepada siswa kemudian membimbing siswa untuk merangkum atau memahami isi soal, membentuk model matematika dari soal dan menyelesaikannya. Kemudian meminta siswa untuk membuat soal baru yang bisa diselesaikan, dan peneliti meminta salah satu siswa untuk menuliskan soal serta jawaban yang telah dibuat.
3. Pada pertemuan berikutnya siswa berkelompok dan secara bergiliran berperan sebagai guru dalam kelompoknya untuk menyelesaikan soal –
soal yang diberikan, dan membuat satu soal baru yang nanti akan dipresentasikan bersama dengan hasil penyelesaian soal yang diberikan oleh peneliti.
4. Selanjutnya setiap wakil dari kelompok harus mempresentasikan hasil diskusi kelompok serta soal yang telah mereka buat.
D. Instrumen Penelitian
1. Desain Pembelajaran
Desain pembelajaran terdiri dari rancangan kegiatan belajar mengajar yang meliputi komponen – komponen sebagai berikut: bidang studi,
pokok bahasan, standar kompetensi, kompetensi dasar, indikator, kegiatan, penilaian, dan pembuatan Rencana Pembelajaran.
2. Lembar kerja siswa
Lembar kerja siswa ini digunakan sebagai bahan diskusi siswa dalam kelompok. Siswa diajak untuk berdiskusi menyelesaikan soal-soal penerapan bentuk aljabar dengan menggunakan reciprocal teaching model. Dengan demikian siswa diharapkan bias terlibat aktif dalam pembelajaran.
3. Tes
Tes adalah serentetan pertanyaan atau latihan yang digunakan untuk mengukur keterampilan , pengetahuan, intelegensi, kemampuan atau bakat yang dimiliki oleh individu atau kelompok. (Arikunto 1989 : 123)
teaching model. Soal-soal pre-tes dan post-tes mencakup tentang aplikasi persamaan dan pertidaksamaan linear.
4. Pertanyaan wawancara
Penelitian ini juga ingin melihat minat siswa terhadap pembelajaran penerapan bentuk alajabar dengan menggunakan reciprocal teaching model untuk meyakinkan peneliti bahwa siswa benar-benar berminat terhadap pembelajaran tersebut, maka peneliti mengadakan wawancara. Wawancara hanya dilakukan pada beberapa siswa saja, wawancara dilakukan setelah pembalajaran penerapan bentuk alajabar dengan reciprocal teaching model selesai diajarkan. Pertanyaan wawancara tersebut adalah sebagai berikut:
a. Apakah kamu merasa senang dengan pembelajaran penerapan bentuk aljabar khususnya tentang aplikasi persamaan dan pertidaksamaan linear satu variabel dengan reciprocal teaching modelini? Mengapa?
b. Apakah kamu merasa terbantu dalam mempelajari penerapan bentuk aljabar ini dengan reciprocal teaching model dalam kelompok diskusi? Mengapa?
c. Dalam diskusi umum ataupun kelompok kamu dituntut untuk aktif berpendapat. Bagaimana perasaan kamu? Apakah merasa senang atau terpaksa? Mengapa?
e. Ketika dalam diskusi kelompok, kamu akan ikut ambil bagian dalam diskusi itu atau kamu hanya menyerahkan semuanya pada teman yang kelompokmu? Mengapa
f. Setelah diadakan diskusi kelompok, setiap kelompok diminta untuk mempresentasikan hasil belajar dalam kelompok di depan kelas. Apakah kamu mau mewakili kelompok kamu untuk presentasi di depan kelas?
E. Validitas
Validitas adalah suatu ukuran yang menunjukkan tingkat-tingkat kevalidan atau kesahihan sesuatu instrumen. Validitas yang akan digunakan dalam penelitian ini adalah validitas isi. Sebuah tes dikatakan memiliki validitas isi apabila mengukur tujuan khusus tertentu yang sejajar dengan materi atau isi pelajaran yang diberikan ( Suharsimi Arikunto 1986 : 58 ). Jadi tes penerapan bentuk aljabar ini dikatakan valid apabila isi dari tes prestasi belajar tersebut mencakup semua materi penerapan bentuk aljabar. Berikut adalah kisi-kisi dari tes yang diberikan kepada siswa :
Tabel 3.1 Tabel Kisi–Kisi Tes
Kompetensi Dasar Iindikator Soal
3.1 Membuat model
matematika dari masalah
yang berkaitan dengan
persamaan dan
pertidaksamaan linear satu
variabel.
1. Mengubah masalah ke
dalam model matematika
berbentuk persamaan linear
satu variabel.
2. Menyelesaikan model
matematika suatu masalah
3.2 Menyelesaikan model
matematika dari masalah
yang berkaitan dengan
persamaan dan
pertidaksamaan linear satu
variabel.
persamaan linear satu
variabel.
3. Mengubah masalah ke
dalam model matematika
berbentuk pertidaksamaan
linear satu variabel.
4. Menyelesaikan model
matematika suatu masalah
yang berkaitan dengan
pertidaksamaan linear satu
variabel.
4,5
F. Analisis Data
Teknik analisis yang digunakan dalam penelitian ini adalah analisa kuantitatif dan kualitatif deskriptif. Untuk analisa kuantitatif akan digunakan data dari hasil pre-tes dan pos-tes yang kemudian dianalisis secara statistik. Sedangkan untuk analisa kualitatif deskriptif akan menggunakan data hasil pengamatan peneliti saat pelaksanaan penelitian. Data hasil penelitian akan dianalisis dengan langkah sebagai berikut : 1. Analisis Hasil Pre-tes dan Pos-tes
mengetahui kemampuan siswa dalam menyelesaikan masalah matematika yang berhubungan dengan penerapan aljabar setelah diberikan pembelajaran dengan menggunakan reciprocal teaching. Penilaian pre-tes dan post-tes berdasarkan kriteria berikut ini :
Tabel.3.2 Tabel Pedoman Pemberian Skor
No . Kualitas pekerjaan Skor
1. Mengerjakan dengan langkah yang lengkap, benar dan hasil
akhir benar
5
2. Mengerjakan dengan langkah lengkap dan benar tetapi hasil
akhir salah
4
3. Mengerjakan dengan langkah yang tidak lengkap dan hasil
akhir benar
3
4. Mengerjakan dengan langkah yang tidak lengkap atau langkah
salah dan hasil akhir salah
2
5. Mengerjakan hanya langkahnya saja (hanya menuliskan
diketahui)
1
6. Tidak mengerjakan sama sekali 0
membentuk suatu pasangan (Walpole 1995 ; Kurniawan, 2008). Untuk menguji hal tersebut digunakan pengujian hipotesis dengan menggunakan uji t-tes Paired Sample dengan bantuan Software SPSS 16.00 for Windows
Uji hipotesis :
H0:μ 1=μ 2 tidak ada peningkatan nilai pre-tes post-tes siswa
setelah penggunaanreciprocal teaching model. H1:μ 1<μ 2 terdapat peningkatan nilai pre-tes post-tes siswa
setelah penggunaanreciprocal teaching model. Dengan selang kepercayaan 95% (α= 0,05)
Kriteria yang digunakan :
a. Pengambilan keputusan berdasarkan nilai thitungdengan ttabel. Tabel 3.3 Pengambilan keputusan berdasarkan nilai thitung
dengan ttabel
Dengan ttabel ( ;v=n−1)dimana n menyatakan banyaknya jumlah subjek penelitian . pada penelitian ini banyaknya subjek penelitian adalah 36 siswa, makav= 36–1 = 35
dengan ttabel
(
0,05;35)
=1,645Tabel 3.4 Pengambilan keputusan berdasarkan angka signifikansi(α)
Akan tetapi sebelum diadakannya pengujian t-tes, peneliti terlebih dulu menguji apakah nilai pre-tes dan nilai post-tes dari satu sample yang sama tersebut berdistribusi normal sehingga dapt menggunakan metode statistik parametrik uji t-tes Paired Sample. Maka peneliti menggunakan pengujian Kolmogorov-Smirnov.
Uji hipotesis :
H0: Data berdistribusi normal H1: Data tidak berdistribusi normal
a. Dengan membandingkan Kormogorov-Smirnov Zhitungdengan Kolmogorov-Smirnov Ztabel:
Tabel 3.5 Kormogorov-Smirnov Zhitungdengan Kolmogorov-Smirnov Ztabel
Kolmogorov-Smirnov Ztabeladalah Z(α)=Z0,05= 1,645 H0diterima : Asymp sign. (2-tailed)>α H0ditolak : Asymp sign. (2-tailed)<α
H0diterima : Kolmogorov-Smirnov Zhitung <
Kolmogorov-Smirnov Ztabel
H0ditolak : Kolmogorov-Smirnov Zhitung>
b. Dengan melihat Absolut (Dtabel), dengan ketentuan : Tabel 3.6 Pengambilan Keputusan dengan Absolut (Dtabel)
Absolut (Dtabel) didapat dengan rumus :
n
D=1,36 di manan
menyatakan banyaknya jumlah subjek penelitian.
Maka Absolut (Dtabel) adalah 0,227 36
c. Dengan melihat angka signifikansi (α), dengan ketentuan : Tabel 3.7 Pengambilan Keputusan dengan Angka signifikansi (α)
2. Analisis Wawancara Minat Siswa
Untuk mengetahui apakah pembelajaran dengan reciprocal teaching model benar-benar menarik minat siswa, maka hasil wawancara yang sudah ada kemudian disimpulkan dengan melihat item pertanyaan dan jawaban dengan sistem coding artinya jawaban yang sama disatukan dan diurutkan dari yang paling banyak muncul. Sampel wawancara ini dipilih berdasarkan kekhasan dan keistimawaan dalam kasus tertentu. Pada penelitian ini beberapa siswa yang aktif
H0diterima : Dhitung< Dtabel H0ditolak : Dhitung> Dtabel
41 BAB IV
PELAKSANAAN, HASIL, DAN PEMBAHASAN HASIL PENELITIAN
A. Deskripsi Pelaksanaan Penelitian 1. Sebelum Pembelajaran
Penelitian ini dilaksanakan di SMP Negeri 4 Depok Sleman. Sampel yang diteliti adalah siswa kelas VII semester I tahun ajaran 2009-2010 yang terdiri dari 36 siswa 19 putra dan 17 putri. Siswa yang terlibat adalah siswa yang telah mempelajari materi persamaan dan pertidaksamaan linear satu variabel.
Sebelumnya peneliti telah melakukan persiapan sebelum pengajaran yaitu menyusun RPP dan lembar kerja atau diskusi siswa yang telah dibahas pada BAB III.
2. Selama Pembelajaran
Pembelajaran diadakan selama 3 kali pertemuan yaitu pada tanggal 18, 22, dan 23 November 2009 masing-masing berlangsung selama 2 jam pelajaran.
Deskripsi pembelajaran dalam tiap pertemuannya dijelaskan sebagai berikut :
a. Pertemuan I
persamaan dan pertidaksamaan linear dari guru matematika mereka. Jadi pre-tes dilakukan untuk mengukur sejauh mana kemanpuan siswa dan tingkat penguasaan materi mereka.
Setelah pre-tes diadakan, kemudian peneliti menjelaskan kembali materi mengenai persamaan dan pertidaksamaan linear satu variabel yang sebelumnya telah di berikan oleh guru matematika mereka dengan menggunakan model pembelajaran yang berbeda yaitu dengan menggunakan reciprocal teaching model.
Peneliti kemudian menjelaskan pada para siswa tentang apa itu reciprocal teaching dan bagaimana prosesnya dalam menyelesaikan soal cerita. Pertama-tama dimulai dengan pengenalan tahapan yang ada dalam reciprocal teaching model yaitu, membaca soal, merangkum atau memahami isi soal dan menyelesaikannya, kemudian membuat soal baru dan menjelaskan tentang soal tersebut. Tetapi dalam pertemuan ini, untuk membuat soal baru langsung dilakukan oleh siswa sendiri.
Peneliti memulai dengan memberikan contoh soal persamaan linear sebagai berikut :
sepatu dan sepasang sandal. Kemudian tentukan harga 3 pasang sepatu dan 5 pasang sandal!
Peneliti membacakan soal tersebut dan siswa mendengarkan dengan seksama, kemudian siswa diajak berdialog untuk memahami isi dari soal untuk membuat model matematikanya dan menyelesaikannya dengan tuntunan peneliti di depan kelas. Kemudian siswa diminta untuk mebuat soal baru beserta penyelesaiannya dan salah satu siswa maju ke depan kelas untuk menuliskan soal beserta penyelesaiannya. Berikut soal yang dibuat oleh siswa :
harga sepatu tiga kali lipat dari harga kaus kaki. Seorang ibu membeli sepasang sepatu dan dua pasang kaus kaki dan ia membayar sebesar Rp. 250.000,00. Berapakah harga sepasang sepatu dan harga kaus kaki?
Jawab : sepasang kaus kaki =p Sepasang sepatu = 3p
Ibu beli sepasang sepatu + 2 pasang kaus kaki = 250.000 3p+ 2p= 250.000
5p= 250.000 p= 250.000 : 5 p= 50.000
jadi harga sepasang kaus kaki = 50.000 dan
Peneliti kemudian mengajak semua siswa untuk melihat hasil pekerjaan yang telah dituliskan di papan tulis dan membahasnya bersama. Setelah itu siswa di berikan contoh soal lagi tentang pertidaksamaan linear. Contoh soalnya adalah sebagai berikut :
Suatu model kerangka balok terbuat dari kawat dengan ukluran panjang (x+10) cm lebar (x – 4 ) cm dan tingginya x cm. Jika panjang kawat yang diperlukan tidak kurang dari 156 cm. Tentukan ukuran minimum (panjang, lebar, tinggi minimum) balok tersebut.
Sama halnya seperti pada contoh soal pertama tentang persamaan linear, peneliti melakukan tanya jawab untuk merangkum informasi apa yang ada pada soal atau memahami isi soal dan membuat model matematikanya kemudian menyelesaikannya bersama –
sama dengan siswa. Seperti pada kegiatan sebelumnya setelah soal diselesaikan peneliti meminta siswa untuk membuat soal baru dan salah satu siswa menuliskan soal tersebut di papan tulis. Berikut soal yang dibuat siswa :
Pesegi panjang mempunyai panjang (x + 7) cm dan lebar (x – 2) cm. Jika kelilingnya tidak kurang dari 50 cm,
tentukan luas minimum persegi panjang tersebut! Jawab:
Diketahui : panjang =x+ 7 Lebar =x–2
2(x+ 7 +x–2 )≥50
2x+ 14 + 2x–4≥50
4x+ 10 ≥50
4x + 10–10 ≥50–10
4x ≥ 40
4 40 4
4x ≥
x ≥ 10
Panjang minimum = 10 + 7 = 17 Lebar minimum = 10–2 = 8 Luas mninimun = 17 × 8 = 136
Pada penelitian hari pertama ini memang sedikit sulit untuk membiasakan siswa berdialog bersama. Banyak yang diam meski sebenarnya mereka tahu apa yang harus mereka jawab. Terkadang mereka hanya berbisik-bisik pada kawan sebelahnya. Tetapi ada siswa yang juga aktif bertanya dan menjawab. Tetapi lama kelamaan siswa mulai terbiasa dan aktif dalam mengikuti proses pembelajaran. Pada akhir pertemuan peneliti meminta siswa untuk mempersiapkan diri karena pada pertemuan berikutnya mereka akan berperan sebagai guru dalam kelompok.
b. Pertemuan II
dalam kelompok. Kelompok ini adalah kelompok tetap diskusi mereka. Siswa dalam kelompok akan bergiliran berperan sebagai guru dan siswa. Setiap kelompok diberikan 4 soal yang harus diselesaikan dan harus membuat satu soal baru. Tetapi dalam kelompok tersebut mereka mempunyai soal pokok yang harus diselesaikan dan akan mereka presentasikan di depan kelas oleh salah seorang wakil dari kelompoknya bersama dengan soal yang telah dibuat. Kelompok satu menyelesaikan soal nomor 1, kelompok 2 soal nomor 2, kelompok 3 soal nomor 3, kelompok 4 soal nomor 4, kelompok lima soal nomor lima, demikian seterusnya.
Dalam kelompok tiga yang terdiri dari 4 orang siswi yaitu : Adinda (S1), Cahya (S7), Fathika (S13), dan Intan (S19) sempat terjadi kebingungan sesaat karena salah satu dari mereka tidak ada yang mau berperan sebagai guru. Berikut transkrip saat mereka kebingungan:
(S1) : siapa yang mau jadi guru nih??
(S13) : kamu aja.
(S1) : enggak mau, aku gak bisa. Kamu aja ya tan!
(S19) : aku juga ga mau. Cahya kamu duluan aja!
(S7) : masa aku? Jangan aku.
sedang belajar.dan akan mendapatkan giliran untuk menjadi guru dalam kelompok.
( Peneliti ) : ada apa ini? Kenapa saling tunjuk? Siapa saja yang mulai
kan sama aja nanti semua kebagian kok. Semakin cepat
kalian mulai semakin baik. Soal-soalnya bisa di kerjakan.
Enggak usah malu.
(S1) : ya udah bu, aku aja yang duluan. Temen-temen tapi kalau aku
salah ngomong jangan di ketawain ya.
(S7) (S13) (S19) : iya enggak.
Akhirnya mereka memulai diskusi mereka dengan salah satu siswa yang menjadi motor atau berperan sebagai guru untuk menyelesaikan soal nomor 1. Mereka bekerja sama dengan baik dan terlihat ada peningkatan dialog karena ternyata ada siswa yang belum mengerti tentang materi persamaan linear dan dia tidak sungkan untuk bertanya pada teman yang berperan sebagai guru tersebut. Berikut transkripnya :
(S1) : teman-teman ini soal yang harus kita kerjakan. Panjang suatu alas
segitiga sama kaki adalah 5 cm kurangnya dari panjang sisi.
Sedangkan kelilingnya adalah 25 cm. Tentukan panjang sisi-sisi
segitiga tersebut!
(dibacakan dengan perlahan dan teman-teman yang lain
mendengarkan)
Udah jelas kan? Yang diketahuinya apa ya?
(S19) : itu loh panjang sisi sama panjang alasnya.
(S7) : diganti pake lambang n aja.
(S1) : hmmm, Apa yang diganti panjang sisi atau panjang alas?
(S19) : panjang alas berarti n-5, gitu ya? kan panjang alas segitiga sama
kaki 5 cm kurangnya dari panjang sisi bener ga sih?
(S1) : hmmm, masa sie? Coba di lihat lagi.
(S13) : kok bisa gitu? Gimana sih? Aku ga ngerti.
(S1) : kita liat bareng-bareng deh panjang alas segitiga sama kaki 5 cm
kurangnya dari panjang sisi gitu. Berati panjang sisinya kita ganti
jadi n terus pnjang alasnya n-5. Ngerti gak?
(S19) : nah iya bener gitu.hehe
(S13) : Ooow iya ngerti. (sambil senyum-senyum)
(S1) : udah ngerti kan, terus keliling segitiga rumusnya apa?.
(S7) : keliling segitiga sama kaki ya?
(S1) : iya apa coba?
(S13) : sisi + sisi + alas. Bener kan? Ayo dihitung.
(mereka masing-masing menghitung)
(S1) : aku udah dapat jawabannya. Kalian dah selesai?
(S19) : aku udah.
(S7) : aku juga udah, ni hasilnya K = sisi + sisi + alas
25 = n + n + n–5
30= 3n
n = 10
(mereka mencocokan jawaban masing-masing)
(S1) : nah klo gitu berarti kita sudah tau bahwa panjang sisi segitiganya
(S7) : iya nih.
(S1) : ya udah yuk, ada yang punya ide kita buat soal kaya gimana?
(S13) : gimana donk bu guru? ( sambil cekikikan)
(S1) : ini kan tentang segitiga, kalo kita buat soal tentang segi empat aja
atau gimana?
(S19) : Buat soal yang gampang aja biar ga bingung. Kaya kemarin aja
yang dicontohin ibunya tuh tentang buku-bukuan atau pensil
gitu.
(S1) : ahhh iya boleh tuh, tentang beli pensil ma pulpen aja ya. Pulpen
bahasa indonesianya apa sih?hehehe
(S7) : iya yang gampang aja. Kayak gitu aja.
(S1) : ya udah harga pulpen eh apa bolpoin ya lebih mahal dari pensil
kan, misal beli 5. yang mana yang 3 yang mana yang 2 tuh pensil
apa pulpen?
(S7) : pensil 3 pulpen 2 aja
(S1) : iya boleh, terusgimana dong…pulpen kan lebih mahal tuh jadi 2
kali lipatnya pensil aja ya. biar enak.
(S19) : Terus gimana 5 barang itu dibeli dengan harga berapa?
(S13) : coba kalo 10.000
(S1) : pulpen nya 2x lipat pensil berarti kalau pulpennya 2 kan jadi 2×2
itu 4,. Jadi 7 pensil harganya 10.000.satu pensilnya berarti…?
(S7) : susah tau ngitungnya
(S13) : hehehe iya susah masa harganya koma-komaan.
(S1) : 10.000 ga bisa, 15.000 jg susah.berapa donk. 7.000 aja gimana?
(S1) : ya dah 21.000 aja kan kalau dibagi 7 jadi 3000
(S7) : terus pulpennya 6.000 ya
(S13) : iya udah gitu aja soalnya.
(S1) : iya jadi gini ya, Harga 2 bolpoint dan 3 pensil sama dengan 21.000.
jika harga bolpoint 2 kali lipat pensil. Berapakah harga bolpoint
dan pensil tersebut.
(S19, S13, S7) : iya iya tulis-tulis.
Dari kelompok ini cukup terlihat kerjasama yang baik, peran guru yang dipegang oleh Adinda (S1) cukup baik dilakukan. Mereka bersama-sama belajar dari tidak tahu menjadi tahu.
Pada kelompok dua, empat, lima, tujuh dan delapan semuanya berjalan dengan baik. Mereka antusias untuk melaksanakan proses diskusi dalam kelompoknya. Dan pada kelompok dua yang terdiri atas sekar (S5), chintami (S8), fajrihani (S11), nisa (25). Mereka sangat antusias untuk berperan sebagai guru dan menyelesaikan setiap soal yang ada.Berikut transkripnya : (S25) : temen-temen aku jadi guru yang pertama ya, nanti abis aku baru
chintami, hani terus sekar.
(S5) : gak mau, aku dulu aja.
(S25) : aku dulu aja ya. sekar nanti soal no 3 aja.
(S11) : iya udah, nisa aja yang mulai duluan.
(S25) : ya udah yuk mulai. Aku bacain soalnya ya. Harga sebuah buku
sama dengan harga 2 buah pensil. Jika seorang anak membeli 3
buah buku dan 2 pensil, maka harganya Rp. 12.000,00.
( soal dibacakan dengan perlahan)
Yang diketahui dari soal ini apa?
(S8) : kita harus ganti pake lambang dulu ya?
(S25) : iya yang diketahuinya kita misalkan pake lambang.
(S5) : kalo pensil kita gantixgimana?
(S25) : iya boleh.(sambil mencatat)
(S11) : terus gimana harga bukunya ga dimisalkan juga? kan sama
dengan harga 2 pensil?
(S25) : iya kan dah kita misalkan untuk pensil kita gantixtrs untuk buku
kan harganya 2 kali pensil berati jadi 2x.
(S5) : iya bener gitu, aku juga mikirnya gitu.
(S25) : terus lanjut ke soal lagi ya, seorang anak membeli 3 buah buku
dan 2 pensil, maka harganya Rp. 12.000,00.
(S8) : jadi 3buku + 2pensil = 12.000 ?
(S11) : kan buku 2x jadi gini dong 3 kali dalam kurung 2x tambah 2x
sama dengan 12.000 (sambil menulis 3(2x) + 2x= 12.000)
(S25) : iya gitu, yuk kita hitung. 3 dikali 2x sama dengan 6x terus d
tambah 2xkan ya jadi 8xsama dengan 12.000.x= 12.000 dibagi
8. Berapa tuh hasilnya?
Serentak menjawab : 1500
(S25) : lanjut ke soal, harga 3 pensil berarti 3×1500
Serentak menjawab : 4500
(S25) : jadi harga 3 pensil 4500. hmmmm, selesai.
(S5) : lanjut ke soal baru aja ya, buat soal presentasinya abis ini aja.
Aku pengen ngerjain soal nomer 3.
(S8) : boleh ya? ya udah deh yuk.
Hal yang sama seperti pada kelompok 2 juga terjadi pada kelompok 5 yang terdiri dari Safira, Dheanisa, Fara, dan Lyoni. Mereka saling berebut menentukan giliran yang menjadi guru dan siapa yang akan maju presentasi di depan kelas. Tetapi karena keterbatasan waktu setiap siswa tidak mendapatkan giliran. Ternyata untuk menjalankan reciprocal teaching model ini dibutuhkan waktu yang cukup banyak.
Masalah terjadi pada kelompok satu dan enam. Dimana dalam kedua kelompok ini terdapat siswa yang cukup sulit untuk dilunakkan. Dalam kelompok sembilan terjadi ketidakcocokan dalam bekerja sama. Ada siswa yang sama sekali tidak dapat bekerja dalam kelompok, dan dia memilih untuk mengerjakan soal itu sendiri. Dalam kelompok enam terdapat siswa yang acuh tak acuh dan tidak menghiraukan apa yang dilakukan oleh teman-teman kelompoknya hal ini terjadi karena dia tidak suka matematika.
masing-masing. Para siswa membutuhkan waktu yang lama dalam mengerjakan soal – soal tersebut dalam kelompok mereka.
Akibatnya diskusi mereka dalam kelompok harus dihentikan dan dilanjutkan dengan presentasi kelompok agar alokasi waktunya tetap mencukupi. Kemudian wakil dari kelompok yang tidak mendapatkan giliran untuk menjadi guru mewakili kelompoknya untuk mempresentasikan hasil pekerjaan mereka di depan kelas.
Dimulai dari kelompok dua diwakili oleh Sekar yang bersedia dan menawarkan diri untuk mempresentasikan pekerjaannya tentang persamaan linear terlebih dahulu. Berikut trasnkrip diskusi presentasi mereka :
(S5) : temen-temen saya wakil dari kelompok dua mau
mempresentasikan hasil kerja kelompok. (kemudian
menuliskan hasil kerja kelompoknya d papan tulis)
Harga pensil =x
Harga buku = 2x
3 buku + 2 pensil = 12.000
3(2x) + 2x= 12.000
6x+2x= 12.000
8x= 12.000
x= 1500
harga 3 buah pensil = 1500 x 3 = 4500
(dia kemudian menjelaskan apa yang dia tulis. Dan semua siswa
yang bertanya dan hanya memberikan respon jawaban iya
benar)
Soal yang kelompok dua buat ternyata hampir mirip dengan apa yang mereka kerjakan. Berikut adalah soalnya dan pembahasan yang di jelaskan oleh wakil kelompok di depan kelas.
Harga sebuah buku gambar sama dengan harga 2 buah buku
tulis. Jika seorang pedagang membeli 4 buah buku gambar dan 6
buku tulis, maka harganya Rp. 18.000,00. Hitunglah harga
masing-masing barang!
Jawab : Harga buku gambar :k
Harga buku tulis : 2k
4 buku gambar + 6 buku tulis = 18.000
4k+ 6(2k) = 18.000
4k+ 12k= 18.000
16k= 18.000
k = 1125
Jadi, harga buku gambar = 1.125
Harga buku tulis = 2 x 1125 = 2250
Berbeda ketika kelompok pertama mempresentasikan hasil kerjanya terdapat kesalahan dalam mengerjakan soal yang kemudian dikoreksi oleh siswi lain. Berikut hasil pekerjaan kelompok pertama:
Umur Ana 25 tahun lebih muda dari umur ibunya. Tujuh tahun kemudian, jumlah umur keduanya 45 tahun. Berapa umur ibu dan Ana sekarang?
n = umur ana n + 32 = 45 n = 45–32
n = 13
umur ibu =13 + 25 = 38 dan umur ana 13 tahun.
Kelompok pertama ini salah dalam mencermati kalimat dalam soal. Mereka tampaknya kurang mengerti maksud dari kalimat dalam soal tersebut. Dan ketika ada salah satu siswa yang bertanya pada mereka tentang hasil pekerjaan mereka itu, mereka pun tidak dapat menjelaskan. Kemudian peneliti meminta siswa yang bertanya tersebut untuk menuliskan jawaban yang sudah dia kerjakan dan menjelaskannya. Siswa tersebut kemudian menuliskan dan menjelaskan jawabannya di papan tulis sebagai berikut :
Umur Ana =x Umur ibu =x+ 25