4. PENGGUNAAN PROJECTION PURSUIT UNTUK
REDUKSI DIMENSI DAN PEMODELAN STATISTICAL
DOWNSCALING
4.1. PendahuluanAnalisis data dengan dimensi besar sering dipengaruhi oleh keadaan data yang disebut curse of dimensionality, yang sering menjadi masalah, terutama kalau dimensinya semakin besar (Scott 1992), sehingga diperlukan data yang lebih banyak. Keadaan data seperti ini mendorong penggunaan suatu metode yang dapat mengatasi masalah tersebut atau yang dapat menghasilkan informasi penting dalam data dengan dimensi yang lebih kecil, yaitu pereduksian dimensi berbasis proyeksi dari peubah berdimensi besar menjadi peubah baru yang berdimensi kecil.
Metode pereduksian dimensi dilakukan dengan tetap mempertahankan struktur informasi penting pada data asal di dalam data tereduksi. PCA dan
Projection Pursuit (PP) dapat digunakan untuk mereduksi dimensi. Hasil reduksi
dimensi dapat diterapkan antara lain untuk pendugaan model regresi berganda. Hasil proyeksi atau pereduksian dimensi dengan PCA, yang disebut komponen-komponen utama, digunakan dalam model PCR, sedangkan hasil reduksi dimensi dengan PP digunakan untuk pemodelan regresi PP atau PPR. Oleh karena itu kedua model ini termasuk dalam kategori model regresi berbasis proyeksi. Model PCR digunakan untuk f(X) linear, sedangkan model PPR untuk pendugaan f(X) nonlinear. Keduanya dapat digunakan untuk keadaan multikolinearitas antar peubah-peubah.
Dalam pemodelan regresi berbasis proyeksi, masalah data berdimensi besar dapat diatasi dengan cara pengepasan sejumlah sekuen fungsi sederhana yang disebut fungsi ridge (Donoho & Johnstone 1989). Setiap fungsi memproyeksikan peubah-peubah prediktor terhadap suatu vektor dan menghubungkan panjang proyeksi ini terhadap peubah respon dengan suatu fungsi pemulus. Jumlah fungsi- fungsi ridge merupakan penduga bagi f( X) pada persamaan 2.1.
Beberapa aplikasi dari metode PP antara lain untuk klasifikasi atau analisis diskriminan, pendugaan fungsi kepekatan, dan pemodelan regresi nonparametrik
(Friedman & Stuetzle 1981), terutama berhubungan dengan struktur data yang nonlinear. Metode ini sering digunakan untuk eksplorasi data (Posse 1995). Dalam bidang ilmu komputer Jimenez & Landgrebe (1999) menggunakan metode PP untuk menganalisis citra satelit. Metode PP dapat digunakan untuk mengatasi struktur nonlinear dalam data berdimensi besar dengan cara pemulusan kernel atau spline. Xia & An (1999) menggunakan metode PP untuk analisis data deret waktu yang nonlinear. PPR memodelkan secara iteratif permukaan regresi (regression surface) sebagai penjumlahan fungsi- fungsi pemulusan dari kombinasi linear peubah-peubah prediktor. Aplikasinya dalam bidang kimia, model PPR memberikan hasil dugaan yang lebih baik daripada model PCR dalam pendugaan konsentrasi atau kandungan protein dalam gandum berdasarkan sejumlah peubah prediktor (absorbans spektrum) yang bersifat multikolinearitas (Malthouse 1995). Dalam Bab ini dibahas tentang aplikasi metode PP dan model PPR dalam bidang klimatologi, khusus nya dalam pemodelan SD, dan pembandingan model PPR dengan model PCR. Kajian ini bertujuan menyusun model PPR dan membandingkannya dengan model PCR.
4.2. Pereduksian Dimensi
Metode PP termasuk ke dalam kelompok metode pereduksian dimensi yang bersifat unsupervised berdasarkan pencarian suatu proyeksi informasi utama (interesting) dari data berdimensi besar (Friedman & Tukey 1974), diacu dalam Li & Sailor (2000). Ide dasar metode PP adalah untuk memperoleh informasi penting dalam data berdimensi besar (banyak peubah prediktor) melalui proyeksi ke data berdimensi lebih kecil dengan cara memaksimumkan fungsi objektif yang disebut Indeks Proyeksi (Projection Index). Informasi dalam data berdimensi kecil mencerminkan informasi yang ada dalam data berdimensi besar. Informasi penting itulah yang akan dicapai (pursue) oleh proyeksinya.
Metode PP berbeda dengan PCA dalam hal prosedur reduksi dimensi. Pereduksian dalam PCA berdasarkan keragaman terbesar dalam data asal. Komponen-komponen utama sebagai hasil reduksi merupakan kombinasi linear dari peubah-peubah asal dengan total keragaman terbesar. Sedangkan metode PP berdasarkan pemaksimuman indeks proyeksi sehingga informasi yang ada dalam
data asal, seperti keadaan data nonlinear, akan tercermin dalam data hasil proyeksi.
Transformasi reduksi dimensi yang biasa digunakan adalah proyeksi linear atau kombinasi linear dari peubah-peubah asal karena proyeksi ini paling sederhana dan mudah diinterpretasi. Jika X = {x1, x2, ... , xp} adalah matriks
berdimensi p yang terdiri dari p vektor peubah asal maka proyeksi linear ℜp à ℜk
adalah:
ZT = A XT, X ∈ ℜp, Z ∈ ℜk, k<p (4.1) di mana A adalah matriks pemetaan atau proyeksi berukuran k×p dengan pangkat k. Matriks A bersifat ortonormal. Jika X adalah peubah acak berdimensi p dengan sebaran F maka Z berdimensi k dengan sebaran FA.
Metode PP menggunakan suatu indeks proyeksi, I(FA), untuk mendapatkan proyeksi A. Indeks proyeksi ini mencirikan struktur yang akan ada dalam proyeksinya, yang dimaksimumkan melalui optimisasi numerik terhadap parameternya. Indeks proyeksi ini bersifat invariant (Huber 1985), yaitu bahwa indeks proyeksi tidak tergantung pada penskalaan dan translasi:
I(sZ+t) = I(Z), s ? 0 (4.2)
di mana s dan t adalah bilangan riil.
4.3. Model Regresi Projection Pursuit
Model PPR bersifat nonparametrik dan termasuk kelompok metode
data-driven di mana model yang diperoleh sesuai dengan karakteristik data. Metode ini
dapat diterapkan untuk data GCM yang bersifat curse of dimensionality dan multikolinearitas dan data curah hujan yang bersifat nonlinear.
Dalam analisis regresi, peubah acak X sebagai prediktor dan Y sebagai peubah respon. Objektif dari analisis regresi adalah menduga nilai harapan E(Y|X) berdasarkan contoh acak {(xi,yi); i=1,2, ... ,n}. Biasanya diasumsikan bahwa bentuk fungsi regresi diketahui sehingga dapat dilakukan pemodelan parametrik. Namun bila fungsi regresi tidak tepat akan menghasilkan model yang tidak sesuai dengan kondisi datanya. Untuk kasus seperti ini diperlukan model nonparametrik.
Pendekatan regresi nonparametrik, seperti kernel dan spline, umumnya berdasarkan rataan lokal dimensi p (local averaging), yaitu pendugaan regresi
pada titik x0 adalah rata-rata respon dari sejumlah pengamatan dengan prediktor-prediktor sekitar x0. Tetapi metode rataan lokal tidak tepat untuk keadaan data yang curse of dimensionality. Kondisi data ini dapat diatasi dengan fungsi polinomial berordo tinggi dengan ukuran contoh besar, atau dengan recursive
partitioning tetapi dengan ukuran contoh yang cukup pada setiap partisi data
pengamatan. Friedman dan Stuetzle (1981) menyarankan penggunaan model PPR untuk mengatasi masalah- masalah pada rataan lokal, fungsi polinomial, dan
recursive partitioning, yaitu dengan menggunakan sejumlah fungsi pemulus dari
hasil proyeksi atau reduksi dimensi seperti pada persamaan 4.7.
Bentuk umum model SD tercantum pada persamaan (2.1). Dalam penelitian ini model SD yang digunakan hanya melibatkan satu peubah sirkulasi atmosfir global (luaran GCM) sebagai prediktor (X) dan satu peubah iklim lokal sebagai prediktan atau peubah respon (y), yaitu:
y(t) = f(X(t ×g)), t=1,2, ... ,n; g=1,2, ... ,p (4.3) di mana: y(t) = peubah iklim lokal (curah hujan),
X(t ×g) = peubah luaran GCM (presipitasi), t = banyaknya waktu (bulanan),
g = banyaknya grid dalam domain GCM (8×8 grid).
Peubah prediktornya hanya satu tetapi datanya ada pada setiap grid dalam suatu domain GCM yang contiguous. Dalam hal ini setiap grid dianggap sebagai peubah prediktor sehingga modelnya adalah model regresi berganda. Data tersebut tidak dapat dimodelkan secara langsung karena adanya korelasi spasial antar grid atau multikolinearitas antar peubah prediktor. Untuk masalah ini diperlukan metode pre-processing terhadap X.
Metode pre-processing akan mentransformasi X(t ×g) menjadi peubah baru Z(k×g) (k<g) sehingga model (4.3) menjadi model berikut.
y(t) = f(Z(t ×k)), t=1,2, ... ,n; k=1,2, ... ,q (4.4) di mana: y(t) = peubah respon,
Z(t ×k) = peubah hasil pre-processing, t = banyaknya waktu,
Selama ini pemodelan SD menggunakan PCR dengan PCA untuk pre-processing. Dengan PCA matriks X akan ditransformasi menjadi Z dengan persamaan (4.1) yang disebut skor komponen utama dengan total keragaman terbesar. Model regresi dibentuk berdasarkan Z seperti berikut.
y = ?0 + ?1 z1 + ?2 z2 + … + ?k zk + d (4.5) atau y = ß0 + ß 1 x1 + ß 2 z2 + … + ß g xg + e (4.6) di mana ß0 = ?0 dan ß i =
∑
= α γ k 1 j jji dan aji = koefisien transformasi.
Dalam metode PP, matriks X juga ditransformasi dengan persamaan (4.1), tetapi prosedur mendapatkan matriks A berbeda dengan prosedur dalam metode PCA. Matriks A diperoleh dengan cara memaksimum indeks proyeksi, I(A), seperti pada persamaan (4.8). Matriks A disebut matriks koefisien proyeksi dan modelnya adalah:
∑
∑
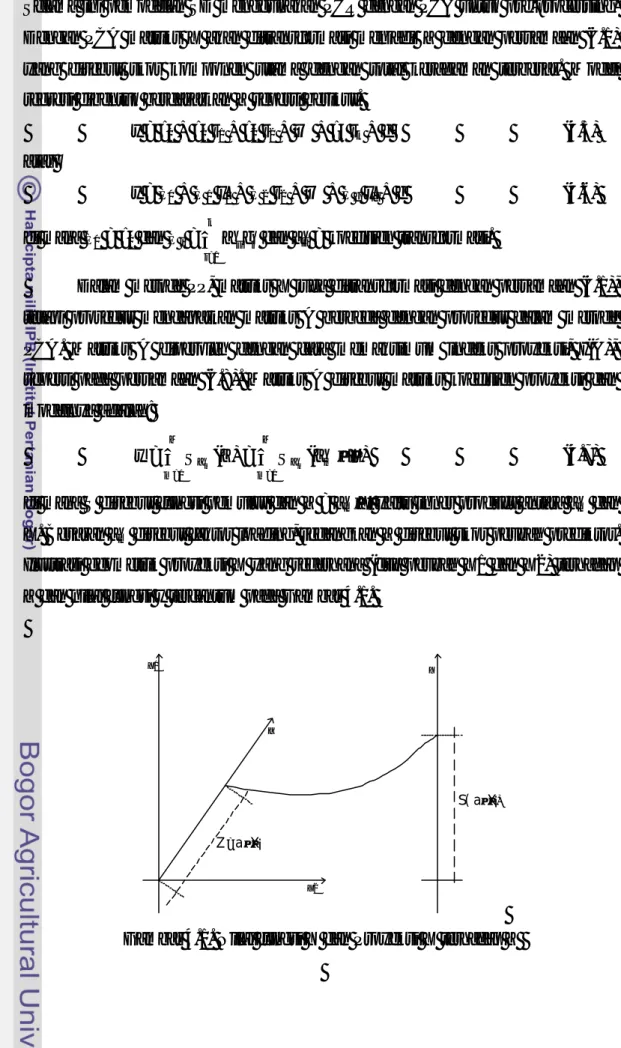
= = • = = M 1 m m M 1 m ) ( ) ( y Sam Z Sam a X (4.7)di mana S disebut fungsi pemulus dan Z = am·X yaitu inner product antara am dan X. Besaran am disebut faktor loading, sedangkan Z disebut skor peubah prediktor. Ilustrasi geometrik proyeksi X yang sederhana (dua peubah X1 dan X2) terhadap Z dan nilai fungsi y tercantum pada Gambar 4.1.
X1 X2 Y α i X a Z= • ) i X S( a•
Pemodelan PPR diawali dengan memaksimumkan indeks proyeksi, mene ntukan fungsi- fungsi peubah tunggal secara empirik berdasarkan proyeksi-proyeksi optimum, serta menjumlahkan fungsi- fungsi tersebut (Jones & Sibson 1987). Johnny, Chan & Shi (1997) menyatakan bahwa metode PP dapat memroses data yang berdimensi besar, tidak berdistribusi normal, dan nonlinear. Fungsi tersebut merupakan kombinasi linear dari peubah-peubah asal (X). Proses penentuan fungsi pemulus ini dilakukan secara iteratif. Malthouse (1995) mengatakan bahwa metode PPR dapat melakukan pendugaan dengan fungsi-fungsi ridge yang kontinu dan adanya kondisi perlu dan cukup bagi pendugaan f(X) dengan penjumlahan sebanyak M fungsi ridge, di mana M<p.
Algoritme penentuan model PPR (Friedman & Stuetzle 1981) adalah: 1) Penentuan nilai awal residual dan nilai M (banyaknya fungsi).
ri ? yi , i=1,2, ... ,n M ? 0
di mana ? yi=0 (peubah respon dibakukan). 2) Penentuan a dan fungsi Sa dalam model.
Untuk kombinasi linear Z = am•X, tentukan fungsi pemulus Sa(Z) sesuai
dengan nilai- nilai Z. Gunakan indeks proyeksi, I(a) berikut.
∑
∑
= = • − − = t 1 i 2 i t 1 i 2 i a i r )) x ( (r 1 ) I( a S a (4.8)Tentukan vektor koefisien aM+1 yang memaksimumkan I(a) atau aM+1 = argmaxa(I(a)) dan fungsi pemulusnya, SαM+1(z).
3) Akhir algoritme.
Jika I(a) lebih kecil dari nilai threshold, maka stop; jika tidak, ubah nilai residual dan nilai M sebagai berikut, kemudian lanjutkan ke langkah 2).
ri ? ri - Sa(Z), i=1,2, ... ,n
M ? M+1.
Fungsi pemulus Sa(Z) ditentukan secara nonparametrik. Bentuk umum
hubungan antara peubah respon dan Z dengan fungsi pemulusnya dapat dituliskan sebagai berikut.
yi = Sa(zi) + ri (4.9) Pada umunya model regresi dalam bentuk seperti berikut:
yi = f(xi) + ei (4.10)
di mana ei adalah iid dengan E(ei)=0 dan f(•) kontinu. Dalam regresi nonparametrik fungsi f (•) diduga dengan Sa(•), yang ditentukan berdasarkan
rataan lokal, yaitu:
S(yi) = AVEi-k=j=i+k(yj) (4.11)
untuk lebar jendela (bandwidth) k tertentu dan dengan formulasi AVE seperti median atau rataan. Pemilihan nilai k sangat menentukan keragaman penduga dan besarnya bias. Nilai k terlalu kecil akan memperbesar ragam penduga, sedangkan nilai k yang terlalu besar akan memperbesar bias. Penentuan fungsi pemulus Sa(•)
menurut Friedman dan Stuetzle (1981):
1) Tentukan median untuk setiap tiga respon secara sekuensial untuk menghilangkan pengaruh data pencilan.
2) Tentukan penduga ragam respon pada setiap titik dengan residual kuadrat rata-rata (average squared residual) dari penduga linear lokal dengan k tertentu. 3) Pemulusan penduga ragam dengan rataan bergerak dan k tetap untuk
menghindari perhitungan lebih dari satu kombinasi linear Z = am•X.
4) Pemulusan sekuen dari tahap 1) dengan pengepasan (fitting) linear lokal dengan nilai k yang diperoleh pada tahap 3).
Hall (1989) menguraikan model PPR secara matematik berdasarkan fungsi kernel (kernel-based PPR) dan sifat penduga PP. Pada dasarnya bahwa solusi PPR
invariant terhadap setiap transformasi baik rotasi maupun penskalaan peubah
prediktor. Berikut ini adalah pendugaan PP untuk mendapatkan proyeksi pertama. Berdasarkan persamaan (4.10), E(yi|xi)=f(x), di mana f(•) disebut fungsi target (Hall 1989). Jika S(•) adalah fungsi pemetaan ℜp à ℜ, f(•) adalah fungsi kepekatan dalam ℜp
, dan X adalah peubah acak berdimensi p, maka untuk suatu skalar z,
Sa(z) = E{f(x)| a•X=z} (4.12)
Proyeksi pertama terhadap f(x) adalah fungsi f1(x)=Sα1(z) di mana a1
meminimumkan L(a) berikut.
sehingga penduga a1 akan meminimumkan penduga L(a), yaitu:
∑
= α • α − = α n 1 i 2 i k Sˆ ( X)} y { n 1 ) ( Lˆ i (4.14)dan penduga proyeksi pertamanya adalah ) X ˆ ( Sˆ ) x ( fˆ1 = α1 α1• (4.15)
Penduga Sˆα(z) akan konvergen terhadap Sa(z) dan konsisten, di mana áˆ1 juga
konvergen terhadap a.
Bentuk model SD (persamaan 4.3) adalah:
yt = f(Xt×g) + et, t=1,2, ... ,n; g=1,2, ... ,p sedangkan model PPR (persamaan 4.7) adalah:
t a • +ε =
∑
= M 1 m m t ( ) y Sam Xtxg sehingga:∑
= • = M 1 m m ) ( f m X Sa a ) X ( di mana: ) X (Sαm αm • = suatu fungsi yang tidak diketahui;
am = (am1, am2, ... , amp) = vektor satuan (arah projection pursuit); Xtg = (xt1, xt2, ... , xtp) = peubah prediktor;
yt = peubah respon;
et = faktor acak dengan E(et) = 0 dan Var(et) = s2; Xtg dan et bebas;
Didefinisikan bahwa:
1). f(X) = E(yt|Xt=X).
2). O = gugus vektor satuan berdimensi p (am). 3). Sa(a•X) = E(yt| a•Xt= a•X), di mana a e O.
Komponen proyeksi pertama dari f(X) adalah S ( 1 X)
1 α •
α , di mana a1 e O meminimumkan L(α) (mengacu pada persamaan 4.8) berikut :
2 t t) S ( X )] X ( f [ E ) ( L α = − α α•
diasumsikan bahwa nilai minimum ini bersifat unik. Selanjutnya misalkan bahwa: ) X X | ) X ( S y ( E ) X ( S(2) t 1 t t 1 α • α• =α• − = • α α α
maka komponen proyeksi keduanya adalah S(2)( 2 X) 2 α • α , di mana a2 e O meminimumkan L(2)(α1,α) berikut: 2 t t 1 t 1 ) 2 ( )] X ( S ) X ( S ) X ( f [ E ) , ( L 1 α • − α• − = α α α α
diasumsikan juga bahwa nilai minimum ini bersifat unik. Dengan cara yang sama dapat diperoleh komponen-komponen proyeksi berikutnya dari f(X). L(α) dapat digunakan untuk mengukur pendekatan Sα(α•X) terhadap f(X), dan L(2)(α1,α) untuk mengukur pendekatan S ( 1 X) S(2)( X)
1 α • + α α•
α terhadap f(X).
Misalkan bahwa {(yt,Xt), 1 = t = n} adalah data pengamatan. Komponen proyeksi pertama S dapat diduga dengan pemulus kernel berikut (Xia & An α 1999): ) X X ( K ( / y ) X X ( K ( ) X ( Sˆ t n 1 t h t t n 1 t h α• −α• α• −α• = • α
∑
∑
= = α (4.16)di mana K(•) adalah suatu fungsi kernel, Kh(•)=K(•/h), dan h adalah lebar jendela (bandwidth). Penduga a1 meminimumkan Lˆ(α) berikut,
2 t t n 1 t t Sˆ ( X )} y { n 1 ) ( Lˆ α = − α< > α• =
∑
(4.17)di mana Sˆα<t>(•) diperoleh dari persamaan (4.16) menggunakan data pengamatan } t s ), X , y
{( s s ≠ . Hal ini untuk mengurangi bias pendugaan αˆ1 (Hall 1989). Jika 1
α meminimumkan S(α) dan penduga αˆ meminimumkan Sˆ(α), maka penduga
αˆ mendekati nilai α1. Keadaan ini menunjukkan bahwa Sˆ(α) mendekati S(α). Hall (1989) menyebutkan bahwa Sˆ(α) konsisten untuk S(α).
Komponen proyeksi kedua dari f(X) diduga dengan Sˆ(α2)(α•X) berikut:
) X X ( K ( / ) X X ( K ( ) X ( Sˆ t n 1 t h ) 1 ( t t n 1 t h ) 2 ( α• =
∑
α• −α• ε∑
α• −α• = = α (4.18) di mana yt Sˆˆ (ˆ1 X) ) 1 ( t = − 1 α • ε α . Penduga αˆ2 meminimumkan Lˆ ( 1, ) ) 2 ( α α berikut: 2 t t 1 ˆ n 1 t t 1 ) 2 ( )} X ( Sˆ ) X ( Sˆ y { n 1 ) , ( Lˆ 1 α • − α• − = α α α α< > =∑
di mana Sˆ(α2<)t>(•) diperoleh dari persamaan (4.18) menggunakan data pengamatan } t s ), X , {( (1) s s ≠
ε . Penduga komponen proyeksi kedua adalah Sˆ(2)(ˆ2 X)
ˆ2 α •
α .
Komponen proyeksi lainnya dapat diperoleh dengan cara yang serupa.
Hall (1989) selanjutnya menguraikan taraf (rate) konvergensi pendugaan
α. Berdasarkan Teorema 4.3 dan 4.4 dalam Hall (1989), untuk suatu penduga αˆ , )
X ˆ (
Sˆαˆ α• konvergen terhadap proyeksi target Sα0(α0 •X) dengan taraf
konvergensi sebesar (nh)−1/2, dengan nilai h optimum sebesar (n)−1/(2r+1), di mana r (=2) menunjukkan turunan ke-r dari fungsi f( X). Uraian yang lebih rinci tercantum pada Hall (1989).
4.4. Bahan dan Metode 4.4.1. Bahan
Datanya sama dengan data yang digunakan pada Bab 3 yaitu data presipitasi luaran GCM dan data curah hujan di stasiun Sukadana. Data presipitasi GCM sebagai matriks X(t ×g) dan curah hujan di stasiun Sukadana sebagai vektor y(t) pada persamaan (4.3).
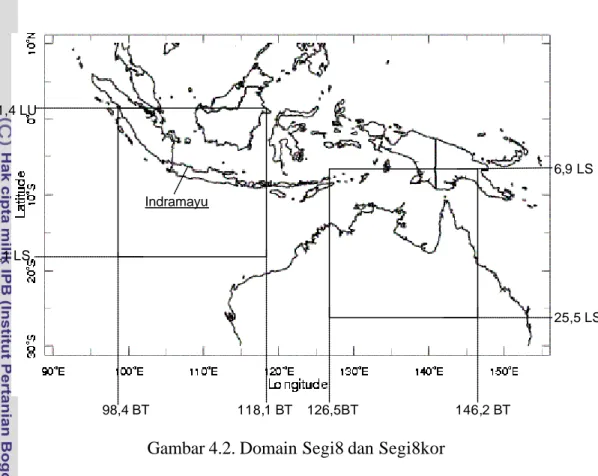
Domain GCM ditentukan berdasarkan Bergant et al (2002), yaitu domain berukuran 8×8 (64 grid), yaitu 1.4o LU – 18.1o LS dan 98.4o BT – 118.1o BT, yang berada tepat di atas Kabupaten Indramayu, selanjutnya disebut domain Segi8. Sebagai pembanding digunakan domain (6.9o–25.5o LS dan 126.5o-146.2o BT) yang ditentukan berdasarkan nilai korelasi tinggi (=0.6) antara sejumlah grid dalam domain dengan curah hujan di stasiun Sukadana, selanjutnya disebut domain Segi8kor. Kedua domain tercantum pada Gambar 4.2.
4.4.2. Metode
Dalam kajian pemodelan SD dengan PPR, dilakukan pendekatan PP untuk
pre-processing sebelum pemodelannya. Hasil pendugaannya akan dibandingkan
dengan hasil pendugaan dengan model PCR, untuk data curah hujan di stasiun Sukadana dengan panjang data historis 35 tahun (1966-2000), 30 tahun (1971-2000), 25 tahun (1976-(1971-2000), 20 tahun (1981-(1971-2000), dan 15 tahun (1986-2000) (Tabel 4.1). Data tahun 1966-2000 digunakan untuk kalibrasi model, sedangkan
data tahun 2001 untuk validasi model. Pembandingan dilakukan berdasarkan RMSEP dan nilai korelasi (r) antara data aktual dengan nilai dugaannya.
Gambar 4.2. Domain Segi8 dan Segi8kor
Tabel 4.1. Tahun Pemodelan untuk Tahun Peramalan 2001 Panjang Data Historis
(tahun) Tahun Pemodelan
35 1966 - 2000
30 1971 – 2000
25 1976 – 2000
20 1981 – 2000
15 1986 - 2000
4.5. Hasil dan Pembahasan
4.5.1. Perbandingan PPR dan PCR
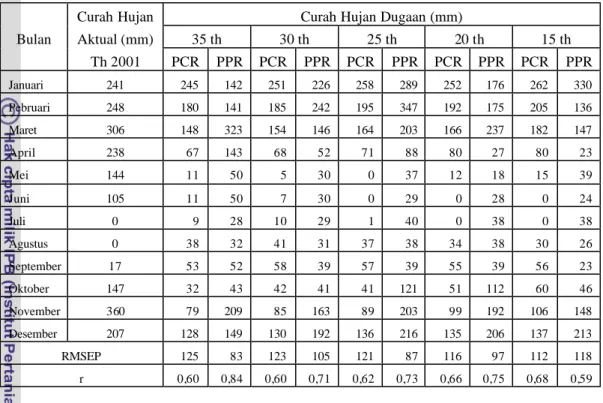
Hasil dugaan curah hujan pada tahun 2001 dengan model PPR dan PCR masing- masing dengan nilai RMSEP dan nilai r tercantum pada Tabel 4.2. Model PCR menggunakan dua atau tiga komponen dengan sekitar 80% keragaman data asal, sedangkan model PPR menggunakan satu fungsi ridge.
1,4 LU 18,1 LS 6,9 LS 25,5 LS 98,4 BT 118,1 BT 126,5BT 146,2 BT Indramayu
Tabel 4.2. Curah Hujan Dugaan berdasarkan Panjang Data Historis (35, 30, 25, 20, dan 15 Tahun) dengan PCR dan PPR: untuk Domain Segi8
Curah Hujan Curah Hujan Dugaan (mm)
Bulan Aktual (mm) 35 th 30 th 25 th 20 th 15 th Th 2001 PCR PPR PCR PPR PCR PPR PCR PPR PCR PPR Januari 241 245 142 251 226 258 289 252 176 262 330 Pebruari 248 180 141 185 242 195 347 192 175 205 136 Maret 306 148 323 154 146 164 203 166 237 182 147 April 238 67 143 68 52 71 88 80 27 80 23 Mei 144 11 50 5 30 0 37 12 18 15 39 Juni 105 11 50 7 30 0 29 0 28 0 24 Juli 0 9 28 10 29 1 40 0 38 0 38 Agustus 0 38 32 41 31 37 38 34 38 30 26 September 17 53 52 58 39 57 39 55 39 56 23 Oktober 147 32 43 42 41 41 121 51 112 60 46 November 360 79 209 85 163 89 203 99 192 106 148 Desember 207 128 149 130 192 136 216 135 206 137 213 RMSEP 125 83 123 105 121 87 116 97 112 118 r 0,60 0,84 0,60 0,71 0,62 0,73 0,66 0,75 0,68 0,59
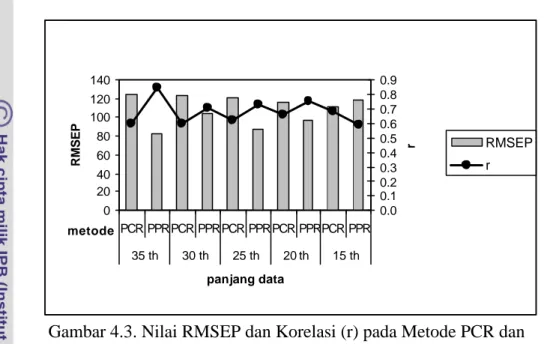
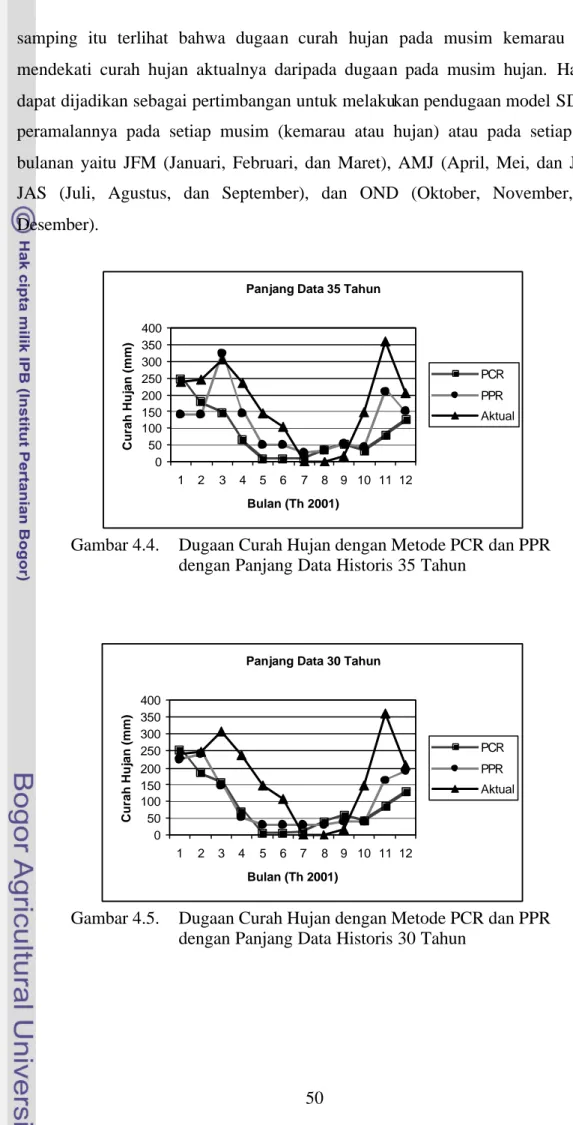
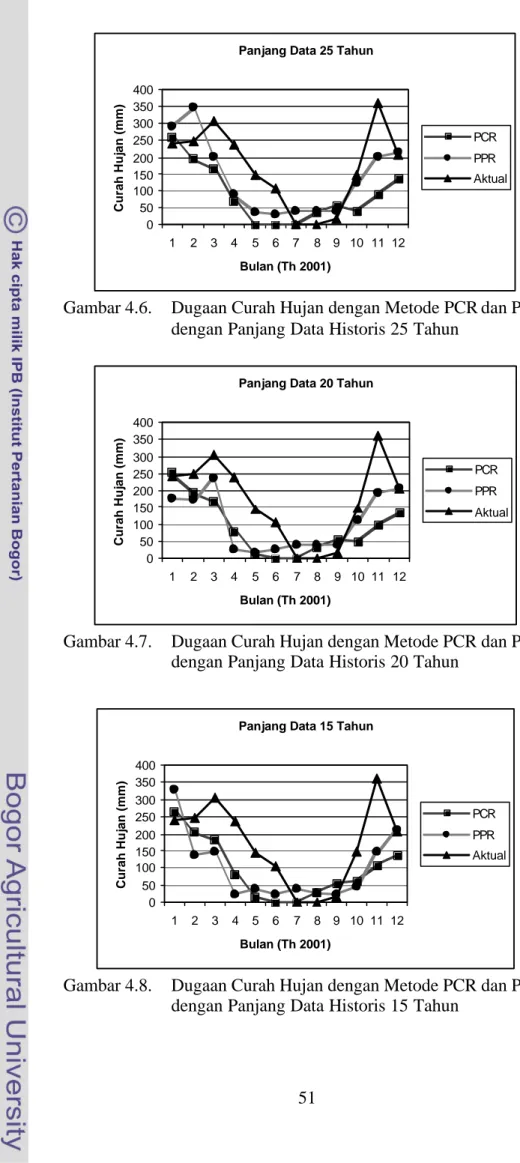
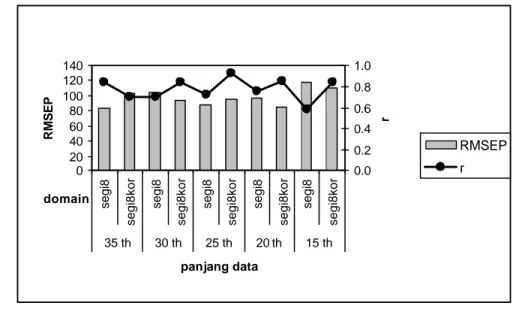
Nilai-nilai RMSEP dan r tersebut untuk setiap panjang data historis (35, 30, 25, 20, dan 15 tahun) di stasiun Sukadana. Secara umum nilai RMSEP dari model PPR lebih kecil dari RMSEP dari model PCR, sedangkan nilai r dari model PPR lebih besar dari nilai r dari model PCR, kecuali untuk panjang data historis 15 tahun di mana nilai RMSEP dari kedua model relatif sama tetapi nilai r dari model PPR (0,59) lebih kecil dari nilai r PCR (0,68). Untuk panjang data historis 35 tahun, nilai RMSEP PPR sebesar 83 dan nilai r PPR sebesar 0,84, sedangkan nilai RMSEP PCR sebesar 125 dan nilai r PCR sebesar 0,60. Untuk panjang data historis 30 tahun, nilai RMSEP PPR sebesar 105 dan nilai r PPR sebesar 0,71, sedangkan nilai RMSEP PCR sebesar 123 dan nilai r PCR sebesar 0,60. Untuk panjang data historis 25 tahun, nilai RMSEP PPR sebesar 87 dan nilai r PPR sebesar 0,73, sedangkan nilai RMSEP PCR sebesar 121 dan nilai r PCR sebesar 0,62. Demikian juga untuk panjang data historis 20 tahun, nilai RMSEP PPR sebesar 97 dan nilai r PPR sebesar 0,75, sedangkan nilai RMSEP PCR sebesar 116 dan nilai r PCR sebesar 0,66. Gambar 4.3 menunjukkan perbandingan nilai-nilai RMSEP dan r dari kedua model. Gambar 4.4 sampai dengan 4.8
masing-masing menunjukkan perbandingan curah hujan aktual pada tahun 2001 dengan curah hujan dugaannya untuk panjang data historis 35, 30, 25, 20, dan 15 tahun.
0 20 40 60 80 100 120 140 PCR PPRPCR PPRPCR PPRPCR PPRPCR PPR 35 th 30 th 25 th 20 th 15 th panjang data RMSEP 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 metode r RMSEP r
Gambar 4.3. Nilai RMSEP dan Korelasi (r) pada Metode PCR dan PPR dengan Berbagai Panjang Data Historis (35, 30, 25, 20, dan 15 tahun)
Berdasarkan hasil tersebut, dalam pendugaan curah hujan model PPR lebih akurat dan pola nilai dugaan lebih mendekati pola data aktualnya daripada model PCR terutama untuk panjang data historis 35, 30, 25, dan 20 tahun. Untuk panjang data historis 15 tahun model PCR (RMSEP=112; r=0,68) lebih baik dari model PPR (RMSEP=118; r=0,59). Pendugaan dengan model PPR untuk panjang data historis 35 tahun (RMSEP=83; r=0,84) lebih baik dari model PPR untuk panjang data historis 30 tahun (RMSEP=105; r=0,71), 25 tahun (RMSEP=87; r=0,73), dan 20 tahun (RMSEP=97; r=0,75). Berdasarkan nilai RMSEP dan r tersebut, untuk pendugaan curah hujan dengan panjang data historis 35 tahun memberikan hasil yang lebih akurat daripada dengan panjang data historis lainnya. Namun demikian panjang data historis yang lebih pendek, seperti 20 tahun, masih dapat digunakan untuk pendugaan curah hujan.
Gambar 4.4 sampai dengan 4.8 memperlihatkan bahwa secara umum dugaan curah hujan lebih rendah dari curah hujan aktual terutama pada bulan-bulan Januari s/d Juni dan Oktober s/d Desember, tetapi dugaan tersebut lebih tinggi dari curah hujan aktual pada bulan-bulan Juli, Agustus, dan September. Di
samping itu terlihat bahwa dugaan curah hujan pada musim kemarau lebih mendekati curah hujan aktualnya daripada dugaan pada musim hujan. Hal ini dapat dijadikan sebagai pertimbangan untuk melakukan pendugaan model SD dan peramalannya pada setiap musim (kemarau atau hujan) atau pada setiap tiga bulanan yaitu JFM (Januari, Februari, dan Maret), AMJ (April, Mei, dan Juni), JAS (Juli, Agustus, dan September), dan OND (Oktober, November, dan Desember).
Panjang Data 35 Tahun
0 50 100 150 200 250 300 350 400 1 2 3 4 5 6 7 8 9 10 11 12 Bulan (Th 2001) Curah Hujan (mm) PCR PPR Aktual
Gambar 4.4. Dugaan Curah Hujan dengan Metode PCR dan PPR dengan Panjang Data Historis 35 Tahun
Panjang Data 30 Tahun
0 50 100 150 200 250 300 350 400 1 2 3 4 5 6 7 8 9 10 11 12 Bulan (Th 2001) Curah Hujan (mm) PCR PPR Aktual
Gambar 4.5. Dugaan Curah Hujan dengan Metode PCR dan PPR dengan Panjang Data Historis 30 Tahun
Panjang Data 25 Tahun 0 50 100 150 200 250 300 350 400 1 2 3 4 5 6 7 8 9 10 11 12 Bulan (Th 2001) Curah Hujan (mm) PCR PPR Aktual
Gambar 4.6. Dugaan Curah Hujan dengan Metode PCR dan PPR dengan Panjang Data Historis 25 Tahun
Panjang Data 20 Tahun
0 50 100 150 200 250 300 350 400 1 2 3 4 5 6 7 8 9 10 11 12 Bulan (Th 2001) Curah Hujan (mm) PCR PPR Aktual
Gambar 4.7. Dugaan Curah Hujan dengan Metode PCR dan PPR dengan Panjang Data Historis 20 Tahun
Panjang Data 15 Tahun
0 50 100 150 200 250 300 350 400 1 2 3 4 5 6 7 8 9 10 11 12 Bulan (Th 2001) Curah Hujan (mm) PCR PPR Aktual
Gambar 4.8. Dugaan Curah Hujan dengan Metode PCR dan PPR dengan Panjang Data Historis 15 Tahun
4.5.2. Perbandingan PPR Berdasarkan Domain Segi8 dan Segi8kor Model PPR dengan domain Segi8 (dm1) dan domain Segi8kor (dm2) menghasilkan dugaan curah hujan pada tahun 2001 untuk setiap domain. Nilai dugaan, RMSEP, dan r untuk setiap domain dan panjang data historis tercantum pada Tabel 4.3.
Tabel 4.3. Curah Hujan Aktual dan Dugaan berdasarkan Panjang Data Historis (35, 30, 25, 20, dan 15 Tahun) dan Domain (Segi8 dan Segi8kor) dengan PPR
Curah Hujan Curah Hujan Dugaan (mm)
Bulan Aktual (mm) 35 th 30 th 25 th 20 th 15 th Th 2001 dm1 dm2 dm1 dm2 dm1 dm2 dm1 dm2 dm1 dm2 Januari 241 142 128 226 144 289 137 176 117 330 159 Pebruari 248 141 330 242 242 347 177 175 138 136 80 Maret 306 323 118 146 161 203 188 237 262 147 184 April 238 143 117 52 101 88 109 27 249 23 72 Mei 144 50 97 30 95 37 93 18 60 39 75 Juni 105 50 55 30 59 29 46 28 60 24 50 Juli 0 28 24 29 35 40 28 38 28 38 48 Agustus 0 32 19 31 22 38 28 38 23 26 26 September 17 52 31 39 22 39 26 39 22 23 27 Oktober 147 43 59 41 26 121 38 112 41 46 34 November 360 209 168 163 176 203 175 192 256 148 203 Desember 207 149 119 192 150 216 117 206 54 213 69 RMSEP 83 103 105 94 87 95 97 84 118 110 r 0,84 0,70 0,71 0,84 0,73 0,93 0,75 0,85 0,59 0,84
Keterangan: d m1 = domain Segi8; d m2 = domain Segi8kor
Secara umum nilai RMSEP dari domain Segi8 lebih kecil dari RMSEP dari domain Segi8kor, sedangkan nilai r dari domain Segi8 lebih besar dari nilai r dari domain Segi8kor, kecuali untuk panjang data historis 35 tahun di mana nilai RMSEP domain Segi8 (83) lebih kecil daripada RMSEP domain Segi8kor (103) dan nilai r domain Segi8 (0,84) lebih besar dari nilai r domain Segi8kor (0,70). Untuk panjang data historis 30 tahun, nilai RMSEP dan r untuk Segi8 masing-masing sebesar 105 dan 0,71, sedangkan nilai RMSEP dan r untuk Segi8kor masing- masing sebesar 94 dan 0,84. Untuk panjang data historis 25 tahun, nilai RMSEP dan r untuk Segi8 sebesar 87 dan 0,73, sedangkan nilai RMSEP dan r Segi8kor sebesar 95 dan 0,93. Untuk panjang data historis 20 tahun, nilai RMSEP
dan r Segi8 sebesar 97 dan 0,75, sedangkan nilai RMSEP dan r Segi8kor sebesar 84 dan 0,85. Demikian juga untuk panjang data historis 15 tahun, nilai RMSEP dan r Segi8 sebesar 118 dan 0,59, sedangkan nilai RMSEP dan r Segi8kor sebesar 110 dan 0,84. Gambar 4.9 menunjukkan perbandingan nilai- nilai RMSEP dan r dari kedua domain.
0 20 40 60 80 100 120 140 segi8 segi8kor segi8 segi8kor segi8 segi8kor segi8 segi8kor segi8 segi8kor 35 th 30 th 25 th 20 th 15 th panjang data RMSEP 0.0 0.2 0.4 0.6 0.8 1.0 domain r RMSEP r
Gambar 4.9. Nilai RMSEP dan Korelasi (r) untuk Domain Segi8 dan Segi8kor dengan Berbagai Panjang Data Historis (35, 30, 25, 20, dan 15 tahun)
Berdasarkan hasil pendugaan curah hujan dengan model PPR, pendugaan dengan domain Segi8kor memberikan hasil yang lebih akurat daripada dengan Segi8 untuk kelima panjang data historis, kecuali untuk panjang data historis 35 tahun di mana Segi8 (RMSEP=83; r=0,84) lebih akurat daripada Segi8kor (RMSEP=103; r=0,70). Untuk pendugaan curah hujan panjang data historis 35 tahun dengan domain Segi8 masih lebih baik daripada panjang data historis lainnya. Pendugaan curah hujan dengan domain Segi8kor untuk panjang data historis yang lebih pendek, seperti 20 tahun, lebih baik daripada dengan Segi8.
Domain Segi8kor ditentukan berdasarkan adanya hubungan (korelasi) yang kuat antara curah hujan pada grid-grid GCM (sebagai prediktor) dengan curah hujan di stasiun Sukadana (sebagai peubah respon). Hal ini berdasarkan pendapat Busuioc et al. (2001) bahwa salah satu syarat dalam pemodelan SD adalah adanya hubungan erat antara prediktan dengan prediktor yang menjelaskan
keragaman iklim lokal dengan baik. Hanya pemilihan grid-grid untuk domain Segi8kor ini masih dilakukan subjektif, belum ada suatu metode yang dapat menentukan domain secara objektif, sehingga domain Segi8 masih digunakan. Penentuan domain Segi8 relatif lebih mudah daripada domain Segi8kor, tanpa harus mengetahui besaran nilai korelasi antara grid- grid GCM dengan stasiun curah hujan.
4.6. Simpulan
1) Secara umum dalam pendugaan curah hujan pada tahun 2001 dengan berbagai panjang data historis di stasiun Sukadana, model PPR memberikan hasil dugaan yang lebih akurat dan pola nilai dugaan lebih mendekati pola data aktualnya daripada model PCR, kecuali untuk panjang data historis 15 tahun. Namun hal ini belum tentu untuk tahun-tahun peramalan lainnya dengan panjang data historis yang sama tetapi periode atau pola data historisnya berbeda. Jika polanya berbeda, maka ada kemungkinan hasil dugaannya juga berbeda. Apalagi kalau ada kejadian ekstrim pada suatu periode tertentu. Dengan demikian diperlukan suatu kajian tentang konsistensi model penduga pada berbagai pola data historis dan tahun peramalan yang berbeda.
2) Pendugaan curah hujan dengan panjang data historis 35 tahun masih lebih akurat daripada panjang data yang lebik pendek (30, 25, 20, dan 15 tahun) tetapi pendugaan dengan panjang data 20 tahun dapat juga digunakan. 3) Penggunaan domain Segi8kor memberikan hasil yang lebih akurat
daripada dengan domain Segi8, namun penentuan Segi8 lebih sederhana daripada Segi8kor. Dalam penentuan domain Segi8kor perlu ditentukan dulu korelasi antara luaran GCM dengan peubah curah hujan, sedangkan penentuan domain Segi8 tidak berdasarkan nilai korelasi.