PERBANDINGAN MODEL PERTUMBUHAN TUMOR
DENGAN METODE PENGOBATAN
VIROTHERAPY DAN RADIOVIROTHERAPY
FAJAR GUMILANG
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2011
ABSTRAK
FAJAR GUMILANG. Perbandingan Model Pertumbuhan Tumor dengan Metode Pengobatan
Virotherapy dan Radiovirotherapy. Dibimbing oleh ALI KUSNANTO dan PAIAN SIANTURI. Tulisan ini membahas tentang analisa kestabilan dan perbandingan model pertumbuhan tumor dengan metode pengobatan virotherapy dan radiovirotherapy. Pengaruh nilai parameter terhadap pertumbuhan virotherapy dan radiovirotherapy tumor diperlihatkan dengan solusi numerik.
Dinamika pertumbuhan tumor dengan metode pengobatan virotherapy dipengaruhi oleh laju kematian sel dan laju reproduksi virus. Sedangkan dinamika pertumbuhan tumor dengan metode pengobatan radiovirotherapy dipengaruhi oleh dosis radiasi dan partikel virus yang bebas menginfeksi tumor. Berdasarkan analisis model terhadap pertumbuhan tumor, terapi yang diberikan tidak dapat mencapai kesembuhan atau sel tumor mati, tetapi hanya dapat memperlambat pertumbuhan sel tumor.
ABSTRACT
FAJAR GUMILANG. Comparison of Tumour Growth Model Under the Virotherapy and Radiovirotherapy Treatments. Supervised by ALI KUSNANTO and PAIAN SIANTURI.
In this paper, the study was about the stability analysis and comparison of tumour growth model under the Virotherapy and Radiovirotherapy treatments. The effect of parameter values on the tumor growth for both methods presented in numerical solutions.
The dynamics of tumour growth under the virotherapy method was affected by the rate of cell death and the rate of virus reproduction. While the dynamics of tumour growth with radiovirotherapy method was affected by the radiation dose and virus particles infecting the tumours. Based on the analysis of models of tumor growth, it is not possible for the therapy to achieve full recovery or to have the whole tumor cells dinimished, but possibly to slow the tumour cell growth.
PERBANDINGAN MODEL PERTUMBUHAN TUMOR
DENGAN METODE PENGOBATAN
VIROTHERAPY DAN RADIOVIROTHERAPY
FAJAR GUMILANG
Skripsi
Sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2011
Judul Skripsi : Perbandingan Model Pertumbuhan Tumor dengan Metode
Pengobatan Virotherapy dan Radiovirotherapy
Nama
: Fajar Gumilang
NIM
: G54070060
Menyetujui,
Pembimbing I
Drs. Ali Kusnanto, M.Si.
NIP. 19650820 199003 1 001
Pembimbing II
Dr. Paian Sianturi
NIP. 19620212 199011 1 001
Mengetahui,
Ketua Departemen Matematika
Dr. Berlian Setiawaty, MS.
NIP. 19650505 198903 2 004
KATA PENGANTAR
Alhamdulillahirobbil’alamin. Penulis mengucapkan puji dan syukur kehadirat Allah SWT atas segala limpahan rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Shalawat serta salam semoga senantiasa tercurah kepada Rosulullah Muhammad SAW beserta keluarga, sahabat dan pengikutnya hingga akhir zaman. Penyusunan karya ilmiah ini juga tidak lepas dari dukungan dan bantuan banyak pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Keluargaku tercinta : Mamah dan Papah yang telah memberikan kasih sayang, didikan, semangat, dukungan baik secara moril, materi, nasihat dan motivasi, serta doa yang tiada henti-hentinya. Doa yang selalu menjadi penerang jalan penulis. Untuk adikku, Tofan Faisal, terima kasih atas doa dan dukungannya,
2. Drs. Ali Kusnanto, M.Si. selaku dosen pembimbing I dan Dr. Paian Sianturi selaku dosen pembimbing II. Terima kasih atas waktu, ilmu yang diberikan dan kesabaran dalam membimbing penulis. Semua ilmu yang Pak Ali dan Pak Paian berikan sangat bermanfaat bagi penulis. Terima kasih,
3. Ir. N. K. Kutha Ardana, M.Sc. selaku dosen penguji. Terima kasih atas waktu dan ilmu yang sangat bermanfaat bagi penulis,
4. Semua dosen Departemen Matematika, terima kasih atas ilmu yang telah diberikan,
5. Pak Yono, Bu Susi, Bu Ade, Pak Bono, Mas Heri, Mas deni dan seluruh staf pegawai Departemen Matematika, terima kasih atas bantuannya dalam memperlancar administrasi akademik bagi penulis di Departemen Matematika,
6. Teman-taman satu bimbingan : Sri, Rachma dan Lazuardi. Terima kasih atas doa, bantuan, dukungan semangat dan nasihatnya,
7. Teman-teman satu kontrakkan : Yasser, Cahya, Suci N Hidayat dan Riza serta Aa Mukhlis dan Teh Novi. Terima kasih atas doa, bantuan, dukungan semangat dan nasihatnya,
8. Teman-teman SMAN 1 Serang (XII IPA 2). Terima kasih atas doa, bantuan, dukungan semangat dan nasihatnya,
9. Teman-teman seperjuangan (Cilegon) : Wawan dan Istri, Eros, Adit, Fredika, Angga, Cecep, Tyo, Yan, Yoki, Ferli, Yulia, Cynthia dan lainnya yang tidak bisa ditulis satu per satu, Terima kasih atas doa, bantuan, dukungan semangat dan nasihatnya,
10.Kakak kelas angkatan 41, 42 dan 43 yang tidak bisa penulis sebutkan satu per satu,
11.Teman-teman angakatan 44 : Mutia, Sri, Rachma, Ayung, Della, Tyas, Rofi, Pandi, Dian tile, Abe, Denda, Imam, Ima, Lili, Yanti, Dora, Lingga, Iyam, Ririh, Sari, Lugina, Ruhiyat, Wahyu, Pepi, Wenti, Tita, Nadiroh, Anis, Yuyun, Nurul N, Nurul A, Istiti, Devi, Deva, Cita, Tanti, Selvi, Fani kodok, Fani R, Ayum, Yuli, Ipul, Puying, Endro, Na’im, Indin, Aqil, Lilis, Tendy, Ikhsan, Yogi, Olih, Arina, Resha, Nurus, Atik, Masay, Siska, nunuy, Lukman, Eka, Aswin, Ali, Aje, Vianey, Gan gan, dan Fikri. Terima kasih atas doa, bantuan, dukungan semangat dan nasihatnya,
12.Adik Kelas angkatan 45 dan 45 yang tidak bisa penulis sebutkan satu per satu, 13.Teman-teman Tim Basket Matematika dan Tim Basket MIPA.
Semoga karya ilmiah ini dapat bermanfaat bagi kita semua, bagi dunia ilmu pengetahuan alam khususnya Matematika dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.
Bogor, Juni 2011
RIWAYAT HIDUP
Penulis lahir di Serang, Banten pada tanggal 19 Maret 1989 sebagai anak pertama dari dua bersaudara, anak dari pasangan Subejo dan Tugi Suprihatin. Tahun 2001 penulis lulus dari SD YPWKS 5 Cilegon. Tahun 2004 penulis lulus dari SMPN 1 Cilegon. Tahun 2007 penulis lulus dari SMAN 1 Serang dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur Ujian Saringan Masuk IPB (USMI). Penulis memilih jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis menjadi asisten dosen mata kuliah Persamaan Diferensial Biasa pada tahun ajaran 2008/2009 dan asisten dosen mata kuliah Persamaan Diferensial Parsial pada tahun ajaran 2009/2010. Selain itu, penulis mengajar Pengantar Matematika dan Kalkulus I di Bimbingan Belajar Gumatika, pengajar Matematika SMA di Private Intesive Studies (PIS), dan pengajar Matematika SMA di Mitra Siswa. Penulis juga aktif pada kegiatan kemahasiswaan Gugus Mahasiswa Matematika (GUMATIKA) sebagai staf Keilmuan (2008/2009), Koordinator Logstran Matematika Ria dalam Kompetisi Sains SMA Se-Indonesia (13-15 November 2009) dan sebagai staf Pengembangan Sumber Daya manusia (2009/2010). Pria kelahiran 22 tahun silam ini juga aktif di kegiatan non akademik sebagai pemain basket di Tim Basket MIPA.
DAFTAR ISI
Halaman
DAFTAR ISI………. vii
DAFTAR TABEL………. viii
DAFTAR GAMBAR……….... viii
DAFTAR LAMPIRAN………. viii
I PENDAHULUAN 1.1 Latar Belakang………... 1
1.2 Tujuan Penulisan……… 1
II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial……… 2
2.2 Titik Tetap……….. 2
2.3 Pelinearan………... 2
2.4 Nilai Eigen dan Vektor Eigen………. 2
2.5 Analisis Kestabilan Titik Tetap……….. 3
III PEMODELAN 3.1 Model Virotherapy……….. 4
3.2 Model Radiovirotherapy………. 5
IV PEMBAHASAN 4.1 Analisis Model Virotherapy……… 7
4.1.1 Penentuan Titik Tetap……….. 7
4.1.2 Analisis Kestabilan Titik Tetap………... 7
4.1.3 Dinamika Populasi Pertumbuhan Tumor……… 8
a. Pertumbuhan Tumor……….. 8
b. Dinamika Populasi untuk 𝛿 > 𝛼……….. 9
c. Dinamika Populasi untuk 𝛿 < 𝛼……….. 10
d. Dinamika Populasi untuk 𝛿 = 𝛼……….. 11
4.1.4 Keberhasilan Terapi……… 11
4.2 Analisis Model Radiovirotherapy……….. 12
4.2.1 Penentuan Titik Tetap………. 12
4.2.2 Analisis Kestabilan Titik Tetap……….. 12
4.2.3 Dinamika Populasi Pertumbuhan Tumor……….... 13
4.2.4 Keberhasilan Terapi……… 15
V SIMPULAN………. 16
VI DAFTAR PUSTAKA……….. 17
DAFTAR TABEL
Halaman
1 Kondisi Kestabilan Titik Tetap……….. 8
DAFTAR GAMBAR
Halaman 1 Skema Diagram Model Virotherapy……….. 42 Skema Diagram Model Radiovirotherapy………. 5
3 Dinamika Populasi Pertumbuhan Tumor………... 9
4 Dinamika Populasi untuk Kondisi 𝛿 > 𝛼………. 9
5 Dinamika Populasi untuk Kondisi 𝛿 < 𝛼………. 10
6 Dinamika Populasi untuk Kondisi 𝛿 = 𝛼………. 11
7 Dinamika Populasi Keberhasilan Terapi (Virotherapy)……… 12
8 Dinamika Populasi 𝑦, 𝑥, 𝑢 dan 𝑣………... 13
9 Dinamika Populasi 𝑦, 𝑥, 𝑢 dan 𝑣 (𝑣 dan 𝜀 ditingkatkan)……….. 14
10 Bidang Fase Hubungan Antara 𝑦, 𝑥, 𝑢 dan 𝑣……… 15
11 Dinamika Populasi Keberhasilan Terapi (Radiovirotherapy)………... 15
DAFTAR LAMPIRAN
Halaman 1 Penentuan Titik Tetap Model Virotherapy………. 192 Penentuan Nilai Eigen dari Persamaan (2), (3), (4)……… 22
3 Penentuan Titik Tetap Model Radiovirotherapy……… 24
4 Penentuan Nilai Eigen dari Persamaan (5), (6), (7), (8)………. 26
5 Kode Mathematica 7 untuk Gambar 3………... 28
6 Kode Maple13 untuk Gambar 4………. 29
7 Kode Maple13 untuk Gambar 5………. 30
8 Kode Maple13 untuk Gambar 6………. 32
9 Kode Maple13 untuk Gambar 7………. 33
10 Kode Maple13 untuk Gambar 8………. 34
11 Kode Maple13 untuk Gambar 9………. 35
12 Kode Maple13 untuk Gambar 10………... 36
I PENDAHULUAN
1.1 Latar BelakangTumor adalah penyakit yang disebabkan oleh pertumbuhan sel-sel jaringan tubuh yang tidak normal. Sel-sel tumor berkembang dengan cepat, tidak terkendali, dan akan terus membelah diri. Sel tumor akan membelah terus meskipun tubuh tidak memerlukannya, sehingga akan terjadi penumpukan sel baru yang disebut tumor ganas.
Gabungan dari sekumpulan genetik dan lingkungan merupakan penyebab dari tumor, contohnya virus. Serangan virus sebenarnya bisa membentuk antibodi (efek positif), namun di sisi lain juga menyebabkan kematian sel (efek negatif). Virus mampu melakukan mutasi dan adaptasi secepat kilat, sehingga dengan mudah virus berkembang biak dalam sel yang dibajaknya kemudian mengubah sel tersebut menjadi medium pengembangbiakan partikel-partikel virus. Hal ini terus menerus dilakukan hingga sel yang ditumpanginya mati.(www.cancerhelp.com)
Dalam dunia kedokteran, para ahli mengkombinasikan efek positif dan negatif dari serangan virus menjadi suatu terapi pengobatan tumor yang disebut virotherapy. Terapi pengobatan tumor tersebut menggunakan virus jenis Measles Virus (MV) yang dapat diatur secara khusus untuk menginfeksi sel tumor, karena ekspresi virus MV sangat tinggi terhadap receptor CD46
yang digunakan oleh virus sebagai alat untuk masuk ke sel tumor target. MV sangat selektif dan mempunyai potensi aktivitas kerusakan sel atau oncolytic (Ding li et al 2006).
Selain itu, terdapat terapi pengobatan tumor yang disebut radiovirotherapy yang merupakan bentuk eksperimen pengobatan
tumor menggunakan penggabungan antara virus dan penyinaran radiasi. Virus diatur ke ekspresi bentuk human sodium iodide symporter (NIS) yang menyediakan sel tumor terinfeksi ke konsentrasi isotop iodide131I. Virus MV-NIS ini menahan aktivitas
oncolytic alami dari virus induk, tetapi mempunyai keuntungan dapat melenyapkan hambatan tumor ke virus ketika dikombinasikan dengan radioidide (Ding li et al 2006).
Ding li (2006) memodelkan secara matematis pertumbuhan tumor virotherapy
dan radiovirotherapy berdasarkan populasi partikel virus dan penyinaran radiasi. Tulisan ini membahas analisis kestabilan dan perbandingan dinamika populasi pertumbuhan tumor virotherapy dan radiovirotherapy
terhadap waktu. Pertama, menentukan titik tetap untuk setiap model. Selanjutnya matriks
Jacobi dengan melakukan pelinearan terhadap setiap variabel. Kemudian menentukan nilai eigen dengan menyelesaikan persamaan karakteristik, nilai eigen digunakan untuk menganalisis kestabilan titik tetapnya.
1.2 Tujuan Penulisan
Tujuan utama penulisan karya ilmiah ini adalah
1. Mengkaji model pertumbuhan tumor
dengan virotherapy dan
radiovirotherapy.
2. Membandingkan dinamika model pertumbuhan tumor virotherapy dan
radiovirotherapy dengan menentukan nilai parameter yang dapat mengontrol kestabilannya.
II LANDASAN TEORI
2.1 Sistem Persamaan DiferensialMisalkan terdapat suatu model dinamika dengan 𝑛 state variabel 𝑥1, 𝑥2, … , 𝑥𝑛 yang
dinyatakan dengan 𝑛 buah persamaan diferensial biasa yang bergantung pada waktu
𝑡 dan vektor parameter p, maka sistem persamaan diferensialnya didefinisikan sebagai: 𝑑𝑥1 𝑑𝑡 = 𝑓1 𝑥1 𝑡 , 𝑥2 𝑡 , … , 𝑥𝑛 𝑡 ; 𝐩 𝑑𝑥2 𝑑𝑡 = 𝑓2 𝑥1 𝑡 , 𝑥2 𝑡 , … , 𝑥𝑛 𝑡 ; 𝐩 ⋮ ⋮ 𝑑𝑥𝑛 𝑑𝑡 = 𝑓𝑛 𝑥1 𝑡 , 𝑥2 𝑡 , … , 𝑥𝑛 𝑡 ; 𝐩 (2.1) (Luenberger 1979) 2.2 Titik Tetap
Misalkan diberikan persamaan diferensial sebagai berikut:
𝑑𝑥
𝑑𝑡 = 𝑥 = 𝑓 𝑥 , 𝑥 ∈ 𝑅
𝑛 (2.2)
Titik 𝑥∗ disebut titik tetap jika memenuhi 𝑓 𝑥∗ = 0
. Titik tetap disebut juga titik kritis atau titik keseimbangan.
(Tu 1994)
2.3 Pelinearan
Misalkan:
𝑥 = 𝑓 𝑥, 𝑦 𝑦 = 𝑔 𝑥, 𝑦
Andaikan 𝑥∗, 𝑦∗ adalah titik tetap
persamaan di atas, maka 𝑓 𝑥∗, 𝑦∗ = 0
dan 𝑔 𝑥∗, 𝑦∗ = 0. Misalkan 𝑢 = 𝑥 − 𝑥∗ dan 𝑣 = 𝑦 − 𝑦∗ maka diperoleh: 𝑢 = 𝑥 𝑢 = 𝑓 𝑥∗+ 𝑢, 𝑦∗+ 𝑣 𝑢 = 𝑓 𝑥∗, 𝑦∗ + 𝑢𝜕𝑓 𝜕𝑥+ 𝑣 𝜕𝑓 𝜕𝑦+ 𝑂 𝑢 2, 𝑣2, 𝑢𝑣 𝑢 = 𝑢𝜕𝑓 𝜕𝑥+ 𝑣 𝜕𝑓 𝜕𝑦+ 𝑂 𝑢 2, 𝑣2, 𝑢𝑣 𝑣 = 𝑦 𝑣 = 𝑔 𝑥∗+ 𝑢, 𝑦∗+ 𝑣 𝑣 = 𝑔 𝑥∗, 𝑦∗ + 𝑢𝜕𝑔 𝜕𝑥+ 𝑣 𝜕𝑔 𝜕𝑦+ 𝑂 𝑢 2, 𝑣2, 𝑢𝑣 𝑣 = 𝑢𝜕𝑔 𝜕𝑥+ 𝑣 𝜕𝑔 𝜕𝑦+ 𝑂 𝑢 2, 𝑣2, 𝑢𝑣
Dalam bentuk matriks:
𝑢 𝑣 = 𝜕𝑓 𝜕𝑥 𝜕𝑓 𝜕𝑦 𝜕𝑔 𝜕𝑥 𝜕𝑔 𝜕𝑦 𝑢𝑣 + 𝑂 𝑢2, 𝑣2, 𝑢𝑣 Matriks 𝑨 = 𝜕𝑓 𝜕𝑥 𝜕𝑓 𝜕𝑦 𝜕𝑔 𝜕𝑥 𝜕𝑔 𝜕𝑦 disebut matriks Jacobi pada titik tetap 𝑥∗, 𝑦∗ . Karena 𝑂 𝑢2, 𝑣2, 𝑢𝑣 → 0 maka dapat diabaikan
sehingga didapat persamaan linear:
𝑢 𝑣 = 𝜕𝑓 𝜕𝑥 𝜕𝑓 𝜕𝑦 𝜕𝑔 𝜕𝑥 𝜕𝑔 𝜕𝑦 𝑢𝑣 (2.3) (Strogatz 1994)
2.4 Nilai Eigen dan Vektor Eigen
Misalkan matriks 𝑨 berukuran 𝑛 × 𝑛, maka suatu vektor taknol X di 𝑅𝑛 disebut
vektor eigen dari 𝑨 jika untuk suatu skalar 𝜆
berlaku:
𝑨𝐗 = 𝜆𝐗 (2.4)
Vektor X disebut vektor eigen yang bersesuaian dengan nilai eigen 𝜆. Untuk mencari nilai eigen dari matriks 𝑨 yang berukuran 𝑛 × 𝑛, maka persamaan (2.4) dapat ditulis sebagai berikut:
𝑨 − 𝜆𝑰 𝐗 = 0 (2.5)
dengan 𝑰 adalah matriks identitas. Persamaan (2.5) mempunyai solusi taknol jika dan hanya jika:
𝑑𝑒𝑡 𝑨 − 𝜆𝑰 = 𝑨 − 𝜆𝑰 = 0 (2.6)
Persamaan (2.6) disebut persamaan karakteristik dari matriks 𝑨.
3
(Anton 1995)
2.5 Analisis Kestabilan Titik Tetap
Misalkan diberikan matriks 𝑨 berukuran
2 × 2 sebagai berikut:
𝑨 = 𝑎 𝑏 𝑐 𝑑
dengan persamaan karakteristik
𝑑𝑒𝑡 𝑨 − 𝜆𝑰 = 0
dan 𝑰 adalah matriks identitas, maka persamaan karakteristiknya menjadi
𝑑𝑒𝑡 𝑎 − 𝜆 𝑏 𝑐 𝑑 − 𝜆 = 0
sedemikian sehingga diperoleh persamaan:
𝜆2− 𝜏𝜆 + Δ = 0
Dengan
𝜏 = 𝑡𝑟𝑎𝑐𝑒 𝑨 = 𝑎 + 𝑑 = 𝜆1+ 𝜆2 Δ = 𝑑𝑒𝑡 𝑨 = 𝑎𝑑 − 𝑏𝑐 = 𝜆1𝜆2
Dengan demikian diperoleh nilai eigen dari matriks 𝑨 sebagai berikut:
𝜆1,2=
𝜏 ± 𝜏2− 4Δ 2
ada tiga kasus untuk nilai Δ: Kasus Δ < 0.
Jika kedua nilai eigen real berbeda tanda maka titik tetap bersifat “sadel”.
Kasus Δ > 0.
𝜏2− 4Δ > 0.
- Jika 𝜏 > 0 dan kedua nilai eigen real bernilai positif maka titik tetap bersifat “simpul tak stabil”.
- Jika 𝜏 < 0 dan kedua nilai eigen real bernilai negative maka titik tetap bersifat “simpul stabil”.
𝜏2− 4Δ < 0.
- Jika 𝜏 > 0 dan kedua nilai eigen imajiner 𝜆1,2= 𝛼 ± 𝑖𝛽 maka titik
tetap bersifat “spiral tak stabil”. - Jika 𝜏 < 0 dan kedua nilai eigen
imajiner 𝜆1,2= 𝛼 ± 𝑖𝛽 maka titik
tetap bersifat “spiral stabil”.
- Jika 𝜏 = 0 dan kedua nilai eigen imajiner murni 𝜆1,2= ±𝑖𝛽 maka
titik tetap bersifat “center”.
𝜏2− 4Δ = 0
.
- Parabola 𝜏2− 4Δ = 0 adalah garis
batas antara simpul dan spiral. Star nodes dan degenerate terletak pada parabola ini. Jika kedua nilai eigen bernilai sama maka titik tetap bersifat “simpul sejati”.
Kasus Δ = 0.
Jika salah satu nilai eigen bernilai nol maka titik asal bersifat “titik tetap tak terisolasi”.
III PEMODELAN
Model yang akan dianalisis merupakan sebuah model yang dibangun berdasarkan pertumbuhan populasi sel tumor. Pada umumnya, pertumbuhan tumor dinyatakan oleh fungsi Gompertz, namun untuk beberapa tumor yang lebih umum model Bertalanffy-Richards (generalized logistic) dapat juga digunakan untuk menjelaskan pertumbuhan tumor. Dalam karya ilmiah ini menggunakan model Bertalanffy-Richards yang diberikan dalam bentuk persamaan:
𝑦 = 𝑟𝑦 1 − 𝑦 𝐾
𝜀
(1) dengan
𝑦 𝑡 menyatakan ukuran populasi sel tumor yang tak terinfeksi virus pada waktu 𝑡.
𝑟 parameter yang menyatakan laju konstan pertumbuhan efektif populasi sel tumor.
𝐾 parameter yang menyatakan ukuran maksimal populasi sel tumor.
𝜀 parameter yang menyatakan bentuk karakteristik pertumbuhan tumor.
3.1 Model Virotherapy
Pada model virotherapy, Ding li (2006) mempertimbangkan dinamika tiga interaksi populasi, yaitu:
1. 𝑦 𝑡 Sel tumor yang tidak terinfeksi virus pada waktu 𝑡.
2. 𝑥 𝑡 Sel tumor yang terinfeksi virus pada waktu 𝑡.
3. 𝑣 𝑡 Partikel virus yang bebas menginfeksi pada waktu 𝑡.
Pemodelan interaksi populasi sel tumor dan partikel virus dinyatakan dalam bentuk persamaan: 𝑦 = 𝑟𝑦 1 − 𝑦+𝑥 𝐾 𝜀 − 𝑘𝑦𝑣 + 𝜌𝑦𝑥 (2) 𝑥 = 𝑘𝑦𝑣 − 𝛿𝑥 (3) 𝑣 = 𝛼𝑥 − 𝑘𝑦𝑣 + 𝜔𝑣 (4) dengan
𝑟 Laju pertumbuhan efektif sel yang tidak terinfeksi (𝑚𝑚3 per hari).
𝐾 Ukuran maksimal sel tumor (𝑚𝑚3). 𝑘 Laju infeksi (𝑚𝑚3 per hari).
𝜌 Laju sel yang bergabung (𝑚𝑚3 per hari). 𝛿 Laju kematian efektif sel yang terinfeksi
(𝑚𝑚3 per hari).
𝜔 Laju virus yang mati (𝑚𝑚3 per hari). 𝛼 Laju produksi virus dari sel tumor yang
terinfeksi (𝑚𝑚3 per hari).
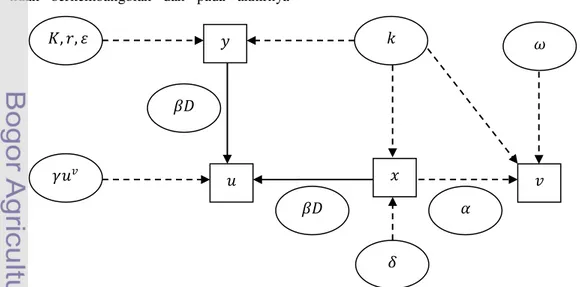
Gambar 1 menyatakan representasi model
virotherapy pada persamaan (2) - (4). Garis panah tebal menandakan populasi bertambah atau populasi berkurang, sedangkan garis putus-putus menunjukkan pengaruh.
Gambar 1 Skema diagram model virotherapy.
𝑦 𝛼 𝜌 𝛿 𝜔 𝐾, 𝑟, 𝜀 𝑘 𝑣 𝑥
5
Populasi sel tumor yang tidak terinfeksi terus berkembang biak. Perkembangbiakan sel-sel ini terjadi karena pengaruh laju pertumbuhan efektif (𝑟), ukuran maksimal tumor (𝐾), dan parameter 𝜀 yang merupakan bentuk karakteristik pertumbuhan tumor. Namun, perkembangbiakan tersebut diikuti oleh laju infeksi 𝑘 > 0 dan laju sel yang bergabung dengan sel yang terinfeksi 𝜌 > 0
yang mengakibatkan populasi sel tumor yang tidak terinfeksi akan berkurang, diberikan oleh penjumlahan 𝑘𝑦𝑣 + 𝜌𝑦𝑥.
Populasi sel tumor yang terinfeksi bertambah karena dipengaruhi oleh laju infeksi. Setelah itu, beberapa sel tumor yang terinfeksi tersebut akan mengalami kematian karena pengaruh laju kematian efektif 𝛿 > 0.
Populasi partikel virus dapat berkembang biak karena pengaruh laju produksi virus dari sel yang terinfeksi, dinyatakan dengan 𝛼𝑥 𝑡
dimana 𝛼 ≥ 0. Proses ini sama seperti populasi sel yang tidak terinfeksi, setelah berkembangbiak, populasi virus akan berkurang karena pengaruh laju infeksi dan laju virus yang mati 𝜔 ≥ 0 .
3.2 Model Radiovirotherapy
Untuk memodelkan pengaruh radiasi pada populasi partikel virus (𝑣), sel tumor yang tidak terinfeksi (𝑦) dan sel tumor yang terinfeksi (𝑥), Ding li (2006) memperkenalkan sel yang dirusak oleh radiasi (𝑢). Sel-sel ini tidak berkembangbiak dan pada akhirnya
mati, namun mereka masih berada ditempat. Nilai kerusakan sel-sel tumor baik yang tidak terinfeksi maupun yang terinfeksi virus setara dengan dosis radiasi (𝐷) yang diserap oleh sel-sel tersebut. Dengan demikian model yang digunakan untuk radiovirotherapy adalah 𝑦 = 𝑟𝑦 1 − 𝑥+𝑦+𝑢 𝐾 𝜖 − 𝑘𝑦𝑣 − 𝛽𝐷𝑦 (5) 𝑥 = 𝑘𝑦𝑣 − 𝛿𝑥 − 𝛽𝐷𝑥 (6) 𝑢 = 𝛽𝐷 𝑥 + 𝑦 − 𝛾𝑢𝑣 (7) 𝑣 = 𝛼𝑥 − 𝜔𝑣 (8) dengan
𝑟 Laju pertumbuhan efektif sel yang tidak terinfeksi (𝑚𝑚3
per hari).
𝐾 Ukuran maksimal sel tumor (𝑚𝑚3). 𝑘 Laju infeksi (𝑚𝑚3 per hari).
𝛿 Laju kematian efektif sel yang terinfeksi (𝑚𝑚3 per hari).
𝜔 Laju virus yang mati (𝑚𝑚3 per hari). 𝛼 Laju produksi virus dari sel tumor yang
terinfeksi (𝑚𝑚3 per hari).
𝐷 Dosis radiasi yang diserap oleh sel (per hari).
𝛽 Tingkat kerusakan se tumor (𝑚𝑚3). 𝛾 Laju kematian efektif sel yang telah rusak
(𝑚𝑚3 per hari).
Gambar 2 menyatakan representasi model pada persamaan (5) - (8). Garis panah tebal menandakan populasi bertambah atau populasi berkurang, sedangkan garis putus-putus menunjukkan pengaruh.
Gambar 2 Skema diagram model radiovirotherapy.
𝛼 𝛽𝐷 𝛾𝑢𝑣 𝜔 𝐾, 𝑟, 𝜀 𝑘 𝛽𝐷 𝛿 𝑦 𝑣 𝑥 𝑢
6
Pada model ini laju infeksi virus ke sel tumor tak terinfeksi (𝑘𝑦𝑣) hanya merupakan pengaruh dari populasi partikel virus dan tidak ikut dalam persamaan populasi partikel virus. Begitu juga dengan laju produksi virus dari sel tumor yang terinfeksi 𝛼𝑥 . Pada model
radiovirotherapy ini, 𝑦 menunjukkan populasi sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi. Populasi partikel virus ditunjukkan oleh 𝑣, 𝑥 menunjukkan populasi sel tumor yang terinfeksi juga tidak rusak oleh radiasi, dan 𝑢 merupakan populasi sel yang rusak akibat radiasi.
Populasi sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi 𝑦 terus berkembang biak karena pengaruh 𝐾, 𝑟, 𝜀. Namun, perkembangbiakan tersebut diikuti oleh laju infeksi 𝑘 dan tingkat kerusakan sel tumor yang tidak terinfeksi akibat radiasi
𝛽𝐷𝑦 yang mengakibatkan populasi sel tumor yang tidak terinfeksi akan berkurang. Untuk populasi sel tumor yang terinfeksi juga tidak rusak oleh radiasi 𝑥 , populasinya terus bertambah karena dipengaruhi oleh laju infeksi. Setelah itu, beberapa sel tumor yang terinfeksi tersebut akan mengalami kematian karena pengaruh laju kematian efektif 𝛿 dan tingkat kerusakan sel tumor yang terinfeksi akibat radiasi 𝛽𝐷𝑥 .
Populasi partikel virus dapat berkembang biak karena pengaruh laju produksi virus dari
sel yang terinfeksi, dinyatakan dengan 𝛼𝑥. Proses ini sama seperti populasi sel yang tidak terinfeksi, setelah berkembangbiak, populasi virus akan berkurang karena pengaruh laju virus yang mati 𝜔 . Dan populasi sel yang rusak akibat radiasi 𝑢 akan terus bertambah karena pengaruh 𝛽𝐷𝑦 + 𝛽𝐷𝑥. Setelah itu, akan mengalami kematian efektif sel yang rusak yang dinyatakan oleh 𝛾𝑢𝑣.
Populasi awal untuk model virotherapy
dan radiovirotherapy yaitu 𝑦 0 = 𝑦0, 𝑣 0 = 𝑣0, 𝑥 0 = 0, dan 𝑢 0 = 0. Model
ini menggunakan beberapa asumsi sebagai berikut:
1. Semua parameter yang digunakan non negatif.
2. Jumlah populasi sel tumor dan virus
𝑦, 𝑥, 𝑣, 𝑢 dalam satuan 𝑚𝑚3 sel
tumor serta semua unit waktu dinyatakan dalam hari.
3. Ukuran maksimal tumor yaitu
1000𝑚𝑚3.
4. Populasi partikel virus dapat menginfeksi populasi sel tumor secara kontinu.
5. Keberhasilan terapi terjadi pada kondisi 𝑦 𝑡 , 𝑥 𝑡 , 𝑣 𝑡 , 𝑢 𝑡 ≤ 1
(diadopsi dalam satuan), walaupun tidak seluruhnya mati.
IV PEMBAHASAN
4.1 Analisis Model Virotherapy4.1.1 Penentuan Titik Tetap Model
Virotherapy
Titik tetap dari persamaan (2) - (4) akan diperoleh dengan menetapkan 𝑦 = 0, 𝑥 = 0, dan 𝑣 = 0 sehingga diperoleh persamaan-persamaan di bawah ini:
𝑟𝑦 1 − 𝑦+𝑥 𝐾 𝜀 − 𝑘𝑦𝑣 + 𝜌𝑦𝑥 = 0 (i) 𝑘𝑦𝑣 − 𝛿𝑥 = 0 (ii) 𝛼𝑥 − 𝑘𝑦𝑣 + 𝜔𝑣 = 0 (iii)
Dengan menyelesaikan persamaan (i) – (iii) secara bersamaan akan diperoleh tiga titik tetap yaitu 𝑇1 0,0,0 , 𝑇2 𝐾, 0,0 , dan
𝑇3 𝑦∗, 𝑥∗, 𝑣∗ dengan 𝑦∗= 𝛿𝜔 𝛼 − 𝛿 𝑘 𝑥∗= 𝜔 𝛼 − 𝛿 𝑣 ∗ 𝑣∗= 𝛼 − 𝛿 𝜔 𝑥 ∗
(Bukti lihat lampiran 1)
4.1.2 Analisis Kestabilan Titik Tetap Model Virotherapy
Misalkan persamaan (2) – (4) dituliskan sebagai berikut: 𝐴 ≔ 𝑦 = 𝑟𝑦 1 − 𝑥 + 𝑦 𝐾 𝜀 − 𝑘𝑦𝑣 + 𝜌𝑦𝑥 𝐵 ≔ 𝑥 = 𝑘𝑦𝑣 − 𝛿𝑥 𝐶 ≔ 𝑣 = 𝛼𝑥 − 𝑘𝑦𝑣 + 𝜔𝑣 (9) Dengan melakukan pelinearan pada persamaan 𝐴, 𝐵, 𝐶 maka akan diperoleh matriks Jacobi sebagai berikut:
𝐽 =
𝐴𝑦 𝐴𝑥 𝐴𝑣 𝐵𝑦 𝐵𝑥 𝐵𝑣 𝐶𝑦 𝐶𝑥 𝐶𝑣
(Bukti lihat lampiran 2)
Analisis Kestabilan di Titik Tetap 𝑻𝟏
Untuk memperoleh kestabilan sistem di titik tetap 𝑇1 0,0,0 terlebih dahulu
melakukan pelinearan pada persamaan (9) maka diperoleh matriks Jacobi:
𝐽 0,0,0 =
𝑟 0 0 0 −𝛿 0 0 𝛼 −𝜔
Nilai eigen akan diperoleh dengan menyelesaikan persamaan karakteristik
𝑑𝑒𝑡 𝐽 0,0,0 − 𝜆𝐼 = 0, sehingga akan diperoleh nilai eigen untuk matriks 𝐽 0,0,0
yaitu:
𝜆1= 𝑟, 𝜆2= −𝛿, 𝜆3= −𝜔
Karena parameter diasumsikan tidak negatif, maka 𝜆1> 0 dan 𝜆2 , 𝜆3< 0.
Sehingga kestabilan titik tetapnya bersifat sadel.
(Bukti lihat lampiran 2)
Analisis Kestabilan di Titik Tetap 𝑻𝟐
Untuk memperoleh kestabilan sistem di titik tetap 𝑇2 𝐾, 0,0 terlebih dahulu
melakukan pelinearan pada persamaan (9) maka diperoleh matriks Jacobi:
𝐽 𝐾,0,0 =
−𝑟𝜀 −𝑟𝜀 − 𝐾𝜌 −𝑘𝐾 0 −𝛿 𝑘𝐾 0 𝛼 −𝑘𝐾 − 𝜔
Nilai eigen akan diperoleh dengan menyelesaikan persamaan karakteristik
𝑑𝑒𝑡 𝐽 𝐾,0,0 − 𝜆𝐼 = 0, sehingga akan diperoleh nilai eigen untuk matriks 𝐽 𝐾,0,0
yaitu: 𝜆1= −𝑟𝜀 𝜆2= −𝑝 + 𝑝2− 4𝑞 2 𝜆3= −𝑝 − 𝑝2− 4𝑞 2 dengan 𝑝 = 𝑘𝐾 + 𝛿 + 𝜔 𝑞 = 𝛿 − 𝛼 𝑘𝐾 + 𝛿𝜔
(Bukti lihat lampiran 2)
Berdasarkan kondisi yang telah diperoleh maka sesuai dengan analisis kestabilan, titik
8
tetap yang diperoleh dipengaruhi oleh laju kematian efektif sel yang terinfeksi 𝛿 dan laju produksi virus dari sel tumor yang terinfeksi 𝛼 sehingga harus diperiksa dari kondisi 𝛿 < 𝛼 dan 𝛿 > 𝛼.
Untuk kasus yang pertama nilai parameter
𝛿 < 𝛼 akan menghasilkan 𝜆1, 𝜆3< 0 dan 𝜆2>0, sehingga dari nilai-nilai eigen yang
diperoleh kestabilan titik tetapnya bersifat sadel. Kasus yang kedua nilai parameter
𝛿 > 𝛼 akan menghasilkan 𝜆1, 𝜆2, 𝜆3< 0,
sehingga dari nilai-nilai eigen yang diperoleh kestabilan titik tetapnya bersifat simpul stabil.
Analisis Kestabilan di Titik Tetap 𝑻𝟑
Untuk memperoleh kestabilan sistem di titik tetap 𝑇3 𝑦∗, 𝑥∗, 𝑣∗
terlebih dahulu melakukan pelinearan pada persamaan (9) dan menyelesaikan persamaan karakteristik
𝑑𝑒𝑡 𝐽 𝑦∗,𝑥∗,𝑣∗ − 𝜆𝐼 = 0, sehingga akan
menghasilkan 𝜆1< 0, 𝜆2 dan 𝜆3 adalah
imajiner murni, sehingga dari nilai-nilai eigen yang diperoleh kestabilan titik tetapnya bersifat spiral stabil.
(Bukti lihat lampiran 2)
Berdasarkan titik tetap yang diperoleh, laju kematian sel yang terinfeksi 𝛿 dan laju produksi virus dari sel yang terinfeksi 𝛼
memengaruhi kestabilan titik tetapnya. Namun, untuk titik tetap 𝑇1 dalam kondisi
apapun kestabilannya bersifat sadel. Berikut adalah tabel kondisi kestabilan dari ketiga titik tetap yang diperoleh. Dari Tabel 1 dapat dilihat bahwa kondisi kestabilan dari titik tetap yang diperoleh tidak mungkin stabil secara bersamaan.
Tabel 1 Kondisi kestabilan titik tetap.
Kondisi 𝑻𝟏 𝑻𝟐 𝑻𝟑
𝛿 > 𝛼 Sadel Simpul
stabil Sadel
𝛿 < 𝛼 Sadel Sadel Spiral stabil
𝛿 = 𝛼 Sadel Simpul
stabil Sadel
4.1.3 Dinamika Populasi Pertumbuhan Tumor dengan Virotherapy
Untuk mengamati pengaruh pertumbuhan populasi sel tumor baik tanpa perlakuan maupun dengan virotherapy maka diperlukan kurva bidang solusi yang menunjukkan hubungan banyaknya populasi dengan variabel waktu. Solusi numerik menggunakan
software Maple 13 dilakukan dengan mensubstitusikan nilai-nilai parameter ke persamaan (2) – (4), sehingga diproleh hubungan antara populasi sel tumor yang tidak terinfeksi, populasi sel terinfeksi, dan populasi partikel virus berdasarkan analisis kestabialn titik tetapnya. Pengaruh yang signifikan pada model virotherapy ini adalah laju kematian sel yang terinfeksi 𝛿 dan laju produksi virus dari sel yang terinfeksi 𝛼 . Namun pada simulasi ini akan diberikan nilai laju infeksi 𝑘 dan laju virus yang mati 𝜔
yang berbeda.
a. Dinamika Populasi Pertumbuhan Tumor
Solusi numerik menggunakan software Mathematica 7 dilakukan dengan mensubstitusikan nilai parameter kontrol 𝑟
dan 𝜀 ke persamaan (1), sehingga diperoleh hubungan antara populasi sel tumor 𝑦
terhadap waktu 𝑡 yang ditunjukkan pada Gambar 3.
Ketika kontrol 𝑟 pada 0.106, 0.206, 0.306
dengan parameter 𝜀 = 2 dan 𝐾 = 1000 serta nilai awal yang diberikan adalah 𝑦 0 = 107.900, maka diperoleh grafik yang menunjukkan bahwa pada nilai 𝑟 yang semakin besar maka pertumbuhan populasi tumor akan semakin cepat pada beberapa waktu tertentu.
Sama halnya dengan kontrol 𝜀 pada 1,2,3
dengan parameter 𝑟 = 0.206 dan 𝐾 = 1000, nilai 𝜀 yang semakin besar maka pertumbuhan populasi tumor akan semakin cepat pada beberapa waktu tertentu. Hal ini menunjukkan bahwa parameter 𝑟 dan 𝜀 pada pertumbuhan populasi tumor mempunyai nilai yang konstan. Berdasarkan hasil plot kontrol 𝑟 dan
𝜀 pada Gambar 3 dapat dijadikan sebagai tolak ukur untuk pertumbuhan tumor dengan
9
Gambar 3 Dinamika populasi pertumbuhan Tumor.
b. Dinamika populasi untuk 𝜹 > 𝛼
Untuk menampilkan plot dinamika populasi diambil nilai parameter yaitu
𝑟 = 0.106, 𝐾 = 1000, 𝜀 = 1.00, 𝑘 = 0.000959, 𝜌 = 0.215, 𝛿 = 0.511, 𝛼 = 0.001, dan 𝜔 = 0.0001. Nilai awal yang diberikan pada kasus ini adalah 𝑦 = 107.900,
𝑥 = 0, dan 𝑣 = 5. Hasil simulasi dapat dilihat pada Gambar 4. Garis putus-putus menunjukkan laju infeksi 𝑘 dan laju virus yang mati 𝜔 ditingkatkan.
Saat laju kematian efektif sel yang terinfeksi yang dihasilkan lebih besar dari pada laju produksi virus dari sel tumor yang terinfeksi maka dinamika populasi sel terinfeksi menunjukkan kenaikan. Namun penurunan populasi virus mengakibatkan populasi sel yang terinfeksi akan mulai turun
pada waktu berikutnya sampai menuju nilai kestabilan di titik tertentu. Lain halnya dengan dinamika populasi sel tumor yang tak terinfeksi, setelah mengalami penurunan jumlah populasi, lalu meningkat terus hingga stabil mencapai ukuran maksimal sel tumor. Pada kasus ini virus terus menyerang sel tumor tak terinfeksi sampai populasinya menurun. Sehingga ketika populasi virus habis, sel tumor tak terinfeksi terus mengalami peningkatan.
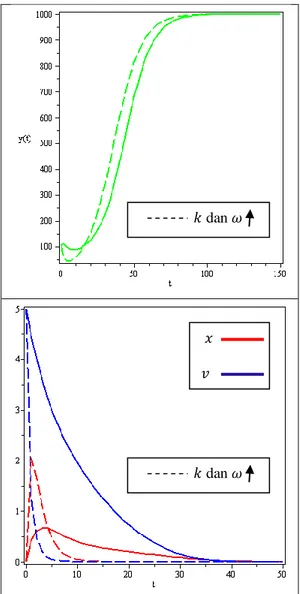
Gambar 4 Dinamika populasi 𝑦, 𝑥. 𝑣 terhadap waktu 𝑡 (pada kondisi 𝛿 > 𝛼).
Ketika laju infeksi 𝑘 dan laju virus yang mati 𝜔 ditingkatkan, yaitu 0.01 dan 0.3
maka akan terjadi peningkatan yang cepat populasi sel terinfeksi. Namun seiring dengan penurunan yang cepat pula dari populasi
0 10 20 30 40 0 200 400 600 800 1000 Waktuhari P o p u l a s i T u m o r mm 3 0 10 20 30 40 0 200 400 600 800 1000 Waktuhari P o p u la s i T u m o r mm 3 𝑟 = 0.106 𝑟 = 0.206 𝑟 = 0.306 𝜀 = 1 𝜀 = 2 𝜀 = 3 𝑥 𝑣 𝑘 dan 𝜔 𝑘 dan 𝜔
10
partikel virus mengakibatkan populasi sel terinfeksi ikut menurun dan stabil menuju nol. Populasi sel tak terinfeksi mencapai ukuran maksimal lebih cepat daripada sebelumnya.
c. Dinamika Populasi untuk 𝜹 < 𝛼
Untuk menampilkan plot dinamika populasi diambil nilai parameter yaitu
𝑟 = 0.106, 𝐾 = 1000, 𝜀 = 1.00, 𝑘 = 0.000959, 𝜌 = 0.215, 𝛿 = 0.511, 𝛼 = 1.3, dan 𝜔 = 0.0001. Nilai awal yang diberikan pada kasus ini adalah 𝑦 = 107.900, 𝑥 = 0, dan 𝑣 = 5. Hasil simulasi dapat dilihat pada Gambar 5. Garis putus-putus menunjukkan laju infeksi 𝑘 dan laju virus yang mati 𝜔
ditingkatkan.
Saat laju kematian efektif sel yang terinfeksi yang dihasilkan lebih kecil dari pada laju produksi virus dari sel tumor yang terinfeksi maka dinamika populasi sel yang tak terinfeksi dan dinamika populasi sel yang terinfeksi mengalami penurunan dan stabil menuju nol. Hal ini bertolak belakang dengan populasi partikel virus yang semakin meningkat seiring dengan bertambahnya waktu.
Ketika laju infeksi 𝑘 dan laju virus yang mati 𝜔 ditingkatkan yaitu 0.01 dan 0.3. Terjadi penurunan populasi sel tumor yang tidak terinfeksi yang diikuti oleh penurunan jumlah virus. Hal ini terjadi pula pada populasi sel yang terinfeksi. Walaupun di awal terapi populasi sel yang terinfeksi meningkat, tetapi karena pengaruh penurunan populasi virus dan sel yang tidak terinfeksi mengakibatkan populasi sel yang terinfeksi ikut menurun.
Sel tumor yang tidak terinfeksi mula-mula mengalami penurunan, namun meningkat seiring berjalannya waktu. Ini disebabkan oleh sel terinfeksi maupun populasi virus mengalami penurunan mencapai nilai minimum dan kurva akan stabil dinilai nol. Namun pada jangka panjang populasi sel tumor tak terinfeksi, sel tumor terinfeksi, dan populasi partikel virus berisolasi secara periodik. Ini berarti terdapat populasi virus yang dapat menginfeksi secara kontinu. Setiap terjadi penurunan populasi sel tumor yang tak terinfeksi, maka populasi virus akan
meningkat bersamaan dengan meningkatnya populasi sel yang terinfeksi.
Gambar 5 Dinamika populasi 𝑦, 𝑥. 𝑣 terhadap waktu 𝑡 (pada kondisi 𝛿 < 𝛼).
𝑥 𝑣 𝑦 𝑥 𝑣 𝑦 𝑥 𝑣 𝑘 dan 𝜔
11
Begitu pun sebaliknya, jika populasi sel yang tak terinfeksi mulai meningkat, maka akan terjadi penurunan pada populasi virus dan populasi sel tumor yang terinfeksi. Meningkatnya populasi sel tak terinfeksi, sel terinfeksi, dan populasi virus semakin bertambahnya waktu semakin kecil dan stabil menuju titik tertentu.
Hubungan populasi sel tumor yang tidak terinfeksi terhadap populasi sel tumor yang terinfeksi menunjukkan kestabilan yang bersifat spiral stabil. Sama halnya dengan hubungan populasi sel tumor yang tak terinfeksi terhadap populasi virus. Populasi sel mulai terinfeksi saat diberikannya partikel virus bebas yang menginfeksi sehingga sel yang tak terinfeksi berkurang populasinya. Namun infeksi yang dilakukan oleh partikel virus tidak mampu membuat sel tumor hilang dari sistem. Kondisi ini menunjukkan bahwa selain perubahan nilai laju kematian sel yang terinfeksi 𝛿 , laju produksi virus dari sel yang terinfeksi 𝛼 , laju infeksi 𝑘 dan laju virus yang mati 𝜔 , waktu (𝑡) juga berpengaruh penting terhadap dinamika pertumbuhan masing-masing populasi.
d. Dinamika populasi untuk 𝜹 = 𝜶
Untuk mengamati pengaruh populasi sel tumor tak terinfeksi, sel tumor terinfeksi, dan populasi virus pada kurun waktu tertentu maka diperlukan kurva yang menunjukkan hubungan banyaknya populasi dengan variabel waktu. Proses penggambaran ini diambil nilai parameter yaitu 𝑟 = 0.106,
𝐾 = 1000, 𝜀 = 1.00, 𝑘 = 0.000959,
𝜌 = 0.215, 𝛿 = 0.511, 𝛼 = 0.511, dan
𝜔 = 0.0001. Nilai awal yang diberikan pada kasus ini adalah 𝑦 = 107.900, 𝑥 = 0, dan
𝑣 = 5. Hasil simulasi dapat dilihat pada Gambar 6. . Garis putus-putus menunjukkan laju infeksi 𝑘 dan laju virus yang mati 𝜔 ditingkatkan.
Sel tumor tak terinfeksi mengalami peningkatan populasi untuk kemudian stabil pada nilai tertentu. Setelah laju infeksi 𝑘 dan laju virus yang mati 𝜔 ditingkatkan, sel tumor tak terinfeksi mengalami penurunan, namun meningkat cepat pada beberapa waktu tertentu, lalu stabil pada ukuran maksimal sel
tumor. Sel tumor yang terinfeksi dan partikel virus akan stabil pada nilai tertentu setelah mengalami peningkatan dan penurunan pada kurun waktu tertentu. Namun setelah laju infeksi 𝑘 dan laju virus yang mati 𝜔
ditingkatkan, sel terinfeksi dan partikel virus menuju nol dengan penurunan populasi yang sangat cepat.
Gambar 6 Dinamika populasi 𝑦, 𝑥. 𝑣 terhadap waktu 𝑡 (pada kondisi 𝛿 = 𝛼).
4.1.4 Dinamika populasi untuk keberhasilan terapi (virotherapy)
Untuk menampilkan plot dinamika populasi diambil nilai parameter yaitu
𝑟 = 0.106, 𝐾 = 1000, 𝜀 = 1.00, 𝑘 = 0.01,
𝜌 = 0.215, 𝛿 = 0.511, 𝛼 = 1.3, dan 𝜔 = 0.3. Nilai awal yang diberikan pada kasus ini
𝑥
𝑣
𝑘 dan 𝜔
12
Adalah 𝑦 = 107.9, 𝑥 = 0, dan 𝑣 = 85. Hasil simulasi dapat dilihat pada Gambar 7.
Populasi sel tidak terinfeksi, sel terinfeksi maupun populasi virus mengalami penurunan mencapai nilai minimum dan kurva akan stabil dinilai nol. Simulasi pada Gambar 7 menunjukkan keberhasilan terapi, karena populasi sel tak terinfeksi, sel terinfeksi dan populasi virus menuju nol hingga hari ke-50. Namun pada jangka panjang, populasinya akan berisolasi periodik kembali, kaena kondisi yang digunakan yaitu 𝜹 < 𝛼.
Gambar 7 Dinamika populasi keberhasilan terapi.
4.2 Analisis Model Radiovirotherapy
4.2.1 Penentuan Titik Tetap Model
Radiovirotherapy
Titik tetap dari persamaan (6) – (9) akan diperoleh dengan menetapkan 𝑦 = 0, 𝑥 = 0,
𝑢 = 0, dan 𝑣 = 0 sehingga diperoleh persamaan-persamaan di bawah ini:
𝑟𝑦 1 − 𝑥+𝑦+𝑢 𝐾 𝜀 − 𝑘𝑦𝑣 − 𝛽𝐷𝑦 = 0 (a) 𝑘𝑦𝑣 − 𝛿𝑥 − 𝛽𝐷𝑥 = 0 (b) 𝛽𝐷 𝑥 + 𝑦 − 𝛾𝑢𝑣= 0 (c) 𝛼𝑥 − 𝜔𝑣 = 0 (d)
Dengan menyelesaikan persamaan (a) – (d) secara bersamaan akan diperoleh dua titik tetap yaitu 𝑇1 𝑦1, 𝑥1, 𝑢1, 𝑣1 dengan
𝑦1= 𝛾 𝛽𝐷 𝑥1= 0 𝑢1= 𝑒𝑥𝑝 ln 𝑟 − 𝛽𝐷𝑟 𝜀 𝐾𝛽𝐷 − 𝛾 𝛽𝐷 𝑣1= 0 dan 𝑇2 𝑦2, 𝑥2, 𝑢2, 𝑣2 = 𝑇2 𝑦∗, 𝑥∗, 𝑢∗, 𝑣∗ .
(Bukti lihat lampiran 3)
4.2.2 Analisis Kestabilan Titik Tetap Model
Radiovirotherapy
Misalkan persamaan (6) – (9) dituliskan sebagai berikut: 𝐴 ≔ 𝑦 = 𝑟𝑦 1 − 𝑥+𝑦+𝑢 𝐾 𝜀 − 𝑘𝑦𝑣 − 𝛽𝐷𝑦 𝐵 ≔ 𝑥 = 𝑘𝑦𝑣 − 𝛿𝑥 − 𝛽𝐷𝑥 𝐶 ≔ 𝑢 = 𝛽𝐷 𝑥 + 𝑦 − 𝛾𝑢𝑣 𝐷 ≔ 𝑣 = 𝛼𝑥 − 𝜔𝑣 (11) Dengan melakukan pelinearan pada persamaan (11), maka akan diperoleh matriks Jacobi sebagai berikut:
𝐽 = 𝐴𝑦 𝐵𝑦 𝐶𝑦 𝐷𝑦 𝐴𝑥 𝐵𝑥 𝐶𝑥 𝐷𝑥 𝐴𝑢 𝐵𝑢 𝐶𝑢 𝐷𝑢 𝐴𝑣 𝐵𝑣 𝐶𝑣 𝐷𝑣
(Bukti lihat lampiran 4)
Analisis Kestabilan di Titik Tetap 𝑻𝟏
Untuk memperoleh kestabilan sistem di titik tetap 𝑇1 𝑦1, 𝑥1, 𝑢1, 𝑣1 terlebih dahulu
melakukan pelinearan pada persamaan (11). Nilai eigen akan diperoleh dengan menyelesaikan persamaan karakteristik
𝑑𝑒𝑡 𝐽 𝑦1,𝑥1,𝑢1,𝑣1 − 𝜆𝐼 = 0, sehingga akan menghasilkan 𝜆1,2= −𝑟𝛾 ± 𝑟2𝛾2− 4𝐾𝛽2𝐷2𝑟𝛾 2𝑘𝛽𝐷 𝑦 𝑥 𝑣
13 𝜆3,4= −𝑍 ± 𝑍2− 4𝛽𝐷𝑄 2𝛽𝐷 dengan 𝑍 = 𝛽2𝐷2+ 𝛽𝐷𝛿 + 𝛽𝐷𝜔 𝑄 = −𝑘𝛼𝛾 + 𝛽2𝐷2𝜔 + 𝛽𝐷𝛿𝜔
(Bukti lihat lampiran 4)
Berdasarkan nilai eigen yang diperoleh, maka 𝜆1, 𝜆2, 𝜆3, 𝜆4< 0. Sehingga kestabilan
titik tetapnya bersifat simpul stabil.
Analisis Kestabilan di Titik Tetap 𝑻𝟐
Untuk memperoleh kestabilan sistem di titik tetap 𝑇2 𝑦2, 𝑥2, 𝑢2, 𝑣2 terlebih dahulu
melakukan peliniearan pada persamaan (11) dan menyelesaikan persamaan karakteristik
𝑑𝑒𝑡 𝐽 𝑦2,𝑥2,𝑢2,𝑣2 − 𝜆𝐼 = 0, sehingga akan
menghasilkan 𝜆1, 𝜆2< 0 dan 𝜆3, 𝜆4 adalah
imajiner murni. Sehingga dari nilai-nilai eigen yang diperoleh kestabilan titik tetapnya bersifat spiral stabil.
(Bukti lihat lampiran 4)
4.2.3 Dinamika Populasi Pertumbuhan Tumor dengan Radiovirotherapy
Solusi numerik menggunakan software Maple 13 dilakukan dengan mensubstitusikan nilai-nilai parameter ke persamaan (6) – (9), sehingga diproleh hubungan antara populasi sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi 𝑦 , populasi partikel virus 𝑣 , populasi sel tumor yang terinfeksi juga tidak rusak oleh radiasi 𝑥 , dan populasi sel yang rusak akibat radiasi 𝑢 .
Untuk menampilkan plot dinamika populasi diambil nilai parameter yaitu
𝑟 = 0.106, 𝐾 = 1000, 𝜀 = 1.00, 𝑘 = 0.104,
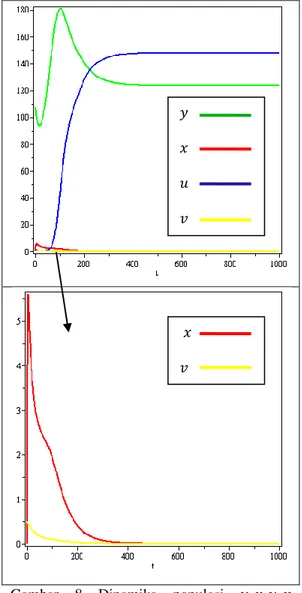
𝛿 = 0.703, 𝛼 = 0.0011, 𝛽 = 0.001, 𝐷 = 150, 𝛾 = 18.57, dan 𝜔 = 0.035. Nilai awal yang diberikan pada kasus ini adalah 𝑦 = 107.900, 𝑥 = 0, 𝑢 = 0, dan 𝑣 = 0.5. Hasil simulasi dapat dilihat pada Gambar 8. Nilai eigen yang diperoleh untuk 𝑇1 yaitu −0.8699, −0.0605, −0.0127, −0.0108 .
Populasi sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi mula-mula mengalami penurunan populasi di awal terapi, namun meningkat tajam dan stabil pada nilai populasi tertentu. Begitu pula dengan populasi
sel tumor yang rusak oleh radiasi. Populasinya meningkat seiring berjalannya waktu dan stabil pada nilai populasi tertentu. Berbeda dengan populasi sel tumor yang terinfeksi dan tidak rusak oleh radiasi. Setelah terjadi peningkatan tajam, kemudian populasinya turun dan stabil menuju nol. Hal ini sejalan dengan populasi partikel virus yang turun terus-menerus hingga stabil menuju nol.
Gambar 8 Dinamika populasi 𝑦, 𝑥. 𝑢, 𝑣
terhadap waktu 𝑡.
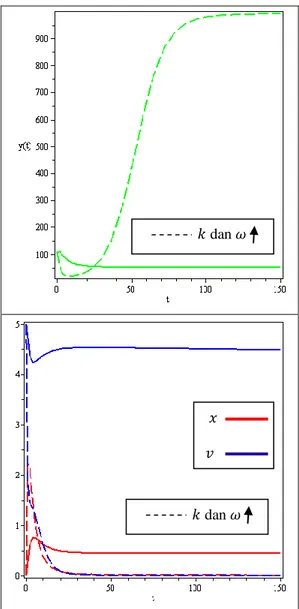
Jika populasi awal partikel virus 𝑣 dan parameter yang menyatakan bentuk karakteristik pertumbuhan tumor 𝜀
ditingkatkan yaitu 𝑣 = 2, 𝜀 = 1.65 serta dosis radiasi yang diserap oleh sel diturunkan nilainya 𝐷 = 0.07 maka akan menghasilkan grafik yang ditunjukkan oleh Gambar 9. Sehingga nilai eigen yang diperoleh untuk 𝑇2
𝑦 𝑥 𝑢 𝑣 𝑥 𝑣
14
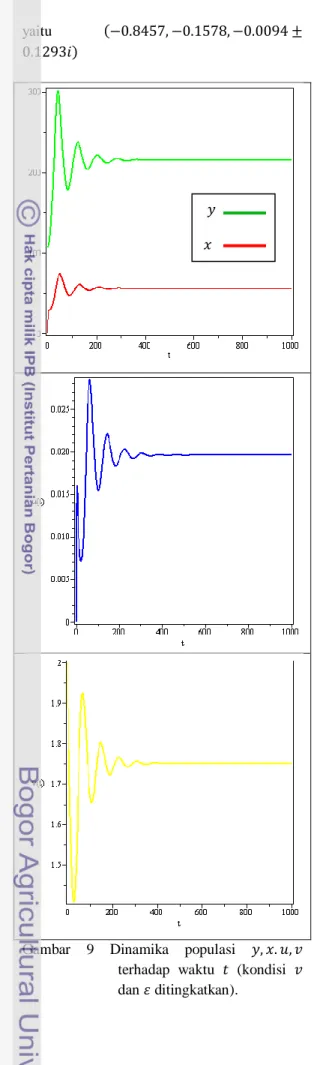
yaitu −0.8457, −0.1578, −0.0094 ± 0.1293𝑖
Gambar 9 Dinamika populasi 𝑦, 𝑥. 𝑢, 𝑣
terhadap waktu 𝑡 (kondisi 𝑣
dan 𝜀 ditingkatkan).
Seperti pertumbuhan tumor virotherapy, dinamika populasi pada Gambar 9 menunjukkan bahwa populasi sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi
𝑦 , populasi partikel virus 𝑣 , populasi sel tumor yang terinfeksi juga tidak rusak oleh radiasi 𝑥 , dan populasi sel yang rusak akibat radiasi 𝑢 berisolasi secara periodik. Ini berarti terdapat populasi partikel virus yang dapat menginfeksi secara kontinu. Masing-masing populasi kemudian stabil pada nilai tertentu. Gambar 10 menunjukkan hubungan populasi partikel virus, populasi sel tumor yang terinfeksi dan tidak rusak oleh radiasi, dan populasi sel yang rusak akibat radiasi terhadap populasi sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi.
𝑦
15
Gambar 10 Bidang fase hubungan antara
𝑦, 𝑥, 𝑢, 𝑣.
4.2.4 Dinamika populasi untuk keberhasilan terapi
Untuk menampilkan plot dinamika populasi diambil nilai parameter yaitu
𝑟 = 0.106, 𝐾 = 1000, 𝜀 = 1.00, 𝑘 = 0.01,
𝛿 = 0.511, 𝛼 = 1.3 𝛽 = 0.215, 𝐷 = 0.07,
𝛾 = 18.57, dan 𝜔 = 0.3. Nilai awal yang diberikan pada kasus ini adalah 𝑦 = 107.900,
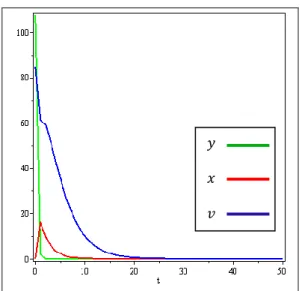
𝑥 = 0, 𝑢 = 0, dan 𝑣 = 5. Hasil simulasi dapat dilihat pada Gambar 11.
Gambar 11 Dinamika populasi keberhasilan terapi.
Populasi sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi 𝑦 , populasi partikel virus 𝑣 , populasi sel tumor yang terinfeksi juga tidak rusak oleh radiasi 𝑥 , dan populasi sel yang rusak akibat radiasi 𝑢
mengalami penurunan mencapai nilai minimum dan kurva akan stabil dinilai nol. Simulasi pada Gambar 11 menunjukkan keberhasilan terapi, karena populasi sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi, populasi partikel virus, populasi sel tumor yang terinfeksi juga tidak rusak oleh radiasi, dan populasi sel yang rusak akibat radiasi menuju nol hingga hari ke-25.
𝑦
𝑥
𝑢
V SIMPULAN
Dari analisis model pertumbuhan tumor dengan virotherapy dan radiovirotherapy
diperoleh beberapa titik tetap. Tiga titik tetap untuk model virotherapy dan dua titik tetap untuk model radiovirotherapy. Kondisi kestabilan dari titik tetap yang diperoleh tidak mungkin stabil secara bersamaan.
Simulasi yang dilakukan dalam karya ilmiah ini dilakukan untuk menunjukkan
implikasi efek virotherapy dan
radiovirotherapy yang signifikan. Untuk dinamika populasi pertumbuhan tumor, parameter laju pertumbuhan efektif sel dan bentuk karakteristik pertumbuhan tumor sangat memengaruhi pertumbuhan sel tumornya. Semakin besar nilai 𝑟 dan 𝜀 maka pertumbuhan populasinya akan semakin cepat menuju ukuran maksimal sel tumor.
Dinamika pertumbuhan tumor dengan
virotherapy dipengaruhi oleh laju kematian sel yang terinfeksi dan laju produksi virus dari sel yang terinfeksi. Pengaruh ditingkatkannya laju
infeksi dan laju virus yang mati menunjukkan semakin cepat populasi sel tumor yang tak terinfeksi mencapai ukuran maksimal sel tumor dan semakin cepat populasi sel tumor terinfeksi dan populasi partikel virus mencapai nilai nol.
Dinamika pertumbuhan tumor dengan
radiovirotherapy masing-masing populasinya mengalami peningkatan terlebih dahulu kemudian stabil menuju nol untuk keberhasilan terapi. Berbeda dengan model
virotherapy yang masing-masing populasinya akan meningkat dalam jangka panjang pada keberhasilan terapi.
Berdasarkan analisis model terhadap model pertumbuhan tumor dengan
virotherapy dan radiovirotherapy, tidak mungkin terapi yang diberikan dapat mencapai penyembuhan atau sel tumor seluruhnya mati, tetapi hanya dapat memperlambat pertumbuhan sel tumor.
DAFTAR PUSTAKA
Anton H. 1995. Aljabar Linear Elementer. Ed ke-5. Terjemahan Pantur Silaban dan I Nyoman Susila. Erlangga, Jakarta. Bajzer Z et al. 2007. Optimization of tumor
virotherapy with recombinant measles virus. Biomathematica Resource, USA. Dingli D et al. 2006. Mathematical modeling
of cancer radiovirotherapy. Mathematical Biosciences 199: 55-78.
http://www.cancerhelp.com/pengobatan-kanker-umum.htm diakses pada tanggal 13 Oktober 2010
Luenberger DG. 1979. Introduction to Dynamic System: Theory, Models, and Applications. John Wiley & Sons: New York.
Strogatz SH. 1994. Nonliniear Dynamics and Chaos, With Application to Physics, Biology, Chemistry, ang Engineering. Addison-Wesley Publising Company, Reading, Massachusets.
Tu PNV. 1994. Dynamical System, An Introduction with Application in Economics and Biology. Springer-Verlag. Heidelberg, Germany.
19
Lampiran 1 Penentuan titik tetap model pertumbuhan tumor dengan virotherapy.
Titik tetap akan diperoleh dengan menetapkan 𝑟𝑦 1 − 𝑦+𝑥 𝐾 𝜀 − 𝑘𝑦𝑣 + 𝜌𝑦𝑥 = 0 (i) 𝑘𝑦𝑣 − 𝛿𝑥 = 0 (ii) 𝛼𝑥 − 𝑘𝑦𝑣 + 𝜔𝑣 = 0 (iii)
Dari persamaan (i) akan diperoleh nilai 𝑦 sebagai berikut:
𝑟𝑦 1 − 𝑦 + 𝑥 𝐾 𝜀 − 𝑘𝑦𝑣 + 𝜌𝑦𝑥 = 0 ↔ 𝑟𝑦 1 − 𝑦 + 𝑥 𝐾 𝜀 − 𝑦 𝑘𝑣 + 𝜌𝑥 = 0 ↔ 𝑦 𝑟 1 − 𝑦 + 𝑥 𝐾 𝜀 − 𝑘𝑣 + 𝜌𝑥 = 0 ↔ 𝑦 = 0 ∩ 𝑟 1 − 𝑦 + 𝑥 𝐾 𝜀 = 𝑘𝑣 + 𝜌𝑥 ↔ 𝑦 = 0 ∩ 1 − 𝑦 + 𝑥 𝐾 𝜀 =(𝑘𝑣 + 𝜌𝑥) 𝑟 ↔ 𝑦 = 0 ∩ 𝑦 + 𝑥 𝐾 𝜀 =𝑟 − 𝑘𝑣 − 𝜌𝑥 𝑟 ↔ 𝑦 = 0 ∩ ln 𝑦 + 𝑥 𝐾 = ln 𝑟 − 𝑘𝑣 − 𝜌𝑥𝑟 𝜀 ↔ 𝑦 = 0 ∩𝑦 + 𝑥 𝐾 = 𝐸𝑥𝑝 ln 𝑟 − 𝑘𝑣 − 𝜌𝑥𝑟 𝜀 ↔ 𝑦 = 0 ∩𝑦 + 𝑥 𝐾 = 𝐸𝑥𝑝 ln 𝑟 − 𝑘𝑣 − 𝜌𝑥𝑟 𝜀 ↔ 𝑦 = 0 ∩ 𝑦 = 𝐸𝑥𝑝 ln 𝑟 − 𝑘𝑣 − 𝜌𝑥𝑟 𝜀 𝐾 − 𝑥
Dari persamaan (ii) akan diperoleh nilai 𝑥 sebagai berikut:
𝑘𝑦𝑣 − 𝛿𝑥 = 0 ↔ 𝛿𝑥 = 𝑘𝑦𝑣
↔ 𝑥 =𝑘𝑦𝑣 𝛿
Dari persamaan (iii) akan diperoleh nilai 𝑣 sebagai berikut:
20
↔ 𝑣 𝑘𝑦 + 𝜔 = 𝛼𝑥 ↔ 𝑣 = 𝛼𝑥
𝑘𝑦 + 𝜔
Substitusi 𝑦 = 0 untuk mendapatkan nilai 𝑥 dan 𝑣.
𝑥 =𝑘𝑦𝑣
𝛿 , karena 𝑦 = 0 maka 𝑥 = 𝑘 0 𝑣
𝛿 = 0 𝑣 = 𝛼𝑥
𝑘𝑦 +𝜔 , karena 𝑦 = 0 dan 𝑥 = 0 maka 𝑣 = 𝛼 0 𝑘 0 +𝜔= 0
Sehingga diperoleh titik tetap 𝑻𝟏 𝒚, 𝒙, 𝒗 = 𝑇1 0,0,0
Substitusi 𝑥 = 0 dan 𝑣 = 0 𝑦 = 𝐸𝑥𝑝 ln 𝑟−𝑘𝑣−𝜌𝑥 𝑟 𝜀 𝐾 − 𝑥, karena 𝑥 = 0 dan 𝑣 = 0 → 𝑦 = 𝐸𝑥𝑝 ln 𝑟−0−0 𝑟 𝜀 𝐾 − 0 → 𝑦 = 𝐸𝑥𝑝 ln 1 𝜀 𝐾 − 0 → 𝑦 = 𝐸𝑥𝑝 0 𝜀 𝐾 − 0 → 𝑦 = 𝐸𝑥𝑝 0 𝐾 − 0 → 𝑦 = 𝐾
Sehingga diperoleh titik tetap 𝑻𝟐 𝒚, 𝒙, 𝒗 = 𝑇2 𝐾, 0,0
Untuk memperoleh titik tetap 𝑇3 𝑦3, 𝑥3, 𝑣3 , substitusikan
𝑦 = 𝐸𝑥𝑝 ln 𝑟 − 𝑘𝑣 − 𝜌𝑥𝑟 𝜀 𝐾 − 𝑥 𝑥 =𝑘𝑦𝑣 𝛿 𝑣 = 𝛼𝑥 𝑘𝑦 + 𝜔
Karena perhitungannya sulit dilakukan secara manual, maka dilakukan perhitungan menggunakan
21 Substitusi 𝑦 = 𝛼 −𝛿 𝑘𝛿𝜔 𝑥 =𝑘𝑦𝑣 𝛿 ↔ 𝑥∗= 𝑘 𝛿𝜔 𝛼 − 𝛿 𝑘 𝑣∗ 𝛿 ↔ 𝑥∗= 𝜔 𝛼 − 𝛿 𝑣 ∗ Substitusi 𝑦 = 𝛿𝜔 𝛼 −𝛿 𝑘 dan 𝑥 ∗= 𝜔 𝛼−𝛿 𝑣 ∗
untuk mendapatkan nilai 𝑣∗
𝑣 = 𝛼𝑥 𝑘𝑦 + 𝜔 ↔ 𝑣∗= 𝛼𝑥 ∗ 𝑘𝑦 + 𝜔 ↔ 𝑣∗= 𝛼 𝜔 𝛼 − 𝛿 𝑣∗ 𝑘 𝛿𝜔 𝛼 − 𝛿 𝑘 + 𝜔 ↔ 𝑣∗= 𝛼 𝛿 𝛼 − 𝛿 𝑣 ∗
Sehingga diperoleh titik tetap 𝑻𝟑 𝒚∗, 𝒙∗, 𝒗∗ dengan
𝑦∗= 𝛿𝜔 𝛼 − 𝛿 𝑘 𝑥∗= 𝜔 𝛼 − 𝛿 𝑣 ∗ 𝑣∗= 𝛼 𝛿 𝛼 − 𝛿 𝑣 ∗
22
Lampiran 2 Penentuan nilai eigen dari persamaan (2), (3), dan (4).
Misalkan persamaan (2), (3), dan (4) dituliskan sebagai berikut: 𝐴 𝑦, 𝑥, 𝑣 = 𝑟𝑦 1 − 𝑦+𝑥 𝐾 𝜀 − 𝑘𝑦𝑣 + 𝜌𝑦𝑥 𝐵 𝑦, 𝑥, 𝑣 = 𝑘𝑦𝑣 − 𝛿𝑥 𝐶 𝑦, 𝑥, 𝑣 = 𝛼𝑥 − 𝑘𝑦𝑣 + 𝜔𝑣
Dengan melakukan pelinearan didapat matriks Jacobi sebagai berikut:
𝐽 = 𝑑𝐴 𝑑𝑦 𝑑𝐴 𝑑𝑥 𝑑𝐴 𝑑𝑣 𝑑𝐵 𝑑𝑦 𝑑𝐵 𝑑𝑥 𝑑𝐵 𝑑𝑣 𝑑𝐶 𝑑𝑦 𝑑𝐶 𝑑𝑥 𝑑𝐶 𝑑𝑣 𝐽 = −𝑘𝑣 + 𝑟 1 − 𝑥 + 𝑦 𝐾 𝜀 −𝑟𝑦 𝑥 + 𝑦 𝐾 −1+𝜀 𝜀 𝐾 − 𝑥𝜌 − 𝑟𝑦 𝑥 + 𝑦𝐾 −1+𝜀 𝜀 𝐾 − 𝑦𝜌 −𝑘𝑦 𝑘𝑣 −𝛿 𝑘𝑦 −𝑘𝑣 𝛼 −𝑘𝑦 − 𝜔
Pelinearan titik tetap 𝑇1 0,0,0 akan diperoleh matriks Jacobi sebagai berikut:
𝐽 0,0,0 =
𝑟 0 0 0 −𝛿 0 0 𝛼 −𝜔
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik 𝑑𝑒𝑡 𝐽 0,0,0 − 𝜆𝐼 = 0
sehingga diperoleh 𝑟 − 𝜆 0 0 0 −𝛿 − 𝜆 0 0 𝛼 −𝜔 − 𝜆 = 0 𝑟 − 𝜆 −𝛿 − 𝜆 −𝜔 − 𝜆 = 0
Jadi nilai eigennya adalah sebagai berikut:
𝜆1= 𝑟 𝜆2= −𝛿 𝜆3= −𝜔
Pelinearan titik tetap 𝑇2 𝐾, 0,0 akan diperoleh matriks Jacobi sebagai berikut:
𝐽 𝐾,0,0 =
−𝑟𝜀 −𝑟𝜀 − 𝐾𝜌 −𝑘𝐾 0 −𝛿 𝑘𝐾 0 𝛼 −𝑘𝐾 − 𝜔
23
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik 𝑑𝑒𝑡 𝐽 𝐾,0,0 − 𝜆𝐼 = 0
sehingga diperoleh −𝑟𝜀 − 𝜆 −𝑟𝜀 − 𝐾𝜌 −𝑘𝐾 0 −𝛿 − 𝜆 𝑘𝐾 0 𝛼 −𝑘𝐾 − 𝜔 − 𝜆 = 0 −𝑟𝜀 − 𝜆 −𝛿 − 𝜆 −𝑘𝐾 − 𝜔 − 𝜆 + 0 + 0 − 0 + −𝑟𝜀 − 𝜆 𝑘𝐾 𝛼 + 0 = 0 ↔ −𝑟𝜀 − 𝜆 −𝛿 − 𝜆 −𝑘𝐾 − 𝜔 − 𝜆 − −𝑟𝜀 − 𝜆 𝑘𝐾 𝛼 = 0 ↔ −𝑟𝜀 − 𝜆 −𝛿 − 𝜆 −𝑘𝐾 − 𝜔 − 𝜆 − 𝑘𝐾 𝛼 = 0 ↔ −𝑟𝜀 − 𝜆 𝜆2+ 𝑘𝐾 + 𝛿 + 𝜔 𝜆 + 𝛼 − 𝛿 𝑘𝐾 + 𝛿𝜔 = 0
Jadi nilai eigennya adalah sebagai berikut:
𝜆1= −𝑟𝜀 𝜆2=−𝑝 + 𝑝 2− 4𝑞 2 𝜆3= −𝑝 − 𝑝2− 4𝑞 2 Dengan 𝑝 = 𝑘𝐾 + 𝛿 + 𝜔 𝑞 = 𝛿 − 𝛼 𝑘𝐾 + 𝛿𝜔
Pelinearan titik tetap 𝑇3 𝑦∗, 𝑥∗, 𝑣∗ dengan mensubstitusikan nilai parameter untuk simulasi
(untuk memudahkan) yaitu: 𝑟 = 0.106, 𝐾 = 1000, 𝜀 = 1.00, 𝑘 = 0.01, 𝜌 = 0.215, 𝛿 = 0.511, 𝛼 = 1.3, dan 𝜔 = 0.3, maka akan diperoleh matriks Jacobi sebagai berikut:
𝐽 𝑦∗,𝑥∗,𝑣∗ =
0.007916 −4.1795 −0.1943 0.0113 −0.511 0.1943 −0.0113 1.3 −0.4943
Jadi nilai eigennya adalah sebagai berikut:
Eigenvalues[{{0.007916,-4.1795,-0.1943},{0.0113,-0.511,0.1943},{-0.0113,1.3,-0.4943}}]
24
Lampiran 3 Penentuan titik tetap model pertumbuhan tumor dengan radiovirotherapy.
Titik tetap akan diperoleh dengan menetapkan 𝑟𝑦 1 − 𝑥+𝑦+𝑢 𝐾 𝜀 − 𝑘𝑦𝑣 − 𝛽𝐷𝑦 = 0 (i) 𝑘𝑦𝑣 − 𝛿𝑥 − 𝛽𝐷𝑥 = 0 (ii) 𝛽𝐷 𝑥 + 𝑦 − 𝛾𝑢𝑣= 0 (iii) 𝛼𝑥 − 𝜔𝑣 = 0 (iv)
Dari persamaan (i) akan diperoleh nilai 𝑦 sebagai berikut:
𝑟𝑦 1 − 𝑦 + 𝑥 + 𝑢 𝐾 𝜀 − 𝑘𝑦𝑣 + 𝛽𝐷𝑦 = 0 ↔ 𝑟𝑦 1 − 𝑦 + 𝑥 + 𝑢 𝐾 𝜀 − 𝑦 𝑘𝑣 + 𝛽𝐷 = 0 ↔ 𝑦 𝑟 1 − 𝑦 + 𝑥 + 𝑢 𝐾 𝜀 − 𝑘𝑣 + 𝛽𝐷 = 0 ↔ 𝑦 = 0 ∩ 𝑟 1 − 𝑦 + 𝑥 + 𝑢 𝐾 𝜀 = 𝑘𝑣 + 𝛽𝐷 ↔ 𝑦 = 0 ∩ 1 − 𝑦 + 𝑥 + 𝑢 𝐾 𝜀 =(𝑘𝑣 + 𝛽𝐷) 𝑟 ↔ 𝑦 = 0 ∩ 𝑦 + 𝑥 + 𝑢 𝐾 𝜀 =𝑟 − 𝑘𝑣 − 𝛽𝐷 𝑟 ↔ 𝑦 = 0 ∩ ln 𝑦 + 𝑥 + 𝑢 𝐾 = ln 𝑟 − 𝑘𝑣 − 𝛽𝐷𝑟 𝜀 ↔ 𝑦 = 0 ∩𝑦 + 𝑥 + 𝑢 𝐾 = 𝐸𝑥𝑝 ln 𝑟 − 𝑘𝑣 − 𝛽𝐷𝑟 𝜀 ↔ 𝑦 = 0 ∩ 𝑦 = 𝐸𝑥𝑝 ln 𝑟 − 𝑘𝑣 − 𝛽𝐷𝑟 𝜀 𝐾 − 𝑥 + 𝑢
Dari persamaan (ii) akan diperoleh nilai 𝑥 sebagai berikut:
𝑘𝑦𝑣 − 𝛿𝑥 − 𝛽𝐷𝑥 = 0 ↔ 𝑥 𝛿 + 𝛽𝐷 = 𝑘𝑦𝑣
↔ 𝑥 = 𝑘𝑦𝑣 𝛿 + 𝛽𝐷
Dari persamaan (iii) akan diperoleh nilai u sebagai berikut:
𝛽𝐷 𝑥 + 𝑦 − 𝛾𝑢𝑣= 0 ↔ 𝛾𝑢𝑣= 𝛽𝐷 𝑥 + 𝑦
25
↔ 𝑢𝑣=𝛽𝐷 𝑥 + 𝑦 𝛾
Dari persamaan (iv) akan diperoleh nilai 𝑣 sebagai berikut:
𝛼𝑥 − 𝜔𝑣 = 0 ↔ 𝑣 =𝛼𝑥 𝜔 Substitusi 𝑦 = 0 ke persamaan 𝑥 = 𝑘𝑦𝑣 𝛿+𝛽𝐷 , maka diperoleh 𝑥1= 0. Substitusi 𝑥 = 0 ke persamaan 𝑣 =𝛼𝑥 𝜔 , maka diperoleh 𝑣1= 0.
Substitusi 𝑥1= 0 dan 𝑣1= 0 ke persamaan 𝑢𝑣= 𝛽𝐷 𝑥 +𝑦 𝛾 , maka diperoleh: 𝑢0=𝛽𝐷 𝑥 + 𝑦 𝛾 ↔ 𝛾 = 𝛽𝐷 𝑥 + 𝑦 ↔ 𝑦 + 𝑥1= 𝛾 𝛽𝐷 Karena 𝑥1= 0, maka 𝑦1= 𝛾 𝛽𝐷 Substitusi 𝑥1= 0, 𝑣1= 0, dan 𝑦1= 𝛾 𝛽𝐷 ke persamaan 𝑦 = 𝐸𝑥𝑝 ln 𝑟−𝑘𝑣−𝛽𝐷𝑟 𝜀 𝐾 − 𝑥 + 𝑢 , maka diperoleh: 𝛾 𝛽𝐷= 𝐸𝑥𝑝 ln 𝑟 − 𝑘 0 − 𝛽𝐷𝑟 𝜀 𝐾 − 0 + 𝑢 ↔ 𝑢 = 𝐸𝑥𝑝 ln 𝑟 − 𝑘 0 − 𝛽𝐷𝑟 𝜀 𝐾 − 𝛾 𝛽𝐷 ↔ 𝑢1= 𝑒𝑥𝑝 ln 𝑟 − 𝛽𝐷𝑟 𝜀 𝐾𝛽𝐷 − 𝛾 𝛽𝐷
Sehingga diperoleh titik tetap 𝑻𝟏 𝒚𝟏, 𝒙𝟏, 𝒖𝟏, 𝒗𝟏 .
Untuk mendapatkan titik tetap 𝑻𝟐 𝒚𝟐, 𝒙𝟐, 𝒖𝟐, 𝒗𝟐 dilakukan dengan perhitungan menggunakan Maple 13 dengan kode sebagai berikut:
26
Lampiran 4 Penentuan nilai eigen dari persamaan (5), (6), (7), dan (8).
Misalkan persamaan (5), (6), (7), dan (8) dituliskan sebagai berikut:
𝐴 𝑦, 𝑥, 𝑢, 𝑣 = 𝑟𝑦 1 − 𝑥+𝑦+𝑢 𝐾 𝜀 − 𝑘𝑦𝑣 − 𝛽𝐷𝑦 𝐵 𝑦, 𝑥, 𝑢, 𝑣 = 𝑘𝑦𝑣 − 𝛿𝑥 − 𝛽𝐷𝑥 𝐶 𝑦, 𝑥, 𝑢, 𝑣 = 𝛽𝐷 𝑥 + 𝑦 − 𝛾𝑢𝑣 𝐷 𝑦, 𝑥, 𝑢, 𝑣 = 𝛼𝑥 − 𝜔𝑣
Dengan melakukan pelinearan didapat matriks Jacobi sebagai berikut:
𝐽 = 𝐴𝑦 𝐵𝑦 𝐶𝑦 𝐷𝑦 𝐴𝑥 𝐵𝑥 𝐶𝑥 𝐷𝑥 𝐴𝑢 𝐵𝑢 𝐶𝑢 𝐷𝑢 𝐴𝑣 𝐵𝑣 𝐶𝑣 𝐷𝑣
Pelinearan titik tetap 𝑇1 𝑦1, 𝑥1, 𝑢1, 𝑣1 akan diperoleh matriks Jacobi sebagai berikut:
(dengan memisalkan 𝜀 = 1 untuk memudahkan)
𝐽 𝑦1,𝑥1,𝑢1,𝑣1 = − 𝑟𝛾 𝐾𝛽𝐷 0 𝛽𝐷 0 − 𝑟𝛾 𝐾𝛽𝐷 −𝛿 − 𝛽𝐷 𝛽𝐷 𝛼 − 𝑟𝛾 𝐾𝛽𝐷 0 0 0 −𝑘𝛾 𝛽𝐷 𝑘𝛾 𝛽𝐷 −𝛾𝐷 −𝜔
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik 𝑑𝑒𝑡 𝐽 𝑦1,𝑥1,𝑢1,𝑣1 −
27 𝜆1,2= −𝑟𝛾 ± 𝑟2𝛾2− 4𝐾𝛽2𝐷2𝑟𝛾 2𝑘𝛽𝐷 𝜆3,4= −𝑍 ± 𝑍2− 4𝛽𝐷𝑄 2𝛽𝐷 dengan 𝑍 = 𝛽2𝐷2+ 𝛽𝐷𝛿 + 𝛽𝐷𝜔 𝑄 = −𝑘𝛼𝛾 + 𝛽2𝐷2𝜔 + 𝛽𝐷𝛿𝜔
(Berapapun nilai parameter yang diberikan, nilai eigen tetap kurang dari nol)
Pelinearan titik tetap 𝑇2 𝑦2, 𝑥2, 𝑢2, 𝑣2 dengan mensubstitusikan nilai parameter untuk
simulasi (untuk memudahkan) yaitu: 𝑟 = 0.106, 𝐾 = 1000, 𝜀 = 1.00, 𝑘 = 0.01, 𝛿 = 0.511,
𝛼 = 1.3𝛽 = 0.215, 𝐷 = 0.07, 𝛾 = 18.57, dan 𝜔 = 0.3., maka akan diperoleh matriks Jacobi sebagai berikut: 𝐽 𝑦2,𝑥2,𝑢2,𝑣2 = −0.001286 0.08938 0.01505 0 −0.001286 −0.52605 0.01505 1.3 −0.001286 0 −0.1573 0 −0.1214 0.1214 0.1067 −0.3
Jadi nilai eigennya adalah sebagai berikut:
Eigenvalues[{{-0.001286,-0.001286,-0.001286,- 0.1214},{0.08938,-0.52605,0,0.1214},{0.01505,0.01505,-0.1573,0.1067},{0,1.3,0,-0.3}}]
{-0.84569,-0.157762,-0.00940817 +0.129254 ,-0.00940817 -0.129254 }
28
Lampiran 5 Kode Mathematica 7 untuk Gambar 3. fajar[r_,K_,_]:=NDSolve[
{y'[t]ry[t](1-(y[t]/K)),y[0]107.900},y[t],{t,0,40}] tes1=fajar[0.106,1000,2];
tes2=fajar[0.206,1000,2]; tes3=fajar[0.306,1000,2];
a=Plot[y[t]/.tes1,{t,0,40},PlotStyle{Blue,Thick},FrameTrue, FrameLabel{"Waktu(hari)","Populasi Tumor(mm3)"}];
b=Plot[y[t]/.tes2,{t,0,40},PlotStyle{Green,Thick},FrameTrue, FrameLabel{"Waktu(hari)","Populasi Tumor(mm3)"}];
c=Plot[y[t]/.tes3,{t,0,40},PlotStyle{Red,Thick},FrameTrue, FrameLabel{"Waktu(hari)","Populasi Tumor(mm3)"}];
Show[a,b,c]
tes4=fajar[0.206,1000,1]; tes5=fajar[0.206,1000,2]; tes6=fajar[0.206,1000,3];
d=Plot[y[t]/.tes4,{t,0,40},PlotStyle{Blue,Thick},FrameTrue, FrameLabel{"Waktu(hari)","Populasi Tumor(mm3)"}];
e=Plot[y[t]/.tes5,{t,0,40},PlotStyle{Green,Thick},FrameTrue, FrameLabel{"Waktu(hari)","Populasi Tumor(mm3)"}];
f=Plot[y[t]/.tes6,{t,0,40},PlotStyle{Red,Thick},FrameTrue, FrameLabel{"Waktu(hari)","Populasi Tumor(mm3)"}];
29
Lampiran 6 Kode Maple 13 untuk Gambar 4.
30
32
33
34
35
36
37