Model Matematika distribusi obat pada penyakit infeksi saluran kemih

(1)

MODEL MATEMATIKA

DISTRIBUSI OBAT PADA PENYAKIT INFEKSI SALURAN KEMIH

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Oleh:

Totok Victor Didik Saputro NIM: 131414092

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(2)

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Oleh:

Totok Victor Didik Saputro NIM: 131414092

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(3)

SKRIPSI

(4)

SKRIPSI

(5)

HALAMAN PERSEMBAHAN

“

Do the Best and Be the Best

… Yes”

~ HMJ PMIPA 2013/2014 ~

“ Keep Smile and Spirit, Let’s Do It

”

~ HMJ PMIPA 2014/2015 ~

“

Siapa Kita? Driyarkara Muda, Driyarkara Muda,

Cerdas dan Humanis Pasti Bisa

”

~ BEMU 2015/2016 ~

Skripsi ini kupersembahkan untuk:

Tuhan Yesus yang senantiasa menyertai langkahku

Ayahku Marsidi dan Ibuku Maria Rais

Mbakku Denok Vivi Angelina

Semua keluargaku

Partner terbaikku Patricia Laras Hernawati

(6)

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 18 Juli 2017 Penulis,

(7)

ABSTRAK

Model matematika diartikan sebagai suatu bentuk representasi matematis dari suatu masalah. Pembentukan model matematika distribusi obat penyakit Infeksi Saluran Kemih (ISK) menggunakan model kompartemen. Model kompartemen merupakan model matematika yang mengestimasi jumlah obat dalam berbagai kompartemen setelah obat dimasukkan ke dalam suatu kompartemen tertentu.

Penelitian ini bertujuan untuk membuat model matematika dan analisis matematika untuk penyembuhan penyakit ISK. Penelitian ini menggunakan metode studi pustaka. Langkah-langkah dalam membentuk model matematika distribusi obat penyakit ISK adalah: 1) Menentukan asumsi-asumsi; 2) Membuat diagram pemberian obat; 3) Membentuk persamaan dari diagram yang dibuat; 4) Membentuk model matematika.

Berdasarkan asumsi-asumsi, dibentuk model matematika distribusi obat penyakit ISK dari tiga kasus yang berbeda. Model matematika yang diperoleh adalah: 1) Kasus I: Pemberian obat melalui oral dan obat dari lambung langsung masuk ke darah adalah � = − � dan ��= � − � ; 2) Kasus II: Pemberian obat melalui oral, sebagian obat dari lambung masuk ke usus dan sebagian masuk ke darah adalah � = − � − � − � − � dan

��₌ _{� −} _� _{; 3) Kasus III: Pemberian obat melalui intravena adalah}

��_{= −} _� _.

Penyembuhan penyakit infeksi saluran kemih menggunakan simulasi model. Penyembuhan ini dilakukan dengan memberikan antibiotik dengan jenis tetrasiklin sebanyak 3 kali sehari selama 8 hari. Bakteri akan berkurang bahkan mati ketika antibiotik jenis tetrasiklin ini diberikan secara teratur dan manusia dikatakan sembuh dari penyakit infeksi saluran kemih.

(8)

ABSTRACT

Mathematical model is interpreted as a form of mathematical representation from a problem. The formation of mathematical model of drug distribution of Urinary Tract Infection (UTI) disease uses compartment model. Compartment model is a mathematical model that estimates drug amount in various compartments after the drug is inserted into a certain compartment. This research aims to form a mathematical model and mathematical analysis for healing of UTI disease. This research uses literature review method. The phases to form the mathematical model of drug distribution of UTI disease are: 1) Determining the assumptions; 2) Making a drug giving diagram; 3) Establishing the equation of the created diagram; 4) Establishing the mathematical model.

Based on the assumptions, the mathematical model of drug distribution of UTI disease is formed from three different cases. The mathematical model that is obtained are: 1) Case I: The drug giving through oral and the drug from stomach

goes straight into blood are � = − � and �� = � − � ; 2) Case II: The drug giving through oral, some drugs from stomach go into the intestine and some go into the blood are � = − � − � − � − � and ��=

� − � ; 3) Case III: The drug giving through intervena is �� = − � . Healing of urinary tract infection disease used model simulation. This healing can be done with tetracycline antibiotic 3 times daily for 8 days. Bacteria will be reduced even die when tetracycline antibiotic given regularly and humans are said to be cured of urinary tract infection.

(9)

LEMBAR PERNYATAAN PERSETUJUAN

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS

Yang bertandatangan di bawah ini, saya mahasiswa Universitas Sanata Dharma dengan:

Nama : Totok Victor Didik Saputro NIM : 131414092

Dengan pengembangan ilmu pengetahuan, saya memberikan karya ilmiah saya kepada Perpustakaan Universitas Sanata Dharma dengan judul:

DISTRIBUSI OBAT PADA PENYAKIT INFEKSI SALURAN KEMIH Beserta perangkat yang diperlukan, bila ada. Dengan demikian, saya memberikan hak untuk menyimpan, mengalihkan ke dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikannya secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu meminta izin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis kepada Perpustakaan Universitas Sanata Dharma. Demikian pernyataan ini saya buat dengan sebenarnya.

Dibuat di Yogyakarta Pada tanggal 18 Juli 2017 Yang menyatakan,

(10)

KATA PENGANTAR

Puji dan syukur penulis haturkan kepada Tuhan Yang Maha Esa, karena berkat dan rahmat-Nya penulis dapat menyelesaikan skripsi ini. Skripsi ini disusun sebagai syarat memperoleh gelar sarjana Pendidikan Matematika.

Penyusunan skripsi ini mendapatkan banyak bantuan dan dukungan dari berbagai pihak. Oleh karena itu, penulis mengucapkan terima kasih kepada pihak-pihak yang telah membantu dan mendukung penyusunan skripsi ini, antara lain adalah sebagai berikut:

1. Bapak Rohandi, Ph. D., selaku Dekan Fakultas Keguruan dan Ilmu Pendidikan.

2. Bapak Dr. M. Andy Rudhito, S. Pd., selaku Ketua Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam.

3. Bapak Dr. Hongki Julie, M. Si., selaku Ketua Program Studi Pendidikan Matematika.

4. Bapak Beni Utomo, M. Sc., selaku dosen pembimbing yang telah membimbing dengan penuh kesabaran, meluangkan waktu, dan pikiran selama proses penyusunan skripsi ini.

5. Ibu Dra. Haniek Sri Pratini, M. Pd., selaku dosen pembimbing akademik yang telah mendampingi dari awal perkuliahan sampai penyusunan skripsi ini.

(11)

7. dr. FX. Budiman sebagai pakar dalam bidang kesehatan yang membantu penyusunan skripsi ini.

8. Ibu Wahyuning Setyani, M. Sc., Apt. sebagai pakar dalam bidang farmasi yang membantu penyusunan skripsi ini.

9. Ibu Ch. Retno Herrani Setyati, M. Biotech sebagai pakar dalam bidang biologi yang membantu menjelaskan mengenai bakteri penyebab terjadinya Infeksi Saluran Kemih.

10.Kedua orangtua saya, Marsidi dan Maria Rais yang dengan sabar membimbing, mendukung, dan memberikan segala cinta kasih dalam kehidupan saya.

11.Kakak saya Denok Vivi Angelina yang selalu mengingatkan dan memberi semangat untuk menyelesaikan skripsi ini.

12.Partner terbaik saya, Patricia Laras Hernawati yang selalu mengingatkan, memberi semangat, dan menghibur ketika sedang jenuh dalam proses menyelesaikan skripsi ini.

13.Yovan Mas Agustias selaku sahabat sekaligus pakar tambahan dalam bidang kesehatan yang membantu penyelesaian skripsi ini.

(12)

15.Sahabat-sahabat saya yang bergabung dalam grup Cah Embuh: Adhi, Cicil, Egi, Ocha, Sepnu, dan Yuse, yang telah berbagi pengalaman selama proses perkuliahan ini.

16.Teman-teman mahasiswa Pendidikan Matematika angkatan 2013 yang telah bersama-sama memulai perjuangan di program studi ini, berbagi pengalaman, ilmu, pengetahuan, dan memberikan semangat sampai penyusunan skripsi ini.

17.Semua pihak yang tidak dapat disebutkan satu per satu dan terlibat dalam proses penyusunan skripsi ini.

18.Universitas Sanata Dharma yang memberikan ruang dan kesempatan untuk menempuh ilmu.

Penulis menyadari bahwa masih banyak kekurangan dalam penyusunan skripsi ini. Oleh karena itu, penulis mengharapkan kritik dan saran dari pembaca untuk menyempurnakan skripsi ini. Semoga skripsi ini berguna bagi para pembaca dan penelitian selanjutnya.

Yogyakarta, 18 Juli 2017

(13)

DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

ABSTRAK ... vi

ABSTRACT ... vii

LEMBAR PERNYATAAN PERSETUJUAN ... viii

KATA PENGANTAR ... ix

DAFTAR ISI ... xii

DAFTAR TABEL ... xiv

DAFTAR GAMBAR ... xv

BAB I PENDAHULUAN ... 1

A. LATAR BELAKANG MASALAH ... 1

B. RUMUSAN MASALAH ... 4

C. PEMBATASAN MASALAH ... 4

D. TUJUAN PENELITIAN ... 5

E. MANFAAT PENELITIAN ... 5

F. SISTEMATIKA PENULISAN ... 5

(14)

A. MODEL MATEMATIKA... 7

B. PERSAMAAN DIFERENSIAL ... 10

C. JALUR PEMBERIAN OBAT ... 14

D. INFEKSI SALURAN KEMIH ... 18

BAB III MODEL MATEMATIKA DISTRIBUSI OBAT PADA PENYAKIT INFEKSI SALURAN KEMIH ... 23

A. MODEL MATEMATIKA DISTRIBUSI OBAT PADA PENYAKIT INFEKSI SALURAN KEMIH ... 23

B. FORMULASI MODEL PEMBERIAN OBAT ... 27

C. FORMULASI MODEL PERTUMBUHAN BAKTERI E. COLI ... 55

BAB IV SIMULASI MODEL MATEMATIKA DISTRIBUSI OBAT PADA PENYAKIT INFEKSI SALURAN KEMIH ... 61

A. SIMULASI MODEL ... 61

B. PROSES PENYEMBUHAN ... 66

BAB V PENUTUP ... 68

A. KESIMPULAN ... 68

B. SARAN... 69

DAFTAR PUSTAKA ... 70

(15)

DAFTAR TABEL

Tabel 2.1 Contoh Persamaan Diferensial Linear dan Tak-Linear ... 11

Tabel 3.1 Daftar Variabel untuk Pemberian Obat melalui Oral ... 24

Tabel 3.2 Daftar Parameter untuk Pemberian Obat melalui Oral ... 24

Tabel 3.3 Daftar Variabel untuk Pemberian Obat melalui Intravena ... 25

Tabel 3.4 Daftar Parameter untuk Pemberian Obat melalui Intravena ... 25

Tabel 4.1 Nilai Variabel dan Parameter untuk Kasus I... 61

Tabel 4.2 Nilai Variabel dan Parameter untuk Kasus II ... 63

(16)

DAFTAR GAMBAR

Gambar 2.1 Diagram Model Kompartemen Pemberian Obat melalui Oral ... 7

Gambar 2.2 Diagram Model Kompartemen Pemberian Obat melalui Intravena 9 Gambar 2.3 Tubuh Manusia untuk Pemberian Obat melalui Intravena ... 15

Gambar 2.4 Obat yang masuk ke darah setelah disuntikan ... 15

Gambar 2.5 Obat yang masuk ke seluruh tubuh ... 16

Gambar 2.6 Tubuh Manusia untuk Pemberian Obat melalui Oral ... 16

Gambar 2.7 Obat dalam Lambung ... 17

Gambar 2.8 Obat dalam Darah ... 17

Gambar 2.9 Obat dalam Usus ... 17

Gambar 2.10 Tempat Terjadinya ISK ... 20

Gambar 3.1 Diagram Pemberian Obat melalui Oral ... 26

Gambar 3.2 Diagram Pemberian Obat melalui Intravena ... 27

Gambar 3.3 Diagram Kompartemen I untuk Kasus I ... 28

Gambar 3.4 Grafik Penyelesaian Kompartemen I untu Kasus I ... 30

Gambar 3.5 Diagram Kompartemen II untuk Kasus I ... 31

Gambar 3.6 Grafik Penyelesaian Kompartemen II untuk Kasus I ... 34

Gambar 3.7 Grafik Penyelesaian Pemberian Obat 8 jam sekali Kasus I ... 35

Gambar 3.8 Diagram Kompartemen I untuk Kasus II ... 37

Gambar 3.9 Grafik Penyelesaian Kompartemen I untuk Kasus II ... 41

Gambar 3.10 Diagram Kompartemen II untuk Kasus II ... 42

Gambar 3.11 Grafik Penyelesaian Kompartemen II untuk Kasus II ... 50

(17)

Gambar 3.13 Diagram Pemberian Obat untuk Kasus III ... 52

Gambar 3.14 Grafik Penyelesaian untuk Kasus III... 54

Gambar 3.15 Grafik Penyelesaian Pemberian Obat 8 jam sekali Kasus III ... 55

Gambar 3.16 Grafik Penyelesaian Pertumbuhan Bakteri ... 57

Gambar 4.1 Grafik Penyelesaian Kasus I ... 62

Gambar 4.2 Grafik Penyelesaian Kasus II ... 64

Gambar 4.3 Grafik Penyelesaian Kasus III ... 65

(18)

BAB I PENDAHULUAN

A. LATAR BELAKANG MASALAH

(19)

dengan proses matematisasi. Matematisasi dibagi menjadi dua hal, yaitu matematisasi vertikal dan matematisasi horisontal. Matematisasi vertikal membawa pemikiran seseorang dari dunia simbol yang tingkatnya sederhana ke dunia simbol yang tingkatannya lebih kompleks, sedangkan matematisasi horisontal membawa pemikiran seseorang dari dunia kehidupan sehari-hari ke dunia simbol-simbol. Inti dari kedua proses matematisasi ini adalah membuat model matematika dari permasalahan yang dihadapi dalam kehidupan sehari-hari (Gravemeijer, 1994).

Model matematika diartikan sebagai suatu bentuk representasi matematis dari suatu masalah. Penyusunan model matematika dimulai dengan membuat asumsi-asumsi yang berkaitan dengan permasalahan. Asumsi ini merupakan pernyataan-pernyataan yang mendukung permasalahan. Asumsi juga menjadi salah satu dasar untuk melakukan langkah selanjutnya dalam membuat pemodelan matematika dan menyelesaikan permasalahan tersebut.

(20)

bawah merupakan infeksi yang terjadi pada uretra dan kandung kemih. Gejala dari kondisi ini meliputi rasa ingin selalu buang air kecil, nyeri atau perih saat buang air kecil, warna urine yang keruh, dan bau urine yang tidak sedap (Novi Praktika, 2009). ISK ini disebabkan oleh bakteri Escherichia Coli atau E. Coli yang umumnya hidup di dalam saluran pencernaan. Bakteri ini dapat masuk ke dalam saluran uretra seseorang ketika kurang baik dalam melakukan pembersihan setelah buang air besar maupun kecil. ISK juga bisa disebabkan oleh iritasi setelah berhubungan seksual dan akibat terganggunya kinerja pengosongan urine oleh kondisi tertentu.

(21)

darah. Pada model dua kompartemen, obat terdistribusi ke dalam dua kompartemen. Kompartemen pertama disebut kompartemen sentral. Kompartemen sentral meliputi darah, cairan ekstraseluler, dan jaringan-jaringan dengan perfusi tinggi. Kompartemen dua merupakan kompartemen perifer. Terdapat jaringan-jaringan yang berkesetimbangan dalam kompartemen ini. Obat yang didistribusikan ke seluruh tubuh masuk ke dalam darah dengan jumlah obat dalam darah dan laju serap obat yang meninggalkan darah menuju organ tubuh lainnya.

Tugas akhir ini membahas mengenai model matematika distribusi obat pada penyakit infeksi saluran kemih dan analisis penyembuhan penyakit infeksi saluran kemih. Metode yang digunakan dalam penyusunan tugas akhir ini adalah metode studi pustaka.

B. RUMUSAN MASALAH

Rumusan masalah dalam penelitian ini adalah:

1. Bagaimana memformulasikan model matematika distribusi obat pada penyakit infeksi saluran kemih?

2. Bagaimana analisis matematika untuk penyembuhan penyakit infeksi saluran kemih?

C. PEMBATASAN MASALAH

(22)

membahas mengenai model matematika distribusi obat pada penyakit infeksi saluran kemih. Model matematika yang sesuai dengan asumsi-asumsi yang dibuat pada penelitian ini adalah model kompartemen.

D. TUJUAN PENELITIAN Tujuan penelitian ini adalah:

1. Membuat model matematika distribusi obat pada penyakit infeksi saluran kemih.

2. Membuat analisis matematika untuk penyembuhan penyakit infeksi saluran kemih.

E. MANFAAT PENELITIAN

Manfaat yang diperoleh dari penelitian ini adalah memberikan sumbangan ilmu berupa materi yang bisa digunakan untuk pembelajaran pemodelan matematika.

F. SISTEMATIKA PENULISAN

Sistematika penulisan ini adalah sebagai berikut:

BAB I PENDAHULUAN

(23)

BAB II LANDASAN TEORI

Pada Bab II akan membahas mengenai teori-teori yang akan digunakan dalam membuat model matematika distribusi obat pada penyakit infeksi saluran kemih. Adapun teori yang digunakan adalah teori mengenai model kompartemen, persamaan diferensial, jalur pemberian obat dan infeksi saluran kemih.

BAB III MODEL MATEMATIKA DISTRIBUSI OBAT PADA PENYAKIT INFEKSI SALURAN KEMIH

Pada Bab III akan membahas mengenai model matematika distribusi obat pada penyakit infeksi saluran kemih.

BAB IV SIMULASI MODEL MATEMATIKA DISTRIBUSI OBAT PADA PENYAKIT INFEKSI SALURAN KEMIH Pada Bab IV akan membahas mengenai simulasi model matematika distribusi obat pada penyakit infeksi saluran kemih.

BAB V PENUTUP

(24)

BAB II

LANDASAN TEORI

A. MODEL MATEMATIKA

Pemodelan matematika merupakan usaha perancangan rumusan matematika yang secara potensial menggambarkan bagaimana mendapatkan penyelesaian masalah matematika yang digeneralisasikan untuk diterapkan pada perilaku atau kejadian alam (Ripno Juli, 2012). Pembentukan model matematika distribusi obat penyakit infeksi saluran kemih berkaitan dengan ilmu dalam bidang farmasi, yaitu farmakokinetik. Farmakokinetik adalah bagian dari ilmu farmakologi yang khusus mempelajari perubahan konsentrasi obat dan metabolitnya di dalam darah dan jaringan sebagai fungsi dari waktu sebagai hasil dari proses yang dilakukan tubuh terhadap obat (Wiwin, 2016). Menurut Teorell, tujuan farmakokinetik adalah untuk menurunkan persamaan matematika yang menerangkan kinetika dan pendistribusian obat ke dalam tubuh. Secara farmakokinetik, dibuatlah model-model yang dapat melihat tubuh sebagai kompartemen. Obat yang diberikan melalui oral, kompartemen pertama terjadi di lambung dan kompartemen kedua terjadi di darah (Belinda Barnes, 2002). Gambar 2.1 menunjukkan diagram model kompartemen untuk pemberian obat melalui oral.

Gambar 2.1 Diagram Model Kompartemen untuk Pemberian Obat Melalui Oral Darah

Lambung

Obat Masuk Pencernaan

(25)

Berdasarkan Gambar 2.1, dapat dibentuk satu persamaan dari masing-masing kompartemen yang terjadi. Laju perubahan obat di dalam lambung dapat dinyatakan dengan

{ ℎ } = {

} − { }

Laju perubahan obat di dalam darah dapat dinyatakan dengan

{ ℎ

ℎ } = { ℎ} − { ℎ }

Misalkan merupakan jumlah obat dalam lambung pada waktu dan merupakan jumlah obat dalam darah pada waktu . Jika diasumsikan pemberian obat hanya dilakukan satu kali, maka laju perubahan obat di dalam lambung adalah sebagai berikut:

= − , = .

dengan adalah jumlah obat dalam kondisi awal, dan > merupakan konstanta laju serap obat dari lambung menuju darah. Jumlah obat dalam darah untuk kondisi awal adalah nol. Jadi, laju perubahan obat di dalam darah adalah sebagai berikut:

= − , = .

(26)

Pada pemberian obat melalui intravena kompartemen hanya terjadi di darah. Obat yang diberikan langsung masuk ke dalam darah dan dengan segera menyebar keseluruh organ tubuh lainnya. Gambar 2.2 menunjukkan diagram model kompartemen untuk pemberian obat melalui intravena.

Berdasarkan Gambar 2.2, laju perubahan obat di dalam darah dapat dinyatakan dengan

{ ℎ

ℎ } = { ℎ} − { ℎ }

Misalkan diasumsikan pemberian obat hanya dilakukan satu kali, sehingga laju perubahan obat di dalam darah adalah sebagai berikut:

= − , = .

dengan > merupakan konstanta laju serap obat dari darah menuju organ tubuh lainnya dan adalah jumlah obat dalam kondisi awal.

Pembentukan model matematika distribusi obat penyakit infeksi saluran kemih menggunakan teori persamaan diferensial. Selain itu, teori persamaan diferensial juga digunakan untuk menentukan penyelesaian model matematika yang dibentuk.

Gambar 2.2 Diagram Model Kompartemen untuk Pemberian Obat Melalui Intravena

Darah Obat Masuk

(27)

B. PERSAMAAN DIFERENSIAL

Persamaan diferensial merupakan persamaan yang melibatkan variabel tak bebas dan derivatif-derivatifnya terhadap variabel-variabel bebas (Didit Budi, 2011). Terbentuknya persamaan diferensial sebagai suatu model matematika berasal dari ketertarikan dan keingintahuan seseorang tentang perilaku atau fenomena perubahan sesuatu di dunia nyata (Kartono, 2012). Dengan memperhatikan banyaknya variabel bebas yang terlibat, ada dua bentuk persamaan diferensial, yaitu persamaan diferensial biasa dan persamaan diferensial parsial (Kartono, 2012).

1. Persamaan Diferensial Biasa

Persamaan diferensial biasa merupakan persamaan diferensial yang hanya melibatkan satu variabel bebas.

Contoh:

+ =

2. Persamaan Diferensial Parsial

Persamaan diferensial parsial merupakan persamaan diferensial yang melibatkan dua atau lebih variabel bebas.

Contoh:

� � +

�

(28)

3. Persamaan Diferensial Linear dan Tak-Linear

Suatu persamaan diferensial dikatakan linear jika tidak ada perkalian antara variabel-variabel tak bebas dan derivatif-derivatifnya. Dengan kata lain, semua koefisiennya adalah fungsi dari variabel-variabel bebas (Didit Budi, 2011).

Suatu persamaan diferensial yang tak-linear dalam beberapa variabel tak bebas dikatakan tak-linear dalam variabel tersebut. Suatu persamaan diferensial yang tak-linear dalam himpunan semua variabel tak bebas secara sederhana dikatakan tak-linear (Didit Budi, 2011).

Tabel 2.1 Contoh Persamaan Diferensial Linear dan Tak-Linear No Persamaan Diferensial Linearitas

1. ′′+ ′+ = cos Linear dalam y

Linear dalam v tetapi tak-linear dalam u karena memuat

(29)

4. Persamaan Diferensial Homogen dan Tak-Homogen

Suatu fungsi , dikatakan homogen berderajad n jika

� , � = �� _, _{. Selanjutnya pandang bentuk persamaan}

diferensial biasa orde pertama,

, + , = .

Persamaan diferensial . dikatakan homogen jika , dan , adalah fungsi homogen dan berderajat sama. Apabila , dan , bukan merupakan fungsi homogen, tidak berderajat sama,

dan persamaan , + , ≠ , maka persamaan

diferensial tersebut dikatakan tak-homogen (Kartono, 2012). Contoh:

− = √ +

Penyelesaian:

Persamaan tersebut dapat disajikan dalam bentuk

√ + + − =

, = √ + + dan , = −

Tunjukkan bahwa , dan , merupakan persamaan homogen.

� , � = √ � + � + �

= √� + � + �

(30)

= �√ + + �

= � √ + +

= � ,

dan

� , � = −

= − �

= � −

= � ,

Jadi, terbukti bahwa persamaan tersebut merupakan persamaan homogen berderajad satu.

5. Penyelesaian Persamaan Diferensial Persamaan diferensial orde-n,

� [ , , , … , �_�] =

dengan F sebagai fungsi real yang argumennya , , , … , �_�.

Misalkan f adalah sebuah fungsi real yang didefinisikan dalam domain bilangan real x dan mempunyai turunan ke-n untuk semua x (Said Munzir, 2009). Fungsi f disebut penyelesaian eksplisit dari persamaan diferensial di atas jika fungsi tersebut memenuhi dua syarat berikut:

(31)

terdefinisi untuk setiap x dalam selang < < , dan

�[ , , ′ _{, … ,} � _{] =}

Sebuah relasi , = disebut penyelesaian implisit dari persamaan di atas jika relasi ini mendefinisikan paling sedikit sebuah fungsi f dalam x. Fungsi ini merupakan penyelesaian eksplisit dari persamaan tadi. Kedua penyelesaian di atas, yakni penyelesaian implisit dan eksplisit dari persamaan diferensial biasanya cukup disebut penyelesaian.

C. JALUR PEMBERIAN OBAT

Model matematika distribusi obat pada penyakit Infeksi Saluran Kemih (ISK) biasanya menggunakan dua kasus jalur pemberian obat, yaitu pemberian obat melalui intravena dan pemberian obat melalui oral.

1. Jalur Pemberian Obat melalui Intravena

(32)

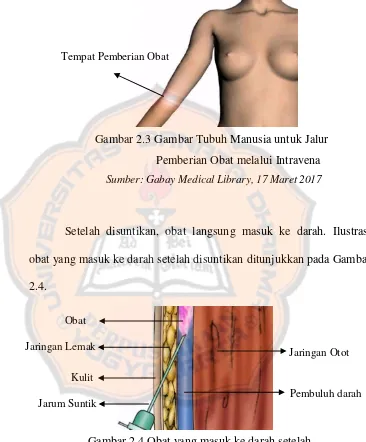
Ilustrasi tempat pemberian obat melalui intravena yang diberikan pada bagian lengan tubuh ditunjukkan pada Gambar 2.3.

Setelah disuntikan, obat langsung masuk ke darah. Ilustrasi obat yang masuk ke darah setelah disuntikan ditunjukkan pada Gambar 2.4.

Setelah masuk ke darah, obat dengan segera tersebar ke seluruh bagian tubuh, termasuk bagian tubuh yang terserang penyakit.

Sumber: Gabay Medical Library, 17 Maret 2017 Gambar 2.3 Gambar Tubuh Manusia untuk Jalur

Pemberian Obat melalui Intravena

Tempat Pemberian Obat

Gambar 2.4 Obat yang masuk ke darah setelah disuntikan

Sumber: Gabay Medical Library, 17 Maret 2017

Jarum Suntik Kulit

Pembuluh darah Jaringan Lemak

Obat

(33)

Ilustrasi obat yang masuk ke seluruh tubuh ditunjukkan pada Gambar 2.5.

2. Jalur Pemberian Obat melalui Oral

Oral merupakan jalur pemberian obat melalui mulut. Jenis obat yang digunakan adalah tetrasiklin. Bentuk obat yang sesuai dengan model matematika dalam penelitian ini adalah kapsul. Ilustrasi pemberian obat melalui oral ditunjukkan pada Gambar 2.6.

Gambar 2.5 Obat yang masuk ke seluruh tubuh Sumber: Gabay Medical Library, 17 Maret 2017

(34)

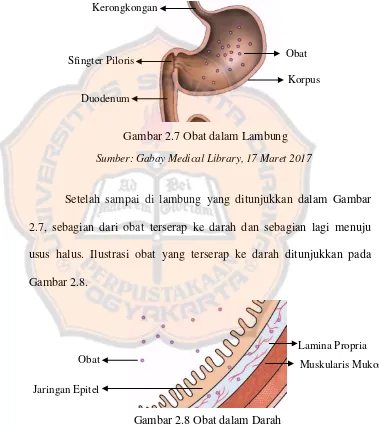
Obat yang diberikan melalui oral masuk melalui mulut dan melewati kerongkongan menuju lambung. Ilustrasi obat dalam lambung ditunjukkan pada Gambar 2.7.

Setelah sampai di lambung yang ditunjukkan dalam Gambar 2.7, sebagian dari obat terserap ke darah dan sebagian lagi menuju usus halus. Ilustrasi obat yang terserap ke darah ditunjukkan pada Gambar 2.8.

Obat yang masuk ke dalam darah akan segera tersebar ke seluruh tubuh dan bagian yang terserang penyakit. Sedangkan, obat

Gambar 2.7 Obat dalam Lambung Sumber: Gabay Medical Library, 17 Maret 2017

Kerongkongan

Obat

Duodenum Sfingter Piloris

Korpus

Gambar 2.8 Obat dalam Darah

Sumber: Gabay Medical Library, 17 Maret 2017

Obat

Jaringan Epitel

(35)

yang masuk ke dalam usus halus sebagian terserap ke dalam darah dan sebagian menuju usus besar. Ketika sampai di usus besar, sebagian obat juga terserap ke dalam darah dan sebagian lagi menuju anus. Ilustrasi obat yang berada dalam usus halus, menuju usus besar, dan di eliminasi melalui anus ditunjukkan pada Gambar 2.9.

D. INFEKSI SALURAN KEMIH

(36)

terjadinya ISK. Bakteri E. Coli dapat menggandakan tubuhnya menjadi dua kali lipat dalam waktu 15 sampai 20 menit (Michael Madigan, 2015). Bakteriuria lebih sering ditemukan pada perempuan. Hal ini karena pendeknya uretra perempuan yang memudahkan mikroorganisme berkolonisasi di perineum dari saluran usus dan genital untuk naik menuju kandung kemih.

Faktor-faktor penyebab terjadinya ISK antara lain kecenderungan menaham urine, iritasi kulit lubang uretra sewaktu berhubungan kelamin, litiasi, dan obstruksi saluran kemih. Selain itu, faktor-faktor lainnya adalah penyakit ginjal polikistik, nekrosis papilar, DM pasca transplantasi ginjal, nefropati analgesik, penyakit Sikle-cell, senggama, kehamilan dan peserta KB dengan tablet progesteron, serta kateterisasi.

(37)

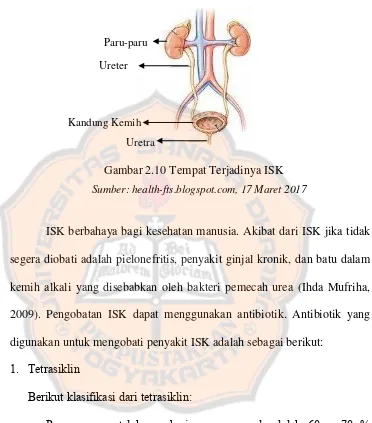
Ilustrasi tempat terjadinya ISK ditunjukkan pada Gambar 2.12.

ISK berbahaya bagi kesehatan manusia. Akibat dari ISK jika tidak segera diobati adalah pielonefritis, penyakit ginjal kronik, dan batu dalam kemih alkali yang disebabkan oleh bakteri pemecah urea (Ihda Mufriha, 2009). Pengobatan ISK dapat menggunakan antibiotik. Antibiotik yang digunakan untuk mengobati penyakit ISK adalah sebagai berikut:

1. Tetrasiklin

Berikut klasifikasi dari tetrasiklin:

a. Penyerapan setelah pemberian secara oral adalah 60 – 70 %

tetrasiklin. Sebagian dari tetrasiklin ini berada di lumen usus,

mengubah flora usus, dan dieksresikan di tinja. Penyerapan

terutama berlangsung di usus halus bagian atas dan terhambat oleh

makanan.

Gambar 2.10 Tempat Terjadinya ISK Sumber: health-fts.blogspot.com, 17 Maret 2017

Paru-paru

Ureter

(38)

b. Tetrasiklin terikat ke protein serum sebanyak 40 – 80 %. Dosis oral

tetrasiklin hidroklorida atau oksitetrasiklin 500 mg setiap 6 jam

menghasilkan kadar darah puncak 4 – 6 mcg/mL.

c. Tetrasiklin yang disuntikan secara intravena memberi kadar yang

sedikit lebih tinggi, tetapi hanya sementara. Kadar puncak 2 – 4

mcg/mL dicapai dengan 200 mg doksisiklin atau monosiklin.

d. Tetrasiklin diekskresikan terutama di empedu dan urine.

Konsentrasi dalam empedu melebihi konsentrasi di serum hingga

sepuluh kali lipat. Sebagian dari obat diekskresikan di empedu

direabsorpsi dari usus (sirkulasi enterohepatik) dan mungkin ikut

serta mempertahankan kadar serum.

e. Sebanyak 10 – 15 % tetrasiklin diekskresikan ke dalam urine,

terutama oleh filtrasi glomerulus. Sebanyak 10 – 40 % obat

diekskresikan di feses.

f. Dosis oral untuk tetrasiklin yang cepat diekskresikan, yang

ekivalen dengan tetrasiklin hidroklorida adalah 0,25 – 0,5 g empat

kali sehari untuk dewasa dan 20 – 40 mg/kg/hari untuk anak (usia 8

tahun atau lebih).

g. Tersedia beberapa tetrasiklin untuk pemberian secara intravena

dalam dosis 0,1 – 0,5 g setiap 6 – 12 jam (serupa dengan dosis

(39)

2. Kloramfenikol

Berikut klasifikasi dari kloramfenikol:

a. Dosis lazim kloramfenikol adalah 50 – 100 mg/kg/hari. Setelah

pemberian oral, kristal kloramfenikol cepat dan tuntas diserap.

b. Dosis oral 1 g menghasilkan kadar darah antara 10 dan 15

mcg/mL.

c. Formulasi parenteral adalah suatu prodrug, kloramfenikol suksinat,

yang terhidrolisis untuk menghasilkan kloramfenikol bebas dengan

kadar darah agak lebih rendah dibandingkan yang dicapai pada

pemberian oral.

d. Kloramfenikol tersebar luas di hampir semua jaringan dan cairan

tubuh, termasuk susunan saraf pusat dan cairan serebrospinal,

sedemikian sehingga konsentrasi kloramfenikol di jaringan otak

mungkin setara dengan konsentrasi di serum. Obat ini mudah

menembus membran sel.

e. Kloramfenikol aktif (sekitar 10 % dari total dosis yang diberikan)

dan produk penguraiannya yang inaktif (sekitar 90 % dari total)

dieliminasi di urine.

f. Sejumlah kecil obat aktif diekskresikan ke dalam empedu dan

(40)

BAB III

A. MODEL MATEMATIKA DISTRIBUSI OBAT PADA PENYAKIT INFEKSI SALURAN KEMIH

Model matematika yang digunakan untuk distribusi obat pada penyakit infeksi saluran kemih adalah model kompartemen. Model kompartemen merupakan model matematika yang mengestimasi jumlah obat dalam berbagai kompartemen setelah obat dimasukkan ke dalam suatu kompartemen tertentu. Model kompartemen dibagi menjadi dua jenis, yaitu model satu kompartemen dan model dua kompartemen. Model matematika ini dibentuk berdasarkan asumsi-asumsi yang ditentukan. Asumsi-asumsi yang digunakan dalam membuat model matematika distribusi obat penyakit infeksi saluran kemih sebagai berikut:

1. Pengobatan manusia yang terserang infeksi saluran kemih bagian atas dan bagian bawah dilakukan di dalam darah.

2. Jalur pemberian obat mempengaruhi proses penyembuhan.

3. Untuk pemberian obat melalui oral, sebagian obat dari lambung langsung masuk ke darah. Selain itu, sebagian lagi melewati usus terlebih dahulu kemudian masuk ke darah.

4. Obat diberikan satu kali dan dalam selang waktu tertentu. 5. Tidak terjadi penularan penyakit.

(41)

Pembentukan model matematika distribusi obat penyakit infeksi

saluran kemih menggunakan dua kasus pemberian obat yang berbeda,

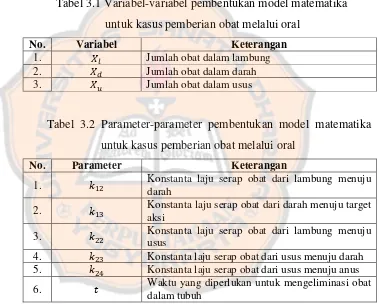
yaitu pemberian obat melalui oral dan intravena. Adapun variabel dan parameter yang digunakan dalam pembentukan model matematika distribusi obat penyakit ISK dengan pemberian obat melalui oral disajikan berturut-turut dalam tabel 3.1 dan 3.2 berikut.

Tabel 3.1 Variabel-variabel pembentukan model matematika untuk kasus pemberian obat melalui oral

No. Variabel Keterangan

1. � Jumlah obat dalam lambung 2. � Jumlah obat dalam darah 3. � Jumlah obat dalam usus

Tabel 3.2 Parameter-parameter pembentukan model matematika untuk kasus pemberian obat melalui oral

No. Parameter Keterangan

1. Konstanta laju serap obat dari lambung menuju darah

2. Konstanta laju serap obat dari darah menuju target aksi

3. Konstanta laju serap obat dari lambung menuju usus

4. Konstanta laju serap obat dari usus menuju darah 5. Konstanta laju serap obat dari usus menuju anus 6. Waktu yang diperlukan untuk mengeliminasi obat

dalam tubuh

(42)

Tabel 3.3 Variabel-variabel pembentukan model matematika untuk kasus pemberian obat melalui intravena No. Variabel Keterangan

1. � Jumlah obat dalam darah

Tabel 3.4 Parameter-parameter pembentukan model matematika untuk kasus pemberian obat melalui intravena

No. Parameter Keterangan

1. Konstanta laju serap obat dari darah menuju target aksi

2. Waktu yang diperlukan untuk mengeliminasi obat dalam tubuh

Pemberian obat dilakukan melalui oral dan intravena. Berikut

penjelasan mengenai pemberian obat melalui oral.

1. Pemberian Obat melalui Oral

Pemberian obat melalui oral melewati mulut, kerongkongan,

lambung, usus halus, usus besar, dan anus. Obat yang sampai di

sebagian lagi menuju bagian tubuh lainnya. Kompartemen kedua

terjadi di darah. Setelah obat sampai di darah, obat kemudian

terdistribusi ke seluruh tubuh, termasuk ke dalam target aksi. Target

aksi merupakan tempat terserangnya penyakit. Dalam kasus ini, yang

(43)

uretra. Ginjal dan ureter merupakan saluran kemih bagian atas,

sedangkan kandung kemih dan uretra merupakan saluran kemih bagian

bawah. Gambar 3.1 merupakan diagram pemberian obat untuk

pengobatan ISK melalui oral.

Selain pemberian obat melalui oral, pembentukan model

matematika distribusi obat penyakit ISK juga melalui intravena. Berikut

penjelasan mengenai pemberian obat melalui intravena.

2. Pemberian Obat melalui Intravena

Pemberian obat melalui intravena langsung menuju darah.

Setelah itu, obat akan masuk dengan segera ke seluruh tubuh termasuk

ginjal, ureter, kandung kemih, dan uretra yang bertindak sebagai target

aksi.

Gambar 3.1 Diagram Pemberian Obat melalui Oral Usus

Lambung

Darah Pemberian

Obat

Target Aksi

(44)

Gambar 3.2 merupakan diagram pemberian obat untuk

pengobatan ISK melalui Intravena.

B. FORMULASI MODEL PEMBERIAN OBAT

Dari Gambar 3.1 dibentuk model matematika yang menunjukkan

pengobatan penyakit infeksi saluran kemih untuk pemberian obat melalui

oral.

1. Kasus I: Pemberian obat melalui oral dan obat dari lambung langsung

masuk ke darah

Asumsi-asumsi yang digunakan untuk membentuk model

matematika pada kasus I adalah sebagai berikut:

a. Pengobatan manusia yang terserang infeksi saluran kemih bagian atas dan bagian bawah sama, yaitu melalui darah.

b. Obat diberikan satu kali dan dalam selang waktu tertentu. Obat diberikan satu kali artinya manusia yang terserang infeksi saluran kemih hanya memasukkan obat ke dalam tubuh satu kali selama

Gambar 3.2 Diagram Pemberian Obat melalui Intravena Darah

Target Aksi Pemberian

(45)

terserang penyakit. Sedangkan, obat yang diberikan selama selang waktu tertentu artinya obat dimasukkan ke dalam tubuh selama selang waktu tertentu sampai manusia yang terserang infeksi saluran kemih dapat dikatakan sembuh.

c. Obat dari lambung langsung menuju darah.

Sebelum didistribusikan ke seluruh tubuh oleh darah, obat

melewati lambung dengan jumlah obat dalam lambung � . Setelah

itu, obat masuk ke dalam darah dengan konstanta laju serap obat dari lambung ke darah . Gambar 3.3 merupakan diagram kompartemen pertama yang terbentuk untuk kasus I.

Berdasarkan Gambar 3.3, laju perubahan obat di dalam lambung dapat dinyatakan dengan

{ ℎ } = { } − {

ℎ } Gambar 3.3 Diagram Kompartemen Pertama untuk Kasus I

Lambung � Pemberian

(46)

dengan:

{ } = , dan

{ −

ℎ

} = �

Sehingga laju perubahan obat di dalam lambung adalah sebagai berikut: �

= − �

�

= − � .

Solusi dari persamaan . adalah �

Substitusikan persamaan ke , sehingga menjadi

� = − + �

(47)

(_{� ) = −}�

�

� = −

� = � − _.

Berikut grafik penyelesaian persamaan . .

Diberikan jumlah awal obat � = , dan konstanta serap obat dari lambung menuju darah = . / . Gambar 3.4 menunjukkan grafik terserapnya obat dalam waktu tertentu yang meninggalkan lambung menuju darah.

(48)

Obat yang berada di lambung kemudian masuk ke darah. Setelah obat yang didistribusikan dari lambung sampai ke darah, obat langsung didistribusikan menuju target aksi. Berikut diagram kompartemen kedua untuk kasus I.

Berdasarkan Gambar 3.5, laju perubahan obat di dalam darah dapat dinyatakan dengan

{ ℎ

ℎ } = { ℎ } − { ℎ }

dengan:

{ _ℎ } = �, dan

{ ℎ } = �

Gambar 3.5 Diagram Kompartemen Kedua untuk Kasus I Darah

�

(49)

Sehingga laju perubahan obat di dalam darah adalah sebagai berikut: �

= � − � .

Substitusikan persamaan . ke persamaan . , sehingga persamaan

menjadi

�

= � − ₋ _�

�

= � − ₋ _{� .}

Persamaan . merupakan persamaan diferensial linear orde satu. Solusi dari persamaan . adalah

�

+ � = � −

Misalkan, = dan = � − , solusi dari persamaan

tersebut adalah

� ∫ � _{= ∫} ∫ �

� ∫ _{= ∫} _� − ∫

� ∫ ₌ _{� ∫} − ∫

� = � ∫ −

� = � ∫ − +

(50)

= − +

− + =

Substitusikan = − + dan =

− + ke persamaan ,

sehingga menjadi

� = _{� ∫ − +}

� =₋ ₊� ∫

� =₋ ₊� +

� = �

− + − + +

� = ₋� −₊ +

� = ₋ �₊− +

� = ₋ � ₊− +

� = ₋ � ₊− + −

Misalkan pada awalnya tidak ada obat dalam darah atau � = , maka persamaan menjadi

(51)

=₋ �₊ +

=₋ ₊� +

= ₋�

� = ₋ � ₊− + ( ₋� ) −

� = ₋ � ₊− + �₋−

� = �₋− − �₋−

� = ₋� − ₋ − _.

(52)

Jumlah awal obat � = , yang terlebih dahulu masuk ke lambung dengan konstanta serap obat dari lambung menuju darah =

. / kemudian masuk ke darah. Gambar 3.6 menunjukkan grafik terserapnya obat dalam waktu tertentu di dalam darah. Grafik tersebut menyatakan bahwa berkurangnya jumlah obat dalam darah setelah melewati lambung.

Misalkan obat diberikan setiap 8 jam sekali, maka grafik

penyelesaian kompartemen kedua untuk kasus I sebagai berikut.

Gambar 3.7 menunjukkan penyelesaian untuk pemberian obat yang

diberikan 8 jam sekali. Setelah 8 jam, obat akan diberikan kembali. Jumlah

obat yang diberikan 8 jam sebelumnya masih tersisa di dalam tubuh,

sehingga ketika obat diberikan kembali setiap 8 jam sekali maka jumlah

(53)

obat akan terus bertambah. Obat akan habis atau hilang di dalam tubuh

ketika pemberian obat dalam waktu 8 jam sekali dihentikan.

2. Kasus II: Pemberian obat melalui oral, sebagian obat dari lambung

masuk ke usus dan sebagian masuk ke darah

Asumsi-asumsi yang digunakan untuk membentuk model

matematika dari kasus II adalah sebagai berikut:

b. Obat diberikan satu kali dan dalam selang waktu tertentu. Obat diberikan satu kali artinya manusia yang terserang infeksi saluran kemih hanya memasukkan obat ke dalam tubuh satu kali selama terserang penyakit. Sedangkan, obat yang diberikan selama selang waktu tertentu artinya obat dimasukkan ke dalam tubuh selama selang waktu tertentu sampai manusia yang terserang infeksi saluran kemih dapat dikatakan sembuh.

(54)

Berikut diagram kompartemen pertama untuk kasus II.

(55)

{ } = �

{

ℎ

} = � , dan

{

ℎ

} = �

Sehingga laju perubahan obat di dalam lambung adalah sebagai berikut: �

= − � − � − � − �

�

= − � − � − � − � .

Jumlah obat dalam lambung sama dengan jumlah obat yang masuk ke dalam lambung dikurangi jumlah obat yang meninggalkan lambung. Obat meninggalkan lambung menuju usus. Secara matematis dapat dituliskan dengan � = � − � , sehingga � = � − �. Oleh karena itu, persamaan . menjadi

�

= − � − � − � − � − � − �

�

(56)

�

= − � − � − � + � − � + �

�

= − � − � + � + � − � − � .

�

+ � + � − � − � = − � − �

�

+ + − − � = − − �

Misalkan, = + − − dan = − − � ,

solusi dari persamaan tersebut adalah

� ∫ � _{= ∫} ∫ �

� ∫ + − − _{= ∫ −} ₋ _� ∫ + − −

� ∫ + − − _{= −} ₋ _{� ∫} ∫ + − −

� + − − _{= −} ₋ _{� ∫} + − −

Misalkan, = + − −

= + − −

(57)

Substitusikan = + − − dan =

+ − − ke

persamaan , sehingga menjadi

� + − − _{= −} ₋ _{� ∫}

+ − −

� + − − ₌ − − �

+ − − ∫

� + − − ₌ − − �

+ − − +

� + − − ₌ − − �

+ − − + − − +

� + − − ₌ − − � + − −

+ − − +

� = ₊− ₋− ₋� + −₊ −₋ ₋ + ₊ ₋ ₋

� = ₊− −₋ ₋� + ₊ ₋ ₋

� = ₊− −₋ ₋� + − + − −

Misalkan � = � , maka persamaan menjadi

� = ₊− −₋ ₋� + − + − −

� = ₊− −₋ ₋� +

(58)

= � + � −₊ � −₋ � +₋ � + �

= ₊ � +₋ �₋

= ₊ +₋ �₋

� = ₊− −₋ ₋� + ₊ +₋ �₋ − + − −

� = ₊− −₋ ₋� + + ₊� −₋ + ₋− − .

(59)

dari lambung menuju usus = . / , konstanta laju serap obat dari usus menuju darah = . / , dan konstanta laju serap obat dari usus menuju organ tubuh lainnya = . / . Gambar 3.9 menunjukkan grafik terserapnya obat dalam waktu tertentu. Sebagian dari obat masuk ke dalam usus dan sebagian lagi menuju darah.

Kompartemen kedua terjadi di darah. Setelah obat yang melewati lambung dan usus sampai ke darah, obat langsung didistribusikan menuju target aksi dengan jumlah obat dalam darah � dan konstanta laju serap obat dari darah ke target aksi . Berikut diagram kompartemen kedua untuk kasus II.

Berdasarkan Gambar 3.10, laju perubahan distribusi obat di dalam darah dapat dinyatakan dengan

{ ℎ

ℎ } = { ℎ } − { ℎ }

Gambar 3.10 Diagram Kompartemen Kedua untuk Kasus II Darah

�

(60)

dengan:

{ _ℎ } = �, dan

(61)

Sehingga laju perubahan obat di dalam darah adalah �

= � − � .

Substitusikan persamaan . ke persamaan . , sehingga persamaan menjadi

�

= ₊− −₋ ₋� + + ₊� −₋ + ₋− − − � .

Persamaan . merupakan persamaan diferensial linear orde satu. Solusi dari persamaan . adalah �

+ � = ₊− −₋ ₋� + + ₊� −₋ + ₋− −

Misalkan, = dan = − − �

+ − − +

+ � − + − − �

+ − − , solusi dari persamaan tersebut

adalah

(62)

� ∫ _{= ∫} − − �

+ − − +

+ � − + − −

+ − − ∫

� = ∫ ₊− −₋ ₋� + + ₊� −₋ + ₋− −

� = ∫ ₊− −₋ ₋� + ∫ + ₊� −₋ + ₋− −

� = ₊− −₋ �₋ ∫ + ₊ +₋ �₋ ∫ − + − −

� = ₊− −₋ �₋ ∫ + ₊ +₋ �₋ ∫ − + − + +

Misalkan, =

=

(63)

= − + − + +

− + − + + =

Substitusikan = , = , = − + − + + , dan =

− + − + + ke persamaan

, sehingga menjadi

� = ₊− −₋ �₋ ∫ + ₊ +₋ �₋ ∫ _{− + − + +}

� = ₊− −₋ �₋ ( ) ∫

+ ₊ +₋ �₋ _{(− + − + + )∫}

� = ₊− −₋ �₋ ( )

(64)

� = ₊− −₋ �₋ ( )

+ ₊ +₋ �₋ _{(− + − + + )} − + − + + ₊

� = ₊− −₋ ₋� ( )

+ + �

+ − − (− + − + + )

− + − + +

+

� = ₊− −₋ ₋� ( )

+ ₊ +₋ �₋ _{(− + − + + )} − − + + ₊ −

Misalkan � = , maka persamaan menjadi

(65)

+ ₊ +₋ �₋ _{(− + − + + )} − − + + ₊ −

= ₊− −₋ ₋� ( ) + ₊ +₋ �₋ _{(− + − + + ) +}

= − ₊− −₋ ₋� ( ) − ₊ +₋ �₋ _{(− + − + + )}

� = ₊− −₋ ₋� ( )

(66)

+ (− ₊− −₋ ₋� ( )

− ₊ +₋ �₋ _{(− + − + + ))} −

� = ₊− −₋ ₋� ( ) − ( ₊− −₋ ₋� ( )) −

+ ₊ +₋ �₋ _{(− + − + + )} − − + +

+ (− ₊ +₋ �₋ _{(− + − + + ))} −

� = ( ₊− −₋ ₋� ( )) − −

(67)

Gambar 3.11 menunjukkan jumlah obat yang tersisa di dalam

darah. Setelah melewati lambung dan masuk ke usus, obat akan terserap

ke dalam darah. Obat yang terserap ke dalam darah akan didistribusikan ke

organ tubuh lainnya.

Misalkan obat diberikan setiap 8 jam sekali, maka grafik

penyelesaian kompartemen kedua untuk kasus II sebagai berikut.

(68)

Grafik pada Gambar 3.12 menunjukkan penyelesaian untuk

pemberian obat yang diberikan 8 jam sekali untuk kasus II. Obat akan

diberikan kembali dalam selang waktu 8 jam. Gambar 3.12 menunjukkan

bahwa dalam selang waktu 8 jam, obat yang tersedia di dalam darah masih

ada. Dengan kata lain, obat akan terus bertambah selama pemberian obat

dalam waktu 8 jam sekali diberikan. Obat akan habis atau hilang ketika

pemberian obat dalam waktu 8 jam sekali dihentikan. Waktu habisnya

obat di dalam tubuh untuk kasus II lebih lama dibandingkan kasus I.

Dari Gambar 3.2 dibentuk model matematika yang menunjukkan

pengobatan penyakit infeksi saluran kemih untuk pemberian obat melalui

intravena.

3. Kasus III: Pemberian obat melalui intravena

Untuk kasus ketiga (III), asumsi-asumsi yang digunakan untuk

membentuk model matematika tersebut adalah sebagai berikut:

(69)

selang waktu tertentu sampai manusia yang terserang infeksi saluran kemih dapat dikatakan sembuh.

c. Obat yang diberikan langsung menuju darah.

Kompartemen yang terbentuk untuk pemberian obat melalui

intravena hanya terjadi di darah. Setelah sampai di darah dengan jumlah

obat dalam darah � , obat didistribusikan lagi menuju target aksi dengan

konstanta laju serap obat dari darah ke target aksi . Berikut diagram

pemberian obat untuk kasus III:

(70)

dengan:

{

ℎ} = ,

dan

{ ℎ

} = �

Sehingga laju perubahan obat di dalam darah adalah sebagai berikut. �

= − �

�

= − � .

Solusi dari persamaan . adalah �

= − �

∫ � � = ∫−

� = − +

Misalkan � = � , maka persamaan menjadi

(� ) = − +

(� ) =

(71)

� = − + �

� − � = −

(�_{� ) = −}

�

� = −

� = � − _.

Berikut grafik penyelesaian persamaan .

Diberikan jumlah awal obat � = , dan konstanta laju serap obat dari darah menuju target aksi = . / . Gambar 3.4 menunjukkan grafik terserapnya obat dalam waktu tertentu yang meninggalkan darah menuju target aksi atau organ tubuh lainnya. Jumlah obat akan berkurang bahkan habis dalam selang waktu tertentu karena tidak diberikan obat kembali.

(72)

Dari penyelesaian kasus III, misalkan pemberian obat dilakukan setiap 8 jam sekali, maka grafik penyelesaian untuk kasus III sebagai berikut.

Gambar 3.15 menunjukkan grafik penyelesaian untuk pemberian

obat yang diberikan 8 jam sekali untuk kasus III. Jumlah obat akan terus

bertambah apabila obat diberikan dalam selang waktu 8 jam sekali. Jika

pemberian obat dalam selang waktu 8 jam sekali dihentikan, maka jumlah

obat yang diberikan untuk kasus III lebih cepat habis dibandingkan dengan

kasus I dan II. Hal ini disebabkan pada kasus III obat langsung masuk ke

dalam darah.

C. FORMULASI MODEL PERTUMBUHAN BAKTERI E. COLI

(73)

juga dipengaruhi oleh konstanta pertumbuhan bakteri. Secara matematis dapat dituliskan sebagai berikut.

≈

= .

dengan:

= konstanta pertumbuhan bakteri, dan = banyaknya bakteri /

Solusi dari persamaan . adalah =

∫ = ∫

= +

Misalkan = , maka persamaan menjadi

( ) = +

=

Substitusikan persamaan ke persamaan sehingga menjadi

= +

− =

( ) =

=

(74)

Misalkan bakteri E. Coli menggandakan tubuhnya menjadi dua kali lipat dalam waktu 20 menit (Michael Madigan, 2015), sehingga secara matematis dapat dituliskan sebagai berikut.

=

= ,

≈ ,

(75)

Penyembuhan dilakukan dengan memberikan antibiotik dengan jenis tetrasiklin yang bekerja dengan cara menghambat sintesis protein bakteri E. Coli terhadap penyakit. Dosis tetrasiklin yang diberikan sebesar , misalnya dosis tetrasiklin dengan jumlah ini dapat membunuh bakteri sebanyak / per jam. Pemberian obat dilakukan setiap 8 jam sekali. Persamaan matematis untuk banyaknya bakteri yang mati dapat dinyatakan dengan

= − .

dengan merupakan konstanta banyaknya bakteri yang mati untuk setiap jam.

Jumlah bakteri E. Coli yang mati sebanding dengan jumlah bakteri yang menyebabkan infeksi dikurangi banyaknya bakteri yang mati akibat antibiotik yang diberikan. Secara matematis dapat dituliskan sebagai berikut.

= − .

dengan:

= konstanta pertumbuhan bakteri, dan = banyaknya bakteri /

(76)

− =−

Misalkan, = − dan = − , solusi dari persamaan tersebut

adalah

∫ � _{= ∫} ∫ �

∫ − _{= ∫ −} ∫ −

− _{= − ∫} −

Misalkan = − ,

= −

− =

Persamaan menjadi

−

= − ∫ −

− ₌− − ∫

− _{= ∫}

(77)

Substitusikan = − ke persamaan , sehingga persamaan menjadi

− ₌ − ₊

= ₋− ₊ ₋

= +

Misalkan = , maka persamaan menjadi

= +

= −

Substitusikan persamaan ke persamaan sehingga menjadi

= + −

(78)

BAB IV

SIMULASI MODEL MATEMATIKA DISTRIBUSI OBAT PADA PENYAKIT INFEKSI SALURAN KEMIH

A. SIMULASI MODEL

1. Kasus I: Pemberian obat melalui oral dan obat dari lambung langsung masuk ke darah

Jika diasumsikan banyaknya dosis obat tetrasiklin untuk pemberian obat melalui oral adalah . , konstanta laju serap obat dari lambung ke darah = . / , jumlah obat dalam lambung � = . , dan konstanta laju serap obat dari darah ke target aksi = . / . Pemberian obat diberikan setiap 8 jam sekali. Nilai-nilai variabel dan parameter tersebut dapat disajikan sebagai berikut.

Tabel 4.1 Nilai-nilai variabel dan parameter kasus I

Variabel Nilai Parameter Nilai

� . . /

(79)

Berikut diberikan penyelesaian kasus I dengan menggunakan matlab.

Gambar 4.1 menunjukkan penyelesaian kasus I. Penyelesaian ini merupakan proses kesembuhan manusia terhadap penyakit ISK untuk pemberian obat melalui oral. Dalam kasus I, dosis tetrasiklin yang diberikan melalui oral sebesar . . Grafik pada Gambar 4.1 menunjukkan jumlah dosis tetrasiklin yang tersisa saat waktu tertentu. Setiap 8 jam sekali, pemberian tetrasiklin dilakukan. Tetrasiklin bekerja dengan cara menghambat sintesis protein bakteri. Berdasarkan Gambar 3.16 menunjukkan grafik pertumbuhan bakteri terhadap penyakit. Dengan pemberian tetrasiklin secara berkesinambungan setiap 8 jam sekali, bakteri akan berkurang bahkan mati karena tidak dapat berkembangbiak. Ketika hal ini terjadi, manusia dapat dikatakan sembuh dari penyakit infeksi saluran kemih.

(80)

2. Kasus II: Pemberian obat melalui oral, sebagian obat dari lambung masuk ke usus dan sebagian masuk ke darah

Jika diasumsikan banyaknya dosis obat tetrasiklin untuk pemberian obat melalui oral adalah . , konstanta laju serap obat dari lambung ke darah = . / , kontanta laju serap obat dari lambung ke usus = . / dengan jumlah obat dalam lambung � = . , konstanta laju serap obat dari usus ke darah = . / , konstanta laju serap obat dari usus ke bagian tubuh lainnya = . / , dan konstanta laju serap obat dari darah ke target aksi = . / . Pemberian obat diberikan setiap 8 jam sekali. Nilai-nilai variabel dan parameter tersebut dapat disajikan sebagai berikut.

Tabel 4.2 Nilai-nilai variabel dan parameter kasus II

� . . /

. /

(81)

Berikut diberikan penyelesaian kasus II dengan menggunakan matlab.

Gambar 4.2 menunjukkan penyelesaian kasus II. Dalam kasus II, dosis tetrasiklin yang diberikan sama seperti kasus I, yaitu . . Pemberian tetrasiklin dilakukan setiap 8 jam sekali. Dalam kasus II, obat yang terserap dalam darah lebih sedikit dibandingkan dengan kasus I. Hal ini karena tidak semua obat yang melewati lambung langsung menuju ke darah, melainkan sebagian dari obat masuk ke dalam usus. Setelah itu obat baru terserap ke dalam darah. Pemberian tetrasiklin secara berkesinambungan dapat menghentikan pertumbuhan bakteri, artinya bakteri semakin berkurang bahkan mati. Dalam keadaan ini, manusia dikatakan sembuh dari penyakit.

(82)

Jika diasumsikan banyaknya dosis obat tetrasiklin untuk pemberian obat melalui intravena adalah . dan konstanta laju serap obat dari darah ke target aksi = . / . Pemberian obat diberikan setiap 8 jam sekali. Nilai-nilai variabel dan parameter tersebut dapat disajikan sebagai berikut.

Tabel 4.3 Nilai-nilai variabel dan parameter kasus III

� . . /

Berikut diberikan penyelesaian kasus III dengan mengggunakan matlab.

Gambar 4.3 menunjukkan penyelesaian kasus III. Penyelesaian ini merupakan proses kesembuhan manusia terhadap penyakit ISK

(83)

untuk pemberian obat melalui intravena. Dalam kasus ini, dosis tetrasiklin yang diberikan melalui intravena sebesar . . Obat yang diberikan melalui intravena langsung masuk ke darah dan segera tersebar ke seluruh bagian tubuh lainnya. Tetrasiklin diberikan setiap 8 jam sekali. Tetrasiklin menghambat sintesis protein bakteri, sehingga dalam rentang waktu tertentu bakteri akan berkurang dan akhirnya mati. Jadi, manusia dapat dikatakan sembuh dari penyakit.

B. PROSES PENYEMBUHAN

Misalnya, banyaknya bakteri E. Coli di dalam tubuh yang menyebabkan terjadinya ISK sebesar . × / . Dosis tetrasiklin yang diberikan sebesar untuk dewasa. Tetrasiklin diberikan 3 kali sehari dalam waktu 8 hari. Delapan hari sama dengan 192 jam. Selama 192 jam ini bakteri akan berkurang bahkan mati (mendekati nol). Banyaknya bakteri yang mati dapat dihitung dengan

(84)

. = .

= .

.

= .

≈

Jadi, bakteri yang mati sebanyak / . Grafik penyembuhan penyakit ISK ditunjukkan pada gambar 4.4 berikut.

Gambar 4.4 menunjukkan grafik penurunan banyaknya bakteri di dalam tubuh yang menyebabkan penyakit ISK. Pemberian obat yang rutin diberikan setiap hari akan menyebabkan hilangnya bakteri E. Coli di dalam tubuh yang terserang penyakit. Dapat diartikan dalam waktu 8 hari bakteri akan berkurang dan manusia dapat dikatakan sembuh dari penyakit ISK.

(85)

BAB V PENUTUP

A. KESIMPULAN

Pengobatan penyakit Infeksi Saluran Kemih (ISK) dapat dibuat model matematika dengan menggunakan model kompartemen. Model matematika ini dibuat dengan tiga kasus yang berbeda. Berdasarkan asumsi-asumsi yang dibuat, diperoleh model matematika dari ketiga kasus tersebut, yaitu:

1. Kasus I: Pemberian obat melalui oral dan obat dari lambung langsung

masuk ke darah

Model matematika yang terbentuk adalah sebagai berikut.

�

= − �

�

= � − �

2. Kasus II: Pemberian obat melalui oral, sebagian obat dari lambung

masuk ke usus dan sebagian masuk ke darah

(86)

�

= − � .

Penyembuhan penyakit infeksi saluran kemih menggunakan simulasi model. Proses penyembuhan ini dilakukan dengan memberikan antibiotik dengan jenis tetrasiklin sebanyak 3 kali sehari selama 8 hari. Bakteri akan berkurang bahkan mati ketika antibiotik jenis tetrasiklin ini diberikan secara teratur dan manusia dikatakan sembuh dari penyakit infeksi saluran kemih.

B. SARAN

(87)

DAFTAR PUSTAKA

Anton, Howard dan Rorres. 2005. Aljabar Linear Elementer Versi Aplikasi (Edisi 8). Jakarta: Erlangga.

Barnes, Belinda and Glenn R. Fulford. 2002. Mathematical Modelling with Case Studies: A Differential Equation Approach Using Maple. London: Taylor & Francis.

Gravemeijer, K.P. E. 1994. Developing Realistic Mathematics Education. Utrecht: CD-β.

Herdwiani, Wiwin, dkk. 2016. Buku Ajar Farmakokinetik Klinik. Jakarta: Trans Info Media.

Iswanto, Ripno Juli. 2012. Pemodelan Matematika: Aplikasi dan Terapannya. Yogyakarta: Graha Ilmu.

Kartono. 2012. Persamaan Diferensial Biasa: Model Matematika Fenomena Perubahan. Yogyakarta: Graha Ilmu.

Kusumah, S. Yaya. 1989. Persamaan Diferensial. Jakarta: Departemen Pendidikan dan Kebudayaan Direktorat Jenderal Pendidikan Tinggi Proyek Pengembangan Lembaga Pendidikan Tenaga Kependidikan. Madigan, Michael, dkk. 2015. Brock Biology of Microorganisms, Fourteenth

Edition. USA: Pearson Education.

(88)

Melliawati, Ruth. 2009. Escherichia Coli dalam Kehidupan Manusia (Jurnal). BioTrens, Vol. 4, No.1.

Mufriha, Ihda. 2009. Analisis Biaya Penggunaan Antibiotik Pada Pasien Infeksi Saluran Kemih Rawat Inap di RSU Pandan Arang Boyolali

Tahun 2008 (Skripsi). Surakarta: Universitas Muhammadiyah Surakarta. Nugroho, Didit Budi. 2011. Persamaan Diferensial Biasa dan Aplikasinya: Penyelesaian Manual dan Menggunakan Maple. Yogyakarta: Graha Ilmu.

Patrianto, Symphorianus Faming. 2016. Model SIR Penyebaran Penyakit Leptospirosis (Skripsi). Yogyakarta: Universitas Sanata Dharma.

Perko, Lawrence. 2001. Differential Equations and Dynamical Systems (Ed. 3). New York: Springer-Verlag.

Priyanto, 2010, Farmakologi Dasar, Edisi II, Lembaga Studi dan Konsultasi Farmakologi, Jakarta.

Olsder, G. J & Woude, J. W. van der. 2004. Mathematical Systems Theory. Netherland: VVSD.

Ross, Shepley L. 1984. Differential Equations Third Edition. Singapore: John Wiley & Sons.

Shargel, L. dan Andrew B.C.YU., 2005, Biofarmasetika dan Farmakokinetika Terapan, Edisi kedua, Airlangga University Press, Surabaya.

(89)

Dr. Kariadi Semarang Tahun 2008 (Skripsi). Semarang: Universitas Diponegoro.