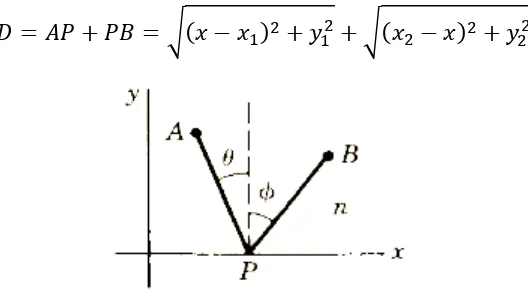
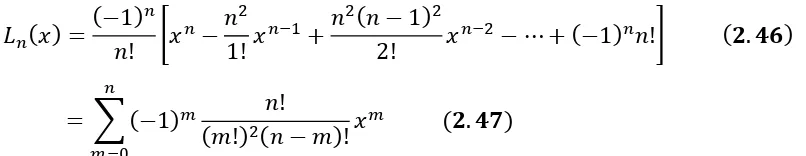Catatan Kuliah :
Fisika Matematika II
Muhammad Fauzi Mustamin
𝛁
𝟐
\𝒊𝒏𝒇𝒕𝒚
press
Muhammad Fauzi Mustamin
Catatan Kuliah: Fisika Matematika 2
Edisi Pertama
KATA PENGANTAR
Berbagai fenomena alam menunjukkan pola keteraturan. Fisika diamanahkan sebagai cabang
pengetahuan untuk menjabarkan keteraturan tersebut. Menggunakan alat matematis,
fenomena-fenomena tersebut diformulasikan sedemikian rupa agar terstruktur untuk dipahami. Hasil kajian
para fisikawan inilah kemudian yang menurun kepada bidang-bidang lain untuk ditelaah lebih
lanjut kajian teknisnya.
Buku ini merupakan kumpulan catatan kuliah saat mengikuti perkuliahan Fisika Matematika II di
program studi Fisika, Universitas Hasanuddin, ditambah dengan hasil telaah otodidak penulis.
Terinspirasi dari hadits Rasulullah, “Ikatlah ilmu dengan menuliskannya”, saya memulai sedikit
demi sedikit menuliskan risalah ini. Setelah beberapa bulan, buku ini akhirnya bisa saya
rampungkan meskipun masih jauh dari kata sempurna untuk menjelaskan luasnya samudera Fisika
Matematika.
Bagi teman-teman, para pembaca sekalian, saran dan feedback selalu dinanti di
muhammadfauzim@gmail.com.
Makassar, Januari 2016
Muhammad Fauzi Mustamin
Kepada dosen-dosen pengajar; Prof. Wira Bahari Nurdin, Bannu, M.Si., dan Dr. Tasrief Surungan,
serta teman-teman sekelas pada mata kuliah Fisika Matematika semester genap 2015, saya
DAFTAR ISI
1. Fungsi Khusus ... 1
1.1 Fungsi Gamma ... 1
1.2 Hubungan Fungsional ... 3
1.3 Fungsi Beta ... 4
1.4 Forulasi Stirling ... 5
2. Persamaan Diferensial Lanjut ... 7
2.1 Persamaan Diferensial Legendre ... 7
2.2 Persamaan Diferensial Bessel... 13
2.3 Persamaan Diferensial Hermite ... 17
2.4 Persamaan Diferensial Lauerre ... 20
2.5 Persamaan Diferensial Chebyshev ... 24
3. Persamaan Diferensial Parsial ... 30
3.1 Persamaan Diferensial Secara Umum ... 30
3.2 Separasi Variabel ... 31
3.3 Superposisi Solusi Terpisah ... 33
3.4 Separasi Variabel pada Kordinat Polar ... 35
4. Fungsi Kompleks ... 42
4.1 Fungsi Variabel Kompleks ... 42
4.2 Hubungan Cauchy-Rieman ... 42
4.3 Integral Kompleks... 44
4.4 Teorema Cauchy ... 45
4.5 Integral Cauchy... 46
4.6 Deret Taylor dan Laurent ... 47
4.8 Integrasi Kontur untuk Integral Tentu ... 53
5. Kalkulus Variasi ... 54
5.1 Persamaan Euler-Lagrange ... 54
5.2 Penggunaan Persamaan Euler-Lagrange ... 57
5.3 Persamaan Lagrange ... 58
5.4 Notasi Variasi ... 60
1.
FUNGSI KHUSUS
1.1 Fungsi Gamma
Fungsi gamma merupakan fungsi spesial yang sering muncul dalam pembahasan suatu fenomena
fisis. Fungsi ini muncul disetiap ekspansi Taylor. Pada pelajaran lebih lanjut, fungsi gamma sering
ditemukan dengan argument setengah bilangan bulat dan dibutuhkan untuk nilai non-integral
secara umum dalam banyak ekspansi, seperti fungsi Bessel untuk urutan bukan bilangan bulat.
Fungsi gamma tidak selalu mendeskripsikan sebuah kuantitas fisis, namun muncul sebagai faktor
dalam ekspansi dari kuantitas fisis yang relevan.
Fungsi gamma memiliki beberapa definisi dalam penggunaannya. Definisi pertama muncul setelah
didefinisikan oleh Euler :
Γ(𝑧) ≡ lim𝑛→∞𝑧(𝑧 + 1)(𝑧 + 2) ∙ ∙ ∙ (𝑧 + 𝑛) 𝑛1 ∙ 2 ∙ 3 ∙ ∙ ∙ 𝑛 𝑧, 𝑧 ≠ 0, −1, −2, … (𝟏. 𝟏)
Dengan melakukan subtitusi 𝑧 = 𝑧 + 1, didapatkan hubungan :
Γ(𝑧 + 1) = 𝑧Γ(𝑧) (𝟏.𝟐)
Dari definisi juga dapat dilihat bahwa :
Γ(1) = lim𝑛→∞1 ∙ 2 ∙ 3 ∙ ∙ ∙ 𝑛(𝑛 + 1) 𝑛 = 11 ∙ 2 ∙ 3 ∙ ∙ ∙ 𝑛
Sehingga membentuk pola
Γ(2) = 1
Γ(3) = 2Γ(2) = 2 Γ(4) = 3Γ(3) = 2 ∙ 3
Atau :
Γ(𝑧) = 1 ∙ 2 ∙ 3 ∙ ∙ ∙ (𝑧 − 1) = (𝑧 − 1)! (𝟏. 𝟑)
Γ(𝑧) = ∫ 𝑒−𝑡 ∞
0
𝑡𝑧−1𝑑𝑡, Re(𝑧) > 0 (𝟏. 𝟒)
Perlu diperhatikan bahwa nilai real dari 𝑧 haruslah konvergen.
Saat fungsi gamma muncul dalam masalah fisis, sering dijumpai dalam beberapa variasi seperti :
Γ(𝑧) = 2 ∫ 𝑒−𝑡2 ∞
0
𝑡2𝑧−1𝑑𝑡, Re(𝑧) > 0 (𝟏. 𝟓)
yang dapat dibuktikan dengan melakukan subtitusi 𝑡 = 𝑡2 pada persamaan (𝟏. 𝟒).
Persamaan (𝟏. 𝟏) dan (𝟏. 𝟒) dapat dibuktikan dengan memperhatikan fungsi dua variabel :
𝐹(𝑧, 𝑛) = ∫ (1 −𝑛)𝑡 𝑛 𝑛
0
𝑡𝑧−1𝑑𝑡, Re(𝑧) > 0 (𝟏. 𝟔)
Dengan 𝑛 adalah bilangan bulat positif. Fungsi tersebut dipilih karena eksponensialnya memiliki
definisi :
Fungsi pada persamaan (𝟏. 𝟔) dapat dilihat memenuhi persamaan (𝟏. 𝟒):
lim
𝑛→∞𝐹(𝑧, 𝑛) = 𝐹(𝑧, ∞) = ∫ 𝑒−𝑡 ∞
0
𝑡𝑧−1𝑑𝑡 = Γ(𝑧) (𝟏. 𝟕)
Sementara dengan melakukan subtitusi = 𝑡/𝑛 :
𝐹(𝑧, 𝑛) = 𝑛𝑧∫(1 − 𝑢)𝑛 1
0
𝑢𝑧−1𝑑𝑢
Persamaan (𝟏. 𝟏) didapatkan dengan integral parsial :
Dengan melakukan sebanyak 𝑛 kali, integral parsialnya diabaikan, kita dapatkan :
𝐹(𝑧, 𝑛) = 𝑛𝑧 𝑛(𝑛 − 1) ∙∙∙ 1
𝑧(𝑧 + 1) ⋯ (𝑧 + 𝑛) ∫ 𝑢𝑧+𝑛−1 1
0
𝑑𝑢
𝐹(𝑧, 𝑛) =𝑧(𝑧 + 1)(𝑧 + 2) ⋯ (𝑧 + 𝑛) 𝑛1 ∙ 2 ∙ 3 ⋯ 𝑛 𝑧
yang merupakan persamaan (𝟏. 𝟏) :
lim
𝑛→∞𝐹(𝑧, 𝑛) = 𝐹(𝑧, ∞) ≡ Γ(𝑧)
1.2 Hubungan Fungsional
Salah satu hubungan relasi yang memenuhi persamaan fungsi gamma adalah persamaan pantulan
(reflection formula) :
Γ(𝑧)Γ(1 − z) =sin 𝑧𝜋 (𝟏. 𝟖)π
Salah satu cara untuk membuktikannya adalah dengan memulai dengan produk dari integral Euler
:
Γ(𝑧 + 1)Γ(1 − z) = ∫ 𝑒−𝑠 ∞
0
𝑠𝑧𝑑𝑠 ∫ 𝑒−𝑡 ∞
0
𝑡−𝑧𝑑𝑡
= ∫(𝑣 + 1)𝑣𝑧𝑑𝑣 2 ∞
0
∫ 𝑢 ∞
0
𝑒−𝑢𝑑𝑢
Yang didapat dari subtitusi 𝑢 = 𝑠 + 𝑡 dan 𝑣 = 𝑠/𝑡. Kita juga membutuhkan Jacobian dari
transformasi ini :
𝐽−1= − |11 1 𝑡 −
𝑠 𝑡2| =
𝑠 + 𝑡 𝑡2 =
(𝑣 + 1)2 𝑢
Integrasi terhadap 𝑢 menjadi sama dengan 1! sementara integrasi terhadap 𝑣 didapatkan dengan
∫(𝑣 + 1)𝑣𝑧𝑑𝑣2 ∞
0
=sin 𝜋𝑧𝜋𝑧
Dengan mengganti Γ(𝑧 + 1) menjadi 𝑧Γ(𝑧) dan didapatkan persamaan (𝟏. 𝟗).
Kasus spesial didapatkan untuk 𝑧 = 1/2, dimana (mengambil akar kuadrat positif)
Γ(1/2) = √𝜋 . (𝟏. 𝟏𝟎)
1.3 Fungsi Beta
Haasil dari fungsi gmma dapat diidentifikasi sebagai penjabaran dari integral yang mengandung
unsur fungsi sin dan cos. Integral tersebut dapat lebih lanjut dimanipulasi untuk mengevaluasi
sebuah angka yang besar dari integral. Hal tersebut menjadi dasar pendefinisian fungsi beta.
Secara umum fungsi beta dalam bentuk integral memiliki formasi :
𝐵(𝑚, 𝑛) = ∫ 𝑥1 𝑚−1
Hubungan fungsi beta dan fungsi gamma dapat dijabarkan dengan melakukan perkalian dua fungsi
= 2 ∫ sin2𝑚−1𝜃 cos2𝑛−1𝜃 𝑑𝜃 𝜋
2
0 Γ(𝑚 + 𝑛)
Untuk bentuk integral cos dan sin, dengan subtitusi 2𝑛 − 1 = 2(𝑛 − 1) + 1 (demikian juga
dengan bagian 𝑚) dapat dijabarkan :
2 ∫ sin2(𝑚−1)+1𝜃 cos2(𝑛−1)+1𝜃 𝑑𝜃
Fungsi beta didapatkan dengan kembali melakukan subtitusi = sin2𝜃 :
∫ sin2(𝑚−1)𝜃 cos2(𝑛−1)𝜃 2 cos 𝜃 sin 𝜃 𝑑𝜃
Sehingga hubungan antara fungsi gamma dan fungsi beta :
𝐵(𝑚, 𝑛) =Γ(𝑚)Γ(𝑛)Γ(𝑚 + 𝑛) (𝟏. 𝟏𝟐)
1.4 Formula Stirling
Sebuah persamaan yang mengandung 𝑛! Ataupun Γ(𝑝) tidak dapat secara sederhana
didiferensialkan. Disini kita menggunakan pendekatan untuk fungsi faktorial atau fungsi Γ yang
disebut persamaan Stirling.
Persamaan ini didapatkan dengan fungsi gamma :
Γ(𝑧 + 1) = 𝑧! = ∫ 𝑡∞ 𝑧
Untuk 𝑧 dengan nilai besar, bentuk logaritma dapat diekspansi menurut deret pangkat :
Sehingga didapatkan :
𝑧! ~ ∫ 𝑒𝑧 ln 𝑧+𝑦√𝑧−(𝑦 2
2 )−𝑧−𝑦√𝑧 ∞
−√𝑧 √𝑧𝑑𝑦
= 𝑒𝑧 ln 𝑧−𝑧√𝑧 ∫ 𝑒−(𝑦 2 2 ) ∞
−√𝑧 𝑑𝑦
= 𝑧𝑧𝑒−𝑧√𝑧 [∫ 𝑒−(𝑦 2 2 ) ∞
−∞ 𝑑𝑦 − ∫ 𝑒
−(𝑦2 )2 −√𝑧
−∞ 𝑑𝑦]
Untuk integral pertama didapatkan √2𝜋. Untuk integral kedua bernilai nol untuk 𝑝 → ∞, dan kita
dapatkan formula Stirling :
𝑧! ~𝑧𝑧𝑒−𝑧√2𝜋𝑧 (𝟏.𝟏𝟒)
Adapun untuk ekspansi asymtot Γ(𝑧 + 1) didapatkan :
Γ(𝑧 + 1) = 𝑧! = 𝑧𝑧𝑒−𝑧√2𝜋𝑧 (1 + 1 12𝑧 +
1
288𝑧2+ ⋯ ) (𝟏. 𝟏𝟓)
Bagian pertama yang merupakan formula Stirling merupakan pendekatan yang baik digunakan
untuk 𝑧 bernilai besar dan bagian keduanya dapat digunakan untuk memperkirakan kesalahan
relatif fungsi tersebut.
Bentuk yang sering dijumpai dalam formula Stirling adalah nilai ln 𝑧! dengan nilai 𝑧 besar. Pada
kasus ini, formula Stirling memberikan hubungan :
ln 𝑧! = ln(𝑧𝑧𝑒−𝑧√2𝜋𝑧) = ln 𝑧𝑧+ ln 𝑒−𝑧+ ln √2𝜋𝑧 = 𝑧 ln 𝑧 − 𝑧 + ln √2𝜋𝑧
Karena nilai 𝑧 besar, bagian ln √2𝜋𝑧 dapat diabaikan sehingga didapatkan persamaan umum :
2.
PERSAMAAN DIFERENSIAL LANJUT
2.1 Persamaan Diferensial Legendre
Persamaan diferensial Legendre memiliki bentuk umum :
(1 − 𝑥)2𝑦′′− 2𝑥𝑦′+ 𝑙(𝑙 + 1)𝑦 = 0 (𝟐. 𝟏)
𝑙 adalah konstanta. Titik singularnya 𝑥 = −1,1, ∞. Pada penggunaan normalnya, variabel 𝑥 biasanya berbentuk kosinus dari sudut kordinat bola yang implikasinya −1 ≤ 𝑥 ≤ 1. Solusi dari
persamaan diferensial ini disebut fungsi Legendre.
Solusi umumnya didapatkan dengan menggunakan konsep ekspansi deret 𝑦 = ∑𝑎𝑛𝑥𝑛.
Substitusikan untuk nilai 𝑦′′, 𝑦′, dan 𝑦 pada persamaan (𝟐. 𝟏) didapatkan :
∑[𝑛(𝑛 − 1)𝑎𝑛𝑥𝑛−2− 𝑛(𝑛 − 1)𝑎𝑛𝑥𝑛− 2𝑛𝑎𝑛𝑥𝑛+ 𝑙(𝑙 + 1)𝑎𝑛𝑥𝑛] ∞
𝑛=0
= 0
Melakukan simplifikasi :
∑{(𝑛 + 2)(𝑛 + 1)𝑎𝑛+2− [𝑛(𝑛 + 1) − 𝑙(𝑙 + 1)]𝑎𝑛}𝑥𝑛 ∞
𝑛=0
= 0
Sehingga didapat hubungan rekursif :
𝑎𝑛+2= [𝑛(𝑛 + 1) − 𝑙(𝑙 + 1)](𝑛 + 1)(𝑛 + 2) 𝑎𝑛 (𝟐. 𝟐)
Nilai 𝑛 = 0,1,2, …. Jika 𝑎0 = 1 dan 𝑎1 = 0 solusi pertama didapat :
𝑦1(𝑥) = 1 − 𝑙(𝑙 + 1)𝑥 2
2! + 𝑙(𝑙 + 1)(𝑙 − 2)(𝑙 + 3) 𝑥4
4! − ⋯ (𝟐. 𝟑)
Serta jika 𝑎0 = 0 fsn 𝑎1 = 1 solusi kedua didapat :
𝑦2(𝑥) = 𝑥 − (𝑙 − 1)(𝑙 + 2)𝑥 3
3! +(𝑙 − 1)(𝑙 + 2)(𝑙 − 3)(𝑙 + 4) 𝑥5
Persamaan tersebut konvergen unutuk |𝑥| < 1 sehingga radius konvergensinya bersatu. Karena
kedua persamaan tersebut bebas secara linear satu sama lain, solusi umum dari persamaan (𝟐. 𝟏)
diperoleh :
𝑦(𝑥) = 𝑐1𝑦1(𝑥) + 𝑐2𝑦2(𝑥)
Dalam banyak aplikasi fisis, parameter 𝑙 pada persamaan Legendre adalah bilangan bulat 𝑙 =
0,1,2, …. Berdampak pada hubungan rekursif :
𝑎𝑙+2 =[𝑙(𝑙 + 1) − 𝑙(𝑙 + 1)](𝑙 + 1)(𝑙 + 2) 𝑎𝑙 = 0
Membuat deretnya terhenti dan didapatkan solusi polynomial dengan orde 𝑙. Secara terpisah, saat
𝑙 genap, 𝑦1(𝑥) tereduksi menjadi sebuah polynomial sementara saat 𝑙 ganjil, 𝑦2(𝑥) yang menjadi polynomial. Solusi ini disebut polynomial Legendre berorde 𝑙. Beberapa polynomial Legendre
awal :
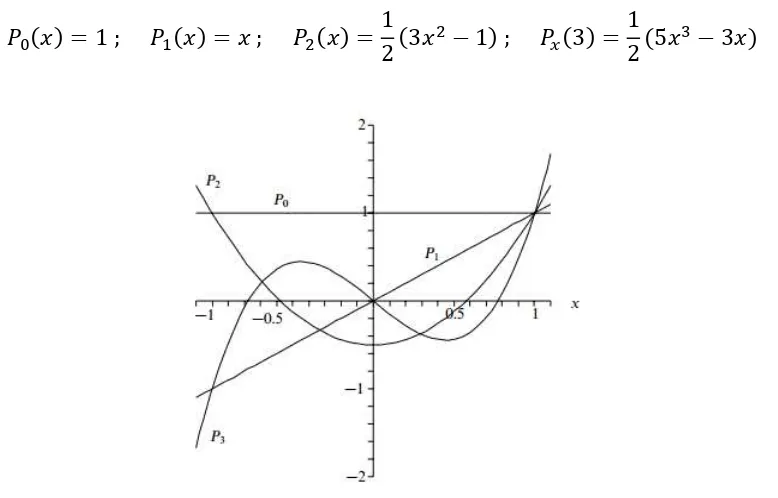
𝑃0(𝑥) = 1 ; 𝑃1(𝑥) = 𝑥 ; 𝑃2(𝑥) =12(3𝑥2− 1) ; 𝑃𝑥(3) =12 (5𝑥3− 3𝑥)
Gambar 2.1 Empat polynomial Legendre awal
2.1.1 Sifat-sifat Polynomial Legendre
Formula Rodrigues merupakan suatu bentuk umum untuk mendefinisikan suatu polynomial.
𝑃𝑙(𝑥) =21𝑙𝑙! 𝑑 𝑙
𝑑𝑥𝑙(𝑥2− 1) (𝟐. 𝟓)
Hal ini dapat dibuktikan dengan memisalkan 𝑢 = (𝑥2− 1)𝑙, sehingga 𝑢′ = 2𝑙𝑥(𝑥2− 1)𝑙−1dan
(𝑥2− 1)𝑢′− 2𝑙𝑥𝑢 = 0
Dengan diferensiasi 𝑙 + 1 kali menggunakan teorema Leibnitz, dapat dilihat hubungan :
[(𝑥2− 1)𝑢𝑙+2+ 2𝑥(𝑙 + 1)𝑢𝑙+1+ 𝑙(𝑙 + 1)𝑢𝑙] − 2𝑙[𝑥𝑢𝑙+1+ (𝑙 + 1)𝑢𝑙] = 0
Atau tereduksi menjadi :
(𝑥2− 1)𝑢𝑙+2+ 2𝑥𝑢𝑙+1− 𝑙(𝑙 + 1)𝑢𝑙 = 0
Mengganti tanda dari persamaan tersebut, didapatkan bentuk yang identic dengan persamaan
Legendre (𝟐. 𝟏) dengan 𝑢𝑙 sebagai variabel terikat. Agar dapat sesuai dengan formula Rodrigues,
kita dapat mengambil bentuk :
𝑢𝑙(𝑥) = 𝑐 𝑙𝑃𝑙(𝑥)
Dimana konstanta 𝑐𝑙 bergatung pada 𝑙. Nilai 𝑙 didapatkan dengan memperhatikan bahwa bagian
dimana turunan ke 𝑙 dari (𝑥2− 1)𝑙 tidak memiliki sebuah faktor 𝑥2− 1, sehingga tidak hilang
pada 𝑥 = 1, adalah (2𝑥)𝑙𝑙! (𝑥2− 1)0. Mengambil 𝑥 = 1, 𝑃𝑙(1) = 1 sehingga 𝑐𝑙 = 2𝑙𝑙! yang
melengkapi formula Rodrigues.
Persamaan Legendre merupakan bentuk Sturm-Lioville dengan 𝑝 = 1 − 𝑥2, 𝑞 = 0, 𝜆 = 𝑙(𝑙 +
1), dan 𝜌 = 1, dan interval alaminya adalah [−1,1]. Karena polynomial Legendre 𝑃𝑙(𝑥) teratur pada titik akhir 𝑥 = ±1, persamaan tersebut orthogonal satu sama lain pada interval tersebut,
sehingga :
∫ 𝑃𝑙(𝑥)𝑃𝑘(𝑥)𝑑𝑥 = {
0 ; 𝑙 ≠ 𝑘 2
2𝑙 + 1 ; 𝑙 = 𝑘 (𝟐. 𝟔)
1
−1
Hal ini dapat dibuktikan dengan menuliskan persamaan diferensial Legendre dengan solusi 𝑃𝑙(𝑥)
dalam bentuk modifikasi :
[(1 − 𝑥2)𝑃
Kalikan dengan 𝑃𝑘(𝑥) lalu integralkan dari = −1 sampai 𝑥 = 1 :
Integralkan secara parsial bagian pertama :
− ∫ 𝑃𝑘′(1 − 𝑥2)𝑃
Membalik aturan untuk 𝑙 dan 𝑘 dan mengurangkan, dapat kita simpulkan :
[𝑘(𝑘 + 1) − 𝑙(𝑙 + 1)] ∫ 𝑃𝑘𝑃𝑙𝑑𝑥 1
−1 = 0
Karena 𝑘 ≠ 𝑙, maka terbukti bahwa syarat orthogonalitas pertama terpenuhi.
Untuk syarat kedua orthogonalitas, dapat dibuktikan dengan menggunakan formula Rodrigues
untuk persamaan Legendre saat = 𝑙 :
Integrasikan secara parsial dengan smua syarat batas habis mereduksi menjadi persamaan :
∫ 𝑃𝑙(𝑥)𝑃𝑙(𝑥)𝑑𝑥 =
Integrasikan bagian integral secara parsial :
Dimana 𝐾𝑙 = ∫ (𝑥−11 2− 1)𝑙𝑑𝑥, sehingga didapat relasi (2𝑙 + 1)𝐾𝑙 = 2𝑙 𝐾𝑙−1 yang menghasilkan
nilai :
𝐾𝑙 =2
2𝑙+1(𝑙!)2
(2𝑙 + 1)!
Sehingga, persamaan orthogonalitas saat 𝑘 = 𝑙 didapatkan :
∫ 𝑃𝑙(𝑥)𝑃𝑙(𝑥)𝑑𝑥 = 1
−1
(2𝑙)! 22𝑙(𝑙!)2
22𝑙+1(𝑙!)2
(2𝑙 + 1)! = 2𝑙 (2𝑙 − 1)!22𝑙(𝑙!)2
22𝑙 2 (𝑙!)2
(2𝑙 + 1)2𝑙(2𝑙 − 1)! =(2𝑙 + 1)2
Sifat lain dari polynomial Legendre adalah fungsi pembangkit. Fungsi pembangkit merupakan alat
yang sangat berguna dalam memanipulasi urutan dari fungsi atau kuantitas dari suatu variabel
bilangan bulat. Kegunaan mendasarnya diimplementasikan pada teori probabilitas.
Secara umum, fungsi pembangkit dari suatu fungsi 𝑓𝑛(𝑥) untuk 𝑛 = 0,1,2, … adalah sebuah fungsi
𝐺(𝑥, ℎ) dimana 𝑥 suatu variabel bebas dengan ℎ variabel dummy sehingga :
𝐺(𝑥, ℎ) = ∑ 𝑓𝑛(𝑥)ℎ𝑛 ∞
𝑛=0
Untuk penerapan di polynomial Legendre, fungsi pembangkitnya :
𝐺(𝑥, ℎ) = (1 − 2𝑥ℎ + ℎ2)−1/2 = ∑ 𝑃 𝑛(𝑥)ℎ𝑛 ∞
𝑛=0
(𝟐. 𝟕)
Dengan melakukan diferensial terhadap 𝑥, didapatkan :
ℎ(1 − 2𝑥ℎ + ℎ2)−3/2 = ∑ 𝑃
𝑛′ℎ𝑛 (𝟐. 𝟖)
serta melakukan diferensial terhadap ℎ :
(𝑥 − ℎ)(1 − 2𝑥ℎ + ℎ2)−3/2 = ∑ 𝑛𝑃
𝑛ℎ𝑛−1 (𝟐. 𝟗)
Persamaan (𝟐. 𝟖)dapat ditulis :
menyamakan koefisien dari ℎ𝑛+1, didapatkan hubungan rekursif :
𝑃𝑛 = 𝑃𝑛+1′ − 2𝑥𝑃𝑛′+ 𝑃𝑛−1′ (𝟐. 𝟏𝟎)
Sementara mengkombinasikan persamaan (𝟐. 𝟖) dan (𝟐. 𝟗) :
(𝑥 − ℎ) ∑ 𝑃𝑛′ℎ𝑛 = ℎ ∑ 𝑛𝑃𝑛ℎ𝑛−1
menyamakan koefisien dari ℎ𝑛 didapatkan hubungan rekursif kedua :
𝑥𝑃𝑛′− 𝑃𝑛−1′ = 𝑛𝑃𝑛 (𝟐. 𝟏𝟏)
Adapun dengan mengkombinasikan (𝟐. 𝟏𝟏) dengan (𝟐. 𝟏𝟎) lalu mengganti 𝑛 dengan 𝑛 − 1 dan
menambahkan dengan , kita dapatkan hubungan rekursif ketiga :
(1 − 𝑥2)𝑃
𝑛′ = 𝑛(𝑃𝑛−1− 𝑥𝑃𝑛) (𝟐. 𝟏𝟐)
2.1.2 Fungsi Legendre Asosiasi
Persamaan umumn dari fungsi Legendre asosiasi adalah :
(1 − 𝑥2)𝑦′′− 2𝑥𝑦′+ [𝑙(𝑙 + 1) − 𝑚2
1 − 𝑥2] 𝑦 = 0 (𝟐. 𝟏𝟑)
Dengan tiga titik singular pada 𝑥 = −1,1, ∞ dan tereduksi menjadi persamaan Legendre normal
saat 𝑚 = 0. Setiap solusi dari persamaan tersebut dikenal dengan fungsi Legendre asosiasi.
Solusi dari ekspansi deret 𝑦 = ∑ 𝑎𝑛𝑥𝑛, dapat diturunkan sesuai dengan persamaan Legendre
normal. Hasil dari langkah tersebut menghasilkan solusi umum yakni fungsi Legendre Asosiasi :
𝑦 = (1 − 𝑥2)𝑚2 𝑑𝑚
𝑑𝑥𝑚𝑃𝑙(𝑥) (𝟐.𝟏𝟒)
atau lebih sering dituliskan sebagai :
𝑃𝑙𝑚(𝑥) = (1 − 𝑥2)𝑚2 𝑑𝑚
𝑑𝑥𝑚𝑃𝑙(𝑥) (𝟐. 𝟏𝟓)
Sama halnya dengan persamaan Legendre, persamaan Legendre asosiasi juga memiliki sifat
∫ 𝑃𝑙𝑚(𝑥) 1
−1 𝑃𝑘
𝑚(𝑥)𝑑𝑥 = {0 ; 𝑙 ≠ 𝑘2
2𝑙 + 1
(𝑙 + 𝑚)!
(𝑙 − 𝑚)! ; 𝑙 = 𝑘 (𝟐. 𝟏𝟔)
Hasil ini didapat dengan menggunakan formula Rodrigues pada persamaan (𝟐. 𝟓)dan persamaan
fungsi Legendre asosiasi (𝟐. 𝟏𝟓).
Sifat lain dari persamaan Legende asosiasi adalah fungsi pembangkit yang memenuhi :
𝐺(𝑥, ℎ) = (2𝑚)!(1 − 𝑥2)
𝑚 2
2𝑚𝑚! (1 − 2ℎ𝑥 + ℎ2)𝑚+12 = ∑ 𝑃𝑛+𝑚 𝑚 ∞
𝑛=0
(𝑥)ℎ𝑛 (𝟐. 𝟏𝟕)
yang diperoleh dari penurunan sebanyak 𝑚 kali dari dari fungsi pembangkit persamaan polynomial
Legendre (𝟐. 𝟕).
Hal terakhir dari sifat persamaan Legendre asosiasi yang perlu diketahui adalah hubungan rekursif.
Beberapa diantaranya :
𝑃𝑛𝑚+1 = 2𝑚𝑥
(1 − 𝑥2)12𝑃𝑛
𝑚+ [𝑚(𝑚 − 1) − 𝑛(𝑛 + 1)]𝑃
𝑛𝑚−1 (𝟐. 𝟏𝟖)
(2𝑛 + 1)𝑥𝑃𝑛𝑚 = (𝑛 + 𝑚)𝑃𝑛−1𝑚 + (𝑛 − 𝑚 + 1)𝑝𝑛+1𝑚 (𝟐. 𝟏𝟗)
(2𝑛 + 1)(1 − 𝑥2)12𝑃
𝑛𝑚 = 𝑃𝑛+1𝑚+1− 𝑃𝑛−1𝑚+1 (𝟐. 𝟐𝟎)
yang berlaku untuk 𝑚 positif maupun negatif.
2.2 Persamaan Diferensial Bessel
Persamaan Bessel memiliki bentuk umum :
𝑥2𝑦′′+ 𝑥𝑦′+ (𝑥2− 𝑣2)𝑦 = 0 (𝟐. 𝟐𝟏)
Memiliki singularitas dititik 𝑥 = 0, ∞. Parameter 𝑣 sebuah konstanta yang ≥ 0. Digunakan pada
persamaan fisis mirip dengan persamaan Legendre, namun untuk kordinat silinder. Persamaan
tersebut dapat disederhanakan :
𝑦′′+1
𝑥 𝑦′+ (1 − 𝑣2
dengan menggunakan solusi deret 𝑦 = 𝑥𝜎∑∞𝑛=0𝑎𝑛𝑥𝑛 yang disubstitusi pada persamaan (𝟐. 𝟐𝟐)
dan dikalikan dengan 𝑥2−𝜎 didapatkan :
∑[(𝜎 + 𝑛)(𝜎 + 𝑛 − 1) + (𝜎 + 𝑛) − 𝑣2] ∞
𝑛=0
𝑎𝑛𝑥𝑛+ ∑ 𝑎𝑛𝑥𝑛+2 ∞
𝑛=0
= 0
yang disederhanakan :
∑[(𝜎 + 𝑛)2− 𝑣2] ∞
𝑛=0
𝑎𝑛𝑥𝑛+ ∑ 𝑎𝑛𝑥𝑛+2 ∞
𝑛=0
= 0
Perhatikan koefisien dari 𝑥0, didapatkan hubungan :
𝜎2− 𝑣2 = 0
sehingga 𝜎 = ±𝑣. Untuk koefisien dari pangkat lebih tinggi :
[(𝜎 + 1)2− 𝑣2]𝑎 1= 0
[(𝜎 + 𝑛)2− 𝑣2]𝑎
𝑛+ 𝑎𝑛−2 = 0 𝑛 ≥ 2
dengan substitusi 𝜎 = ±𝑣, didapatkan hubungan rekursif :
(1 ± 2𝑣)𝑎1 = 0 (𝟐. 𝟐𝟑)
𝑛(𝑛 ± 2𝑣)𝑎𝑛+ 𝑎𝑛−2 = 0 𝑛 ≥ 2 (𝟐. 𝟐𝟒)
Persamaan (𝟐. 𝟐𝟑) memberikan dampak 𝑎1 = 0.
Sekarang solusi umum dari persamaan Bessel terdapat dua syarat : saat 𝑣 sebuah bilangan bulat
dan saat bukan bilangan bulat.
2.2.1 Fungsi Bessel untuk 𝒗 Bukan Bilangan Bulat
Saat 𝑣 bukan bilangan bulat, 𝜎1 = 𝑣 dan 𝜎2 = −𝑣 tidak akan berubah oleh sebuah bilangan bulat
sehingga didapatkan dua solusi independen dalam bentuk deret Frobenius. Kondisi khusus saat
𝑣 = 𝑚/2 untutk 𝑚 = 1,3,5, …, dan 𝜎1− 𝜎2 = 2𝑣 = 𝑚 adalah bilangan bulat ganjil positif.
𝑎𝑛 = −𝑛(𝑛 ± 2𝑣) untuk 𝑛 = 2,4,6, … ,𝑎𝑛−2
= 0 untuk 𝑛 = 1,3,5, …,
Mengambil nilai 𝑎0 = 1 pada setiap kasus, didapatkan dua solusi :
𝑦±𝑣(𝑥) = 𝑥±𝑣[1 − 𝑥 2
2(2 ± 2𝑣) +
𝑥4
2 × 4(2 ± 𝑣)(4 ± 2𝑣) − ⋯]
dengan bantuang fungsi gamma, dapat dituliskan :
𝑎0 = 2±𝑣Γ(1 ± v)1
yang merupakan generalisasi dari fungsi faktorial.
Pemaparan tersebut mengantarkan pada dua solusi persamaan Bessel yang biasa dilambangkan
𝐽𝑣(𝑥) dan 𝐽−𝑣(𝑥) :
𝐽𝑣(𝑥) =Γ(𝑣 + 1) (1 𝑥2) 𝑣
[1 −𝑣 + 1 (1 𝑥2)2+(𝑣 + 1)(𝑣 + 2)1 2! (1 𝑥2)4− ⋯ ]
atau
𝐽𝑣(𝑥) = ∑ (−1) 𝑛
𝑛! Γ(𝑣 + 𝑛 + 1) ( 𝑥 2)
𝑣+2𝑛 ∞
𝑛=0
(𝟐. 𝟐𝟓)
serta solusi keduanya
𝐽−𝑣(𝑥) = ∑ (−1) 𝑛
𝑛! Γ(𝑛 − 𝑣 + 1) ( 𝑥 2)
2𝑛−𝑣 ∞
𝑛=0
(𝟐. 𝟐𝟔)
Fungsi 𝐽𝑣(𝑥) dan 𝐽−𝑣(𝑥) disebut juga solusi fungsi Bessel jenis pertama. Sehingga untuk 𝑣 bukan
bilangan bulat, persamaan diferensial Bessel mempunyai solusi umum :
𝑦(𝑥) = 𝑐1 𝐽𝑣(𝑥) + 𝑐2 𝐽−𝑣(𝑥)
2.2.2 Fungsi Bessel untuk 𝒗 Bilangan Bulat
Saat 𝑣 berupa bilangan bulat, solusi Bessel tipe pertama tidak memenuhi syarat tersebut. Saat
𝐽−𝑣(𝑥) = (−1)𝑣𝐽𝑣(𝑥)
Sehingga keduanya bergantung secara linear. Hal ini membuat kedua fungsi 𝐽𝑣(𝑥) dan 𝐽−𝑣(𝑥)
solusi umum pada jenis pertama tidak sesuai, sehingga didefinisikan fungsi :
𝑌𝑣(𝑥) =𝐽𝑣(𝑥) cos 𝑣𝜋 − 𝐽sin 𝑣𝜋 −𝑣(𝑥) (𝟐. 𝟐𝟕)
yang disebut fungsi Bessel jenis kedua dengan orde 𝑣 atau biasa dikenal dengan fungsi Neumann.
Kombinasi linear dari fungsi Bessel dari jenis pertama dan jenis kedua berkesesuaian dengan :
𝐻𝑣(1)(𝑥) = 𝐽𝑣(𝑥) + 𝑖𝑌𝑣(𝑥), 𝐻𝑣(2)(𝑥) = 𝐽𝑣(𝑥) − 𝑖𝑌𝑣(𝑥) (𝟐. 𝟐𝟖)
keduanya disebut sebagai fungsi Hankel tiper pertama dan tipe kedua.
2.2.3 Sifat-sifat Fungsi Bessel 𝑱𝒗(𝒙)
Karena tidak memiliki batas tertentu, fungsi Bessel dapat dimislkan berada pada batas [𝑎, 𝑏] untuk
menyelidiki sifat ortogonalitasnya. Bentuk umum dari sifat ortogonalitas fungsi Bessel :
∫ 𝑥𝐽𝑣(𝛼𝑥)𝐽𝑣(𝛽𝑥)𝑑𝑥 = 𝑏
𝑎 {
0 ; 𝛼 ≠ 𝛽 1
2[(𝑥2− 𝑣2
𝛼2) 𝐽𝑣2(𝛼𝑥) + 𝑥2[𝐽𝑣′(𝛼𝑥)]2]𝑏𝑎 ; 𝛼 = 𝛽 (𝟐. 𝟐𝟗)
Untuk menentukan kondisi batas dari hasil pertama, saat 𝛼 ≠ 𝛽, didefinisikan fungsi 𝑓(𝑥) =
𝐽𝑣(𝛼𝑥) dan 𝑔(𝑥) = 𝐽𝑣(𝛽𝑥) yang harus memenuhi kondisi :
𝑥2𝑓′′+ 𝑥𝑓′ + (𝛼2𝑥2− 𝑣2)𝑓 = 0
𝑥2𝑔′′+ 𝑥𝑔′+ (𝛽2𝑥2− 𝑣2)𝑔 = 0
Selain itu, juga terdapat hubungan rekursif :
𝑑
𝑑𝑥[𝑥𝑣𝐽𝑣(𝑥)] = 𝑥𝑣𝐽𝑣−1(𝑥) (𝟐.𝟑𝟎) 𝑑
𝑑𝑥[𝑥−𝑣𝐽𝑣(𝑥)] = −𝑥−𝑣𝐽𝑣+1(𝑥) (𝟐.𝟑𝟏)
Ekspansi turunan pada ruas kiri persamaan (𝟐. 𝟑𝟎)dan bagi dengan 𝑥𝑣−1 :
Serta dengan ekspansi turunan pada ruas kiri persamaan (𝟐. 𝟑𝟏) dan kalikan dengan 𝑥𝑣+1 :
𝑥𝐽𝑣′(𝑥) − 𝑣𝐽𝑣(𝑥) = −𝑥𝐽𝑣+1(𝑥) (𝟐.𝟑𝟑)
Tambahkan (𝟐. 𝟑𝟐) dengan (𝟐. 𝟑𝟑) didapatkan :
𝐽𝑣−1(𝑥) − 𝐽𝑣+1(𝑥) = 2𝐽𝑣′(𝑥) (𝟐. 𝟑𝟒)
Serta dengan mengurangkan (𝟐. 𝟑𝟐) dengan (𝟐. 𝟑𝟑) didapatkan :
𝐽𝑣−1(𝑥) + 𝐽𝑣+1(𝑥) =2𝑣𝑥 𝐽𝑣(𝑥) (𝟐. 𝟑𝟓)
Sifat lain dari funsi Bessel jenis pertama adalah fungsi pembagkit yang memenuhi persamaan :
𝐺(𝑥, ℎ) = 𝑒[𝑥2(ℎ−1ℎ)]= ∑ 𝐽𝑛(𝑥)ℎ𝑛 ∞
𝑛=−∞
(𝟐. 𝟑𝟔)
Dengan menggunakan fungsi pembangkit tersebut, fungsi Bessel dapat dijabarkan dalam bentuk
integral :
𝐽𝑛(𝑥) = 1𝜋∫ cos(𝑛𝜃 − 𝑥 sin 𝜃) 𝜋
0 𝑑𝜃 (𝟐. 𝟑𝟕)
2.3 Persamaan Diferensial Hermite
Persamaan Hermite memiliki bentuk umum :
𝑦′′− 2𝑥𝑦′+ 2𝑣𝑦 = 0 (𝟐. 𝟑𝟖)
dengan singularitas di titik 𝑥 = ∞. Parameter 𝑣 adalah bilangan real, meski lebih sering berupa
bilangan bulat pada pengaplikasian. Persamaan Hermite muncul dalam mendeskripsikan fungsi
gelombang dari osilasi harmonik. Setiap solusi dari persamaan ini disebut fungsi Hermite.
Karena 𝑥 = 0 adalah titik biasa dari persamaan, kita bias mencari dua solusi independen dalam
bentuk deret pangkat :
𝑦 = ∑ 𝑎𝑚𝑥𝑚 ∞
dengan melakukan substitusi pada persamaan Hermite, diperoleh bentuk :
∑[(𝑚 + 2)(𝑚 + 1)𝑎𝑚+2+ 2(𝑣 − 𝑚)𝑎𝑚] ∞
𝑚=0
𝑥𝑚= 0
yang menghasilkan hubungan rekursif :
𝑎𝑚+2= −(𝑚 + 2)(𝑚 + 1) 𝑎2(𝑣 − 𝑚) 𝑚
Jika dipilih 𝑣 = 𝑛 dimana 𝑛 adalaha bilanga bulat positif, dapat dilihat 𝑎𝑛+2 = 𝑎𝑛+4= ⋯ = 0,
sehingga satu solusi dari persamaan Hermite adalah polynomial dengan orde 𝑛. Untuk 𝑛 genap,
dipilih 𝑎0= (−1)𝑛2𝑛!/ (𝑛/2)!, sementara untuk 𝑛 ganjil digunakan 𝑎1 = (−1)𝑛−12 2𝑛!/ [1
2(𝑛 −
1)] !. Pilihan ini memungkinkan solusi umum ditulis sebagai :
𝐻𝑛(𝑥) = (2𝑥)𝑛− 𝑛(𝑛 − 1)(2𝑥)𝑛−1+𝑛(𝑛 − 1)(𝑛 − 2)(𝑛 − 3)2! (2𝑥)𝑛−4− ⋯
Atau disederhanakan :
𝐻𝑛(𝑥) = ∑(−1)𝑚 𝑛
2
𝑚=0
𝑛!
𝑚! (𝑛 − 2𝑚)!(2𝑥)𝑛−2𝑚 (𝟐. 𝟑𝟗)
dimana 𝐻𝑛(𝑥) disebut polynomial Hermite dan notasi 𝑛/2 menotasikan bagian bilangan bulat
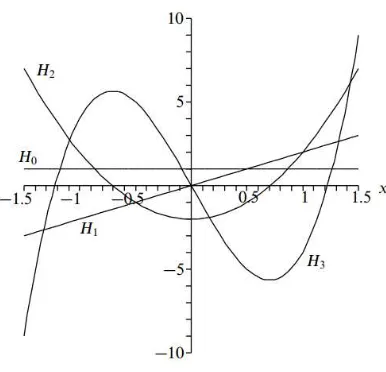
dari 𝑛/2 . Dapat pula dilihat hubungan 𝐻𝑛(−𝑥) = (−1)𝑛𝐻𝑛(𝑥). Beberapa nilai pertama dari
polynomial Hermite :
Gambar 2.2 Skema beberapa nilai pertama polynomial Hermite
2.3.1 Sifat-sifat Polynomial Hermite
Sifat pertama adalah formula Rodrigues dari polynomial Hermite :
𝐻𝑛(𝑥) = (−1)𝑛𝑒𝑥2 𝑑 𝑛
𝑑𝑥𝑛(𝑒−𝑥
2
) (𝟐. 𝟒𝟎)
Didapatkan dengan menggunakan teorema Leibniz.
Karena polynomial Hermite 𝐻𝑛(𝑥) merupakan solusi dari persamaan Hermite dan memiliki
interval alami [−∞, ∞], keduanya harus orthogonal berdasarkan pada fungsi pemberat 𝜌 = 𝑒−𝑥2 :
∫ 𝐻𝑛(𝑥)𝐻𝑘(𝑥)𝑒−𝑥2 ∞
−∞ 𝑑𝑥 = {
0 ; 𝑛 ≠ 𝑘
2𝑛𝑛! √𝜋 ; 𝑛 = 𝑘 (𝟐. 𝟒𝟏)
yang dapat dibuktikan dengan menggunakan formula Rodrigues.
Hal lain dari polynomial Hermite yang penting diketahui adalah fungsi pembangkit yang sesuai
dengan persamaan :
𝐺(𝑥, ℎ) = 𝑒2ℎ𝑥−ℎ2
= ∑𝐻𝑛𝑛!(𝑥)
∞
𝑛=0
ℎ𝑛 (𝟐. 𝟒𝟐)
𝐻𝑛+1(𝑥) = 2𝑥𝐻𝑛(𝑥) − 2𝑛𝐻𝑛−1(𝑥) (𝟐. 𝟒𝟑)
𝐻𝑛′(𝑥) = 2𝑛𝐻𝑛−1(𝑥) (𝟐. 𝟒𝟒)
2.4 Persmaan Diferensial Laguerre
2.4.1 Persamaan Umum dan Solusi Umu
Persamaan Laguerre memiliki bentuk umum :
𝑥𝑦′′+ (1 − 𝑥)𝑦′+ 𝑣𝑦 = 0 (𝟐. 𝟒𝟓)
yang memiliki sigularitas regular pada 𝑥 = 0 dan titik singularitas esensinya pada 𝑥 = ∞.
Parameter 𝑣 merupakan bilangan real, meski pada penggunaannya dalam aplikasi fisika hampir
selalu menggunakan bilangan genap. Persamaan Laguerre ini muncul dalam mendeskripsikan
fungsi gelombang atom hidrogen. Setiap solusi dari persamaan Laguerre disebut fungsi Laguerre.
Karena 𝑥 = 0 merupakan titik singular regular persamaan tersebut, kita dapat mencari solusi
dalam bentuk deret Frobenius :
𝑦(𝑥) = ∑ 𝑎𝑚𝑥𝑚+𝜎 ∞
𝑚=0
Substitusi ke persamaan (𝟐. 𝟒𝟓)dan membagi dengan 𝑥𝜎−1, kita dapatkan :
∑[(𝑚 + 𝜎)(𝑚 + 𝜎 − 1) + (1 − 𝑥)(𝑚 + 𝜎) + 𝑣𝑥]𝑎𝑚𝑥𝑚 = 0 ∞
𝑚=0
Substitusi 𝜎 = 0 dan membuat koefisien 𝑥𝑚+1 lenyap, didapatkan hubungan rekursif :
𝑎𝑚+1= (𝑚 + 1)𝑚 − 𝑣2𝑎𝑚
Ingat bahwa 𝑣 merupakan bilangan bulat dalam aplikasi fisis. Sehingga, jika 𝑣 = 𝑛, dimana 𝑛
adalah bilangan bulat positif, didapatkan 𝑎𝑛+1= 𝑎𝑛+2 = ⋯ = 0, dan solusi dari persamaan
Laguerre adalah sebuah polynomial orde 𝑛. Secara koncensional, dengan memilih 𝑎0 = 1
𝐿𝑛(𝑥) =(−1) 𝑛
𝑛! [𝑥𝑛− 𝑛2
1! 𝑥𝑛−1+
𝑛2(𝑛 − 1)2
2! 𝑥𝑛−2− ⋯ + (−1)𝑛𝑛!] (𝟐. 𝟒𝟔)
= ∑(−1)𝑚 𝑛!
(𝑚!)2(𝑛 − 𝑚)! 𝑥𝑚 𝑛
𝑚=0
(𝟐. 𝟒𝟕)
dimana 𝐿𝑛(𝑥) disebut juga 𝑛 polynomial Laguerre. Perlu dicatat bahwa 𝐿𝑛(0) = 1. Beberapa nilai
awal dari polynomial Laguerre adalah :
𝐿0(𝑥) = 1; 𝐿1(𝑥) = −𝑥 + 1; 2! 𝐿2(𝑥) = 𝑥2− 4𝑥 + 2; 3! 𝐿3(𝑥) = −𝑥3+ 9𝑥2− 18𝑥 + 6
Gambar 2.3 Skema beberapa nilai awal polynomial Laguerre
2.4.2 Sifat-sifat Polynomial Laguerre
Sifat pertama adalah formula Rodrigues polynomial Laguerre :
𝐿𝑛(𝑥) =𝑒 𝑥
𝑛! 𝑑𝑛
𝑑𝑥𝑛(𝑥𝑛𝑒−𝑥) (𝟐. 𝟒𝟕)
yang dapat diturunkan dari persamaan Leibniz.
Sifat selanjutnya adalah ortogonalitas dari polynomial Laguerre. Karena polynomial Laguerre
adalah solusi dari suatu persamaan dengan regular pada titik akhirnya, polynomial tersebut
∫ 𝐿𝑛(𝑥)𝐿𝑚(𝑥)𝑒−𝑥 ∞
0 𝑑𝑥 = {0 , 𝑛 ≠ 𝑚1 , 𝑚 = 𝑚 (𝟐. 𝟒𝟖)
yang diperoleh dengan menurunkan formula Rodrigues polynomial Laguerre.
Hal lain adalah bentuk dari fungsi pembangkit. Untuk polynomial Laguerre, fungsi pembangkitnya
memenuhi persamaan :
𝐺(𝑥, ℎ) =𝑒−𝑥ℎ1 − ℎ/(1 − ℎ) = ∑ 𝐿𝑛(𝑥)ℎ𝑛 ∞
𝑛=0
(𝟐. 𝟒𝟗)
Dari fungsi pembangkit tersebut, dengan menurunkan terhadap 𝑥 dan ℎ, kita dapat memperoleh
hubunganrekursif berkaitan dengan polynomial Laguerre. Bebeapa bentuk rekursif dari
polynomial Laguerre adalah sebagai berikut :
(𝑛 + 1)𝐿𝑛+1(𝑥) = (2𝑛 + 1 − 𝑥)𝐿𝑛(𝑥) − 𝑛𝐿𝑛−1(𝑥) (𝟐.𝟓𝟎)
𝐿𝑛−1(𝑥) = 𝐿′𝑛−1(𝑥) − 𝐿′𝑛(𝑥) (𝟐. 𝟓𝟏)
𝑥𝐿′𝑛(𝑥) = 𝑛𝐿𝑛(𝑥) − 𝑛𝐿𝑛−1(𝑥) (𝟐. 𝟓𝟐)
Hubungan pertama dan kedua didapatkan dari fungsi pembangkit sementara hubungan ketiga
merupakan kombinasi dari hubungan pertama dan kedua.
2.4.3 Fungsi Laguerre Asosiasi
Persamaan Laguerre asosiasi memiliki bentuk umum :
𝑥𝑦′′+ (𝑚 + 1 − 𝑥)𝑦′+ 𝑛𝑦 = 0 (𝟐. 𝟓𝟑)
Titik singularitas regulat di 𝑥 = 0 dan titik singularitas esensi 𝑥 = ∞. Nilai 𝑛 dan 𝑚 dalam aplikasi
fisis adalah bilangan bulat positif. Digunakan pada aplikasi mekanika kuantum. Setiap solusi dari
persamaan ini disebut fungsi Laguerre asosiasi.
Solusi untuk 𝑛 dan 𝑚 positif diberikan oleh polynomial Laguerre asosiasi :
𝐿𝑚𝑛 = (−1)𝑚 𝑑 𝑚
𝑑𝑥𝑚𝐿𝑛+𝑚(𝑥) (𝟐. 𝟓𝟒)
Pembuktian ini dapat dilakukan dengan melakukan substitusi 𝐿𝑛(𝑥) pada persamaan Laguerre non
𝑥𝐿′′𝑛+𝑚+ (1 − 𝑥)𝐿′𝑛+𝑚 + (𝑛 + 𝑚)𝐿𝑛+𝑚 = 0
Turunkan 𝑚 kali dengan teorema Leibniz lalu mengurutkannya kita dapatkan :
𝑥𝐿(𝑚+2)𝑛+𝑚 + (𝑚 + 1 − 𝑥)𝐿(𝑚+1)𝑛+𝑚 + 𝑛𝐿(𝑚)𝑛+𝑚 = 0
Kalikan dengan (−1)𝑚 dan dengan 𝐿𝑚𝑛 = (−1)𝑚𝐿(𝑚)𝑛+𝑚, didapatkan :
𝑥(𝐿𝑚𝑛)′′+ (𝑚 + 1 − 𝑥)(𝐿𝑚𝑛)′+ 𝑛𝐿𝑚𝑛 = 0
yang memperlihatkan bahwa 𝐿𝑚𝑛 adalah solusi dari persamaan (𝟐. 𝟓𝟒).
Beberapa nilai awal dari polynomial Laguerre asosiasi adalah :
𝐿𝑚0(𝑥) = 1
𝐿1𝑚(𝑥) = −𝑥 + 𝑚 + 1
2! 𝐿𝑚2(𝑥) = 𝑥2− 2(𝑚 + 2)𝑥 + (𝑚 + 1)(𝑚 + 2)
Secara umum, polynomial Laguerre asosiasi biasa memiliki bentuk :
𝐿𝑚𝑛(𝑥) = ∑(−1)𝑘 𝑛
𝑘=0
(𝑛 + 𝑚)!
𝑘! (𝑛 − 𝑘)! (𝑘 + 𝑚)! 𝑥𝑘 (𝟐. 𝟓𝟓)
2.4.4 Sifat-sifat Polynomial Laguerre Asosiasi
Formula Rodrigues dari polynomial Laguerre asosiasi diberikan oleh :
𝐿𝑚𝑛(𝑥) =𝑒 𝑥𝑥−𝑚
𝑛! 𝑑𝑛
𝑑𝑥𝑛(𝑥𝑛+𝑚𝑒−𝑥) (𝟐. 𝟓𝟔)
yang didapatkan dari turunan ke 𝑛 dengan teorema Leibniz.
Dengan fungsi pemberat 𝜌 = 𝑥𝑚𝑒−𝑥, sifat ortogonalitas polynomial Laguerre asosiasi dapat
dituliskan :
∫ 𝐿𝑚𝑛(𝑥)𝐿𝑚𝑘(𝑥)𝑥𝑚𝑒−𝑥𝑑𝑥 = {
0 , 𝑛 ≠ 𝑘 (𝑛 + 𝑚)!
𝑛! , 𝑛 = 𝑘
∞
0 (𝟐. 𝟓𝟕)
Adapun fungsi pembangkit dari polynomial Laguerre asosiasi diberikan oleh persamaan :
𝐺(𝑥, ℎ) =(1 − ℎ)𝑒−𝑥ℎ/(1−ℎ)𝑚+1 = ∑ 𝐿𝑚𝑛(𝑥)ℎ𝑛 ∞
𝑛=0
(𝟐. 𝟓𝟖)
yang didapatkan dengan menurunkan fungsi pembangkit polynomial Laguerre biasa sebanyak 𝑚
kali terhadap 𝑥 dan menggunakan persamaan (𝟐. 𝟓𝟒).
Dari persamaan fungsi pembangkit polynomial Laguerre asosisasi tersebut dapat diturunkan
hubungan rekursif :
(𝑛 + 1)𝐿𝑚𝑛+1(𝑥) = (2𝑛 + 𝑚 + 1 − 𝑥)𝐿 𝑛
𝑚(𝑥) − (𝑛 + 𝑚)𝐿 𝑛−1
𝑚 (𝑥) (𝟐. 𝟓𝟗)
𝑥(𝐿𝑚𝑛)′(𝑥) = 𝑛𝐿𝑚𝑛(𝑥) − (𝑛 − 𝑚)𝐿𝑚𝑛−1(𝑥) (𝟐. 𝟔𝟎)
2.5 Persamaan Diferensial Chebyshev
2.5.1 Persamaan Umum dan Solusi Umum
Persamaan Chebysehev memiliki bentuk umum :
(1 − 𝑥2)𝑦′′− 𝑥𝑦′+ 𝑣2𝑦 = 0 (𝟐. 𝟔𝟏)
dengan titik singularitas di 𝑥 = −1, 1, ∞. Solusi dari persamaan diferensial ini disebut sebagai
fungsi Chebyshev.
Solusi umumnya didapatkan melalui solusi deret 𝑦 = ∑∞𝑚=0𝑎𝑚𝑥𝑚 dimana dengan substitusi 𝑥 =
cos 𝜃 persamaan Chebyshev (dengan 𝑣 = 𝑛) menjadi :
𝑑2𝑦
𝑑𝜃2+ 𝑛2𝑦 = 0
Membentuk persamaan osilasi harmonik dengan solusi cos 𝑛𝜃 dan sin 𝑛𝜃. Hal ini membuat solusi
linear dari persamaan Chebyshev menjadi :
𝑇𝑛(𝑥) = cos(𝑛 cos−1𝑥) dan 𝑈𝑛(𝑥) = sin(𝑛 cos−1𝑥) (𝟐. 𝟔𝟐)
Dengan 𝑇𝑛(𝑥) adalah polynomial sementara 𝑈𝑛(𝑥) bukan polynomial. Hal ini dapat ditunjukkan
dengan mencari bentuk ekspansi dari perpaduan kedua fungsi tersebut.
𝑇𝑛(𝑥) + 𝑖𝑈𝑛(𝑥) = cos 𝑛𝜃 + 𝑖 sin 𝑛𝜃
= (cos 𝜃 + 𝑖 sin 𝜃)𝑛
= (𝑥 + 𝑖√1 − 𝑥2)𝑛
Dimana |𝑥| ≤ 1.
Dengan konsep ekspansi binomial :
(𝑎 + 𝑏)𝑛 = ∑ (𝑛
𝑚)
𝑛
𝑚=0
𝑎𝑛−𝑚𝑏𝑚 (𝟐. 𝟔𝟑)
Bentuk superposisi kompleksnya didapatkan :
𝑇𝑛(𝑥) + 𝑖𝑈𝑛(𝑥) = ∑ (𝑛𝑚) 𝑛
𝑚=0
𝑥𝑛−𝑚(1 − 𝑥2)𝑚/2
Atau dalam bentuk ekspansinya :
𝑇𝑛(𝑥) = 𝑥𝑛− (𝑛2) 𝑥𝑛−2(1 − 𝑥2) + (𝑛4)𝑥𝑛−4(1 − 𝑥2)2− ⋯ (𝟐. 𝟔𝟒)
𝑈𝑛(𝑥) = √1 − 𝑥2[(𝑛1) 𝑥𝑛−1− (𝑛3) 𝑥𝑛−3(1 − 𝑥2) + (𝑛5) 𝑥𝑛−5(1 − 𝑥2)2− ⋯ ] (𝟐. 𝟔𝟓)
Dimana (𝑚𝑛) = 𝑛!
𝑚!(𝑛−𝑚)! adalah koefisien binomial, 𝑇𝑛(𝑥) bentuk pertama polynomial Chebyshev,
dan 𝑈𝑛(𝑥) bentuk kedua polynomial Chebyshev.
Beberapa nilai awal untuk polynomial Chebyshev bentuk pertama :
Gambar 2.4 Beberapa nilai awal polynomial Chebyshev bentuk pertama
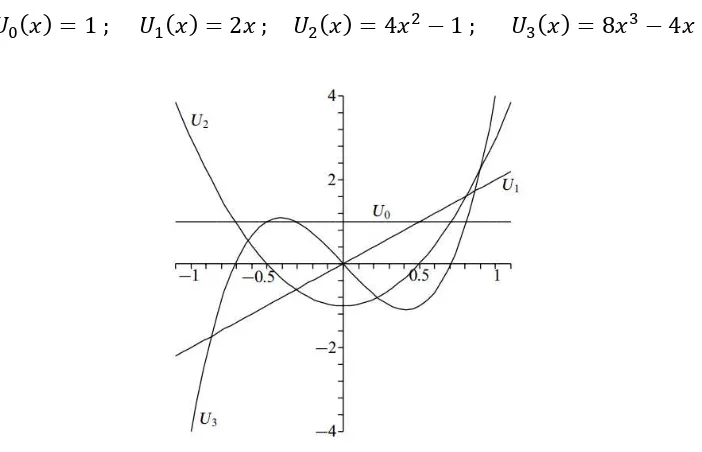
Sedang beberapa nilai awal untuk polynomial Chebyshev bentuk kedua :
𝑈0(𝑥) = 1 ; 𝑈1(𝑥) = 2𝑥 ; 𝑈2(𝑥) = 4𝑥2− 1 ; 𝑈3(𝑥) = 8𝑥3− 4𝑥
Gambar 2.4 Beberapa nilai awal polynomial Chebyshev bentuk kedua
Bentuk lain didapatkan saat mensubstitusikan 𝑥 = cos 𝜃, maka 𝑇𝑛(𝑥) = cos 𝑛𝜃. Dari persamaan
euler :
𝑒𝑖𝑛𝜃+ 𝑒−𝑖𝑛𝜃 = 2 cos 𝑛𝜃
Sehingga 𝑇𝑛(𝑥) = 1
2(𝑒𝑖𝑛𝜃+ 𝑒−𝑖𝑛𝜃) = 1
atau
𝑇𝑛(𝑥) =12{(𝑥 + 𝑖 √1 − 𝑥2) 𝑛
+ (𝑥 − 𝑖 √1 − 𝑥2)𝑛}
Dengan teorema binomial :
(𝑥 ± 𝑖 √1 − 𝑥2)𝑛 = ∑ 𝐶𝑟𝑛 𝑛
𝑟=0
𝑥𝑛−𝑟(±𝑖√1 − 𝑥2)𝑟
sehingga
𝑇𝑛(𝑥) = 12 {∑ 𝐶𝑟𝑛 𝑛
𝑟=0
𝑥𝑛−𝑟(+𝑖√1 − 𝑥2)𝑟+ ∑ 𝐶𝑟𝑛 𝑛
𝑟=0
𝑥𝑛−𝑟(−𝑖√1 − 𝑥2)𝑟}
= 12 ∑ 𝐶𝑟𝑛 𝑛
𝑟=0
𝑥𝑛−𝑟(𝑖)𝑟(1 − 𝑥2)𝑟/2{1 + (−1)𝑟}
Hanya berlaku untuk 𝑟 genap, sehingga :
𝑇𝑛(𝑥) = ∑ 𝐶𝑟𝑛 𝑛
𝑟=0
𝑥𝑛−𝑟(𝑖)𝑟(1 − 𝑥2)𝑟/2
Dengan memisalkan 𝑟 = 2𝑠
𝑇𝑛(𝑥) = ∑ 𝐶2𝑠𝑛 𝑛/2
𝑠=0
𝑥𝑛−2𝑠(𝑖)2𝑠(1 − 𝑥2)𝑠
Sehingga solusi pertama dalam bentuk polynomial:
𝑇𝑛(𝑥) = ∑ 𝐶2𝑟𝑛 𝑛/2
𝑟=0
𝑥𝑛−2𝑟(−1)𝑟(1 − 𝑥2)𝑟 (𝟐. 𝟔𝟔)
Dengan melakukan langkah serupa, solusi kedua dalam bentuk polynomial adalah :
𝑈𝑛(𝑥) = ∑ 𝐶2𝑟+1𝑛 (𝑛−1)/2
𝑟=0
2.5.2 Sifat-sifat Polynomial Chebyshev
Polynomial Cheyshev dapat dituliskan dalam bentuk formula Rodrigues :
𝑇𝑛(𝑥) = (−1)
Sementara sifat orthogonalitasnya memenuhi persamaan :
Sementara saat ≠ 𝑛 :
∫ 𝑇𝑛(𝑥)𝑇𝑚(𝑥)(1 − 𝑥2)−1/2𝑑𝑥 = 1
−1
1 2 ([
1
𝑛 + 𝑚 sin(𝑛 + 𝑚)𝜃] 𝜋0 + [ 1
𝑛 − 𝑚 sin(𝑛 − 𝑚)𝜃] 𝜋0) = 0
Sifat lain yang penting diketahui adalah fungsi pembangkit polynomial Chebyshev. Bentuk
umunya adalah :
𝐺1(𝑥, ℎ) =1 − 2𝑥ℎ + ℎ1 − 𝑥ℎ 2 = ∑ 𝑇𝑛(𝑥)ℎ𝑛 ∞
𝑛=0
(𝟐. 𝟕𝟏)
𝐺2(𝑥, ℎ) =1 − 2𝑥ℎ + ℎ1 2 = ∑ 𝑈𝑛(𝑥)ℎ𝑛 ∞
𝑛=0
(𝟐. 𝟕𝟐)
yang dapat diturunkan untuk mendapatkan bentuk lain persamaan polynomial :
𝑇𝑛(𝑥) =𝑛2 ∑(−1)𝑚 𝑛
2
𝑚=0
(𝑛 − 𝑚 − 1)!
𝑚! (𝑛 − 2𝑚)!(2𝑥)𝑛−2𝑚 (𝟐. 𝟕𝟑)
𝑈𝑛(𝑥) = ∑(−1)𝑚 𝑛
2
𝑚=0
(𝑛 − 𝑚)!
𝑚! (𝑛 − 2𝑚)!(2𝑥)𝑛−2𝑚 (𝟐. 𝟕𝟒)
Sementara hubungan rekursif dapat diporeleh dari :
𝑇𝑛(𝑥) = 𝑇𝑛(cos 𝜃) = cos 𝑛𝜃
3. PERSAMAAN DIFERENSIAL PARSIAL
Persamaan diferensial parsial merupakan persamaan yang menghubungkan fungsi tidak diketahui (variabel bergantung) dari dua atau lebih variabel terhadap turunan parsial dengan mengacu pada variabel tersebut. Variabel tidak bergantung yang paling sering dijumpai adalah posisi dan waktu.
3.1 Persamaan Diferensial Parsial Secara Umum
Kebanyakan PDP pada gejala fisis merupakan orde kedua dan linear. Untuk mendapat kesan terhadap bentuk umumnya, berikut diperkenalkan beberapa bentuk PDP dalam sistem fisis.
Persamaan gelombang,
∇2𝑢 = 1
𝑐2
𝜕2𝑢
𝜕𝑡2 (𝟑. 𝟏)
Mendeskripsikan fungsi posisi dan waktu perpindahan dari titik kesetimbangan 𝑢(𝐫, 𝑡), dari tali atau membran bergetar, gas atau cairan. Persamaannya juga muncul pada elektromagnetik, dimana 𝑢 dapat merupaan medan listrik atau medan magnet dalam gelombang elektromagnetik atau arus maupun tegangan sepanjang garis transmisi. Nilai 𝑐 merupakan kecepatan rambat gelombang.
Persamaan difusi,
𝜅∇2𝑢 = 𝜕𝑢
𝜕𝑡 (𝟑. 𝟐)
Mendeskripsikan temperature 𝑢 pada suatu wilayah tanpa mengandung sumber panas. Persamaan ini juga berlaku untuk difsui kimia dengan konsentrasi 𝑢(𝐫, 𝑡). Konstanta 𝜅 disebut difusifitas. Persamaannya jeas terlihat terdiri dari tiga variabel spasial berorde dua dan satu variabel waktu berorde satu.
Persamaan Laplace,
𝜅∇2𝑢 = 0 (𝟑. 𝟑)
Didapatkan dengan pada kondisi 𝜕𝑢/𝜕𝑡 = 0 pada persamaan difusi, dan mendeskripsikan, misalnya, distribusi temperature steady-state pada sebuah padatan dimana tidak ada sumber panas. Persamaan Laplace juga dapat digunakan dalam mendeskripsikan potensial gravitasi pada wilayah tidak ada benda atau potensial listrik pada wilayah tidak adanya muatan. Lebih jauh, aplikasinya dapat diterapkan pada fluida tidak tertekan dengan tidak ada sumber.
Persamaan Poisson,
juga mendeskripsikan situasi fisis sama dengan persamaan Laplace, namun pada wilayah mengandung benda, muatan, atau sumber panas atau cairan. Fungsi 𝜌(𝐫) disebut rapat sumber dan pada aplikasi fisis biasanya mengandung konstanta fisis. Misalnya, jika 𝑢 adalah potensial listrik pada suatu daerah dalam ruang, dimana 𝜌 adalah rapat muatan listrik, maka ∇2𝑢 = −𝜌(𝐫)/𝜖0, dengan 𝜖0 permitivitas ruang hampa.
Persamaan Schrodinger,
−2𝑚 ∇ℏ2 2𝑢 + 𝑉(𝐫)𝑢 = 𝑖ℏ𝜕𝑢
𝜕𝑡 (𝟑. 𝟓)
Mendeskripsikan fungsi mekanika kuantum 𝑢(𝐫, 𝑡) dari partikel non-relaivistik bermassa 𝑚, ℏ adalah konstanta Planck dibagi 2𝜋. Seperti persamaan difusi, bentuknya juga berorde dua dalam tiga variabel spasial dan berorde satu dalam waktu.
3.2 Separasi Variabel
Misalkan kita mencari solusi 𝑢(𝑥, 𝑦, 𝑧, 𝑡) untuk persamaan diferensial parsial dalam kordinat Kartesian. Bentuk awalnya dapat dimisalkan dalam bentuk
𝑢(𝑥, 𝑦, 𝑧, 𝑡) = 𝑋(𝑥)𝑌(𝑦)𝑍(𝑧)𝑇(𝑡) (𝟑. 𝟔)
Solusi dengan bentuk seperti ini dikatakan terpisah dengan variabel 𝑥, 𝑦, 𝑧 dan 𝑡, dan mencari solusinya disebot motode separasi variabel.
Untuk persamaan diferensial parsial secara umum, kelihatannya sulit mendapatkan solusi terpisah. Namun untuk beberapa persamaan umum dan persamaan fisis, memiliki solusi dengan bentuk ini. Untuk menjabarkan lebih jauh, dapat ditinjau persamaan gelombang dalam tiga dimensi
∇2𝑢(𝐫) = 1
dengan substitusi persamaan (3.6) didapatkan
𝑑2𝑋
dan lebih mudah dilihat dengan notasi
𝑋′′𝑌𝑍𝑇 + 𝑋𝑌′′𝑍𝑇 + 𝑋𝑌𝑍′′𝑇 = 1
𝑐2𝑋𝑌𝑍𝑇′′ (𝟑. 𝟏𝟎)
𝑋′′
Bentuk ini merupakan dasar dari metoda separasi variabel. Bagian pertama hanya bergantung pada 𝑥, bagian kedua pada 𝑦, bagian ketiga pada 𝑧, serta bagian sisi kanan persamaan hanya bergantung pada 𝑡. Persamaan (3.7) dapat dipenuhi untuk semua 𝑥, 𝑦, 𝑧 dan 𝑡 jika setiap bagian tidak bergantung terhadap variabel bebas namun haruslah sebuah konstanta.
Untuk mengilustrasikan pemisalan, dipilih −𝑙2, −𝑚2, −𝑛2 untuk tiga konstanta pertama. Konstanta yang berhubungan dengan sisi sebelah kanan persamaan haruslah memenuhi −𝜇2 = −(𝑙2+ 𝑚2+ 𝑛2). Penjabaran ini kemudian membuat persamaan (3.7) dapat dituliskan dalam
Penyederhanaan ini merupakan alat untuk mengasumsikan sebuah solusi terpisah, PDP memiliki turunan terhadap empat variabel bebas dalam satu persamaan, telah direduksi menjadi empat PDB terpisah. Persamaannya dihubungkan dengan empat parameter konstan yang memenuhi ungkapan aljabar. Konstanta ini disebut juga konstanta separasi.
Solusi umum dari persamaan (3.8) kemudian dapat langsung dideduksi
𝑋(𝑥) = 𝐴𝑒𝑖𝑙𝑥+ 𝐵𝑒−𝑖𝑙𝑥
𝑌(𝑦) = 𝐶𝑒𝑖𝑚𝑦 + 𝐷𝑒−𝑖𝑚𝑦 (𝟑. 𝟏𝟑)
𝑍(𝑧) = 𝐸𝑒𝑖𝑛𝑧+ 𝐹𝑒−𝑖𝑛𝑧
𝑇(𝑡) = 𝐺𝑒𝑖𝑐𝜇𝑡+ 𝐻𝑒−𝑖𝑐𝜇𝑡
dengan 𝐴, 𝐵, … , 𝐻 adalah konstanta, diperoleh dengan menggunakan syarat batas dari suatu solusi. Bentuk alternatif solusinya dapat pula dituliskan
𝑋(𝑥) = 𝐴′cos 𝑙𝑥 + 𝐵′sin 𝑙𝑥
𝑌(𝑦) = 𝐶′cos 𝑚𝑦 + 𝐷′sin 𝑚𝑦 (𝟑. 𝟏𝟒)
𝑍(𝑧) = 𝐸′cos 𝑛𝑧 + 𝐹′sin 𝑛𝑧
𝑇(𝑡) = 𝐺′cos(𝑐𝜇𝑡) + 𝐻′sin(𝑐𝜇𝑡)
dimana 𝐴′, 𝐵′, … , 𝐻′ merupakan konstanta lain. Pemilihan bentuk dalam merepresentasikan solusi bergantung pada permasalahannya.
Sebagai gambaran, dengan memasukkan syarat batas misalnya, didapatkan solusi
𝑋(𝑥) = 𝑒𝑖𝑙𝑥 𝑌(𝑦) = 𝑒𝑖𝑚𝑦
𝑍(𝑧) = 𝑒𝑖𝑛𝑧 𝑇(𝑡) = 𝑒−𝑖𝑐𝜇𝑡
𝑢(𝑥, 𝑦, 𝑧, 𝑡) = 𝑒𝑖𝑙𝑥𝑒𝑖𝑚𝑦𝑒𝑖𝑛𝑦𝑒−𝑖𝑐𝜇𝑡
= 𝑒𝑖(𝑙𝑥+𝑚𝑦+𝑛𝑦−𝑐𝜇𝑡)
Dalam notasi konvensional teori gelombang, 𝑙, 𝑚, 𝑛 adalah komponen dari vektor gelombang 𝐤, dimana besarnya 𝑘 = 2𝜋/𝜆, dengan 𝜆 panjang gelombang. Adapun 𝑐𝜇 adalah frekuensi sudut 𝜔 dari gelombang. Sehingga, persamaannya dapat dituliskan
𝑢(𝑥, 𝑦, 𝑧, 𝑡) = 𝑒𝑖(𝑘𝑥𝑥+𝑘𝑦𝑦+𝑘𝑧𝑧−𝜔𝑡) = 𝑒𝑖(𝐤∙𝐫−𝜔𝑡)
Metode separasi variabel ini dapat diaplikasikan untuk banyak PDP yang muncul pada fenomena fisis.
3.2 Superposisi Solusi Terpisah
Saat persamaan diferesial parsial berbentuk linear (seperti persamaan Laplace, Schrodinger, difusi dan gelombang), solusi matematis dapat dibentuk dari prinsip superposisi untuk nilai berbeda setiap konstanta separasi. Mengambil dua variabel misalnya
𝑢𝜆𝑖(𝑥, 𝑦) = 𝑋𝜆1(𝑥)𝑌𝜆1(𝑦)
merupakan solusi PDP dengan memberikan konstanta separasi variabel 𝜆1, maka hasil superposisi
𝑢(𝑥, 𝑦) = 𝑎1𝑋𝜆1(𝑥)𝑌𝜆1(𝑦) + 𝑎2𝑋𝜆2(𝑥)𝑌𝜆2(𝑦) + ⋯ = ∑ 𝑎𝑖𝑋𝜆𝑖(𝑥)𝑌𝜆𝑖(𝑦)
𝑖
(𝟑. 𝟏𝟓)
juga merupakan solusi untuk setiap konstanta 𝑎𝑖, dengan 𝜆𝑖 adalah nilai yang memenuhi konstanta separasi 𝜆, diberikan oleh syarat batas. Nilai dari superposisi merupakan hasil dari syarat batas, katakanlah 𝑢(𝑥, 𝑦) memiliki bentuk tertentu 𝑓(𝑥) pada 𝑦 = 0, dapat ditemukan dengan memilih konstanta 𝑎𝑖 sedemikian rupa
𝑓(𝑥) = ∑ 𝑎𝑖𝑋𝜆𝑖(𝑥)𝑌𝜆𝑖(0)
𝑖
Secara umum, hal ini akan memungkinkan fungsi 𝑋𝜆𝑖(𝑥) membentuk kumpulan fungsi, seperti halnya fungsi sinusoidal pada deret Fourier.
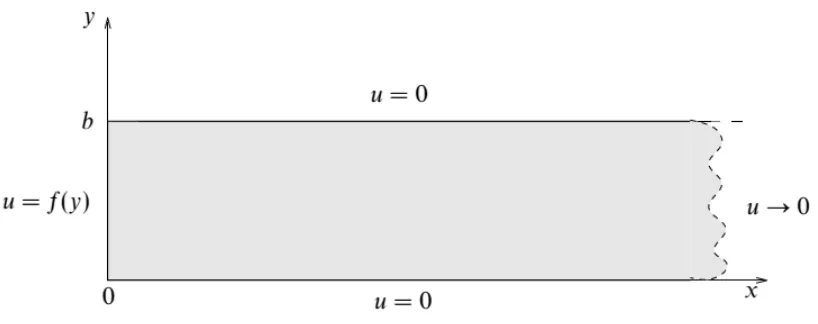
Gambar 3.1 Semi-takberhingga plat logam dengan setiap sisi bertemperatur tetap
Saat temperatur dari logam di 𝑥 = 0 juga tetap dan diberikan oleh 𝑓(𝑦), distribusi temperatur keadaan tunak 𝑢(𝑥, 𝑦) dari logam dapat dicari dengan menggunakan persamaan difusi
𝜅 (𝜕𝜕𝑥2𝑢2+𝜕𝜕𝑦2𝑢2) =𝜕𝑢𝜕𝑡
Namun karena kondisinya tunak, 𝜕𝑢/𝜕𝑡 = 0, membuat persamaannya direduksi menjadi persamaan Laplace
𝜕2𝑢
𝜕𝑥2+
𝜕2𝑢
𝜕𝑦2 = 0
Menggunakan asumsi 𝑢(𝑥, 𝑦) = 𝑋(𝑥)𝑌(𝑦), solusinya dapat dipenuhi oleh persamaan
𝑋(𝑥) = 𝐴𝑒𝑖𝑙𝑥+ 𝐵𝑒−𝑖𝑙𝑥, 𝑌(𝑦) = 𝐶𝑒𝑖𝑚𝑦+ 𝐷𝑒−𝑖𝑚𝑦
atau
𝑋(𝑥) = 𝐴′cos 𝑙𝑥 + 𝐵′sin 𝑙𝑥 , 𝑌(𝑦) = 𝐶′cos 𝑚𝑦 + 𝐷′sin 𝑚𝑦
Pada kasus ini, persamaan haruslah memenuhi syarat batas 𝑢(𝑥, 0) = 0 = 𝑢(𝑥, 𝑏) dan terlihat solusi sinusoidal pada bagian 𝑦 cukup sesuai. Lebih jauh, karena syarat lain 𝑢(∞, 𝑦) = 0 maka solusi dari bagian 𝑥 dapat dipilih dalam bentuk eksponensial. Solusi terpisah dari kasus ini kemudian dapat dituliskan
𝑢(𝑥, 𝑦) = (𝐴𝑒𝜆𝑥+ 𝐵−𝜆𝑥)(𝐶 cos 𝜆𝑦 + 𝐷 sin 𝜆𝑦)
𝑢(𝑥, 𝑦) = 𝐵𝑒−𝜆𝑥sin 𝜆𝑦
Namun dengan kondisi lain, 𝑢(𝑥, 𝑏) = 0, mengharuskan 𝜆 = 𝑛𝜋/𝑏, dengan 𝑛 bilangan bulat positif. Hal ini membuat terdapat 𝑛 buah solusi dari persamaan.
Menggunakan prinsip superposisi, solusi umum untuk memenuhi syarat batas dapat dituliskan
𝑢(𝑥, 𝑦) = ∑ 𝐵𝑛𝑒−𝑛𝜋𝑥𝑏 sin𝑛𝜋𝑦𝑏 ∞
𝑛=1
(𝟑. 𝟏𝟔)
untuk suatu konstanta 𝐵𝑛. Bilangan bulat 𝑛 negatif tidak disertakan karena akan membuat solusinya divergen saat 𝑥 → ∞. Syarat batas tersisa adalah 𝑢(0, 𝑦) = 𝑓(𝑦), dan mengharuskan konstanta 𝐵𝑛 memenuhi
𝑓(𝑦) = ∑ 𝐵𝑛sin𝑛𝜋𝑦𝑏 ∞
𝑛=1
Bentuk ini tidak lain adalah ekspansi deret Fourier untuk bagian sinus, sehingga konstanta 𝐵𝑛 dapat ditelusuri dengan
𝐵𝑛 =2𝑏∫ 𝑓(𝑦) 𝑏
0 sin (
𝑛𝜋𝑦 𝑏 ) 𝑑𝑦
dengan 𝑓(𝑦) = 𝑢0, maka
𝐵𝑛 = 2𝑏∫ 𝑢0 𝑏
0 sin (
𝑛𝜋𝑦 𝑏 ) 𝑑𝑦 =2𝑏 [−𝑢0𝑛𝜋 cos (𝑏 𝑛𝜋𝑦𝑏 )]𝑏0
= −2𝑢𝑛𝜋0[cos 𝑛𝜋 − 1]
= −2𝑢𝑛𝜋0[(−1)𝑛− 1] = {4𝑢𝑛𝜋 𝑛 ganjil0
0 𝑛 genap
Dengan substitusi pada (3.12), didapatkan solusi akhirakhir
𝑢(𝑥, 𝑦) = ∑ 4𝑢𝑛𝜋 𝑒0 −(𝑛𝜋𝑥𝑏 )sin (𝑛𝜋𝑦
𝑏 )
𝑛 ganjil
3.3 Separasi Variabel pada Kordinat Polar
Banyak PDP mengandung operator ∇2, seperti di persamaan gelombang, persamaan difusi, persamaan Schrodinger dan persamaan Poisson. Pada pembahasan kalkulus vektor, bentuk operator ∇2 untuk koordinat bidang polar, silinder dan bola secara berurut diberikan oleh
∇2=1
Persamaan paling sederhana dengan ∇2 adalah persamaan Laplace,
∇2𝑢(𝒓) = 0 (𝟑. 𝟐𝟎)
Dari penjabaran persamaan ini dapat diperoleh penjabaran untuk bentuk persamaan lain yang lebih kompleks.
3.3.1 Persamaan Laplace di Bidang Polar
Misalkan untuk mecari solusi (𝟑. 𝟐𝟎) pada lingakaran 𝜌 = 𝑎. Pencarian solusi akan mengarah
membuat persamaannya dapat dipisah menjadi dua bentuk PDB
𝜌
Pertama, untuk 𝑛 ≠ 0, persamaan (𝟑. 𝟐𝟐) memiliki bentuk umum
Φ(𝜙) = 𝐴𝑒𝑖𝑛𝜙+ 𝐵𝑒−𝑖𝑛𝜙 (𝟑. 𝟐𝟑)
Sementara persamaan (𝟑. 𝟐𝟏) berbentuk persamaan homogeny
𝜌2𝑃′′+ 𝜌𝑃′− 𝑛2𝑃 = 0
yang dapat diselesaikan dengan menggunakan deret pangkat 𝜌, atau dapat juga dengan substitusi 𝜌 = 𝑒𝑡 untuk mendapatkan
𝑃(𝜌) = 𝐶𝜌𝑛+ 𝐷𝜌−𝑛 (𝟑. 𝟐𝟒)
Substitusi ulang (𝟑. 𝟐𝟑) dari persamaan azimuthal (𝟑. 𝟐𝟐), dapat dilihat bahwa jika 𝚽, dan kemudian 𝑢, memilliki nilai tunggal dan tidaklah berubah ketika 𝜙 meningkat 2𝜋 maka 𝑛 haruslah bilangan bulat. Secara matematis, nilai lain dari 𝑛 memungkinkan, namun ini tidaklah mendeskripsikan situasi fisis yang ril. Dari hasil ini, diperoleh solusidari persamaan Laplace dua dimensi
𝑢(𝜌, 𝜙) = (𝐴 cos 𝑛𝜙 + 𝐵 sin 𝑛𝜙)(𝐶𝜌𝑛 + 𝐷𝜌−𝑛)
dengan 𝐴, 𝐵, 𝐶, 𝐷 adalah suatu konstanta dan 𝑛 adalah bilangan bulat.
Ketika 𝑛 = 0 solusi (𝟑. 𝟐𝟏) dan (𝟑. 𝟐𝟐)adalah
Φ(𝜙) = 𝐴𝜙 + 𝐵 𝑃(𝜌) = 𝐶 ln 𝜌 + 𝐷
Namun, agar 𝑢 = 𝑃Φ bernilai tunggal, kita perlukan 𝐴 = 0, sehingga solusi untuk 𝑛 = 0 adalah
𝑢(𝜌, 𝜙) = 𝐶 ln 𝜌 + 𝐷 .
Melakukan superposisi terhadap solusi untuk nilai 𝑛 berbeda-beda, solusi umum persamaan Laplace pada bidang polar adalah
𝑢(𝜌, 𝜙) = (𝐶0ln 𝜌 + 𝐷0) + ∑(𝐴𝑛cos 𝑛𝜙 + 𝐵𝑛sin 𝑛𝜙)(𝐶𝑛𝜌𝑛+ 𝐷𝑛𝜌−𝑛) ∞
𝑛=1
(𝟑. 𝟐𝟓)
3.3.2 Persamaan Laplace pada Silinder
Dalam koordinat silinder, persamaan Laplace secara umum berbentuk
1
Seperti sebelumnya, solusinya dapat dimisalkan
𝑢(𝜌, 𝜙, 𝑧) = 𝑃(𝜌)Φ(𝜙)𝑍(𝑧)
dimana saat disubstitusi ke (𝟑. 𝟐𝟔) dan melakukan pembagian terhadap 𝑢 = 𝑃Φ𝑍 memberikan
1
Bagian terakhir hanya bergantung terhadap 𝑧, sementara bagian pertama dan kedua secara berurut bergantung pada 𝜌 dan 𝜙. Mengambil konstanta separasi 𝑘2, diperoleh
Mengalikan persamaan kedua dengan 𝜌2, diperoleh
𝜌 Mengambil konsanta separasi 𝑚2, didapatkan
1 Φ
𝑑2Φ
𝑑𝜙2 = −𝑚2, (𝟑. 𝟐𝟕)
Persamaan pada sudut azimuth 𝜙 memiliki solusi yang tidak asing lagi
Φ(𝜙) = 𝐶 cos 𝑚𝜙 + 𝐷 sin 𝑚𝜙
Sama halnya pada dua dimensi, sifat nilai tunggal dari 𝑢 membuat 𝑚 haruslah suatu bilangan bulat. Namun saat 𝑚 = 0, solusinya memberikan
Φ(𝜙) = 𝐶𝜙 + 𝐷 .
Bentuk ini sesuai untuk sebuah solusi dengan simetri aksial (𝐶 = 0) atau sebuah nilai banyak, seperti potensial skalar magnet diasosiasikan dengan arus 𝐼.
Terakhir, persamaan dengan 𝜌, (𝟑. 𝟐𝟖), bisa ditransformasikan ke dalam persamaan Bessel berorde 𝑚 dengan menuliskan 𝜇 = 𝑘𝜌. Hal ini memberikan solusi
𝑃(𝜌) = 𝐴𝐽𝑚(𝑘𝜌) + 𝐵𝑌𝑚(𝑘𝜌) .
Dari pembahasan persamaan Bessel, 𝑌𝑚(𝑘𝜌) singular pada 𝜌 = 0, sehingga saat mencari solusi persamaan Laplace pada koordinat silinder dalam suatu daerah dengan 𝜌 = 0, nila 𝐵 = 0.
Solusi separasi variabel keseluruhan untuk persamaan Laplace ∇2𝑢 = 0 pada silinder dapat dituliskan
𝑢(𝜌, 𝜙, 𝑧) = [𝐴𝐽𝑚(𝑘𝜌) + 𝐵𝐽𝑚(𝑘𝜌)][𝐶 cos 𝑚𝜙 + 𝐷 sin 𝑚𝜙][𝐸𝑒−𝑘𝑧 + 𝐹𝑒𝑘𝑧]. (𝟑. 𝟐𝟗)
Prinsip superposisi dapat diterapkan untuk membangun solusi lebih umum dengan menambahkannya bersama dengan solusi (𝟑. 𝟐𝟗) untuk nilai memungkinkan dari konstanta separasi 𝑘 dan 𝑚.
3.3.3 Persamaan Laplace pada Bola
Dalam koordinat bola, persamaan Laplace, ∇2= 0, memiliki bentuk
1
yang merupakan persamaan dengan aplikasi luas dalam fisika.
Sulusinya dimisalkan
𝑢(𝑟, 𝜃, 𝜙) = 𝑅(𝑟)Θ(𝜃)Φ(𝜙) .
Substitusi ke persamaan (𝟑. 𝟑𝟎) dan dibagi dengan 𝑢 = 𝑅ΘΦ, kemudian mengalikannya dengan 𝑟2, diperoleh
1
Persamaan (𝟑. 𝟑𝟐) merupakan persamaan homogen,
𝑟2𝑑2𝑅 serta solusi untuk persamaan radial
𝑅(𝑟) = 𝐴𝑟𝜆1 + 𝐵𝑟𝜆2 ,
dengan 𝜆1+ 𝜆2 = −1 dan 𝜆1𝜆2 = −𝜆. Dapat pula diambil 𝜆1 dan 𝜆2 sebagai 𝑙 dan −(𝑙 + 1), memberikan 𝜆 bentuk 𝑙(𝑙 + 1).
Sampai disini, telah diperoleh informasi dari solusi faktor pertama dari keseluruhan solusi, dimana bentuknya
Kalikan dengan sin2𝜃 serta melakukan pengurutan ulang diperoleh
[sin 𝜃Θ 𝑑𝜃 (sin 𝜃𝑑 𝜕Θ𝜕𝜃) + 𝑙(𝑙 + 1) sin2𝜃] + 1
Φ 𝜕2Φ
𝜕𝜙2 = 0 . (𝟑. 𝟑𝟓)
Mengambil konstanta pemisah 𝑚2, persamaan dalam sudut azimut 𝜙 memiliki solusi yang sama untuk solusi dalam bentuk silinder, yaitu
Φ(𝜙) = 𝐶 cos 𝑚𝜃 + 𝐷 sin 𝑚𝜃 .
Ketunggalan nilai dari 𝑢 membuat nilai 𝑚 haruslah bilangan bulat. Untuk 𝑚 = 0, didapatkan Φ(𝜙) = 𝐶𝜙 + 𝐷.
sin 𝜃 Θ
𝑑
𝑑𝜃 (sin 𝜃 𝑑Θ
𝑑𝜃 ) + 𝑙(𝑙 + 1) sin2𝜃 = 𝑚2 . (𝟑. 𝟑𝟔)
Perubahan variabel bebas dari 𝜃 menjadi 𝜇 = cos 𝜃, sin 𝜃 = (1 − 𝜇2)1/2 membuat persamaan ini tereduksi ke bentuk khusus. Memberikan
𝜇 = cos 𝜃 , 𝑑𝜇𝑑𝜃 = − sin 𝜃 , 𝑑𝜃 = −𝑑 (1 − 𝜇2)1/2 𝑑
𝑑𝜇 , persamaan untuk 𝑀(𝜇) ≡ Θ(𝜃) dapat dituliskan
𝑑
𝑑𝜇 [(1 − 𝜇2) 𝑑𝑀
𝑑𝜇 ] +[𝑙(𝑙 + 1) − 𝑚2
1 − 𝜇2] 𝑀 = 0 . (𝟑. 𝟑𝟔)
Persamaan khusus ini disebut persamaan Legendre asosiasi. Saat 𝑚 = 0, persamaan ini tereduksi menjadi persamaan Legendre dan memiliki solusi
𝑀(𝜇) = 𝐸𝑃𝑙(𝜇) + 𝐹𝑄𝑙(𝜇) . (𝟑. 𝟑𝟕)
Solusinya diberikan oleh fungsi Legendre asosiasi 𝑃𝑙𝑚(𝜇) dan 𝑄𝑙𝑚(𝜇), dimana
𝑃𝑙𝑚(𝜇) = (1 − 𝜇2)|𝑚|/2 𝑑|𝑚|
𝑑𝜇|𝑚|𝑃𝑙𝑚 , (𝟑. 𝟑𝟖)
demikian juga untuk 𝑄𝑙𝑚. Dari hasil ini kemudian diperoleh
𝑀(𝜇) = 𝐸𝑃𝑙𝑚+ 𝐹𝑄
𝑙𝑚 (𝟑. 𝟑𝟗)
dengan 𝑚 haruslah bilangan bulat, 0 ≤ |𝑚| ≤ 𝑙. Perlu dicatat, jika solusi untuk persamaan Laplace terbatas saat 𝜇 = cos 𝜃 = ±1 (misalnya pada sumbu polar dimana 𝜃 = 0, 𝜋), mengharuskan konstanta 𝐹 = 0 pada (𝟑. 𝟑𝟕) dan (𝟑. 𝟑𝟗) karena 𝑄𝑙𝑚 divergen pada ±1.
Dari penjabaran tersebut, solusi dari setiap tiga PDB yang terdiri dari 𝑅, Θ dan Φ telah didapatkan. Solusi total dari persamaan Laplace dengan separasi variabel pada koordinat bola kemudian memiliki bentuk
𝑢(𝑟, 𝜃, 𝜙) = (𝐴𝑟𝑙 + 𝐵𝑟−(𝑙+1))(𝐶 cos 𝑚𝜙 + 𝐷𝜙)[𝐸𝑃
𝑙𝑚(cos 𝜃) + 𝐹𝑄𝑙𝑚(cos 𝜃)], (𝟑. 𝟒𝟎)
4. FUNGSI KOMPLEKS
4.1 Fungsi Variabel Kompleks
Suatu fungsi 𝑓(𝑧) dikatakan fungsi variabel kompleks 𝑧 jika setiap nilai 𝑧 pada suatu daerah tertentu di 𝑅 (pada diagram Argand) memiliki satu atau lebih nilai 𝑓(𝑧). Fungsi 𝑓(𝑧) dapat berupa fungsi yang terdiri dari bagian ril dan bagian imajiner, dimana secara umum merupakan fungsi 𝑥 dan 𝑦.
𝑓(𝑧) = 𝑢(𝑥, 𝑦) + 𝑖𝑣(𝑥, 𝑦) (𝟒. 𝟏)
Fungsi 𝑓(𝑧) dengan nilai tunggal pada domain 𝑅 dapat didiferensialkan pada titik 𝑧 saat turunannya
𝑓′(𝑧) = lim
Δz→0[
𝑓(𝑧 + Δz) − 𝑓(𝑧)
Δ𝑧 ] (𝟒. 𝟐)
ada dan unik. Hal ini berarti nilainya tidak bergantung pada arah di diagram Argand dimana Δ𝑧 menuju nol.
Perhatikan fungsi 𝑓(𝑧) = 𝑥2− 𝑦2+ 𝑖2𝑥𝑦 = (𝑥 + 𝑖𝑦)2 = 𝑧2. Dengan mencoba persamaan (𝟒. 𝟐),
𝑓′(𝑧) = lim
Δ𝑧→0[
(𝑧 + Δ𝑧)2− 𝑧2
Δ𝑧 ]
= limΔ𝑧→0[Δ𝑧(2𝑧 + Δ𝑧)Δ𝑧 ] 𝑓′(𝑧) = 2𝑧
terlihat bahwa 𝑓(𝑧) = 𝑧2 terdiferensiasi untuk semua 𝑧 berhingga.
Sebuah fungsi dengan nilai tunggal dan dapat didiferensialkan pada semua titik di domain 𝑅 dikatakan analitik di 𝑅. Suatu fungsi juga dapat memiliki satu atau lebih titik yang tidak analitik meski titik lain pada domain 𝑅 analitik. Titik yang tidak analitik ini disebut juga singularitas dari 𝑓(𝑧).
4.2 Hubungan Cauchy-Rieman
Jika suatu limit
𝐿 = limΔ𝑧→0[𝑓(𝑧 + Δ𝑧) − 𝑓(𝑧)
Δz ] (𝟒. 𝟑)
Saat memisalkan 𝑓(𝑧) = 𝑢(𝑥, 𝑦) + 𝑖𝑣(𝑥, 𝑦) dan Δ𝑧 = Δ𝑥 + 𝑖Δ𝑦, maka
𝑓(𝑧 + Δ𝑧) = 𝑢(𝑥 + Δ𝑥, 𝑦 + Δ𝑦) + 𝑖𝑣(𝑥 + Δ𝑥, 𝑦 + Δ𝑦) dan dengan menerapkan limit pada persamaan (𝟒. 𝟑),
𝐿 = limΔ𝑥,Δ𝑦→0[𝑢(𝑥 + Δ𝑥, 𝑦 + Δ𝑦) + 𝑖𝑣(𝑥 + Δ𝑥, 𝑦 + Δ𝑦) − 𝑢(𝑥, 𝑦) − 𝑖𝑣(𝑥, 𝑦) Kedua kesamaan ini dikenal dengan hubungan Cauchy-Riemann.
Hubungan ini dapat digunakan dala menentukan keanalitikan suatu fungsi. Dari persamaan di atas untuk 𝑓(𝑧) = 𝑥2− 𝑦2+ 𝑖2𝑥𝑦,
Terlihat bahwa jika suatu fungsi 𝑓(𝑧) analitik, maka fungsi tersebut haruslah memenuhi hubungan Cauchy-Riemann.
Hasil penting lain dari hubungan Cauchy-Riemann adalah saat mendiferensialkan hubungan ini dengan suatu variabel bebas.
dimana 𝑢 dan 𝑣 secara terpusah adalah solusi dai persamaan Laplace pada dua dimensi
Sebelum lebih jauh, untuk suatu titik dimana 𝑓(𝑧) tidak analitik pada diagram Argand, titik tersebut disebut sebagai titik singular fungsi kompleks 𝑓(𝑧). Saat 𝑓(𝑧) analitik disemua rentang domain namun terdapat titik singular hanya di 𝑧 = 𝑧0, maka 𝑧0 disebut titik singular terisolasi.
4.3 Integral Kompleks
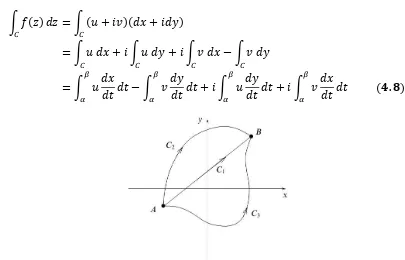
Proses integrasi untuk bilangan ril sudah biasa dilakukan. Berkenaan dengan diperkenalkannya bilangan kompleks, tentu tinjauan integral bilangan kompleks menjadi perlu untuk diperbincangkan. Karena bidang-𝑧 terdiri dari dua dimensi, terdapat kebebasan lebih tinggi serta ambiguitas dengan integral bilangan kompleks. Jika fungsi 𝑓(𝑧) bernilai tunggal dan kontinu pada suatu daerah 𝑅 di bidang kompleks, maka dapat didefinisikan integral kompleks dari 𝑓(𝑧) antara dua titik 𝐴 dan 𝐵 sepanjang suatu kurva di 𝑅; nilainya akan bergantung pada lintasan yang diambil antara 𝐴 dan 𝐵. Namun untuk suatu lintasan, terdapat perbedaan tetapi memikul hubungan nilai integral satu dengan yang lain tidak bergantung pada lintasan mana yang dipilih.
Misalkan lintasan 𝐶 dideskripsikan oleh parameter ril kontinu 𝑡(𝛼 ≤ 𝑡 < 𝛽) yang memberi posisi 𝐶 sebelumnya dengan persamaan
𝑥 = 𝑥(𝑡), 𝑦 = 𝑦(𝑡)
dengan 𝑡 = 𝛼 dan 𝑡 = 𝛽 bergantung pada titik 𝐴 dan 𝐵. Maka integral sepanjang lintasan 𝐶 dari fungsi kontinu 𝑓(𝑧) dituliskan
∫ 𝑓(𝑧)
𝐶 𝑑𝑧 (𝟒. 𝟕)
dan secara eksplisit sebagai penjumlahan dari integral ril
∫ 𝑓(𝑧)
𝐶 𝑑𝑧 = ∫ (𝑢 + 𝑖𝑣)(𝑑𝑥 + 𝑖𝑑𝑦)𝐶
= ∫ 𝑢 𝑑𝑥
𝐶 + 𝑖 ∫ 𝑢 𝑑𝑦𝐶 + 𝑖 ∫ 𝑣 𝑑𝑥𝐶 − ∫ 𝑣 𝑑𝑦𝐶
= ∫ 𝑢𝛽 𝑑𝑥𝑑𝑡 𝑑𝑡
𝛼 − ∫ 𝑣
𝑑𝑦 𝑑𝑡 𝑑𝑡
𝛽
𝛼 + 𝑖 ∫ 𝑢
𝑑𝑦 𝑑𝑡 𝑑𝑡
𝛽
𝛼 + 𝑖 ∫ 𝑣
𝑑𝑥 𝑑𝑡 𝑑𝑡
𝛽
𝛼 (𝟒. 𝟖)