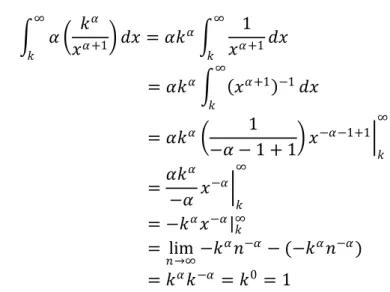PENDUGA TERBAIK UNTUK DISTRIBUSI PARETO DENGAN MENGGUNAKAN TEOREMA BATAS BAWAH CRAMMER-RAO SKRIPSI

i PENDUGA TERBAIK UNTUK DISTRIBUSI PARETO DENGAN MENGGUNAKAN TEOREMA BATAS BAWAH CRAMMER-RAO

SKRIPSI

Diajukan Untuk Memenuhi Sebagian Persyaratan Mencapai Derajat Sarjana S-1

OLEH: RISKA JULIANI

F1A1 11 031

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS HALU OLEO

KENDARI 2016

iii KATA PENGANTAR

Segala puji bagi Allah S.W.T atas segala rahmat, taufik, karunia dan hidayah-Nya sehingga penulis dapat menyelesaikan skripsi ini dengan judul “Penduga Terbaik untuk Distribusi Pareto dengan Menggunakan Teorema Batas Bawah Crammer Rao” serta salawat dan salam penulis haturkan atas Nabi Muhammad ShallallahuAlaihi Wasallam, keluarga, sahabat dan para pengikutnya. Penulis menyadari bahwa dalam penulisan skripsi ini tidak dapat terselesaikan tanpa bimbingan dan arahan dari Ibu Dr.rer.nat. Wayan Somayasa, S.Si., M.Si selaku pembimbing I dan Bapak Rasas Raya, S.Si., M.Si selaku pembimbing II yang telah banyak meluangkan waktunya untuk membimbing dan mengarahkan penulis sejak dari perencanaan hingga terselesaikannya skripsi ini serta memberikan dorongan dan motivasi kepada penulis. Oleh karena itu penulis mengucapkan banyak terima kasih.

Ucapan terima kasih juga disampaikan kepada yang tersayang ayah anda Umar dan ibunda Nartin yang telah mendukung dan memberikan doa yang tulus ikhlas serta kasih sayangnya kepada penulis sehingga skripsi ini selesai, saudara-saudaraku Rulis, Rajes, Rosa dan Resvina yang selalu memberikan doa dan semangat, semua itu penulis mendoakan menjadi pahala serta catatan amal kebaikan disisi Allah Subhanahu WaTa’ala.

Suatu hal yang tidak terlupakan atas dorongan dan bimbingannya, serta arahan dan bantuan kepada penulis, maka patutlah kiranya penulis menyampaikan ucapan terima kasih dan penghargaan kepada semua pihak khususnya:

iv 1. Rektor Universitas Halu Oleo, Bapak Prof. Dr. Ir. H. Usman Rianse, M.S. 2. Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Halu

Oleo, Bapak Dr. Muh. Zamrun F., S.Si.,M.Si., M.Sc.

3. Kepala Laboratorium Komputasi Matematika F-MIPA Universitas Halu Oleo, Ibu Norma Muhtar, S.Si.,M.Si.

4. Kepala Perpustakaan F-MIPA Universitas Halu Oleo, Ibu Dra. Hj. Indrawati, M.Si.

5. Segenap Staf Administrasidan Tata Usaha di Lingkungan F-MIPA Universitas Halu Oleo atas segala bentuk bantuan yang diberikan kepada penulis selama studi.

6. Ketua Jurusan Matematika F-MIPA Universitas Halu Oleo, Bapak La Gubu, S.Si.,M.Si. dan sekretaris jurusan Matematika, Bapak Rasas Raya, S.Si,. M.Si.

7. Bapak dan Ibu Dosen Jurusan Matematika serta seluruh staf pengajar di lingkungan F-MIPA Universitas Halu Oleo.

8. Rasas Raya, S.Si., M.Si selaku penasehat akademik yang telah memberikan pengarahan dan bimbingan dalam memprogramkan mata kuliah.

9. La Gubu, S.Si.,M.Si., Dr. Asrul Sani, M.Sc dan Lilis Laome, S.Si., M.Si selaku dewan penguji.

10. Sahabat selalu menemaniku dalam suka dan duka: Sitti Sardianti, Mega Puspita, Andi Nurul Musahida, Ridayani, Halma dan Hijrawati.

11. Teman-teman Matematika Angkatan 2011: Nini Karlis Kartini, S.Mat (NingNonk), Ade Rahayu Putri, S.Mat (AyhuBusu), Wa Ode Syarfin Tala, S.Mat (Fio), Wa Ode Desi Nurhasnawati, S. Mat (Desmon) dan Wahyu

v Mustikaningrum, S.Mat (Wahyu), Kasliono, S.Mat, Kalfin, S.Mat, Wayan Eka Murtiawan, S.Mat, Edicun BJ, Rahmat Budianto, Raful Sudirman, S.Mat, Sartika, Samsir, S.Mat, Gafur, S.Mat, Takim, S.Mat, Peni, Arif, Usman, S.Mat, Rina A.S, S.Mat, CitrawanFitri, S.Mat, Ully Hidayati, S.Mat, Mayan, S.Mat, Eka Rahmi Syamsuddin,S.Mat, Wiwi, S.Mat, Risna, Bibi, S.Mat, Silfi, S.Mat, Cici, Ririn, Nining, Cakra Purnawati dan lain-lain yang telah memberikan dorongan moral dan spiritual serta kebersamaan yang tidak terlupakan selama mengikuti perkuliahan.

12. Senior-senior Matematika: Kak Yudi’08, Kak Ansar’08, Kak Alip’08, Kak Gusti’09, KakAgusman’09, Kak Uthy’09, Kak Aim’09,Kak Kiki’09,Kak Fadly’06, Kak Diana’10, Kak Harma’10, Kak Abi’10, Kak Derma’10,Kak Uju’10, Kak Ardy Arr’10, Kak Ulfa’10, Kak Rendi’10 dan semuanya yang tidak dapat disebutkan satu persatu.

13. Junior Matematika Angkatan 2012 dan 2013: Rahmadin La Oga, Syech Muh. Syam, Ilham, Nela, Yacobus, Fadil, Selfiana, Mail, Guslan, Irfan dan semuanya yang tidak dapat disebutkan satu persatu.

14. Teman-teman KKN di Desa Tawarombadaka, KOLTIM: Ramadhan, Irma, Amni, Herlia, Esti, Hato, Jamsir, Sariani, Mujur, Nurlan, Rio, Ito Purnomo, Nasrun dan seluruh keluarga besar Desa Tawarombadaka, KOLTIM.

15. Teman-teman dan sepupuku : Ima, Arsi, Indry, Tamara, Anjeli, Sesilya, Lusni, Irenk, Ega, Maun, Obink, Rahmat, yang selalu memberikan semangat. Selanjutnya penulis menyadari bahwa penulisan skripsi ini masih jauh dari kesempurnaan. Sehingga dengan senang hati dan segala kerendahan hati penulis menerima segala saran yang sifatnya membangun demi penyempurnaannya.

vi Akhir kata penulis berharap semoga skripsi ini dapat bermanfaat bagi semua pihak yang membutuhkan.

Kendari, 1 April 2016

vii DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN PENGESAHAN ... ii

KATA PENGANTAR ... iii

DAFTAR ISI ... vii

DAFTAR GAMBAR ... ix DAFTAR LAMPIRAN ... x ABSTRAK ... xi ABSTRACT ... xii BAB I PENDAHULUAN 1.1 LatarBelakang... 1 1.2 RumusanMasalah ... 3 1.3 TujuanPenelitian ... 3 1.4 ManfaatPenelitian ... 3

BAB II TINJAUAN PUSTAKA 2.1 Fungsi Distribusi ... 4

2.2 Distribusi Pareto ... 5

2.3 Metode Estimasi Parameter ... 9

2.3.1 Metode Momen ... 9

2.3.2 Metode Maksimum Likelihood ... 10

2.3.2.1 Kasus Satu Parameter... 11

2.3.2.2 Kasus k Parameter ... 12

2.4 Kriteria Memilih Estimator ... 12

2.4.1 Ketakbiasan ... 12

2.4.2 Keterkonsentrasian dan UMVUE ... 13

BAB III METODE PENELITIAN 3.1 Waktu dan Tempat Penelitian ... 16

viii BAB IV HASIL DAN PEMBAHASAN

4.1 Metode Momen Dalam Menduga Parameter Distribusi

Pareto ... 18

4.2 Metode Maksimum Likelihood Dalam Menduga Parameter Distribusi Pareto... 21

4.3 Penduga terbaik (UMVUE) ... 24

4.3.1 Penduga Tak Bias Untuk Distribusi Pareto ... 24

4.3.2 Penduga dengan variansi minimum... 24

4.3.2.1 Ketaksamaan Cramer Rao untuk distribusi Pareto………. 25

4.4 Penduga Interval Menggunakan Metode Momen Berdasarkan Data Sampel Acak Sederhana ... 28

4.5 Informasi Data ... 29 4.6 Analisis Data ... 31 BAB V PENUTUP 5.1 Kesimpulan ... 32 5.2 Saran ... 32 DAFTAR PUSTAKA ... 33 LAMPIRAN

ix DAFTAR GAMBAR

Halaman Gambar 4.1. Grafik pdf distribusi Pareto untuk berbagai nilai 𝛼 ... 21 Gambar 4.2. Desain Pengeboran Daerah Eksplorasi PT. Antam ... 32 Gambar 4.3. Pola Kandungan Nikel ... 32

x DAFTAR LAMPIRAN

Halaman Lampiran 1. Data Persentase Kandungan Nikel di PT. ANTAM ... 38 Lampiran 2. Program menghitung estimasi interval. ... 39 Lampiran 3. Simulasi perhitungan pdf distribusi Pareto ... 40

xi PENDUGA TERBAIK UNTUK DISTRIBUSI PARETO DENGAN MENGGUNAKAN TEOREMA BATAS BAWAH CRAMER-RAO

Oleh

Riska Juliani F1A1 11 031

Abstrak

Distribusi Pareto disebut juga dengan distribusi power law. Jika sebuah kumpulan data memiliki distribusi power-law, maka dikatakan bahwa data-data tersebut tidak sensitif terhadap rata-rata atau standar deviasi dari data tersebut atau dengan kata lain, data itu tidak bersifat acak. Penelitian ini bertujuan untuk merumuskan metode estimasi parameter-parameter dalam distribusi Pareto dengan menggunakan metode momen dan maksimum likelihood serta menentukan penduga terbaik (UMVUE) dalam distribusi Pareto menggunakan Teorema Batas Bawah Cramer-Rao. Metode yang digunakan untuk mengecek sifat UMVUE suatu penduga adalah ketaksamaan Cramer-Rao. Hasil penelitian menunjukkan bahwa penduga untuk parameter fungsi distribusi Pareto bukan merupakan UMVUE sehingga bukan penduga terbaik untuk distribusi Pareto.

Kata kunci : distribusi Pareto, metode penduga momen, metode penduga maksimum likelihood, dan UMVUE.

xii THE BEST ESTIMATION FOR PARETO DISTRIBUTION USING

CRAMER RAO LOWER BOUNDED THEOREM

By

Riska Juliani F1A1 11 031

Abstract

Pareto distribution is called as law distribution. When the data have power-law distribution so said the those data isn’t sensitive to average or standart deviation from those data or in other word the data is not random. The aim of this research is formulate estimation parameter methods in the Pareto distribution using the moment method, the maximum likelihood method, and determine the best estimate (UMVUE) in the Pareto distribution using the Cramer Rao Lower Bounded method. The method which is used to checking the UMVUE of the estimate is inequality Cramer Rao. The result is the estimation for parameter function of Pareto distribution isn’t UMVUE so that isn’t the best estimate for Pareto distribution.

Keywords : Pareto distribution, the moment estimate method, the maximum

1 BAB I

PENDAHULUAN

1.1 Latar Belakang

Statistika merupakan ilmu pengetahuan yang berhubungan dengan teknik pengumpulan, pengolahan atau penganalisa dan penarikan kesimpulan berdasarkan kumpulan data dan penganalisa yang dilakukan (Sudjana, 1996).

Statistika dibagi menjadi dua yakni statistika deskriptif dan statistika inferensial. Statistika deskriptif merupakan metode-metode yang berkaitan dengan pengumpulan dan penyajian sekumpulan data, sehingga dapat memberikan informasi yang berguna. Statistika inferensial merupakan statistika yang berkenaan dengan cara penarikan kesimpulan berdasarkan data yang diperoleh dari sampel untuk menggambarkan karakteristik atau ciri dari suatu populasi. Penarikan kesimpulan dapat dilakukan dengan cara penduga parameter (Supranto, 1985).

Ada dua jenis penduga parameter, yakni penduga titik dan penduga interval. Penduga titik dari sebuah parameter adalah sebuah nilai yang diperoleh dari sampel dan digunakan sebagai penduga dari parameter yang nilainya tidak diketahui. Sedangkan penduga interval sebuah parameter 𝜃 merupakan suatu interval nilai sedemikian hingga nilai-nilai yang mungkin dari parameter itu akan tercakup dalam interval itu dengan peluang tertentu (Suryani, 2009).

Dalam penduga titik ada beberapa metode yang digunakan diantaranya metode momen dan metode maksimum likelihood. Karena ada beberapa metode untuk menentukan penduga titik, maka suatu parameter dapat memiliki lebih dari

2 satu penduga titik. Ada beberapa kriteria untuk menentukan penduga mana yang terbaik antara lain ketakbiasan, penduga dengan variansi minimum, efisiensi, dan statistik cukup (Somayasa, 2001:76-77).

Distribusi Pareto merupakan model distribusi peluang dari suatu variabel kontinu. Distribusi Pareto memiliki dua parameter yang biasa disebut parameter skala dan parameter bentuk. Distribusi Pareto umumnya digunakan dalam bidang sosial, ekonomi, bisnis, asuransi, maupun politik (Arnold, 2004). Salah satu contoh penerapannya adalah dalam mempelajari karakteristik iklim ekstrim dan terjadinya perubahan iklim. Untuk mengetahui cara menduga parameter bentuk dan skala digunakan metode Maximum Likelihood Estimation (MLE). Metode ini dapat digunakan dalam mengeksplorasi karakteristik curah hujan di wilayah penelitian, dan mengidentifikasi perubahan iklim (sari dan sutikno, 2013).

Para peneliti maupun administrator dalam bidang bisnis, pendidikan, pemerintahan, ekonomi, maupun bidang lain, semuanya berkepentingan dalam masalah pendugaan. Misalnya dalam menduga banyaknya siswa yang memasuki perguruan tinggi periode mendatang atau proporsi pemilih yang akan memilih salah satu diantara dua calon presiden dalam pemilihan umum tahun lalu. Penduga ini biasanya dilakukan pada parameter suatu populasi. Untuk mengambil kesimpulan dari masalah-masalah tersebut maka perlu melakukan penduga parameter-parameter yang belum diketahui harga sebenarnya (Malik, 2011).

Dari fungsi distribusi Pareto dapat dicari penduga parameter dengan menggunakan metode maksimum likelihood. Untuk menentukan ukuran kebaikan suatu penduga pada distribusi Pareto, dapat digunakan Teorema Batas Bawah Cramer Rao (Zulfa, 2006).

3 Penduga terbaik yaitu penduga tak bias dan bervariansi minimum. Penduga tak bias terbaik UMVU (Univormly Minimum Variance Unbiased) diperoleh jika setiap penduga tak bias memenuhi batas bawah Crammer Rao. Pada penelitian ini penulis tertarik untuk melakukan penelitian lebih lanjut tentang “Penduga Terbaik Untuk Distribusi Pareto dengan Menggunakan Teorema Batas Bawah Cramer-Rao” sebagai bahan tugas akhir.

1.2 Rumusan Masalah

Rumusan masalah dalam penelitian ini adalah :

1. Bagaimana merumuskan estimasi parameter-parameter dalam distribusi Pareto dengan menggunakan metode momen dan maksimum likelihood ? 2. Bagaimana mengecek UMVUE penduga parameter distribusi Pareto

mengunakan Teorema Batas Bawah Crammer-Rao ? 1.3 Tujuan Penelitian

Tujuan yang hendak dicapai dari penelitian ini adalah :

1. Merumuskan estimasi parameter-parameter dalam distribusi Pareto dengan menggunakan metode momen dan maksimum likelihood .

2. Menentukan penduga terbaik (UMVUE) dalam distribusi Pareto menggunakan Teorema Batas Bawah Cramer-Rao.

1.4 Manfaat Penelitian

Adapun manfaat dari penelitian ini diharapkan dapat memberikan informasi yang bermanfaat tentang hasil penduga terbaik (UMVUE) dari distribusi Pareto dengan menggunakan metode momen dan maksimum likelihood sehingga memenuhi Batas Bawah Cramer Rao.

4 BAB II

TINJAUAN PUSTAKA

Variabel acak 𝑋 dibedakan menjadi dua jenis, yaitu varibel acak diskrit dan variabel acak kontinu. Variabel acak diskrit adalah variabel acak yang mempunyai nilai-nilai terhitung (countable). Jadi, variabel acak diskrit 𝑋 dapat bernilai 𝑥₁, … , 𝑥_𝑛 ∈ 𝑅. Sedangkan variabel acak kontinu adalah variabel acak yang nilai-nilainya tak terhitung (uncountable). Jadi nilai-nilai vaiabel acak kontinu 𝑋 dapat merupakan semua nilai dalam satu interval misalnya [a, b] atau 𝑅, dimana banyaknya bilangan yang terkandung pada interval tersebut adalah tak terhingga atau tak terbilang (Walpole dan Myers, 1995:53).

2.1 Fungsi Distribusi

Definisi 2.1 (Walpole dan Myers, 1995:77) Himpunan pasangan terurut {𝑥, 𝑓 𝑥 } merupakan fungsi peluang atau distribusi peluang variabel acak diskrit 𝑋 jika untuk setiap kemungkinan hasil 𝑥 memenuhi:

1. 𝑓 𝑥 ≥ 0. 2. 𝑓(𝑥)𝑥 = 1

3. 𝑃 𝑋 = 𝑥 = 𝑓 𝑥

Maka distribusi peluang dari 𝑋 tersebut disebut distribusi peluang variabel acak diskrit 𝑋.

Definisi 2.2 (Walpole dan Myers, 1995:85) Fungsi 𝑓(𝑥) adalah distribusi peluang variabel acak kontinu 𝑋, yang didefinisikan di atas himpunan semua bilangan real 𝑅, bila:

5 1. 𝑓 𝑥 ≥ 0 untuk semua 𝑥 ∈ 𝑅,

2. _−∞∞ 𝑓 𝑥 𝑑𝑥 = 1,

3. 𝑃 𝑎 < 𝑋 < 𝑏 = 𝑓 𝑥 𝑑𝑥_𝑎𝑏 .

Dalam banyak soal diperlukan menghitung peluang bahwa nilai amatan variabel acak 𝑋 akan lebih kecil atau sama dengan suatu bilangan real 𝑥. Bila 𝐹 𝑥 = 𝑃(𝑋 ≤ 𝑥) untuk setiap bilangan real 𝑥, maka 𝐹(𝑥) disebut sebagai fungsi distribusi kumulatif variabel acak 𝑋 (Walpole dan Myers, 1995:79).

Definisi 2.3 (Walpole dan Myers, 1995:79) Distribusi kumulatif 𝐹(𝑥) suatu variabel acak diskrit 𝑋 dengan distribusi peluang 𝑓(𝑥) dinyatakan dengan

𝐹 𝑥 = 𝑃 𝑋 ≤ 𝑥 = _𝑡≤𝑥𝑓(𝑡) untuk −∞ < 𝑥 < ∞.

Definisi 2.4 (Walpole dan Myers, 1995:87) Distribusi kumulatif 𝐹(𝑥) suatu variabel acak kontinu 𝑋 dengan fungsi peluang 𝑓 𝑥 diberikan dengan

𝐹 𝑥 = 𝑃 𝑋 ≤ 𝑥 = _−∞𝑥 𝑓 𝑡 𝑑𝑡 Untuk −∞ < 𝑥 < ∞. 2.2 Distribusi Pareto

Distribusi Pareto berasal dari nama seorang ekonom yaitu Vilfredo Pareto (1848-1923) yang mengamati bahwa 80% kekayaan di Milan dimiliki oleh hanya 20% dari penduduknya. Distribusi Pareto disebut juga dengan distribusi power law. Jika sebuah kumpulan data memiliki distribusi power-law, maka dikatakan bahwa data-data tersebut tidak sensitif terhadap rata-rata atau standar deviasi dari data tersebut atau dengan kata lain, data itu tidak bersifat acak (Yosef, 2005). Distribusi Pareto sering dipakai pada persoalan uji hidup, seperti waktu sampai rusak atau umur suatu komponen yang diukur dari suatu waktu tertentu sampai rusak (Jamilah, Firdaus & Sugiarto, S., 2014).

6 Definisi 2.5 (Malik, 2011)

1. Jika 𝑋 adalah variabel acak berdistribusi Pareto, maka fungsi kepadatan peluang (pdf) dari variabel acak Pareto dengan parameter 𝑘 dan 𝛼 adalah:

𝑓 𝑥 = 𝛼 𝑘𝛼

𝑥𝛼 +1 ; 𝑥 ≥ 𝑘

0 ; 𝑥 < 𝑘

2. Jika 𝑋 adalah variabel acak berdistribusi Pareto, maka fungsi distribusi kumulatif (CDF) dari variabel acak Pareto dengan parameter 𝑘 dan 𝛼 adalah : 𝐹 𝑥 = 1 − 𝑘 𝑥 𝛼 ; 𝑥 ≥ 𝑘 0 ; 𝑥 < 𝑘 dimana 𝑘 > 0 dan 𝛼 > 0 adalah parameternya.

3. Jika 𝑋 adalah variabel acak berdistribusi Pareto, maka probabilitas bahwa 𝑋 lebih besar dari beberapa nilai 𝑥 dengan parameter skala 𝑘 dan parameter bentuk 𝛼 diberikan oleh :

𝑃 𝑋 > 𝑥 = 𝑘 𝑥 𝛼 ; 𝑥 ≥ 𝑘 1 ; 𝑥 < 𝑘 dimana 𝑘 > 0 dan 𝛼 > 0 adalah parameternya. Bukti : 𝑓 𝑥 = 𝛼 𝑘𝛼 𝑥𝛼 +1 ; 𝑥 ≥ 𝑘 0 ; 𝑥 < 𝑘 𝐹 𝑥 = 𝛼 𝑘 𝛼 𝑥𝛼 +1 𝑑𝑥 𝑥 𝑘 =

𝛼

𝑘𝛼 𝑥𝛼+1 −1 𝑥 𝑘 𝑑𝑥

7 =

𝛼

𝑘𝛼 _𝑥−𝛼−1 𝑥 𝑘 𝑑𝑥 =

𝛼

𝑘𝛼 1 −𝛼 − 1 + 1 𝑥 −𝛼−1+1 𝑘 𝑥 =

𝛼

𝑘 𝛼 −𝛼 𝑥 −𝛼 𝑘 𝑥 = − 𝑘𝛼𝑥−𝛼 _𝑘𝑥 = −𝑘𝛼𝑥−𝛼 − −𝑘𝛼_𝑘−𝛼 = −𝑘𝛼𝑥−𝛼 + 1 = 1 − 𝑘𝛼_𝑥−𝛼 = 1 −𝑘 𝛼 𝑥𝛼. Teorema 2.6 (Malik, 2011)

1. Andaikan X adalah variabel acak berdistribusi Pareto, maka: 𝜇 = 𝐸 𝑋 = 𝛼𝑘 𝛼 − 1, 𝛼 > 1 Bukti : 𝐸 𝑋 = 𝑥 𝑓 𝑥 𝑑𝑥 𝑘 −∞ + 𝑥 𝑓 𝑥 𝑑𝑥 ∞ 𝑘 = 0 + 𝑥 𝑓 𝑥 𝑑𝑥 ∞ 𝑘 = 𝛼𝑘 𝛼 𝑥𝛼𝑑𝑥 ∞ 𝑘 = 𝛼𝑘𝛼 1 𝑥𝛼𝑑𝑥 ∞ 𝑘 = 𝛼𝑘𝛼 𝑥−𝛼𝑑𝑥 ∞ 𝑘 = 𝛼𝑘𝛼 1 −𝛼 + 1𝑥 −𝛼+1 ∞ 𝑘 = 𝛼𝑘𝛼𝑘 −𝛼+1 𝛼 − 1 = 𝛼𝑘 𝛼 − 1 .

8 2. Andaikan X adalah variabel acak berdistribusi Pareto, maka:

𝑉𝑎𝑟 𝑋 = 𝑘 𝛼 − 1 2 _𝛼 𝛼 − 2, 𝛼 > 2 Bukti : 𝐸 𝑋2 = 𝑥2 _{𝑓 𝑥 𝑑𝑥} 𝑘 −∞ + 𝑥2 𝑓 𝑥 𝑑𝑥 ∞ 𝑘 = 0 + 𝑥2 𝑓 𝑥 𝑑𝑥 ∞ 𝑘 = 𝛼 𝑘 𝛼 𝑥𝛼 −1𝑑𝑥 ∞ 𝑘 = 𝛼𝑘𝛼 1 𝑥𝛼 −1𝑑𝑥 ∞ 𝑘 = 𝛼𝑘𝛼 𝑥−𝛼+1𝑑𝑥 ∞ 𝑘 = 𝛼𝑘𝛼 1 −𝛼 + 2𝑥 −𝛼+2 ∞ 𝑘 = 𝛼𝑘𝛼𝑘 −𝛼+2 𝛼 − 2 = 𝛼𝑘 2 𝛼 − 2 . 𝑉𝑎𝑟 𝑋 = 𝐸 𝑋 − 𝐸(𝑋) 2 = 𝐸 𝑋2− 2𝑋𝐸 𝑋 + 𝐸 𝑋 2 = 𝐸 𝑋2 − 2 𝐸 𝑋 2_{+ 𝐸 𝑋} 2 = 𝐸 𝑋2 _{− [𝐸 𝑋 ]}2 = 𝛼𝑘 2 𝛼 − 2− 𝛼𝑘 𝛼 − 1 2 = 𝛼𝑘 2 _{𝛼 − 1} 2_{− 𝛼𝑘} 2 _{𝛼 − 2} 𝛼 − 1 2 _{𝛼 − 2} = 𝑘 2_{[𝛼 𝛼 − 1} 2_{− 𝛼}2 _{𝛼 − 2 ]} 𝛼 − 1 2 _{𝛼 − 2} = 𝑘 2_[𝛼(𝛼2_{− 2𝛼 + 1) − 𝛼}2 _{𝛼 − 2 ]} 𝛼 − 1 2 _{𝛼 − 2} = 𝑘 2 _𝛼3_{− 2𝛼}2_{+ 𝛼 − 𝛼}3_{− 2𝛼}2 𝛼 − 1 2 _{𝛼 − 2} = 𝑘 𝛼 − 1 2 𝛼 𝛼 − 2

9 2.3 Metode Estimasi Parameter

Keakuratan penduga parameter tergantung pada ukuran sampel dan metode yang digunakan untuk penduga parameter. Statistik yang dihitung dari sampel yang digunakan untuk menduga parameter populasi disebut penduga. Suatu penduga yang baik mempunyai sifat-sifat: tak bias, konsisten dan efisien. Statistik yang digunakan untuk menduga parameter populasi 𝜃 disebut suatu penduga titik untuk 𝜃, dinotasikan 𝜃 . Ada 3 metode yang banyak digunakan untuk penduga parameter dari populasi yaitu metode maximum likelihood, metode momen dan metode kuadrat terkecil (Walpole, 1995).

2.3.1 Metode Momen

Misalkan 𝑋~𝑓_𝑥 . ; 𝜃₁, … , 𝜃_𝑘 , 𝜃₁, … , 𝜃_𝑘 ∈ Ɵ adalah populasi yang menjadi perhatian kita dan 𝜃₁, … , 𝜃_𝑘 adalah parameter-parameter yang tidak

diketahui. Momen ke 𝑗 dari populasi ini terhadap titik pusat adalah 𝜇_𝑗′ = 𝐸(𝑋𝑗). Biasanya 𝜇_𝑗′ bergantung pada 𝜃1, … , 𝜃𝑘 karena itu kita notasikan

sebagai 𝜇_𝑗′ = 𝜇_𝑗′(𝜃1, … , 𝜃𝑘). 𝑗 = 1, … , 𝑘. Misalkan 𝑋1, … , 𝑋𝑛 adalah sampel acak

dari populasi 𝑓𝑥 . ; 𝜃1, … , 𝜃𝑘 , 𝜃1, … , 𝜃𝑘 ∈ Ɵ. Karena 𝜇𝑗′ sangat dekat dengan

𝑀_𝑗′, penduga 𝜃 ₁, … , 𝜃 _𝑘 dapat diturunkan dengan menyelesaikan sistem persamaan 𝜇_𝑗′ = 𝜇_𝑗′ 𝜃₁, … , 𝜃_𝑘 = 𝑀_𝑗′_{, 𝑗 = 1, … , 𝑘, (2.1)}

secara simultan untuk 𝜃₁, … , 𝜃_𝑘 dimana 𝑀_𝑗′ adalah momen ke j sampel. Selanjutnya penduga yang diperoleh dengan cara seperti ini kita sebut sebagai penduga metode momen (moment method estimator) disingkat MME.

10 2.3.2 Metode Maksimum Likelihood

Definisi 2.7 (Somayasa, 2008) Misalkan 𝑋₁, … , 𝑋_𝑛 merupakan n variabel acak dengan 𝑋₁~ 𝑓𝑥_𝑖 . ; 𝜃1, … , 𝜃𝑘 , 𝜃1, … , 𝜃𝑘 , 𝑖 = 1, … , 𝑛. Misalkan 𝑥1, … , 𝑥𝑛

merupakan data atau realisasi dari 𝑋1, … , 𝑋𝑛. Fungsi 𝐿 ∶ Ɵ →𝑅≥0, sedemikian

hingga 𝐿 𝜃1, … , 𝜃𝑘 = 𝑓𝑥1, … , 𝑥𝑛 𝑥1, … , 𝑥𝑛; 𝜃1, … , 𝜃𝑘 disebut fungsi likelihood.

Sebagai kejadian yang lebih khusus, jika 𝑋₁, … , 𝑋_𝑛 merupakan suatu sampel acak, maka :

𝐿 𝜃1, … , 𝜃𝑘 = 𝑛𝑖=1𝑓𝑥𝑖 𝑥𝑖; 𝜃1, … , 𝜃𝑘 . (2.2)

Selanjutnya, nilai-nilai dari 𝜃₁, … , 𝜃_𝑘 ∈ Ɵ yang dinyatakan sebagai 𝜃 ₁, … , 𝜃 _𝑘 sedemikian hingga

𝐿 𝜃 ₁, … , 𝜃 _𝑘 = max_{(𝜃1,…,𝜃𝑘)∈ Ɵ} 𝐿 𝜃₁, … , 𝜃_𝑘 , (2.3) disebut penduga dengan likelihood terbesar (Maximum likelihood estimator). Biasanya (𝜃 1,...,𝜃 k) merupakan fungsi dari data 𝑥1, … , 𝑥𝑛 , misalkan sebagai

𝜃 i = 𝜃_𝑖(𝑥₁, … , 𝑥_𝑛), 𝑖 = 1, … , 𝑘. Jika fungsi-fungsi ini kita terapkan terhadap sampel acak 𝑋1, … , 𝑋𝑛 , maka 𝜃 i = 𝑡𝑖 𝑋1, … , 𝑋𝑛 disebut penduga dengan

likelihood terbesar (MLE) untuk 𝜃𝑖, 𝑖 = 1, … , 𝑘.

Dari persamaan (2.3) adalah jelas bahwa permasalahan menentukan MLE adalah termasuk permasalahan optimasi. Nilai-nilai dari (𝜃 1,...,𝜃 k) memberikan global maksimum dari 𝐿 𝜃₁, … , 𝜃_𝑘 yang memaksimumkan 𝐿 𝜃₁, … , 𝜃_𝑘 juga memaksimumkan log-likelihood ln 𝐿 𝜃₁, … , 𝜃_𝑘 saja (Somayasa, 2008).

11 2.3.2.1Kasus satu parameter (𝒌 = 𝟏)

Jika ruang parameter Ɵ merupakan interval terbuka, dan jika 𝐿 . terdeferensialkan pada Ɵ, maka titik-titik ekstrim adalah titik-titik yang merupakan penyelesaian dari persamaan

𝑑 ln 𝐿(𝜃)

𝑑𝜃

= 0.

(2.4)

Andaikan 𝜃 merupakan satu-satunya penyelesaian, maka titik 𝜃 adalah MLE, jika

𝑑2ln 𝐿(𝜃)

𝑑𝜃

< 0. (2.5)

Jika penyelesaian dari persamaan (2.4) tidak tunggal, misalkan sebagai 𝜃 1, … , 𝜃 𝑚, 𝑚 ∈ 𝑁 dan semuanya memenuhi persamaan (2.5) maka MLE adalah

𝜃 = 𝑎𝑟𝑔 max𝜃𝐿 𝜃 . (2.6)

Contoh 2.8 Misalkan 𝑋₁, … , 𝑋_𝑛 adalah sampel acak dari populasi 𝑋~𝑃𝑂𝐼 𝜆 , 𝜆 > 0. fungsi likelihood dari datanya adalah

ln 𝐿 𝜆 = 𝑒 −𝜆_𝜆𝑥𝑖 𝑥𝑖! 𝑛 𝑖=1 = 𝑒 −𝜆_𝜆 𝑛𝑖=1𝑥𝑖 𝑥𝑖! 𝑛 𝑖=1 . Fungsi log-likelihoodnya adalah

ln 𝐿( 𝜆) = −𝑛𝝀 + 𝒙_𝒊𝒍𝒏 𝝀 − 𝒙_𝒊! 𝒏 𝒊=𝟏 𝒏 𝒊=𝟏 ⇒𝑑 ln 𝐿 𝜆 𝑑𝜆 = 0 ⇔ −𝑛 + 1 𝜆 𝑥𝑖 = 0 ⇔ 𝜆 = 𝑥 , 𝑛 𝑖=1

selanjutnya uji turunan ke dua pada titik 𝜆 = 𝑥 memberikan 𝑑2ln 𝐿 𝜆 𝑑𝜆2 = − 1 𝑥 2 𝑥𝑖 𝑛 𝑖=1 = −𝑛 𝑥 < 0. Jadi MLE untuk 𝛌 adalah 𝜆 = 𝑥 (Somayasa, 2008).

12 2.3.2.2Kasus 𝒌 parameter

Misalkan ruang parameter Ɵ merupakan himpunan terbuka ruang Euclid𝑅𝑘 dan 𝐿 . terdeferensialkan pada 𝑅𝑘_{. Titik-titik ekstrim adalah titik-titik yang}

merupakan penyelesaian dari sistem persamaan

𝜕 ln 𝐿 𝜃1,…,𝜃𝑘

𝜕𝜃𝑗

= 0, 𝑗 = 1, … , 𝑘. (2.7)

Selanjutnya apakah titik-titik ekstrim ini memberikan nilai maksimum, harus diverifikasi. Untuk kasus 𝑘 = 2, kita gunakan alat dari kalkulus sebagai berikut. Misalkan 𝐿(𝜃₁, 𝜃₂) terdeferensialkan sampai order kedua, dan misalkan (𝜃 ₁, 𝜃 ₂) merupakan penyelesaian tunggal dari persamaan (2.7). Misalkan

𝐷 𝜃₁, 𝜃₂ ∶= 𝜕2ln 𝐿(𝜃1,𝜃2) 𝜕𝜃₁2 𝜕2ln 𝐿(𝜃1,𝜃2) 𝜕𝜃₂2 − 𝜕2ln 𝐿(𝜃1,𝜃2) 𝜕𝜃1𝜕𝜃2 , (2.8) jika 𝐷(𝜃 ₁, 𝜃 ₂) > 0 dan 𝜕 2_{ln 𝐿(𝜃} 1,𝜃2)

𝜕𝜃12 (𝜃 1, 𝜃 2) < 0, maka (𝜃 1, 𝜃 2) merupakan MLE.

Dalam kasus penyelesaian dari persamaan (2.7) tidak tunggal, semua penyelesaian harus diverifikasi apakah dia merupakan titik maksimum atau bukan. Selanjutnya MLE adalah titik (𝜃 ₁, 𝜃 ₂) dengan 𝐿(𝜃 ₁, 𝜃 ₂) terbesar (Somayasa, 2008).

2.4 Kriteria Memilih Estimator 2.4.1 Ketakbiasan

Definisi 2.9 (Somayasa, 2008) Misalkan 𝑋₁, … , 𝑋_𝑛 merupakan sampel acak dari populasi 𝑓_𝑥 . ; 𝜃 , 𝜃 ∈ Ɵ ⊂ 𝑅. Misalkan 𝜏 ∶ Ɵ → 𝑅 merupakan fungsi real pada ruang parameter. Suatu penduga 𝑇 ≔ 𝑡(𝑋1, … , 𝑋𝑛) disebut penduga tak bias jika

𝐸 𝑇 = 𝜏 𝜃 , ∀𝜃 𝜖 Ɵ. Sebaliknya, jika kondisi ini tidak dipenuhi, kita sebut 𝑇 penduga bias.

13 2.4.2 Keterkonsentrasian dan UMVUE

Definisi 2.10 (Somayasa, 2008) Misalkan 𝑇₁ dan 𝑇₂ merupakan penduga (tidak harus tak bias) untuk 𝜏(𝜃). 𝑇₁ dikatakan lebih terkonsentrasi disekitar 𝜏(𝜃) dari pada 𝑇₂ jika untuk setiap 𝜀 > 0 berlaku,

𝑃 𝑇₁− 𝜏(𝜃) < 𝜀 ≥ 𝑃 𝑇₂− 𝜏(𝜃) < 𝜖 . (2.9) Definisi 2.11 (Somayasa, 2008) Misalkan 𝐴_𝑟(𝜃) merupakan himpunan semua penduga (tidak harus tak bias) untuk 𝜏(𝜃). 𝑇∗ dikatakan paling terkonsentrasi disekitar 𝜏(𝜃) jika untuk setiap 𝜀 > 0 berlaku,

𝑃 𝑇1− 𝜏(𝜃) < 𝜀 = 𝑇𝜖𝐴𝑟(𝜃 )𝑃 𝑇1− 𝜏(𝜃) < 𝜀 𝑠𝑢𝑝

. (2.10) Catatan, misalkan 𝑈_𝑟(𝜃) merupakan himpunan penduga tak bias untuk 𝜏(𝜃). Dengan ketaksamaan Chebychev diperoleh

𝑃 𝑇₁− 𝜏(𝜃) < 𝜀 ≥ 1 −𝑉𝑎𝑟 (𝑇)

𝜀2 , ∀𝜀> 0. (2.11)

Jadi berdasarkan persamaan (2.11), jika 𝑇∗ ∈ 𝑈_𝑟(𝜃) maka 𝑇∗ merupakan penduga tak bias yang paling terkonsentrasi disekitar 𝜏(𝜃) dibandingkan dengan penduga lainnya di dalam 𝑈𝑟(𝜃). Jika dipenuhi

𝑉𝑎𝑟 𝑇∗ = 𝑇∈𝑈𝑟 (𝜃 )𝑉𝑎𝑟 𝑇 , ∀𝜀𝜖 Ɵ 𝑖𝑛𝑓

, (2.12) kriteria ini menghasilkan suatu konsep baru dalam pemilihan penduga terbaik, yaitu konsep penduga tak bias dengan variansi minimum seragam (univormly minimum variance unbiased estimator), disingkat UMVUE. Selanjutnya penduga tak bias yang memenuhi persamaan (2.12) disebut UMVUE.

14 Teorema 2.12 Batas bawah Cramer-Rao (Somayasa, 2008) Misalkan 𝑋₁, … , 𝑋_𝑛 merupakan sampel acak dari 𝑓 . ; 𝜃 , 𝜃 𝜖 Ɵ. Jika 𝑇 ≔ 𝑡(𝑋1, … , 𝑋𝑛) merupakan

penduga tak bias untuk 𝜏(𝜃), dan jika 𝜏′ 𝜃 ≔ 𝑑𝜏(𝜃)/𝑑𝜃 ada, maka batas bawah Cramer-Rao untuk 𝜏(𝜃) adalah

𝑉𝑎𝑟(𝑇) ≥ 𝜏′ 𝜃 2 𝑛𝐸 𝜕 𝜕𝜃ln 𝑓(𝑋𝑖;𝜃) 2 (2.13)

Bukti. Pertama-tama didefinisikan suatu fungsi 𝑢 ∶ 𝑅𝑛 _{→ 𝑅, dimana}

𝑢 𝑥₁, … , 𝑥_𝑛; 𝜃 ≔ 𝜕 𝜕𝜃ln 𝑓( 𝑥1, … , 𝑥𝑛; 𝜃) = 1 𝑓 𝑥1, … , 𝑥𝑛; 𝜃 𝜕 𝜕𝜃𝑓(𝑥1, … , 𝑥𝑛; 𝜃) = 𝑢 𝑥1, … , 𝑥𝑛; 𝜃 𝑓 𝑥1, … , 𝑥𝑛; 𝜃 = 𝜕 𝜕𝜃𝑓 𝑥1, … , 𝑥𝑛; 𝜃 .

Selanjutnya di definisikan suatu kuantitas acak yang masih bergantung pada 𝜃, yaitu 𝑈 ≔ 𝑢(𝑋₁, … , 𝑋_𝑛; 𝜃). Maka 𝐸 𝑈 = … 𝑢( ∞ −∞ ∞ −∞ 𝑥₁, … , 𝑥_𝑛; 𝜃) 𝑓 𝑥₁, … , 𝑥_𝑛; 𝜃 𝑑𝑥₁… 𝑑𝑥_𝑛 = _−∞∞ … _−∞∞ _𝜕𝜃𝜕 ( 𝑓 𝑥1, … , 𝑥𝑛; 𝜃 𝑑𝑥1… 𝑑𝑥𝑛 = 𝜕 𝜕𝜃 … ∞ −∞ 𝑓 𝑥1, … , 𝑥𝑛; 𝜃 𝑑𝑥1… 𝑑𝑥𝑛 ∞ −∞ = 𝜕 𝜕𝜃 1 = 0.

Pada perhitungan ekspektasi dari U, pertukaran tanda integral dan diferensial dapat dilakukan karena domain dari integran-nya bergantung pada 𝜃. Dari asumsi T tak bias terhadap 𝜏(𝜃), diperoleh

15 𝜏′ _{𝜃 =} 𝜕 𝜕𝜃 E(T) =𝜕 𝜕𝜃 … ∞ −∞ 𝑡 𝑥1, … , 𝑥𝑛 𝑓 𝑥1, … , 𝑥𝑛; 𝜃 𝑑𝑥1… 𝑑𝑥𝑛 ∞ −∞ = … _−∞∞ 𝑡 𝑥1, … , 𝑥𝑛 𝜕 𝜕𝜃 𝑓 𝑥1, … , 𝑥𝑛; 𝜃 𝑑𝑥1… 𝑑𝑥𝑛 ∞ −∞ = … _−∞∞ 𝑡 𝑥₁, … , 𝑥_𝑛 𝑢 𝑥1, … , 𝑥𝑛; 𝜃 𝑓 𝑥1, … , 𝑥𝑛; 𝜃 𝑑𝑥1… 𝑑𝑥𝑛 ∞ −∞ = 𝐸(𝑇𝑈).

Dari kedua hasil diatas diperoleh 𝐶𝑜𝑣 𝑇, 𝑈 = 𝐸 𝑇 𝐸 𝑈 = 𝑟′ _{𝜃 . Pada sisi lain,}

ketaksamaan Cauchy-Schwars memberikan 𝐶𝑜𝑣(𝑇, 𝑈) 2 _{≤ 𝑉𝑎𝑟 𝑇 𝑉𝑎𝑟 𝑈 ,}

sehingga 𝑉𝑎𝑟 𝑇 ≥ 𝐶𝑜𝑣 𝑇,𝑈 2

𝑉𝑎𝑟 𝑈 =

𝜏′ 𝜃 2

𝑉𝑎𝑟 𝑈 . Selanjutnya verifikasi lebih lanjut bentuk

dari 𝑉𝑎𝑟 𝑈 . Mengingat 𝑋1, … , 𝑋𝑛 adalah sampel acak, maka

𝑉𝑎𝑟 𝑈 = 𝑉𝑎𝑟 𝜕 𝜕𝜃ln 𝑓 𝑋𝑖; 𝜃 𝑛 𝑖=1 = 𝑉𝑎𝑟 𝜕 𝜕𝜃ln 𝑓(𝑋𝑖; 𝜃) 𝑛 𝑖=1 = 𝑉𝑎𝑟 𝑛 𝑖=1 𝜕 𝜕𝜃ln 𝑓 𝑋𝑖; 𝜃 = 𝑛𝐸 𝜕 𝜕𝜃ln 𝑓(𝑋𝑖; 𝜃) 2

16 BAB III

METODE PENELITIAN

3.1 Waktu dan Tempat Penelitian

Penelitian ini berlangsung dari bulan Agustus 2015 sampai dengan Maret 2016. Penelitian ini berlokasi di Perpustakaan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Halu Oleo.

3.2 Metode dan Prosedur Penelitian

Metode yang diterapkan dalam penyelesaian penelitian ini yaitu metode kepustakaan (library research). Metode ini digunakan peneliti untuk menyeleksi teori-teori yang dapat mendukung pokok permasalahan yang dimunculkan pada penelitian ini, agar pembahasannya dapat diselesaikan secara tuntas. Teori-teori pendukung tersebut telah dibahas pada Bab II. Adapun lngkah-langkah yang dilakukan dalam penelitian ini adalah sebagai berikut :

1. Merumuskan prosedur estimasi parameter dalam distribusi Pareto dengan menggunakan Metode momen.

 Menentukan momen pertama dan kedua dari distribusi Pareto.

 Menyelesaikan persamaan momen pertama dan kedua untuk mendapatkan penduga metode momen dari distribusi Pareto.

2. Merumuskan prosedur estimasi parameter dalam distribusi Pareto dengan menggunakan Metode Maksimum Likelihood.

17  Membentuk fungsi kepadatan peluang bersama distribusi Pareto ke

dalam fungsi likelihood.

 Membentuk fungsi likelihood kedalam fungsi maksimum likelihood (log likelihood).

 Memaksimumkan fungsi maksimum likelihood dengan menurunkan fungsi maksimum likelihood terhadap parameter yang mengikutinya.  Melakukan uji turunan kedua untuk memastikan fungsi likelihood

telah maksimum.

3. Menentukan penduga terbaik dalam distribusi Pareto menggunakan Teorema Batas Bawah Crammer-Rao.

 Menunjukkan penduga distribusi Pareto adalah tak bias untuk 𝜏 𝛼 .  Menggunakan ketaksamaan Cramer-Rao untuk menunjukkan bahwa

penduga dari distribusi Pareto adalah penduga tak bias dan bervariansi minimum (UMVUE).

4. Penduga interval kepercayaan dari distribusi Pareto. 5. Membuat kesimpulan.

18 BAB IV

HASIL DAN PEMBAHASAN

Penelitian ini membahas permasalahan merumuskan prosedur estimasi parameter dari distribusi Pareto dengan menggunakan metode momen dan metode likelihood, serta menentukan penduga terbaik (UMVUE).

4.1 Metode momen dalam menduga parameter distribusi Pareto.

Pada Bab II sudah diketahui fungsi kepadatan peluang (pdf) dari variabel acak Pareto dengan parameter 𝑘 > 0 dan α > 0 adalah

𝑓 𝑥 = 𝛼

𝑘𝛼

𝑥𝛼 +1 ; 𝑥 ≥ 𝑘

0 ; 𝑥 < 𝑘 , (4.1) dimana fungsi 𝑓(𝑥) pada Persaman (4.1) adalah distribusi peluang variabel acak kontinu 𝑋, yang didefinisikan di atas himpunan semua bilangan real 𝑅 :

1. 𝑓 𝑥 ≥ 0 untuk semua 𝑥 ∈ 𝑅. 2. _−∞∞ 𝑓 𝑥 𝑑𝑥 = 1 Bukti : 𝛼 𝑘 𝛼 𝑥𝛼 +1 𝑑𝑥 = 𝛼𝑘 𝛼 1 𝑥𝛼 +1 ∞ 𝑘 ∞ 𝑘 𝑑𝑥 = 𝛼𝑘𝛼 𝑥𝛼 +1 −1 ∞ 𝑘 𝑑𝑥 = 𝛼𝑘𝛼 1 −𝛼 − 1 + 1 𝑥 −𝛼−1+1 𝑘 ∞ = 𝛼𝑘 𝛼 −𝛼 𝑥 −𝛼 𝑘 ∞ = −𝑘𝛼𝑥−𝛼 _𝑘∞ = lim 𝑛→∞−𝑘 𝛼_𝑛−𝛼 _{− (−𝑘}𝛼_𝑛−𝛼₎ = 𝑘𝛼𝑘−𝛼 = 𝑘0 = 1 1 2 3 4 5 6 7 8 9 10 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

Grafik Fungsi Kepadatan Peluang Distribusi Pareto untuk K = 1 alpha=1 alpha=3 alpha=5

19 Gambar 1. Grafik Pdf distribusi Pareto untuk berbagai nilai α

Sedangkan mean dan variansinya adalah

𝜇 = 𝐸 𝑋 = 𝛼𝑘 𝛼 − 1, 𝑉𝑎𝑟 𝑋 = 𝑘 𝛼 − 1 2 𝛼 𝛼 − 2.

Adapun langkah-langkah menduga parameter dengan metode momen adalah sebagai berikut :

Langkah I : Menentukan momen pertama dan kedua dari distribusi Pareto. 𝜇_𝑗′ = 𝐸 𝑋𝑗 _{, 𝑗 = 1,2, … , 𝑘 . Untuk 𝑗 = 1 maka 𝐸 𝑋 =} 𝛼𝑘 𝛼−1= 𝑋 𝛼𝑘 = (𝛼 − 1) 𝑋 𝛼𝑘 = 𝑋 𝛼 − 𝑋 𝑋 = 𝛼𝑋 − 𝛼𝑘 𝑋 = 𝛼(𝑋 − 𝑘) 𝛼 = 𝑋 (𝑋 −𝑘) . (4.2)

20 𝑗 = 2 maka 𝐸 𝑋2 = 𝑘 𝛼−1 2 𝛼 𝛼−2+ 𝛼𝑘 𝛼−1 2 = 𝑋 (4.3)

Langkah II : Menyelesaikan Persamaan (4.3) dengan mensubstitusi 𝛼 = 𝑋

(𝑋 −𝑘). 𝐸 𝑋2 ₌ 𝑘 𝛼 − 1 2 𝛼 𝛼 − 2+ 𝛼𝑘 𝛼 − 1 2 𝑋 = 𝑘 𝑋 𝑋 − 𝑘− 1 2 𝑋 𝑋 − 𝑘 𝑋 𝑋 − 𝑘− 2 + 𝑋 𝑋 − 𝑘𝑘 𝑋 𝑋 − 𝑘− 1 2 𝑋 = 𝑘(𝑋 − 𝑘) 𝑋 − (𝑋 − 𝑘) 2 𝑋 𝑋 − 𝑘 𝑋 − 𝑘 𝑋 − 2 (𝑋 − 𝑘)+ 𝑋 𝑘 𝑋 − 𝑘 𝑋 − 𝑘 𝑋 − (𝑋 − 𝑘) 2 𝑋 = 𝑘(𝑋 − 𝑘) 𝑘 2 𝑋 −(𝑋 − 𝑘)+ 𝑋 𝑘 𝑘 2 𝑋 = 𝑋 − 𝑘 2_𝑋 −(𝑋 − 𝑘) + 𝑋 2 𝑋 = − 𝑋 − 𝑘 𝑋 + 𝑋 2 𝑋 − 𝑋 2 = − 𝑋 2− 𝑋 𝑘 𝑋 − 𝑋 2 _{= −𝑋} 2_{+ 𝑋 𝑘} 𝑋 𝑘 = 𝑋 − 𝑋 2+ 𝑋 2 𝑘 =𝑋 𝑋 .

Jadi, penduga metode momen untuk 𝛼 dan k adalah 𝑘 =𝑋

𝑋 , sehingga

𝛼 =

𝑋 (𝑋 −𝑘)

=

𝑋 𝑋 −𝑋 𝑋

=

_{𝑋 2−𝑋} 𝑋 𝑋

=

𝑋 2 𝑋 2_−𝑋 . (4.4)

21 4.2 Metode Maksimum Likelihood dalam Menduga Parameter Distribusi

Pareto.

Adapun langkah-langkah menduga dengan metode maksimum likelihood adalah sebagai berikut:

Langkah I: Menentukan fungsi kepadatan peluang dari distribusi Pareto. Fungsi kepadatan peluang dari distribusi Pareto,

𝑓 𝑥 = 𝛼 𝑘

𝛼

𝑥𝛼+1 . (4.5)

Fungsi kepadatan peluang distribusi Pareto Persamaan (4.5) digunakan untuk mencari fungsi kepadatan peluang bersama dari peubah acak 𝑋1, 𝑋2, 𝑋3, … , 𝑋𝑛,

yaitu

𝑓 𝑥1, … , 𝑥𝑛; 𝛼, 𝑘 = 𝑛𝑖=1𝑓 𝑥𝑖; 𝛼, 𝑘 . (4.6)

Langkah II: Membentuk fungsi kepadatan peluang bersama pada Persamaan (4.6) kedalam fungsi likelihood 𝐿 𝛼, 𝑘 . Sehingga fungsi likelihood dari fungsi kepadatan peluang bersamanya adalah

𝐿 𝛼, 𝑘 = 𝑓 𝑥_𝑖; 𝛼, 𝑘 𝑛 𝑖=1 = 𝛼𝑘 𝛼 𝑥1𝛼+1 . 𝛼𝑘 𝛼 𝑥2𝛼+1 … 𝛼𝑘 𝛼 𝑥𝑛𝛼+1 = 𝛼𝑘 𝛼 𝑥_𝑖𝛼+1 𝑛 𝑖=1 = 𝛼𝑛𝑘𝑛𝛼 1 𝑥_𝑖𝛼 +1 𝑛 𝑖=1 . (4.7)

22 Langkah III: Membentuk fungsi likelihood pada Persamaan (4.7) kedalam fungsi ln 𝐿 𝛼, 𝑘 yang dinamakan dengan fungsi maksimum likelihood (log likelihood), sehingga fungsi maksimum likelihood dari fungsi likelihood tersebut diperoleh

𝐿 𝛼, 𝑘 = ln 𝐿 𝛼, 𝑘 = 𝑙𝑛 𝛼𝑛𝑘𝑛𝛼 1 𝑥_𝑖𝛼+1 𝑛 𝑖=1 = 𝑙𝑛 𝛼𝑛 + ln 𝑘𝑛𝛼 + 𝑙𝑛 𝑥_𝑖−𝛼−1 𝑛 𝑖=1 = 𝑛 𝑙𝑛 𝑎 + 𝑛𝛼 𝑙𝑛 𝑘 − 𝛼 + 1 𝑙𝑛 𝑥_𝑖 . 𝑛 𝑖=1 (4.8) Langkah IV: Memaksimumkan fungsi maksimum likelihood dengan menurunkan fungsi maksimum likelihood terhadap parameter yang mengikutinya yakni α, k kemudian menyamakan dengan 0.

Distribusi Pareto ini mempunyai dua parameter yang tidak diketahui yakni α dan k. 𝜕 𝜕𝑘ln 𝐿 𝛼, 𝑘 = 0 𝜕 𝜕𝑘 𝑛 𝑙𝑛 𝑎 + 𝑛𝛼 𝑙𝑛 𝑘 − (𝛼 + 1) 𝑙𝑛 𝑥𝑖 𝑛 𝑖=1 = 0 𝑛𝛼 𝑘 = 0 𝑘 = 0

Karena dapat dilihat ln 𝐿 𝛼, 𝑘 tidak terdeferensialkan terhadap k pada titik dimana ln 𝐿 𝛼, 𝑘 mencapai maksimum, maka MLE untuk k yaitu 𝑘 = min 𝑥_𝑖. Selanjutnya dari persamaan log likelihood diatas diturunkan terhadap parameter 𝛼 dengan mensubtitusi nilai parameter k serta menyamakan dengan nol maka diperoleh

23  Untuk kasus jika parameter k diketahui cukup dengan mengestimasi

parameter 𝜶.

Sehingga untuk nilai α dapat dicari dengan mendiferensialkan fungsi ln 𝐿 𝛼, 𝑘 terhadap parameter yang mengikutinya yakni :

𝜕 𝜕𝛼ln 𝐿 𝛼, 𝑘 = 0 𝜕 𝜕𝛼 𝑛 𝑙𝑛 𝑎 + 𝑛𝛼 𝑙𝑛 𝑘 − (𝛼 + 1) 𝑙𝑛 𝑥𝑖 𝑛 𝑖=1 = 0 𝑛 𝛼+ 𝑛 ln 𝑘 − 𝑙𝑛 𝑥𝑖 = 0 𝑛 𝑖=1 𝑛 𝛼= ln 𝑥𝑖 𝑛 𝑖=1 − 𝑛 ln 𝑘 . (4.9) Langkah V: Melakukan uji turunan kedua untuk memastikan fungsi likelihood pada fungsi 𝜕 𝜕𝛼ln 𝐿 𝛼, 𝑘 telah maksimum, 𝜕2 𝜕𝛼2ln 𝐿 𝛼, 𝑘 = 𝜕 𝜕𝛼 𝑛 𝛼+ 𝑛 ln 𝑘 − ln 𝑥𝑖 𝑛 𝑖=1 𝛼= 𝑛 ln 𝑥 𝑖−ln 𝑘 𝑖 = −𝑛𝛼−2 𝛼= 𝑛 ln 𝑥𝑖 𝑖−ln 𝑘 = −𝑛 𝑛 𝑖 ln 𝑥𝑖− ln 𝑘 −2 = −𝑛 𝑖 ln 𝑥𝑖− ln 𝑘 𝑛 2 = − 𝑖 ln 𝑥𝑖− ln 𝑘 2 𝑛 < 0, karena − ln 𝑥𝑖 𝑖−ln 𝑘 2

𝑛 < 0maka penduga likelihood maksimum untuk 𝛼 adalah

𝛼 = 𝑛

24 4.3 Penduga Terbaik (UMVUE)

Untuk menentukan suatu penduga adalah UMVUE maka penduga tersebut harus penduga tak bias dan bervariansi minimum. Sebuah penduga tak bias akan mencapai variansi minimum diantara semua penduga tak bias lainnya, apabila variansi dari penduga itu lebih besar atau sama dengan batas bawah Cramer-Rao. 4.3.1 Penduga tak bias untuk distribusi Pareto

Suatu penduga 𝑇 dikatakan penduga tak bias untuk 𝜏 𝜃 , jika 𝐸 𝑇 = 𝜏 𝜃 , untuk semua 𝜃 ∈ 𝛺. Sebaliknya 𝑇 dikatakan penduga bias untuk 𝜏 𝜃 , jika 𝐸 𝑇 ≠ 𝜏 𝜃 . Akan tetapi, penduga bias ini dapat diubah menjadi penduga tak bias, apabila ruas kanan dikalikan atau ditambahkan dengan konstanta tertentu. 𝐸 𝑋 = 1 𝑛 𝐸(𝑥𝑖) = 1 𝑛 𝛼𝑘 𝛼 − 1= 1 𝑛 𝑛 𝛼𝑘 𝛼 − 1 = 𝛼𝑘 𝛼 − 1 , maka, 𝑋 merupakan penduga tak bias untuk 𝜏 𝛼 = 𝛼𝑘

𝛼−1

.

4.3.2 Penaksir dengan Variansi Minimum

Untuk membahas penaksir sebuah parameter yang mempunyai variansi minimum, harus dibandingkan dua buah penaksir dalam hal variansinya. Dalam hal ini, kedua penaksir tersebut semuanya harus merupakan penaksir tak bias. Misalkan ada dua penaksir tak bias 𝜃 ₁ dan 𝜃 ₂ untuk 𝜃. Jika 𝜃 ₁ mempunyai variansi yang lebih kecil dibandingkan dengan 𝜃 ₂, maka 𝜃 ₁ dikatakan penaksir tak bias bervariansi minimum. Sebuah penaksir tak bias lainnya, apabila variansi dari penakisir itu sama dengan batas bawah Cramer Rao.

25 4.3.2.1Ketaksamaan Cramer-Rao untuk distribusi Pareto

Salah satu cara untuk mengetahui suatu penduga adalah penduga terbaik yaitu dengan menggunakan ketaksamaan Cramer-Rao. Batas bawah Cramer-Rao untuk 𝜏 𝛼 . 𝜕𝜏 𝛼 𝜕𝛼 = 𝜕 _{𝛼 − 1}𝛼𝑘 𝜕𝛼 =𝑘 𝛼 − 1 − 𝛼𝑘 𝛼 − 1 2 =𝛼𝑘 − 𝑘 − 𝛼𝑘 𝛼 − 1 2 = −𝑘 𝛼 − 1 2 . 𝑓 𝑥𝑖; 𝛼, 𝑘 = 𝛼𝑛𝑘𝑛𝛼 1 𝑥𝑖𝛼 +1 𝑛 𝑖=1 ln 𝑓 𝑥𝑖; 𝛼, 𝑘 = 𝑛 ln 𝛼 + 𝛼 𝑛 ln 𝑘 − 𝑥𝑖𝛼+1 𝑛 𝑖=1 = 𝑛 𝑙𝑛 𝑎 + 𝑛𝛼 𝑙𝑛 𝑘 − (𝛼 + 1) 𝑙𝑛 𝑥𝑖 𝑛 𝑖=1 𝜕 ln 𝑓 𝑥𝑖; 𝛼, 𝑘 𝜕𝛼 = 𝑛 𝛼+ 𝑛 ln 𝑘 − ln 𝑥𝑖 𝑛 𝑖=1 𝜕 ln 𝑓 𝑥𝑖; 𝛼, 𝑘 𝜕𝛼 2 = 𝑛 𝛼+ 𝑛 ln 𝑘 − ln 𝑥𝑖 𝑛 𝑖=1 2 = 𝑛 𝛼 2 + 𝑛 ln 𝑘 − ln 𝑥𝑖 𝑛 𝑖=1 2 − 2𝑛 𝛼 𝑛 ln 𝑘 − ln 𝑥𝑖 𝑛 𝑖=1 = 𝑛 𝛼 2 + 𝑛 ln 𝑘 2+ ln 𝑥𝑖 𝑛 𝑖=1 2 − 2 𝑛 ln 𝑘 ln 𝑥𝑖 𝑛 𝑖=1 +2𝑛 𝛼 𝑛 ln 𝑘 − ln 𝑥𝑖 𝑛 𝑖=1

26 𝐸 𝜕 ln 𝑓 𝑥𝑖; 𝛼, 𝑘 𝜕𝛼 2 = 𝐸 𝑛 𝛼 2 + 𝐸( 𝑛 ln 𝑘 2) + 𝐸 ln 𝑥𝑖 𝑛 𝑖=1 2 − 2 𝑛 ln 𝑘 ln E( 𝑥𝑖) 𝑛 𝑖=1 + 2 𝑛 𝛼 𝐸 𝑛 ln 𝑘 − ln 𝑥𝑖 𝑛 𝑖=1 = 𝑛 𝛼 2 + 𝑛 ln 𝑘 2+ 𝑣𝑎𝑟 ln 𝑥𝑖 𝑛 𝑖=1 − 2 𝑛 ln 𝑘 ln 𝛼𝑘 𝛼 − 1 𝑛 𝑖=1 +2 𝑛 𝛼 𝐸 (𝑛 ln 𝑘) − ln 𝐸(𝑥𝑖 𝑛 𝑖=1 ) = 𝑛 𝛼 2 + 𝑛 ln 𝑘 2+ ln 𝑣𝑎𝑟 𝑥𝑖 𝑛 𝑖=1 − 2 𝑛 ln 𝑘 𝑛 𝑙𝑛 𝛼𝑘 𝛼 − 1 +2𝑛 𝛼 𝑛 ln 𝑘 − ln 𝛼𝑘 𝛼 − 1 𝑛 𝑖=1 = 𝑛 𝛼 2 + 𝑛 ln 𝑘 2_{+ 𝑛} 𝑘 𝛼 − 1 2 _𝛼 𝛼 − 2− 2𝑛 2_{ln 𝑘 ln 𝛼𝑘 − 𝑙𝑛 𝛼 − 1} +2𝑛 𝛼 𝑛 ln 𝑘 − 2𝑛2 𝛼 (ln 𝛼𝑘 − 𝑙𝑛 𝛼 − 1 ) = 𝑛 2 𝛼2+ 𝑛 ln 𝑘 2+ 𝑛 𝑘 𝛼 − 1 2 _𝛼 𝛼 − 2+ 2 𝑛2 𝛼 ln 𝑘 − ln 𝛼𝑘 − 𝑙𝑛 𝛼 − 1 2𝑛2ln 𝑘 +2𝑛 2 𝛼 .

Untuk𝑘 = 1, maka ln 𝑘 = 0 sehingga

= 𝑛 2 𝛼2+ 0 + 𝑛 𝑘 𝛼 − 1 2 _𝛼 𝛼 − 2+ 0 − 0 − 𝑙𝑛 𝛼 − 1 (2𝑛 2_{(0) +}2𝑛2 𝛼 ) = 𝑛 2 𝛼2− ln 𝛼 − 1 2_𝛼 𝛼 + 𝑙𝑛 𝛼 − 1 2𝑛2 𝛼 = 𝑛 2 𝛼2+ 𝑛 𝑘 𝛼 − 1 2 𝛼 𝛼 − 2+ 𝑙𝑛 𝛼 − 1 2𝑛2 𝛼 . Diketahui 𝜏 𝛼 = 𝛼𝑘 𝛼−1, maka τ ′ _{𝛼 =} −𝑘 𝛼−1 2.

27 𝐶𝑅𝐿𝐵 = τ ′ _𝛼 2 𝑛 𝐸 𝜕 ln 𝑓 𝑥_𝜕𝛼𝑖; 𝛼, 𝑘 2 = −𝑘 𝛼 − 1 2 𝑛 𝑛_𝛼22+ 𝑛 _{𝛼 − 1}𝑘 2 𝛼 𝛼 − 2+ 𝑙𝑛 𝛼 − 1 2𝑛 2 𝛼 = −𝑘 𝛼 − 1 2 𝑛3 𝛼2 + 𝑛 2_𝑘2_𝛼 𝛼 − 1 2_{(𝛼 − 2)} + 𝑙𝑛 𝛼 − 1 2𝑛 3 𝛼 = − 𝑘 𝛼 − 1 2 𝛼2 _{𝛼 − 1} 2_{(𝛼 − 2)} 𝛼 − 1 2 _{𝛼 − 2 𝑛}3_{+ 𝑛}2_𝑘2_𝛼3_{+ 𝛼 𝛼 − 1} 2 _{𝛼 − 2 2𝑛}3_{ln 𝛼 − 1} = − 𝑘 𝛼 2_{(𝛼 − 2)} 𝛼 − 1 2 _{𝛼 − 2 𝑛}3_{+ 𝑛}2_𝑘2_𝛼3_{+ 𝛼 𝛼 − 1} 2 _{𝛼 − 2 2𝑛}3_{ln 𝛼 − 1} = − 𝑘 𝛼 2 _{𝛼 − 2} 𝛼2_{− 2𝛼 + 1 𝛼 − 2 𝑛}3_{+ 𝑛}2_𝑘2_𝛼3_{+ 𝛼 𝛼}2_{− 2𝛼 + 1 𝛼 − 2 2𝑛}3_{ln 𝛼 − 1} = − 𝑘 𝛼 2 _{𝛼 − 2} 𝛼3_{− 2𝛼}2_{− 2𝛼}2_{+ 4𝛼 + 𝛼 − 2 𝑛}3_{+ 𝑛}2_𝑘2_𝛼3_{+ 𝛼 𝛼}3_{− 2𝛼}2_{− 2𝛼}2_{+ 4𝛼 + 𝛼 − 2 2𝑛}3_{ln 𝛼 − 1} =− 𝑘 𝛼 2 _{𝛼 − 2} 𝛼3_{+ 4𝛼}2_{+ 5𝛼 − 2 𝑛}3_{+ 𝑛}2_𝑘2_𝛼3_{+ 2𝑛}3_{𝛼 ln 𝛼 − 1 𝛼}3_{+ 4𝛼}2_{+ 5𝛼 − 2} = − 𝑘 𝛼 2 _{𝛼 − 2} 1 + 2𝛼 ln 𝛼 − 1 𝛼3_{+ 4𝛼}2_{+ 5𝛼 − 2 𝑛}3_{+ 𝑛}2_𝑘2_𝛼3 . Jadi, 𝐶𝑅𝐿𝐵 = τ ′ _𝛼 2 𝑛 𝐸 𝜕 ln 𝑓_𝜕𝛼𝑥𝑖;𝛼,𝑘 2

= −

𝑘 𝛼2 𝛼−2 1+2𝛼 ln 𝛼−1 𝛼3_+4𝛼2_{+5𝛼−2 𝑛}3_{+ 𝑛}2_𝑘2_𝛼3 .

𝑉𝑎𝑟 𝑋 = 𝑘 𝛼 − 1 2 _𝛼 𝛼 − 2 𝑛 = 𝑘 𝛼 − 1 2 _𝛼 𝛼 − 2 1 𝑛 = 𝑘 2_𝛼 𝑛 𝛼 − 1 2 _{𝛼 − 2} . Karena 𝑉𝑎𝑟 𝑋 = 𝑘2𝛼 𝑛 𝛼−1 2 _𝛼−2 ≠ CRLB =− 𝑘 𝛼2 𝛼−2 1+2𝛼 ln 𝛼−1 𝛼3_+4𝛼2_{+5𝛼−2 𝑛}3_{+ 𝑛}2_𝑘2_𝛼3

dapat disimpulkan bahwa 𝑋 bukan merupakan UMVUE untuk 𝛼 = 𝛼𝑘

28 4.4 Penduga interval menggunakan metode momen berdasarkan data

sampel acak sederhana

Misalkan 𝑋₁, . . . , 𝑋_𝑛 adalah sampel acak sederhana berukuran n dari distribusi Pareto dengan fungsi densitas pada Persamaan (4.1) karena parameter skala diketahui yaitu k=1 maka fungsi densitas peluang dari distribusi Pareto pada persamaan (4.1) menjadi

𝑓 𝑥 = 𝛼𝑥− 𝛼+1 ; 𝑥 ≥ 1, 𝛼 > 0 (4.11) Dari Persamaan (4.11) diperoleh rata-rata dan variansi dari distribusi Pareto diperoleh 𝜇 = 𝐸 𝑋 = 𝛼 𝛼 − 1, (4.12) 𝑉𝑎𝑟 𝑋 = 1 𝛼 − 1 2 _𝛼 𝛼 − 2; 𝛼 > 2 (4.13) Kemudian akan dibentuk penduga interval untuk 𝛼 dengan terlebih dahulu mencari penduga titik dari 𝛼 dengan menggunakan metode momen yang dinotasikan dengan 𝛼 . Diketahui bahwa variabel acak 𝑋 berdistribusi Pareto dengan rata-rata dan variansi pada persamaan (4.12) dan (4.13), dengan menggunakan metode momen yaitu

𝜇 = 𝜇₁ = 𝐸(𝑋) Dimana 𝜇 = 𝜇₁ = 1 𝑛 𝑋𝑖 𝑛 𝑖=1 , sehingga 𝐸 𝑋 = 𝑋

Untuk mendapatkan penaksir titik 𝛼 , dengan menylesaikan persamaan

𝛼 = 𝑋 (𝑋 − 𝑘)= 𝑋 𝑋 −𝑋 𝑋 = 𝑋 𝑋 2_{− 𝑋} 𝑋 = 𝑋 2 𝑋 2_{− 𝑋}

29 Ryttgard [7] telah menunjukkan bahwa 𝛼 berdistribusi normal secara asimptotik dengan 𝑁 𝛼,𝛼2

𝑛 +

𝛼

𝑛 𝛼−2 jika 𝛼 > 2 atau dapat dinotasikan dengan

𝑛

𝛼

− 𝛼

𝛼2₊ 𝛼

𝛼 − 2

𝑑

→𝑁 0,1 .

Sehingga dari persamaan diatas dapat dibentuk penduga interval dua sisi yaitu :

𝛼− 𝑍 𝛼0 2 𝛼2 𝑛 + 𝛼 𝑛 𝛼 − 2 , 𝛼+ 𝑍 𝛼20 𝛼2 𝑛 + 𝛼 𝑛 𝛼 − 2 (4.14) Jadi persamaan diatas interval kepercayaan untuk 𝛼 disekitar 100 1 − 𝛼 %. (Jamilah, Firdaus & Sugiarto, S., 2014).

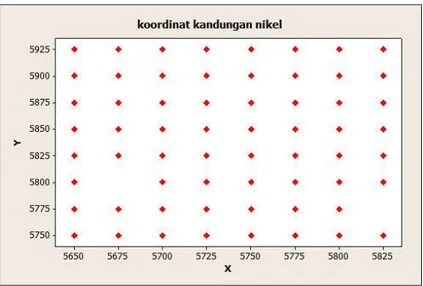
4.5 Informasi Data.

Data yang digunakan dalam tugas akhir ini diperoleh dari (Murtiawan, 2015) yaitu data posisi kandungan nikel (Ni) di Pomalaa (Lampiran 1). Data posisi nikel yang dinyatakan dalam titik koordinat ,x y dengan satuan meter

 

m

dan kandungan nikel dengan satuan persen

 

% . Data terdiri dari 62 titik pengeboran dengan jarak antar titik pengeboran yaitu 25 meter. Rancangan atau desain pengeboran yang dilakukan berbentuk grid teratur seperti terlihat pada Gambar 4.1.

30 Gambar 4.1. Desain Pengeboran Pada Daerah Eksplorasi PT. Antam.

Gambar 4.1. Mempresentasekan suatu plot posisi dari persentase kandungan nikel yang diperoleh dari hasil pengeboran oleh PT. Antam pada daerah ekplorasinya. Pola keadaan kandungan nikel pada tiap titik pengeboron dapat dilihat pada Gambar 4.2.

Gambar 4.2. Pola Kandungan Nikel

Pada Gambar 4.2 sumbu 𝑋 dan 𝑌 menyatakan posisi dari titik pengeboran pada daerah eksplorasi. Sedangkan sumbu vertikal menyatakan persentase kandungan nikel. Gambar 4.2 menunjukkan bahwa persentase kandungan nikel

31 berubah-ubah seiring dengan perubahan posisi (koordinat) titik pengeboran 𝑥, 𝑦 pada daerah ekplorasi tersebut.

4.6 Analisis data

Langkah awal untuk mengkontruksikan interval kepercayaan untuk  sesuai Persamaan (4.14) mengharuskan populasi berdistribusi normal, sehingga perlu dilakukan uji kenormalan untuk sampel persentase kandungan nikel.

Berdasarkan penelitian yang dilakukan sebelumnya, data persentase kandungan nikel bersifat stasioner order dua yang berarti memiliki distribusi yang sama. Berdasarkan uji Kolmogorov-Smirnov yaitu untuk mengecek data berdistribusi normal, maka pada tingkat signifikansi 5% data persentase kandungan nikel berdistribusi normal (Murtiawan, 2015).

Selajutnya interval kepercayaan 95% untuk  dengan menerapkan Persamaan (4.14) yang diimplementasikan dalam program yang ditulis dalam software Matlap-2007 (Lampiran 2). Sehingga diperoleh interval kepercayaan kepercayaan 95% untuk  berkisaran diantara 24,8926 dan 27,5139 dengan nilai estimasi untuk  3 sebesar 26,2033.

32 BAB V

PENUTUP

5.1 Kesimpulan

Berdasarkan hasil pembahasan dapat disimpulkan bahwa

1. parameter-parameter yang ditaksir dalam distribusi Pareto menghasilkan penduga metode momen dan maksimum likelihood yang terdiri dari : a. Untuk penduga metode momen untuk parameter 𝛼 dan k yaitu :

𝑘 =𝑋 𝑋 𝛼 = 𝑋 𝑋 − 𝑘 = 𝑋 𝑋 −𝑋 𝑋 = 𝑋 𝑋 2_{− 𝑋} 𝑋 = 𝑋 2 𝑋 2 _{− 𝑋}

b. Untuk penduga metode maksimum likelihood untuk parameter k diketahui maka didapatkan parameter 𝛼 yaitu :

𝛼 = 𝑛

ln 𝑥𝑖 𝑖 − ln 𝑘

2. Distribusi Pareto yang memiliki 𝑇 = 𝑋 , maka 𝑇 bukan merupakan UMVUE untuk fungsi parameternya sehingga bukan penduga terbaik untuk 𝜏 𝛼 .

5.2 Saran

Untuk penelitian selanjutnya disarankan mencari penduga terbaik dengan UMVUE pada distribusi yang lain seperti distribusi pareto terpotong, weibull, distribusi keluarga eksponensial serta menduga parameter dengan menggunakan metode yang lain pula seperti metode bayes, metode regresi ridge, dan metode kuadrat terkecil.

33 DAFTAR PUSTAKA

Arnold, B.C., 2004. Pareto Distributions. John Wiley & Sons. New York.

Jamilah, Firdaus & Sugiarto, S. 2014. Penduga Interval Parameter Bentuk Dari Distribusi Pareto Berdasarkan Metode Momen Dan Maksimum Likelihood.

Fakultas Matematika Dan Ilmu Pengetahuan Alam Universitas Riau. Pekanbaru.

Malik, M. 2011. Estimasi Parameter Distribusi Pareto dengan Metode Kuadrat Terkecil,Maximum Product of Spacing dan Regresi Ridge.(Skripsi). Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara. Medan.

Murtiawan, W. E. 2015. Estimasi Data Spasial Menggunakan Metode Ordinary Kriging. Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Halu Oleo. Kendari.

Rusydah, I. F. 2009. Estimator Tak Bias Terbaik pada Fungsi Distribusi Kontinu dengan Teorema Batas Bawah Crammer Rao.(Skripsi). Fakultas Sains dan Teknologi Universitas Islam Maulana Malik Ibrahim. Malang.

Rytgaard, M. 1990. Estimation in the Pareto Distribution. Journal of International Actuarial Association, 20:201-205.

Sari Y. D. W dan Sutikno. 2013. Estimasi Parameter Generalized Pareto Distribution Pada Kasus Identifikasi Perubahan Iklim Di Sentra Produksi Padi Jawa Timur. Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Sepuluh November. Surabaya.

Somayasa, W. 2001. Statistika Elementer. Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Halu Oleo. Kendari.

Somayasa, W. 2008. Diktat Statistika Matematika I. Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Halu Oleo. Kendari.

Sudjana M. A. 1996. Metoda Statistika edisi 6. Tarsito. Bansung.

Supranto M. A, J. 1985. Pengantar Probabilita Dan Statistik Induktif Jilid 2. Erlangga. Jakarta.

Suryani, I. 2009. Penduga Tak Bias Variansi Minimum untuk Distribusi Kontinu (Skripsi). Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Halu Oleo. Kendari.

34 Walpole, E. R dan Myers, H. R. 1995. Ilmu Peluang dan Statistika untuk Insinyur

dan Ilmuwan. Edisi 4. ITB Bandung. Bandung.

Walpole, E. R. 1995. Pengantar Statistika. Edisi 3. PT Gramedia Pustaka Utama. Jakarta.

Yosef, Z. B. 2005. Power Laws and Small World Phenomenon. Diakses tanggal 4 April 2015 . https://en.wikipedia.org/wiki/Pareto_principle.

Zulfa, I. 2006. Aplikasi Teorema Crammer-Rao Lower Bound Untuk Estimator Tak Bias Terbaik Pada Distribusi Keluarga Eksponensial. Diakses 14 Februari 2015. www.google.com.

36 Lampiran 1. Data Persentase Kandungan Nikel di PT.ANTAM, Pomalaa.

No X Y Nikel No X Y Nikel 1 5825 5925 0,39 32 5650 5850 0,74 2 5800 5925 0,86 33 5825 5825 0,71 3 5775 5925 0,94 34 5800 5825 1,03 4 5750 5925 1,22 35 5775 5825 1,03 5 5725 5925 0,88 36 5750 5825 1,22 6 5700 5925 1,13 37 5725 5825 1,08 7 5675 5925 0,92 38 5700 5825 1,01 8 5650 5925 0,82 39 5675 5825 1,19 9 5825 5900 0,54 40 5650 5825 1,14 10 5800 5900 0,65 41 5825 5800 0,73 11 5775 5900 0,88 42 5800 5800 0,80 12 5750 5900 1,17 43 5775 5800 1,48 13 5725 5900 1,24 44 5750 5800 1,02 14 5700 5900 1,11 45 5725 5800 1,35 15 5675 5900 1,23 46 5700 5800 1,15 16 5650 5900 1,16 47 5650 5800 0,90 17 5825 5875 0,59 48 5800 5775 1,36 18 5800 5875 1,11 49 5775 5775 1,23 19 5775 5875 1,43 50 5750 5775 1,06 20 5750 5875 1,13 51 5725 5775 1,27 21 5725 5875 1,14 52 5700 5775 1,14 22 5700 5875 0,98 53 5675 5775 1,04 23 5675 5875 0,93 54 5650 5775 1,10 24 5650 5875 1,30 55 5825 5750 0,96 25 5825 5850 0,81 56 5800 5750 0,82 26 5800 5850 0,97 57 5775 5750 0,90 27 5775 5850 1,25 58 5750 5750 1,14 28 5750 5850 1,01 59 5725 5750 1,05 29 5725 5850 1,02 60 5700 5750 1,10 30 5700 5850 1,66 61 5675 5750 0,94 31 5675 5850 1,47 62 5650 5750 0,83 Sumber: Skripsi estimasi data spasial menggunakan metode ordinary kriging

37 Lampiran 2. Program menghitung penduga interval.

clear all;

clc;

format short

t11=xlsread('data X1.xlsx');%perintah untuk membaca file dari

excel

t2=xlsread('data Y.xlsx');

a=mean(t2) A=a/(a-1) z=(3^2)/62; z1=3/62; Z=sqrt(z+z1); Ib=A-1.95*Z Ia=A+1.95*Z Hasil Run a = 3 A_het = 26.2033 batas_bawah = 24.8926 batas_atas = 27.5139

38 Lampiran 3. Simulasi perhitungan pdf distribusi Pareto untuk alpa=1,3,5 dan k=1. > x=seq(1,8,by=0.25) > alpa1=1 > alpa2=3 > alpa3=5 > k=1 > k1=k^alpa1 > x1=x^(alpa1+1) > pdf=alpa1*(k1/x1) > k2=k^alpa2 > x2=x^(alpa2+1) > pdf1=alpa2*(k2/x2) > k3=k^alpa3 > x3=x^(alpa3+1) > pdf2=alpa3*(k3/x3) > plot(pdf2,type="b",ylab="PDF") > lines(pdf1,type="b",col=2) > lines(pdf,type="b",col=4)

> title(main="Grafik Distribusi Pareto") Hasil Run > pdf [1] 1.00000000 0.64000000 0.44444444 0.32653061 0.25000000 0.19753086 [7] 0.16000000 0.13223140 0.11111111 0.09467456 0.08163265 0.07111111 [13] 0.06250000 0.05536332 0.04938272 0.04432133 0.04000000 0.03628118 [19] 0.03305785 0.03024575 0.02777778 0.02560000 0.02366864 0.02194787 [25] 0.02040816 0.01902497 0.01777778 0.01664932 0.01562500 > pdf1 [1] 3.0000000000 1.2288000000 0.5925925926 0.3198667222 0.1875000000 [6] 0.1170553269 0.0768000000 0.0524554334 0.0370370370 0.0268898148 [11] 0.0199916701 0.0151703704 0.0117187500 0.0091952922 0.0073159579 [16] 0.0058931408 0.0048000000 0.0039489719 0.0032784646 0.0027444156 [21] 0.0023148148 0.0019660800 0.0016806134 0.0014451275 0.0012494794

39 [26] 0.0010858485 0.0009481481 0.0008315999 0.0007324219

> pdf2

[1] 5.000000e+00 1.310720e+00 4.389575e-01 1.740771e-01 7.812500e-02 [6] 3.853673e-02 2.048000e-02 1.156043e-02 6.858711e-03 4.242969e-03 [11] 2.719955e-03 1.797970e-03 1.220703e-03 8.484699e-04 6.021365e-04 [16] 4.353197e-04 3.200000e-04 2.387889e-04 1.806317e-04 1.383448e-04 [21] 1.071674e-04 8.388608e-05 6.629639e-05 5.286246e-05 4.249930e-05 [26] 3.443039e-05 2.809328e-05 2.307596e-05 1.907349e-05