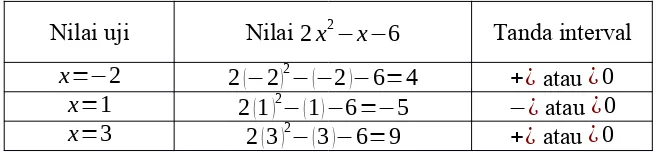Jenis-Jenis Akar Persamaan Kuadrat

A. Jenis-Jenis Akar Persamaan Kuadrat

Sifat dari kedua akar tersebut sangat dipengaruhi oleh nilai b2 −4ac yang disebut diskriminan (D). Jika a , b , dan c adalah jenis bilangan real,

diskriminan (D)=b2−4ac. Sehingga akar-akar persamaan kuadrat tersebut

dapat ditunjukkan sebagai berikut: Sehingga kedua akar persamaan tersebut adalah:

Apabila D<0_{, maka persamaan kuadrat ax}2_{+bx+c=0 mempunyai} akar-akar bilangan imaginer atau tidak real.

3. Jika b2

−4ac>0, artinya D>0. Akan diperoleh: x_1,2=−b ±_2a√D

x₁=−b+_2a√D dan x₂=−b−_2a√D

Apabila nilai D>0, maka persamaan kuadrat ax2_{+bx+c=0 mempunyai} akar-akar real berbeda. Apabila a , b , dan c adalah bilangan rasional, maka akan diperoleh:

a. Apabila b2

−4ac=r2 (bilangan kuadrat), maka akan diperoleh: x_1,2=−b ±_2a√D

x1,2=−b ±

√

r 2

2a x_1,2=−b ±_2a√r

x1=−b+r_2a dan x2=−b−r_2a

Apabila nilai D=r2_{, maka persamaan kuadrat ax}2

+bx+c=0 mempunyai akar-akar rasional.

b. Apabila b2

−4ac=r (bukan bilangan kuadrat), maka akan diperoleh: x_1,2=−b ±_2a√D

x_1,2=−b ±_2a√r

x₁=−b+_2a√r dan x₂=−b−_2a√r

Apabila nilai D=r, maka persamaan kuadrat ax2

+bx+c=0 mempunyai akar-akar irrasional.

4. Jika b2

−4ac ≥0, artinya D ≥0. Akan diperoleh: x_1,2=−b ±_2a√D

Apabila nilai D ≥0, maka persamaan kuadrat ax2_+bx

+c=0 mempunyai akar-akar real.

Contoh 1:

Tentukanlah jenis akar-akar persamaan berikut ini dengan memperhatikan

diskriminan!

1. x2−2x+1=0 2. x2+5x+7=0 3. 2x2+x−3=0

Penyelesaian: 1. x2

−2x+1=0 D=b2

−4ac¿(−2)2−4.1 .1¿4−4=0

Diskriminan (D)=0, maka persamaan x2−2x+1=0 mempunyai akar yang sama. Jadi, x1=x2⇔ akar-akar real dan sama.

Diuji dengan menggunakan akar-akar persamaan kuadrat

x=−b ±

√

₂b_a2−4ac¿−(−₂2)±0¿2₂¿1 Jadi, x1=1atau x2=1

2. x2+5x+7=0

D=b2−4ac¿52−4.1.7¿25−28=−3 Diskriminan (D)=−3<0, persamaan x2

+5x+7=0,mempunyai kedua akar imajiner.

3. 2x2+x−3=0

D=b2−4ac¿12−4.2.(−3)¿1+24 ¿25

Diskriminan (D)=25, _{maka persamaan 2x}2+x−3=0 mempunyai kedua akar real yang berbeda.

x=−b ±

√

b menyebabkan persamaan tersebut mempunyai akar-akar kembar.

Penyelesaian: 1. x2

+(p+1)x+9=0

Jika ingin mencari akar yang sama, diskriminan(D)>0. a=1,b=(p+1)x , c=9

(p)2−4.1.(p+3)=0p2−4(p+3)=0p2−4p+12=0 (p−6) (p+2)=0

p=6atau p=−2

Nilai p yang memenuhi adalah p=6 atau p=−2. Jika p=6, persamaan tersebut menjadi:

x2

Diuji dengan menggunakan akar-akar persamaan kuadrat

x=−b ±

√

b

Penyelesaian atau himpunan penyelesaian dari pertidaksamaan kuadrat dalam variabel x ditentukan dengan 2 cara, yaitu dengan menggunakan sketsa grafik fungsi kuadrat dan garis bilangan.

1. Menyelesaikan pertidaksamaan kuadrat dengan menggunakan garis bilangan

Langkah-langkah yang diperlukan adalah sebagai berikut:

a. Langkah 1 yaitu mengubah pertidaksamaan dalam bentuk baku, apabila bentuk pertidaksamaan masih belum baku.

b. Langkah 2 yaitu menentukan nilai diskriminan terlebih dahulu. 1) Jika D<0 dan a<0, bentuk pertidaksamaan ax2

+bx+c<0 disebut definit negatif.

2) Jika D<0 dan a>0, bentuk pertidaksamaan ax2+bx+c<0 disebut definit positif.

3) Jika D=0, ada satu penyebab nol di ruas kiri. 4) Jika D>0, ada dua penyebab nol di ruas kiri

c. Langkah 3 yaitu menentukan nilai-nilai pembuat nol pada interval pertidaksamaan.

d. Langkah 4 yaitu menggambar nilai-nilai nol yang diperoleh pada langkah 3 pada diagram garis bilangan. Perhatikan contoh garis bilangan di bawah ini:

e. Langkah 5 yaitu menentukan tanda-tanda interval yang diperoleh pada langkah 4 dengan cara mengambil nilai uji yang berada dalam masing-masing interval.

Contoh:

1. Tentukan himpunan penyelesaian pertidaksamaan kuadrat berikut ini dengan menggunakan garis bilangan.

a. x2

−4x←3 b. x2

−4x+3≤0 c. x2−4x+3>0 d. x2−4x+3≥0

2. Tentukan himpunan penyelesaian pertidaksamaan kuadrat 2x2−x+6≥0 dengan menggunakan garis bilangan.

Penyelesaian:

1. Langkah untuk menyelesaikan pertidaksamaan x2−4x←3 adalah: a. Langkah 1 yaitu mengubah pertidaksamaan dalam bentuk baku.

x2−4x←3 x2−4x+3<0

b. Langkah 2 yaitu menentukan nilai diskriminan, yaitu: x2−4x+3<0

a=1,b=−4,dan c=3 Diskriminan (D)=b2−4ac

¿(−4)2−4.1 .3 ¿16−12

¿8

Diskriminan D=8>0_{, sehingga pertidaksamaan x}2_−4x←3 mempunyai aka-akar real. Sehingga pertidaksamaan tersebut mempunyai penyelesaian.

c. Langkah 3: menentukan nilai-nilai pembuat nol pada interval pertidaksamaan.

x2−4x+3=0(x−1) (x−3)=0 x=1 atau x=3

membagi garis bilangan menjadi 3 interval, yaitu: x<1,1<x<3,_dan x>1. _{Perhatikan gambar di bawah ini:}

e. Langkah 5 yaitu menentukan tanda-tanda interval yang diperoleh pada langkah 4 dengan cara mengambil nilai uji yang berada dalam masing-masing interval. Dalam contoh ini, diambil:

x=0 (berada dalam interval x<1¿ x=2 (berada dalam interval 1<x<3¿ x=4 (berada dalam interval x>3¿ Hasilnya dapat dilihat` pada tabel di bawah ini.

Nilai uji Nilai x2−4x+3 Tanda interval x=0 (0)2−4(0)+3=3 +¿ atau ¿0 x=2 (2)2−4(2)+3=−1 −¿ atau ¿0 x=4 (4)2−4(4)+3=3 +¿ atau ¿0 Berdasarkan hasil perhitungan pada tabel di atas, tanda-tanda interval dapat dituliskan dalam interval yang sesuai.

Perhatikan gambar di bawah ini.

f. Langkah 6 yaitu berdasarkan tanda-tanda interval pada gambar di atas, maka interval yang memenuhi pertidaksamaan x2

−4x+3<0 adalah 1<x<3.

Jadi, himpunan penyelesaiannya adalah HP={x|1<x<3}

Perlu dicatat bahwa tand-tanda interval 1<x<3di atas dapat pula digunakan untuk mnenentukan penyelesaian pertidaksamaan-pertidaksamaan berikut:

b. Pertidaksamaan x2

−4x+3≤0

Himpunan penyelesaiaannya adalah HP={x|1≤ x ≤3} c. Pertidakasamaan x2

−4x+3>0

d. Pertidaksamaan x2

−4x+3≥0

Himpunan penyelesaiannya adalah HP={x|1≤1atau x ≥3} 2. Langkah untuk menyelesaikan pertidaksamaan 2x2_−x−6≥0

a. Langkah 1 yaitu menentukan nilai diskriminan, yaitu:

2x2

−x−6≥0 a=2,b=−1,dan c=−6 Diskriminan (D)=b2−4ac

¿(−1)2−4.2.(−6) ¿1−(−48)

¿1+48 ¿49

Diskriminan D=49>0, sehingga pertidaksamaan

2x2−x−6≥0mempunyai aka-akar rasional. Sehingga pertidaksamaan tersebut mempunyai penyelesaian.

b. Langkah 2: menentukan nilai-nilai pembuat nol pada interval pertidaksamaan.

2x2−x−6=0(2x+3) (x−2)=0

2x=−3 atau x=2

x=−₂3 atau x=2

c. Langkah 3 yaitu menggambar nilai-nilai nol pada diagram garis bilangan, yaitu:

d. Langkah 4 yaitu menentukan tanda-tanda interval dengan cara mengambil nilai uji yang berada dalam masing-masing interval. Dalam contoh ini, diambil:

x=−2 (berada dalam interval x←3₂¿

Nilai uji Nilai 2x2_{−x−6 Tanda interval} x=−2 2(−2)2−(−2)−6=4 +¿ atau ¿0

x=1 2(1)2−(1)−6=−5 −¿ atau ¿0 x=3 2(3)2−(3)−6=9 +¿ atau ¿0

Berdasarkan hasil perhitungan pada tabel di atas, tanda-tanda interval dapat dituliskan dalam interval yang sesuai. Perhatikan gambar di bawah ini.

e. Langkah 5 yaitu berdasarkan tanda-tanda interval pada gambar, maka interval yang memenuhi pertidaksamaan 2x2−x−6≥0

adalah x←3₂ atau x>2.

Jadi, himpunan penyelesaiannya adalah HP=

{

x

|

x←3₂atau x>2

}

2. Menyelesaikan pertidaksamaan kuadrat dengan menggunakan

sketsa grafik fungsi kuadrat

Fungsi kuadrat ditentukan dengan rumus f(x)=ax2+bx+c. Fungsi kuadrat yang ditentukan dengan rumus x2

Berdasarkan sketsa grafik parabola y=x2

−4x+3 pada gambar di atas dapat ditetapkan sebagai berikut:

a. Parabola di atas sumbu X(y>0) untuk x dalam selang x<1 atau

Dengan demikian, sketsa grafik fungsi kuadrat f(x)=x2−4x+3 atau parabola y=x2−4x+3 dapat digunakan untuk menentukan penyelesaian atau himpunan penyelesaian

pertidaksamaan-pertidaksamaan kuadrat berikut ini: digunakan untuk menentukan penyelesaian pertidaksamaan kuadrat ax2_+bx+c

<0,ax2+bx+c ≤0,ax2+bx+c>0, dan ax2+bx+c ≥0.

Secara umum penyelesian atau himpunan penyelesaian pertidaksamaan kuadrat dengan menggunakan sketsa grafik fungsi kuadrat dapat ditentukan melalui langkah-langkah sebagai berikut:

Gambarlah sketsa grafik kuadrat f(x)=ax2+bx+c atau parabola y=ax2+bx+c. Jika ada, carilah titik-titik potong dengan sumbu x .

b. Langkah 2:

Berdasarkan sketsa grafik yang diperoleh pada langkah 1, dapat ditetapkan selang atau interval yang memenuhi pertidaksamaan kuadrat ax2_+bx+c

<0,ax2+bx+c ≤0,ax2+bx+c>0, atau ax2_{+bx+c ≥0.}

Contoh 2:

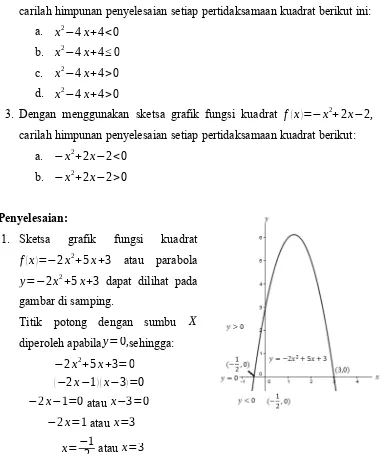
1. Dengan menggunakan sketsa grafik fungsi kuadrat f(x)=−2x2+5x+3, carilah himpunan penyelesaian setiap pertidaksamaan kuadrat berikut:

2. Dengan menggunakan sketsa grafik fungsi kuadrat f(x)=x2−4x+4, carilah himpunan penyelesaian setiap pertidaksamaan kuadrat berikut ini:

a. x2−4x+4<0 b. x2−4x+4≤0 c. x2−4x+4>0 d. x2

−4x+4>0

3. Dengan menggunakan sketsa grafik fungsi kuadrat f(x)=−x2+2x−2, carilah himpunan penyelesaian setiap pertidaksamaan kuadrat berikut:

a. −x2+2x−2<0 b. −x2+2x−2>0

Penyelesaian:

1. Sketsa grafik fungsi kuadrat f(x)=−2x2+5x+3 atau parabola y=−2x2+5x+3 dapat dilihat pada gambar di samping.

Titik potong dengan sumbu X diperoleh apabilay=0,sehingga:

−2x2+5x+3=0 (−2x−1) (x−3)=0 −2x−1=0_atau x−3=0

−2x=1_ataux=3 x=−₂1 atau x=3

Grafik fungsi kuadrat f(x)=−2x2+5x+3 dapat dilihat pada gambar di samping ini:

Sehingga dapat ditetapkan:

a. Himpunan penyelesaian pertidaksamaan kuadrat −2x2+5x+3<0 adalah:

b. Himpunan penyelesaian pertidaksamaan kuadrat −2x2

+5x+3≤0

adalah HP=

{

x

|

x ≤−1₂atau x ≥3, x∈R

}

.

c. Himpunan penyelesaian pertidaksamaan kuadrat −2x2+5x+3>0

adalah HP=

{

x

|

−₂1<x<3, x∈R

}

.

d. Himpunan penyelesaian pertidaksamaan kuadrat −2x2

+5x+3≥0

adalah HP=

{

x

|

−₂1≤ x ≤3, x∈R

}

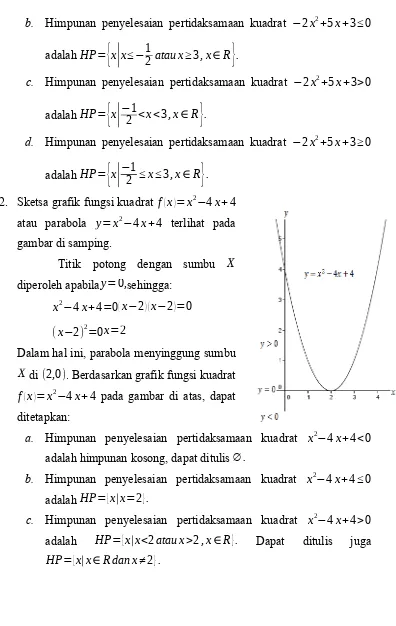
. 2. Sketsa grafik fungsi kuadrat f(x)=x2−4x+4

atau parabola y=x2−4x+4 terlihat pada gambar di samping.

Titik potong dengan sumbu X diperoleh apabilay=0,sehingga:

x2−4x+4=0(x−2) (x−2)=0 (x−2)2=0x=2

Dalam hal ini, parabola menyinggung sumbu X di (2,0). Berdasarkan grafik fungsi kuadrat f(x)=x2−4x+4 pada gambar di atas, dapat ditetapkan:

a. Himpunan penyelesaian pertidaksamaan kuadrat x2−4x+4<0 adalah himpunan kosong, dapat ditulis ∅.

b. Himpunan penyelesaian pertidaksamaan kuadrat x2−4x+4≤0 adalah HP={x|x=2}.

c. Himpunan penyelesaian pertidaksamaan kuadrat x2

d. Himpunan penyelesaian pertidaksamaan kuadrat x2

−4x+4≥0 adalah HP={x|x ≤2atau x ≥2, x∈R}. Dapat ditulis juga HP={x|x∈R}.

3. Sketsa grafik fungsi kuadrat f(x)=−x2+2x−2atau parabola y=−x2

+2x−2dapat dilihat pada gambar di bawah ini. Titik potong dengan sumbu X

diperoleh apabilay=0,sehingga: −x2+2x−2=0

Nilai diskriminan D=b2 −4ac a=(−1), b=2,dan c=−2

D=(2)2−4(−1)(−2)¿4−8¿−4 Karena D<0, maka parabola tidak memotong maupun menyinggung sumbu X . Berdasarkan Sketsa grafik fungsi kuadrat f(x)=−x2+2x−2 dapat ditetapkan:

a. Himpunan penyelesaian

pertidaksamaan kuadrat

−x2+2x−2<0 adalah HP={x|x∈R}.

b. Himpunan penyelesaian pertidaksamaan kuadrat −x2

+2x−2>0 adalah himpunan kosong.

Wirodikromo, Sartono. 2007. Matematika Untuk Kelas X. Jakarta: Penerbit Erlangga.