Perhitungan Parameter Gelombang Suara Untuk Sumber Berbentuk Sembarang Menggunakan Metoda Elemen Batas Dengan Program Matlab.

(1)

i

Universitas Kristen Maranatha

PERHITUNGAN PARAMETER GELOMBANG SUARA

UNTUK SUMBER BERBENTUK SEMBARANG

MENGGUNAKAN METODA ELEMEN BATAS

DENGAN PROGRAM MATLAB

Garry Paulin Setiawan

Email : garrypsetiawan@yahoo.com

Jurusan Teknik Elektro, Fakultas Teknik, Universitas Kristen Maranatha

Jalan Prof. drg. Suria Sumantri, MPH 65

Bandung 40164, Indonesia

ABSTRAK

Metoda Elemen Batas telah digunakan untuk memecahkan berbagai

masalah pada bidang akustik, seperti pada industri otomotif yang melibatkan

radiasi suara dari mesin yang bergetar, prediksi medan akustik pada interior ruang

kendaraan, medan akustik pada rongga muffler, dan sebagainya. Keunggulan dari

Metoda Elemen Batas adalah penurunan dimensi persoalan yang dihadapi.

Persoalan dimensi tiga yang melibatkan volume diperlakukan seperti persoalan

dua dimensi yang hanya melibatkan permukaan benda.

Pada tugas akhir ini dibuat program dengan MATLAB untuk menghitung

nilai parameter gelombang suara yang melibatkan benda berbentuk sembarang

dengan menggunakan Metoda Elemen Batas. Parameter akustik yang terlibat

adalah kecepatan potensial dan kecepatan partikel. Program dibuat untuk

penyelesaian masalah radiasi dan penghamburan gelombang suara dari sumber

yang bergetar serta masalah invers untuk menentukan parameter akustik pada

sumber berdasarkan informasi akustik di titik-titik medan. Di samping itu

program yang dibuat juga melibatkan kasus ruang setengah tak berhingga untuk

radiasi dan penghamburan gelombang suara dari sumber yang bergetar. Program

(2)

ii

dilakukan meliputi masalah radiasi dan penghamburan dengan melibatkan

beberapa bentuk geometri sumber benda (bola, kubus, silinder).

Hasil uji kasus menunjukkan kesesuaian antara hasil dari program

MATLAB dengan hasil dari program FORTRAN. Program MATLAB juga

menyajikan pembuatan grafik secara langsung dari hasil perhitungan program

(output) yaitu pembuatan pola radiasi tekanan dan distribusi tekanan pada

permukaan benda atau di titik-titik medan yang dikehendaki.

(3)

iii

CALCULATION OF ACOUSTIC PARAMETERS

INVOLVING BODIES OF ARBITRARY SHAPE

USING BOUNDARY ELEMENT METHOD

WITH MATLAB PROGRAM

Garry Paulin Setiawan

Email : garrypsetiawan@yahoo.com

Jurusan Teknik Elektro, Fakultas Teknik, Universitas Kristen Maranatha

Jalan Prof. drg. Suria Sumantri, MPH 65

Bandung 40164, Indonesia

ABSTRACT

Boundary Element Method (BEM) has been used to solve various

problems in acoustics, such as in automotive industry involving sound radiation

from vibrating engines, the prediction of acoustic field on the vehicle interior

space, the acoustic field in the cavity of muffler, and so forth. The advantage of

BEM is the reduction of the dimension of the problems. Three-dimensional

problems involving volume is treated as two-dimensional problems which

involves only the surface of the body.

In this project, a program was made in MATLAB code to calculate the

acoustic parameters involving bodies of arbitrary shape using Boundary Element

Method. The acoustic parameters involved are velocity potential and particle

velocity. The program was made for solving problems involving radiation and

scattering of acoustic waves from vibrating bodies and inverse problems to

determine the acoustic parameters on the body based on the acoustic information

in the field points. In addition the program also handles half space problems for

radiation and scattering of acoustic waves from vibrating bodies. The program

was developed based on an existing FORTRAN program. Test cases including

radiation and scattering problems involving some shapes of the bodies were

(4)

iv

Good aggrement was obtained between the MATLAB program calculation

and those yield by the FORTRAN program calculation. MATLAB also provides

post processing for plotting the result of the calculation such as the radiation

pattern of pressure and pressure distribution on the surface of bodies or on the

desired field points.

(5)

viii

DAFTAR ISI

ABSTRAK ...i

ABSTRACT ...iii

KATA PENGANTAR ...v

DAFTAR ISI ...viii

DAFTAR GAMBAR ...xii

BAB I. PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Rumusan Masalah ... 1

1.3 Tujuan ... 1

1.4 Batasan Masalah ... 1

1.5 Spesifikasi Alat Yang Digunakan ... 1

1.6 Sistematika Pembahasan ... 2

BAB II. LANDASAN TEORI 2.1 Teori Akustik Dasar ... 5

2.2 Formulasi Metoda Elemen Batas ... 6

2.3 Persamaan Integral Helmholtz pada Penghamburan Gelombang Akustik ... 8

(6)

ix

2.5 Metode CHIEF (Combined Helmholtz Integral Equation Formulation)

... 10

2.6 Diskritisasi Permukaan dengan Elemen Isoparametrik ... 11

2.7 Implementasi Numerik ... 13

2.8 Solusi Persamaan Matriks ... 14

2.9 MATLAB VS FORTRAN ... 17

BAB III. ALUR KERJA PROGRAM DAN DISKRITISASI PERMUKAAN 3.1 Alur Kerja Program Direct BEM ... 19

3.2 Alur Kerja Program Inverse BEM ... 20

3.3 Alur Kerja Program Halfspace BEM ... 22

3.4 Diskritisasi Permukaan ... 22

3.4.1 Diskritisasi permukaan bola ... 22

3.4.2 Diskritisasi permukaan kubus... 23

3.4.3 Diskritisasi permukaan silinder ... 24

BAB IV. UJI KASUS 4.1 Bola Bergetar Homogen ... 26

4.2 Bola Berosilasi ... 27

4.3 Penghamburan Gelombang Bidang pada Bola Keras ... 29

4.4 Radiasi Kubus Bergetar ... 31

4.5 Radiasi Silinder Bergetar ... 32

(7)

x

4.7 Radiasi Bola Bergetar Homogen dengan Kehadiran Kubus Diam ... 42

4.8 Radiasi Silinder Bergetar Homogen dengan Kehadiran Silinder Diam 47 4.9 Radiasi Kubus Bergetar pada Salah Satu Sisinya ... 51

4.10 Kasus Radiasi dari Dua Bola Bergetar Homogen... 53

4.11 Kasus Radiasi Bola Homogen pada Ruang Setengah Tak Hingga (Half Space) ... 55

4.12 Kasus Penghamburan Gelombang Bidang Terhadap Bola Keras pada Ruang Setengah Tak Hingga (Half Space) ... 57

4.13 Pola Radiasi Kubus Bergetar pada Ruang Setengah Tak Hingga (Half Space) ... 59

4.14 Kasus Silinder Bergetar pada Ruang Setengah Tak Hingga (Halfspace) ... 60

4.15 Kasus Inversi Bola Bergetar Homogen ... 61

4.16 Kasus Inversi Bola Berosilasi ... 62

4.17 Kasus Inversi untuk Penghamburan Gelombang Bidang pada Bola Keras ... 63

4.18 Kasus Inversi pada Kubus Bergetar ... 64

4.19 Kasus Inversi untuk Penghamburan pada Kubus Diam ... 65

4.20 Kasus Inversi untuk Bola Bergetar Homogen dan Bola Diam ... 65

4.21 Kasus Inversi pada Dua Kubus Bergetar ... 66

BAB V. KESIMPULAN DAN SARAN 5.1 Kesimpulan ... 67

(8)

xi

DAFTAR PUSTAKA

LAMPIRAN

Lampiran A ...A-1

(9)

xii

DAFTAR GAMBAR

Gambar 2.1. Ilustrasi kasus eksterior (kiri) dan kasus interior (kanan) ... 7

Gambar 2.2 Ilustrasi kasus penghamburan gelombang akustik ... 8

Gambar 2.3. Ilustrasi kasus akustik pada ruang setengah tak berhingga ... 9

Gambar 2.4 Elemen isoparametrik dan koordinat lokal tiap node ... 11

Gambar 3.1. Alur kerja program direct BEM ... 19

Gambar 3.2. Alur kerja program inverse BEM ... 21

Gambar 3.3. Diskritisasi permukaan bola ... 23

Gambar 3.4. Diskritisasi permukaan kubus ... 23

Gambar 3.5. Diskritisasi permukaan silinder ... 24

Gambar 4.1. Konfigurasi bola bergetar homogen ... 26

Gambar 4.2. Pola radiasi kecepatan potensial bola bergetar homogen pada penampang bidang yz, R=1, r=2, untuk (a) k=1, (b) k= 3.14159 .... 27

Gambar 4.3. Konfigurasi bola berosilasi... 28

Gambar 4.4. Pola radiasi kecepatan potensial bola berosilasi pada penampang bidang yz, k=1 dan r=2 ... 28

Gambar 4.5. Konfigurasi penghamburan gelombang bidang pada bola keras (rigid) yang diam ... 29

(10)

xiii

Gambar 4.7. Pola radiasi kecepatan potensial penghamburan gelombang bidang

pada bola diam pada penampang bidang xz, r=5 untuk (a) k=2 dan

(b) k=3.14159... 30

Gambar 4.8. Pola radiasi kecepatan potensial penghamburan gelombang bidang

pada bola diam pada penampang bidang xz dengan 354 node pada

r=5 untuk (a) k=2 dan (b) k=3.14159 ... 31

Gambar 4.9 Tekanan pada permukaan kubus bergetar untuk k=1 ... 32

Gambar 4.10 Konfigurasi silinder bergetar ... 33

Gambar 4.11. Pola radiasi kecepatan potensial dari silinder bergetar pada

penampang bidang yz, r=3 untuk (a) k=1 dan (b) k=2 ... 33

Gambar 4.12. Konfigurasi bola bergetar homogen dengan kehadiran bola diam . 34

Gambar 4.13. Ilustrasi uji kasus bola bergetar dengan kehadiran bola diam dengan

(a) jari-jari kedua bola sama (R1=R2=1), (b) jari-jari bola kedua

lebih kecil (R2=0.5,R1=1), (c) jari-jari bola kedua lebih besar

(R2=2,R1=1) ... 35

Gambar 4.14. Pola radiasi kecepatan potensial dari bola bergetar dengan

kehadiran bola diam pada penampang bidang yz, r=2, R1=R2=1,

k=1, untuk jarak (a) d=3, (b) d=4 (c) d=5 (d) d=6 ... 36

kehadiran bola diam pada penampang bidang yz, r=2, R1=1,R2=2

k=1, untuk jarak (a) d=3, (b) d=5 (c) d=6 (d) d=7 ... 37

kehadiran bola diam pada penampang bidang yz, r=2, R1=1,R2=0.5

(11)

xiv

kehadiran bola diam pada penampang bidang yz, R1=1,R2=1, k=1,

jarak d=3, untuk jarak titik ukur (a) r=1.75, (b) r=1.5, (c) r=1.25 ... 39

jarak d=2.5, untuk jarak titik ukur (a) r=1.75, (b) r=1.5, (c) r=1.25 39

jarak d=3, untuk jarak titik ukur (a) r=2, (b) r=1.5, (c) r=1.25 ... 40

jarak d=2.5, untuk jarak titik ukur (a) r=1.5, (b) r=1.25 ... 40

kehadiran bola diam pada penampang bidang yz, R1=1,R2=0.5, k=1,

jarak d=3, untuk jarak titik ukur (a) r=2, (b) r=1.5 ... 41

jarak d=2.5, untuk jarak titik ukur (a) r=1.5, (b) r=1.25 ... 41

Gambar 4.23. Konfigurasi bola bergetar dengan kehadiran kubus diam ... 42

Gambar 4.24. Ilustrasi uji kasus bola bergetar dengan kehadiran kubus diam untuk

jari-jari bola pertama (a) R1=1, (b) R1=2, (c) R1=0.5 ... 43

kehadiran kubus diam pada penampang bidang yz, R1=1, k=1, jarak

(12)

xv

titik ukur r=3, untuk jarak kedua benda (a) d=4, (b) d=5, (c) d=6 ... 44

kehadiran kubus diam pada penampang bidang yz, R1=0.5, k=1,

jarak titik ukur r=1.5, untuk jarak kedua benda (a) d=4, (b) d=6, (c)

d=7 ... 45

kedua benda d=3, untuk jarak titik ukur (a) r=1.75, (b) r=1.5, (c)

r=1.25 ... 46

kedua benda d=4, untuk jarak titik ukur (a) r=3, (b) r=2.75, (c)

r=2.25 ... 46

kehadiran kubus diam pada penampang bidang yz, R1=0.5, k=1,

jarak kedua benda d=2.5, untuk jarak titik ukur (a) r=1.5, (b) r=1, (c)

r=0.75 ... 47

Gambar 4.31. Konfigurasi silinder bergetar homogen (silinder 1) dan silinder

diam (silinder 2) ... 47

Gambar 4.32. Ilustrasi uji kasus silinder dengan kehadiran silinder kedua yang

diam dengan (a) besar kedua silinder sama, (b) silinder kedua lebih

(13)

xvi

Gambar 4.33. Pola radiasi kecepatan potensial dari silinder bergetar dengan

kehadiran silinder diam pada penampang bidang yz, R1=R2=2,

L1=L2=4, k=1, jarak titik ukur r=3, untuk jarak kedua benda (a) d=4,

(b) d=7, (c) d=9 ... 49

kehadiran silinder diam pada penampang bidang yz, R1=2,R2=4,

L1=4,L2=8, k=1, jarak titik ukur r=3, untuk jarak kedua benda (a)

d=7, (b) d=9, (c) d=12 ... 50

kehadiran silinder diam pada penampang bidang yz, R1=2,R2=1,

L1=4,L2=2, k=1, jarak titik ukur r=3, untuk jarak kedua benda (a)

d=4, (b) d=5, (c) d=6 ... 50

Gambar 4.36. Ilustrasi kubus yang bergetar pada salah satu sisinya dengan sisi

yang bergetar adalah sisi yang diarsir ... 51

Gambar 4.37. Pola radiasi kecepatan potensial dari kubus bergetar satu sisi untuk

penampang (a) bidang xy, (b) bidang xz, (c) bidang yz ... 51

Gambar 4.38. Pola radiasi kecepatan potensial dari kubus bergetar dua sisi untuk

Gambar 4.39. Pola radiasi kecepatan potensial dari kubus bergetar tiga sisi untuk

Gambar 4.40. Pola radiasi kecepatan potensial dari kubus bergetar empat sisi

untuk penampang (a) bidang xy, (b) bidang xz, (c) bidang yz ... 52

Gambar 4.41. Pola radiasi kecepatan potensial dari kubus bergetar lima sisi untuk

(14)

xvii

Gambar 4.42. Konfigurasi dua bola bergetar homogen ... 53

Gambar 4.43. Pola radiasi kecepatan potensial dari dua bola bergetar homogen

pada penampang bidang yz, R1=R2=1, k=1, r=2, untuk jarak (a)

d=3, (b) d=4, (c) d=5 ... 54

Gambar 4.44. Grafik nilai tekanan terhadap posisi titik y untuk x=0,z=0, pada

kasus dua bola bergetar homogen, R1=R2=1, d=12. ... 54

Gambar 4.45. Konfigurasi bola bergetar homogen pada Halfspace ... 55

Gambar 4.46. Pola radiasi kecepatan potensial dari radiasi bola bergetar homogen

pada Halfspace untuk penampang bidang yz, B=3, k=1, untuk (a)

r=2 , (b) r=3 ... 56

Gambar 4.47. Pola radiasi kecepatan potensial dari radiasi bola bergetar homogen

pada Halfspace untuk penampang bidang yz, k=1, r=2,untuk (a)

B=10, (b) B=30, (c) B=50 ... 56

Gambar 4.48. Konfigurasi penghamburan gelombang bidang terhadap bola keras

pada Halfspace ... 57

Gambar 4.49. Pola radiasi kecepatan potensial dari penghamburan gelombang

bidang terhadap bola keras (rigid) pada Halfspace untuk penampang

bidang xz, B=3, k=1, untuk (a) r=2 , (b) r=3 ... 58

Gambar 4.50. Pola radiasi kecepatan potensial dari penghamburan gelombang

bidang terhadap bola keras (rigid) pada Halfspace untuk penampang

bidang xz, B=30, r=5, untuk (a) k=1 , (b) k=0.1 ... 58

(15)

xviii

Gambar 4.52. Pola radiasi kecepatan potensial dari radiasi kubus bergetar pada

Halfspace untuk penampang bidang yz, k=1, r=2, untuk (a) B=2, (b)

B=10, (c) B=30 ... 59

Gambar 4.53. Konfigurasi silinder bergetar pada Halfspace ... 60

Gambar 4.54. Pola radiasi kecepatan potensial dari radiasi silinder bergetar pada

B=10, (c) B=50 ... 60

Gambar 4.55. Pola radiasi kecepatan potensial dari radiasi silinder bergetar pada

B=10, (c) B=50 ... 61

Gambar 4.56. Distribusi kecepatan potensial pada sumber bola yang bergetar

homogen k=1 ... 62

Gambar 4.57. Distribusi kecepatan potensial pada sumber bola yang bergetar

homogen k=3.14159 ... 62

Gambar 4.58. Distribusi kecepatan potensial pada sumber bola yang berosilasi

k=1 ... 63

Gambar 4.59. Distribusi kecepatan potensial pada bola untuk kasus penghamburan

gelombang bidang terhadap bola keras, k=1 ... 64

Gambar 4.60. Distribusi kecepatan potensial pada kubus bergetar k=1 ... 64

Gambar 4.61. Distribusi kecepatan potensial pada kubus untuk kasus

penghamburan, k=1 ... 65

Gambar 4.62. Distribusi kecepatan potensial pada bola untuk kasus bola bergetar

(16)

xix

Gambar 4.63. Distribusi kecepatan potensial pada kasus dua kubus bergetar, k=1

(17)

A-1

LAMPIRAN A

PERBANDINGAN HASIL DARI PROGRAM FORTRAN

DENGAN MATLAB

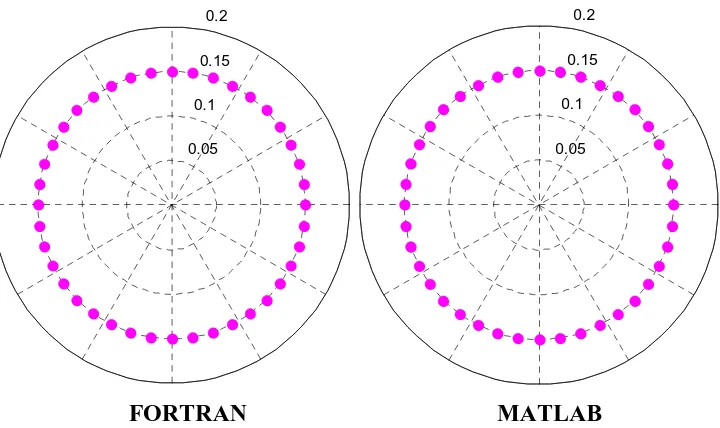
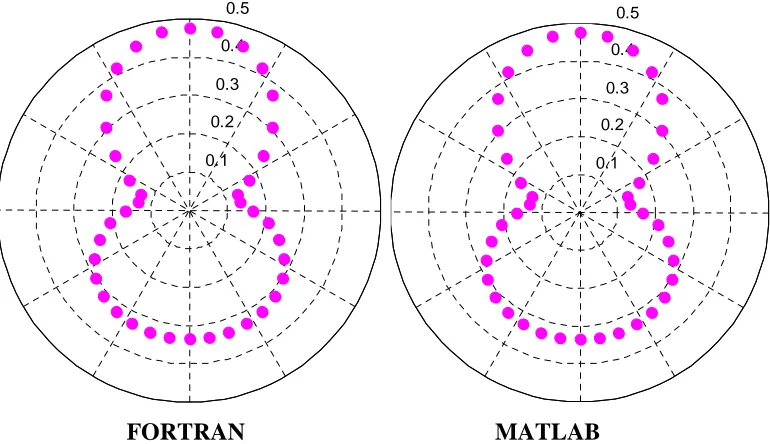
Berikut adalah perbandingan beberapa hasil dari program BEM Fortran

dengan hasil program MATLAB. Konfigurasi kasus sama seperti pada bab IV.

FORTRAN MATLAB

Gambar A.1. Pola radiasi kecepatan potensial dari bola bergetar homogen k=1,

r=2.

Gambar A.2. Pola kecepatan potensial tekanan dari bola bergetar homogen

k=3.14159, r=2, dengan satu titik CHIEF pada titik pusat.

(18)

A-2

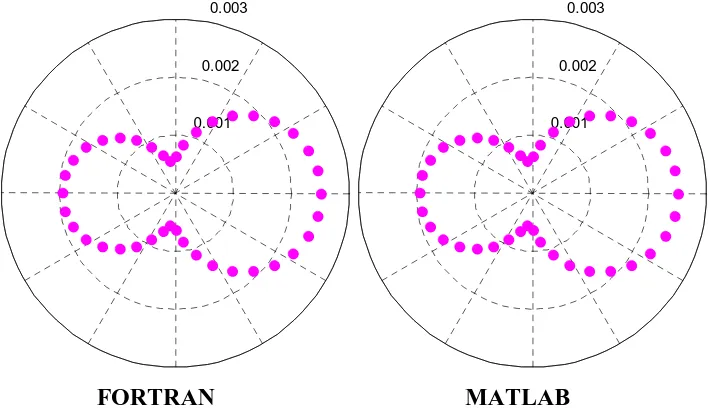
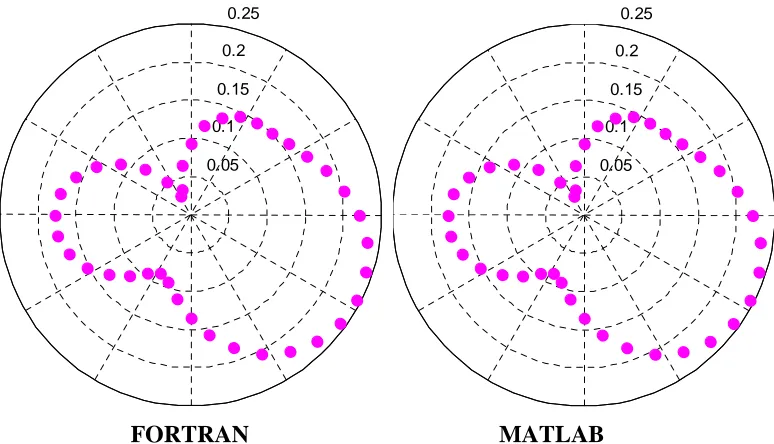
Gambar A.3. Pola kecepatan potensial yang terhambur dari penghamburan

gelombang bidang pada bola diam r=5, untuk k=1

Gambar A.4. Pola kecepatan potensial yang terhambur dari penghamburan

gelombang bidang pada bola diam r=5, untuk k=0.1.

(19)

A-3

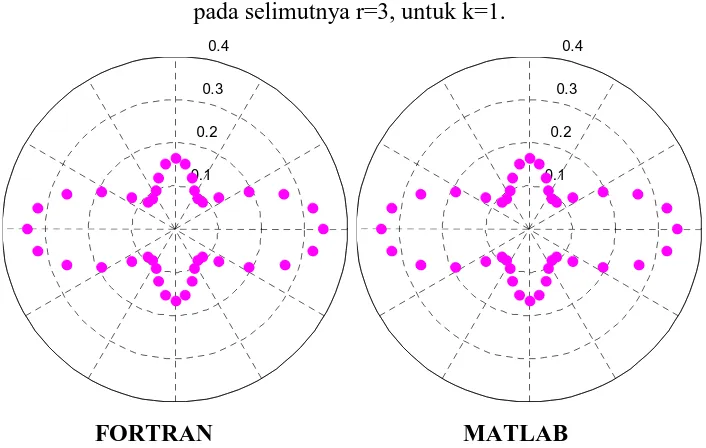
Gambar A.5. Pola radiasi kecepatan potensial dari silinder bergetar homogen

pada selimutnya r=3, untuk k=1.

Gambar A.6. Pola radiasi kecepatan potensial dari silinder bergetar homogen

pada selimutnya r=3, untuk k=2.

(20)

A-4

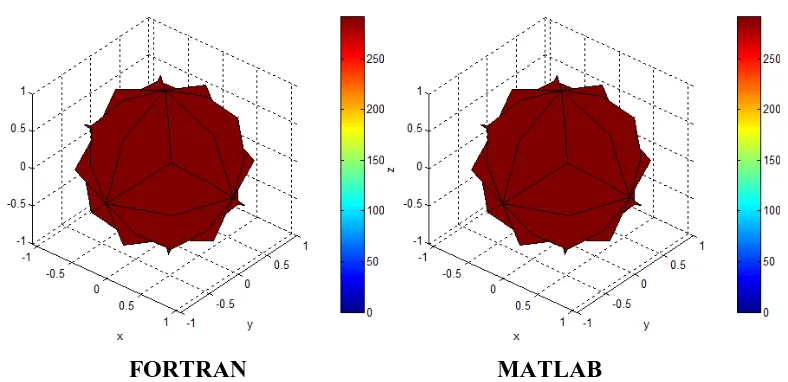
Gambar A.7. Distribusi kecepatan potensial pada kasus inverse untuk kubus

bergetar dengan diskritisasi 20 node dan 6 elemen pada k=1.

Gambar A.8. Distribusi kecepatan potensial pada kasus inverse untuk bola

(21)

A-5

Gambar A.9. Pola radiasi kecepatan potensial dari bola bergetar homogen pada

ruang setengah tak berhingga (Half Space) untuk B=3, r=2, k=1.

Gambar A.10. Pola radiasi kecepatan potensial dari bola bergetar homogen pada

ruang setengah tak berhingga untuk B=3, r=3, k=1.

(22)

A-6

Gambar A.11. Pola kecepatan potensial terhambur dari penghamburan

gelombang bidang pada bola keras pada ruang setengah tak berhingga untuk B=3,

r=2, k=1.

Gambar A.12. Pola kecepatan potensial terhambur dari penghamburan

gelombang bidang pada bola keras pada ruang setengah tak berhingga untuk B=3,

(23)

B-1

LAMPIRAN B

GEOMETRI PERMUKAAN BENDA DAN TITIK UKUR

B.1 Bola dengan Diskritisasi 50 Node dan 24 Elemen

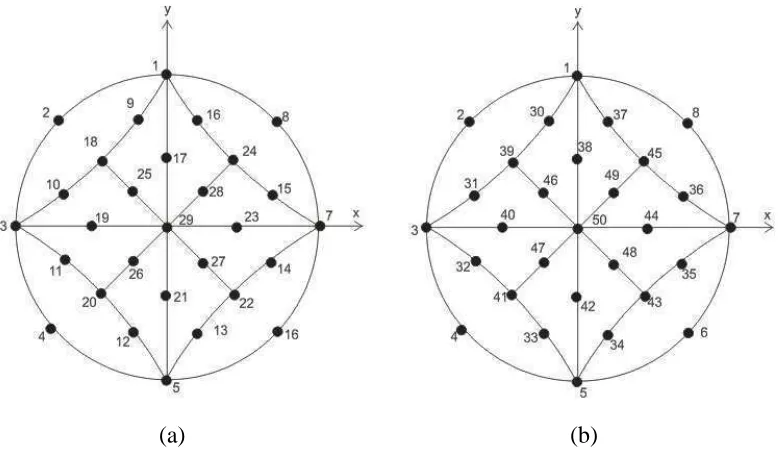
Permukaan bola didiskritisasi menjadi 50 node dan 24 elemen seperti pada

gambar 3.3b. Nomor global masing-masing node diberikan pada gambar B.1.

(a) (b)

Gambar B.1. Nomor global tiap node dilihat dari atas. (a) Node 29 adalah node

(24)

B-2

B.1.1 Nomor global dan koordinat titik bola dengan 50 node

NGN adalah nomor global node yang diberikan pada gambar B.1.

(25)

B-3

B.1.2 Nomor elemen dan hubungan nomor lokal dengan nomor global node

(26)

B-4

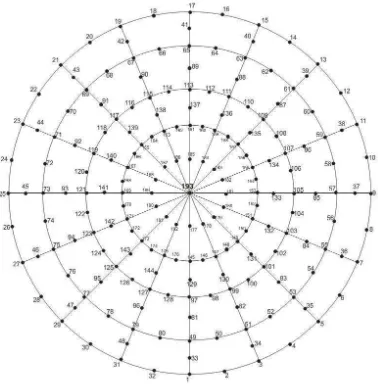
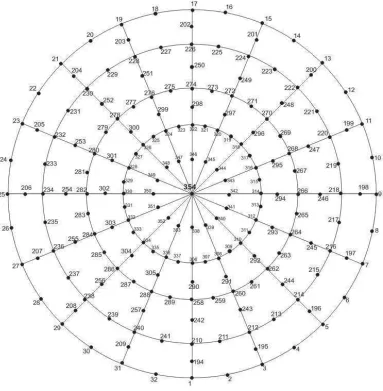
B.2 Bola dengan Diskritisasi 354 Node dan 128 Elemen

Permukaan bola didiskritisasi menjadi 354 node dan 128 elemen seperti

pada gambar 3.3a. Nomor global masing-masing node diberikan pada gambar B.2

dan B.3.

Gambar B.2. Nomor global tiap node dilihat dari atas. Node 193 adalah node

(27)

B-5

Gambar B.3. Nomor global tiap node dilihat dari atas. Node 354 adalah node

(28)

B-6

B.2.1 Nomor global dan koordinat titik bola dengan 354 node

(29)

(30)

(31)

(32)

(33)

(34)

B-12

(35)

(36)

(37)

(38)

B-16

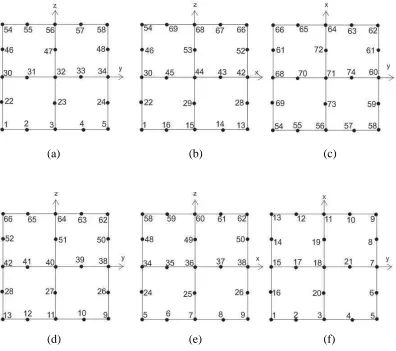
B.3 Kubus dengan Diskritisasi 74 Node dan 24 Elemen

Permukaan kubus didiskritisasi menjadi 74 node dan 24 elemen seperti

pada gambar 3.4. Nomor global masing-masing node diberikan pada gambar B.4.

(a) (b) (c)

(d) (e) (f)

Gambar B.4. Nomor global pada sisi kubus, (a) sisi depan kubus, (b) sisi kiri

kubus, (c) sisi atas kubus, (d) sisi belakang kubus, (e) sisi kanan kubus, (f) sisi

(39)

B-17

B.3.1 Nomor global dan koordinat titik kubus dengan 74 node

(40)

B-18

(41)

B-19

B.4 Kubus dengan Diskritisasi 290 Node dan 96 Elemen

Permukaan kubus didiskritisasi menjadi 290 node dan 96 elemen seperti

pada gambar 3.4. Nomor global masing-masing node diberikan pada gambar B.5,

B.6 dan B.7.

(a) (b)

Gambar B.5. Nomor global tiap node pada setiap sisi kubus. (a) Sisi depan

(42)

B-20

(a) (b)

Gambar B.6. Nomor global tiap node pada setiap sisi kubus. (a) Sisi kiri kubus,

(b) Sisi kanan kubus.

(a) (b)

Gambar B.7. Nomor global tiap node pada setiap sisi kubus. (a) Sisi atas kubus,

(43)

B-21

B.4.1 Nomor global dan koordinat titik kubus dengan 290 node

(44)

(45)

(46)

(47)

(48)

B-26

NGN x y z NGN x y z

252 -0.25 -1 0.5 272 0.5 1 0

253 -0.5 -1 0.5 273 0.25 1 0

254 -0.75 -1 0.5 274 0 1 0

255 0.5 -1 0.75 275 -0.25 1 0

256 0 -1 0.75 276 -0.5 1 0

257 -0.5 -1 0.75 277 -0.75 1 0

258 0.5 1 -0.75 278 0.5 1 0.25

259 0 1 -0.75 279 0 1 0.25

260 -0.5 1 -0.75 280 -0.5 1 0.25

261 0.75 1 -0.5 281 0.75 1 0.5

262 0.5 1 -0.5 282 0.5 1 0.5

263 0.25 1 -0.5 283 0.25 1 0.5

264 0 1 -0.5 284 0 1 0.5

265 -0.25 1 -0.5 285 -0.25 1 0.5

266 -0.5 1 -0.5 286 -0.5 1 0.5

267 -0.75 1 -0.5 287 -0.75 1 0.5

268 0.5 1 -0.25 288 0.5 1 0.75

269 0 1 -0.25 289 0 1 0.75

(49)

B-27

(50)

(51)

(52)

B-30

B.5 Silinder dengan Diskritisasi 42 Node dan 16 Elemen

Permukaan silinder didiskritisasi menjadi 42 node dan 16 elemen seperti

pada gambar 3.3b. Nomor global masing-masing node diberikan pada gambar

B.8.

(a) (b)

(c) (d)

Gambar B.8. Nomor global pada silinder, (a) tutup silinder atas, (b) tutup silinder

(53)

B-31

B.5.1 Nomor global dan koordinat titik silinder dengan 42 node

(54)

B-32

Kasus Eksterior

No El. Node 1 Node 2 Node 3 Node 4 Node 5 Node 6 Node 7 Node 8

1 1 3 3 29 26 2 3 27

2 29 3 3 5 28 27 3 4

3 1 9 11 3 2 6 10 7

4 3 11 13 5 4 7 12 8

5 9 17 19 11 10 14 18 15

6 11 19 21 13 12 15 20 16

7 17 25 25 19 18 22 25 23

8 19 25 25 21 20 23 25 24

9 21 25 25 40 41 24 25 42

10 40 25 25 17 39 42 25 22

11 17 9 36 40 39 14 35 38

12 40 36 13 21 41 38 37 16

13 9 1 32 36 35 6 31 34

14 36 32 5 13 37 34 33 8

15 1 29 29 32 31 26 29 30

(55)

1

BAB I

PENDAHULUAN

1.1 Latar Belakang

Akustik merupakan cabang yang penting dari sains fisika. Medan akustik

terdapat pada berbagai media di mana gelombang suara merambat. Persamaan

gelombang akustik linier dapat digunakan untuk memodelkan masalah akustik

dalam media udara atau air. Pada banyak situasi gelombang akustik yang ada pada

medan akustik adalah gelombang harmonik terhadap waktu, sehingga persamaan

gelombang akustik linier dapat diturunkan menjadi persamaan Helmholtz [12].

Persamaan Helmholtz merupakan persamaan diferensial parsial. Solusi

analitik dapat dicari dalam permasalahan tertentu yang melibatkan sumber suara

atau objek dengan bentuk geometris yang reguler seperti bola atau tabung. Untuk

benda-benda yang tidak reguler (tidak teratur) bentuk geometrisnya, solusi

analitik sulit diperoleh. Dalam hal ini untuk dapat mencari solusi permasalahan

digunakan metoda numerik.

Metoda numerik tersebut misalnya adalah Metoda Elemen Hingga (Finite

Element Method), Metoda Elemen Batas (Boundary Element Method) dan

lain-lain. Metoda Elemen Batas (MEB) hanya melibatkan permukaan benda atau

sumber yang terkait sedangkan Metode Elemen Hingga melibatkan seluruh

volume benda. Dengan Metoda Elemen Batas persoalan tiga dimensi yang

melibatkan volume diperlakukan seperti persoalan dua dimensi yang hanya

melibatkan permukaan benda. Jadi Metoda Elemen Batas dapat menurunkan

dimensi persoalan yang harus dipecahkan.

MEB telah digunakan untuk memecahkan berbagai masalah pada bidang

akustik, seperti pada industri otomotif yang melibatkan radiasi suara dari mesin

atau benda yang bergetar, penghamburan suara dari permukaan yang tidak

reguler, prediksi medan akustik ruang penumpang dari suatu kendaraan, medan

(56)

2

menyelesaikan permasalahan radiasi dan penghamburan suara pada ruang

setengah tak berhingga [7] dan yang menyangkut benda axisymmetric [5].

Formulasi MEB dalam akustik berdasarkan pada persamaan integral

Helmholtz permukaan. Pada awal perkembangan metoda ini, implementasi

numerik dari persamaan integral Helmholtz mengasumsikan variabel akustik

memiliki besar yang konstan pada tiap elemen. Setelah melalui perkembangan

terus-menerus, para ilmuwan (A.F.Seybert, B.Soenarko, F.J.Rizzo dan

D.J.Shippy), memperkenalkan implementasi numerik yang menggunakan elemen

isoparametrik [6] dengan memanfaatkan fungsi interpolasi (fungsi bentuk) yang

sama untuk variabel-variabel akustik maupun permukaan geometris. Fungsi

interpolasi yang digunakan diadopsi dari Metoda Elemen Hingga yaitu fungsi

interpolasi kuadratik.

Perangkat lunak (Software) yang sudah ada untuk menyelesaikan

perhitungan akustik dari benda yang tidak reguler (tidak teratur) bentuk

geometrisnya kebanyakan dibuat dengan menggunakan bahasa pemrograman

Fortran. Salah satunya adalah BEMAP (Boundary Element Methods for Acoustic

Prediction) untuk menghitung radiasi suara dari benda yang bergetar [9]. Bahasa

Fortran merupakan bahasa pemrograman yang sudah dari dulu digunakan di

kalangan ilmuwan karena kemampuannya dalam menyelesaikan masalah-masalah

di bidang teknik dan sains. Akan tetapi seiring dengan bermunculannya bahasa

pemrograman yang baru seperti pascal, C, dan masih banyak lainnya,

perkembangan bahasa Fortran tersebut menjadi lambat (terakhir sampai versi

Fortran 2008). Dewasa ini berkembang program MATLAB (Matrix Laboratory),

di mana MATLAB sendiri mempunyai kemampuan yang sama dengan bahasa

Fortran akan tetapi mekanisme pemrogramannya lebih mudah dan sederhana.

Oleh karena itu melalui tugas akhir ini, akan dibuat perangkat lunak tersebut

(57)

3

1. 2 Rumusan Masalah

Masalah yang akan dibahas pada tugas akhir ini adalah :

Bagaimana mengembangkan pemograman MATLAB untuk dapat memecahkan

persoalan perhitungan parameter gelombang suara dari radiasi dan hamburan yang

melibatkan sumber berbentuk sembarang menggunakan metode elemen batas.

1.3 Tujuan

Tujuan dari tugas akhir ini adalah membuat perangkat lunak (Software)

menggunakan MATLAB untuk perhitungan parameter gelombang suara yang

ditimbulkan oleh radiasi dan hamburan dari benda berbentuk sembarang dengan

menggunakan Metoda Elemen Batas (Boundary Element Method). Perangkat

lunak yang akan dibuat bersumber pada bahasa pemrograman Fortran dari

program yang sudah ada.

1.4 Batasan Masalah

Ada pun batasan – batasan masalah dalam tugas akhir ini adalah :

1. Persoalan yang dibahas adalah dalam lingkup akustik linier.

2. Massa jenis medium dianggap uniform.

3. Sumber dianggap diam atau tidak bergerak.

4. Medium dalam keadaan diam (tidak ada aliran).

5. Uji kasus yang dilakukan hanya meliputi masalah eksterior.

1.5 Spesifikasi Alat Yang Digunakan

Perangkat lunak (Software) yang digunakan pada tugas akhir ini adalah

(58)

4

1.6 Sistematika Pembahasan

Sistematika pembahasan pada laporan tugas akhir ini adalah

BAB I Pendahuluan, menjelaskan latar belakang masalah, tujuan tugas

akhir, rumusan masalah, batasan masalah, alat yang digunakan dan

sistematika pembahasan.

BAB II Landasan teori, membahas tentang formulasi Metoda Elemen

Batas, metoda CHIEF, solusi persamaan matriks dan penyelesaian

persamaan matriks dengan metoda faktorisasi LU dan SVD.

BAB III Memberikan penjelasan tentang tiga program yang dibuat yaitu

program Direct BEM, Inverse BEM, dan Halfspace BEM. Selain

itu memberikan macam-macam disktritisasi yang digunakan pada

tugas akhir ini.

BAB IV Membahas beberapa uji kasus yang dilakukan untuk kasus radiasi,

penghamburan untuk beberapa geometri(bola,kubus,silinder). Uji

kasus radiasi dan penghamburan juga dilakukan untuk kasus

Halfspace.

BAB V Memberikan kesimpulan dari tugas akhir ini dan saran untuk

pengembangan lebih lanjut.

Lampiran A Memberikan perbandingan hasil-hasil dari program FORTRAN

dengan program MATLAB untuk pola radiasi dan penghamburan

pada beberapa kasus.

Lampiran B Memberikan koordinat node dan hubungan antara nomor global

dan nomor lokal node dari beberapa geometri yang digunakan

(59)

67

menghitung parameter akustik yaitu kecepatan potensial dan kecepatan partikel

dengan menggunakan Metoda Elemen Batas. Program yang dibuat dapat

menyelesaikan masalah direct akustik, masalah inversi akustik, dan masalah direct

akustik pada ruang setengah tak berhingga. Uji kasus meliputi masalah radiasi dan

penghamburan dengan melibatkan beberapa bentuk geometri sumber benda yang

terkait. Dari hasil tugas akhir ini dapat disimpulkan

1. Program perhitungan parameter akustik dengan menggunakan Metoda

Elemen Batas telah berhasil dibuat ke dalam MATLAB. Program yang dibuat

berdasarkan program dalam bahasa Fortran yang telah ada. Simulasi uji kasus

yang telah dilakukan menunjukkan hasil yang sesuai antara hasil dari

program MATLAB dengan hasil dari program Fortran.

2. Kemudahan dari program MATLAB telah dimanfaatkan yakni pembuatan

grafik secara langsung baik dua dimensi maupun tiga dimensi. Grafik dua

dimensi yaitu pola radiasi kecepatan potensial dan pola penghamburan dapat

langsung dibuat dari data hasil perhitungan program. Selain itu distribusi

tekanan pada permukaan benda dapat divisualisasikan dengan baik menjadi

(60)

68

5.2 Saran

Beberapa saran yang dapat diberikan untuk penelitian lebih lanjut adalah

1. Metoda Elemen Batas sangat bermanfaat untuk kasus-kasus frekuensi rendah.

Pada kasus frekuensi tinggi diperlukan diskritisasi yang semakin banyak. Hal

ini akan berimbas pada sistem persamaan matriks yang semakin besar yang

kemudian akan menyebabkan waktu komputasi yang semakin lama. Oleh

karena itu perlu dikembangkan sebuah metoda untuk mengatasi hal tersebut.

Salah satunya adalah metoda Multilevel Fast Multipole Method (MLFMM) di

mana elemen-elemen hasil diskritisasi dikelompokkan ke dalam

cluster-cluster[1]. Metoda ini dengan Metoda Elemen Batas diyakini dapat

mengurangi waktu komputasi tanpa mengurangi keakuratan hasil.

2. Pembuatan program dengan MATLAB dapat dilanjutkan pada

(61)

69

DAFTAR PUSTAKA

[1] Bapat, M.S., L. Shen, Y.J. Liu, Adaptive fast multipole boundary element

method for three-dimensional half-space acoustic wave problems.

Engineering Analysis with Boundary Elements 33, Mei 2009, hal

1113-1123.

[2] Cheng, C. Y. R. dan A. F. Seybert, Recent Applications of The Boundary

Element Method to Problems in Acoustics, Proceedings SAE Noise and

Vibration Conference, Tranverse City, Michigan, 1987, hal 389-398.

[3] Juhl, Peter, The Boundary Element Method for Sound Field Calculations,

Disertasi Ph.D., The Acoustics Laboratory, Technical University of

Denmark, 1993.

[4] Kreyzig, Erwin, Advanced Engineering Mathematics, Edisi 9, John Wiley &

Sons, Singapur, 2006.

[5] Seybert, A.F. dan B.Soenarko, A Special Integral Equation Formulation for

Acoustic Radiation and Scattering for Axisymmetric Bodies and Boundary

Conditions. J. Acoust. Soc. Am. 80(4), Oktober 1986, hal 1241-1247.

[6] Seybert, A.F., B.Soenarko, F.J.Rizzo dan D.J.Shippy, An Advanced

Computational Method for Radiation and Scattering of Acoustic Waves in

Three Dimensions., J. Acoust. Soc. Am. 77(2), February 1985, hal 362-368.

[7] Seybert, A.F. dan B.Soenarko, Radiation and Scattering of Acoustic Waves

from Bodies of Arbitrary Shape in a Three Dimensional Half Space,

Transaction of the ASME, Februari 1988.

[8] Seybert, A.F. dan C.Y.R.Cheng, Application of the Boundary Element

Method to Acoustic Cavity Response and Muffler Analysis. Journal of

Vibration, Acoustics, Stress and Reliability in Design, January 1987, hal

15-21.

[9] Seybert, A. F. dan R. Khurana, Calculation of The Sound Intensity and

Sound Radiation Efficiency of Structures From Vibration Data,

(62)

70

[10] Trucco, Emanuele, Introductory Techniques for 3-D Computer Vision,

Prentice Hall, 1998.

[11] Wibowo, Bong Juwono, Solusi Masalah Invers Akustik Tiga Dimensi

dengan Menggunakan Metoda Elemen Batas, Tugas Akhir, Jurusan Teknik

Fisika, Intitut Teknologi Bandung, 1997.

[12] Wu, T. W., Boundary Element Acoustics: Fundamentals and Computer