PEMODELAN RISIKO KEJADIAN MALNUTRISI PADA PASIEN ANAK PENDERITA PENYAKIT INFEKSI SALURAN PERNAFASAN AKUT DENGAN PENDEKATAN MULTIVARIATE ADDAPTIVE REGRESSION
SPLINE
(Studi Kasus di Rumah Sakit Umum Haji Surabaya)
SKRIPSI
INTAN PRATIWI UTAMI
PROGRAM STUDI S1-STATISTIKA DEPARTEMEN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
PEMODELAN RISIKO KEJADIAN MALNUTRISI PADA PASIEN ANAK PENDERITA PENYAKIT INFEKSI SALURAN PERNAFASAN AKUT DENGAN PENDEKATAN MULTIVARIATE ADDAPTIVE REGRESSION
SPLINE
(Studi Kasus di Rumah Sakit Umum Haji Surabaya)
SKRIPSI
INTAN PRATIWI UTAMI
PROGRAM STUDI S1 STATISTIKA DEPARTEMEN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
PEDOMAN PENGGUNAAN SKRIPSI
Skripsi ini tidak dipublikasikan, namun tersedia di perpustakaan dalam
lingkungan Universitas Airlangga, diperkenankan untuk dipakai sebagai referensi
kepustakaan, tetapi pengutipan harus seijin penulis dan harus menyebutkan
sumbernya sesuai kebiasaan ilmiah. Dokumen skripsi ini merupakan hak milik
KATA PENGANTAR
Assalamu’alaikum wr.wb Puji syukur kehadirat Allah SWT yang telah
melimpahkan rahmat-Nya sehingga penulis dapat menyelesaikan skripsi yang
berjudul “Pemodelan Risiko Kejadian Malnutrisi Pada Pasien Anak Penderita
Infeksi Saluran Pernafasan Akut dengan Pendekatan Multivariate Addaptive Regression Spline (Studi Kasus di RSU Haji Surabaya)”. Dalam kesempatan ini penulis menyampaikan ucapan terima kasih kepada:
1. Orang tua dan keluarga tercinta yang selalu memberikan doa, dukungan, dan
kepercayaan sehingga penulis dapat menyelesaikan skripsi ini.
2. Dr. Ardi Kurniawan, M.Si dan Dr. Nur Chamidah, M.Si selaku dosen
pembimbing I dan dosen pembimbing II yang senantiasa membimbing dan
membantu dengan tulus dan sabar dalam penyelesaian skripsi ini.
3. Drs. Eko Tjahjono, M.Si selaku dosen wali yang selalu memberikan
penjelasan, pengarahan, dan saran demi kesuksesan menjadi mahasiswa.
4. Sahabat Redaksi, Ilmi dan teman statistika angkatan 2012 yang selalu
memberikan doa dan semangat dalam penyelesaian skripsi ini.
Penulis berharap semoga skripsi ini dapat bermanfaat bagi perkembangan
ilmu pengetahuan dan teknologi.
Surabaya, Juni 2016
Penulis,
vii
Intan Pratiwi Utami, 2016. Pemodelan Risiko Kejadian Malnutrisi Pada Pasien Anak Penderita Penyakit Infeksi Saluran Pernafasan Akut Dengan Pendekatan Multivariate Addaptive Regression Spline (Studi Kasus Di Rumah Sakit Umum Haji Surabaya) Skripsi dibawah Dr. Ardi Kurniawan, M.Si dan Dr. Nur Chamidah, M.Si. Program Studi S1-Statistika, Departemen Matematika, Fakultas Sains dan Teknologi, Universitas Airlangga, Surabaya.
ABSTRAK
Masa anak-anak merupakan fase dimana membutuhkan tumbuh kembang dan perhatian dengan baik. Namun kesehatan pada masa anak-anak akan rentan terkena penyakit, virus dan infeksi apabila tidak didukung dengan lingkungan dan asupan makanan. Penyakit penyerta yang sering terjadi adalah Infeksi Saluran Pernafasan Akut (ISPA). Malnutrisi adalah keadaan dimana tubuh tidak mendapat asupan gizi yang cukup, malnutrisi dapat juga disebut keadaan yang disebabkan oleh ketidakseimbangan di antara pengambilan makanan dengan kebutuhan gizi untuk mempertahankan kesehatan. Berbagai penelitian tentang malnutrisi rumah sakit telah banyak dilakukan dengan menggunakan metode kohort retrospektif. Tujuan skripsi ini yaitu untuk menganalisis dan menginterpretasikan dari model berdasarkan faktor yang berpengaruh signifikan terhadap risiko kejadian malnutrisi pada pasien anak penderita Infeksi Saluran Pernafasan Akut (ISPA).
Metode yang digunakan dalam penelitian ini adalah metode Multivariate Adaptive Regression Spline (MARS). Penelitian ini menggunakan 38 data tidak malnutrisi dan 22 data malnutrisi dengan variabel prediktor sebanyak 6 variabel. Hasil dari penelitian ini adalah faktor-faktor yang berpengaruh terhadap risiko kejadian malnutrisi pada pasien anak penderita ISPA di RSU Haji Surabaya pada tahun 2015- Mei 2016 antara lain jenis kelamin, lama perawatan, usia, Indeks Massa Tubuh (IMT), kelas perawatan, jenis pasien. Model terbaik yang didapatkan pada kombinasi BF=12, MI=3, dan MO=1 dengan nilai GCV minimum 0,225 dan R square sebesar 97,06%.
Intan Pratiwi Utami, 2016. Risk modeling Genesis Children Malnutrition in Patien ts Disease Patients With Acute Respiratory Tract Infection Addaptive Multivariat e Regression Spline Approach (Case Study in RSU Haji Surabaya). This skripsi is under supervised by Dr. Ardi Kurniawan, M.Si and Dr. Nur Chamidah, M.Si, S1-Statistics Courses, Matematics Departement, Faculty of Sains and Technology, Ai rlangga University, Surabaya.
ABSTRACT
Childhood is a phase which requires the growth and attention well. But he alth in childhood will be prone to diseases, viruses and infections if not supported by environmental and food intake. Morbidities that often happens is Acute Respir atory Infection (ARI). Malnutrition is a condition where the body does not get ade quate nutrition, malnutrition can also be called a condition caused by an imbalanc e between taking meals with nutritional needs to maintain health. Various studies on malnutrition hospitals have been carried out using the method of retrospective cohort. The purpose of this paper is to analyze and interpret than models based on factors that significantly influence the risk of occurrence of malnutrition in pediatr ic patients with acute respiratory infection (ARI). The method used in this researc h is the method of Multivariate Adaptive Regression Spline (MARS). This study u ses data from malnutrition 38 and 22 predictor variables of data malnutrition by as much as 6 variables. The results of this study are the factors that influence the risk of occurrence of malnutrition in pediatric patients with ARI in RSU Haji Surabaya in 2015- May 2016 include gender, length of treatment, age, body mass index (B MI), a class of treatments, types patient. The best model obtained in combination BF = 12, MI = 3, and MO = 1 with a minimum value of 0,225 GCV and R square of 97.06%.
DAFTAR ISI
Halaman
HALAMAN JUDUL ... i
LEMBAR PERNYATAAN ... ii
LEMBAR PENGESAHAN ... iii
PEDOMAN PENGGUNAAN SKRIPSI ... iv
LEMBAR ORISINALITAS ... v
KATA PENGANTAR ... vi
ABSTRAK ... vii
ABSTRACT ... viii
DAFTAR ISI ... ix
DAFTAR GAMBAR ... xii
DAFTAR TABEL ... xiii
DAFTAR LAMPIRAN ... xiv
BAB I PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Rumusan Masalah ... 4
1.3 Tujuan ... 4
1.4 Manfaat ... 5
BAB II TINJAUAN PUSTAKA ... 6
2.1 Malnutrisi Rumah Sakit ... 6
2.2 Status Gizi ... 9
2.4 Regresi Logistik ... 12
2.5 Regresi Nonparametrik ... 13
2.6 Regresi Spline ... 14
2.7 Multivariate Adaptive Regression Spline ... 15
2.8 Klasifikasi MARS ... 19
2.9 Pengujian Koefisien Fungsi Basis Model MARS ... 22
2.10 Penentuan Nilai Cut Off Probability ... 23
2.11 Odds Ratio ... 24
2.12 Ketepatan Klasifikasi dan nilai Press’sQ ... 25
2.13 Software MARS ... 27
2.14 Software R ... 28
BAB III METODE PENELITIAN ... 30
3.1 Sumber Data ... 30
3.2 Variabel Penelitian ... 30
3.3 Langkah – Langkah Analisis ... 31
BAB IV HASIL DAN PEMBAHASAN ... 34
4.1 Deskriptif Statistik Pasien Anak Penderita ISPA ... 34
4.2 Model Regresi Logistik Biner pada Risiko Kejadian Malnutrisi Menggunakan Pendekatan MARS ... 36
4.3 Interpretasi Fungsi Basis dalam Model MARS ... 42
BAB V KESIMPULAN DAN SARAN ... 51
5.1 Kesimpulan ... 51
DAFTAR PUSTAKA ... 53
DAFTAR GAMBAR
Nomor Judul Gambar Halaman
4.1 Jenis Kelamin pada Pasien Anak ISPA 34
4.2 Kelas Perawatan pada Pasien Anak ISPA 35
4.3 Jenis Pasien pada Pasien Anak ISPA 35
DAFTAR TABEL
Nomor Judul Tabel Halaman
2.1 Nilai Ketergantungan model y terhadap xj 24
2.2 Ketepatan Klasifikasi Model MARS 26
3.1 Variabel Penelitian 30
4.1 Model pada Kejadian Malnutrisi dengan MARS
(BF=12) 36
4.2 Model pada Kejadian Malnutrisi dengan MARS
(BF=18) 37
4.3 Model pada Kejadian Malnutrisi dengan MARS
(BF=24) 38
4.4 Tingkat Kepentingan Variabel Prediktor 40
4.5 Uji Parsial atau Individu Model MARS 42
4.6 Odds Ratio pada Fungsi Basis 45
4.7 Ketepatan klasifikasi berdasarkan APPER pada data
in sample 48
4.8 Ketepatan klasifikasi berdasarkan APPER pada data
DAFTAR LAMPIRAN
Lampiran 1 Data Sekunder Rekam Medis Pasien Anak Penderita ISPA di
RSU Haji Surabaya (in sample)
Lampiran 2 Data Sekunder Rekam Medis Pasien Anak Penderita ISPA di
RSU Haji Surabaya (out sample)
Lampiran 3 Output Model Optimal Program MARS dengan Fungsi Basis 12
Lampiran 4 Output Model Optimal Program MARS dengan Fungsi Basis 18
Lampiran 5 Output Model Optimal Program MARS dengan Fungsi Basis 24
Lampiran 6 Program Penentuan Nilai Cut Off Probabiliy Data In Sample pada
OSS-R
Lampiran 7 Output Perbandingan Ketepatan Klasifikasi data in sample pada setiap Cut Point
Lampiran 8 Uji Ketepatan Klasifikasi data In Sample
Lampiran 9 Program Penentuan Nilai Cut Off Probabiliy Data Out Sample pada OSS-R
Lampiran 10 Uji Ketepatan Klasifikasi data Out Sample
BAB I PENDAHULUAN
1.1 Latar Belakang
Derajat kesehatan suatu bangsa dipengaruhi oleh kesehatan. Kesehatan
dibutuhkan sejak manusia lahir untuk bisa tumbuh kembang. Masa anak-anak
merupakan fase dimana membutuhkan tumbuh kembang dan perhatian dengan
baik. Namun kesehatan pada masa anak-anak akan rentan terkena penyakit, virus
dan infeksi apabila tidak didukung dengan lingkungan dan asupan makanan.
Penyakit penyerta yang sering terjadi adalah Infeksi Saluran Pernafasan Akut
(ISPA), diare persisten, cacingan, tuberculosis, malaria dan HIV/AIDS (Krisnansari, 2010). Oleh karena itu, tingkat pelayanan kesehatan harus lebih
bermutu dan prima, namun dapat dijangkau oleh seluruh masyarakat agar
terwujud derajat kesehatan yang tinggi bagi bangsa Indonesia. Hal ini tentu akan
berdampak pada pelayanan gizi di suatu rumah sakit yang menuntut ahli gizi
untuk memberikan pelayanan gizi dengan kualitas terbaik.
Tujuan utama asupan gizi adalah mencegah terjadinya penurunan berat
badan pasien seminimal mungkin dengan harapan dapat menurunkan risiko
komplikasi, morbiditas dan mortalitas. Malnutrisi adalah keadaan dimana tubuh
tidak mendapat asupan gizi yang cukup, malnutrisi dapat juga disebut keadaan
yang disebabkan oleh ketidakseimbangan di antara pengambilan makanan dengan
kebutuhan gizi untuk mempertahankan kesehatan. Hal ini terjadi karena asupan
makan terlalu sedikit ataupun pengambilan makanan yang tidak seimbang.
dikatakan bahwa tingginya prevalensi malnutrisi rumah sakit mencerminkan
kualitas pelayanan suatu rumah sakit. Malnutrisi dapat terjadi sejak sebelum
pasien masuk rumah sakit maupun terjadi setelah pasien masuk rumah sakit.
Penyebab malnutrisi umumnya kompleks dan multifaktor. Gangguan yang timbul
akan menyebabkan dan memperberat komplikasi, antara lain respon yang tidak
adekuat terhadap modalitas terapi lain, menurunkan imunitas dan selanjutnya akan
meningkatkan angka morbiditas dan mortalitas. Selain dampak medis, juga
mengakibatkan peningkatan biaya pengobatan dan lama rawat. Varian lama rawat
dipengaruhi oleh beberapa faktor antara lain: Keparahan penyakit, mekanisme
koping, jenis penyakit, mutu pelayanan dan status akhir pasien.
Fakta menunjukkan bahwa insiden kasus malnutrisi di Indonesia cukup
tinggi di beberapa rumah sakit diantaranya balita yang dirawat di RSU Dr.
Pirngadi Medan menderita malnutrisi sebesar 38% dan di RS Dr. Sutomo
Surabaya terdapat 47% terserang MRS (Rianlego, 2014). Keadaan ini akan dapat
memperburuk status kesehatan anak, yang akan berakibat lanjut pada
terhambatnya proses penyembuhan anak di rumah sakit.
Penelitian tentang MRS pernah dilakukan oleh Khreshna (2013) dengan
judul Model Prediksi Statistika Sebagai “Alarm Malnutrisi Anak” Untuk
Mendeteksi Risiko Kejadian Malnutrisi didapat di Rumah Sakit. Penelitian lain
dilakukan oleh Juliaty (2013) menyatakan bahwa anak yang dirawat lebih dari
satu minggu dengan penyakit kronis dan diagnosis multipel mempunyai faktor
risiko MRS 1,2 kali lebih besar dibandingkan anak yang dirawat kurang dari
MRS dibanding penyakit non infeksi, penelitian ini menggunakan metode kohort
retrospektif. Salah satu penyakit yang sering menyerang anak yang menderita gizi
kurang adalah Infeksi Saluran Pernapasan Akut (ISPA).
Analisis regresi merupakan salah satu metode statistika yang dapat
menggambarkan ketergantungan atau mencari hubungan fungsional antara satu
variabel respon dengan satu atau lebih variabel prediktor, sehingga analisis regresi
tepat untuk memodelkan tingkat risiko kejadian malnutrisi pada pasien anak
penderita ISPA dengan variabel respon berskala nominal yang mempunyai dua
kategori yaitu mengalami MRS (Y 1) dan tidak mengalami MRS (0), sedangkan
variabel prediktornya adalah faktor-faktor yang diduga mempengaruhi risiko
kejadian malnutrisi pada pasien anak penderita ISPA adalah jenis kelamin, lama
perawatan, usia, Indeks Massa Tubuh (IMT), kelas perawatan, jenis pasien.
Metode Multivariate Adaptive Regression Splines (MARS) adalah salah satu pendekatan regresi nonparametrik dan merupakan pengembangan metode
Regresi Partisi Rekursif (RPR) dengan menggunakan fungsi basis spline. MARS merupakan salah satu metode alternatif untuk pemodelan bagi data berdimensi
tinggi, memiliki variabel prediktor banyak dan ukuran sampel yang besar. MARS
dapat menambahkan atau melibatkan banyak interaksi antar variabel
(Friedman,1991). Model MARS memiliki power dan fleksibilitas dalam memodelkan hubungan yang hampir aditif atau yang melibatkan interaksi
beberapa variabel prediktor. Model dapat direpresentasikan dalam bentuk yang
mengidentifikasi secara terpisah kontribusi aditif dan model dihubungkan dengan
Berdasarkan uraian di atas, akan diteliti bentuk model kejadian malnutrisi
pada pasien anak penderita penyakit infeksi saluran pernafasan akut di RSU Haji
Surabaya dengan menggunakan pendekatan MARS.
1.2 Rumusan masalah
Berdasarkan latar belakang diatas, maka permasalahan yang akan dibahas
dalam skripsi ini adalah sebagai berikut:
1. Bagaimana mendeskripsikan data kejadian malnutrisi dari pasien anak
penderita ISPA yang dirawat di RSU Haji Surabaya berdasarkan faktor-faktor
yang diduga mempengaruhi?
2. Bagaimana mengestimasi model kejadian malnutrisi berdasarkan faktor-faktor
yang diduga mempengaruhi dengan menggunakan metode MARS?
3. Bagaimana menganalisis dan menginterpretasikan model berdasarkan faktor
yang berpengaruh signifikan terhadap kejadian malnutrisi dengan
menggunakan metode MARS?
1.3 Tujuan
Berdasarkan rumusan masalah diatas, maka tujuan dalam skripsi ini adalah
sebagai berikut:
1. Mendeskripsikan data kejadian malnutrisi dari pasien anak penderita ISPA
yang dirawat di RSU Haji Surabaya berdasarkan faktor-faktor yang diduga
2. Mengestimasi model kejadian malnutrisi berdasarkan faktor-faktor yang
diduga mempengaruhi dengan menggunakan metode MARS.
3. Menganalisis dan menginterpretasi model berdasarkan faktor yang
berpengaruh signifikan terhadap kejadian malnutrisi dengan menggunakan
metode MARS.
1.4 Manfaat
Manfaaat dari penulisan skripsi ini adalah sebagai berikut:
1. Bagi peneliti, mendapatkan ilmu dan pengetahuan tentang pengaplikasian
metode MARS khususnya dalam dunia kesehatan dengan kejadian malnutrisi
pada anak penderita penyakit ISPA.
2. Bagi pemerintah dan instansi terkait diharap bisa meningkatkan kualitas
layanan untuk mencegah dan meminimalisir angka morbiditas dan mortalitas
anak penderita penyakit ISPA dari faktor-faktor yang mempengaruhi.
3. Bagi pembaca, secara umum dapat mengetahui pentingnya pengetahuan
BAB II
TINJAUAN PUSTAKA
Tinjauan pustaka yang digunakan dalam skripsi ini adalah penjelasan
mengenai malnutrisi rumah sakit dan metode Multivariate Adaptive Regression Splines (MARS).
2.1 Malnutrisi Rumah Sakit
Malnutrisi Rumah Sakit (MRS) adalah terjadinya malnutrisi pada pasien
yang sedang dirawat di rumah sakit. Prevalensi terjadinya MRS pasien rawat inap
cukup tinggi dan dikatakan bahwa tingginya prevalensi malnutrisi rumah sakit
mencerminkan kualitas pelayanan suatu rumah sakit. Malnutrisi adalah keadaan
dimana tubuh tidak mendapat asupan gizi yang cukup, malnutrisi dapat juga disebut
keadaan yang disebabkan oleh ketidakseimbangan di antara pengambilan makanan
dengan kebutuhan gizi untuk mempertahankan kesehatan. Hal ini terjadi karena
asupan makan terlalu sedikit ataupun pengambilan makanan yang tidak seimbang.
Selain itu, kekurangan gizi dalam tubuh berakibat terjadinya malabsorpsi makanan
atau kegagalan metabolik.
Banyaknya kejadian malnutrisi pada pasien di rumah sakit sering tidak
teratasi dengan baik, bila keadaan berlanjut lama, tubuh akan melakukan proses
adaptasi seperti menurunnya nafsu makan dan memperlambat metabolik.
Malnutrisi dapat mempengaruhi fungsi dan penyembuhan setiap organ, seperti
perubahan berat badan, fungsi jantung dan ginjal menurun, gangguan sistem saluran
yang menurun, penurunan kapasitas fungsional dan kondisi metabolisme, serta
depresi pada pasien, sehingga penting menjadi perhatian bagi rumah sakit untuk
melakukan perbaikan status gizi melalui pemenuhan kebutuhan energi untuk
mendukung proses kesembuhan pasien.
Malnutrisi Rumah Sakit akan mempengaruhi banyak hal, diantaranya
adalah waktu perawatan yang semakin lama, proses penyembuhan yang semakin
lambat, biaya perawatan yang terus meningkat, dan peningkatan mortalitas. Berikut
merupakan variabel-variabel yang mempengaruhi terjadinya MRS pada pasien
anak penderita ISPA diantaranya adalah:
1. Jenis kelamin
Menurut Almatsier (2005), tingkat kebutuhan pada anak laki-laki lebih
banyak jika dibandingkan dengan perempuan. Begitu juga dengan kebutuhan
energi, sehingga laki-laki mempunyai peluang untuk menderita KEP yang lebih
tinggi daripada perempuan apabila kebutuhan akan protein dan energinya tidak
terpenuhi dengan baik. Kebutuhan yang tinggi ini disebabkan aktivitas anak
laki-laki lebih tinggi dibandingkan dengan anak perempuan sehingga membutuhkan gizi
yang tinggi.
2. Usia pasien anak ketika masuk RS
Umur faktor umur sangat penting dalam penentuan status gizi. Kesalahan
penentuan umur akan menyebabkan interpretasi status gizi menjadi salah. Hasil
pengukuran tinggi badan dan berat badan menjadi tidak berarti bila tidak disertai
umur digunakan adalah tahun umur penuh (completed year) untuk anak umur 5-14
tahun digunakan bulan usia penuh (completed month).
3. Indeks Masa Tubuh (IMT)
Body Mass Indeks merupakan indeks antropometri yang sering digunakan untuk menilai status gizi individu maupun masyarakat karena cukup peka untuk
menilai status gizi orang dewasa di atas 18 tahun. IMT dapat dihubungkan dengan
persen lemak tubuh. IMT dihitung dengan pembagian berat badan (dalam kg) oleh
tinggi badan (dalam meter) pangkat dua. Korelasi berat badan dengan jumlah total
lemak tubuh cukup erat, kendati sebagian orang dengan lean body mass yang tinggi
bisa memberikan IMT yang tinggi walaupun orang tersebut tidak gemuk (Hartono,
2000).
Pengukuran IMT dapat dikategorikan dalam 3 kategori, menurut WHO
1998 adalah sebagai berikut:
1. Kategori kurus apabila kekurangan berat badan tingkat berat kurang dari 17,0.
2. Kategori normal apabila range IMT dibatas ambang 18,5 – 25,0.
3. Kategori gemuk apabila kelebihan berat badan tingkat berat lebih dari 27,0.
Masalah gizi disebabkan oleh banyak faktor yang saling terkait baik secara
langsung maupun tidak langsung. Kemiskinan dan kurang gizi merupakan suatu
fenomena yang saling terkait, oleh karena itu meningkatkan status gizi suatu
masyarakat erat kaitannya dengan peningkatan ekonomi. Tingkat sosial ekonomi
mempengaruhi macam makanan tambahan dan waktu pemberian, tetapi juga pada
2.2 Status Gizi
Gizi berasal dari bahasa Arab “Qizzi” adalah suatu proses organisme
menggunakan makanan yang dikonsumsi secara normal melaui proses digesti,
absorpsi, transportasi, penyimpanan, metabolisme dan pengeluaran zat-zat yang
tidak digunakan untuk mempertahankan kehidupan, pertumbuhan dan fungsi
normal dari organ, serta menghasilkan energi (Hartriyanti & Triyanti, 2007).
Penilaian status gizi pada pasien di rumah sakit sangat penting untuk
dilakukan, terutama pasien dengan resiko malnutrisi yang tinggi. Identifikasi dan
skrining malnutrisi secara dini dapat mendukung ketepatan intervensi gizi oleh ahli
gizi terhadap pasien sehingga outcome pasien yang lebih baik dan efektivitas biaya
kesehatan secara keseluruhan dapat diwujudkan. Salah satu penilaian status gizi
secara langsung adalah antropometri.
Antropometri secara umum merupakan ukuran tubuh. Sedangkan sudut
pandang gizi, Jelliffe (1966) mengungkapkan bahwa antropometri gizi
berhubungan dengan berbagai macam pengukuran dimensi tubuh dan komposisi
tubuh dari berbagai tingkat umur dan tingkat gizi. Penggunaan antropometri,
khususnya pengukuran berat badan pernah menjadi prinsip dasar pengkajian gizi
dalam asuhan medik. Untuk mengkaji status gizi secara akurat, beberapa
pengukuran secara spesifik diperlukan dan pengukuran ini mencakup pengukuran
berat badan (Andy Hartono, 2000). Berikut pengukuran antropometri:
1. Berat Badan
Berat badan merupakan ukuran antropometri yang terpenting dan paling
mineral pada tulang. Berat badan seseorang sangat dipengaruhi oleh beberapa
faktor antara lain : umur, jenis kelamin, aktifitas fisik, dan keturunan (Krisnansari,
2014). Berat badan merupakan ukuran antropometrik yang terpenting, dipakai pada
setiap kesempatan memeriksa kesehatan pada semua kelompok umur. Berat badan
merupakan hasil peningkatan/penurunan semua jaringan yang ada pada tubuh,
antara lain tulang, otot, lemak, cairan tubuh dan lain-lainnya. Berat badan dipakai
sebagai indikator terbaik pada saat ini untuk mengetahui keadaan gizi, pengukuran
objektif dan dapat diulangi, dapat digunakan timbangan apa saja yangrelatif murah,
mudah dan tidak memerlukan banyak waktu.
1. Tinggi Badan (TB)
Tinggi badan merupakan parameter yang penting bagi keadaan gizi yang
telah lalu dan keadaan sekarang jika umur tidak diketahui dengan tepat. Tinggi
badan merupakan antropometri yang menggambarkan keadaan pertumbuhan
skeletal. Dalam keadaan normal, tinggi badan tumbuh bersamaan dengan
pertambahan umur. Pertumbuhan tinggi badan, tidak seperti berat badan, relatif
kurang sensitif terhadap masalah defisiensi gizi dalam waktu pendek. Dalam
penilaian status gizi tinggi badan dinyatakan sebagai indeks sama halnya dengan
berat badan. Sedangkan indeks yang digunakan untuk menentukan penilaian status
gizi adalah sebagai berikut:
1. BB/U : Berat badan menurut umur
2. PB/U : Panjang badan menurut umur
3. TB/U : Tinggi badan menurut umur
Masing-masing indeks tersebut mempunyai standard baku rujukan untuk
menilai gizi masyarakat atau seseorang. Terdapat banyak standard baku yang
digunakan di dunia internasional, salah satunya adalah menurut standard Baku
Antropometri WHO-NCHS kategori status gizi BB/U (Z-Score) sebagai berikut:
1. > +2 SD : BB lebih (gizi lebih)
2. -2 SD s/d +2 SD : BB normal (gizi normal)
3. -3 SD s/d <-2 SD : BB rendah
4. <-3 SD : BB sangat rendah (gizi buruk)
2.3 Infeksi Saluran Pernafasan Akut
Infeksi Saluran Pernapasan Akut (ISPA) merupakan penyebab masalah
kesehatan paling umum yang terjadi di dunia. WHO telah memperkirakan bahwa
terdapat 14-15 juta kematian anak karena infeksi pernapasan akut. Meskipun
penyakit ini belum didefinisikan ke dalam kelompok penyakit, namun infeksi
pernapasan akut termasuk di dalamnya batuk influenza, pneumonia, bronkhitis, dan
sejumlah penyakit infeksi lainnya. Kebanyakan infeksi pernapasan ditemukan di
bagian dunia yang lebih dingin atau di dataran tinggi pada daerah tropis (Webber
2005). ISPA dapat bersifat akut atau kronik. Istilah ISPA atau Acute Respiratory
Infection (ARI) meliputi tiga unsur yaitu:
1. Infeksi yaitu masuknya mikroorganisme ke dalam tubuh manusia dan
berkembang biak sehingga menimbulkan gejala penyakit.
2. Saluran pernapasan yaitu organ mulai dari hidung hingga alveoli. ISPA secara
bawah (termasuk jaringan paru-paru) dan organ adenoksa saluran pernapasan
(sinus-sinus, rongga telinga tengah dan pleura).
3. Infeksi akut yaitu infeksi yang berlangsung sampai dengan 14 hari. Batas 14 hari
diambil untuk menujukkan proses akut meskipun untuk beberapa penyakit yang
digolongkan dalam ISPA. Proses ini dapat berlangsung lebih dari 14 hari
(Depkes 2004 dalam Fitriyani 2008).
2.4 Regresi Logistik
Analisis regresi logistik adalah analisis yang digunakan untuk melihat
hubungan antara variabel respon kategorik dengan variabel-variabel prediktor
kategorik maupun kontinu. Variabel respon dalam regresi logistik dapat berbentuk
dikotomus (biner) maupun polikotomus dengan skala data ordinal atau nominal
(Agresti, 1990). Regresi logistik dengan variabel respon berskala ordinal disebut
regresi logistik ordinal, sedangkan jika variabel respon berskala nominal dengan 2
kategori disebut regresi logistik dikotomus, dan kategori lebih dari 2 disebut regresi
logistik polikotomus.
Regresi logistik digunakan untuk pengklasifikasian sejumlah obyek ke
dalam beberapa kelompok. Regresi logistik dikotomus, respon 𝑌 terdiri dari 2
kategori (misalkan 0 dan 1). Kondisi tersebut mengakibatkan respon 𝑌 berdistribusi
Bernoulli. Distribusi Bernoulli untuk variabel random biner berbentuk:
1 ( | ) (x) (1y (x) )y
P Y y X x , y0,1 (2.1)
Model regresi logistik dikotomus dapat terdiri dari banyak variabel
prediktor yang dikenal sebagai model multivariabel. Model regresi logistik
multivariabel dengan p variabel prediktor adalah
Proses pendugaan parameter dari regresi logistik menggunakan metode
Maximum Likelihood Estimation. Menurut Agresti (2002) metode Maximum Likelihood Estimation memberikan nilai duga bagi dengan cara
memaksimumkan fungsi likelihood dan mensyaratkan bahwa data mengikuti sebaran Bernoulli. Fungsi likelihood untuk model regresi logistik biner adalah:
1
Dari (2.3) diperoleh fungsi log likelihood ℓ(𝛽) = 𝑙𝑛𝐿(𝛽) adalah
1
karena turunan parsial pertama terhadap parameter j yang diperoleh berbentuk
implisit dan berupa fungsi non linier, maka untuk mengestimasi parameternya
digunakan metode iterasi Newton-Raphson multivariat.
2.5 Regresi Nonparametrik
Regresi nonparametrik digunakan untuk mengetahui hubungan variabel
diketahui bentuknya. Misalkan data berpasangan (𝑥𝑖, 𝑦𝑖), 𝑖 = 1,2, … , n
diasumsikan memenuhi model regresi nonparametrik sebagai berikut:
𝑦𝑖 = 𝑓(𝑥𝑖) + 𝜀𝑖 , 𝑖 = 1,2, … , 𝑛, (2.5)
dengan 𝜀𝑖 sebuah error random yang saling independen memiliki mean 0
dan varians 𝜎2. 𝑓(𝑥
𝑖) adalah fungsi regresi yang tidak diketahui bentuknya yang
akan diestimasi (Eubank, 1999).
2.6 Regresi Spline
Diasumsikan data berpasangan {(𝑥1𝑦1), (𝑥2, 𝑦2), … , (𝑥𝑛, 𝑦𝑛)} memenuhi
model regresi nonparameterik pada persamaan (2.5). Estimator spline dengan orde
ke k dan titik knot 𝜏1, 𝜏2, … , 𝜏K adalah suatu fungsi 𝑓 yang dinyatakan sebagai
berikut:
𝑓(𝑥) = ∑𝑘+𝐾𝑝=0𝛽𝑝𝜙𝑝(𝑥) (2.6)
dengan 𝜷 = (𝛽0,𝛽1, … , 𝛽k+K)𝑇 adalah vektor koefisien dan 𝜙0,𝜙1, … , 𝜙k+K
adalah suatu fungsi yang didefinisikan sebagai berikut:
𝜙𝑝(𝑥) = { 𝑥
𝑝
(𝑥 − 𝜏𝑝−𝑘)+𝑘
𝑢𝑛𝑡𝑢𝑘 0 ≤ 𝑝 ≤ 𝑘 𝑢𝑛𝑡𝑢𝑘 + 1 ≤ 𝑝 ≤ 𝑘 + K
dengan 𝑘 adalah orde polinomial, 𝐾 adalah banyaknya knot dan
(𝑥 − 𝜏𝑝−𝑘)+𝑘 = {(𝑥 − 𝜏𝑝−𝑘)
𝑘
0
, 𝑥 ≥ 𝜏
𝑝−𝑘, 𝑥 < 𝜏
𝑝−𝑘Spline merupakan potongan-potongan polinomial dengan segmen-segmen
polinomial berbeda digabungkan bersama knot 𝜏1, 𝜏2, … , 𝜏K dengan suatu cara yang
Selanjutnya dengan menggunakan data sebanyak 𝑛, maka model regresi
spline dari persamaan (2.6) dapat ditulis menjadi
𝑓(𝑥1) = 𝛽0 + 𝛽1𝑥1 + ⋯ + 𝛽𝑘𝑥1𝑘+ 𝛽𝑘+1(𝑥1− 𝜏1)+𝑘 + ⋯ + 𝛽𝑘+𝐾(𝑥1− 𝜏𝐾)+𝑘
𝑓(𝑥2) = 𝛽0+ 𝛽1𝑥2 + ⋯ + 𝛽𝑘𝑥2𝑘+ 𝛽𝑘+1(𝑥2− 𝜏1)+𝑘+ ⋯ + 𝛽𝑘+𝐾(𝑥2− 𝜏𝐾)+𝑘
⋮
𝑓(𝑥𝑛) = 𝛽0+ 𝛽1𝑥𝑛 + ⋯ + 𝛽𝑘𝑥𝑛𝑘+ 𝛽𝑘+1(𝑥𝑛− 𝜏1)+𝑘 + ⋯ + 𝛽𝑘+𝐾(𝑥𝑛 − 𝜏𝐾)+𝑘
Dalam bentuk matriks, model regresi spline dapat ditulis sebagai berikut :
[
sebagai metode baru yang mengakomodasi pembangunan model-model prediksi
yang lebih akurat untuk variabel-variabel respon kontinu maupun kategorik biner.
Model MARS difokuskan untuk mengatasi permasalahan dimensi yang tinggi dan
diskontinuitas pada data. MARS merupakan pengembangan dari pendekatan
Recursive Partition Regression (RPR) yang menghasilkan model yang tidak kontinu pada knot (Friedman, 1991).
Beberapa hal yang diperhatikan dalam membangun model MARS yaitu:
merupakan awal dari segmen yang lain. Di setiap titik knot, diharapkan adanya
kontinuitas dari fungsi basis antar satu region dengan region lainnya. Minimum
observasi (MO) antara knot adalah 0, 1, 2 dan 3 observasi.
2. Basis Function (BF) atau fungsi basis, yaitu selang antar knot yang berurutan. Pada umumnya BF yang dipilih berbentuk polinomial dengan turunan yang
kontinu pada setiap titik knot. Maksimum BF yang diijinkan adalah dua sampai
empat kali jumlah variabel prediktornya.
3. Interaction (interaksi), yaitu hasil perkalian silang antar variabel yang saling berkorelasi. Jumlah maksimum interaksi (MI) yang diperbolehkan adalah 1, 2
atau 3. Jika MI > 3 akan dihasilkan model yang semakin kompleks dan model
akan sulit untuk diinterpretasi.
Dalam Friedman (1991) disebutkan bahwa model MARS merupakan
kombinasi dari spline dan rekursif partisi. Pemodelan regresi spline
diimplementasikan dengan membentuk kumpulan fungsi basis yang dapat
mencapai pendekatan spline orde ke-q dan mengestimasi koefisien fungsi basis
tersebut menggunakan least-squares (kuadrat terkecil).
Sebagai contoh, untuk kasus univariate (𝑣 = 1), salah satu bentuk fungsi basis adalah:
1
1
, k
q q
j
k
x x t (2.7)
Dengan {𝑡𝑘}1𝑘 adalah titik knots yang diharapkan terdapat kontinuitas dari
umumnya fungsi basis yang dipilih adalah berbentuk polinomial dengan derivatif
yang kontinu pada setiap titik knots.
Alternatif untuk menyelesaikan kasus – kasus dimensi tinggi yaitu data yang
memiliki jumlah variabel prediktor sebesar 3 n 20 atau multivariat adalah menggunakan pendekatan secara komputasi (Adaptive Computation). Dalam
statistika, algoritma adaptive computation diterapkan untuk pendekatan suatu fungsi yang didasarkan pada dua paradigma, yaitu Project Persuit Regression (PPR) dan Recursive Partitioning Regression (RPR). RPR juga merupakan pendekatan dari fungsi f yang tidak diketahui dengan:
0
a adalah parameter dari fungsi basis ke-𝑚
M adalah banyaknya fungsi basis
0
,
Secara umum persamaan (2.10) dapat dituliskan sebagai berikut:
0
Persamaan (2.11) menunjukkan bahwa penjumlahan suku pertama meliputi
semua fungsi basis untuk satu variabel prediktor, penjumlahan suku kedua meliputi
semua fungsi basis untuk interaksi antara dua variabel prediktor, penjumlahan suku
ketiga meliputi semua fungsi basis untuk interaksi antara tiga variabel prediktor dan
seterusnya.
Persamaan ini dikenal dengan dekomposisi ANOVA dari model MARS.
Interpretasi model MARS melalui dekomposisi ANOVA adalah merepresentasikan
variabel yang masuk dalam model, baik untuk satu variabel maupun interaksi antar
variabel.
Berdasakan persamaan (2.10) dan (2.11), maka model MARS dapat ditulis
sebagai berikut:
Pada pemodelan MARS, penentuan knots dilakukan secara otomatis dari
maksimum. Kriteria pemilihan fungsi basis pada forward stepwise adalah dengan meminimumkan Mean Squared Error (MSE). Untuk memenuhi konsep parsemoni
(model yang sederhana) dilakukan backward stepwise, yaitu memilih fungsi basis
yang dihasilkan dari algoritma forward stepwise dengan meminimumkan nilai Generalized Cross-Validation (GCV) (Friedman dan Silverman, 1989). Berikut ini diberikan fungsi GCV yang didefinisikan yaitu:
x adalah variabel independen/prediktor
i
Klasifikasi pada MARS didasarkan pada pendekatan analisis regresi
logistik. Kriteria yang digunakan adalah kuadrat terkecil dari residual untuk
menghubungkan variabel prediktor X dengan variabel respon 𝑌 biner (0,1). Jika
dengan pendekatan kuadrat terkecil mendekati probabilitas dari populasi 1. Model
Persamaan (2.14) adalah sama dengan persamaan model regresi logistik
respon biner, dengan fungsinya dapat di dekati dengan estimator MARS.
Pendugaan parameter model MARS dengan peubah respon biner dilakukan
melalui metode Maximum Likelihood Estimation. Menurut Kriner (2007) MARS
dengan peubah respon biner dan nilai peluang peubah responnya P Y( i 1) dan
( i 0) 1
P Y maka fungsi kemungkinan yang akan dimaksimalkan adalah:
Setelah dilakukan turunan pertama terhadap am maka didapatkan hasil
sebagai berikut:
Pada model MARS klasifikasi didasarkan pada pendekatan analisis regresi
logistik, model MARS adalah sebagai berikut:
Apabila variabel repon berupa biner, maka harus digunakan titik potong (cut
2.9 Pengujian Koefisien Fungsi Basis Model MARS
Pada model MARS dilakukan pengujian koefisien BF yang meliputi uji
serentak dan uji individu. Pengujian koefisien yang dilakukan secara bersamaan
atau serentak terhadap fungsi yang terdapat dalam model MARS ini bertujuan untuk
mengetahui apakah secara umum model MARS yang terpilih merupakan model
yang sesuai dan menunjukkan hubungan yang tepat antara variabel prediktor
dengan variabel respon. Hipotesis yang digunakan sebagai berikut.
0: 1 1 M 0
H a a a
1:
H paling tidak ada satu aM 0 , 1,2, ,j m
Statistik uji yang digunakan adalah nilai F yang diperoleh dari tabel ordinary least squares results hasil dari output pengolahan MARS. Kriteria jika 𝑝 −
𝑣𝑎𝑙𝑢𝑒 < ∝ maka 𝐻0 ditolak, artinya paling sedikit ada satu 𝛼𝑗 yang tidak sama
dengan nol sehingga dikatakan model yang diperoleh sesuai dan menunjukkan
hubungan yang tepat antara variabel prediktor dengan variabel respon.
Sedangkan pengujian yang dilakukan secara parsial (individu) ini bertujuan
untuk mengetahui apakah setiap variabel prediktor mempunyai pengaruh signifikan
terhadap variabel respon pada fungsi basis yang terbentuk di dalam model, selain
itu juga untuk mengetahui apakah model yang memuat parameter tersebut telah
mampu menggambarkan keadaan data yang sebenarnya.
Hipotesisnya sebagai berikut.
0: j 0
H a
1:
Statistik uji yang digunakan adalah nilai |t| pada tabel ordinary least square
hasil dari output pengolahan MARS. Nilai |t| dibandingkan dengan nilai dengan
derajat bebas v n k dan tingkat signifikansi 𝛼. Dengan daerah kritis jika 𝑝 −
𝑣𝑎𝑙𝑢𝑒 < ∝, maka 𝐻0 ditolak, artinya ada pengaruh setiap variabel prediktor dengan
variabel respon pada BF di dalam model (Cholifah, 2013).
2.10 Penentuan Nilai Cut Off Probability
Berdasarkan Kalhori, et al. (2010), Cut off Probability merupakan titik poin
yang digunakan untuk mengukur akurasi model dengan mengklasifikasikan hasil
estimasi status pasien anak penderita ISPA. Misal diberikan data
{(𝑥𝑗𝑖)𝑗=1𝑝 , 𝑦𝑖} 𝑖=1 𝑛
dimana 𝑦 = {0 , 𝑡𝑖𝑑𝑎𝑘 𝑀𝑅𝑆 1 , 𝑀𝑅𝑆 (2.17)
dengan menerapkan persamaan (2.2) pada data tersebut maka akan diperoleh 𝜇̂𝑖(𝑥)
sebagai bentuk estimator model data in sample. Proses validasi dilakukan dengan menghitung 𝜇̂𝑖(𝑥) untuk setiap nilai cut off probability dari 0 sampai 1 dengan
increment 0,01 sehingga dapat diperoleh titik poin terbaik, yaitu titik dimana jumlah tertinggi klasifikasi yang benar telah dilakukan. Untuk setiap cut off probability di
atas, dapat dihitung nilai error sebagai berikut :
𝐸(𝑌|𝑋) = ∑(𝑌(𝑥𝑖) ≠ 𝑦𝑖)
𝑛
𝑖=1
(2.18)
Untuk 𝜇̂𝑖(𝑥) ≥ cut off probability maka hasil prediksi adalah 1, dan jika 𝜇̂𝑖(𝑥) <
2.11 Odds Ratio
Odds ratio merupakan ukuran risiko atau kecenderungan untuk mengalami kejadian tertentu antara satu kategori dengan kategori lainnya, didefinisikan sebagai
ratio dari odds untuk xj 1 terhadapxj 0. Odds ratio ini menyatakan risiko atau kecenderungan pengaruh observasi dengan xj 1 adalah berapa kali lipat jika dibandingkan dengan observasixj 0. Interpretasi variabel bebas yang berskala kontinu dari koefisien j pada model regresi logistik adalah setiap kenaikan c unit
pada variabel bebas akan menyebabkan risiko terjadinyay1 , adalah exp c
.j kali lebih besar.Odds ratio dilambangkan dengan 𝜃, didefinisikan sebagai perbandingan dua nilai odds xj 1 danxj 0 , sehingga:
Nilai ketergantungan model y terhadap 𝑥𝑗 dapat dilihat dalam Tabel 2.1.
Dari Tabel 2.1, maka diperoleh nilai odds ratio:
Jadi nilai exp
j dapat diartikan bahwa risiko terjadinya peristiwa1
y pada kategori xj 1 adalah sebesar exp
j risiko terjadinya peristiwa 1y pada kategorixj 0(Hosmer dan Lemeshow, 2000).
2.12 Ketepatan Klasifikasi dan nilai Press’Q
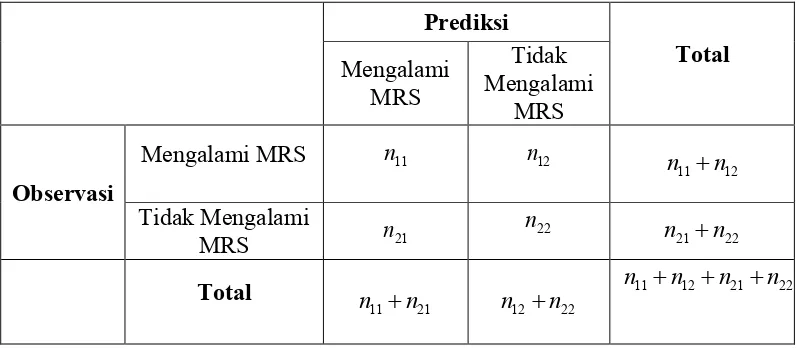
Ketepatan klasifikasi model MARS dilihat berdasarkan nilai Apparent Error Rate (APPER) yang merupakan suatu nilai yang digunakan untuk melihat peluang kesalahan dalam mengklasifikasi objek. Berikut ini disajikan hasil
Tabel 2.2. Ketepatan Klasifikasi Model MARS
Rumus yang digunakan dalam menghitung peluang kesalahan dalam
pengklasifikasian objek adalah sebagai berikut:
Untuk mengetahui kestabilan dalam ketepatan klasifikasi tentang sejauh
mana kelompok-kelompok dapat dipisahkan dengan menggunakan variabel yang
ada maka dapat diuji dengan membandingkan nilai Press’s Q dengan nilai tabel Chi
Square yang berderajat bebas 1. Untuk menguji digunakan hipotesa adalah: H0 : Hasil klasifikasi model tidak stabil/tidak konsisten
H1 : Hasil klasifikasi model stabil/konsisten
Apabila nilai Press’s Q yang diperoleh lebih besar daripada nilai Chi Square
dengan derajat bebas 1, maka H0 ditolak dan disimpulkan bahwa model yang
2 ’
1
N nK
Press sQ
N K
(2.22)
dengan
𝑁 adalah jumlah total sampel
𝑛 adalah jumlah individu yang tepat diklasifikasi
𝐾 adalah jumlah Kelompok
(Johnson dan Dean, 2007)
2.13 Software MARS
Software MARS merupakan suatu program statistik untuk menganalisis data multivariate dengan dimensi yang tinggi. Di dalam software MARS juga terdapat fungsi spline dan adaptif yang bertujuan untuk mengkontinukan suatu data,
serta terdapat interaksi dalam hubungan antar variabelnya. Data yang dijalankan
oleh software MARS antara lain data seleksi, data transformasi, deteksi interaksi, dan secara otomatis dilakukan dengan kecepatan yang tinggi.
Prosedur software MARS dibangun dari model regresi yang fleksibel oleh
fungsi spline (fungsi basis) pada interval yang berbeda dari variabel prediktor.
Kedua variabel yang digunakan pada titik akhir dari interval untuk setiap variabel
disebut knot, yang diperoleh melalui prosedur yang lengkap dengan algoritma yang
langkah. Software MARS juga dapat melakukan pencarian untuk interaksi antar variabel dimana pada setiap tingkat interaksi harus dipertimbangkan.
Model MARS yang optimal dipilih berdasarkan dua tahap. Tahap pertama
model dibangun dengan penambahan BF (efek utama yang baru, knot, atau
interaksi) sampai model tersebut optimal. Tahap kedua, BF yang memiliki
kontribusi yang kecil terhadap model yang akan dihapus sampai mencapai model
yang optimal serta ditemukan nilai variannya. Software MARS mudah digunakan
karena terdapat tampilan Graphical User Interface (GUI) sehingga pengguna dapat
mengontrol variabel bentuk fungsional serta interaksi yang digunakan.
2.14 Software R
Software R adalah suatu kesatuan software yang terintegrasi dengan beberapa fasilitas untuk manipulasi, perhitungan dan penampilan grafik yang
handal. R berbasis pada bahasa pemrograman S versi gratis sejenis S-Plus, yang
dikembangkan oleh AT dan T Bell Laboratories (sekarang Lucent Technologies)
pada akhir tahun 1970.. Software R cocok untuk riset, baik statistik, ekonomi, komputasi numerik dan pemrograman komputer.
Software R mempunyai karakteristik tersendiri, selalu dimulai dengan prompt “>” pada console-nya yang mempunyai beberapa kelebihan adalah efektif
dalam pengelolaan data dan fasilitas penyimpanan, lengkap dalam operator
dikembangkan sesuai kebutuhan dan bersifat terbuka, setiap orang dapat
menambahkan fitur tambahan dalam bentuk paket ke dalam software R.
Beberapa perintah internal yang digunakan dalam R adalah:
a. length( )
Merupakan perintah untuk menunjukkan banyaknya data.
b. matrix(a,b,c)
Merupakan perintah untuk membentuk sebuah matriks yang anggotanya a
dengan jumlah baris sebanyak b dan jumlah kolom sebanyak c.
Bentuknya: matrix(…,…,…)
c. cat( )
Merupakan perintah untuk menuliskan argumentasi dalam bentuk karakter dan
kemudian mencetak hasil atau yile yang telah ditetapkan.
Bentuknya: cat(“…”)
d. if-else
Merupakan perintah untuk menjalankan pernyataan pertama jika kondisi
benar dan pernyataan kedua akan dieksekusi jika kondisi bernilai salah.
Bentuknya: if(kondisi)
pernyataan pertama
BAB III
METODOLOGI PENELITIAN
Pada bab ini akan dijelaskan langkah analisis yang dilakukan serta sumber
data yang digunakan dalam skripsi ini.
3.1 Sumber Data
Data yang digunakan dalam skripsi ini adalah data sekunder dari hasil
rekam medis pasien anak penderita ISPA yang menjalani rawat inap di RSU Haji
Surabaya pada tahun 2015 – Mei 2016. Data yang digunakan berjumlah 60 pasien,
yaitu untuk tidak mengalami malnutrisi rumah sakit sebanyak 38 pasien dan 22
pasien untuk mengalami Malnutrisi Rumah Sakit (MRS). Data tersebut dibagi
menjadi dua, yaitu 34 pasien digunakan untuk pemodelan yang terdiri dari 19
pasien tidak MRS dan 15 pasien MRS, dan 26 pasien digunakan untuk uji
validasi, yang terdiri dari 19 pasien tidak MRS dan 7 pasien MRS.
3.2 Variabel Penelitian
Variabel penelitian yang akan digunakan dalam skripsi ini dijelaskan pada
Tabel 3.1 sebagai berikut:
Tabel 3.1. Variabel Penelitian
Variabel Keterangan Variabel Tipe
Y
Malnutrisi Rumah Sakit
Kategorik 0 untuk tidak mengalami malnutrisi rumah sakit
Lanjutan Tabel 3.1
Variabel Keterangan Tipe Variabel
X1
Jenis Kelamin
Kategorik 0 untuk laki-laki
1 untuk perempuan
X2 Lama perawatan di Rumah Sakit (Hari) Kontinu
X3 Usia pasien ketika masuk rumah sakit (Tahun) Kontinu
X4 Indeks Massa Tubuh (mmHg) Kontinu
X5
Kelas Perawatan
Kategorik 0 untuk kelas IIIA
1 untuk kelas IIA
2 untuk kelas IA (Sapire, Ruby, Emerald, Paviliun)
X6
Jenis Pasien
Kategorik 0 untuk JPS-SKM SBY
1 untuk JKN-NON PBI 2 untuk JKN-PBI 3 untuk UMUM
3.3 Langkah-langkah Analisis
Berdasarkan tujuan skripsi ini, maka dilakukan pengolahan data dengan
langkah-langkah sebagai berikut:
1. Mendeskripsikan data kejadian malnutrisi dari pasien anak penderita ISPA
yang dirawat di RSU Haji Surabaya berdasarkan faktor-faktor yang diduga
mempengaruhi dengan langkah-langkah:
a. Membuat histogram antara kejadian malnutrisi rumah sakit dengan variabel
jenis kelamin (X1), lama perawatan (X2), usia (X3), IMT (X4), Kelas
2. Mengestimasi model kejadian malnutrisi berdasarkan faktor-faktor yang
diduga mempengaruhi dengan menggunakan metode MARS dengan langkah
sebagai berikut:
a. Menentukan data yang digunakan sebagai in sample untuk memperoleh model dan sebagai out sample untuk memprediksi.
b. Menentukan nilai maksimum BF antara 12 sampai dengan 24.
c. Menentukan jumlah maksimum interaksi (MI) yaitu 1, 2, dan 3, dengan
asumsi bahwa jika MI>3 akan menghasilkan model yang semakin kompleks
dan nilai GCV akan semakin meningkat, serta menentukan minimum
observasi yaitu 0, 1, 2 dan 3.
d. Mendapatkan model terbaik dengan trial and errror sampai diperoleh model optimal dengan GCV minimum dengan rumus pada persamaan (2.13).
e. Mendapatkan model terbaik dan diubah menjadi model logit seperti
persamaan (2.14).
f. Menguji signifikansi dari koefisien fungsi basis pada model logit MARS
dengan uji serentak dan uji individu.
3. Menganalisis dan menginterpretasi model berdasarkan faktor yang
berpengaruh signifikan terhadap kejadian malnutrisi dengan menggunakan
metode MARS dengan langkah sebagai berikut:
a. Menghitung nilai APPER pada persamaan (2.21) menggunakan model
b. Mendapatkan nilai cut of probability terbaik berdasarkan nilai ketepatan klasifikasi terbesar.
c. Menghitung ketepatan klasifikasi model yang diperoleh pada data in sampel berdasarkan APPER dan menguji kestabilan klasifikasi dengan uji Press’Q dengan nilai chi-square derajat bebas 1.
d. Mengaplikasikan model MARS pada data out sample guna memprediksi dengan mensubstitusikan fungsi basis yang telah diperoleh sesuai faktor yang
mempengaruhi ke model MARS sehingga menemukan nilai peluang yang
diperoleh dengan titik potong yang telah ditentukan.
e. Menghitung ketepatan klasifikasi model yang diperoleh pada data out sampel
BAB IV
HASIL DAN PEMBAHASAN
4.1 Deskriptif Statistik Pasien Anak Penderita ISPA
Deskripstif statistik risiko kejadian malnutrisi dilakukan untuk mengetahui
karakteristik pasien anak penderita Infeksi Saluran Pernafasan Akut (ISPA). Dalam
mendeskripsikan sebaran suatu variabel, digunakan beberapa bentuk penyajian data,
yaitu dengan tabel, diagram lingkar, dan diagram batang.
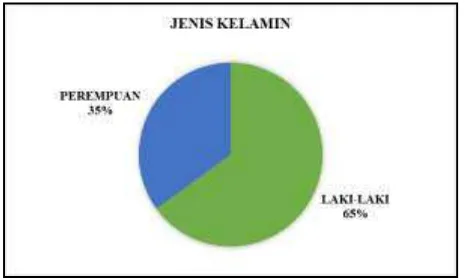
Salah satu faktor yang terkait dengan risiko kejadian malnutrisi adalah jenis
kelamin, berikut ini merupakan gambaran diagram lingkar jenis kelamin pasien
pasien anak penderita ISPA di RSU Haji Surabaya:
Gambar 4.1 Jenis Kelamin pada Pasien Anak ISPA
Berdasarkan Gambar 4.1 merupakan diagram lingkar deskripsi jenis
kelamin pasien anak ISPA di RSU Haji Surabaya, dapat diketahui bahwa jumlah
pasien berjenis kelamin perempuan sejumlah 21 pasien (35%) lebih kecil
Selain faktor jenis kelamin, faktor kelas perawatan dapat menjadi salah satu
faktor yang mempengaruhi risiko kejadian malnutrisi. Variabel kelas perawatan
disajikan pada Gambar 4.2 sebagai berikut:
Gambar 4.2 Kelas Perawatan pada Pasien Anak ISPA
Berdasarkan Gambar 4.2 merupakan diagram lingkar deskripsi kelas
perawatan pada pasien anak ISPA di RSU Haji Surabaya, bahwa jumlah pasien
kelas IIIA sejumlah 27 pasien (45%) lebih banyak dari pasien kelas IIA sejumlah
23 pasien (38%) dan lebih banyak dari pasien kelas IA sejumlah 10 pasien (17%).
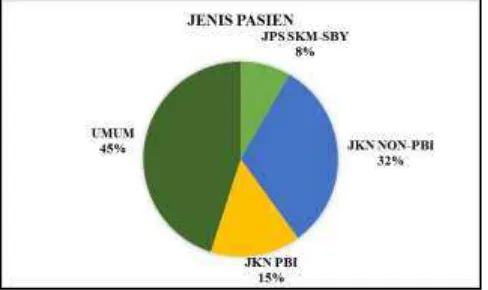
Faktor jenis pasien dapat menjadi salah satu faktor yang mempengaruhi
risiko kejadian malnutrisi. Variabel jenis pasien pada Gambar 4.3 sebagai berikut:
Berdasarkan Gambar 4.3 merupakan diagram lingkar deskripsi jenis pasien
pada pasien anak ISPA di RSU Haji Surabaya, dapat diketahui bahwa jumlah pasien
umum sejumlah 27 pasien (45%) lebih banyak dari jumlah pasien JKN Non-PBI
sejumlah 19 pasien (32%) lebih banyak dari jumlah pasien JKN PBI sejumlah 9
pasien (15%) dan lebih banyak dari jumlah pasien JPS SKM-SBY sejumlah 5
pasien (8%).
4.2 Model Regresi Logistik Biner pada Risiko Kejadian Malnutrisi Menggunakan Pendekatan MARS
Pembentukan model regresi logistik biner pada tingkat risiko kejadian
malnutrisi menggunakan pendekatan MARS dengan Basis Function (BF) yang digunakan adalah dua sampai empat kali variabel prediktor yaitu 12, 18 dan 24.
Nilai maksimum interaksi (MI) sebesar 1,2 dan 3 serta nilai minimum observasi
(MO) yang digunakan yaitu 0, 1, 2 dan 3. Berdasarkan Lampiran 3, terdapat
kombinasi dengan fungsi basis 12, maksimum interaksi dan minimum observasi
dengan melalui trial and error maka hasil yang diperoleh oleh variabel prediktor
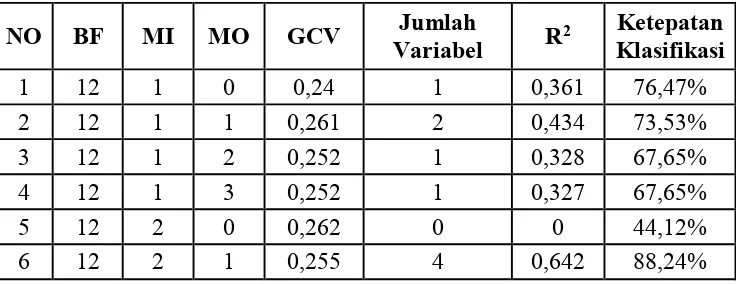
ditampilkan pada Tabel 4.1.
Tabel 4.1 Model pada Kejadian Malnutrisi dengan MARS (BF=12)
NO BF MI MO GCV Variabel Jumlah R2 Ketepatan
Klasifikasi
1 12 1 0 0,24 1 0,361 76,47%
2 12 1 1 0,261 2 0,434 73,53%
3 12 1 2 0,252 1 0,328 67,65%
4 12 1 3 0,252 1 0,327 67,65%
5 12 2 0 0,262 0 0 44,12%
Lanjutan Tabel 4.1
NO BF MI MO GCV VARIABEL JUMLAH R2 Ketepatan
Klasifikasi
7 12 2 2 0,255 4 0,642 88,24%
8 12 2 3 0,262 0 0 44,12%
9 12 3 0 0,262 0 0 44,12%
10*) 12 3 1 0,225 5 0,779 97,06%
11 12 3 2 0,255 4 0,642 88,24%
12 12 3 3 0,262 0 0 44,12%
Berdasarkan Tabel 4.1, diperoleh model MARS pada tingkat risiko kejadian
malnutrisi dengan fungsi basis 12 (dua kali jumlah variabel prediktor) diperoleh
model terbaik yaitu pada nomor 10 (BF=12, MI=3, MO= 1) yang memiliki nilai
GCV minimal sebesar 0,225 dengan R2 sebesar 0,779 dan variabel prediktor yang
masuk dalam model sebanyak 5.
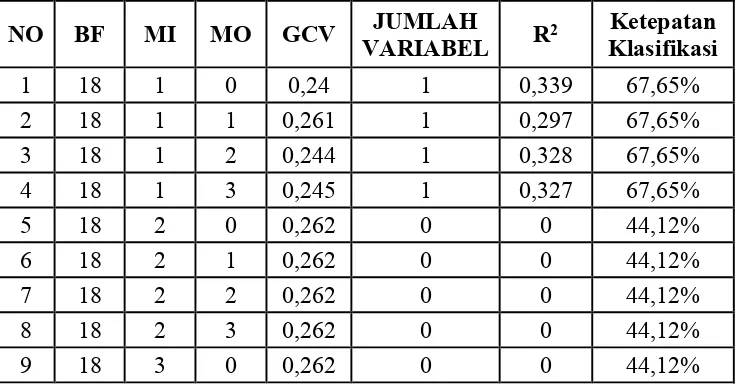
Berdasarkan Lampiran 4, terdapat kombinasi dengan fungsi basis 18,
maksimum interaksi dan minimum observasi dengan melalui trial and error maka
hasil yang diperoleh oleh variabel prediktor ditampilkan pada Tabel 4.2.
Tabel 4.2 Model pada Kejadian Malnutrisi dengan MARS (BF=18)
NO BF MI MO GCV VARIABEL JUMLAH R2 Ketepatan
Klasifikasi
1 18 1 0 0,24 1 0,339 67,65%
2 18 1 1 0,261 1 0,297 67,65%
3 18 1 2 0,244 1 0,328 67,65%
4 18 1 3 0,245 1 0,327 67,65%
5 18 2 0 0,262 0 0 44,12%
6 18 2 1 0,262 0 0 44,12%
7 18 2 2 0,262 0 0 44,12%
8 18 2 3 0,262 0 0 44,12%
Lanjutan Tabel 4.2
NO BF MI MO GCV VARIABEL JUMLAH R2 Ketepatan
Klasifikasi
10*) 18 3 1 0,236 5 0,779 97,06%
11 18 3 2 0,262 0 0 44,12%
12 18 3 3 0,262 0 0 44,12%
Berdasarkan Tabel 4.2, diperoleh model MARS pada tingkat risiko kejadian
malnutrisi dengan fungsi basis 18 (tiga kali jumlah variabel prediktor) diperoleh
model terbaik yaitu pada nomor 10 (BF= 18, MI= 3, MO= 1) yang memiliki nilai
GCV minimum sebesar 0,236 dengan R2 sebesar 0,779 dan variabel prediktor yang
masuk dalam model sebanyak 5.
Berdasarkan Lampiran 5, terdapat kombinasi dengan fungsi basis 24,
maksimum interaksi dan minimum observasi dengan melalui trial and error maka
hasil yang diperoleh oleh variabel prediktor ditampilkan pada Tabel 4.3.
Tabel 4.3 Model pada Kejadian Malnutrisi dengan MARS (BF=24)
NO BF MI MO GCV VARIABEL JUMLAH R2 Ketepatan
Klasifikasi
1 24 1 0 0,24 1 0,339 67,65%
2 24 1 1 0,261 1 0,297 67,65%
3 24 1 2 0,244 1 0,328 67,65%
4 24 1 3 0,245 1 0,327 67,65%
5 24 2 0 0,262 0 0 44,12%
6 24 2 1 0,262 0 0 44,12%
7 24 2 2 0,262 0 0 44,12%
8 24 2 3 0,262 0 0 44,12%
Lanjutan Tabel 4.3
NO BF MI MO GCV VARIABEL JUMLAH R2 Ketepatan
Klasifikasi
10*) 24 3 1 0,236 5 0,779 97,06%
11 24 3 2 0,262 0 0 44,12%
12 24 3 3 0,262 0 0 44,12%
Berdasarkan Tabel 4.3, diperoleh model MARS pada tingkat risiko kejadian
malnutrisi dengan fungsi basis 24 (empat kali jumlah variabel prediktor) diperoleh
model terbaik yaitu pada nomor 10 (BF= 24, MI= 3, MO=1) yang memiliki nilai
GCV minimum sebesar 0,236 dengan R2 sebesar 0,779 dan variabel prediktor yang
masuk dalam model sebanyak 5.
Dari keseluruhan model yang diperoleh dengan cara trial and error serta kombinasi antara nilai BF, MI dan MO untuk variabel prediktor berdasarkan nilai
GCV yang paling minimum maka model pendekatan MARS terbaik dipilih dan
dianggap paling sesuai dari model yang ada yaitu terjadi pada model nomor 10 pada
basis function 12 dengan nilai BF=12, MI=3 dan MO=1. Model MARS terbaik yang diperoleh untuk kejadian malnutrisi yaitu sebagai berikut:
0,06 0,222* 2 0,109* 5 0,126* 6 0,145* 9 0,12* 11
Y BF BF BF BF BF (4.1)
Berdasarkan dari persamaan 4.1 diperoleh model logit untuk tingkat risiko
kejadian malnutrisi pada pasien anak ISPA yaitu sebagai berikut:
0,06 0,222* 2 0,109* 5 0,126* 6 0,145* 9 0,12* 11 0,06 0,222* 2 0,109* 5 0,126* 6 0,145* 9 0,12* 11 ( )
1
BF BF BF BF BF
BF BF BF BF BF
e x
e
(4.2)
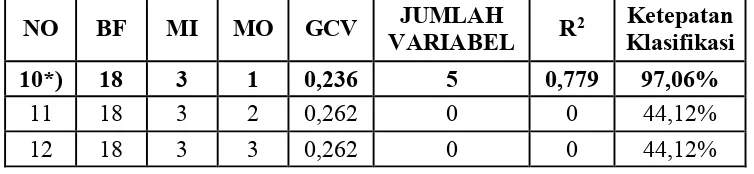
Berdasarkan Lampiran 3, pada output MARS dengan Fungsi Basis 12,
Tabel 4.4. Tingkat Kepentingan Variabel Prediktor
Variabel Tingkat Kepentingan -GCV
X5 100% 0,466
X6 82,45% 0,389
X4 39,18% 0,262
X1 21,56% 0,236
X2 21,56% 0,236
Berdasarkan pada Tabel 4.4, dapat diketahui bahwa jika variabel
X5 dimasukkan dalam model maka nilai GCV akan berkurang sebesar 0,466, X6
dimasukkan dalam model maka nilai GCV akan berkurang sebesar 0,389, X4
dimasukkan dalam model maka nilai GCV akan berkurang sebesar 0,262, X1
dimasukkan dalam model maka nilai GCV akan berkurang sebesar 0,236,
X2dimasukkan dalam model maka nilai GCV akan berkurang sebesar 0,236.
Pada Tabel 4.4, dapat diketahui juga bahwa variabel prediktor yang
berpengaruh terhadap variabel respon tingkat risiko kejadian malnutrisi yaitu kelas
perawatan (X5), jenis pasien (X6), Indeks Massa Tubuh (X4), jenis kelamin (X1),
lama perawatan (X2). Dalam penelitian ini diketahui pula tingkat kepentingan
variabel yaitu kelas perawatan sebesar 100%, jenis pasien sebesar 82,45%, Indeks
Massa Tubuh (IMT) sebesar 39,18%, jenis kelamin sebesar 21,56%, lama
perawatan sebesar 21,56%.
Berdasarkan model pada persamaan (4.1) diperoleh beberapa basis fungsi
yang terdapat interaksi tiga variabel prediktor yaitu X1, X4, X6.
Model MARS yang telah diperoleh dari keenam faktor dilakukan pengujian
a. Uji Serentak Koefisien Fungsi Basis Model MARS
Pengujian secara serentak atau bersamaan terhadap fungsi basis yang
terdapat dalam model MARS bertujuan untuk mengetahui apakah secara umum
model yang terpilih merupakan model yang sesuai dan menunjukkan hubungan
yang tepat antara variabel prediktor dan respon.
Hipotesis yang digunakan yaitu sebagai berikut:
H0 : a2=a5= a6= a9= a11=0
H1 : paling tidak ada satu aj ≠ 0
dengan aj merupakan fungsi basis yang masuk dalam model dan
j=2, 5, 6, 9, 11.
Berdasarkan hasil pengolahan MARS dapat diketahui bahwa nilai F sebesar
19,727. Informasi selengkapnya dapat dilihat pada tabel ordinary least squares results pada Lampiran 3. Dengan menggunakan α sebesar 0,05 diperoleh F0,05(5, 28)
sebesar 2,56. Daerah kritis yang dihasilkan F > F0,05(5,28), maka keputusan yang
diambil yakni menolak H0 yang artinya paling sedikit ada satu aj tidak sama dengan
nol atau dapat dinyatakan bahwa minimal terhadap satu fungsi basis ′a' yang
memuat variabel prediktor yang berpengaruh terhadap variabel respon.
b. Uji Parsial Koefisien Fungsi Basis Model MARS
Uji selanjutnya yaitu uji secara parsial atau individu yang bertujuan untuk
mengetahui apakah fungsi basis yang tebentuk mempunyai pengaruh signifikan
terhadap model, selain itu juga untuk mengetahui apakah model yang memuat
fungsi basis tersebut mampu menggambarkan keadaan data sebenarnya. Hipotesis
H0 : aj = 0
H1 : aj ≠ 0
dengan aj merupakan fungsi basis yang masuk dalam model dan
j=2, 5, 6, 9, 11. Menggunakan α sebesar 0,05 maka diperoleh nilai ttabel = t(∝ 2⁄ ,v)=
𝑡(0,025,29) sebesar 2,045. Tolak H0 apabila nilai |t| > 𝑡(0,025,29).
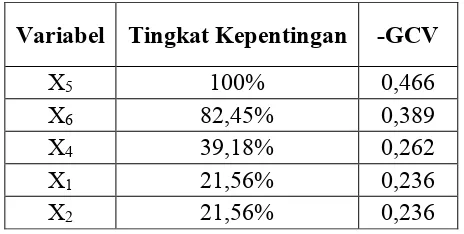
Berdasarkan Lampiran 3, pada tabel ordinary least squares results, berikut
disajikan hasil pengujian parsial model MARS pada tabel 4.5.
Tabel 4.5. Uji Parsial atau Individu Model MARS
Parameter Estimasi Standar Error tstatistik Keputusan
Basis Fungsi 2 0,222 0,028 7,821 Tolak H0
Basis Fungsi 5 -0,109 0,025 -4,344 Tolak H0
Basis Fungsi 6 -0,126 0,03 -4,218 Tolak H0
Basis Fungsi 9 0,145 0,027 5,399 Tolak H0
Basis Fungsi 11 0,12 0,016 7,408 Tolak H0
Berdasarkan Tabel 4.5, terlihat bahwa semua fungsi mempunyai nilai
signifikan sehingga keputusan yang diambil yakni menolak H0 yang berarti semua
fungsi basis dalam model berpengaruh signifikan terhadap model.
4.3 Interpretasi Fungsi Basis dalam Model MARS
Model terbaik untuk faktor yang mempengaruhi tingkat risiko kejadian
malnutrisi pada pasien anak penderita ISPA dituliskan pada persamaan (4.2).
Persamaan tersebut menggambarkan kejadian risiko kejadian malnutrisi pada
pasien anak penderita ISPA berdasarkan malnutrisi atau tidaknya pasien karena
yang mempengaruhi variabel respon, dengan melalui beberapa interaksi yang telah
dilakukan maka didapatkan banyaknya fungsi basis yang merupakan komponen
interaksi dari fungsi basis lainnya yaitu BF2, BF5, BF6, BF9, dan BF11. Model yang
tertulis pada persamaan (4.2) sebagai berikut:
1. BF1 = max(0, X4− 17,810) = {X0, X4− 17,810, untuk X4 > 17,810 4 yang lain
Artinya nilai koefisien 𝐵𝐹1 akan bernilai X4− 17,810 jika nilai X4 > 17,810
yang akan berpeluang mengalami kenaikan kejadian malnutrisi sebesar 55%, dan
lainnya akan bernilai 0 jika X4 < 17,810.
2. BF2 = max(0, 17,810 − X4) = {17,810 − X0, X4, untuk X4 < 17,810 4 yang lain
Artinya nilai koefisien 𝐵𝐹2 akan bernilai 17,810 − X4 jika nilai X4 < 17,810
yang akan berpeluang mengalami kenaikan kejadian malnutrisi sebesar 55%, maka
nilai 𝐵𝐹2 akan bernilai 0 jika 𝑋4 > 17,810 adalah seorang pasien anak penderita
ISPA yang memiliki IMT lebih dari 17,810 kg/m2.
3. BF3 = (X1 = 0) ∗ BF2
= (X1 = 0) ∗ (max(0, 17,810 − X4))
= {17,810 − X0, X4, untuk X1 = 0, X4 < 17,810
4 yang lain
Artinya nilai koefisien BF3 akan bernilai jika nilai X1 berada pada kategori 0 dan
X4 < 17,810 yang akan berpeluang mengalami kenaikan kejadian malnutrisi
sebesar 55%, maka nilai BF3 akan bernilai 0 jika X1 = 1 dan X4>17,810.
4. BF5 = max (0, X2− 5) ∗ BF3
= {1, untuk X0, X2 > 5, X1 = 0, dan X4 < 17,810
2, X1, X4 yang lain
Artinya nilai koefisien BF5 akan bernilai jika X2 lebih dari 5 hari, X1 berada pada
kategori 0, dan X4 < 17,810 yang akan berpeluang mengalami kenaikan kejadian
malnutrisi sebesar 55%, maka nilai BF5 akan bernilai 0 dengan X2 kurang dari 5
hari, 𝑋1 berada pada kategori 1, X4 lebih dari 17,810 kg/m2.
5. BF6 = max (0, 5 − X2) ∗ BF3
= max (0, 5 − X2) ∗ (X1 = 0) ∗ (max(0, 17,810 − X4))
= {1, untuk X0, X2 < 5, X1 = 0, dan X4 < 17,810
2, X1, X4 yang lain
Artinya nilai koefisien BF6 akan bernilai jika X2 kurang dari 5 hari, X1 berada
pada kategori 0, dan X4 < 17,810 yang akan berpeluang mengalami kenaikan
kejadian malnutrisi sebesar 55%, maka nilai BF6 akan bernilai 0 jika X2 > 5
adalah lama perawatan lebih dari 5 hari, 𝑋1 berada pada kategori 1, X4 lebih dari
17,810 kg/m2.
6. BF9 = (X6 = 1)*BF1
= (X6 = 1)*max(0, X4 − 17,810)
= { X0, X4− 17,810 , untuk X6=1, X4 > 17,810 4 yang lain
Artinya nilai koefisien BF9 akan bernilai jika nilai X6 berada pada kategori 1 dan
X4 > 17,810 yang akan berpeluang mengalami penurunan kejadian malnutrisi
sebesar 55% , maka nilai BF9 akan bernilai 0 jika X6 berada pada kategori 0, 2, 3
dan X4 kurang dari 17,810 kg/m2.
= (X6 = 0||X6 = 2||X6 = 3)*max(0, X4− 17,810)
= { 1 0, X, untuk X6=0, X6=2, X6=3, X4 > 17,810 4 yang lain
Artinya nilai koefisien BF10 akan bernilai 1 jika nilai X6 berada pada kategori 0, 2,
3 dan X4 > 17,810 yang akan berpeluang mengalami penurunan kejadian
malnutrisi sebesar 55%, maka nilai BF10 akan bernilai 0 jika X6 berada pada
kategori 1 dan X4 kurang dari 17,810 kg/m2.
8. BF11 = (X5 = 0)*BF10
= (X5 = 0)*(X6 = 0||X6 = 2||X6 = 3)*max(0, X4− 17,810)
= { 1 , untuk X5=0, X6=0, X6=2, X6=3, X4 > 17,810
0, X4 yang lain
Artinya nilai koefisien BF11 akan bernilai 1 jika nilai X5 berada pada kategori 0,
nilai X6 berada pada kategori 0, 2, 3 dan X4 > 17,810 yang akan berpeluang
mengalami penurunan kejadian malnutrisi sebesar 55%, maka nilai BF11 akan
bernilai 0 jika X5 berada pada kategori 1, 2 dan X6 berada pada kategori 1 dan X4
kurang dari 17,810 kg/m2.
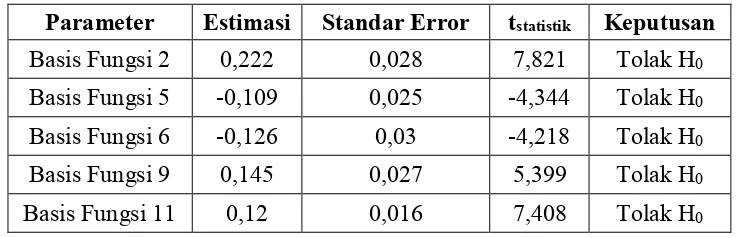
Odds ratio merupakan ukuran risiko atau kecenderungan untuk mengalami kejadian tertentu antara satu kategori dengan kategori lain. Berikut tabel odds ratio
dalam Tabel 4.6 adalah sebagai berikut:
Tabel 4.6.Odds Ratio pada Fungsi Basis No. Fungsi Basis Koefisien Odds Ratio
1 BF2 0,222 1,248
2 BF5 -0,109 0,896
3 BF6 -0,126 0,882
4 BF9 0,145 1,156