BAB II
KAJIAN PUSTAKA
A. JARINGAN SYARAF TIRUAN
1. Definisi Jaringan Syaraf Tiruan
Jaringan syaraf tiruan (artificial neural network) adalah model komputasi yang terinspirasi secara biologis, jaringan syaraf tiruan terdiri dari beberapa elemen pengolahan (neuron) dan ada hubungan antara neu-ron (Shanmuganathan, 2016). Jaringan syaraf tiruan dapat digambarkan sebagai model matematis dan komputasi untuk fungsi aproksimasi non-linear, klasifikasi data cluster dan regresi non-parametrik atau sebuah simulasi dari korelasi model syaraf biologi.
Model jaringan syaraf ditunjukkan dengan kemampuan dalam emulasi, analisis, prediksi, dan asosiasi. Kemampuan yang dimiliki jarin-gan syaraf tiruan dapat digunakan untuk belajar dan menghasilkan aturan atau operasi dari beberapa contoh atau input yang dimasukkan dan mem-buat prediksi tentang kemungkinan output yang akan muncul atau me-nyimpan karakteristik dari input yang disimpan kepada jaringan syaraf tiruan.
dikenal dan sering digunakan dalam paradigma jaringan syaraf tiruan ada-lah perambatan galat mundur / backpropagation (Hermawan, 2006).
Dalam menentukan jumlah neuron yang digunakan dalam lapisan tersembunyi terdapat beberapa aturan atau metode yaitu jumlah neuron da-lam lapisan tersembunyi baiknya diantara ukuran lapisan masukan dan lapisan keluaran, jumlah neuron dalam lapisan tersembunyi sebaiknya 2/3 dari ukuran lapisan masukan di tambah ukuran lapisan keluaran, dan jumlah neuron dalam lapisan tersembunyi sebaiknnya lebih kecil atau ku-rang dari dua kali ukuran masukan (Heaton, 2008)
2. Arsitektur Jaringan Syaraf Tiruan
Jaringan syaraf tiruan dirancang dengan menggunakan suatu aturan yang bersifat menyeluruh (general rule) dimana seluruh model jaringan memiliki konsep dasar yang sama. Arsitektur sebuah jaringan akan menen-tukan keberhasilan target yang akan dicapai karena tidak semua permasa-lahan dapat diselesaikan dengan arsitektur yang sama. Berikut macam – macam arsitektur jaringan syaraf tiruan :
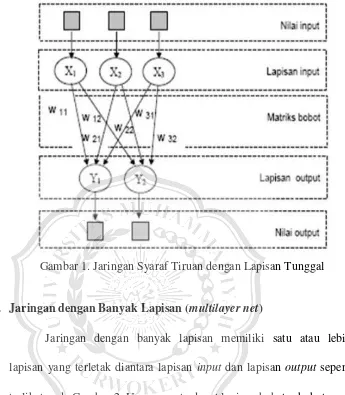
a. Jaringan dengan Lapisan Tunggal (single layer net)
Gambar 1. Jaringan Syaraf Tiruan dengan Lapisan Tunggal
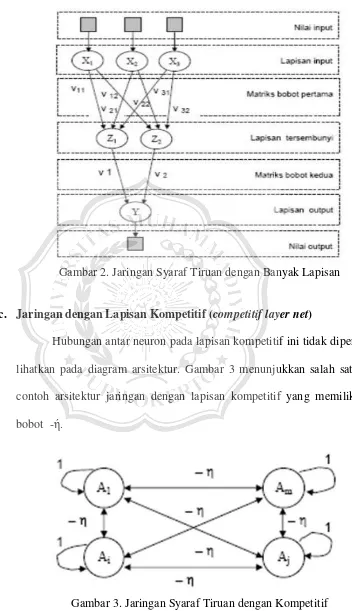
b. Jaringan dengan Banyak Lapisan (multilayer net)
Jaringan dengan banyak lapisan memiliki satu atau lebih
lapisan yang terletak diantara lapisan input dan lapisan output seperti
terlihat pada Gambar 2. Umumnya terdapat lapisan bobot – bobot yang
terletak antara 2 lapisan yang bersebelahan. Jaringan dengan banyak
lapisan dapat menyelesaikan permasalahan yang lebih sulit dari pada
Gambar 2. Jaringan Syaraf Tiruan dengan Banyak Lapisan
c. Jaringan dengan Lapisan Kompetitif (competitif layer net)
Hubungan antar neuron pada lapisan kompetitif ini tidak diper-lihatkan pada diagram arsitektur. Gambar 3 menunjukkan salah satu contoh arsitektur jaringan dengan lapisan kompetitif yang memiliki bobot -ή.
3. Implementasi Jaringan Syaraf Tiruan
Beberapa hasil penelitian implemantasi jaringan syaraf tiruan dian-taranya adalah :
a. Mustafidah, dkk. (2013a), menerapkan jaringan syaraf tiruan untuk memprediksi tingkat validitas soal dengan menggunakan algoritma pelatihan trainlm dan menghasilkan pengenalan pola data dengan memiliki kecocokan sebesar 85.54% dengan tingkat error 0.00063347. b. Menerapkan jaringan syaraf tiruan untuk prediksi prestasi belajar ma-hasiswa Program Studi Teknik Informatika Universitas Muhammadi-yah Purwokerto didasarkan atas nilai-nilai dalam mata pelajaran yang diujikan dalam Ujian Nasional saat di SLTA. Dalam penelitian ini dil-akukan pembandingan tingkat keoptimalan dari algoritma pelatihan traingd, traingdm, learngd, dan learngdm. Dengan rata-rata masing-masing algoritma yaitu learngd : 0.0215, learngdam: 0.0163, traingd : 0.0211, dan traingdm : 0.0267 (Mustafidah, dkk, 2013b).
B. ALGORITMA PEMBELAJARAN BACKPROPAGATION
Menurut Kusumadewi (2003), Backpropagation merupakan algoritma pembelajaran yang terawasi dan biasanya digunakan oleh perceptron dengan banyak lapisan untuk mengubah bobot – bobot yang terhubung dengan neuron – neuron yang ada pada lapisan tersembunyi. Algoritma backpropagation
per-ambatan maju, neuron – neuron diaktifkan dengan menggunakan fungsi akti-fasi yang dapat dideferensikan seperti sigmoid, persamaan dan perhitungan – perhitungan pada persamaan (1), (2), (3) :
( ) ... (1)
dengan : ( ) ( ) ( ) atau tangen sigmoid :
( )
atau ( )
... (2)
dengan ( ) ( ) ( ) atau purelin : ( )
( ) ... (3)
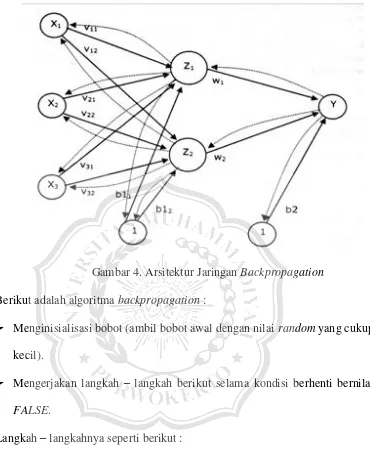
Gambar 4. Arsitektur Jaringan Backpropagation Berikut adalah algoritma backpropagation :
Menginisialisasi bobot (ambil bobot awal dengan nilai random yang cukup
kecil).
Mengerjakan langkah – langkah berikut selama kondisi berhenti bernilai
FALSE.
Langkah – langkahnya seperti berikut :
1. Untuk tiap pasangan elemen yang akan dilakukan : Feedforward :
a. Tiap – tiap unit input (Xi, i = 1,2,3,…,n) menerima sinyal dan
meneruskan sinyal tersebut kesemua unit pada lapisan yang ada diat-asnya (lapisan tersembunyi).
∑ ... (4) Kemudian gunakan fungsi aktivasi untuk menghitung sinyal output pada persamaan (5).
( ) ... (5)
Dan mengirimkan sinyal tersebut kesemua unit di lapisan atasnya (unit – unit output).
c. Tiap – tiap unit output (Yk, k = 1,2,3,…,m) menjumlahkan sinyal – sinyal input terbobot pada persamaan (6).
∑ ... (6) Gunakan fungsi aktivasi untuk menghitung sinyal output pada persamaan (7).
( ) ... (7)
Dan kirimkan sinyal tersebut ke semua unit di lapisan atasnya (unit – unit output).
Backpropagation:
d. Tiap – tiap unit output (Yk, k = 1,2,3,…,m) menerima target pola yang berhubungan dengan pola input pembelajaran, menghitung informasi error pada persamaan (8).
( ) ( ) ... (8)
Kemudian dihitung koreksi bobot (yang nantinya akan digunakan untuk memperbaiki nilai ) pada persamaan (9).
Selain itu hitung juga koreksi bias (yang nantinya akan digunakan untuk memperbaiki nilai awal ) pada persamaan (10).
... (10)
Mengirim ini ke unit – unit yang ada pada lapisan bawahnya. e. Tiap – tiap unit tersembunyi (Zj, j = 1,2,3,…,p) menjumlahkan delta
input (dari unit – unit yang berada pada lapisan atasnya) pada persa-maan (11).
∑ ... (11) Mengalikan nilai tersebut dengan turunan dari fungsi aktiva-sinya untuk menghitung informasi error pada persamaan (12).
( ) ... (12)
Kemudian menghitung koreksi bobot (yang nantinya akan digunakan untuk memperbaiki nilai ) pada persamaan (13).
... (13)
Selain itu hitung juga koreksi bias (yang nantinya akan digunakan untuk memperbaiki nilai ) pada persamaan (14).
... (14)
f. Tiap – tiap unit output (Yk, k = 1,2,3,…,p) memperbaiki bias dan b
o-botnya (j = 0,1,2,…,p) pada persamaan (15).
( ) ( ) ... (15) Tiap – tiap unit tersembunyi (Zj, j = 1,2,3,…,p) memperbaiki b i-as dan bobotnya (i = 0,1,2,3,…,n) pada persamaan (16).
Jaringan backpropagation telah dikembangkan oleh Mustafidah, dkk. (2014), yaitu menguji dengan menggunakan 12 algoritma backpropa-gation diantaranya adalah algoritma Fletcher-Reeves Update, Polak-Ribiere, Powell-Beale Restarts, Scaled Conjugate Gradient, Gradient Descent dengan Momentum dan Adaptive Learning Rate, Resilent Backpropagation, BFGS, One Step Secant, Levenberg-Marquardt, dari 12 algoritma pelatihan dipilih algoritma yang paling optimal berdasarkan pola data uji validitas.
Penelitian selanjutnya dikembangkan oleh Mustafidah & Suwarsito (2015b), yaitu menguji dengan 12 algoritma dan dipilih algoritma yang paling optimal berdasarkan error yang dihasilkan. Berdasarkan penelitian keduanya algoritma pelatihan yang paling optimal adalah algoritma pelati-han trainlm.
C. ALGORITMA LEVENBREG-MARQUARDT
Berdasarkan penelitian yang telah dilakukan oleh Mustafidah & Harjono (2017), jaringan syaraf tiruan khususnya metode backpropogation banyak digunakan untuk memecahkan masalah. Dan pada penelitian tersebut telah di uji bahwa algoritma yang paling optimal adalah algoritma Levenberg-Marquardt.
Algoritna Levenberg-Marquardt dirancang menggunakan pendekatan turunan kedua tanpa harus menghitung matriks Hessian. Apabila jaringan saraf feedforward menggunakan fungsi kinerja sum of square, maka matriks Hessian dapat didekati sebagai berikut pada persamaan (17).
H = J’ * J ... (17)
dan gradien dapat dihitung sebagai berikut pada persamaan (18).
Gw = J’ * e ... (18)
dimana J adalah matriks Jacobian yang berisi turunan pertama dari error jaringan terhadap bobot, dan e adalah suatu vektor yang berisi error jaringan. Matriks Jacobian dapat dihitung dengan teknik backpropagation standar, yang lebih sederhana dibandingkan dengan matriks Hessian.
Algoritma Levenberg-Marquardt menggunakan pendekatan untuk menghitung matriks Hessian, melalui perbaikan metode Newton pada persa-maan (19).
gradient descent dengan learning rate yang sangat kecil. Metode Newton san-gan cepat dan akurat untuk mendapatkan error minimum, oleh karena itu di-harapkan algoritma sesegera mungkin dapat mengubah nilai m menjadi 0 (Kusumadewi, 2004).
D. MEAN SQUARED ERROR (MSE)
Mean Squared Error atau disingkat dengan MSE adalah metode yang menghasilkan kesalahan – kesalahan yang kemungkinan lebih baik untuk kesalahan kecil, tetapi terkadang menghasilkan perbedaan besar. Nilai MSE dapat dianalogikan sebagai varian ditambah dengan kuadrat bias dari suatu model. Dimana adalah model yang dievaluasi dan adalah model sebenarnya. Jika tidak ada bias antara model yang dibangun dengan model sebenarnya (unbiased model), maka MSE sepadan dengan varian dari model. Semakin kecil varian suatu model, semakin robust model tersebut dalam melakukan peramalan (Lehmann, E. L. & Casella, 1998).
Perhitungan kesalahan atau error merupakan pengukuran bagaimana jaringan dapat belajar dengan baik sehingga jika dibandingkan dengan pola yang baru akan dengan mudah dikenali. Kesalahan pada keluaran jaringan merupakan selisih antara keluaran sebenarnya (current output) dan keluaran yang diinginkan (desired output). Selisih yang dihasilkan antara keduanya ditemukan dengan cara dihitung menggunakan suatu persamaan. Suatu error dapat dihitung dengan MSE (Mean Squared Error). MSE merupakan fungsi kinerja jaringan yang mengukur kinerja berdasarkan rata-rata dari kuadrat er-ror. (Kusumadewi, 2004).
∑ ∑ ( )
... (20)
= nilai keluaran jaringan syaraf
= nilai target yang diinginkan untuk setiap keluaran = jumlah seluruh pola
= jumlah keluaran
E. MATLAB
Matlab (Matrix Laboratory) merupakan salah satu bahasa pemograman yang dikembangkan oleh MathWorks.Inc. Matlab tidak hanya berfungsi se-bagai bahasa pemograman, tetapi sekaligus sese-bagai alat visualisasi, yang berhubungan langsung dengan ilmu matematika. Oleh karena itu, matlab se-makin banyak digunakan oleh para programer yang menghendaki kepraktisan dalam membuat program (Paulus & Nataliani, 2007).
Perangkat lunak ini menawarkan kemudahan dan kesederhanaan dalam menyelesaikan permasalahan yang berhubungan dengan vektor dan matriks. Memperoleh inversi dan menyelesaikan persamaan linier merupakan contoh permasalahan yang dapat dipecahkan dengan cara yang sangat singkat dan mudah sekali. Untuk menangani persoalan – persoalan spesifik, matlab me-nyediakan sejumlah toolbox yang bisa dipakai untuk mempermudah perhi-tungan, misalnya toolbox neural network yang bisa dipakai untuk fungsi – fungsi yang berkaitan dengan jaringan syaraf tiruan (Irawan, 2012).
pelatihan Backpropagation dapat menggunakan perintah trainada beberapa parameter pelatihan yang dapat digunakan diantaranya yaitu:
1. net.trainParam.show : dipakai untuk menampilkan frekuensi pe-rubahan MSE (default : setiap 25 epoh).
2. net.trainParam.epochs : dipakai untuk menentukan jumlah epoh maksimum pelatihan (default : 100 epoh).
3. net.trainParam.goal : dipakai untuk menentukan batas nilai MSE
agar iterasi dihentikan. Iterasi akan berhenti jika MSE < batas yang diten-tukan dalam net.trainParam.goal atau jumlah epoh mencapai batas
yang ditentukan dalam net.trainParam.epochs.
4. net.trainParam.lr : dipakai untuk menentukan laju pemahaman (α = learning rate). Default = 0.01. Semakin besar nilai α , semakin cepat pula proses pelatihan. Akan tetapi jika α terlalu besar, maka algoritma
menjadi tidak stabil dan mencapai titik minimum lokal.
5. net.trainParam.time : dipakai untuk membatasi lama pelatihan (dalam detik). Pelatihan akan dihentikan jika lamanya melebihi nilai yang
ditentukan dari net.trainParam.time.
F. SPSS
Sejak dikeluarkannya SPSS dengan versi under DOS sampai sekarang dengan versi under Windows, sudah dikembangkan SPSS sampai generasi atau re-lease 17 yang paling baru dengan penambahan fasilitas yang makin lengkap seperti grafik pengendali untuk Quality control dan penambahan fasilitas un-tuk link S-Plus yaitu Package Statistika terbaru yang sangat cocok untuk tujuan ilmiah dan pengembangannya, tidak hanya pengolahan data semata. SPSS berfungsi untuk membantu memproses data – data statistik secara cepat dan tepat, serta menghasilkan berbagai output yang dikehendaki oleh para pengambil keputusan. Statistik dapat diartikan sebagai suatu kegiatan yang bertujuan untuk mengumpulkan data, meringkas atau menyajikan data kemudian menganalisis data dengan menggunakan metode tertentu, dan menginterpretasikan hasil dari analisa tersebut.
G. ANAVA
dimana MST = Mean Square of Treatment MSE = Mean Square of Error