PENGARUH MODEL PEMBELAJARAN KOOPERATIF TIPE
ROUND
ROBIN BRAINSTORMING
BERBANTUAN
HYPNOTEACHING
TERHADAP KEMAMPUAN KOMUNIKASI MATEMATIS
SISWA KELAS X SMA NEGERI 3 SALATIGA
JURNAL
Disusun untuk memenuhi syarat memperoleh gelar Sarjana Pendidikan
Disusun oleh:
Merlista Suryanti Ndaong (202013087)
PROGRAM STUDI PENDIDIKAN MATEMATIKA
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS KRISTEN SATYA WACANA
SALATIGA
PENGARUH MODEL PEMBELAJARAN KOOPERATIF TIPE ROUND ROBIN BRAINSTORMING BERBANTUAN HYPNOTEACHING
TERHADAP KEMAMPUAN KOMUNIKASI MATEMATIS SISWA KELAS X SMA NEGERI 3 SALATIGA
Merlista Suryanti Ndaong1, Kriswandani2
Program Studi Pendidikan Matematika Fakultas Keguruan dan Ilmu Pendidikan Universitas Kristen Satya Wacana, Jl. Diponegoro 52-60, Salatiga 50711 1
Mahasiswa Pendidikan Matematika FKIP UKSW, email: [email protected] 2
Dosen Pendidikan Matematika FKIP UKSW, email: [email protected]
ABSTRAK
Penelitian yang berjenis penelitian eksperimen semu ini bertujuan untuk mengetahui ada tidaknya pengaruh model pembelajaran kooperatif tipe Round Robin Brainstorming berbantuan Hypnoteaching terhadap kemampuan komunikasi matematis siswa kelas X SMA Negeri 3 Salatiga. Populasi dalam penelitian ini adalah semua siswa Kelas X SMA Negeri 3 Salatiga. Teknik pengambilan sampel dilakukan dengan cluster random sampling dan diperoleh dua kelas, yaitu kelas X MIA 3 sebagai kelas eksperimen dengan jumlah 30 siswa dan kelas X MIA 4 sebagai kelas kontrol dengan jumlah 31 siswa. Desain penelitian yang digunakan adalah Nonequivalent Control Group Design. Pengumpulan data dalam penelitian ini menggunakan tes kemampuan komunikasi matematis berupa pretest dan posttest, kemudian data dianalisis menggunakan uji non parametrik Mann-Whitney. Berdasarkan hasil analisis uji non parametrik Mann-Whitney posttest diperoleh nilai signifikansi 0,000<0,05 yang berarti Model Pembelajaran Kooperatif tipe Round Robin Brainstorming berbantuan hypnoteaching berpengaruh terhadap kemampuan komunikasi matematis Siswa Kelas X SMA Negeri 3 Salatiga.
Kata Kunci: Model Pembelajaran Kooperatif tipe Round Robin Brainstorming, Hypnoteaching, Kemampuan Komunikasi Matematis
PENDAHULUAN
Matematika merupakan mata pelajaran yang penting untuk dipelajari. Hal ini terbukti
dengan diajarkannya mata pelajaran matematika pada jenjang SD, SMP maupun SMA. Sebagai
mata pelajaran yang penting, matematika memiliki beberapa tujuan. Tujuan mata pelajaran
matematika yang tertuang dalam Permendiknas Nomor 22 Tahun 2006 tentang Standar Isi adalah
agar siswa memiliki kemampuan (1) memahami konsep matematika, (2) menggunakan
penalaran, (3) memecahkan masalah, (4) mengkomunikasikan gagasan, (5) memiliki sikap
menghargai kegunaan matematika dalam kehidupan (Zaini dan Marsigit, 2014). Selain itu,
National Council of Teacher of Mathematics (NCTM) dalam Nuraeni dan Luritawaty (2016)
penalaran dan pembuktian, komunikasi matematis, keterkaitan dalam matematika, dan
representasi. Hal ini berarti bahwa komunikasi matematis merupakan salah satu kemampuan
siswa yang harus diperhatikan dalam pembelajaran matematika.
Komunikasi dalam matematika merupakan kemampuan mendasar yang harus dimiliki
pelaku dan pengguna matematika selama belajar, mengajar, dan meng-asses matematika
(Lindquist dan Elliot dalam Kusnaeni dan Retnawati, 2013). Ansari dalam Fadilah dkk (2013)
menyatakan komunikasi matematis merupakan kemampuan yang dapat menyertakan dan memuat
berbagai kesempatan siswa untuk berkomunikasi dalam bentuk merefleksikan benda-benda
nyata, gambar, atau ide-ide matematika, membuat model situasi atau persoalan menggunakan
metode tertulis, konkrit, grafik, dan aljabar, menggunakan keahlian membaca, menulis, dan
menelaah, untuk menginterpretasikan dan mengevaluasi ide-ide, simbol, istilah, serta informasi
matematika, merespon suatu pernyataan/persoalan dalam bentuk argumen yang meyakinkan.
Menurut Ontario Ministry of Education’s dalam Zaini dan Marsigit (2014), berkomunikasi
matematika adalah menyampaikan makna melalui lisan, ditulis, dan bentuk visual misalnya,
memberikan penjelasan alasan atau pembenaran hasil secara lisan atau tertulis;
mengkomunikasikan ide-ide matematika dan solusi secara tertulis, dengan menggunakan angka
dan simbol aljabar; dan secara visual, menggunakan gambar, diagram, grafik, tabel, grafik, dan
materi konkret. Ansari dalam Juanda, dkk (2014) menyatakan bahwa komunikasi matematis
merupakan: (1) kekuatan sentral bagi siswa dalam merumuskan konsep dan strategi matematika,
(2) modal keberhasilan bagi siswa terhadap pendekatan dan penyelesaian dalam eksplorasi dan
investigasi matematika, dan (3) wadah bagi siswa dalam berkomunikasi dengan temannya untuk
memperoleh informasi, membagi pikiran dan penemuan, curah pendapat, menilai dan
mempertajam ide untuk meyakinkan yang lain. Komunikasi dalam matematika menolong guru
memahami kemampuan siswa dalam menginterpretasi dan mengekspresikan pemahamannya
tentang konsep dan proses matematika yang mereka pelajari, seperti yang dikemukakan Peressini
dan Bassett dalam Sapitri dan Hartono (2015) bahwa tanpa komunikasi dalam matematika guru
akan memiliki sedikit keterangan, data, dan fakta tentang pemahaman siswa dalam melakukan
proses dan aplikasi matematika. Oleh karena itu, kemampuan komunikasi matematis siswa adalah
kemampuan siswa dalam mengkomunikasikan gagasan dengan pembicaraan lisan, catatan,
simbol, tabel, grafik, diagram, atau media lain untuk memperjelas keadaan atau masalah (Zaini
Kemampuan komunikasi matematis siswa kelas X SMA Negeri 3 Salatiga sebagian besar
berada pada kategori sedang. Dari data pretest diperoleh bahwa sebagian besar siswa dari 61
siswa yang diteliti pada kelas eksperimen (X MIA 3) dan kelas kontrol (X MIA 4) termasuk
dalam kategori kemampuan komunikasi matematis sedang yaitu sebanyak 53 orang sedangkan
kategori kemampuan komunikasi matematis tinggi sebanyak 7 orang dan 1 orang termasuk dalam
kategori kemampuan komunikasi matematis rendah. Berdasarkan hasil wawancara dan observasi
yang dilakukan, diperoleh informasi bahwa masih sedikit siswa yang berani mengemukakan ide
di kelas, sebagian besar masih diam sehingga guru harus aktif dalam memberikan
pertanyaan-pertanyaan pancingan agar siswa bisa mengemukakan pendapat. Sebagian besar siswa juga sulit
berkonsentrasi dalam belajar sehingga cukup sulit untuk mengendalikan kelas. Presentasi di kelas
pun masih didominasi oleh beberapa siswa tertentu saja yang tergolong berkemampuan akademik
cukup tinggi. Kesiapan awal siswa di sebagian besar kelas juga kurang sehingga guru harus
menunggu beberapa saat untuk menenangkan kegaduhan kelas sebelum memulai pembelajaran.
Selain itu, menyelesaikan soal cerita juga merupakan salah satu kesulitan bagi siswa karena
biasanya siswa sulit untuk menerjemahkan soal cerita ke dalam model matematika terutama
soal-soal uraian ataupun karena kebiasaan soal-soal-soal-soal ujian yang berorientasi pada soal-soal pilihan ganda
bukan pada soal uraian. Sekalipun dalam proses pembelajaran guru juga menekankan pentingnya
proses mengkomunikasikan gagasan baik lisan maupun tertulis secara sistematis namun sebagian
besar siswa masih cenderung mengutamakan hasil akhir tanpa komunikasi matematis yang
sistematis. Oleh karena itu, kemampuan komunikasi matematis ini perlu dikembangkan dalam
pembelajaran di kelas karena merupakan hal yang penting bagi guru maupun siswa.
Salah satu alernatif pembelajaran yang diduga mampu mempengaruhi kemampuan
komunikasi matematis siswa ialah dengan penggunaan model pembelajaran kooperatif
(cooperative learning) disertai metode yang tepat. Hal ini senada dengan Adun dan Iwan (Aeni,
2013) yang menyatakan bahwa salah satu alasan cooperative learning digunakan adalah ketika
akan memperbaiki kemampuan berkomunikasi siswa.
Roger, dkk dalam Huda (2014) menyatakan bahwa pembelajaran kooperatif merupakan
aktivitas pembelajaran kelompok yang diorganisir oleh satu prinsip bahwa pembelajaran harus
didasarkan pada perubahan informasi secara sosial di antara kelompok-kelompok pembelajar
yang di dalamnya setiap pembelajar bertanggung jawab atas pembelajarannya sendiri dan
pembelajaran kooperatif adalah Round Robin Brainstorming. Round Robin Brainstorming
merupakan model pembelajaran yang memberikan kesempatan kepada setiap siswa untuk
mengemukakan pendapat atau jawaban secara berurutan atas permasalahan atau pertanyaan yang
telah diajukan oleh guru sebelumnya. Sebagaimana yang dikemukakan oleh Rohmah (2015)
bahwa dalam pelaksanaan Round Robin Brainstorming, setiap siswa diharuskan menyampaikan
ide atau jawaban dari permasalahan yang diberikan. Langkah-langkah kegiatan pembelajaran
Round Robin Brainstorming dalam Tampubolon (2014) adalah (1) guru membagi kelompok
dengan anggota 4-5 orang, satu orang dalam kelompok bertugas sebagai pencatat; (2) guru
mengajukan pertanyaan/masalah dan setiap kelompok mendapat giliran menjawab pertanyaan
tersebut; (3) siswa mencatat semua jawaban dari setiap kelompok; (4) hasil catatan tersebut
didiskusikan bersama untuk mendapatkan kesimpulan akhir; dan (5) penilaian dilaksanakan
untuk keberhasilan pembelajaran. Sedangkan menurut Magre dan Joshi (2013),
langkah-langkahnya adalah sebagai berikut: (1) kelas dibagi ke dalam kelompok-kelompok kecil yang
terdiri dari 4-6 siswa per kelompok dengan satu orang ditunjuk sebagai pencatat; (2) sebuah
pertanyaan diajukan oleh guru dengan banyak kemungkinan jawaban dan siswa diberikan waktu
untuk memikirkan jawabannya, (3) setelah waktu berpikir selesai, anggota-anggota kelompok
berbagi tanggapan atau jawaban dengan gaya round robin satu sama lain; (4) pencatat menuliskan
semua jawaban dari anggota-anggota kelompok; dan (5) orang di samping pencatat (searah jarum
jam) memberikan jawaban dan pencatat menuliskannya kemudian orang lain dalam kelompok
secara berurutan (searah jarum jam) memberikan jawaban sampai waktu habis. Oleh karena itu,
model pembelajaran kooperatif tipe Round Robin Brainstorming diharapkan mampu
mempengaruhi kemampuan komunikasi matematis siswa dalam pembelajaran di kelas.
Model pembelajaran yang diharapkan mampu mempengaruhi kemampuan komunikasi
matematis siswa juga tentu harus disertai metode pembelajaran yang menyenangkan dan efektif.
Salah satu metode pembelajaran yang dapat digunakan adalah metode hypnoteaching.
Hypnoteaching yaitu menyajikan materi pelajaran dengan menggunakan bahasa-bahasa bawah
sadar dan merupakan metode baru dalam dunia pendidikan untuk mencapai keberhasilan dalam
proses kegiatan belajar mengajar (Hasbullah dan Rahmawati, 2015). Noer (2010) menyatakan
bahwa hypnoteaching merupakan perpaduan dari konsep aktivitas belajar mengajar dengan ilmu
hipnosis, sehingga dalam hypnoteaching guru menggunakan bahasa persuasif sebagai alat
proses belajar mengajar dalam hal ini yaitu hypnoteaching dapat memotivasi siswa,
meningkatkan kemampuan berkonsentrasi, kepercayaan diri, kedisiplinan dan keorganisasian.
Oleh karena itu, dapat disimpulkan bahwa pembelajaran matematika dengan model pembelajaran
kooperatif tipe Round Robin Brainstorming berbantuan hypnoteaching merupakan pembelajaran
berbasis kelompok yang diawali dengan masalah yang diberikan oleh guru dan masing-masing
siswa dalam kelompok diberi kesempatan untuk memberi tanggapan ataupun menjawab,
kemudian dalam prosesnya guru menggunakan hypnoteaching untuk memfokuskan siswa pada
pembelajaran serta mensugesti siswa dalam membangun kepercayaan diri agar siswa berani
berpendapat dan memanfaatkan kesempatan mengembangkan kemampuan komunikasi
matematisnya sebaik mungkin.
Berdasarkan permasalahan tersebut maka dapat dirumuskan tujuan penelitian ini yaitu
untuk mengetahui ada tidaknya pengaruh model pembelajaran kooperatif tipe Round Robin
Brainstorming berbantuan hypnoteaching terhadap kemampuan komunikasi matematis siswa
Kelas X SMA Negeri 3 Salatiga.
METODE PENELITIAN
Jenis penelitian ini adalah eksperimen semu (Quasi Experimental). Penelitian eksperimen
semu bertujuan untuk mendapatkan informasi dari eksperimen yang sebenarnya dalam keadaan
yang tidak memungkinkan untuk mengontrol dan atau memanipulasi semua variabel yang relevan
(Slameto, 2015:137). Hal ini senada dengan Sugiyono (2009:114) yang menyatakan bahwa
dalam eksperimen semu terdapat kelompok kontrol tetapi tidak dapat sepenuhnya mengontrol
variabel-variabel luar yang mempengaruhi pelaksanaan eksperimen. Model pembelajaran yang
akan digunakan di kelas eksperimen adalah model pembelajaran kooperatif tipe round robin
brainstorming berbantuan hypnoteaching sementara pada kelas kontrol digunakan model
pembelajaran konvensional.
Penelitian ini dilaksanakan di SMA Negeri 3 Salatiga yang terletak di Jalan Kartini No.34,
Kota Salatiga, Provinsi Jawa Tengah. Penelitian ini dilaksanakan pada Semester 2 Tahun Ajaran
2016-2017. Populasi dalam penelitian ini adalah semua siswa Kelas X SMA Negeri 3 Salatiga.
Adapun teknik pengambilan sampel dilakukan dengan cluster random sampling dan diperoleh
dua kelompok siswa, yaitu kelas X MIA 3 sebagai kelas eksperimen dengan jumlah siswa 36
30 siswa dan kelas X MIA 4 sebagai kelas kontrol dengan jumlah siswa 35 orang tetapi 4 orang
tidak mengikuti pretest sehingga jumlah siswa dalam kelas kontrol menjadi 31 orang. Desain
penelitian yang digunakan adalah Nonequivalent Control Group Design.
Pengumpulan data dalam penelitian ini menggunakan tes kemampuan komunikasi
matematis yang diberikan kepada kedua kelas. Tes ini terdiri dari pretest dan posttest. Pretest
diberikan sebelum penerapan model pembelajaran kooperatif tipe Round Robin Brainstorming,
sedangkan posttest diberikan setelah penerapan model pembelajaran kooperatif tipe Round Robin
Brainstorming. Hal ini bertujuan untuk mengetahui pengaruh model pembelajaran kooperatif tipe
Round Robin Brainstorming berbantuan Hypnoteaching terhadap kemampuan komunikasi
matematis siswa Kelas X SMA Negeri 3 Salatiga. Adapun instrumen yang digunakan dalam
penelitian ini adalah instrumen tes kemampuan komunikasi matematis yang berupa tes uraian
tertulis yang diberikan saat pretest dan posttest. Instrumen yang digunakan divalidasi terlebih
dahulu oleh para ahli (expert judgement) yaitu 1 dosen pendidikan matematika dan 2 guru
matematika.
Untuk mengetahui kemampuan komunikasi matematis siswa, penelitian ini menggunakan
rubrik penskoran hasil modifikasi oleh Kurniawan (2016) yang dibuat berdasarkan Maryland
Math Communication Rubric, Maine Holistic Rubric, dan QUASAR Communication Mathematic
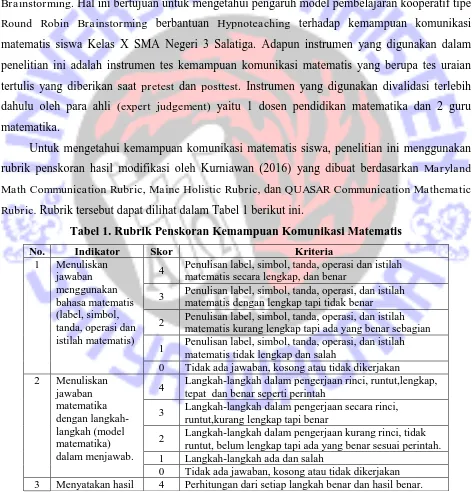
Rubric. Rubrik tersebut dapat dilihat dalam Tabel 1 berikut ini.
Tabel 1. Rubrik Penskoran Kemampuan Komunikasi Matematis No. Indikator Skor Kriteria
4 Penulisan label, simbol, tanda, operasi dan istilah matematis secara lengkap, dan benar
3 Penulisan label, simbol, tanda, operasi, dan istilah matematis dengan lengkap tapi tidak benar
2 Penulisan label, simbol, tanda, operasi, dan istilah matematis kurang lengkap tapi ada yang benar sebagian
1 Penulisan label, simbol, tanda, operasi, dan istilah matematis tidak lengkap dan salah
0 Tidak ada jawaban, kosong atau tidak dikerjakan 2 Menuliskan
4 Langkah-langkah dalam pengerjaan rinci, runtut,lengkap, tepat dan benar seperti perintah
3 Langkah-langkah dalam pengerjaan secara rinci, runtut,kurang lengkap tapi benar
2 Langkah-langkah dalam pengerjaan kurang rinci, tidak runtut, belum lengkap tapi ada yang benar sesuai perintah. 1 Langkah-langkah ada dan salah
perhitungan dari langkah-langkah setiap jawaban suatu pernyataan
3 Perhitungan dari setiap langkah 75 % benar dan hasil akhir salah
2 Perhitungan dari setiap langkah 25 % benar dan hasil salah
1 Perhitungan dari setiap langkah salah tapi ada pekerjaan, tidak kosong
0 Tidak ada jawaban, kosong atau tidak dikerjakan
PEMBAHASAN
A. Kondisi Sebelum diberi Perlakuan
Hasil pretest dan posttest kemampuan komunikasi matematis siswa yang diperoleh dari
kelas eksperimen dan kelas kontrol dikelompokkan berdasarkan tiga kategori yaitu tinggi, sedang
dan rendah. Adapun interval untuk masing-masing kategori adalah sebagai berikut jika
dimisalkan x adalah skor kemampuan komunikasi matematis yang diperoleh siswa.
Tinggi : 4 ≤ � ≤ 6
Sedang : ≤ � ≤ 4
Rendah : − ≤ � ≤ 9
Deskripsi kategori kemampuan komunikasi matematis awal (pretest) pada kelas eksperimen dan kelas kontrol dapat dilihat pada Tabel 2 sebagai berikut.
Tabel 2. Kategori Kemampuan Komunikasi Matematis Awal (Pretest)
Berdasarkan Tabel 2, diperoleh bahwa sebagian besar siswa dari kelas eksperimen maupun kelas
kontrol termasuk dalam kategori kemampuan komunikasi matematis sedang. Pada kelas
eksperimen, terdapat 3 siswa yang termasuk dalam kategori kemampuan komunikasi matematis
tinggi, 27 siswa dengan kategori kemampuan komunikasi matematis sedang dan tidak ada siswa
yang termasuk dalam kategori kemampuan komunikasi matematis rendah. Sedangkan pada kelas
kontrol dengan 31 siswa yang mengikuti pretest, 4 siswa termasuk dalam kategori kemampuan
komunikasi matematis tinggi, 26 siswa dengan kategori kemampuan komunikasi matematis
sedang dan 1 siswa termasuk dalam kategori kemampuan komunikasi matematis rendah.
Kelas N
Banyaknya Siswa pada Kategori Kemampuan Komunikasi Matematis
Tinggi Sedang Rendah
Eksperimen 30 3 27 0
Kontrol 31 4 26 1
Kemampuan komunikasi matematis untuk kondisi awal dapat diketahui perbedaannya
dengan menggunakan uji beda rerata untuk kedua kelas menggunakan statistika non parametrik
Mann-Whitney. Adapun hasil analisisnya dapat dilihat pada tabel 3.
Tabel 3. Uji Non Parametrik Mann-Whitney Skor Kemampuan Komunikasi Matematis Awal (Pretest)
Test Statisticsa
Skor Kemampuan Komunikasi Matematis
Awal Gabungan
Mann-Whitney U 356.000
Wilcoxon W 852.000
Z -1.576
Asymp. Sig.
(2-tailed) .115
a. Grouping Variable: Kode
Berdasarkan Tabel 3 terlihat bahwa nilai signifikan (2-tailed) adalah 0,115 > 0,05 sehingga dapat
disimpulkan bahwa tidak terdapat perbedaan nilai rerata untuk kedua kelas tersebut yang berarti
rata-rata kelas kontrol dan kelas eksperimen sama. Hal ini menunjukkan bahwa kedua kelas
memiliki kemampuan awal yang sama sehingga dapat diberikan perlakuan yang berbeda.
B. Kondisi Setelah diberi Perlakuan
Deskripsi hasil posttest kemampuan komunikasi matematis siswa pada kelas eksperimen
dan kelas kontrol yang telah dikategorikan dapat dilihat pada Tabel 4 berikut ini.
Tabel 4. Kategori Kemampuan Komunikasi Matematis Akhir (Posttest)
Berdasarkan Tabel 4, diperoleh hasil bahwa dari 30 siswa kelas eksperimen terdapat 20 siswa
dengan kategori kemampuan komunikasi matematis tinggi, 10 siswa dengan kategori
kemampuan komunikasi matematis sedang dan tidak ada siswa yang termasuk dalam kategori
kemampuan komunikasi matematis rendah. Sedangkan dari 31 siswa kelas kontrol terdapat 6
siswa dengan kategori kemampuan komunikasi matematis tinggi, 24 dengan kategori
Kelas N
Banyaknya Siswa pada Kategori Kemampuan Komunikasi Matematis
Tinggi Sedang Rendah
Eksperimen 30 20 10 0
Kontrol 31 6 24 1
kemampuan komunikasi matematis sedang dan 1 siswa dengan kategori kemampuan komunikasi
matematis rendah.
Uji beda rerata untuk kedua kelas menggunakan statistika non parametrik Mann-Whitney.
Hasil analisis dapat dilihat pada table 5.
Tabel 5. Uji Non Parametrik Mann-Whitney Skor Kemampuan Komunikasi Matematis Akhir (Posttest)
Test Statisticsa
Skor Kemampuan Komunikasi Matematis Akhir
Gabungan
Mann-Whitney U 157.000
Wilcoxon W 653.000
Z -4.449
Asymp. Sig.
(2-tailed) .000
a. Grouping Variable: Kode
Berdasarkan Tabel 5 terlihat bahwa nilai signifikan (2-tailed) adalah 0,000 < 0,05 sehingga dapat
disimpulkan terdapat perbedaan nilai rerata untuk kedua kelas tersebut yang berarti rata-rata kelas
kontrol dan kelas eksperimen berbeda. Pada pretest jumlah siswa kelas eksperimen yang
termasuk dalam kategori kemampuan komunikasi matematis tinggi adalah 3 siswa sedangkan
pada posttest meningkat menjadi 20 siswa. Begitupun dengan kelas kontrol, jumlah siswa yang
termasuk kategori kemampuan komunikasi matematis tinggi pada pretest yaitu 4 siswa
meningkat menjadi 6 siswa pada posttest. Hal ini menunjukkan bahwa kemampuan komunikasi
matematis siswa pada kedua kelas mengalami peningkatan. Hal ini dapat diartikan bahwa setelah
diberi perlakuan, kemampuan komunikasi matematis siswa kelas eksperimen lebih baik daripada
kemampuan komunikasi matematis siswa kelas kontrol, sehingga dapat disimpulkan bahwa
model pembelajaran kooperatif tipe round robin brainstorming berbantuan hypnoteaching
berpengaruh terhadap kemampuan komunikasi matematis siswa kelas X SMA Negeri 3 Salatiga.
KESIMPULAN
Berdasarkan hasil penelitian dan pembahasan maka dapat disimpulkan bahwa model
pembelajaran kooperatif tipe round robin brainstorming berbantuan hypnoteaching berpengaruh
terhadap kemampuan komunikasi matematis siswa kelas X SMA Negeri 3 Salatiga. Hal ini
terlihat dari nilai signifikan uji Mann-Whitney adalah 0,000 < 0,05 yang menunjukkan bahwa
peningkatan kemampuan komunikasi matematis yang signifikan pada kelas eksperimen (siswa
berkemampuan komunikasi matematis tinggi sebanyak 3 siswa meningkat menjadi 20 siswa)
dibandingkan dengan kelas kontrol (siswa berkemampuan komunikasi matematis tinggi sebanyak
4 siswa meningkat menjadi 6 siswa).
DAFTAR PUSTAKA
Aeni, Nur. 2013. Perbandingan Hasil Belajar Tipe-Tipe Model Kooperatif dalam Pembelajaran Bilangan Pecahan pada Siswa Kelas VII SMP Negeri 1 Patampanua Kabupaten Pinrang. Tugas Akhir Program Magister (TAPM). Jakarta: Universitas Terbuka. [Online]. Diunduh dari http://www.pustaka.ut.ac.id/dev25/pdftesis2/41377.pdf pada 21 Juli 2016, pukul 09:58 WIB.
Fadilah dkk. 2013. Kemampuan komunikasi Matematis siswa Sekolah Menengah Pertama dan Madrasah Tsanawiyah pada Materi Fungsi di P. Brandan Kabupaten Langkat. Dalam Jurnal Pendidikan Matematika PARADIKMA, Volume 5, Nomor 2. [Online]. Diunduh dari http://download.portalgaruda.org/article.php?article=148990&val=5571&title=KEMAMP UAN%20%20KOMUNIKSI%20%20MATEMATIS%20%20SISWA%20SEKOLAH%20 %20MENENGAH%20%20PERTAMA%20%20DAN%20MADRASAH%20%20%20TSA NAWIYAH%20%20%20%20PADA%20%20MATERI%20FUNGSI%20DI%20P.BRAN DAN%20KABUPATEN%20LANGKAT pada 22 Mei 2016 pukul 01:08 WIB.
Hasbullah dan Eva Yuni Rahmawati. 2015. Pengaruh penerapan metode hypnoteaching terhadap motivasi belajar mahasiswa universitas Indraprasta PGRI. Dalam Jurnal Formatif, Volume 5, Nomor 1. [Online]. Diunduh dari http://journal.lppmunindra.ac.id/index.php/Formatif/article/viewFile/163/156 pada 30 Mei 2016 pukul 01:44 WIB.
Huda, Miftahul. 2014. Cooperative Learning – Metode, Teknik, Struktur dan Model Terapan. Yogyakarta: Pustaka Pelajar.
Jaya, Novian Triwidia. 2010. Hypnoteaching “Bukan Sekedar Mengajar”. Bekasi: D-Brain.
Juanda, M., dkk. 2014. Peningkatan Kemampuan Pemecahan Masalah dan Komunikasi Matematis Siswa SMP melalui Model Pembelajaran Means-ends Analysis (MeA). Dalam Jurnak Kreano FMIPA UNNES, Volume 5, Nomor 2, Desember 2014. [Online]. Diunduh dari
http://download.portalgaruda.org/article.php?article=350712&val=5678&title=Peningkatan %20Kemampuan%20Pemecahan%20Masalah%20dan%20Komunikasi%20Matematis%20 Siswa%20SMP%20melalui%20Model%20Pembelajaran%20Means-ends%20Analysis pada 23 Juni 2016 pukul 16:47 WIB.
http://repository.uksw.edu/bitstream/123456789/9866/2/T1_202012065_Full%20text.pdf pada 23 Januari 2017, pukul 06:24 WIB.
Kusnaeni dan Heri Retnawati. 2013. Problem Possing dalam Setting Kooperatif Tipe TAI Ditinjau dari Kemampuan Komunikasi dan Pemecahan Masalah. Dalam Pythagoras: Jurnal Pendidikan Matematika, Volume 8, Nomor 1, Juni 2013. Diunduh dari http://journal.uny.ac.id/index.php/pythagoras/article/viewFile/8492/7005 pada 23 Juni 2016, pukul 16:48 WIB.
Magre, Sunita dan Susheel Joshi. 2013. Co-operative Learning: Theorical Bases and Its Types. Dalam Golden Reserach Thoughts Volume 2, Issue. 11, May 2013. [Online]. Diunduh dari http://aygrt.isrj.org/UploadedData/2425.pdf pada 28 Juni 2016 pukul 11:15 WIB.
Noer, Muhammad. 2010. Hypnoteaching for Succes Learning. Yogyakarta: Pedagogia.
Nuraeni, Reni dan Irena Puji Luritawaty. 2016. Mengembangkan Kemampuan Komunikasi Matematik Siswa. Dalam Jurnal Mosharafa – Jurnal Pendidikan Matematika STKIP Garut, Volume 8, Nomor 2, April 2016. Diunduh dari http://jurnalmtk.stkip-garut.ac.id/data/edisi8/vol2/Reni.pdf pada 30 Juli 2016 pukul 21:32 WIB.
Rohmah, Maya Siti. 2015. Pendekatan Brainstorminground-robin untuk meningkatkan kemampuan komunikasi matematis siswa SMP. Dalam Infinity - Jurnal Ilmiah Program Studi Matematika STKIP Siliwangi Bandung, Volume 4, Nomor 2, September 2015.
[Online]. Diunduh dari
http://e-journal.stkipsiliwangi.ac.id/index.php/infinity/article/view/82/79 pada 30 Mei 2016 pukul 20:21 WIB.
Sapitri dan Hartono. 2015. Keefektifan Cooperative Learning STAD dan GI ditinjau dari Kemampuan Berpikir Kritis dan Komunikasi Matematis. Dalam Jurnal Riset Pendidikan Matematika, Volume 2, Nomor 2, November 2015. [Online]. Diunduh dari http://journal.uny.ac.id/index.php/jrpm/article/viewFile/7346/6328 pada 21 Mei 2016 pukul 23:23 WIB.
Slameto. 2015. Metodologi Penelitian dan Inovasi Pendidikan. Salatiga: Satya Wacana University Press.
Sugiyono. 2009. Metode Penelitian Pendidikan (Pendekatan Kuantitatif, Kualitatif, dan R&D). Bandung: Alfabeta.
Tampubolon, Saur. 2014. Penelitian Tindakan Kelas sebagai Pengembangan Profesi Pendidik dan Keilmuan. Jakarta: Erlangga.
Zaini, Ahmad dan Marsigit. 2014. Perbandingan Keefektifan Pembelajaran Matematika dengan Pendekatan Matematika Realistik dan Konvensional ditinjau dari Kemampuan Penalaran dan Komunikasi Matematik Siswa. Dalam Jurnal Riset Pendidikan Matematika, Volume 1,
Nomor 2, November 2014. [Online]. Diunduh dari: