commit to user
BAB IV
HASIL DAN PEMBAHASAN
Pada bab ini disajikan deskripsi data, k-means clustering, uji stasioneri-tas data masing-masing cluster, orde model VAR, model VAR-GSTAR dengan pembobot normalisasi korelasi silang, serta validasi model. Selanjutnya model VAR-GSTAR dengan pembobot normalisasi korelasi silang diterapkan pada data curah hujan di 29 Kabupaten/Kotamadya Jawa Tengah.
4.1
Deskripsi Data
Pada subbab ini dijelaskan deskripsi data curah hujan di 29 kabupaten/kota madya di Jawa Tengah yang diperoleh dari BMKG kelas I. Data curah hujan digu-nakan untuk menerapkan model VAR-GSTAR sebanyak 1392 data. Data curah hujan tertinggi berada di Kabupaten Purbalingga sebesar 1919 mm dan data curah hujan terendah bernilai 0 yang berarti pada daerah tersebut tidak turun hujan. Rata-rata curah hujan bulanan tertinggi berada di Kabupaten Pekalongan sebesar 374.938 mm. Sebaran data curah hujan tertinggi di Kota Pekalongan ka-rena Kota Pekalongan memiliki simpangan baku terbesar sebesar 359.883 mm.
Efek saling mempengaruhi antar lokasi dilihat dari nilai korelasi data curah yang tinggi. Oleh karena itu data curah hujan di 29 Kabupaten/Kotamadya Jawa Tengah dapat digunakan untuk menerapkan model VAR-GSTAR.
4.2
2-means Clustering
Data curah hujan bulanan 29 kabupaten/kotamadya di Jawa Tengah me-miliki keragaman tinggi sehingga diperlukan clustering. Hal ini diperlukan
un-commit to user
hampir sama. Metode yang dipergunakan dalam clustering adalah k-means (Mac-Queen, [11]), dengan jarak euclidean sebagai ukuran kesamaan objek yang ditun-jukkan pada persamaan (2.1).
Ukuran yang dipertimbangkan untuk merepresentasikan karakteristik curah hujan, digunakan ukuran tinggi dan rendah. Oleh karena itu, ditentukan k seba-nyak 2 cluster. Berdasarkan pewilayahan dengan k-means clustering ditentukan k sebanyak 2 cluster.
Cara menentukan karakteristik curah hujan menggunakan jarak euclidean. Untuk menentukan jarak euclidean pada masing-masing lokasi diawali dengan menentukan 2 pusat cluster terlebih dahulu. Setelah menentukan 2 pusat cluster kemudian menghitung jarak euclidean. Hal ini dilakukan secara berulang hingga diperoleh pusat cluster bernilai tetap.
Berdasarkan pengelompokkan curah hujan dengan 2-means clustering, ter-bentuk 2 cluster yaitu cluster rendah dan cluster tinggi. Cluster rendah me-nerangkan wilayah dengan curah hujan rendah, sedangkan cluster tinggi mene-rangkan wilayah curah hujan tinggi yang ditunjukkan pada Tabel 4.1.
Tabel 4.1. Wilayah curah hujan dengan 2-means untuk masing-masing cluster
Cluster Wilayah
Rendah Brebes, Tegal, Pemalang, Batang, Kendal, Demak, Jepara, Kudus, Pati, Grobogan, Rembang, Blora
Sragen, Karanganyar, Klaten, Wonogiri, Kota Semarang Tinggi Cilacap, Banyumas, Purbalingga, Pekalongan,
Banjarnegara, Kebumen, Wonosobo, Purworejo,
Temanggung, Magelang, Kabupaten Semarang, Boyolali
Hasil pewilayahan curah hujan di Jawa Tengah dengan 2-means cluste-ring pada Tabel 4.1 menunjukkan bahwa cluster rendah terdiri atas 17 kabupa-ten/kotamadya dan cluster tinggi terdiri atas 12 kabupakabupa-ten/kotamadya. Untuk memperjelas hasil penyebaran wilayah curah hujan yang merupakan hasil dari 2-means clustering ditunjukkan pada Gambar 4.1 .
commit to user
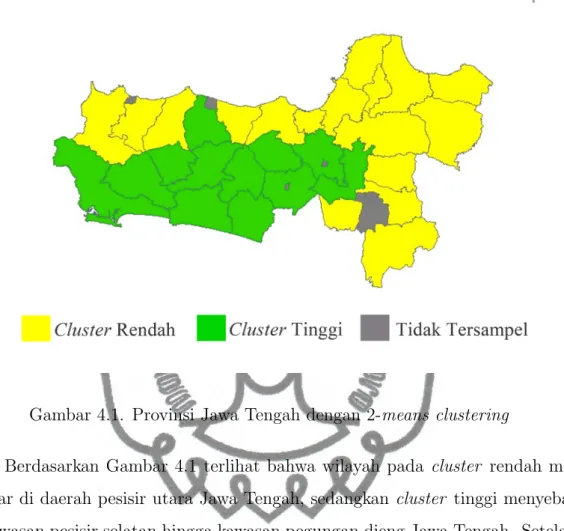
Gambar 4.1. Provinsi Jawa Tengah dengan 2-means clustering
Berdasarkan Gambar 4.1 terlihat bahwa wilayah pada cluster rendah me-nyebar di daerah pesisir utara Jawa Tengah, sedangkan cluster tinggi meme-nyebar di kawasan pesisir selatan hingga kawasan pegungan dieng Jawa Tengah. Setelah terbentuk 2 cluster, data curah hujan pada masing-masing cluster dapat diterap-kan dalam model VAR-GSTAR. Dalam menerapditerap-kan data tersebut, kestasioneran data harus dipenuhi.
4.3
Uji Stasioneritas Data
Asumsi yang digunakan pada model VAR-GSTAR adalah data stasioner. Untuk mengetahui kestasioneran data curah hujan pada masing-masing cluster digunakan statistik uji IPS sesuai persamaan (2.3). Dalam uji IPS digunakan nilai ADF dari masing masing lokasi. Nilai ADF diperoleh dari persamaan (2.4). Nilai ADF pada masing-masing lokasi untuk cluster rendah ditunjukkan pada
commit to user
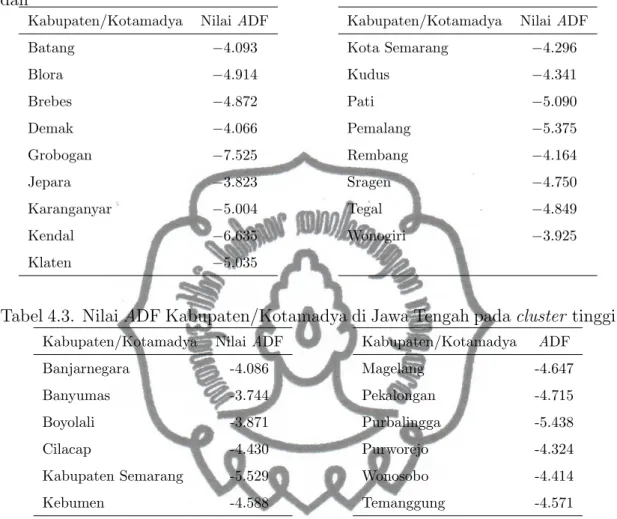
Tabel 4.2. Nilai ADF Kabupaten/Kotamadya di Jawa Tengah pada cluster ren-dah
Kabupaten/Kotamadya Nilai ADF Kabupaten/Kotamadya Nilai ADF
Batang −4.093 Kota Semarang −4.296
Blora −4.914 Kudus −4.341 Brebes −4.872 Pati −5.090 Demak −4.066 Pemalang −5.375 Grobogan −7.525 Rembang −4.164 Jepara −3.823 Sragen −4.750 Karanganyar −5.004 Tegal −4.849 Kendal −6.635 Wonogiri −3.925 Klaten −5.035
Tabel 4.3. Nilai ADF Kabupaten/Kotamadya di Jawa Tengah pada cluster tinggi
Kabupaten/Kotamadya Nilai ADF Kabupaten/Kotamadya ADF
Banjarnegara -4.086 Magelang -4.647
Banyumas -3.744 Pekalongan -4.715
Boyolali -3.871 Purbalingga -5.438
Cilacap -4.430 Purworejo -4.324
Kabupaten Semarang -5.529 Wonosobo -4.414
Kebumen -4.588 Temanggung -4.571
Berdasarkan Tabel 4.2 dan Tabel 4.3, kemudian ditentukan nilai uji IPS menggunakan persamaan (2.3) dengan α = 0.05 yang ditunjukkan pada Tabel 4.4.
Tabel 4.4. Nilai uji IPS untuk masing-masing cluster Cluster Cluster Rendah Cluster Tinggi nilai IPS (t) −4.868 −4.529
nilai t 1.960 1.960
Tabel 4.4 menunjukkan bahwa cluster rendah dan cluster tinggi memiliki nilai|t| > 1.960. Dengan demikian, data curah hujan untuk cluster 1 dan cluster 2 menunjukkan bahwa H0 ditolak. Hal ini berarti data curah hujan
commit to user
4.4
Orde Model VAR
Penentuan orde waktu model VAR-GSTAR diperoleh dari orde model VAR. Orde model VAR ditentukan dengan panjang lag optimal berdasarkan nilai AIC terkecil (2.7). Nilai AIC untuk masing-masing lag disajikan pada Tabel 4.5.
Tabel 4.5. Nilai AIC masing-masing lag pada cluster tinggi dan cluster rendah AIC
Cluster lag 0 lag 1 lag 2 Rendah 200.452 195.272
-Tinggi 151.835 152.290 149.694
Berdasarkan Tabel 4.5 menunjukkan bahwa nilai AIC ditampilkan hanya pada lag-lag tertentu. Hal ini dikarenakan nilai AIC pada lag-lag selanjutnya memiliki nilai yang berulang seperti lag-lag sebelumnya. Menurut Wutsqa dan Suhartono [6] untuk mengidentifikasi orde waktu dalam model VAR-GSTAR di-gunakan nilai AIC terkecil dari orde model VAR. Oleh karena itu orde waktu model VAR-GSTAR pada cluster rendah adalah 1 dan cluster tinggi adalah 2.
4.5
Model VAR-GSTAR dengan Pembobot Normalisasi
Korelasi Silang
Pada penelitian ini dipilih pembobot normalisasi korelasi silang, karena me-nurut Suhartono dan Atok [18], pembobot tersebut memberikan semua kemung-kinan hubungan antar ruang. Pembobot normalisasi korelasi silang yang digu-nakan untuk model VAR-GSTAR diperoleh dari nilai korelasi data curah hujan setiap lokasi dengan lokasi lain sesuai persamaan (2.5). Nilai korelasi masing-masing lokasi diperoleh dengan menghitung persamaan (2.6). Pada Tabel 4.6 ditunjukkan nilai korelasi 5 lokasi pada cluster rendah.
commit to user
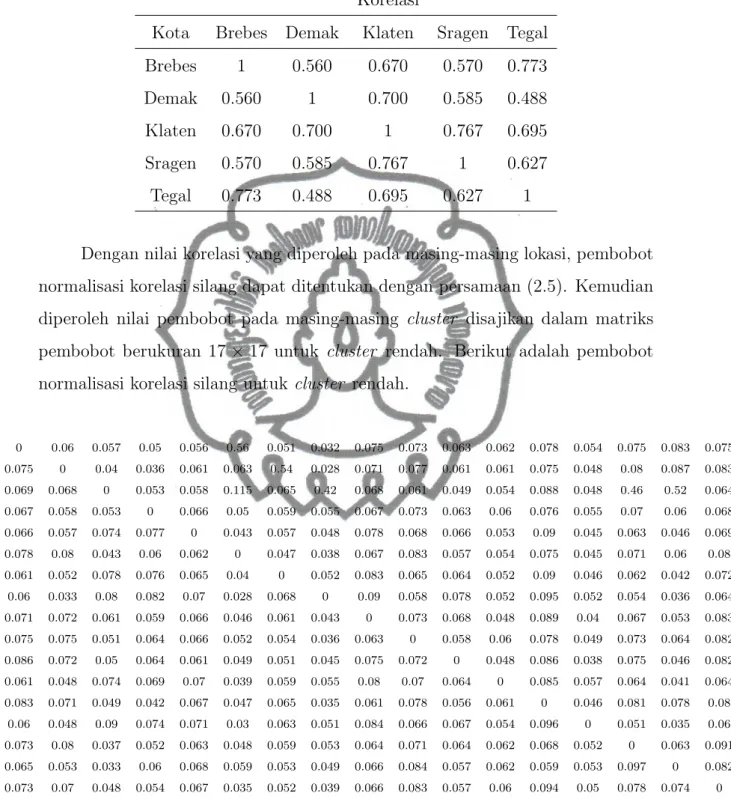
Tabel 4.6. Nilai korelasi 5 lokasi pada cluster rendah Korelasi
Kota Brebes Demak Klaten Sragen Tegal
Brebes 1 0.560 0.670 0.570 0.773
Demak 0.560 1 0.700 0.585 0.488
Klaten 0.670 0.700 1 0.767 0.695
Sragen 0.570 0.585 0.767 1 0.627
Tegal 0.773 0.488 0.695 0.627 1
Dengan nilai korelasi yang diperoleh pada masing-masing lokasi, pembobot normalisasi korelasi silang dapat ditentukan dengan persamaan (2.5). Kemudian diperoleh nilai pembobot pada masing-masing cluster disajikan dalam matriks pembobot berukuran 17× 17 untuk cluster rendah. Berikut adalah pembobot normalisasi korelasi silang untuk cluster rendah.
W1(1) = 0 0.06 0.057 0.05 0.056 0.56 0.051 0.032 0.075 0.073 0.063 0.062 0.078 0.054 0.075 0.083 0.075 0.075 0 0.04 0.036 0.061 0.063 0.54 0.028 0.071 0.077 0.061 0.061 0.075 0.048 0.08 0.087 0.083 0.069 0.068 0 0.053 0.058 0.115 0.065 0.42 0.068 0.061 0.049 0.054 0.088 0.048 0.46 0.52 0.064 0.067 0.058 0.053 0 0.066 0.05 0.059 0.055 0.067 0.073 0.063 0.06 0.076 0.055 0.07 0.06 0.068 0.066 0.057 0.074 0.077 0 0.043 0.057 0.048 0.078 0.068 0.066 0.053 0.09 0.045 0.063 0.046 0.069 0.078 0.08 0.043 0.06 0.062 0 0.047 0.038 0.067 0.083 0.057 0.054 0.075 0.045 0.071 0.06 0.08 0.061 0.052 0.078 0.076 0.065 0.04 0 0.052 0.083 0.065 0.064 0.052 0.09 0.046 0.062 0.042 0.072 0.06 0.033 0.08 0.082 0.07 0.028 0.068 0 0.09 0.058 0.078 0.052 0.095 0.052 0.054 0.036 0.064 0.071 0.072 0.061 0.059 0.066 0.046 0.061 0.043 0 0.073 0.068 0.048 0.089 0.04 0.067 0.053 0.083 0.075 0.075 0.051 0.064 0.066 0.052 0.054 0.036 0.063 0 0.058 0.06 0.078 0.049 0.073 0.064 0.082 0.086 0.072 0.05 0.064 0.061 0.049 0.051 0.045 0.075 0.072 0 0.048 0.086 0.038 0.075 0.046 0.082 0.061 0.048 0.074 0.069 0.07 0.039 0.059 0.055 0.08 0.07 0.064 0 0.085 0.057 0.064 0.041 0.064 0.083 0.071 0.049 0.042 0.067 0.047 0.065 0.035 0.061 0.078 0.056 0.061 0 0.046 0.081 0.078 0.08 0.06 0.048 0.09 0.074 0.071 0.03 0.063 0.051 0.084 0.066 0.067 0.054 0.096 0 0.051 0.035 0.06 0.073 0.08 0.037 0.052 0.063 0.048 0.059 0.053 0.064 0.071 0.064 0.062 0.068 0.052 0 0.063 0.091 0.065 0.053 0.033 0.06 0.068 0.059 0.053 0.049 0.066 0.084 0.057 0.062 0.059 0.053 0.097 0 0.082 0.073 0.07 0.048 0.054 0.067 0.035 0.052 0.039 0.066 0.083 0.057 0.06 0.094 0.05 0.078 0.074 0 .
Berdasarkan matriks pembobot pada cluster 1, nilai pembobot W13 pada
daerah 1 dan 3 untuk satu periode sebelumnya memiliki hubungan sebesar 0.057. Selain pada cluster rendah, nilai korelasi juga dihitung untuk cluster tinggi. Nilai
commit to user korelasi pada cluster tinggi ditunjukkan pada Tabel 4.7.
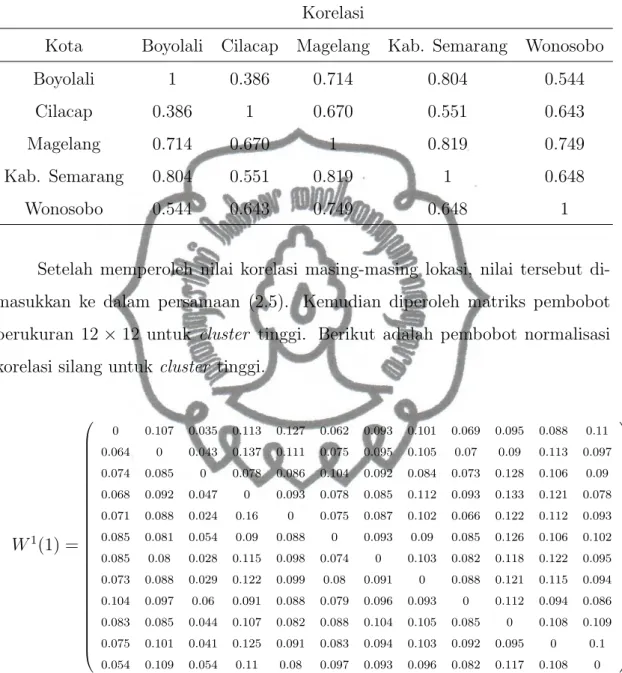
Tabel 4.7. Nilai korelasi 5 lokasi pada cluster tinggi Korelasi
Kota Boyolali Cilacap Magelang Kab. Semarang Wonosobo
Boyolali 1 0.386 0.714 0.804 0.544
Cilacap 0.386 1 0.670 0.551 0.643
Magelang 0.714 0.670 1 0.819 0.749
Kab. Semarang 0.804 0.551 0.819 1 0.648
Wonosobo 0.544 0.643 0.749 0.648 1
Setelah memperoleh nilai korelasi masing-masing lokasi, nilai tersebut di-masukkan ke dalam persamaan (2.5). Kemudian diperoleh matriks pembobot berukuran 12× 12 untuk cluster tinggi. Berikut adalah pembobot normalisasi korelasi silang untuk cluster tinggi.
W1(1) = 0 0.107 0.035 0.113 0.127 0.062 0.093 0.101 0.069 0.095 0.088 0.11 0.064 0 0.043 0.137 0.111 0.075 0.095 0.105 0.07 0.09 0.113 0.097 0.074 0.085 0 0.078 0.086 0.104 0.092 0.084 0.073 0.128 0.106 0.09 0.068 0.092 0.047 0 0.093 0.078 0.085 0.112 0.093 0.133 0.121 0.078 0.071 0.088 0.024 0.16 0 0.075 0.087 0.102 0.066 0.122 0.112 0.093 0.085 0.081 0.054 0.09 0.088 0 0.093 0.09 0.085 0.126 0.106 0.102 0.085 0.08 0.028 0.115 0.098 0.074 0 0.103 0.082 0.118 0.122 0.095 0.073 0.088 0.029 0.122 0.099 0.08 0.091 0 0.088 0.121 0.115 0.094 0.104 0.097 0.06 0.091 0.088 0.079 0.096 0.093 0 0.112 0.094 0.086 0.083 0.085 0.044 0.107 0.082 0.088 0.104 0.105 0.085 0 0.108 0.109 0.075 0.101 0.041 0.125 0.091 0.083 0.094 0.103 0.092 0.095 0 0.1 0.054 0.109 0.054 0.11 0.08 0.097 0.093 0.096 0.082 0.117 0.108 0
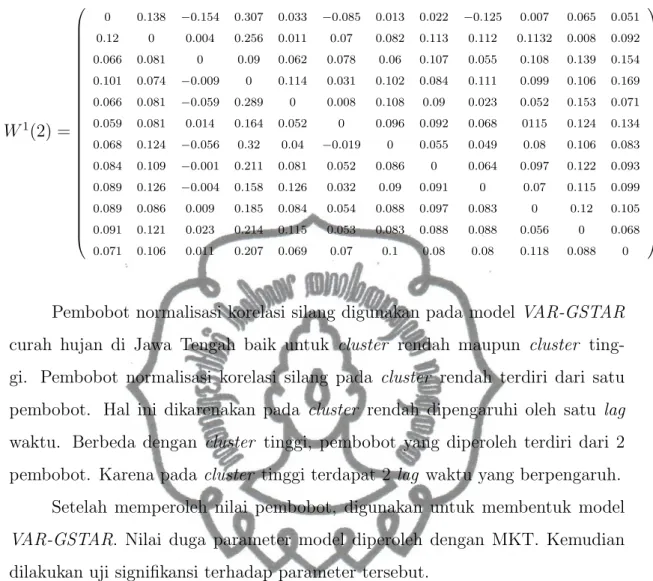
commit to user W1(2) = 0 0.138 −0.154 0.307 0.033 −0.085 0.013 0.022 −0.125 0.007 0.065 0.051 0.12 0 0.004 0.256 0.011 0.07 0.082 0.113 0.112 0.1132 0.008 0.092 0.066 0.081 0 0.09 0.062 0.078 0.06 0.107 0.055 0.108 0.139 0.154 0.101 0.074 −0.009 0 0.114 0.031 0.102 0.084 0.111 0.099 0.106 0.169 0.066 0.081 −0.059 0.289 0 0.008 0.108 0.09 0.023 0.052 0.153 0.071 0.059 0.081 0.014 0.164 0.052 0 0.096 0.092 0.068 0115 0.124 0.134 0.068 0.124 −0.056 0.32 0.04 −0.019 0 0.055 0.049 0.08 0.106 0.083 0.084 0.109 −0.001 0.211 0.081 0.052 0.086 0 0.064 0.097 0.122 0.093 0.089 0.126 −0.004 0.158 0.126 0.032 0.09 0.091 0 0.07 0.115 0.099 0.089 0.086 0.009 0.185 0.084 0.054 0.088 0.097 0.083 0 0.12 0.105 0.091 0.121 0.023 0.214 0.115 0.053 0.083 0.088 0.088 0.056 0 0.068 0.071 0.106 0.011 0.207 0.069 0.07 0.1 0.08 0.08 0.118 0.088 0 .
Pembobot normalisasi korelasi silang digunakan pada model VAR-GSTAR curah hujan di Jawa Tengah baik untuk cluster rendah maupun cluster ting-gi. Pembobot normalisasi korelasi silang pada cluster rendah terdiri dari satu pembobot. Hal ini dikarenakan pada cluster rendah dipengaruhi oleh satu lag waktu. Berbeda dengan cluster tinggi, pembobot yang diperoleh terdiri dari 2 pembobot. Karena pada cluster tinggi terdapat 2 lag waktu yang berpengaruh.
Setelah memperoleh nilai pembobot, digunakan untuk membentuk model VAR-GSTAR. Nilai duga parameter model diperoleh dengan MKT. Kemudian dilakukan uji signifikansi terhadap parameter tersebut.
Uji signifikansi parameter memiliki hipotesis H0 : parameter-parameter
lo-kasi tidak signifikan dan H1 : parameter-parameter lokasi signifikan. Keputusan
uji sigifikansinya yaitu H0 ditolak apabila nilai|thitung| > t(α2;n) dengan α = 0.05.
Karena terdapat paling tidak satu parameter ruang waktu yang tidak signifikan, seperti pada Tabel 4.8 kolom ke-4 untuk cluster rendah (halaman 27) dan Tabel 4.9 kolom ke-8 untuk cluster tinggi (halaman 27), dilakukan regresi stepwise.
Tabel 4.10 (halaman28) menunjukkan hasil pendugaan parameter dengan metode stepwise, begitu pula pada Tabel 4.11 (halaman 28). Semua parameter ruang waktu masing-masing cluster yang diperoleh dari regresi dengan metode stepwise telah signifikan. Hal ini dilihat dari nilai thitung dengan taraf sigifikansi
commit to user T ab el 4.8. P endugaan parameter dan uji signifik ansi mo del V AR-GST AR (1 1 ) pada cluster rendah P arameter Nilai duga thitung Kesimpulan P arameter Nilai duga thitung Kesimpulan c ϕ 1 10 − 0 .054 − 0 .240 Tidak signifik an c ϕ 1 11 0.570 3.000 Signifik an c ϕ 2 10 0.176 0.880 Tidak signifik an c ϕ 2 11 0.478 2.450 Signifik an c ϕ 3 10 0.362 1.940 Tidak signifik an c ϕ 3 11 0.355 1.850 Tidak signifik an c ϕ 4 10 0.413 1.370 Tidak signifik an c ϕ 4 11 0.182 0.740 Tidak signifik an c ϕ 5 10 − 0 .110 − 0 .510 Tidak signifik an c ϕ 5 11 0.897 3.320 Signifik an c ϕ 6 10 0.732 4.070 Signifik an c ϕ 6 11 -0.050 − 0 .240 Tidak signifik an c ϕ 7 10 0.158 0.980 Tidak signifik an c ϕ 7 11 0.541 2.620 Signifik an c ϕ 8 10 0.194 1.240 Tidak signifik an c ϕ 8 11 0.388 2.070 Signifik an c ϕ 9 10 − 0 .072 − 0 .260 Tidak signifik an c ϕ 9 11 0.852 2.750 Signifik an c ϕ 10 10 0.381 1.290 Tidak signifik an c ϕ 10 11 0.345 1.170 Tidak signifik an c ϕ 11 10 − 0 .008 − 0 .030 Tidak signifik an c ϕ 11 11 0.720 2.480 Signifik an c ϕ 12 10 − 0 .089 − 0 .470 Tidak signifik an c ϕ 12 11 1.092 3.760 Signifik an c ϕ 13 10 − 0 .170 − 0 .890 Tidak signifik an c ϕ 13 11 1.317 4.890 Signifik an c ϕ 14 10 − 0 .115 − 0 .640 Tidak signifik an c ϕ 14 11 0.788 3.630 Signifik an c ϕ 15 10 0.221 1.180 Tidak signifik an c ϕ 15 11 0.522 2.630 Signifik an c ϕ 16 10 0.048 0.230 Tidak signifik an c ϕ 16 11 0.615 2.880 Signifik an c ϕ 17 10 0.340 1.270 Tidak signifik an c ϕ 17 11 0.362 1.420 Tidak signifik an
commit to user T ab el 4.9. P endugaan parameter dan uji signifik ansi mo del V AR-GST AR (21 ) pada cluster tinggi P arameter Nilai duga thitung Kesimpulan P arameter Nilai duga thitung Kesimpulan c ϕ 1 10 0.493 2.050 Signifik an c ϕ 1 20 − 0 .302 − 1 .480 Tidak signifik an c ϕ 2 10 0.349 1.620 Tidak signifik an c ϕ 2 20 − 0 .013 − 0 .060 Tidak signifik an c ϕ3 10 − 0 .086 − 0 .680 Tidak signifik an c ϕ3 20 0.178 1.630 Tidak signifik an c ϕ4 10 0.257 2.040 Signifik an c ϕ4 20 − 0 .194 − 1 .650 Tidak signifik an c ϕ5 10 − 0 .148 − 0 .740 Tidak signifik an c ϕ5 20 − 0 .021 − 0 .120 Tidak signifik an c ϕ 6 10 0.665 2.280 Signifik an c ϕ 6 20 − 0 .060 − 0 .210 Tidak signifik an c ϕ 7 10 0.116 0.500 Tidak signifik an c ϕ 7 20 − 0 .322 − 1 .590 Tidak signifik an c ϕ 8 10 0.055 0.250 Tidak signifik an c ϕ 8 20 0.089 0.430 Tidak signifik an c ϕ 9 10 0.405 1.450 Tidak signifik an c ϕ 9 20 − 0 .359 − 1 .360 Tidak signifik an c ϕ 10 10 0.334 0.970 Tidak signifik an c ϕ 10 20 − 0 .184 − 0 .550 Tidak signifik an c ϕ 11 10 0.294 0.860 Tidak signifik an c ϕ 11 20 − 0 .508 − 1 .460 Tidak signifik an c ϕ 12 10 0.330 2.070 Signifik an c ϕ 12 20 − 0 .105 − 0 .640 Tidak signifik an c ϕ1 11 0.067 0.890 Tidak signifik an c ϕ1 21 0.244 1.080 Tidak signifik an c ϕ2 11 0.404 1.660 Tidak signifik an c ϕ2 21 − 0 .212 − 0 .880 Tidak signifik an c ϕ3 11 1.239 4.030 Signifik an c ϕ3 21 − 0 .831 − 3 .370 Signifik an c ϕ 4 11 1.308 5.430 Signifik an c ϕ 4 21 − 0 .239 − 0 .800 Tidak signifik an c ϕ 5 11 1.003 3.810 Signifik an c ϕ 5 21 − 0 .218 − 0 .850 Tidak signifik an c ϕ 6 11 0.237 0.600 Tidak signifik an c ϕ 6 21 − 0 .284 − 0 .800 Tidak signifik an c ϕ 7 11 0.683 2.590 Signifik an c ϕ 7 21 0.038 0.330 Tidak signifik an c ϕ 8 11 1.242 3.330 Signifik an c ϕ 8 21 − 0 .556 − 1 .860 Tidak signifik an c ϕ 9 11 0.340 1.190 Tidak signifik an c ϕ 9 21 0.093 0.390 Tidak signifik an c ϕ 10 11 0.594 1.660 Tidak signifik an c ϕ 10 21 − 0 .206 0.710 Tidak signifik an c ϕ11 11 0.551 1.760 Tidak signifik an c ϕ11 21 0.102 0.360 Tidak signifik an c ϕ12 11 0.751 3.020 Signifik an c ϕ12 21 − 0 .370 − 1 .720 Tidak signifik an
commit to user
Tabel 4.10. Pendugaan parameter signifikan dan thitung model VAR-GSTAR (11)
pada cluster rendah menggunakan metode stepwise
Parameter Nilai duga thitung Parameter Nilai duga thitung
c ϕ110 0.389 3.070 ϕc1510 0.529 5.170 c ϕ2 10 0.478 4.320 ϕc 16 10 0.457 4.360 c ϕ5 10 0.484 5.470 ϕc311 0.547 5.090 c ϕ7 10 0.457 5.320 ϕc411 0.360 3.370 c ϕ9 10 0.545 5.540 ϕc611 0.567 5.150 c ϕ11 10 0.509 4.900 ϕc811 0.451 4.180 c ϕ12 10 0.514 7.100 ϕc1011 0.571 5.250 c ϕ13 10 0.604 7.640 ϕc1711 0.530 4.920 c ϕ14 10 0.390 4.300
Tabel 4.11. Pendugaan parameter signifikan dan thitung model VAR-GSTAR (21)
pada cluster tinggi menggunakan metode stepwise
Parameter Nilai duga thitung Parameter Nilai duga thitung
c ϕ1 10 0.522 4.368 ϕc711 0.608 6.578 c ϕ2 10 0.581 6.020 ϕc811 1.350 6.441 c ϕ6 10 0.647 7.334 ϕd1111 0.523 5.778 c ϕ9 10 0.584 5.439 ϕc1211 0.745 3.036 c ϕ10 10 0.620 6.153 ϕc420 -0.188 -2.163 c ϕ12 10 0.316 1.990 ϕc321 -0.609 -2.848 c ϕ3 11 1.151 5.199 ϕc821 -0.448 -2.269 c ϕ411 1.514 9.857 ϕc1221 -0.421 -2.254 c ϕ5 11 0.677 7.394
Karena semua parameter ruang waktu yang telah signifikan, model VAR-GSTAR untuk cluster rendah dan tinggi mudah diperoleh. Agar lebih jelas model 2.2 dituliskan kembali yaitu, Zi(t) =
∑p k=1 ∑λs l=0 ∑n i=1Φ i klW l(k)Z i(t− k) + ei(t).
commit to user b ZBre b ZT eg b ZBat b ZBlo b ZDem b ZGrob b ZJ ep b ZRem b ZKen b ZKla b ZKotse b ZKud b ZP em b ZP at b ZKra b ZSra b ZW on = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.633 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.587 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.670 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.457 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.679 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.663 ZBre(t− 1) ZT eg(t− 1) ZBat(t− 1) ZBlo(t− 1) ZDem(t− 1) ZGrob(t− 1) ZJ ep(t− 1) ZRem(t− 1) ZKen(t− 1) ZKla(t− 1) ZKotse(t− 1) ZKud(t− 1) ZP em(t− 1) ZP at(t− 1) ZKra(t− 1) ZSra(t− 1) ZW on(t− 1) + 0.503 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.597 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.743 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.683 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.747 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.683 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.936 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1.07 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.638 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.697 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.629 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
commit to user 0 0.06 0.057 0.05 0.056 0.56 0.051 0.032 0.075 0.073 0.063 0.062 0.078 0.054 0.075 0.083 0.075 0.075 0 0.04 0.036 0.061 0.063 0.54 0.028 0.071 0.077 0.061 0.061 0.075 0.048 0.08 0.087 0.083 0.069 0.068 0 0.053 0.058 0.115 0.065 0.42 0.068 0.061 0.049 0.054 0.088 0.048 0.46 0.52 0.064 0.067 0.058 0.053 0 0.066 0.05 0.059 0.055 0.067 0.073 0.063 0.06 0.076 0.055 0.07 0.06 0.068 0.066 0.057 0.074 0.077 0 0.043 0.057 0.048 0.078 0.068 0.066 0.053 0.09 0.045 0.063 0.046 0.069 0.078 0.08 0.043 0.06 0.062 0 0.047 0.038 0.067 0.083 0.057 0.054 0.075 0.045 0.071 0.06 0.08 0.061 0.052 0.078 0.076 0.065 0.04 0 0.052 0.083 0.065 0.064 0.052 0.09 0.046 0.062 0.042 0.072 0.06 0.033 0.08 0.082 0.07 0.028 0.068 0 0.09 0.058 0.078 0.052 0.095 0.052 0.054 0.036 0.064 0.071 0.072 0.061 0.059 0.066 0.046 0.061 0.043 0 0.073 0.068 0.048 0.089 0.04 0.067 0.053 0.083 0.075 0.075 0.051 0.064 0.066 0.052 0.054 0.036 0.063 0 0.058 0.06 0.078 0.049 0.073 0.064 0.082 0.086 0.072 0.05 0.064 0.061 0.049 0.051 0.045 0.075 0.072 0 0.048 0.086 0.038 0.075 0.046 0.082 0.061 0.048 0.074 0.069 0.07 0.039 0.059 0.055 0.08 0.07 0.064 0 0.085 0.057 0.064 0.041 0.064 0.083 0.071 0.049 0.042 0.067 0.047 0.065 0.035 0.061 0.078 0.056 0.061 0 0.046 0.081 0.078 0.08 0.06 0.048 0.09 0.074 0.071 0.03 0.063 0.051 0.084 0.066 0.067 0.054 0.096 0 0.051 0.035 0.06 0.073 0.08 0.037 0.052 0.063 0.048 0.059 0.053 0.064 0.071 0.064 0.062 0.068 0.052 0 0.063 0.091 0.065 0.053 0.033 0.06 0.068 0.059 0.053 0.049 0.066 0.084 0.057 0.062 0.059 0.053 0.097 0 0.082 0.073 0.07 0.048 0.054 0.067 0.035 0.052 0.039 0.066 0.083 0.057 0.06 0.094 0.05 0.078 0.074 0 ZBre(t− 1) ZT eg(t− 1) ZBat(t− 1) ZBlo(t− 1) ZDem(t− 1) ZGrob(t− 1) ZJ ep(t− 1) ZRem(t− 1) ZKen(t− 1) ZKla(t− 1) ZKotse(t− 1) ZKud(t− 1) ZP em(t− 1) ZP at(t− 1) ZKra(t− 1) ZSra(t− 1) ZW on(t− 1) .
commit to user b ZCil b ZBys b ZP ur b ZP ek b ZBan b ZKeb b ZW sb b ZP wj b ZT em b ZM ag b ZKase b ZBoy = 0.522 0 0 0 0 0 0 0 0 0 0 0 0 0.581 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.647 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.584 0 0 0 0 0 0 0 0 0 0 0 0 0.620 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.320 ZCil(t− 1) ZBys(t− 1) ZP ur(t− 1) ZP ek(t− 1) ZBan(t− 1) ZKeb(t− 1) ZW sb(t− 1) ZP wj(t− 1) ZT em(t− 1) ZM ag(t− 1) ZKase(t− 1) ZBoy(t− 1) + 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1.151 0 0 0 0 0 0 0 0 0 0 0 0 1.514 0 0 0 0 0 0 0 0 0 0 0 0 0.677 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.608 0 0 0 0 0 0 0 0 0 0 0 0 1.350 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.523 0 0 0 0 0 0 0 0 0 0 0 0 0.745 0 0.107 0.035 0.113 0.127 0.062 0.093 0.101 0.069 0.095 0.088 0.11 0.064 0 0.043 0.137 0.111 0.075 0.095 0.105 0.07 0.09 0.113 0.097 0.074 0.085 0 0.078 0.086 0.104 0.092 0.084 0.073 0.128 0.106 0.09 0.068 0.092 0.047 0 0.093 0.078 0.085 0.112 0.093 0.133 0.121 0.078 0.071 0.088 0.024 0.16 0 0.075 0.087 0.102 0.066 0.122 0.112 0.093 0.085 0.081 0.054 0.09 0.088 0 0.093 0.09 0.085 0.126 0.106 0.102 0.085 0.08 0.028 0.115 0.098 0.074 0 0.103 0.082 0.118 0.122 0.095 0.073 0.088 0.029 0.122 0.099 0.08 0.091 0 0.088 0.121 0.115 0.094 0.104 0.097 0.06 0.091 0.088 0.079 0.096 0.093 0 0.112 0.094 0.086 0.083 0.085 0.044 0.107 0.082 0.088 0.104 0.105 0.085 0 0.108 0.109 0.075 0.101 0.041 0.125 0.091 0.083 0.094 0.103 0.092 0.095 0 0.1 0.054 0.109 0.054 0.11 0.08 0.097 0.093 0.096 0.082 0.117 0.108 0 ZCil(t− 1) ZBys(t− 1) ZP ur(t− 1) ZP ek(t− 1) ZBan(t− 1) ZKeb(t− 1) ZW sb(t− 1) ZP wj(t− 1) ZT em(t− 1) ZM ag(t− 1) ZKase(t− 1) ZBoy(t− 1)
commit to user 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 −0.188 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ZCil(t− 2) ZBys(t− 2) ZP ur(t− 2) ZP ek(t− 2) ZBan(t− 2) ZKeb(t− 2) ZW sb(t− 2) ZP wj(t− 2) ZT em(t− 2) ZM ag(t− 2) ZKase(t− 2) ZBoy(t− 2) + 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 −0.0609 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 −0.448 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 −0.421 0 0.138 −0.154 0.307 0.033 −0.085 0.013 0.022 −0.125 0.007 0.065 0.051 0.12 0 0.004 0.256 0.011 0.07 0.082 0.113 0.112 0.1132 0.008 0.092 0.066 0.081 0 0.09 0.062 0.078 0.06 0.107 0.055 0.108 0.139 0.154 0.101 0.074 −0.009 0 0.114 0.031 0.102 0.084 0.111 0.099 0.106 0.169 0.066 0.081 −0.059 0.289 0 0.008 0.108 0.09 0.023 0.052 0.153 0.071 0.059 0.081 0.014 0.164 0.052 0 0.096 0.092 0.068 0115 0.124 0.134 0.068 0.124 −0.056 0.32 0.04 −0.019 0 0.055 0.049 0.08 0.106 0.083 0.084 0.109 −0.001 0.211 0.081 0.052 0.086 0 0.064 0.097 0.122 0.093 0.089 0.126 −0.004 0.158 0.126 0.032 0.09 0.091 0 0.07 0.115 0.099 0.089 0.086 0.009 0.185 0.084 0.054 0.088 0.097 0.083 0 0.12 0.105 0.091 0.121 0.023 0.214 0.115 0.053 0.083 0.088 0.088 0.056 0 0.068 0.071 0.106 0.011 0.207 0.069 0.07 0.1 0.08 0.08 0.118 0.088 0 ZCil(t− 2) ZBys(t− 2) ZP ur(t− 2) ZP ek(t− 2) ZBan(t− 2) ZKeb(t− 2) ZW sb(t− 2) ZP wj(t− 2) ZT em(t− 2) ZM ag(t− 2) ZKase(t− 2) ZBoy(t− 2)
Model VAR-GSTAR (11) pada cluster rendah dan VAR-GSTAR (21)
pa-da cluster tinggi dengan pembobot normalisasi korelasi silang digunakan untuk validasi data curah hujan bulan September 2014 sampai Desember 2014.
4.6
Asumsi White Noise Model VAR-GSTAR untuk 2
Cluster
Setelah memperoleh model VAR-GSTAR pada masing-masing cluster, di-lakukan uji untuk asumsi sisaan bersifat white noise dan medi-lakukan validasi mo-del. Hasil sisaan yang diperoleh dari model VAR-GSTAR untuk masing-masing cluster dilakukan pengujian sisaan white noise. Uji white noise yang digunakan
commit to user
Tabel 4.12. Nilai LB pada model VAR-GSTAR (11) pada cluster rendah
Lag 1 2 3
Nilai LB 19.631 20.954 23.347
χ2
(0.095;k) 0.004 0.103 0.352
Kesimpulan white noise white noise white noise
Tabel 4.13. Nilai LB pada model VAR-GSTAR (21) pada cluster tinggi
Lag 1 2 3
Nilai LB 1.227 2.541 2.554
χ2
(0.095;k) 0.004 0.103 0.352
Kesimpulan white noise white noise white noise
Berdasarkan Tabel 4.12 dan 4.13, model VAR-GSTAR (11) pada cluster 1
dan VAR-GSTAR (21) pada cluster 2 memiliki sisaan white noise. Kemudian
se-telah masing-masing model memiliki sisaan white noise, dilakukan validasi model menggunakan RMSE untuk mengetahui ukuran kebaikan model.
4.7
Validasi Model VAR-GSTAR untuk 2 Cluster
Setelah masing-masing model pada setiap cluster memiliki sisaan white noi-se, kemudian dilakukan validasi model. Validasi model digunakan sebagai ukuran kebaikan model. Salah satu cara validasi model dengan menentukan nilai RSME. Besarnya nilai RMSE dihitung berdasarkan persamaan (2.10). Data curah hujan di Jawa Tengah memiliki nilai RMSE yaitu 173.312 untuk cluster 1 dan 203.272 untuk cluster 2. Karena nilai RMSE bernilai ratusan dengan data mencapai ribuan, nilai RMSE dikatakan kecil sehingga model baik untuk digunakan.