Teori dan Contoh Pengembangan Soal-soal Daya Matematis *

(1)

*Disampaikan dalam workshop Peningkatan Kompetensi Pedagogik Mahasiswa Pendidikan Matematika, UIN Sunan Gunung Djati, Bandung, 16 Juli 2016

1

Teori dan Contoh Pengembangan Soal-soal Daya Matematis*

Al Jupri

Departemen Pendidikan Matematika, FPMIPA, Universitas Pendidikan Indonesia

e-mail: aljupri@upi.edu

Abstrak

Artikel ini mengulas secara praktis tentang cara mengembangkan soal-soal daya matematis. Pengembangan soal ini diperlukan sebab aspek-aspek daya matematis sangat relevan dengan tujuan pembelajaran matematika yang tertuang dalam kurikulum di Indonesia. Sebagai landasan teoretis pengembangan soal, aspek-aspek daya matematis, seperti pemecahan masalah, penalaran, koneksi dan komunikasi matematis, diuraikan secara secara ringkas dan seperlunya. Selanjutnya, kami sajikan cara-cara praktis — seperti teknik adopsi, adaptasi dan kreasi mandiri — beserta contohnya dalam mengembangkan soal-soal daya matematis. Di bagian akhir, kami simpul dan diskusikan aspek teoretis dan praktis dari aktivitas pengembangan soal, baik sebagai acuan untuk proses pembelajaran maupun untuk penelitian di masa yang akan datang. Dengan cara ini, kami berharap artikel ini dapat bermanfaat bagi peningkatan kompetensi pedagogik dan profesional para (calon) guru matematika.

Kata Kunci: Daya matematis, komunikasi matematis, koneksi matematis, pemecahan masalah, penalaran matematis.

1. Pengantar

Ditinjau dari sisi kognitif penguasaan materi matematika, ada empat tujuan pembelajaran yang perlu dicapai, yaitu siswa diharapkan dapat: (1) menjelaskan dan menggunakan keterkaitan antar konsep dalam pemecahan masalah; (2) menggunakan penalaran dalam mengidentifikasi pola, membuat generalisasi dan menyusun bukti matematis; (3) melakukan pemecahan masalah; dan (4) mengomunikaskan gagasan dengan menggunakan simbol, tabel, diagram atau media lain yang relevan (Dediknas, 2006). Secara ringkas keempat tujuan pembelajaran ini berturut-turut disebut sebagai kemampuan koneksi matematis, penalaran matematis, pemecahan masalah dan komunikasi matematis. Sedangkan bila ditinjau dari sisi afektif, tujuan pembelajaran matematika adalah agar siswa dapat memiliki sikap positif – seperti ulet, percaya diri, rasa ingin tahu, perhatian, dan minat – terhadap matematika. Bila kita cermati dengan seksama, lima tujuan pembelajaran tersebut serupa dengan aspek-aspek daya matematis (mathematical power) yang tertuang dalam dokumen National Council of Teachers of Mathematics tahun 1989 (NCTM, 1989). Dengan demikian, secara sederhana, kita dapat mengatakan bahwa tujuan pembelajaran matematika yang perlu digapai siswa Indonesia adalah aspek-aspek daya matematis.

(2)

2

Sebagai tujuan pembelajaran, aspek-aspek daya matematis tersebut perlu dipupuk dan dikembangkan guru agar dikuasai para siswa. Cara untuk mencapai ini, salah satunya, adalah dengan menyediakan soal-soal matematika yang mencakup aspek-aspek tersebut dalam proses pembelajaran matematika di kelas. Namun demikian, para guru, yang seringkali masih bergantung pada uraian buku teks dan terbiasa menerapkan pendekatan pengajaran tradisional, mengalami kesulitan dalam menyelesaikan dan mengembangkan permasalahan matematika yang menuntut kemampuan pemecahan masalah, penalaran dan komunikasi matematis (Jupri, Drijvers & Van den Heuvel-Panhuizen, 2014; Sembiring, Hadi & Dolk, 2008). Hal ini menimbulkan satu pertanyaan penting yang perlu segera dicari pemecahannya: Bagaimanakah cara mengembangkan soal-soal matematika yang memuat aspek kemampuan pemecahan masalah, penalaran dan komunikasi matematis? Dengan perkataan lain, kita perlu mencari cara untuk mengembangkan soal-soal daya matematis yang dapat diterapgunakan dalam proses pembelajaran.

Untuk menjawab pertanyaan tersebut, artikel ini mengajukan gagasan praktis yang dapat diterapkan guru dalam pengembangan soal-soal daya matematis, khususnya untuk empat aspek yang mengukur kemampuan kognitif penguasaan materi. Aspek disposisi matematis tidak dibahas dalam artikel ini sebab hal tersebut merupakan sisi afektif sebagai akibat dari berbagai aspek lainnya. Untuk tujuan ini, pertama kami ulas secara ringkas tentang keempat aspek daya matematis. Kemudian, kami sajikan cara-cara pengembangan soal beserta contoh-contohnya. Dan akhirnya, kami simpul dan diskusikan aspek teoretis dan praktis pengembangan soal-soal tersebut.

2. Daya Matematis

Menurut NCTM (NCTM, 1989) daya matematis yang perlu dievaluasi meliputi kemampuan siswa dalam hal: menerapkan pengetahuan dan keterampilan dalam menyelesaikan permasalahan baik dalam matematika ataupun di luar matematika (aspek pemecahan masalah); menggunakan bahasa matematis untuk mengomunikasikan gagasan (aspek komunikasi matematis); menggunakan penalaran dan analisis (aspek penalaran matematis); pengetahuan dan pemahaman terhadap kaitan antar konsep dan prosedur matematis (aspek koneksi matematis); dan disposisi terhadap matematika. Proses mengevaluasi daya matematis tak hanya mengukur tentang banyaknya pengetahuan yang dimiliki siswa, tetapi juga mencakup seberapa jauh siswa dapat mengintegrasikan berbagai aspek daya matematis tersebut secara fleksibel, misalnya, kapan perlu menerapkan

(3)

3

penalaran, kapan pula perlu mengomunikasikan gagasan, dan seterusnya dalam situasi yang relevan.

Meskipun proses mengevaluasi aspek-aspek daya matematis itu tak bisa secara terpisah dan terisolasi, beberapa peneliti (seperti Kastberg, D’Ambrosio, Mcdermott & Saada, 2005; Rowan & Robles, 1998) menyarankan penggunaan, misalnya, pertanyaan-pertanyaan yang dapat menggali tiap aspek daya matematis secara spesifik. Misalnya, untuk mengevaluasi aspek penalaran matematis, pertanyaan-pertanyaan yang dapat diajukan, di antaranya, adalah pertanyaan tentang pola yang terbentuk dari susunan barisan bilangan tertentu, tentang alasan yang mendasari dari langkah-langkah proses penyelesaian soal dan pembuktian matematis. Atas dasar inilah, berikut kami uraikan berbagai indikator esensial aktivitas-aktivitas yang mengukur empat aspek daya matematis tersebut, khususnya ditinjau dari sisi kognitif penguasaan materi matematika.

Pemecahan Masalah

Sesuai tujuan pembelajaran matematika yang termuat dalam kurikulum, indikator esensial aktivitas pemecahan masalah meliputi: kemampuan memahami masalah, merancang model matematika, menyelesaikan model, dan menafsirkan solusi yang diperoleh (Depdiknas, 2006). Contoh 1 dan Contoh 2 merupakan soal-soal yang bila diselesaikan akan memenuhi indikator-indikator dari pemecahan masalah tersebut.

Contoh 1. Jumlah dua buah bilangan adalah 20 dan hasil kalinya adalah 25. Tentukanlah jumlah kuadrat dari kedua bilangan tersebut! (Kurniawan & Suryadi, 2007).

Contoh 2. Diketahui berikut merupakan gambar konsep sebuah mesjid yang akan dibangun. Penampang kubah berupa setengah lingkaran dan menyinggung segitiga siku-siku , dengan ∠ = 90°. Jika diketahui = 5 meter, maka panjang jari-jari penampang kubah tersebut adalah...

Sumber soal: KSM MA, tingkat propinsi, tahun 2014 (Departemen Agama RI, 2014) Penalaran Matematis

Indikator esensial aktivitas penalaran matematis yang termuat dalam kurikulum, di antaranya, adalah: aktivitas menemukan pola dan sifat—misalnya barisan bilangan; aktivitas membuat generalisasi secara induktif; aktivitas menyusun pembuktian matematis secara deduktif; dan aktivitas memberi penjelasan terhadap gagasan atau pernyataan matematis tertentu (Depdiknas, 2006). Contoh 3 dan Contoh 4 merupakan soal-soal yang

(4)

4

mengevaluasi kemampuan siswa dari aspek penalaran yang sesuai dengan indikator-indikator tersebut. Contoh 3 sesuai dengan indikator-indikator aktivitas memberi penjelasan terhadap pernyataan matematis. Sedangkan Contoh 4 sesuai dengan indikator aktivitas menyusun bukti matematis.

Contoh 3. Periksalah benar atau tidaknya proses penyelesaian persamaan berikut, dan berikan penjelasan secukupnya!

= 3 ⇒ 2 + 1 = 3(4 + 2) ⇒ 2 + 1 = 12 + 6 ⇒ 10 = −5 ⇒ = − = −.

Jadi, penyelesaian persamaan = 3 adalah = −. (Adaptasi dari Arcavi, 2005).

Contoh 4.Diketahui jajar genjang . Melalui pertengahan ditarik garis dari sampai memotong perpanjangan di . Buktikan bahwa = ! (Budhi, 2008).

Koneksi Matematis

Indikator kunci dari kemampuan koneksi matematis, di antaranya, mencakup kemampuan siswa dalam: mengaitkan satu konsep dengan konsep lain; mengaitkan antara satu algoritma/prosedur dan prosedur matematis lain; mengaitkan antara suatu konsep dan prosedur atau sebaliknya; dan menggunakan aneka kaitan ini secara akurat, fleksible dan efisien dalam pemecahan masalah (Depdiknas, 2006). Contoh 5 merupakan soal yang sesuai dengan indikator mengaitkan antara dua konsep, yaitu konsep logaritma dan konsep fungsi kuadrat. Contoh 6 adalah soal yang sesuai indikator mengaitkan antara, misalnya, konsep persamaan garis lurus (aljabar) dan geometri.

Contoh 5. Nilai maksimum dari () = log (5 + ) + log(3 − ) adalah…

(Seno, 2003). Contoh 6. Perhatikan gambar berikut. Diketahui bahwa AB menggambarkan sebuah gedung bertingkat, CD menyatakan tinggi sebuah rumah bertingkat, dan garis-garis BC serta AD menggambarkan tali-tali. Jika AB = 10 meter, CD = 6 meter dan AC = 8 meter, berapakah tinggi h? A B C D h

(5)

5

Komunikasi Matematis

Secara umum, kemampuan berkomunikasi dapat dikelompokkan menjadi komunikasi verbal dan komunikasi non-verbal. Komunikasi verbal mencakup komunikasi lisan dan tulisan, sedangkan komunikasi non-verbal mencakup, misalnya, gerak mata, gerak tangan, dan gerakan anggota tubuh lainnya. Komunikasi yang dibahas dalam artikel ini meliputi komunikasi verbal saja, khususnya komunikasi tertulis dalam matematika. Indikator kemampuan komunikasi matematis yang sesuai kurikulum, di antaranya, meliputi kemampuan: (1) membaca, memahami, dan mengungkapkan kembali suatu ide matematis tertentu, baik dalam bentuk simbol, diagram, gambar, atau tulisan dengan menggunakan gagasan sendiri—tanpa mengurangi makna ide matematis mula-mula; (2) menjelaskan gagasan tertentu berdasarkan hasil melihat, membaca, mendengar, dan berdiskusi; dan (3) menyampaikan ide tertentu dengan simbol, tabel, diagram, gambar, atau tulisan (Depdiknas, 2006). Contoh 7 adalah soal yang menekankan aspek komunikasi matematis yang sesuai indikator mengungkapkan gagasan tertulis ke dalam simbol matematis. Contoh 8 adalah soal yang tampaknya sesuai dengan indikator pertama.

Contoh 7. Jumlah tiga bilangan asli berurutan adalah 120. Tentukan: (i) model matematika yang menggambarkan pernyataan tersebut; (ii) Tentukan bilangan terkecil dari bilangan-bilangan asli tersebut! (Adaptasi dari Budhi, 2007)

Contoh 8. Dari tempat A Tom berjalan ke arah timur sejauh 1 km, kemudian 2 km ke utara, lalu 1 km ke timur, terus 1 km ke utara, lalu 1 km ke timur, terakhir 1 km ke utara sampai tempat B. Gambarkan situasi perjalanan Tom dari A ke B. Lalu, tentukan jarak antara A dan B tersebut! (Adaptasi dari Tim Psikolog, 2006).

3. Cara Mengembangkan Soal-soal Daya Matematis

Berdasarkan pengalaman dalam mengembangkan soal-soal yang memenuhi indikator-indikator aspek pemecahan masalah, penalaran, koneksi ataupun komunikasi matematis, kami mencatat terdapat tiga cara berbeda yang dapat dilakukan: Adopsi, Adaptasi, dan Kreasi Mandiri (orisinal).

Cara adopsi dilakukan dengan cara mengambil dan menggunakan secara langsung suatu soal untuk keperluan kita tanpa melakukan perubahan apapun terhadap soal yang diadopsi. Namun demikian, cara ini bukan berarti mudah untuk dilakukan. Untuk dapat melakukan adopsi soal, kita harus mampu mencocokan antara indikator-indikator yang ingin dicapai dan soal-soal yang akan diadopsi. Untuk meyakinkan diri apakah suatu soal

(6)

6

yang diadopsi sesuai indikator yang diperlukan, kita tentunya harus mampu menyelesaikan soal tersebut dengan benar.

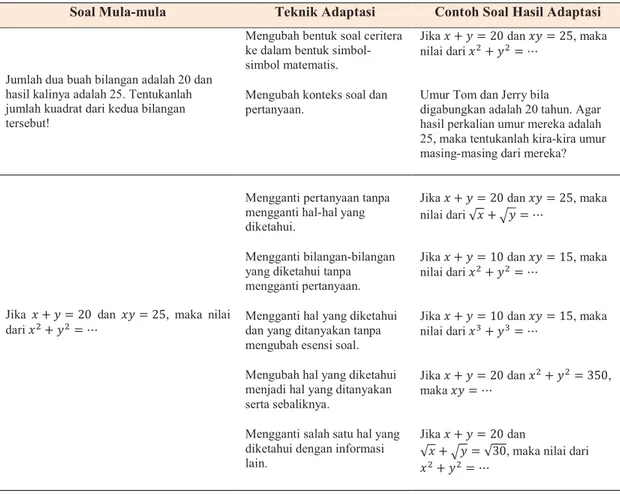
Cara adaptasi soal dilakukan dengan cara menyesuaikan soal yang akan digunakan sesuai keperluan kita, tanpa mengubah makna esensial dari soal mula-mula. Teknik adaptasi yang dapat dilakukan, misalnya, adalah dengan mengganti bilangan yang diketahui tanpa mengubah bentuk soal; memodifikasi konteks soal agar sesuai situasi kekinian dan dapat dikenal siswa; menyajikan soal dengan cara berbeda, misalnya, dengan mengubah soal bentuk ceritera ke dalam bentuk simbol-simbol matematis; mengganti hal yang diketahui dan yang ditanyakan tanpa mengubah esensi soal, ataupun dengan menambah pertanyaan dari soal mula-mula. Tentu masih banyak teknik-teknik adaptasi lain yang dapat dikembangkan, misalnya, dengan mengubah hal yang diketahui menjadi hal yang ditanyakan dan sebaliknya. Hal ini kami serahkan kepada pembaca untuk menambahkan sendiri. Tabel 1 berikut menyajikan aneka contoh bentuk adaptasi soal dari soal pemecahan masalah Contoh 1.

Tabel 1. Contoh pengembangan soal dengan cara adaptasi

Soal Mula-mula Teknik Adaptasi Contoh Soal Hasil Adaptasi

Jumlah dua buah bilangan adalah 20 dan hasil kalinya adalah 25. Tentukanlah jumlah kuadrat dari kedua bilangan tersebut!

Mengubah bentuk soal ceritera ke dalam bentuk simbol-simbol matematis.

Jika + $ = 20 dan $ = 25, maka nilai dari + $= ⋯

Mengubah konteks soal dan pertanyaan.

Umur Tom dan Jerry bila

digabungkan adalah 20 tahun. Agar hasil perkalian umur mereka adalah 25, maka tentukanlah kira-kira umur masing-masing dari mereka?

Mengganti pertanyaan tanpa mengganti hal-hal yang diketahui.

Jika + $ = 20 dan $ = 25, maka nilai dari & + '$ = ⋯

Mengganti bilangan-bilangan yang diketahui tanpa mengganti pertanyaan.

Mengganti hal yang diketahui dan yang ditanyakan tanpa mengubah esensi soal.

Jika + $ = 10 dan $ = 15, maka nilai dari (+ $(= ⋯

Mengubah hal yang diketahui menjadi hal yang ditanyakan serta sebaliknya.

Jika + $ = 20 dan + $= 350, maka $ = ⋯

Mengganti salah satu hal yang diketahui dengan informasi lain.

Jika + $ = 20 dan

& + '$ = &30, maka nilai dari

(7)

7

Cara kreasi mandiri (orisinal) adalah cara mengembangkan soal berdasarkan hasil pemikiran mandiri. Suatu soal dikatakan orisinal/asli bila soal tersebut belum pernah ada sebelumnya—baik bentuk atau tipenya. Namun demikian, keaslian suatu soal tidak mudah dideteksi. Selain itu, cara ini tampaknya agak sukar dilakukan oleh kebanyakan orang. Untuk dapat melakukannya diperlukan kemampuan berpikir kreatif asli, dan sepertinya merupakan hasil perenungan mendalam terhadap suatu konsep dan permasalahan tertentu. Sebagai contoh, berikut kami sajikan Contoh 9 sebagai soal hasil kreasi mandiri kami dalam pokok bahasan persamaan dan fungsi kuadrat dan kami pandang sebagai soal yang mengukur kemampuan koneksi matematis. Meski kami sendiri tidak tahu apakah soal tersebut dapat dikatakan sebagai soal orisinal atau tidak, setidaknya soal tersebut dikembangkan berdasarkan indikator koneksi matematis seperti yang tertuang dalam kurikulum.

Contoh 9. Diketahui fungsi dan ) dengan () = ( − 1)( + 1) dan )() = ( + 1)( − 3). Tentukan: (i) Gambar grafik dari () dan )(); (ii) Selesaikan

persamaan () = )(); (iii) Jelaskan kaitan antara grafik , grafik ) dan penyelesaian dari

persamaan bagian (ii).

4. Simpulan dan Diskusi

Berdasarkan uraian pada bagian-bagian sebelumnya, maka dapat ditarik tiga kesimpulan berikut. Pertama, dari tiga cara praktis pengembangan soal daya matematis: adopsi, adaptasi dan kreasi mandiri, kami memandang bahwa cara adaptasi merupakan cara paling potensial yang dapat dilakukan oleh para (calon) guru matematika. Sebabnya adalah karena cara ini menjembatani antara kemampuan mengadopsi, yang sekedar memungut dan menggunakan soal dari sumber tertentu, dan kemampuan berpikir kreatif sederhana, yaitu melakukan inovasi kecil-kecilan terhadap sesuatu. Kemampuan berpikir kreatif sederhana ini diyakini dapat dilakukan oleh para guru di tengah tugas mengajar yang seringkali menyita waktu. Cara adaptasi dapat dipandang sebagai bentuk kreatif dari cara adopsi yang dapat melahirkan suatu produk yang inovatif (Leung & Silver, 1997): untuk dapat melakukan adaptasi, maka kita perlu melakukan adopsi; dan untuk dapat melakukan adopsi, kita perlu mencocokkan antara indikator yang dituju dan soal yang tersedia. Langkah terakhir ini tentunya bisa dilakukan bila kita mampu menyelesaikan soal yang akan diadopsi dengan benar.

Kedua, mengingat begitu potensialnya cara adaptasi dapat dilakukan para guru, kami memandang perlu penelitian mendalam tentang hal ini. Misalnya, kajian tentang

(8)

8

pengembangan soal-soal untuk tiap aspek daya matematis yang sesuai tujuan kurikulum matematika. Hasil dari penelitian ini kami duga dapat digunakan para guru matematika dalam menjalankan tugas mengajar dan mengevalusi keberhasilan belajar siswa, serta dapat dijadikan sebagai rujukan untuk penelitian pengembangan soal lanjutan: baik di jenjang pendidikan dasar, menengah ataupun tinggi. Penelitian pengembangan soal ini dapat dilakukan secara continu, misalnya, untuk tiap pokok bahasan yang diamanatkan dalam kurikulum matematika.

Ketiga, meski cara kreasi mandiri tidak mudah dilakukan, kami mendorong para (calon) guru untuk mencobanya. Selain mampu berpikir kreatif, syarat untuk melakukan cara mandiri itu tidak mudah: perlu menguasai pokok bahasan matematika yang akan dibuat soal-soalnya; dan dapat menganalisis, mensintesis serta mengevaluasi soal-soal yang dibuat. Kami percaya hal ini bisa berhasil dikerjakan bila kita terus berusaha dengan kerja keras yang tidak mengenal putus asa.

Dengan melakukan pengembangan soal, baik dengan adopsi, adaptasi atau kreasi mandiri, kami meyakini bahwa hal ini merupakan salah satu cara bagi kita, para (calon) guru, untuk terus belajar dan meningkatkan mutu kompetensi diri: baik kompetensi pedagogik ataupun kompetensi profesional. Dengan cara ini, semoga pendidikan matematika di tanah air kita akan maju dan berkembang.

Referensi

Arcavi, A. (2005). Developing and using symbol sense in mathematics. For the Learning of Mathematics, 14(3), 24–35.

Budhi, W. S. (2007). Matematika untuk SMP kelas VII semester 1. Jakarta: Erlangga. Budhi, W. S. (2008). Matematika untuk SMP kelas VII semester 2. Jakarta: Erlangga. Departemen Agama RI. (2014). Berkas soal Kompetisi Sains Madrasah tingkat Propinsi

bidang matematika Madrasah Aliyah. Jakarta: Departemen Agama RI.

Depdiknas (2006). Kurikulum tingkat satuan pendidikan sekolah menengah pertama. Jakarta: Departemen Pendidikan Nasional.

Jupri, A., Drijvers, P., & van den Heuvel-Panhuizen, M. (2014). Difficulties in initial algebra learning in Indonesia. Mathematics Education Research Journal, 26(4), 683-710.

(9)

9

Kastberg, S. E., D’Ambrosio, B., Mcdermot, G., & Saada, N. (2005). Contexts matters in assessing students’ mathematical power. For the Learning of Mathematics, 25(2), 10 –15.

Kurniawan, & Suryadi. (2007). Siap juara olimpiade matematika SMP. Jakarta: Erlangga. Leung, S. S., & Silver, E. A. (1997). The role of task format, mathematics knowledge, and

creative thinking on the arithmetic problem posing of prospective elementary school teachers. Mathematics Education Research Journal, 9 (1), 5 – 24.

NCTM (1989). Principles and standards for school mathematics: Evaluation standard 4-Mathematical power. Diambil pada 12 Juli 2016 dari

http://www.fayar.net/east/teacher.web/math/Standards/previous/CurrEvStds/evals4.htm Rowan, T.E., & Robles, J. (1998). Using questions to help children build mathematical

power. Teaching Children Mathematics, 4(9), 504 – 509.

Sembiring, R. K., Hadi, S., & Dolk, M. (2008). Reforming mathematics learning in Indonesian classrooms through RME. ZDM, The International Journal on Mathematics Education, 40(6), 927 – 939.

Seno, H. (2003). Metode smart solution matematika. Yogyakarta: Andi dan Primagama. Tim Psikolog. (2006). Latihan psikotes dalam bentuk logika matematika: Persiapan masuk

PTN, STT Telkom, atau calon pegawai/karyawan. Bandung: Pustaka Setia.