Metode Simpleks Diperbaiki (Revised Simplex Method) Materi Bahasan

TI2231 Penelitian Operasional I 1

Metode Simpleks Diperbaiki (Revised Simplex Method)

Kuliah 05

Materi Bahasan

① Dasar-dasar aljabar dari metode simpleks

② Metode simpleks yang diperbaiki

TI2231 Penelitian Operasional I 3

① Dasar-dasar Aljabar Metode Simpleks

Dasar-dasar Metode Simpleks

• Dalam PL, ruang solusi layak (feasible solution space) dikatakan membentuk himpunan konveks (convex set) jika segmen garis yang menghubungkan dua titik yang layak terletak dalam himpunan tersebut.

• Suatu titik ekstrem (extreme point) dari himpunan konveks adalah titik layak yang tidak dapat terletak pada suatu segmen garis yang menghubungkan dua titik sebarang yang layak dalam himpunan tersebut.

• Titik ekstrem sama dengan titik pojok (corner point).

TI2231 Penelitian Operasional I 5

Convex dan Nonconvex Set

x’

x”

x”

x’

Convex set Nonconvex set

Convex Combination

• Dalam solusi PL secara grafis, telah ditunjukkan bahwa solusi optimal selalu berkaitan dengan titik ekstrem (pojok) yang layak dari ruang solusi.

• Tiap titik yang layak dapat ditentukan sebagai

fungsi dari titik-titik ekstrem.

TI2231 Penelitian Operasional I 7

• Diberikan titik-titik ekstrem x

₁

, x

₂

, x

₃

, x

₄

, x

₅

dan x

₆

titik yang layak x dapat dinyatakan sebagai kombinasi konveks (convex

combination) dari titik-titik ekstrem

menggunakan

dimana

6 6 5 5 4 4 3 3 2 2 1

1x x x x x x

x 























6

1

5 4 3 2

1























0 ,

, , ,

,

_{2 3 4 5 6}

1

    





• Notasi matriks dari PL x : vektor n dari variabel

A : matriks (m x n) dari koefisien pembatas c : vektor n dari koefisien fungsi tujuan

• Masalah PL

cx z

(Min) Max

b Ax 



0

x

Dari Titik-Titik Ekstrem ke Solusi Basis

TI2231 Penelitian Operasional I 9

• Solusi basis dari Ax = b ditentukan dengan menetapkan n – m variabel sama dengan 0 dan

memecahkan m persamaan dalam m variabel yang tak diketahui.

• Hubungan antara definisi geometris dari titik-titik ekstrem dan definisi aljabar dari solusi basis:

Titik-titik ekstrem {x| Ax = b} Solusi basis Ax = b

• Dengan menetapkan pembatas tak negatif x 0,

• Sistem Ax = b dapat dinyatakan dalam bentuk vektor

• Vektor P_jadalah kolom ke j dari A.

• Himpunan bagian dari m vektor dikatakan membentuk suatu basis B jika dan hanya jika m vektor adalah independen linier.

• Matriks B adalah nonsingular.

• Jika x_B adalah himpunan dari m variabel yang berkaitan dengan vektor nonsingular B, maka x_B harus merupakan solusi basis.



 n 

j jx

1

b P

TI2231 Penelitian Operasional I 11

• Dalam kasus ini

• Diberikan B^-1adalah invers dari B, solusi basis dinyatakan dengan

• Jika B^-1b 0, maka x_Badalah layak.

b Bx_B 

b B x_B  ^1

• Definisi mengasumsikan bahwa terdapat n – m variabel sebagai nonbasis pada level 0.

• Sistem dengan m persamaan dan n variabel tak diketahui, jumlah maksimum dari solusi basis (layak dan tak layak) adalah

 

!

!

! n m m C_n^m n

 

TI2231 Penelitian Operasional I 13

Tentukan dan klasifikasikan (sebagai layak dan tak layak) dari semua solusi basis untuk sistem persamaan linier berikut:



 























 











2 4 2

2 2

1 3 1

3 2 1

x x x



 







 







 





 2

4 2

2 3 1

2 1

x

x 

 







 







 





 



 





4 / 3

4 / 7 2 4 8 / 1 4 / 1

8 / 3 4 / 1

2 1

x x



 







 







 











2 4 2

2 1 3

3 2

x

x 

 





 



 







 









 



 





4 / 7

4 / 3 2 4 8 / 3 4 / 1

8 / 1 4 / 1

3 2

x x (P₁, P₂)

(P₂, P₃)

(P₁, P₃) Bukan basis

Layak

Tak layak

B Bx_B= b Solusi Status

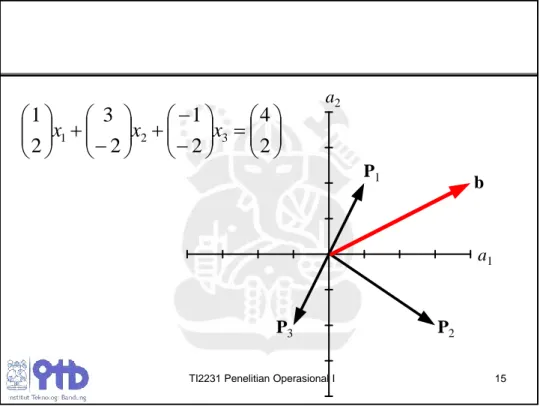
TI2231 Penelitian Operasional I 15

a₂

a₁ P₁ b

P₂ P₃



 







 







 



 





 



 





2 4 2

1 2

3 2

1

3 2

1 x x

x

Tabel Simpleks dalam Bentuk Matriks (1)

• Misalkan diberikan PL sebagai berikut:

• Misalkan B adalah basis layak dari sistem Ax = b, x0.

• Misalkan x_Bberkaitan dengan himpunan variabel basis dengan c_B adalah vektor koefisien fungsi tujuannya.

cx z

Max

b Ax 



0

x

TI2231 Penelitian Operasional I 17

xB

Pj

B^1

j B

cj c B^1P

b B^1

b B c_B ^1

Basis x_j Solusi

• Diberikan P_jadalah vektor ke j dari A, kolom tabel simpleks yang berkaitan dengan variabel x_jdapat dinyatakan dengan

Tabel Simpleks dalam Bentuk Matriks (2)

② Metode Simpleks yang Diperbaiki

TI2231 Penelitian Operasional I 19

• Metoda simplex melakukan perhitungan pada seluruh tabel pada tiap iterasi.

• Padahal, informasi yang dibutuhkan hanya:

– Koefisien fungsi tujuan relatif

– Kolom yang berkaitan dengan variabel yang masuk basis (kolom pivot)

– Variabel basis saat ini dan nilainya (konstanta ruas kanan)

Masalah PL

Memaksimumkan Z = 3x₁+ 2x₂

dengan pembatas-pembatas:

x₁+ 2x₂6 2x₁+ x₂ 8 – x₁ + x₂ 1 x₂ 2 x₁≥ 0, x₂≥ 0

TI2231 Penelitian Operasional I 21

Rumusan Bentuk Baku

Memaksimumkan Z = 3x₁+ 2x₂

dengan pembatas-pembatas:

x₁ + 2x₂+ x₃ = 6 2x₁+ x₂ + x₄ = 8 – x₁ + x2 + x₅ = 1 x₂ + x₆= 2

x₁ ≥ 0, x₂≥ 0, x₃≥ 0, x₄ ≥ 0, x₅≥ 0, x₆ ≥ 0

Solusi Basis Layak Awal (1)

















  0 1 2 1

P1



















1 1 1 2

P2



















0 0 0 1

P3



















0 0 1 0

P4



















0 1 0 0

P5



















1 0 0 0

P6

















 2 1 8 6

b

TI2231 Penelitian Operasional I 23

^{P P P P}  ^I

B 





















1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1

6 5 4 3



















 

1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1

1 I

B

x_B= (x₃, x₄, x₅, x₆)

Maka,



















 ^ 2 1 8 6

1b B b



0,0,0,0



B  c

Pemeriksaan optimalitas (1)

Pengali simplex (simplex multiplier):

    ^0,0,0,0

1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1 0 , 0 , 0 , 0 ,

,

, _{4 5 6} ¹

3 





















 c B^

π     _B

TI2231 Penelitian Operasional I 25

Pemeriksaan optimalitas (2)

Koefisien fungsi tujuan relatif untuk variabel non basis:

  3

0 1 2 1 0 , 0 , 0 , 0

1 3

1

1 

















 





c πP c

  2

0 1 2 1 0 , 0 , 0 , 0

2 2

2

2 

















 





c πP c

Karena terdapat c_j 0 maka solusi belum optimal.

Penentuan variabel yang masuk basis

Variabel yang masuk basis: x₁ karena mempunyai koefisien fungsi tujuan relatif paling positif

TI2231 Penelitian Operasional I 27

















 

















 



















 ^

0 1 2 1

0 1 2 1

1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1

1 1

1 B P

P

4 , 2, ,8 1

min 6 



 



  

  bersesuaian dengan variabel x₄





















































 ^

2 1 8 6

2 1 8 6

1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1

1b B b

Penentuan basis baru

















 0 1 0 0 0

1 0 1 0 0

2 0 0 1 0

1 0 0 0 1















 

0 1 0 0 0

0 0 1 2 / 1 0

1 0 0 2 / 1 0

0 0 0 2 / 1 1















 

 

1 0 0 0

0 1 2 / 1 0

0 0 2 / 1 0

0 0 2 / 1 1 B 1



x ,x,x ,x





x ^{c }



^0,3,0,0



TI2231 Penelitian Operasional I 29

Solusi baru



x₃,x₁,x₅,x₆



B 

x ^c_B ^



^0,3,0,0



















































 























 ^

2 5 4 2

2 1 8 6

1 0

0 0

0 1

2 / 1 0

0 0

2 / 1 0

0 0

2 1 1

1

6 5 1 2

b B b x_B

x x x x

 

¹²

2 1 8 6

1 0

0 0

0 1

2 / 1 0

0 0

2 1 0

0 0

2 1 1

0 , 0 , 3 ,

1 0 































 



c_BB^b Z

Pemeriksaan optimalitas (1)

Pengali simplex (simplex multiplier):

    0,3/2,0,0

1 0 0 0

0 1 2 / 1 0

0 0 2 / 1 0

0 0 2 / 1 1 0 , 0 , 3 , 0 ,

,

, _{1 5 6} ¹

3 















 





 c B^

π     _B

TI2231 Penelitian Operasional I 31

Koefisien fungsi tujuan relatif untuk variabel non basis:

  1/2

1 1 1 2 0 , 0 , 2 / 3 , 0

2 2

2

2 























c πP c

  3/2

0 0 1 0 0 , 0 , 2 / 3 , 0

4 0

4

4 























c πP c

Karena terdapat c_j 0 maka solusi belum optimal.

Penentuan variabel yang masuk basis

Variabel yang masuk basis: x₂ karena mempunyai koefisien fungsi tujuan relatif paling positif

TI2231 Penelitian Operasional I 33

Penentuan variabel yang keluar basis

















































 



 ^

1 2 / 3

2 / 1

2 / 3

1 1 1 2

1 0 0 0

0 1 2 / 1 0

0 0 2 / 1 0

0 0 2 / 1 1

2 1

2 B P

P

3 / 1 4 ,2 2 / 3 , 5 2 / 1 , 4 2 / 3

min 2 



 



 

 bersesuaian dengan variabel x₃

















































 



 ^

2 5 4 2

2 1 8 6

1 0 0 0

0 1 2 / 1 0

0 0 2 / 1 0

0 0 2 / 1 1

1b B b

Penentuan basis baru















 

1 1 0 0 0

2 3 0 1 2 1 0

2 1 0 0 2 1 0

2 3 0 0 2 1 1

























 

1 0

3 1 3 2

0 1

1 1

0 0

3 2 3 1

0 0

3 1 3 2 B 1



x ,x ,x ,x





x c 



^2,3,0,0



























0 1 0 3 1 3 2

0 0 1 1 1

0 0 0 3 2 3 1

1 0 0 3 1 3 2

TI2231 Penelitian Operasional I 35



x₂,x₁,x₅,x₆



B 

x ^c_B ^



^2,3,0,0



















































































 ^

3 2

3 3 10

3 4

2 1 8 6

1 0

3 1 3 2

0 1

1 1

0 0

3 2 3 1

0 0

3 1 3 2

1

6 5 1 2

b B b x_B

x x x x

 

38 3

2 1 8 6

1 0

3 1 3 2

0 1

1 1

0 0

3 2 3 1

0 0

3 1 3 2 0 , 0 , 3 ,

1 2 











































c_BB^b Z

Pemeriksaan optimalitas (1)

Pengali simplex (simplex multiplier):

    1/3,4/3,0,0

1 0 3 / 1 3 / 2

0 1 1 1

0 0 3 / 2 3 / 1

0 0 3 / 1 3 / 2 0 , 0 , 3 , 2 ,

,

, _{1 5 6} ¹

2 





























 c B^

π     _B

TI2231 Penelitian Operasional I 37

Pemeriksaan optimalitas (2)

Koefisien fungsi tujuan relatif untuk variabel non basis:

  1/3

0 0 0 1 0 , 0 , 3 / 4 , 3 / 1

3 0

3

3 























c πP c

  4/3

0 0 1 0 0 , 0 , 3 / 4 , 3 / 1

4 0

4

4 























c πP c

Karena semua c_j 0 maka solusi optimal.

Solusi optimal

















































































 ^

3 / 2

3 3 / 10

3 / 4

2 1 8 6

1 0 3 / 1 3 / 2

0 1 1 1

0 0 3 / 2 3 / 1

0 0 3 / 1 3 / 2

1

6 5 1 2

b B b x

x x x x

B

  38/3 3

/ 2

3 3 / 10

3 / 4 0 , 0 , 3 ,

2 



















c_Bb Z

TI2231 Penelitian Operasional I 39

• Mengurangi waktu komputasi

• Menghemat memori komputer

• Mempermudah pemahaman untuk topik lanjutan dari pemrograman linier (teori dualitas, analisis sensitivitas)

Hubungan Tabel Simpleks dengan Matriks B^-1(Iterasi 0)

c_B

3 2 0 0 0 0

Konstanta x₁ x₂ x₃ x₄ x₅ x₆

0 x₃ 1 2 1 0 0 0 6

0 x₄ 2 1 0 1 0 0 8

0 x₅ -1 1 0 0 1 0 1

0 x₆ 0 1 0 0 0 1 2

3 2 0 0 0 0 Z = 0

Basis c_j

c Baris

TI2231 Penelitian Operasional I 41

Hubungan Tabel Simpleks dengan Matriks B^-1(Iterasi 1)

c_B

3 2 0 0 0 0

Konstanta x₁ x₂ x₃ x₄ x₅ x₆

0 x₃ 0 3/2 1 -1/2 0 0 2

3 x₁ 1 1/2 0 1/2 0 0 4

0 x₅ 0 3/2 0 1/2 1 0 5

0 x₆ 0 1 0 0 0 1 2

0 1/2 0 -3/2 0 0 Z = 12

Basis c_j

c Baris

Hubungan Tabel Simpleks dengan Matriks B^-1(Iterasi 2)

c_B

3 2 0 0 0 0

Konstanta x₁ x₂ x₃ x₄ x₅ x₆

2 x₂ 0 1 2/3 -1/3 0 0 4/3

3 x₁ 1 0 -1/3 2/3 0 0 10/3

0 x₅ 0 0 -1 1 1 0 3

0 x₆ 0 0 -2/3 1/3 0 1 2/3

0 0 -1/3 -4/3 0 0 Z = 12²/₃

Basis c_j

c Baris