HIMPUNAN MODUL PERKULIAHAN. Pengertian dan berbagai macam bentuk himpunan Operasi dasar himpunan

(1)

MODUL PERKULIAHAN

HIMPUNAN

 Pengertian dan berbagai macam

bentuk himpunan

 Operasi dasar himpunan

Fakultas Program Studi Tatap Muka Kode MK Disusun Oleh

Ilmu Komputer Sistem Informasi

01

87004 Tim Dosen

Abstract

Kompetensi

Himpunan adalah konsep dasar dari semua cabang matematika. Himpunan merupakan sekumpulan objek yang mempunyai syarat tertentu dan jelas. Berbagai macam jenis himpunan, misal himpunan kosong, himpunan yang sama dsb. Operasi himpunan misal irisan, gabungan, pengurangan dsb.

Mahasiswa mampu memahami dan dapat membedakan berbagai macam bentuk himpunan dan menggambarkannya dalam bentuk diagram Venn

(2)

HIMPUNAN

A. Pengertian dan Bentuk himpunan

Himpunan adalah konsep dasar dari semua cabang matematika. George Cantor dianggap sebagai bapak teori himpunan. Himpunan adalah sekumpulan objek yang mempunyai syarat tertentu dan jelas. Objek yang dimaksud dapat berupa bilangan, manusia, hewan, tumbuhan, Negara dan sebagainya.Objek ini selanjutnya dinamakan

anggota atau elemen dari himpunan itu. Syarat tertentu dan jelas dalam menentukan

anggota suatu himpunan ini sangat penting karena untuk membedakan mana yang menjadi anggota himpunan dan mana yang bukan merupakan anggota himpunan. Inilah yang kemudian dinamakan himpunan yang terdefinisi dengan baik (well-defined set).

B. Penyajian bentuk himpunan :

a. Enumerasi Contoh :

 Himpunan empat bilangan asli pertama: A = {1, 2, 3, 4}.

 Himpunan lima bilangan genap positif pertama: B = {4, 6, 8, 10}.  C = {kucing, a, Amir, 10, paku}

 R = { a, b, {a, b, c}, {a, c} }  C = {a, {a}, {{a}} }

 K = { {} }

 Himpunan 100 buah bilangan asli pertama: {1, 2, ..., 100 }  Himpunan bilangan bulat ditulis sebagai {…, -2, -1, 0, 1, 2, …}.

b. Simbol-simbol Baku Contoh :

P = himpunan bilangan bulat positif = { 1, 2, 3, ... } N = himpunan bilangan alami (natural) = { 1, 2, ... } Z = himpunan bilangan bulat = { ..., -2, -1, 0, 1, 2, ... } Q = himpunan bilangan rasional

(3)

R = himpunan bilangan riil

C = himpunan bilangan kompleks

c. Notasi Pembentuk himpunan

Notasi: { xsyarat yang harus dipenuhi oleh x } Contoh :

A adalah himpunan bilangan bulat positif yang kecil dari 5 A = { x | x adalah bilangan bulat positif lebih kecil dari 5}

atau

A = { x | x P, x< 5 }

Yang ekivalen dengan A = {1, 2, 3, 4}

M = { x | x adalah mahasiswa yang mengambil kuliah IF2151}

d. Diagram Venn Contoh : Misalkan U = {1, 2, …, 7, 8}, A = {1, 2, 3, 5} dan B = {2, 5, 6, 8}. Diagram Venn: U 1 ₂ 5 3 6 8 4 7 A B

Jumlah elemen di dalam A disebut cardinal dari himpunan A. Dan dinotasikan dengan n(A) atau A

C. Bentuk/Jenis Himpunan 1. Himpunan Kosong

(4)

 Notasi :  atau {}

Contoh

(i) E = {x | x<x }, maka n(E) = 0

(ii) P = {orang Indonesia yang pernah ke bulan }, maka n(P) = 0 (iii) A = {x | x adalah akar persamaan kuadrat x2_{+ 1 = 0}, n(A) = 0}

 himpunan {{ }} dapat juga ditulis sebagai {}

 himpunan {{ }, {{ }}} dapat juga ditulis sebagai {, {}}

 {} bukan himpunan kosong karena ia memuat satu elemen yaitu himpunan kosong.

2. HimpunanBagian (Subset)

 Himpunan A dikatakan himpunan bagian dari himpunan B jika dan hanya jika setiap elemen A merupakan elemen dari B.

 Dalam hal ini, B dikatakan superset dari A.  Notasi: A  B  Diagram Venn:

U

A

B

Contoh : (i) { 1, 2, 3}  {1, 2, 3, 4, 5} (ii) (ii) {1, 2, 3}  {1, 2, 3} (iii) NZRC

(5)

B = { (x, y) | 2x + y< 4, x 0 dany 0 }, maka B  A.

TEOREMA 1. Untuk sembarang himpunan A berlaku hal-hal sebagai berikut:

(a) A adalah himpunan bagian dari A itu sendiri (yaitu, AA). (b) Himpunan kosong merupakan himpunan bagian dari A ( A). (c) Jika AB dan BC, maka AC

 A dan AA, maka dan A disebut himpunan bagian tak sebenarnya (improper subset) dari himpunan A.

Contoh: A = {1, 2, 3}, maka {1, 2, 3} dan  adalah improper subset dari A.  A  B berbeda dengan A  B

(i) A  B : A adalah himpunan bagian dari B tetapi A  B. A adalah himpunan bagian sebenarnya (proper subset) dari B.

Contoh: {1} dan {2, 3} adalah proper subset dari {1, 2, 3}

(ii) AB : digunakan untuk menyatakan bahwa A adalah himpunan bagian (subset) dari B yang memungkinkan A = B.

3. Himpunan yang Sama

 A = B jika dan hanya jika setiap elemen A merupakan elemen B dan sebaliknya setiap elemen B merupakan elemen A.

 A = B jika A adalah himpunan bagian dari B dan B adalah himpunan bagian dari A. Jika tidak demikian, maka A  B.

 Notasi : A = B  AB dan BA

Contoh

(i) Jika A = { 0, 1 } dan B = { x | x (x – 1) = 0}, maka A = B (ii) Jika A = { 3, 5, 8, 5 } dan B = {5, 3, 8 }, maka A = B (iii) Jika A = { 3, 5, 8, 5 } dan B = {3, 8}, maka AB

Untuk tiga buah himpunan A, B dan C berlaku aksioma berikut: (a) A = A, B = B, dan C = C

(b) jika A = B, maka B = A

(6)

4. Himpunan yang Ekivalen

 Himpunan A dikatakan ekivalen dengan himpunan B jika dan hanya jika cardinal dari kedua himpunan tersebut sama.

 Notasi : A ~ BA = B

Contoh

Misalkan A = { 1, 3, 5, 7 } dan B = { a, b, c, d }, maka A ~ B sebabA = B = 4

5. Himpunan Saling Lepas

 Dua himpunan A dan B dikatakan saling lepas (disjoint) jika keduanya tidak memiliki elemen yang sama.

 Notasi : A // B  Diagram Venn:

U

A B

Contoh

Jika A = { x | xP, x< 8 } dan B = { 10, 20, 30, ... }, makaA // B.

6. Himpunan Kuasa

 Himpunan kuasa (power set) dari himpunan A adalah suatu himpunan yang elemennya merupakan semua himpunan bagian dari A, termasuk himpunan kosong dan himpunan A sendiri.

 Notasi : P(A) atau 2A

 JikaA = m, makaP(A) = 2m.

Contoh

Jika A = { 1, 2 }, maka P(A) = { , { 1 }, { 2 }, { 1, 2 }}

(7)

Himpunan kuasa dari himpunan kosong adalah P() = {}, dan himpunan kuasa dari himpunan {} adalah P({}) = {, {}}.

D. Operasi Himpunan

a. Irisan

Notasi : A  B = { xxA dan xB }

Contoh :

1. Jika A = {2, 4, 6, 8, 10} dan B = {4, 10, 14, 18}, maka A∈B = {4, 10} 2. Jika A = { 3, 5, 9 } dan B = { -2, 6 }, maka AB = .

b. Gabungan

Notasi : AB = { xxA atau xB }

Contoh :

1. Jika A = { 2, 5, 8 } dan B = { 7, 5, 22}, maka AB = { 2, 5, 7, 8, 22 } 2. A = A

c. Komplemen

(8)

Contoh :

Misalkan U = {1, 2, 3, ..., 9 },

1. Jika A = {1, 3, 7, 9}, maka

A

= {2, 4, 6, 8}

2. JikaA = { x | x/2 P, x< 9 }, maka

A

= { 1, 3, 5, 7, 9 } contoh :

A = himpunan semua mobil buatan dalam negeri B = himpunan semua mobil impor

C = himpunan semua mobil yang dibuat sebelum tahun 1990

D = himpunan semua mobil yang nilai jualnya kurang dari Rp 100 juta E = himpunan semua mobil milik mahasiswa universitas tertentu

1. “mobil mahasiswa di universitas ini produksi dalam negeri atau diimpor dari luar negeri”  (E∈A)  (E∈B) atau E∈ (AB)

2. “semua mobil produksi dalam negeri yang dibuat sebelum tahun 1990 yang nilai jualnya kurang dari Rp 100 juta” A∈C∈D

3. “semua mobil impor buatan setelah tahun 1990 mempunyai nilai jual lebih dari Rp 100 juta” 

C



D



B

d. Selisih

Notasi : A – B = { xxA dan xB } = A ∈

B

Contoh :

1. Jika A = { 1, 2, 3, ..., 10 } danB = { 2, 4, 6, 8, 10 }, maka

A – B = { 1, 3, 5, 7, 9 } dan B – A = 

2. {1, 3, 5} – {1, 2, 3} = {5}, tetapi {1, 2, 3} – {1, 3, 5} = {2}

(9)

Notasi: AB = (AB) – (A∈B) = (A – B)  (B – A) Contoh :

Jika A = { 2, 4, 6 } dan B = { 2, 3, 5 }, maka AB = { 3, 4, 5, 6 }

Contoh :

U = himpunan mahasiswa

P = himpunan mahasiswa yang nilai ujian UTS di atas 80 Q= himpunan mahasiswa yang nilai ujian UAS di atas 80

Seorang mahasiswa mendapat nilai A jika nilai UTS dan nilai UAS

keduanya diatas 80, mendapat nilai B jika salah satu ujian di atas 80, dan mendapat nilai C jika kedua ujian di bawah 80.

1. “Semua mahasiswa yang mendapat nilai A” : P∈Q 2. “Semua mahasiswa yang mendapat nilai B” : PQ

3. “Semua mahasiswa yang mendapat nilai C” : U – (PQ)

DaftarPustaka

1. Firrar Utdirartatmo, Teori Bahasa dan Otomata, Graha Ilmu, Yogyakarta, Edisi 2, 2005. 2. Jonhson, Ricard, Discrete Mathematics. Prentice Hall Int, New Jersey, 2001

3. Sri Kusumadewi, Hari Purnomo, Aplikasi Logika Fuzzy, Graha Ilmu, Yogyakarta, 2004. 4. Klin, George J dan Tina A. Folger, Fuzzy Sets, Uncertainty and Information, Prentice Hall

Int, New Jersey, 1998.

(10)

MODUL PERKULIAHAN

INKLUSI EKSKLUSI

HIMPUNAN

 Definisi pada teori himpunan

 Prinsip inklusi-eksklusi.

02

87004 Tim Dosen

(11)

Dalam matematika prinsip Inklusi dan Eksklusi merupakan perluasan ide dalam Diagram Venn beserta operasi irisan dan gabungan.

Mahasiswa mampu memahami prinsip inklusi – eksklusi dan definisi pada teori himpunan

INKLUSI EKSKLUSI HIMPUNAN

1. Prinsip Inklusi – Eksklusi.

Operasi penggabungan dua buah himpunan akan menghasilkan himpunan baru yang anggotanya berasal dari kedua himpunan tersebut. Pada operasi tersebut mungkin saja ada anggota himpunan yang sama pada kedua himpunan pembentuk himpunan baru tersebut. Misal jika A adalah himpunan bilangan prima yang lebih kecil dari 10 dan B himpunan bilangan ganjil kurang dari sepuluh. Maka ada bilangan {3,5,7} yang menjadi anggota di A dan di B. Pada operasi gabungan dua himpunan, banyaknya anggota himpunan baru yang terbentuk akan ada dua elemen himpunan {3,5,7} yang berasal dari A dan B. Elemen ini merupakan elemen bersama antara A dan B yang dalam himpunan dapat ditentukan sebagai operasi irisan A ∩ B. Sehingga untuk kasus dimana ada elemen bersama antara A dan B, maka banyaknya anggota himpunan baru tersebut seharusnya jumlah elemen penggabungan dikurang jumlah elemen bersama. Secara himpunan dapat dituliskan sebagai berikut.

| A U B | = |A | + |B| - |A ∩ B |

Prinsip ini dikenal dengan nama prinsip inklusi – eksklusi.

(12)

U

A B

| A U B | = |A | + |B| - | A ∩ B |

Teorema. Misalkan A dan B himpunan maka A U B berhingga dan

| A U B | = |A | + |B| - | A ∩ B |

atau dengan menggunakan operasi beda setangkup jumlah elemen himpunan baru tersebut dapat ditentukan dengan operasi berikut.

| A  B | = |A | + |B| - | A ∩ B |

Berapa banyaknya bilangan bulat antara 1 dan 100 yang habis dibagi 3 atau 5? Penyelesaian:

A = himpunan bilangan bulat yang habis dibagi 3, B = himpunan bilangan bulat yang habis dibagi 5,

AB = himpunan bilangan bulat yang habis dibagi 3 dan 5 (yaitu himpunan

bilangan bulat yang habis dibagi oleh KPK – Kelipatan Persekutuan Terkecil – dari 3 dan 5, yaitu 15),

(13)

Yang ditanyakan adalah AB.

A = 100/3 = 33, B = 100/5 = 20, AB = 100/15 = 6

AB = A + B – AB = 33 + 20 – 6 = 47

Jadi, ada 47 buah bilangan yang habis dibagi 3 atau 5.

prinsip inklusi-eksklusi pada dua himpunan dapat dikembangkan untuk lebih dari dua himpunan.

Contoh : Di antara bilangan bulat antara 101 – 600 (termasuk 101 dan 600 itu sendiri), berapa banyak bilangan yang habis dibagi oleh 4 atau 5 namun tidak keduanya? Penyelesaian: Diketahui: U = 500 A = 600/4 – 100/4 = 150 – 25 = 125 B = 600/5 – 100/5 = 120 – 20 = 100 A B = 600/20 – 100/20 = 30 – 5 = 25 yang ditanyakan A B_{ = ?}

Hitung terlebih dahulu

AB = A + B – 2A B = 125 + 100 – 50 = 175

untuk mendapatkan

(14)

Jika A,B,C merupakan himpunan berhingga maka AB C berhingga. AB C = A + B+| C | – AB-AC- BC + ABC Untuk r buah himpunan.

Teorema

Jika A1,A2... An adalah bilangan berhingga, maka A1A2 … Ar =



i Ai –



  i j r 1 AiAj +



   i j k r 1

AiAjAk + … + (-1)r-1A1A2 … Ar

Contoh : Berapa banyaknya bilangan bulat antara 1 dan 100 yang habis dibagi 3 atau 5?

Jawab

P = himpunan bilangan bulat yang habis dibagi 3, Q = himpunan bilangan bulat yang habis dibagi 5,

n(PQ) = himpunan bilangan bulat yang habis dibagi 3 dan 5 ( yaitu himpunan bilangan bulat yang habis dibagi olek KPK / kelipatan persekutuan terkecil dari 3 dan 5 yaitu 15. Ditanyakan n (A B)??? n (A) = 100/3 = 33 n (B) = 100/5 = 20 n (A B) = 100/15 = 6 maka n (A  B) = n (A) + n (B) – n (A  B) = 33 + 20 -6 = 47

(15)

2. Prinsip Inklusif dan Eksklusif pada 3 himpunan atau lebih

Prinsip Inklusi dan Eksklusi merupakan perluasan ide dalam Diagram Venn beserta operasi irisan dan gabungan, namun dalam pembahasan kali ini konsep tersebut diperluas, dan diperkaya dengan ilustrasi penerapan yang bervariasi dalam matematika kombinatorik. Kita awali dengan sebuah ilustrasi:

Sebuah perkuliahan umum dihadiri oleh 20 mahasiswa yang memiliki kegemaran membaca dan 30 mahasiswa yang memiliki kegemaran menulis. Berapa mahasiswa di dalam perkuliahan tersebut yang memiliki kegemaran membaca atau menulis?

Dari permasalahan ini terlihat bahwa informasi yang diketahui belum memadai. Banyaknya mahasiswa yang memiliki kegemaran membaca atau menulis hanya dapat diketahui jika banyaknya mahasiswa yang menggemari kedua kegiatan tersebut diketahui.

Prinsip Inklusi-Eksklusi

Banyaknya anggota himpunan gabungan antara himpunan A dan himpunan B merupakan jumlah banyaknya anggota dalam himpunan tersebut dikurangi banyaknya anggota di dalam irisannya. Dengan demikian,

n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

Contoh

1. Dalam sebuah program studi pendidikan matematika yang terdiri atas 350 mahasiswa, terdapat 175 mahasiswa yang mengambil mata kuliah persamaan diferensial dan 225 mahasiswa yang mengambil mata kuliah analisis kompleks, dan 50 mahasiswa yang mengambil mata kuliah persamaan diferensial dan analisis kompleks. Ada berapa mahasiswa di dalam perkuliahan itu jika setiap mahasiswa mengambil mata kuliah persamaan diferensial, analisis kompleks, atau kedua-duanya?

Penyelesaian:

(16)

dan B menyatakan mahasiswa yang mengambil mata kuliah analisis kompleks. Maka A B merupakan himpunan mahasiswa yang mengambil kedua mata kuliah tersebut. Banyaknya mahasiswa di dalam kelas itu yang mengambil mata kuliah persamaan diferensial, analisis kompleks, atau kedua-duanya adalah

n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

= 175 + 225 – 50 = 350

Ini berarti, terdapat 350 mahasiswa di dalam kelas yang mengambil mata kuliah persamaan diferensial, analisis kompleks, atau kedua-duanya. Karena banyaknya siswa keseluruhan di dalam kelas tersebut adalah 350 mahasiswa, artinya tidak terdapat mahasiswa yang tidak memilih salah satu dari kedua konsentrasi itu.

2. Di sebuah jurusan dalam suatu perguruan tinggi terdapat 134 mahasiswa tingkat 3. Dari sekian banyak mahasiswa tersebut, 87 di antaranya mengambil mata kuliah teori graf diskrit, 73 mengambil mata kuliah matematika ekonomi, dan 29 mengambil mata kuliah teori graf dan matematika ekonomi. Berapa banyak mahasiswa yang tidak mengambil sebuah mata kuliah baik dalam teori graf maupun dalam matematika ekonomi? Penyelesaian:

Untuk menentukan banyaknya mahasiswa tingkat 3 yang tidak mengambil mata kuliah teori graf ataupun matematika ekonomi, kurangilah banyaknya mahasiswa yang mengambil mata kuliah dari salah satu mata kuliah ini dari keseluruhan banyaknya mahasiswa tingkat 1.

Misalkan A merupakan himpunan semua mahasiwa tingkat 3 yang mengambil mata kuliah teori graf, dan B adalah himpunan mahasiswa yang mengambil mata kuliah matematika ekonomi.

Maka n(A)=87, n(B)=73, dan n(A ∩ B) = 29. Banyaknya mahasiswa tingkat 3 yang mengambil mata kuliah teori graf atau matematika ekonomi adalah

(17)

= 87 + 73 – 29 = 160-29 = 131

Ini artinya terdapat sebanyak 134–131 = 3 mahasiswa tingkat 3 yang tidak mengambil mata kuliah teori graf ataupun matematika ekonomi.

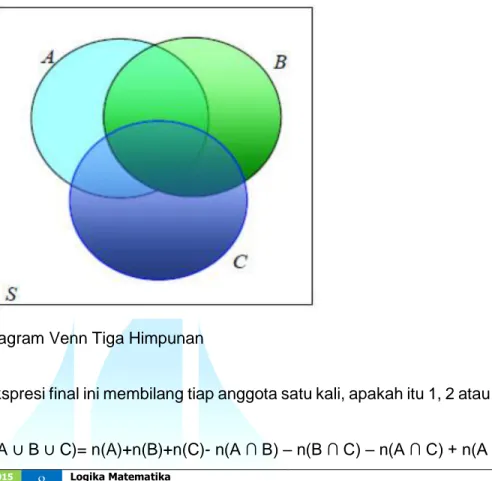
Dalam bagian berikutnya akan diuraikan bagaimana cara-cara menentukan banyaknya anggota dalam gabungan antara himpunan terhingga dari sebuah himpunan. Hasil ini kemudian akan dikembangkan menjadi sebuah prinsip yang dinamakan Prinsip Inklusi-Eksklusi. Sebelum membicarakan gabungan dari n himpunan, dengan n sebagai bilangan bulat positif, sebuah rumusan bagi banyaknya anggota dalam gabungan 3 himpunan A, B, dan C akan diturunkan. Untuk menyusun rumus ini perlu diingat bahwa n(A)+n(B)+n(C) membilang tiap anggota tepat satu kali dari ketiga himpunan tersebut satu kali, anggota yang tepat 2 kali dari himpunan-himpunan itu adalah dua kali, dan anggota-anggota dalam 3 himpunan-himpunan tersebut 3 kali.

Ilustrasikan dari permasalahan gabungan dari 3 himpunan

Diagram Venn Tiga Himpunan

(18)

Teorema (Prinsip Inklusi-Eksklusi)

Daftar Pustaka

(19)

MODUL PERKULIAHAN

HUKUM DAN

PEMBUKTIAN

HIMPUNAN

o Hukum pada himpunan

o Prinsip dualitas.

o Pembuktian pernyataan himpunan

03

87004 Tim Dosen

Abstract

Kompetensi

Hukum pada himpunan adalah sifat-sifat (properties) himpunan. Dua konsep yang berbeda dapat saling dipertukarkan

Mahasiswa mampu memahami dan dapat membuktikan pernyataan himpunan

(20)

benar. Prinsip ini merupakan prinsip dualitas.

Hukum dan Pembuktian Himpunan

A. Hukum pada himpunan.

Hukum pada himpunan adalah sifat-sifat (properties) himpunan. Hukum himpunan sering disebut sebagai hukum aljabar himpunan. Berikut adalah hukum aljabar pada himpunan.

Hukum identitas :

A = A AU = A

Hukum null / dominasi: A =  AU = U Hukum komplemen: AA_{= U} AA =  Hukum idempoten: AA = A AA = A Hukum involusi:

)

( A

_{= A}

Hukum penyerapan (absorpsi): A  (A  B) = A A  (A  B) = A Hukum komutatif: A  B = B  A A  B = B  A Hukum asosiatif: A  (B  C) = (A  B)  C A  (B  C) = (A  B)  C Hukum distributif: A  (B  C) = (A  B)  (A  C) A  (B  C) = (A  B)  (A  C) Hukum De Morgan: B A  = A B B A  = A B Hukum 0/1  = U

U

= 

(21)

B. Prinsip dualitas.

Prinsip Dualitas dikatakan berlaku pada saat dua konsep yang berbeda dapat saling

dipertukarkan namun tetap memberikan jawaban yang benar.

Contoh: Di Amerika kemudi mobil di kiri depan, Inggris (juga Indonesia) kemudi mobil di kanan depan.

Peraturan:

(a) di Amerika Serikat,

 mobil harus berjalan di bagian kanan jalan,

 pada jalan yang berlajur banyak, lajur kiri untuk mendahului,  bila lampu merah menyala, mobil belok kanan boleh langsung (b) di Inggris,

 mobil harus berjalan di bagian kiri jalan,

 pada jalur yang berlajur banyak, lajur kanan untuk mendahului,  bila lampu merah menyala, mobil belok kiri boleh langsung

Prinsip dualitas:

Konsep kiri dan kanan dapat dipertukarkan pada kedua negara tersebut sehingga peraturan yang berlaku di Amerika Serikat menjadi berlaku pula di Inggris

(Prinsip Dualitas pada Himpunan). Misalkan S adalah suatu kesamaan (identity) yang melibatkan himpunan dan operasi-operasi seperti  ,  dan komplemen. Jika S* diperoleh dari S dengan mengganti .

   ,    ,    U,  U  ,

(22)

Sedangkan komplemen dibiarkan seperti semula, maka kesamaan S* juga benar dan disebut dual dari kesamaan S.

Hukum identitas:

A   = A

Dualnya:

A  U = A

Hukum null / dominasi:

A   =  Dualnya: A  U = U Hukum komplemen: A A_{= U} Dualnya: A A=  Hukum idempoten: A  A = A Dualnya: A  A = A Hukum penyerapan: A  (A  B) = A Dualnya: A  (A  B) = A Hukum komutatif: A  B = B  A Dualnya: A  B = B  A Hukum asosiatif: A  (B  C) = (A  B)  C Dualnya: A  (B  C) = (A  B)  C Hukum distributif: A  (B  C)=(A  B)  (A  C) Dualnya: A  (B  C) = (A  B)  (A  C) Hukum De Morgan:

B

A 

=

A



B

Dualnya:

B

A 

=

A



B

(23)

Hukum 0/1



_{= U}

Dualnya:

U

= 

C. Pembuktian Pernyataan Himpunan.

 Pernyataan himpunan adalah argumen yang menggunakan notasi himpunan.  Pernyataan dapat berupa:

1. Kesamaan (identity)

Contoh : Buktikan “A (BC) = (AB)  (AC)” 2. Implikasi

Contoh: Buktikanbahwa “Jika A  B = dan A  (B  C) maka selalu berlaku bahwa A  C”.

1. Pembuktian dengan menggunakan diagram Venn

Misalkan A, B, dan C adalah himpunan.

BuktikanA (BC) = (AB)  (AC) dengan diagram Venn.

(24)

Kedua digaram Venn memberikan area arsiran yang sama. Terbukti bahwa A (BC) = (AB)  (AC).

 Diagram Venn hanya dapat digunakan jika himpunan yang digambarkan tidak banyak jumlahnya.

 Metode ini mengilustrasikan ketimbang membuktikan fakta. Diagram Venn tidak dianggap sebagai metode yang valid untuk pembuktian secara formal.

2. Pembuktian dengan menggunakan table keanggotaan

Misalkan A, B, dan C adalah himpunan.

Buktikan bahwa A  (BC) = (AB)  (AC).

Bukti: A B C BC A (BC) AB AC (AB)  (AC) 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1

Karena kolom A (BC) dan kolom (AB)  (AC) sama, makaA  (BC) = (AB)  (AC).

3. Pembuktian dengan menggunakan aljabar himpunan.

Misalkan A dan B himpunan. Buktikan bahwa (AB)  (A

B

) = A

Bukti:

(25)

= AU (Hukum komplemen) = A (Hukum identitas)

Misalkan A dan B himpunan. Buktikan bahwa A (B – A) = AB

Bukti:

A (B – A) =A (B

A

) (Definisi operasi selisih) = (AB)  (A

_A

) (Hukum distributif) = (AB) U (Hukum komplemen) = AB (Hukum identitas)

Buktikan bahwa untuk sembarang himpunan A dan B, bahwa (i) A (AB) = AB dan

(ii) A (AB) = AB

Bukti:

(i) A (

A

B) = ( A

A

)  (AB) (Hukum distributif) = U (AB) (Hukum komplemen)

= AB (Hukum identitas)

(ii) adalah dual dari (i)

A (

A

B) = (A

A

)  (AB) (Hukum distributif) =  (AB) (Hukum komplemen) = AB (Hukum identitas)

4. Pembuktian dengan menggunakan definisi

 Metode ini digunakan untuk membuktikan pernyataan himpunan yang tidak berbentuk kesamaan, tetapi pernyataan yang berbentuk implikasi. Biasanya di dalam implikasi tersebut terdapat notasi himpunan bagian ( atau ).

(26)

Contoh. Misalkan A dan B himpunan. Jika AB =  dan A (BC) maka buktikan

bahwa AC.

Bukti:

(i) Dari definisi himpunan bagian, PQ jika dan hanya jika setiap x P juga xQ. Misalkan xA. Karena A  (BC), maka dari definisi himpunan bagian, x juga  (B C).

Dari definisi operasi gabungan (), x (BC) berarti xB atau xC. (ii) Karena xA dan AB = , maka xB

Dari (i) dan (ii), xC harus benar. Karenax A juga berlaku x C, maka dapat disimpulkan A C .

Uji kompetensi :

1. Buktikan (A B) B

a. Menggunakan diagram Venn b. Menggunakan tabel keanggotaan c. Kesamaan

2. Buktikan (A B) B

a. Menggunakan diagram Venn b. Menggunakan tabel keanggotaan c. Kesamaan

(27)

Daftar Pustaka

(28)

MODUL PERKULIAHAN

RELASI DAN FUNGSI

 Relasi

 Fungsi

 Jenis fungsi

04

87004 Tim Dosen

Abstract

Kompetensi

Dalam matematika hubungan antara elemen suatu himpunan dengan himpunan lainnya yang dinyatakan dalam bentuk struktur disebut relasi. Cara yang paling mudah untuk menyatakan hubungan antara elemen

- Mahasiswa mampu memahami pengertian fungsi dan sifat-sifatnya. - Mahasiswa mampu menentukan

komposisi fungsi dari dua fungsi - Mahasiswa mampu menentukan

(29)

himpunan adalah dengan himpunan pasangan terurut.

RELASI DAN FUNGSI

D. Relasi.

Hubungan antara elemen suatu himpunan dengan himpunan lainnya yang dinyatakan dalam bentuk struktur disebut relasi. Cara yang paling mudah untuk menyatakan hubungan antara elemen himpunan adalah dengan himpunan pasangan terurut. Himpunan ini dapat diperoleh lewat perkalian kartesian dengan Notasi : A X B = {(x, y) | x e A dan y e B }

Contoh.

(i) Misalkan C = { 1, 2, 3 }, dan D = { x, y }, maka C X D = { (1, x), (1, y), (2, x), (2, y), (3, x), (3, y) } (ii) Misalkan A = B = himpunan semua bilangan riil, maka A X B = himpunan semua titik di bidang datar.

Invers dari R dinotasikan dengan R-1_{adalah relasi dari B ke A yang terdiri dari} pasangan-pasangan terurut yang berkebalikan dengan R, yaitu R-1_{= { (b, a)| (a, b) e R }. Dengan kata lain, b R}-1_{a jika dan hanya jika a R b.}

Contoh : A = { 1,2 } B = { a,b,c } C = { c,d } Tentukanlah : a. (A X B)  (A X C) b. A X (B  C)

(30)

Jawab

a. A X B = { (1, a), (1, b), (1, c), (2, a), (2, b), (2, c) } A X C = { (1, c), (1, d), (2, c), (2, d) }

Maka (A X B)  (A X C) = { (1, c), (2, c) } b. Dalam hal ini B  C = { c }

Maka A X (B  C) = { (1, c), (2, c) }

Perhatikan bahwa (A X B)  (A X C) = A X (B  C). Hal ini berlaku untuk sembarang himpunan A, B, dan C. Contoh :

Misalkan R adalah relasi dari A = { 1, 2, 3, 4 } ke B = { x, y, z } didefinisikan oleh R = { (1, y), (1, z), (3, y), (4, x), (4, z) }

Tentukan domain dan range dari R Tentukan relasi invers R-1_{dari R}

JAWAB

Domain dari R terdiri dari elemen-elemen pertama dari pasangan terurut R, dan rangenya terdiri dari elemen-elemen keduanya. Maka domain (R) = { 1, 3, 4 } dan range (R) = { x, y, z }.

R-1_{didapatkan dengan menukarkan urutan dari pasangan-pasangan terurut di R.} Maka

R-1_{= { (y, 1), (z, 1), (y, 3), (x, 4), (z, 4) }}

Komposisi Relasi

Misalkan A, B, C adalah himpunan-himpunan, dan misalkan R adalah sebuah relasi dari A ke B dan misalkan S adalah sebuah relasi dari B ke C. dengan begitu, R adalah subset dari A X B dan S adalah subset dari B X C. maka R dan S akan memberikan sebuah relasi dari A ke C yang dinyatakan dengan R ○ S dan didefinisikan A (R ○ S) c jika untuk sembarang b e B kita dapatkan a R b dan b S c.

Dengan demikian,

R ○ S = { (a, c) ada b e B dimana (a, b) e R dan (b, c) e S } Relasi R ○ S disebut komposisi dari S dan dinyatakan dengan RS.

(31)

1. Misalkan

K = { 1,2,3 }, M = { A, B, C } dan N = { X, Y, Z }

Perhatikan relasi R dari K ke M dan S dari M ke N berikut R = { (1, B), (2, A), (3, C) }

Dan S = { (A, Y), (B, X), (C, Z) }

Tentukan relasi komposisi R ○ S!

Gambarlah diagram panah dari R dan S seperti berikut ini :

Pada gambar diatas ada panah dari 1 ke B yang diikuti panah dari B ke X. maka 1 (R ○ S) X karena 1RB dan B S X. dengan demikian (1,X) anggota dari R○ S. Dengan cara yang sama sebuah path dari 2 ke A ke Y dan path dari 3 ke C ke Z. Maka (2, Y) dan (3, Z) juga anggota dari R ○ S. Tidak ada pasangan lain yang menjadi anggota R ○ S. maka

R ○ S = { (1, X), (2, y), (3, z) }

Definisi :

Sebuah relasi pada sebuah himpunan A disebut relasi ekivalen jika dan hanya jika relasi tersebut bersifat refleksif, simetris dan transitif.

Contoh : Misal himpunan A adalah himpunan string kata dalam kosa kata bahasa Indonesia.

R adalah relasi pada himpunan A, dimana untuk A (b, a)∈A, a R b (a berelasi dengan b) jika dan hanya jika l(a) = l(b), dimana l(x) adalah panjang kata x. Apakah R adalah relasi ekivalen?

(32)

jika (a, a) ε R untuk setiap a ε A ...(*)

Karena untuk setiap string kata a berlaku l(a) = l(a), maka syarat (*) terpenuhi, sehingga R bersifat refleksif

(ii) Syarat R bersifat simetris :

jika untuk semua (a, b) ε A, jika (a, b) ε R, maka (b, a) ε R ...(**) Karena untuk setiap string kata a, b berlaku :

jika l(a)=l(b), maka l(b) = l(a),

maka syarat (**) terpenuhi, sehingga R bersifat simetris.

(iii) Syarat R bersifat transitif:

jika (a, b) ε R dan (b, c) ε R, maka (a, c) ε R, untuk a, b, c ε A ..(***) Karena untuk setiap string kata a, b, c berlaku :

jika l(a) = l(b) dan l(b) = l(c), maka l(a) = l(c), maka syarat (***) terpenuhi, sehingga R bersifat transitif.

Jadi R adalah relasi ekivalen

Partial Ordering

Sebuah relasi R pada sebuah himpunan S disebut partial order jika relasi ini bersifat bersifat refleksif, antisimetris, dan transitif.

Contoh .

Tunjukkan bahwa relasi lebih besar atau sama dengan adalah partial order pada himpunan bilangan bulat!

R dapat kita definisikan sebagai

(i) Untuk semua bilangan bulat tentu saja berlaku, yang artinya untuk semua bilangan bulat a, maka (a, a). Sehingga R bersifat refleksif

(ii) Jika berlaku dan maka tentu a = b, yang artinya (a, b) dan (b, a) aa ≥ ab ≥ R∈→ (a = b). Sehingga R bersifat antisimetris

(iii) Jika yang berarti jika (a, b) dan (b, c) ba ≥ ab ≥ ca ≥ R∈ maka (a, c) R∈.

Sehingga R bersifat transitif. Karena R bersifat refleksif, antisimetris dan transitif, maka R adalah Partial Order.

(33)

E. Fungsi

Fungsi merupakan kejadian khusus dari relasi. Hubungan antara fungsi, relasi dan hasil kali kartesian dari himpunan X ke himpunan Y digambarkan sbb

Andaikan setiap elemen dari himpunan A dipetakan secara unik ke suatu elemen di himpunan B, kumpulan dari pemetaan-pemetaan ini disebut fungsi atau pemetaan dari A ke B. Kita menyatakan sebuah fungsi f dari A ke B dengan f : A  B. Kita menuliskan f(a) untuk elemen di B yang mana f memetakan ke a  A, f(a) adalah nilai fungsi di a atau petaan a di bawah f. Istilah fungsi dan pemetaan seringkali digunakan dengan pengertian yang sama, meskipun ada sumber-sumber yang mengganti istilah fungsi untuk suatu nilai real atau pemetaan bernilai kompleks, yaitu yang memetakan suatu himpunan ke dalam bilangan real R atau C.

Pada f : A B

Himpunan A adalah domain dari f. Himpunan B adalah kodomain dari f. Himpunan dari semua nilai pemetaan f disebut image (range) dari f dan dinyatakan dengan Im f atau f (A).

Im f = { b e B terdapat a e A sedemikian hingga f (a) = b }

Contoh :

Andaikan A adalah himpuan dari mahasiswa –mahasiswa di kampus. Tentukan manakah dari pemetaan berikut yang mendefinisikan sebuah fungsi pada himpunan A.

a) Setiap mahasiswa memetakan usianya b) Setiap mahasiswa memetakan gurunya c) Setiap mahaiswa memetakan jenis kelaminnya

(34)

Jawab :

Suatu kumpulan pemetaan adalah sebuah fungsi pada A dimana setiap a e A dipetakan tepat ke satu elemennya, sehingga

a) Ya, karena setiap mahsiswa mempunyai satu dan hanya satu usia

b) Ya, jika setiap mahasiswa hanya memiliki satu guru. Tidak, jika ada mahasiswa yang memiliki guru lebih dari satu.

c) Ya, karena setiap mahasiswa hanya memiliki satu jenis kelamin. d) Tidak, jika ada mahasiswa yang belum menikah

Contoh :

Diketahui fungsi f dari G = { A, B, C, D } ke H = { X, Y, Z, W } yang didefinisikan oleh gambar di bawah ini.

Tentukanlah

a) image (range) dari setiap elemen di G b) image (range) dari f

c) grafik dari f, tuliskan f sebagai himpunan dari pasangan-pasangan terurut.

Jawab

a) panah menyatakan image (range) dari suatu elemen, sehingga f (A) = Y, f (B) = X, f (C) = Z, f (D) = Y

b) Image f(G) dari f terdiri dari semua nilai pemetaan. Hanya X, Y, Z yang muncul sebagai nilai pemetaan, sehingga f(G) = { X,Y,Z }

c) Pasangan terurut (A, f (A)), dimana A G adalah bentuk grafik f. maka f = { (A,Y), (B,X), (C,Z), (D,Y) }

(35)

Pada fungsi f yang memetakan A ke B dan fungsi g yang memetakan B ke C, dimana kodomain dari f adalah domain dari g. Komposisi fungsi f dan g ditulis dengan g ○ f adalah fungsi dari A ke C yang didefinisikan oleh

(g ○ f) (a) || g (f (a))

untuk mendapatkan range dari a di bawah g ○ f, pertama kita mencari range a di bawah f kemudian tentukan range dari f (a) di bawah g.

Misalkan fungsi f K L dan g L  M didefinisikan oleh gambar berikut .

Tentukan komposisi fungsi !

Kita gunakan defisi komposisi fungsi untuk menghitung (g ○ f) (A) = g (f (A)) = g (Y) = T

(g ○ f) (B) = g (f (B)) = g (X) = S (g ○ f) (C) = g (f (C)) = g (Y) =T

Perhatikan bahwa diperoleh jawaban yang sama jika kita mengikuti arah panah pada diagram.

A  Y  T, B  X  S, C  Y T

Injektif, Bijektif dan Surjektif

Misalkan f adalah suatu fungsi dari X ke Y. f disebut fungsi injektif (one to one) bila dan hanya bila setiap anggota Y paling banyak hanya mempunyai satu kawan di X. Fungsi surjektif apabila setiap anggota Y mempunyai kawan di X. Kawan tersebut tidak harus tunggal. Fungsi bijektif apabila fungsi tersebut injektif dan sekaligus surjektif

(36)

Fungsi Invers

Diketahui suatu fungsi f : X  Y adalah suatu fungsi. Dari contoh-contoh sebelumnya tampak bahwa relasi dari Y ke X belum tentu merupakan fungsi. Akan tetapi jika fungsi f : X  Y adalah suatu fungsi bijektif, maka setiap elemen y E Y mempunyai tepat satu kawan di X. Ini berarti bahwa relasi dari Y ke X merupakan fungsi juga. Fungsi dari Y ke X disebut invers fungsi f (f1)

(37)

Daftar Pustaka

(38)

MODUL PERKULIAHAN

PROPOSISI dan

KUANTOR

O PROPOSISI

O NEGASI PROPOSISI

o KUANTOR

05

87004 Tim Dosen

Abstract

Kompetensi

Ilmu logika lebih mengarah kepada bentuk kalimat (sintaks) dari pada arti kalimat itu sendiri (sematik). Kalkulus proposisi merupakan metoda komputasi untuk menentukan apakah proposisi/kalimat yang ditinjau nilai benar/salah (true/false). Kuantor universal menunjukkan bahwa setiap objek dalam semestanya

Mahasiswa mampu memahami dan membedakan bentuk-bentuk proposisi dan kuantor.

(39)

mempunyai sifat kalimat yang menyatakannya. Kuantor eksistensial menunjukkan bahwa diantara objek-objek (term–term) dalam semestanya, paling sedikit ada ada satu term/objek yang memenuhi sifat kalimat yang menyatakannya.

Proposisi dan Kuantor

G. PROPOSISI

Ilmu logika berhubungan dengan kalimat-kalimat (argumen). Dengan menggunakan aturan-aturan tertentu maka pernyataan yang terdiri dari argumen-argumen bisa bernilai benar atau salah. Ilmu logika lebih mengarah kepada bentuk kalimat (sintaks) dari pada arti kalimat itu sendiri (sematik).

1. Proposisi

Kata merupakan rangkaian huruf yang mengandung arti, sedangkan kalimat adalah kumpulan kata yang disusun menurut aturan tata bahasa dan mengandung arti. Di dalam matematika tidak semua pernyataan yang bernilai benar atau salah saja yang digunakan dalam penalaran. Pernyataan disebut juga kalimat deklaratif yaitu kalimat yang bersifat menerangkan dan disebut juga proposisi. Pernyataan/ Kalimat Deklaratif/ Proposisi adalah kalimat yang bernilai benar atau salah tetapi tidak keduanya

Berikut adalah beberapa contoh proposisi:  4 + 1 = 5

 9 adalah bilangan prima

 Jakarta adalah ibukota negara Indonesia.

Kalimat-kalimat diatas adalah proposisi karena dapat diketahui nilai kebenarannya. Kalimat (a) dan (c) bernilai benar, sedangkan kalimat (b) bernilai salah.

Contoh berikut ini adalah kalimat-kalimat yang bukan merupakan proposisi: a. Dimana letak pulau Bali?

b. x + y = 2

c. Siapa namamu? d. x > 5

Tetapi pernyataan berikut :“Untuk sembarang bilangan bulat n ≥ 0, maka 2n adalah bilangan genap.” dan “x + y = y + x untuk setiap x dan y bilangan riil”

(40)

adalah proposisi, karena pernyataan pertama adalah cara lain untuk menyatakan bilangan genap dan pernyataan kedua walaupun tidak menyebutkan nilai x dan y, tetapi pernyataan tersebut benar untuk nilai x dan y berapapun. Proposisi biasanya dilambangkan dengan huruf kecil seperti p, q, r, dan seterusnya.

Misalnya,

p : 6 adalah bilangan genap. q : 2 + 3 = 7

r : 2 < 5

2. Kalkulus Proposisi

Kalkulus proposisi merupakan metoda komputasi untuk menentukan apakah proposisi/kalimat yang ditinjau nilai benar/salah (true/false). Dengan demikian pada kalkulus proposri yang dipelajari adalah bagaimana menentukan nilai kebenaran suatu kalimat (True/False). Satu atau lebih proposisi dapat dikombinasikan untuk menghasilkan proposisi baru. Operator yang digunakan untuk mengkombinasikan proposisi disebut operator logika. Operator logika dasar yang digunakan adalah dan (and), atau (or), dan tidak (not). Proposisi baru yang diperoleh dari pengkombinasian tersebut dinamakan proposisi majemuk (compound proposition). Dalam logika dikenal 5 buah operator berikut ini.

a. Konjungsi

Konjungsi merupakan operator pada kalkulus proporsi dengan lambang ˄. Operator ini memiliki tabel kebenaran seperti berikut ini.

Contoh :

Diketahui proposisi berikut ini: p : Langit mendung

(41)

q : Adi membawa jas hujan.

p ˄ q : Langit mendung dan Adi membawa jas hujan.

b. Disjungsi

Disjungsi merupakan operator pada kalkulus proporsi dengan lambang ˅. Operator ini memiliki tabel kebenaran seperti berikut ini.

Kalimat disjungsi dapat mempunyai 2 arti yaitu :

c. Inklusif OR

Yaitu jika “p benar atau q benar atau keduanya true” Contoh :

p : 7 adalah bilangan prima q : 7 adalah bilangan ganjil

p  q : 7 adalah bilangan prima atau ganjil

Benar bahwa 7 bisa dikatakan bilangan prima sekaligus bilangan ganjil.

d. Eksklusif OR

Yaitu jika “p benar atau q benar tetapi tidak keduanya”. Contoh :

p :Saya akan melihat pertandingan bola di TV. q :Saya akan melihat pertandingan bola di lapangan.

(42)

Hanya salah satu dari 2 kalimat penyusunnya yang boleh bernilai benarya itu jika “Saya akan melihat pertandingan sepak bola di TV saja atau di lapangan saja tetapi tidak keduanya.

e. Negasi

Negasi merupakan operator pada kalkulus proporsi dengan lambang

~

atau



. Operator ini memiliki tabel kebenaran seperti berikut ini.

f. Implikasi

Implikasi merupakan operator pada kalkulus proporsi dengan lambang →. Operator ini memiliki tabel kebenaran seperti berikut ini.

(43)

Misalkanada 2 pernyataan p dan q, untuk menunjukkan atau membuktikan bahwa jika p bernilai benar akan menjadikan q bernilai benar juga, diletakkan kata “JIKA” sebelum pernyataan pertama lalu diletakkan kata “MAKA” sebelum pernyataan kedua sehingga didapatkan suatu pernyataan majemuk yang disebut dengan Implikasi /Pernyataan bersayarat dinotasikan dengan simbol “”.

Notasi pq dapat dibaca : 1. Jika p maka q

2. q jika p

3. p adalah syarat cukup untuk q 4. q adalah syarat perlu untuk p

Contoh :

p : Pak Budi adalah seorang pemilik usaha pertambakan.

q : Pak Budi adalah seorang wiraswasta.

p q : Jika Pak Budi adalah pemilik usaha pertambakan. Maka pastilah dia seorang wiraswasta.

g. bi-implikasi

bi-implikasi merupakan operator pada kalkulus proporsi dengan

lambang⇔. Operator ini memiliki tabel kebenaran seperti berikut ini.

Biimplikasi atau bikondosional adalah pernyataan majemuk dari dua pernyataan p dan q yang dinyatakan dengan notasi “p  q” yang bernilai sama

(44)

dengan (p q)  (q  p) sehingga dapat dibaca “ p jika dan hanya jika q” atau “p bila dan hanya bila q”. Biimplikasi 2 pernyataan hanya akan bernilai benar jika implikasi kedua kalimat penyusunnya sama-sama bernilai benar. Contoh :

p :Dua garis saling berpotongan adalah tegaklurus. q :Dua garis saling membentuk sudut 90 derajat.

p q : Dua garis saling berpotongan adalah tegak lurus jika dan hanya jika dua garis saling membentuk sudut 90 derajat.

H. NEGASI PROPOSISI

Misal proposisi “ Pak Saman makan nasi dan minum es teh manis”. Suatu konjungsi akan bernilai benar jika kedua kalimat penyusunnya yaitu p dan q bernilai benar, sedangkan negasi adalah pernyataan yang bernilai salah jika pernyataan awalnya bernilai benar dan bernilai benar jika pernyataan awalnya bernilai salah.

Oleh karena itu negasi dari : “Pak Saman makan nasi dan minum es teh manis” adalah suatu pernyataan majemuk lain yang salah satu komponennya merupakan negasi dari komponen pernyataan awalnya. Jadi negasinya adalah: “Pak Saman tidak makan nasi dan tidak minum es teh manis”.

Disini berlaku hukum De Morgan yaitu : (pq) ekuivalen dengan pq  Negasi Disjungsi

Contoh : “Pak Saman makan nasi dan minum es teh manis”

Suatu disjungsi akan bernilai salah hanya jika kedua komponen penyusunnya bernilai salah, selain itu bernilai benar. Sehingga negasi dari kalimat diatas adalah : “ Tidak benar bahwa Pak Saman makan nasi dan minum es teh manis” atau dapat juga dikatakan “Pak Saman tidak makan nasi dan tidak minum es teh manis. Disini berlaku hukum De Morgan yaitu : (pq) pq

(45)

 Negasi Implikasi

Misal proposisi “Jika hari hujan maka Pak Saman membawa payung”.

Untuk memperoleh negasi dari pernyataan diatas, kita dapat mengubah bentuknya ke dalam bentuk disjungsi kemudian dinegasikan, yaitu :

p q pq

Maka negasinya

( p q) (pq)  pq

 Negasi biImplikasi

Biimplikasi atau bikondisional adalah pernyataan majemuk dari dua pernyataaan p dan q yang dinotasikan dengan p  q  (p  q)  (q  p) sehingga : (p  q)  [(p  q)  (q  p)]  [(pq )  (qp)]  (pq ) (qp) (p  q)  (pq )  (qp) I. Kuantor 1. Kuantor Universal

Kuantor universal menunjukkan bahwa setiap objek dalam semestanya mempunyai sifat kalimat yang menyatakannya. Kita dapat meletakkan kata-kata “Untuk semua/setiap x” di depan kalimat terbuka yang mengandung variabel x untuk menghasilkan kalimat yang mempunyai suatu nilai kebenaran. Nilai x ditentukan berdasarkan semesta pembicaraannya. Kuantor universal disimbolkan dengan “∀”. Kuantor universal mengindikasikan bahwa sesuatu bernilai benar untuk semua individual-individualnya.

(46)

Misal kalimat : “Semua gajah mempunyai belalai” , maka jika predikat “mempunyai belalai” diganti dengan simbol B maka dapat ditulis :

G(x) ⇒ B(x),

dibaca “Jika x adalah gajah, maka x mempunyai belalai”. Tetapi kalimat di atas belum kalimat berkuantor karena kalimat diatas belum memuat kata “semua”. Untuk itu perlu ditambahkan simbul kuantor universal sehingga menjadi

(∀x)(G(x) ⇒ B(x))

jadi sekarang dapat dibaca ” Untuk semua x, jika x adalah gajah, maka x mempunyai belalai”.

Pernyataan-pernyataan yang berisi kata ”semua”, ”setiap”, atau kata lain yang

sama artinya, mengindikasikan adanya pengkuantifikasian secara universal,

maka dipakai kuantor universal.

Misalnya jika diketahui pernyataan logika, ”Setiap mahasiswa harus belajar dari buku teks”, jika ingin ditulis dalam logika predikat, maka ditentukan misal B untuk “ harus belajar dari buku teks”, sehingga jika ditulis B(x), berarti “x harus belajar dari buku teks”. Kata “Setiap mahasiswa” mengindikasikan bernilai benar untuk setiap x, maka penulisan yang lengkap adalah:

(∀x) Bx

dibaca “Untuk setiap x, x harus belajar dari buku teks”. Akan tetapi notasi diatas belum sempurna karena x belum menunjuk mahasiswa, maka harus lebih ditegaskan dan sebaiknya ditulis :

(∀x)(M(x) ⇒ B(x)),

dibaca “Untuk setiap x, jika x mahasiswa, maka x harus belajar dari buku teks”. Langkah untuk melakukan pengkuantoran universal:

1. Carilah lingkup (scope) dari kuantor universalnya, yaitu “Jika x adalah mahasiswa, maka x harus rajin belajar”. Selanjutnya akan ditulis: mahasiswa(x) ⇒ harus rajin belajar(x).

2. Berilah kuantor universal di depannya (∀x)(mahasiswa(x) ⇒ harus rajin belajar(x)). Kemudian ubah menjadi suatu fungsi (∀x)(M(x) ⇒ B(x)) Contoh :

Jika diketahui persamaan x+3>10, dengan x adalah himpunan bilangan bulat positif A > 5. Tentukan nilai kebenaran (∀x∈A) x+3>10. Untuk menentukan nilai kebenarannya, maka harus dicek satu persatu.

(47)

A={1,2,3,4}. Jika kuantor universal, maka untuk semua nilai A yang dimasukkan harus memenuhi persamaan yaitu x+3>10

Untuk A=1, maka 1+3>10 ≡ 4>10 Memenuhi A=2, maka 2+3>10 ≡ 5>10 Memenuhi A=3, maka 3+3>10 ≡ 6>10 Memenuhi A=4, maka 4+3>10 ≡ 7>10 Memenuhi

Karena semua himpunan A memenuhi, maka (∀x) x+3>10 bernilai benar. Tapi jika ada satu saja nilai A yang tidak memenuhi, misalnya dimasukkan A=8, sehingga 8+3>10 ≡ 11>10, dimana hasilnya salah maka (∀x) x+3>10 bernilai salah. Nilai x yang menyebabkan suatu kuantor bernilai salah disebut dengan contoh penyangkal atau counter example.

2. Kuantor Eksistensial (Existensial Quantifier)

Kuantor eksistensial menunjukkan bahwa diantara objek-objek (term–term) dalam semestanya, paling sedikit ada ada satu term/objek yang memenuhi sifat kalimat yang menyatakannya. Ada beberapa kata yang dapat digunakan misal “Terdapat…..”, “Beberapa x bersifat…..”, “Ada……”, “Paling sedikit ada satu x………” di depan kalimat terbuka yang mengandung variabel x. Kuantor eksistensial disimbolkan dengan ”∃”. Kuantor eksistensial mengindikasikan bahwa sesuatu kadang-kadang bernilai benar untuk individu-individualnya, misal ” Ada pelajar yang memperoleh beasiswa berprestasi ”.

Cara menentukan kuantor Eksistensial

1. Carilah scope dari kuantor-kuantor eksistensialnya.

“Ada x yang adalah pelajar, dan x memperoleh beasiswa berprestasi “. Selanjutnya akan ditulis :

Pelajar(x) ∧ memperoleh beasiswa berprestasi (x) 2. Berilah kuantor eksisitensial di depannya

(∃x) (Pelajar(x)∧ memperoleh beasiswa berprestasi(x)) Ubahlah menjadi suatu fungsi.

(∃x)(P(x) ∧ B(x))

(48)

“Beberapa orang rajin beribadah”.

Jika ditulis dengan menggunakan logika predikat, maka: ”Ada x yang adalah orang, dan x rajin beribadah”. (∃x)(Orang(x) ∧ rajin beribadah(x))

(∃x)(O(x) ∧ I(x)) Contoh :

“Ada binatang yang tidak mempunyai kaki”.

“Terdapat x yang adalah binatang dan x tidak mempunyai kaki”. (∃x)(binatang(x) ∧ tidak mempunyai kaki(x))

(∃x)(B(x) ∧￢K(x)) Contoh :

Misalkan B adalah himpunan bilangan bulat. Tentukan nilai kebenaran (∃x ∈ B)(x2=x).

(∃x ∈ B)(x2=x) dapat dibaca “Terdapat x yang adalah bilangan bulat dan x memenuhi x^2=x”. (∃x ∈ B)(x^2=x) akan bernilai benar jika dapat ditunjukkan paling sedikit ada satu bilangan bulat yang memenuhi x^2=x.

Misal x= -1, maka 〖-1〗^2 = 1 Tidak memenuhi x= 1, maka 〖(1)〗^2=1 Memenuhi

Karena ada satu nilai yang memenuhi, yaitu x=1, maka pernyataan di atas bernilai benar.

3. Kuantor Ganda

Domain atau semesta pembicaraan penafsiran kuantor sangat penting untuk menentukan jenis kuantor yang akan digunakan serta mempengaruhi penulisan simbolnya. Misal pernyataan “Setiap orang mencintai Jogjakarta”

Selanjutnya, dapat ditulis simbolnya dengan logika predikat (∀x)C(x,j). Simbol tersebut dapat dibaca “Untuk semua y, y mencintai Jogjakarta”. Persoalan yang terjadi adalah domain penafsiran seseorang untuk y bisa berbeda-beda. Ada orang yang menganggap y adalah manusia, tetapi mungkin orang lain menganggap y bisa mahluk hidup apa saja dan mungkin y bisa menjadi benda apa saja. Tentu saja domain penafsiran semacam ini kacau karena yang dimaksudkan pasti hanya orang atau manusia. Oleh karena itu, untuk memastikan

(49)

bahwa domain penafsiran hanya orang, penulisan simbol harus diperbaiki seperti berikut :

(∀y)(O(y)⇒ C(y,j) )

Sekarang simbol tersebut dapat dibaca ”Untuk semua y jika y adalah orang, maka y mencintai Jogjakarta”.

Untuk menulis simbol yang tepat, memang harus menempatkan terlebih dahulu domain penafsiran karena domain penafsiran Sangat mempengaruhi penulisan dan sekaligus menghindari terjadinya ambiguitas. Contoh domain penafsiran yang bersifat umum antara lain manusia, binatang, tumbuh-tumbuhan, bilangan prima, bilangan asli, dan sebagainya, yang nantinya akan menggunakan kuantor universal. Akan tetapi jika tidak semuanya, misalnya beberapa manusia, atau satu manusia saja, akan memakai kuantor yang berbeda yaitu kuantor eksisitensial. Untuk dua kuantor yang berbeda pada satu penulisan simbol yang berasal dari satu pernyataan dapat dilihat pada contoh berikut.

Misal “Setiap orang dicintai oleh seseorang”

Dengan notasi simbol logika predikat, akan ditullis seperti berikut (∀x)(∃y)C(y,x)

Yang dapat dibaca ”Untuk semua x, terdapat y dimana y mencintai x”

X dan Y sebenarnya menunjuk domain penafsiran yang sama yaitu orang, dan pada simbol tersebut ternyata dibedakan. Penulisan tersebut lebih baik lagi jika bisa memakai variable yang sama. Maka pernyataan diatas secara lengkap dapat ditulis :

(∀x)(O(x)⇒ (∃x)(O(y)∧ C(y,x) ) )

Misal H(x)∶ x hidup , M(x)∶ x mati

(∀x)(H(x) ∨ M(x)) dibaca “Untuk semua x, x hidup atau x mati” Akan tetapi jika ditulisnya (∀x)(H(x)) ∨ M(x) maka dibaca “Untuk semua x hidup, atau x mati”. Pada “x mati”, x tidak terhubung dengan kuantor universal, yang terhubung hanya”x hidup”. Perhatikan penulisan serta peletakan tanda kurungnya. Sehingga umum, hubungan antara penempatan kuantor ganda adalah sebagai berikut :

(50)

(∃x)(∃y) P(x,y) ≡ (∃y)(∃x) P(x,y) (∃x)(∀y) P(x,y) ≡ (∀y)(∃x) P(x,y)

Ingkaran kalimat berkuantor ganda dilakukan dengan cara yang sama seperti ingkaran pada kalimat berkuantor tunggal.

￢[(∃x)(∀y) P(x,y)] ≡ (∀x)(∃y) ￢P(x,y) ￢[(∀x)(∃y) P(x,y)] ≡ (∃x)(∀y) ￢P(x,y)

Contoh:

Misal : “Ada seseorang yang mengenal setiap orang”. Untuk menentukan bentuk simbolnya.

1. Jadikan potongan pernyataan ”x kenal y”, maka akan menjadi K(x,y) yang berarti “ x kenal y”.

2. Jadikan potongan pernyataan ”x kenal semua y”, sehingga menjadi (∀y) K(x,y).

3. Jadikan pernyataan “ada x, yang x kenal semua y”, sehingga menjadi (∃x)(∀y) K(x,y)

(51)

Daftar Pustaka

(52)

MODUL PERKULIAHAN

TAUTOLOGI DAN

KONTRADIKASI

O TAUTOLOGI

O INGKARAN KONVERS, INVERS, DAN KONTRAPOSISI

O PENYEDERHANAAN LOGIKA

o MODUS PONEN

o MODUS TOLLENS

06

87004 Tim Dosen

Abstract

Kompetensi

Tautologi adalah suatu bentuk kalimat yang selalu bernilai benar tidak peduli bagaimanapun nilai kebenaran masing-masing kalimat

- Mahasiswa mampu memahami pengertian bentuk-bentuk tautologi dan kontradikasi

(53)

penyusunnya, Sebaliknya kontradiksi adalah suatu bentuk kalimat yang selalu bernilai salah, tidak peduli bagaimanapun nilai kebenaran masing-masing kalimat penyusunnya.

- Mahasiswa mampu memahami penarikan kesimpulan secara valid.

Tautologi dan Kontradikasi

A. TAUTOLOGI, KONTRADIKSI DAN CONTIGENT

Tautologi adalah suatu bentuk kalimat yang selalu bernilai benar (True) tidak peduli bagaimanapun nilai kebenaran masing-masing kalimat penyusunnya, sebaliknya kontradiksi adalah suatu bentuk kalimat yang selalu bernilai salah (False), tidak peduli bagaimanapun nilai kebenaran masing-masing kalimat penyusunnya. Dalam tabel kebenaran, suatu tautologi selalu bernilai True pada semua barisnya dan kontradiksi selalu bernilai False pada semua baris. Kalau suatu kalimat tautologi diturunkan lewat hukum-hukum yang ada maka pada akhirnya akan menghasilkan True, sebaliknya kontradiksi akan selalu bernilai False.Jika pada semua nilai kebenaran menghasilkan nilai F dan T, maka disebut formula campuran (contingent).

Contoh

1. Tunjukkan bahwa p(p) adalah tautologi!

p p p(p)

T T T

T F T

F T T

2. Tunjukkan bahwa (pq)  [(p) (q)] adalah tautologi! p q p q pq p q (pq)  [(p)  (q)]

T T F F T F T

T F F T T F T

F T T F T F T

F F T T F T T

(54)

p q p q pq p q (pq)  [(p)  (q)]

T T F F T F F

T F F T T F F

F T T F T F F

F F T T F T F

4. Tunjukkan bahwa [(pq)  r]  p adalah contingent!

p q r pq (pq)  r [(pq)  r]  p T T T T T T T T F T T T T F T F F T T F F F F T F T T F T F F T F F T F F F T F T F F F F F T F

B. INGKARAN KONVERS, INVERS DAN KONTRAPOSISI

Contoh :

Tentukan ingkaran atau negasi konvers, invers, dan kontraposisi dari implikasi berikut. “Jika suatu bendera adalah bendera RI maka bendera tersebut berwarna merah dan putih”

Penyelesaian

Misal p : Suatu bendera adalah bendera RI

q : Bendera tersebut berwarna merah dan putih

maka kalimatnya menjadi p  q atau jika menggunakan operator dan maka p  q ekuivalen(sebanding/) dengan p  q. Sehingga :

(55)

Implikasi : (pq) p  q

Negasinya : (pq)  pq

Kalimatnya :“ Suatu bendera adalah bendera RI dan bendera tersebut tidak berwarna merah dan putih”.

2) Negasi dari konvers

Konvers : qp qp

Negasinya : (qp)  qp

Kalimatnya : “Ada/Terdapat bendera berwarna merah dan putih tetapi bendera tersebut bukan bendera RI”.

3) Negasi dari invers

Invers : p q (p)q)  pq

Negasinya : (pq) pq

Kalimatnya : “Suatu bendera bukan bendera RI atau bendera tersebut berwarna merah dan putih”.

4) Negasi dari kontraposisi

Kontraposisi : q p (q)p  qp

Negasinya : (qp) qp

Kalimatnya : “ Suatu bendera tidak berwarna merah dan putih dan bendera tersebut adalah bendera RI”.

C. FORMULA

Pada tautologi, dan juga kontradiksi, dapat dipastikan bahwa jika dua buah ekspresi logika adalah tautologi, maka kedua buah ekspresi logika tersebut ekuivalen secara logis, demikian pula jika keduanya kontradiksi. Persoalannya ada pada contingent, karena memiliki semua nilai T dan F. Tetapi jika urutan T dan F atau sebaliknya pada tabel kebenaran tetap pada urutan yang sama maka tetap disebut ekuivalen secara logis.

(56)

Contoh :

1. Badu tidak pandai, atau dia tidak jujur.

2. Adalah tidak benar jika Badu pandai dan jujur.

Secara intuitif dapat ditebak bahwa kedua pernyataan di atas sebenarnya sama, tetapi bagaimana jika dibuktikan dengan menggunakan tabel kebenaran berdasarkan ekspresi logika. Pembuktian pernyataan diatas dapat diakukan dengan tahapan berikut.

1. Ubah dahulu argumen di atas kedalam bentuk ekspresi/notasi logika. Misal : A = Badu pandai

B = Badu jujur Maka kalimatnya menjadi 1. AB

2. (AB)

2. Buat tabel kebenarannya

A B A B AB AB (AB)

T T F F T F F

T F F T F T T

F T T F F T T

F F T T F T T

Perhatikan ekspresi di atas!

Meskipun kedua ekspresi logika di atas memiliki nilai kebenaran yang sama, ada nilai T dan F, keduanya baru dikatakan ekuivalen secara logis jika dihubungkan dengan perangkai ekuivalensi dan akhirnya menghasilkan tautologi.

3. Tambahkan perangkai biimplikasi untuk menghasilkan tautologi

AB (AB) AB (AB)

(57)

T T T

Jika hasilnya adalah tautologi (bernilai T semua), maka dikatakan bahwa kedua argumen tersebut ekuivalen secara logis.

Selain dengan menggunakan tabel kebenaran, menentukan dua buah argumen adalah ekuivalen secara logis dapat juga menggunakan hukum-hukum ekuivalensi logika yang dapat dilihat pada formula berikut.

Identitas p1 p p0 p Ikatan p1 T p0 0 Idempoten ppp ppp Negasi pp 1 pp 0 Negasi Ganda p p Komutatif pq qp pq qp Asosiatif (pq)r p(qr) (pq)rp(qr) Distributif p(qr)  (pq)(pr) p(qr)  (pq)(pr) De Morgan’s (pq) p q (pq) p q Aborbsi p(pq)  p p(pq)  p Contoh :

1. Buktikan ekuivalensi kalimat di bawah ini dengan hukum-hukum ekuivalensi. (pq)  (pq) p Penyelesaian (pq)  (pq)  (p(q))  (pq)  (pq)  (pq) p  (qq) p  T p Terbukti

(58)

Dalam membuktikan ekuivalensi pq ada 3 macam cara yang bisa dilakukan : 1. P diturunkan terus menerus (dengan menggunakan hukum-hukum ekuivalensi

logika yang ada).

2. Q diturunkan terus-menerus (dengan menggunakan hukum-hukum ekuivalensi logika yang ada), sehingga didapat P.

3. P dan Q diturunkan secara terpisah sehingga akhirnya didapat R

Sebagai aturan kasar, biasanya bentuk yang lebih kompleks yang diturunkan ke dalam bentuk yang sederhana. Jadi jika p kompleks maka aturan (1) yang dilakukan. Sebaliknya jika q yang lebih kompleks maka aturan (2) yang dilakukan. Aturan (3) digunakan jika p dan q sama-sama kompleks.

D. PENYEDERHAAN LOGIKA

Operasi penyederhanaan menggunakan hukum-hukum ekuivalensi logis. Selanjutnya perhatikan operasi penyederhanaan berikut dengan hukum yang digunakan tertulis di sisi kanannya. Penyederhanaan ekspresi logika atau bentuk-bentuk logika ini dibuat sesederhana mungkin dan sudah tidak dimungkinkan dimanipulasi lagi.

Contoh 1: p (p q)

p (p q) ingat pq pq

(p)(p q) ingat pq pq

 p  (p  q) Hk. Negasi ganda dan De Morgan

 (pp)  (pq) Hk. Distributif p(pq) Hk. Idempoten ppp p Hk. Absorbsi Contoh 2: p(pq)  (p1) (pq) Hk.Identitas p(1q) Hk.Distributif  p1 Hk.Identitas

(59)

p Hk.Identitas Contoh 3: (pq)  (qp)  (pq)  (qp) ingat pq pq  (pq)  (pq) Hk. Komutatif  [(pq) p]  [(pq)q] Hk. Distributif  [(pp)(pq)]  [(pq)(qq)] Hk. Distributif  [0(pq)]  [(pq)0] Hk. Kontradiksi  (pq)(pq) Hk. Identitas

Operasi penyederhanaan dengan menggunakan hukum-hukum logika dapat digunakan untuk membuktikan suatu ekspresi logika, Tautologi, Kontradiksi, maupun Contingent. Jika hasil akhir penyederhanaan ekspresi logika adalah 1, maka ekspresi logika tersebut adalah tautologi. Jika hasil yang diperoleh adalah 0, berarti ekspresi logika tersebut kontradiksi. Jika hasilnya tidak 0 ataupun 1, maka ekspresi logikanya adalah contingent.

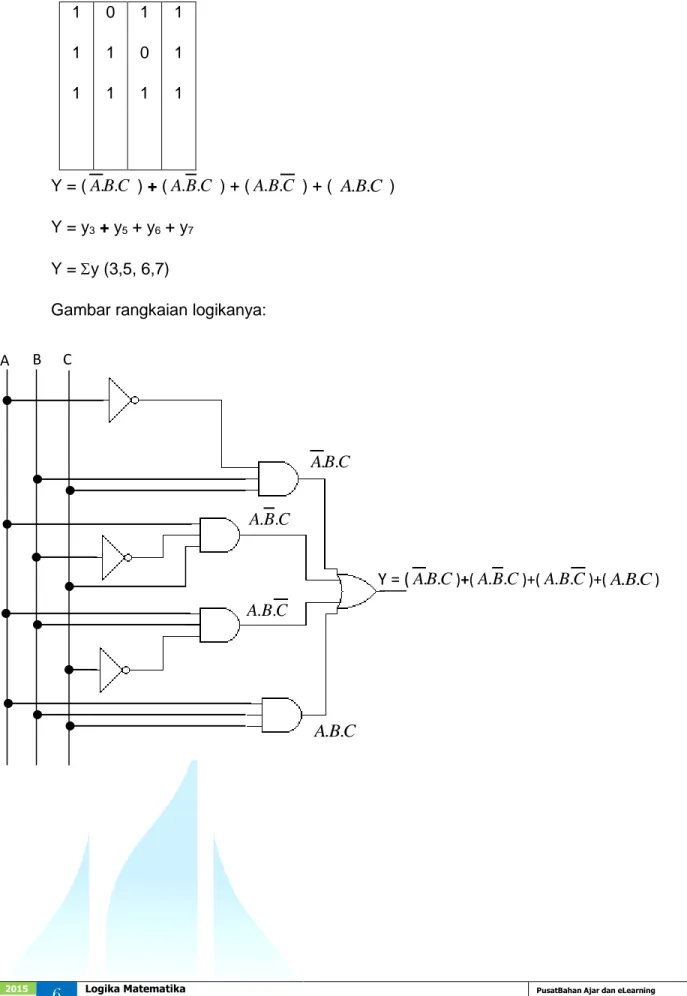
Contoh 1: [(pq)p]q

 [(pq)p]  q ingat pq pq

[(pq)p]  q ingat pq pq

 [(pq)p]  q Hk. Negasiganda dan De Morgan  [(pp)(qp)]  q Hk. Distributif

 [1(pq)]  q Hk. Idempoten dan komutatif

 (pq)q Hk. Identitas

p(qq) Hk. Assosiatif

p1 ` Hk. Idempoten

 1 Hk. Identitas

(60)

(pq)  [(p)  (q)]  (pq)(pq)  [(pq)p][(pq)q] Hk. Distributif  [(pp)(qp)][(pq)(qq)] Hk. Distributif  [0(qp)][(pq)0] Hk. Negasi  (pq)(pq) Hk. Idempoten  (pp)(qq) Hk. Assosiatif  00 Hk. Negasi  0 Hk. Idempoten

Hasil akhir 0, maka ekspresi logika di atas adalah kontradiksi.

Contoh 3: [(pq)p] q  [(pp)(qp)] q Hk. Distributif  [0  (qp)] q Hk. Negasi  (qp) q Hk. Identitas (qp) q ingat pq pq  (qp) q Hk. De Morgan  (qq)p Hk. Assosiatif qp Hk. Idempoten

Hasilnya bukan 0 atau 1, ekspresi logika di atas adalah contingent

E. ATURAN PENARIKAN KESIMPULAN

1. MODUS PONEN

Modus ponen atau penalaran langsung adalah salah satu metode inferensi dimana jika diketahui implikasi ” Bila p maka q ” yang diasumsikan bernilai benar dan antasenden (p) benar. Supaya implikasi pq bernilai benar, maka q juga harus bernilai benar.

Modus Ponen : pq , p ├ q Atau dapat juga ditulis

(61)

pq p

――――  q

Jika digit terakhir suatu bilangan adalah 0, maka bilangan tersebut habis dibagi 10 Digit terakhir suatu bilangan adalah 0

Bilangan tersebut habis dibagi 10

2. MODUS TOLLENS

Bentuk modus tollens mirip dengan modus ponen, hanya saja premis kedua dan kesimpulan merupakan kontraposisi premis pertama modus ponen. Hal ini mengingatkan bahwa suatu implikasi selalu ekuivalen dengan kontraposisinya.

Modus Tollens : pq, q ├ p Atau dapat juga ditulis

pq q ―――― p Contoh :

Jikad digit terakhir suatu bilangan adalah 0, maka bilangan tersebut habis dibagi 10

Suatu bilangan tidak habis dibagi 10 Digit terakhir bilangan tersebut bukan 0