PERMAINAN DUA ORANG BERJUMLAH TIDAK NOL DAN METAGAME TANPA KERJASAMA

PERMAINAN DUA ORANG BERJUMLAH TIDAK NOL DAN

METAGAME TANPA KERJASAMA

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana

Program Studi Matematika

Disusun oleh: PUJI ASTUTI NIM : 023114031

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

TWO-PERSON NON-ZERO-SUM GAMES AND

METAGAME WITHOUT COOPERATION

Thesis

Presented as Partial Fulfillment of the Requirements To Obtain the SARJANA SAINS Degree

In Mathematics

by: PUJI ASTUTI

Student number : 023114031

MATHEMATICS DEPARTMENT SAINS AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY YOGYAKARTA

2008

Percayalah pada Tuhan dengan segenap hatimu,

dan janganlah bersandar pada pergertianmu sendiri.

Amsal 3:5

Kupersembahkan Skripsiku ini kepada :

Tuhan Yesus Kristus yang senatiasa menyertaiku,sumber harapan dan kekuatanku.

Kedua orang tuaku atas cinta dan doa yang tiada henti.

Mas Sun, Mbak Asih, Nug, dan Bowo.

Yang terkasih Albertus Aan Oky atas dukungan, doa, perhatian, dan cinta.

Serta Almamaterku tercinta.

Punyailah iman yang dapat melihat kesempatan dalam kesulitan,

dan bukan melihat kesulitan dalam kesempatan.

Yakinilah dibalik semua kesulitan ada rencana indah yang Tuhan telah siapkan.

-nn-

Seribu kata tidak akan meninggalkan kesan yang begitu dalam dibandingkan dengan satu perbuatan.

-Henrik Ibsen-

Selalu ada jalan untuk melakukan yang lebih baik. Temukanlah !

-Thomas Alfa Edison-

Letakkan segala sesuatunya pada Tuhan sehingga Dia mengambil alih

semuanya. Kerjakan bagianmu dengan baik, maka Dia akan mengerjakan

bagian dengan sangat baik.

-nn-

ABSTRAK

Permainan dua orang berjumlah tidak nol merupakan permainan yang dilakukan oleh dua pemain dengan hasil permainan salah satu pemain tidak selalu negatif dari hasil permainan pemain yang lain. Hasil permainan dari permainan tersebut merupakan suatu pasangan ekuilibrium. Pasangan ekuilibrium dari permainan tersebut dapat dibentuk dengan mencari hasil yang optimal dari strategi-strategi campuran yang digunakan masing-masing pemain. Cara lain yang dapat digunakan adalah dengan metode Swastika, yaitu menentukan peluang dari masing-masing strategi sehingga diperoleh nilai permainan harapan dari para pemainnya.

Metagame tanpa kerjasama untuk dua pemain merupakan permainan yang strateginya didasarkan pada permainan yang sedang berlangsung. Hal ini karena penyelesaian permainan yang didasarkan pada teori permainan hasilnya tidak selalu sama dengan permainan yang sedang terjadi. Strategi salah satu pemain merupakan fungsi reaksi untuk strategi pemain lainnya. Dari strategi tersebut dapat ditentukan hasil rasional untuk masing-masing pemain. Pasangan ekuilibrium dari metagame didapatkan melalui irisan hasil rasional dari masing-masing pemain.

ABSTRACT

Two-person non-zero-sum games is a game with two players and the outcomes of one player is not always negative from the other player’s outcomes. The outcomes of the game is an equilibrium pairs. The equilibrium pairs from the game can be determined by finding the optimal outcomes from mix strategies which is used by each player. Another way can be used is Swastika method, which determines probability of each strategy so it gains the expected value of the game.

Metagame without cooporation for two players is a games which is based on the actual game being played . It is because the game solving is based on the game theory which the outcomes is not always the same with the playing game. These are games where the players strategies are really reaction functions to the other players strategies. From the strategy it can be determine the rational outcomes for each player. The equilibrium pairs from metagame is gained from each players rational outcomes section.

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus, atas berkat dan kasih karunia yang telah diberikan sehingga penulis dapat menyelesaikan skripsi yang bejudul ” Permainan Dua Orang Berjumlah Tidak Nol Dan Metagame Tanpa Kerjasama”.

Dalam proses penulisan skripsi ini banyak hambatan yang dialami oleh penulis. Namun, berkat bantuan dan dukungan dari banyak pihak, akhirnya skripsi ini dapat terselesaikan. Oleh karena itu penulis ingin mengucapkan terima kasih kepada:

1. Ibu Lusia Krismiyati Budiasih, S.Si, M.Si, selaku dosen pembimbing skripsi dan selaku ketua program studi Matematika FST USD Yogyakarta yang telah memberikan banyak saran dan yang telah meluangkan waktu, pikiran, nasihat, tenaga, serta memberikan kesabarannya sehingga penulis dapat sampai pada tahap penyusunan skripsi ini. (matatih buangeeeet ya bu….. :))

2. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc, selaku dekan FMIPA dan dosen pembimbing akademik yang telah memberikan bimbingan, saran, nasehat, dan dukungan selama ini.

3. Ir. Gregorius Heliarko, S.J., S.S., BST., M.A., M.Sc. Selaku Dekan Fakultas Sains dan Teknologi Universitas Sanata Dharma.

4. Bapak dan Ibu Dosen FMIPA yang telah memberikan ilmu pengetahuan yang sangat berguna bagi penulis.

5. Mas Tukijo , Ibu Suwarni dan Ibu Linda yang telah memberikan pelayanan administrasi dan urusan – urusan akademik kepada penulis selama masih kuliah.

6. Romo Dr. Frans Susilo, SJ, selaku kepala perpustakaan yang telah menyediakan fasilitas dan kemudahan selama penulis kuliah.

7. Perpustakaan USD dan Staf yang telah memberikan fasilitas dan kemudahan kepada penulis.

8. Bapak dan ibu tercinta : Ibu Karpini dan Bapak Basuki yang selalu mendoakan penulis dan memberikan dukungan yang tak pernah berhenti dalam segala hal.

9. Mas Sun, Mbak Narsih, Sinuk, Bowo, Mas Sugeng, Mbak Ari dan sikecil Lintang terima kasih buat persaudaraan ini semoga kita dapat selalu menjaganya. Tuhan berkati kita.

10. Albertus Aan Oky Dwi Hatmoko yang telah memberikan banyak cinta, pengertian, waktu, kesabaran, nasehat, semangat (cayo-cayo ijup...:), perhatian, serta kasih sayangnya kepada penulis. Terima kasih buat doa yang tiada henti untuk penulis, saran, pengetahuan, kebersamaan dan kenangan indah yang telah diberikan kepada penulis.

11.Saudara dan sahabat penulis : Yulita, Minul, Ika, Teguh, Mas Wawan, Mas Aga terima kasih untuk kesempatan hidup yang Tuhan berikan sehingga penulis bisa lalui bersama kalian, terima kasih untuk doa dan kasih sayangnya serta dukungan yang tak pernah berhenti.

12.Aan, Bani, Taim, Markus, Galih, Tato, (genk mawut) terima kasih atas persahabatan, kenangan, dukungan, semangat, dan perjalanan hidup yang sangat berarti yang kalian berikan untuk penulis (kapan bisa main bareng-bareng lagi...???). Untuk Ridwan dan Katrin (asyik bisa main bareng-bareng kalian).

13.Teman – teman Kost ‘ICHA’, mbak Nia, Lusae, Via, Indri, Tecca, Tiehna, Ratih, Cicil, Siane, Ana, Erita dan untuk teman dikost baru Yemima terima kasih buat keceriaan yang boleh dibagi bersama penulis.

14.Teman – teman angkatan 2002, Amelia, Lenta, Debby, Priska, Retno, Sari, Vida, Lili, Dani, Ika, Feliks, Archi, Aning, Desi, Deon, Nunung, Chea, Wuri, Rita, Asih, dan Palma yang sudah memberikan segala keceriaan dalam melewati kebersamaan selama di Matematika USD.

15.Seluruh teman – teman di Prodi Matematika, kakak angkatan dan adik angkatan.

16.Teman – teman KKN: Angga, Wiwik, Lisna, Suko, Suro, Beny, Mina, dan Tyas yang memberi warna hidup yang baru selama KKN.

17.Teman – teman di Persekutuan Ekklesia Blok 8, terima kasih untuk doanya sehingga penulis bisa menyelesaikan skripsi ini.

18.Pak Mardi dan Ibu yang memberikan nasehat, pengalaman hidup, dan semangat.

19.Kost Kodok Ijo : Didit, Topan, Sumin, Bayu yang memberi keceriaan. 20.Ririn yang memberikan bantuan dan pengertian kepada penulis. Semangat

dan selamat berjuang.

Penulis juga mengucapkan terima kasih kepada semua pihak yang telah membantu penulis dalam penulisan skripsi ini yang tidak disebutkan di sini.

Yogyakarta, Januari 2008

Penulis

DAFTAR ISI

Halaman

HALAMAN JUDUL……….... i

HALAMAN JUDUL DALAM BAHASA INGGRIS ………. ii

HALAMAN PERSETUJUAN PEMBIMBING………... iii

HALAMAN PENGESAHAN……….. iv

HALAMAN PERSEMBAHAN ………... v

PERNYATAAN KEASLIAN KARYA ……….. vii

ABSTRAK……….. viii

ABSTRACT……… ix

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ………... x

KATA PENGANTAR ……… xi

DAFTAR ISI……….. xv

BAB I PENDAHULUAN……… 1

A. Latar Belakang………. 1

B. Rumusan Masalah……… 3

C. Pembatasan Masalah………... 4

D. Tujuan Penulisan………. 4

E. Metode Penulisan……….... 4

F. Manfaat Penulisan………... 5

G. Sistematika Penulisan………. 5

BAB II PERMAINAN DUA ORANG BERJUMLAH TIDAK NOL… 6

A. Permainan Berjumlah Tidak Nol………. 7

B. Permainan Tanpa Kerjasama..………... 7

C. Strategi Campuran……… 15

D. Teorema Nash………... 21

E. Metode Swastika Untuk Menemukan Pasangan Ekuilibrium 28

BAB III METAGAME TANPA KERJASAMA UNTUK DUA PEMAIN 48

A. Metagame dan Metaekuilibria………….……… 49

B. Teorema Metarasionalitas..………... 65

C. Simetri Metaekuilibria………..…………. 78

D. Analisis Pilihan………...………. 81

E. Analisis Pilihan Yang Berlaku Untuk Strategi Pasar……… 84

BAB IV PENUTUP……….………... 103

DAFTAR PUSTAKA……….. 106

BAB I PENDAHULUAN

A. Latar Belakang Masalah

Dalam kehidupan sehari-hari sering dijumpai kegiatan-kegiatan yang bersifat kompetitif yang diwarnai dengan suatu keadaan persaingan (konflik). Persaingan ini dapat dilakukan diantara dua orang atau sejumlah orang (grup). Persaingan ini dapat disebut sebagai suatu permainan (game). Dari persaingan yang banyak terjadi dalam kehidupan sehari-hari, muncullah sebuah Teori Permainan.

mendapatkan perhatian yang begitu besar dan digunakan pada bidang ekonomi, politik , olahraga, militer, dan bidang-bidang lainnya.

Masih banyak kegiatan-kegiatan lain yang bersifat kompetitif , namun tidak setiap keadaan persaingan dapat disebut sebagai permainan, hanya persaing-an ypersaing-ang memenuhi kriteria atau ciri-ciri tertentu saja ypersaing-ang dapat disebut sebagai permainan. Kriteria atau ciri-ciri tersebut adalah:

1. Terdapat persaingan kepentingan diantara pemain (pelaku). 2. Jumlah pemain terbatas.

3. Setiap pemain mempunyai sejumlah pilihan atau tindakan yang terbatas yang disebut strategi.

4. Aturan permainan di dalam memilih tindakan diketahui oleh setiap pemain.

5. Hasil permainan dipengaruhi oleh tindakan-tindakan yang dibuat oleh semua pemain. Hasil untuk seluruh kombinasi tindakan yang mungkin dilakukan tersebut dapat didefinisikan secara numeris.

Permainan dapat diklasifikasikan dalam beberapa cara, bergantung pada faktor-faktor tertentu. Salah satunya adalah jumlah keuntungan atau kerugian dari pemain yang diklasifikasikan sebagai permainan berjumlah nol (zero-sum game) dan permainan bejumlah tidak nol (non zero-sum game). Faktor yang lain dapat ditentukan dari adanya kerjasama yang dilakukan dalam permainan tersebut yang diklasifikasikan dalam permainan dengan kerjasama dan permainan tanpa kerjasama. Dalam bab selanjutnya yang akan dibahas lebih lanjut adalah

permainan berjumlah tidak nol tanpa kerjasama. Permainan berjumlah tidak nol tanpa kerjasama merupakan permainan yang hasil permainannya bukan merupakan negatif dari hasil pemain lainnya dan dalam permainan tersebut tidak terdapat kerjasama diantara para pemainnya.

Penyelesaian dalam permainan terkadang membuat hasil yang diperoleh tidak seperti yang diperkirakan. Dapat diasumsikan bahwa setiap pemain mencoba memprediksikan strategi apa yang akan digunakan oleh lawannya. Hal ini akan menuju pada hasil nyata yang stabil dimana masing-masing pemain dapat memprediksikan dengan tepat strategi yang digunakan dan hasil yang akan dicapai oleh pemain lain.

Metagame merupakan pengembangan dari Teori Permainan, dimana metagame adalah strategi permainan yang titik ekuilibriumnya didapat berdasarkan pada permainan yang sebenarnya. Metagame merupakan permainan yang strategi para pemainnya benar-benar merupakan reaksi untuk strategi pemain lain. Dalam metagame setiap pemain memberikan reaksi untuk strategi yang dipilih oleh pemain lainnya.

B. Perumusan Masalah

Permasalahan yang dibahas dalam skripsi ini dapat dirumuskan sebagai berikut:

1. Bagaimana penyelesaian permainan berjumlah tidak nol tanpa kerjasama? 2. Bagaimana metode penyelesaian Metagame berjumlah tidak nol tanpa

kerjasama untuk dua pemain?

3. Bagaimana aplikasi Metagame dalam penggunaannya pada Strategi Pasar?

C. Pembatasan Masalah

Dalam skripsi ini dibatasi oleh beberapa hal sebagai berikut :

1. Teori permainan yang dibahas hanya yang terkait langsung dengan permasalahan dalam permainan berjumlah tidak nol.

2. Pembahasan masalah dalam skripsi ini dibatasi pada permainan tanpa kerjasama, dimana hanya terdapat dua pemain dalam setiap permainan. 3. Strategi permainan yang digunakan terbatas.

D. Tujuan Penulisan

Skripsi ini bertujuan untuk :

1. Merumuskan model matematika untuk setiap masalah dalam suatu permainan.

2. Menyelesaikan permainan dengan menggunakan Metagame untuk dua pemain berjumlah tidak nol, sehingga setiap pemain dapat memprediksi dengan tepat strategi dan hasil yang dicapai oleh para pemain lain.

E. Metode Penulisan

Penulisan skripsi ini menggunakan metode studi pustaka, yaitu dengan menggunakan buku-buku yang telah dipublikasikan, sehingga tidak ditemukan hal

baru.

F. Manfaat Penulisan

Manfaat yang diharapkan dari penulisan skripsi ini adalah agar penulis dan pembaca mengetahui cara menyelesaikan suatu masalah permainan dengan Metagame.

G. Sistematika Penulisan

Bab I. Pendahuluan. Pada bagian ini akan dibahas mengenai latar belakang masalah, perumusan masalah, pembatasan masalah, tujuan penulisan, metode penulisan, manfaat penulisan, dan sistematika penulisan skripsi ini.

Bab II. Permainan Dua Orang Berjumlah Tidak Nol. Pada bagian ini akan dibahas mengenai permainan tidak berjumlah nol, permainan tanpa kerjasama, strategi campuran, Teorema Nash, dan penyelesaian permainan menggunakan metode Swastika untuk menemukan pasangan ekuilibrium.

Bab III. Metagame Tanpa Kerjasama Untuk 2 Pemain. Pada bagian ini akan dibahas mengenai metagame dan metaekuilibria, teorema metarasionalitas, simetri metaekuilibria, analisis pilihan, dan analisis pilihan yang berlaku untuk strategi pasar.

Bab IV. Penutup. Pada bagian ini berisi mengenai kesimpulan dan saran.

BAB II

PERMAINAN DUA ORANG BERJUMLAH TIDAK NOL

Teori permainan (game theory) adalah bagian dari ilmu pengetahuan yang berkaitan dengan pengambilan keputusan pada saat dua pihak atau lebih berada dalam kondisi persaingan atau konflik. Pihak-pihak tersebut selanjutnya disebut sebagai pemain. Para pemain yang bersaing diasumsikan bersifat rasional dan cerdas, artinya masing-masing pemain akan melakukan strategi atau tindakan yang rasional untuk memenangkan persaingan tersebut, dan masing-masing pemain juga mengetahui strategi pemain lawannya.

kerjasama dan permainan tanpa kerjasama. Dalam penulisan ini hanya akan dibahas mengenai permainan berjumlah tidak nol tanpa kerjasama.

A. Permainan berjumlah tidak nol

Pada permainan berjumlah nol untuk dua pemain hasil permainan untuk salah satu pemain merupakan negatif dari hasil permainan untuk pemain lainnya. Untuk permainan berjumlah nol n pemain, penjumlahan dari hasil permainan pemain 1 sampai pemain n harus sama dengan nol.

Pada permainan berjumlah tidak nol untuk dua pemain, hasil dari permainan untuk pemain 1 bukan merupakan negatif dari hasil permainan untuk pemain 2. Tetapi hasil permainannya dapat ditulis sebagai pasangan, misalkan (A,B), dengan A adalah hasil dari pemain 1 dan B adalah hasil dari pemain 2. Untuk permainan n pemain tidak berjumlah nol maka hasil permainannya dapat ditulis sebagai pasangan

(

)

dengan masing-masing adalah hasil dari pemain i.

n

A A

A₁, ₂,..., A_i

B. Permainan Tanpa Kerjasama

dinyatakan dengan sebuah matriks yang strategi-strategi pemainnya dinyatakan dengan baris dan kolom dalam matriks yang bersangkutan.

Definisi 2.2.1

Strategi murni adalah satu-satunya strategi yang digunakan dalam suatu permainan.

Permainan yang menggunakan dua atau lebih strategi murni disebut dengan permainan yang menggunakan strategi campuran.

Definisi 2.2.2

Misalkan x dan y masing-masing adalah strategi yang digunakan pemain 1 dan pemain 2, maka hasil untuk pemain i dapat dituliskan sebagai

(x,y)

i

e

Hasil permainan merupakan hasil terbaik yang diperoleh kedua pemain.

Definisi 2.2.3

Contoh 2.2.1

Misalkan suatu permainan dengan dua pemain, dengan pemain 1 menggunakan strategi

(

x₁,x₂

)

dan pemain 2 menggunakan strategi

(

y₁,y₂

)

. Maka matriks hasil untuk pemain 1 tersebut dapat dituliskan sebagai berikut :

Strategi pemain 2

1

y y₂

1

x e_i

(

x₁,y₁

)

e_i

(

x₁,y₂

)

Strategi

pemain 1

2

x e_i

(

x₂,y₁

)

e_i

(

x₂,y₂

)

Definisi 2.2.4

Misalkan suatu hasil permainan dituliskan dengan e

(

x_i,y_j

)

. Jika hasil e₁

(

x_i,y_j

)

merupakan keuntungan dari pemain 1 maka paling tidak pemain 1 mendapatkan hasil _y

{

e

(

x_i y_j

)

}

j ,

min ₁ untuk sebarang strategi yang digunakan pemain 2. Kriteria maksimin adalah memilih strategi yang memaksimalkan hasil tersebut di atas, yakni

i

x

(

)

{

i j

}

y x

L e x y

v

j

i min ,

max ₁

= .

Definisi 2.2.5

Misalkan suatu hasil permainan dituliskan dengan e

(

x_i,y_j

)

. Jika hasil e₂

(

x_i,y_j

)

merupakan kerugian dari pemain 2, maka paling tidak pemain 2 mendapatkan hasil _x

{

e

(

x_i y_j

)

}

i ,

minimaks adalah memilih strategi yang meminimumkan hasil tersebut di atas, yakni

j

y

(

)

{

i j

}

x y

U e x y

v

i

jmax ,

min ₂

= .

Definisi 2.2.6

Nilai maksimin adalah hasil dari permainan yang diperoleh dengan memaksimumkan minimum keuntungan dari strategi baris yang dimainkan pemain 1.

Nilai minimaks adalah hasil dari permainan yang diperoleh dengan meminimumkan maksimum kerugian dari strategi kolom yang dimainkan pemain 2.

Definisi 2.2.7

Titik sadel merupakan titik keseimbangan dari suatu permainan dengan nilai maksimin sama dengan nilai minimaks.

Suatu permainan yang hanya menggunakan strategi murni mempunyai titik sadel.

Definisi 2.2.8

Misalkan permainan yang dimainkan oleh dua pemain. Saat pemain 1 menggunakan strategi , yaitu strategi yang terbaik dari pemain 1. Dan saat pemain 2 menggunakan strategi , yaitu strategi yang terbaik dari pemain 2.

merupakan titik ekuilibrium dari permainan tersebut, yaitu titik keseimbangan saat kedua pemain menggunakan strategi yang terbaik dari permainan.

* x

* y )

Contoh 2.2.2 (Permainan Prisoner’s Dilemma)

Dua orang ditangkap polisi karena mencuri barang milik orang lain. Kemudian dilakukan wawancara secara terpisah oleh polisi. Mereka berdua tahu jika mereka tetap diam maka polisi tidak mendapatkan cukup bukti untuk menghukum mereka atas pencurian tersebut, dan mereka hanya mendapatkan satu tahun hukuman penjara karena perbuatan mereka. Jika mereka berdua mengakui bahwa mereka mencuri, maka masing-masing mendapatkan sembilan tahun hukuman penjara. Jika salah satu mengakui dan yang lain tetap diam, maka yang mengakui menjadi bukti dan akan dibebaskan, sedangkan yang tetap diam akan mendapatkan hukuman sepuluh tahun penjara. Apa yang sebaiknya mereka lakukan?

Penyelesaian :

Dalam permainan ini strategi murni yang digunakan pemain 1 adalah A1 = mengakui dan A2 = tidak mengakui. Sedangkan strategi pemain 2 adalah B1 = mengakui dan B2 = tidak mengakui. Misalkan banyaknya hukuman dinyatakan dengan –n tahun, maka matriks hasil dari permainan di atas dapat dituliskan sebagai berikut :

Pemain 2

BB1 : Mengakui BB2 : Tidak mengakui

A1 : Mengakui (-9,-9) (0,-10)

Pemain 1

Jika keduanya mengakui mencuri berarti strategi yang digunakan adalah dan masing-masing akan mendapatkan hukuman 9 tahun penjara, dituliskan dengan

(

A1,B1

)

(

1,

)

9

1 A B =−

e dan e2

(

A,B1

)

=−9. Jika keduanya tidak

mengakui mencuri berarti strategi yang digunakan adalah

(

A₂,B₂

)

dan setiap pemain akan mendapatkan hukuman 1 tahun penjara dituliskan dengan

dan

(

2,

)

1

1 A B =−

e e2

(

A,B2

)

=−1. Jika salah satu mengakui dan yang lain tidak

mengakui mencuri berarti yang mengakui akan dibebaskan dan yang tidak mengakui akan mendapatkan hukuman 10 tahun penjara, dengan demikian strategi yang digunakan adalah

(

A₁,B₂

)

dan

(

A₂,B₁

)

dan hasilnya dapat dituliskan dengan e1

(

A1,B

)

=0 , e2

(

A,B2

)

=−10 dan e1

(

A2,B

)

=−10 , e2

(

A,B1

)

=0.

Akan dicari penyelesaian permainan tersebut, yaitu dengan cara mencari nilai minimaks dan nilai maksimin untuk setiap pemain. Matrik hasil untuk pemain 1 adalah:

Minimum baris -9 → maks -10

Maksimum -9 0

1

B B₂

1

A -9 0

2

A -10 -1

kolom ↓

min

Dengan demikian hasil permainan untuk pemain 1 adalah dan

mempunyai titik sadel karena nilai maksimin sama dengan nilai minimaks. Sebaliknya matriks hasil untuk pemain 2 adalah sebagai berikut :

(

1, 1

)

9

1 A B =−

Minimum baris -9 → maks -10

Maksimum -9 0

1

A A₂

1

B -9 0

2

B -10 -1

kolom ↓

min

Dengan demikian hasil permainan untuk pemain 2 e₂

(

A₁,B₁

)

=−9 dan juga mempunyai titik sadel. Hasil permainan untuk kedua pemain dinyatakan dengan

(

,

) (

, ,

) {

} 9, 9

{e₁ A₁ B₁ e₂ A₁ B₁ = − −

}

dan ini merupakan titik ekuilibrium dari permainan ini. Maka penyelesaian dari permainan ini adalah jika kedua pemain saling mengakui bahwa mereka mencuri.

Akan dicari penyelesaian permainan Prisoner’s Dilemma menggunakan kriteria maksimin dan kriteria minimaks. Dengan menggunakan kriteria maksimin

(

)

{

i j

}

y x

L e x y

v

j

imin ,

max 1

= hasil permainan untuk pemain 1 adalah

(

)

{

}

(

) (

)

{

}

{

(

) (

}

{

}

(

) (

)

{

}

(

)

{

9, 9

}

0 , 10 dan 9 , 9 max 1 , 1 , 0 , 10 min dan 10 , 0 , 9 , 9 min max , min max ₁ − − = − − − = − − − − − − = = i j j i j i x y y x j i y x

L e x y

v

)

Dengan menggunakan kriteria minimaks v_{U y x}

{

e

(

x_i y_j

)

}

i

jmax ,

min ₂

= hasil

permainan untuk pemain 2 adalah

(

)

{

}

(

) (

)

{

}

{

(

) (

}

{

}

(

) (

)

{

}

(

)

{

9, 9

}

0 , 10 , 9 , 9 min 1 , 1 , 10 , 0 max dan 0 , 10 , 9 , 9 max min , max min ₂ − − = − − − = − − − − − − = = j i i j i j y x x y j i x y

U e x y

v

Dapat dilihat bahwa hasil permainan dengan menggunakan kriteria maksimin sama dengan hasil permainan dengan menggunakan kriteria minimaks, yaitu

({

−9,−9

)}

=

= _U

L v

v . Maka permainan Prisoner’s Dilemma tersebut mempunyai

titik ekuilibrium karena v_L=v_U.

Definisi 2.2.9

Dalam permainan tanpa kerjasama untuk n pemain, misalkan adalah strategi

campuran yang digunakan oleh pemain i. n pasang strategi campuran , ,..., , adalah n pasang ekuilibrium untuk strategi campuran jika untuk semua strategi – strategi yang lain, yaitu , ,…, berlaku :

* i

x

* 1

x x₂*

* n

x

1

y y₂ y_n

(

) (

* *

)

2 * 1 *

* * 2 *

1, ,..., i,..., n i , ,..., i,..., n

i x x x x e x x y x

e ≥ , 1 ≤ i ≤ n .

Definisi 2.2.10

Misalkan pada permainan yang dimainkan oleh dua pemain,X adalah himpunan strategi campuran untuk pemain 1, Y adalah himpunan strategi campuran untuk pemain 2. Suatu pasangan strategi adalah pasangan ekuilibrium untuk permainan tidak berjumlah nol jika untuk setiap

Y X ∈

∈ *

* x ,y

Y X ∈

∈ y

x , :

( ) (

)

( ) (

* * * * * *

y , x y

, x

y , x y

x,

2 2

1 1

e e

e e

≤ ≤

)

Contoh 2.2.3

Dari permainan Prisoners Dilemma pada contoh 2.2.2 didapatkan pasangan ekuilibrium

{

e₁

(

x*,y*

) (

,e₂ x*,y*

)

}

=

{

−9,−9

}

.

{

−9,−9

}

adalah pasangan ekuilibrium untuk permainan tidak berjumlah nol tersebut jika untuk setiap

berlaku :

Y X ∈

∈ y

x ,

( ) (

)

( ) (

* * * * * *

y , x y

, x

y , x y

x,

2 2

1 1

e e

e e

≤ ≤

)

Dari permainan pada contoh 2.2.2 tersebut didapatkan hasil untuk pemain 1 adalah e₁

( )

x,y* =−10 dan hasil untuk pemain 2 adalah e₂

( )

x*,y =−10. Didapatkan untuk pemain 1 berlaku e₁

( ) (

x,y* ≤e₁ x*,y*

)

≡−10<−9 dan untuk pemain 2 berlaku e₂

( ) (

x*,y ≤e₂ x*,y*

)

≡−10<−9. Maka menurut definisi 2.2.9 untuk permainan Prisoners Dilemma berlaku e₁

( ) (

x,y* ≤e₁ x*,y*

)

≡−10<−9 dan

( ) (

*, ₂ *, *

)

10 9

2 x y ≤e x y ≡− < −

e . Dengan pasangan ekuilibriumnya adalah

.

{

−9,−9

}

C. Strategi Campuran

Von Neumann menyarankan salah satu cara untuk menyelesaikan kasus dimana dengan menggunakan strategi campuran. Suatu strategi campuran terdiri atas seni percobaan acak setiap waktu dalam permainan tersebut dan untuk menentukan strategi yang akan digunakan pemain setiap saat. Strategi murni terdiri dari beberapa strategi murni dengan probabilitas tertentu.

U

L v

Contoh 2.3.1 (Permainan Poker sederhana)

Dalam permainan Poker yang sederhana strategi yang digunakan para pemain akan ditunjukkan dalam tabel berikut :

Strategi

1

I Pemain 1 percaya ketika pemain 2 berkata ’Ace’ Pemain 1

2

I Pemain 1 tidak percaya ketika pemain 2 berkata ’Ace’

1

II Pemain 2 berkata ’Two’ ketika mempunyai ’Two’ Pemain 2

2

II Pemain 2 berkata ’Ace’ ketika mempunyai ’Two’

Dari strategi di atas akan didapatkan hasil permainan sebagai berikut.

Jika pemain 1 menggunakan strategi dan pemain 2 menggunakan strategi , maka pemain 1 akan mendapatkan -1 jika pemain 2 menunjukkan ’Ace’. Tetapi jika pemain 2 menunjukkan ’Two’ maka saat itu juga pemain 1 mendapatkan +1. Harapan mendapatkan ’Ace’ adalah

1

I II₁

2

1 _{dan harapan mendapatkan ’Two’ juga} 2 1 _,

maka nilai yang diharapkan adalah 1.

( )

1.₂1 0

2

1+ − = _.

Jika pemain 1 menggunakan strategi dan pemain 2 menggunakan strategi , maka pemain 1 mendapatkan nilai -1.

1

I II₂

Jika pemain 1 menggunakan strategi dan pemain 2 menggunakan strategi , maka ketika pemain 2 menunjukkan ’Ace’ pemain 1 kalah -2. Jika pemain 2 menunjukkan ’Two’ pemain 1 menang +1. Maka nilai harapannya adalah

2

I II₁

2 1 2

1 2

Yang terakhir jika pemain 1 menggunakan strategi dan pemain 2 menggunakan strategi , maka pemain 1 akan mendapatkan -2 ketika pemain 2 mendapatkan ’Ace’. Tetapi jika kartu tersebut adalah ’Two’ maka pemain 1 mendapatkan +2. Kemudian, nilai harapannya adalah

2

I

2

II

0 2 . 2

. ₂1

2

1 − + = _.

Maka matriks hasilnya dapat ditunjukkan sebagai berikut :

Pemain 2

1

II II₂

1

I 0 -1

Pemain 1

2

I - ₂1 ₀

Dalam permainan Poker, pemain 1 akan melempar koin untuk menentukan strategi yang akan digunakan. Apabila muncul ”kepala” maka yang digunakan adalah strategi . Dan bila muncul ”ekor” maka akan menggunakan strategi . Probabilitas pemain 1 menggunakan strategi dan strategi masing-masing adalah

1

I I₂

1

I I₂

2 1 _.

Hasil permainan dari matriks di atas menunjukkan jika pemain 2 menggunakan strategi maka peluang pemain 1 menang jika menggunakan strategi adalah 0 dan peluang pemain 1 menang jika menggunakan strategi adalah -

1

II I₁

2

I ₂1 _.

menang jika menggunakan strategi adalah -1. Dan jika menggunakan strategi adalah 0.

1

I

2

I

Hasil yang diharapkan pemain 1 jika pemain 2 menggunakan strategi adalah (0 x

1

II

2 1_{) +}

(-2 1 _x

2 1 _{) =}

-4

1 _{. Dan hasil yang diharapkan pemain 1 jika pemain 2}

menggunakan strategi II₂ adalah (-1 x ₂1 _{) + (0 x} 2 1 _{) =}

-2

1 _{. Dalam permainan}

tersebut digunakan strategi campuran, yakni pemain 1 menggunakan strategi campuran

(

I₁,I₂

)

dan pemain 2 menggunakan strategi campuran

(

II₁,II₂

)

.

Strategi murni adalah satu-satunya strategi yang digunakan dalam suatu permainan. Misalkan pemain 1 mempunyai n strategi murni, susunan strategi campuran X bisa dinyatakan dengan n-tuple x=

(

x₁,x₂,...,x_n

)

dimana

, dan n i

x_i ≥0, =1,2,...,

(2.3.1)

∑

=

= n

i i

x

1

1

Persamaan (2.3.1) digunakan untuk menentukan strategi campuran dan setiap strategi murni dalam strategi campuran tersebut mempunyai probabilitas . Sedangkan jika pemain 2 mempunyai m strategi murni, susunan strategi campuran Y bisa dinyatakan dengan m-tuple

i

x

(

y₁,y₂,...,y_m

)

=

y dimana ,

dan

m i

y_i ≥0, =1,2,...,

∑

=

= m

i i

y

1

1 (2.3.2)

Apabila pemain 1 memainkan strategi x=

(

x₁,x₂,...,x_n

)

dan pemain 2

memainkan strategi hasil yang diharapkan untuk pemain 1

adalah :

(

y1,y2,...,ym =

y

)

)

( )

∑∑

= =

= m

j n

i

j ij ie y

x e

1 1

1x,y (2.3.3)

Contoh 2.3.2

Dalam permainan Poker yang sederhana, misalkan pemain 1 memainkan strategi dan pemain 2 memainkan strategi

(

x −x

= ,1

x y=

(

y,1− y

)

, dan matriks hasilnya

adalah

Pemain 2

1

II II₂

y 1-y

1

I x 0 -1

Pemain 1

2

I 1-x - ₂1 ₀

Nilai harapan hasil pemain 1 adalah

( )

(

) (

)

(

)(

)

xy y x

xy y x xy

y x y

x y

x xy e

2 3 2 1

2 1 2 1

2 1

1 , 0. 1. 1 1 0 1 1

+ − − =

+ − − =

− − + − − − −

=

y x

Jika pemain 1 memainkan strategi

( )

₃2 3 1_,

*=

x , yakni _x=₃1 _{artinya bahwa pemain 1}

bermain dengan menggunakan strategi I_{1 3}1 _{kali banyaknya permainan yang dia}

lakukan. Maka dari persamaan (2.3.4) diperoleh

(

)

₃1

1 x*,y = −

e , untuk semua y∈Y (2.3.5)

Hal ini secara tidak langsung menyatakan bahwa pemain 1 yakin hasilnya paling sedikit − ₃1 _{jika memainkan . Artinya bahwa dia akan kalah paling tidak}

adalah

* x

3 1 _.

Jika pemain 2 memainkan

( )

1₃ 3 2_,

*=

y , yakni _y=₃2 _{artinya pemain 2 bermain}

dengan menggunakan strategi II₁ adalah ₃2 _{kali jumlah permainan yang}

dimainkannya. Maka dari persamaan (2.3.4) memberikan

(

)

31

1 x,y* =−

e , untuk semua x∈X (2.3.6)

Jadi, jika pemain 2 memainkan dia meyakinkan pemain 1 bahwa pemain 1 tidak dapat memperoleh hasil lebih dari

* y

3 1

− dengan strategi apapun yang

dimainkan. Pemain 1 akan kalah ₃1_.

Dari contoh di atas jika pemain 1 menggunakan strategi maka hasilnya akan kurang dari atau sama dengan hasil pemain 2 jika pemain 2 menggunakan strategi . Penyelesaian optimal permainan ini adalah pemain 2 memainkan strategi campuran

* x

* y

( )

₃1 3 2_,

*=

y dan pemain 1 memainkan strategi

campuran

(

₃2 3 1_,

*=

)

D. Teorema Nash

Definisi 2.4.1

Semesta pembicaraan adalah R. Dengan titik x merupakan x∈R dan himpunan .

R S⊂

Untuk p∈R dan r<0. Kitar p dengan radus r adalah

( ) (

p r p r p r

) {

x x-p r

N , = − , + = ∈R:| |<

}

. Atau kitar titik p dengan radius r adalah interval terbuka dengan ujung-ujung p-r dan p+r.

Definisi 2.4.2

Titik p adalah titik limit himpunan S jika untuk setiap r<0 terdapat titik q dengan q≠ p,q∈S dan q∈N

( )

p,r .

Definisi 2.4.3

Himpunan S dikatakan tertutup jika semua titik limitnya anggota dari S. Atau (S tertutup) ⇔(p titik limit S ⇒p∈S) .

Contoh 2.4.1

Definisi 2.4.4

Himpunan S disebut terbatas jika himpunan tersebut mempunyai batas atas atau batas bawah.

Contoh 2.4.2

i. Misalkan himpunan S=

{

x|0≤x≤1

}

maka S adalah himpunan terbatas karena himpunan S akan menuju ke 1 dan terbatas pada 1 saja, tidak akan melewati 1. Dengan kata lain, anggota-anggota himpunan S akan berada dintara 0 dan 1, batas bawah 0 dan batas atas 1.

Definisi 2.4.5

Himpunan S disebut konveks jika untuk setiap pasangan dari titik , dalam S membentuk segmen garis

1

x x₂

[x₁ ,x₂] = { : = x x αx₁ + βx₂, α≥0,β≥0,α+β=1} untuk semua S.

y y

x

Contoh 2.4.3

i. Misalkan himpunan S=

{

x,y|x2+y2≤4

}

adalah himpunan konveks. Untuk menunjukkan hal tersebut, ambil dua titik dalam S

(

)

(

,

)

4

4 , 2 2 2 1 2 1 2 2 2 1 2 1 ≤ + ⇒ ∈ = ≤ + ⇒ ∈ = v v S v v u u S u u v u

Himpunan S disebut konveks jika memenuhi definisi 2.4.5

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⇒ ∈ + 2 1 2 1 2 1 2 1 v v u u v v u u S β α β α β α β

αu v

Maka :

(

) (

)

(

)

2

(

)

(

)

4

4 2 2 4 2 2 4 2 2 2 1 2 2 2 1 1 2 2 2 1 2 2 2 2 2 1 2 2 2 1 1 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 1 2 1 1 2 1 2 2 2 2 2 1 1 ≤ + + + + + ≤ + + + + + ≤ + + + + + ≤ + + + v v v u v u u u v v v u v u u u v v u u v v u u v u v u β αβ α β β αβ αβ α α β αβ α β αβ α β α β α

Karena α ≥0,β ≥0,α +β =1 dan u₁2+u₂2 ≤4,v₁2+v₂2 ≤4

Maka

(

)

(

)

(

)

4

2 4 4 2 2 1 1 2 2 2 1 2 2 2 2 1 2 ≤ + ≤ + ≤ + v u v u v v u u αβ β α

Sehingga α2

(

u₁2+u₂2

)

+2αβ

(

u₁v₁+u₂v₂

)

+β2

(

v₁2 +v₂2

)

≤4 Oleh karena itu αu+βv ∈S maka himpunan S konveks.

Definisi 2.4.6

Fungsi f kontinu jika fungsi tersebut berkelanjutan tanpa perubahan yang mendadak.

Contoh 2.4.5

i. Misalkan himpunan S=

{

x|0≤x≤1

}

dan diberikan fungsi . Himpunan S disebut kontinu karena setiap nilai x antara 0 dan 1 jika dipetakan ke dalam fungsi f(x) maka akan mendapatkan nilai yang saling berdekatan dan dapat dihubungkan sebagai garis lurus.

( )

x x f =1−

ii. Misalkan diberikan himpunan S=

{

x|−1≤x≤1

}

dengan persamaan

( )

2

x x

f = . Himpunan S disebut kontinu karena setiap nilai dalam x jika dipetakan ke dalam fungsi f(x) akan mendapatkan nilai yang berkelanjutan tanpa ada perubahan yang mendadak.

Gambar dibawah ini mengambarkan himpunan S yang tertutup, terbatas, konveks dan fungsi f yang berlaku dalam himpunan S tersebut kontinu.

S

f

Teorema 2.4.1 (Teorema titik tetap Brouwer)

Jika f suatu fungsi yang memetakan titik-titik pada himpunan S yang tertutup, terbatas dan konveks dalam ruang Euclides ke dalam himpunan S dan jika f adalah fungsi kontinu maka sekurang-kurangnya ada satu titik dalam S yang dipetakan ke dirinya sendiri (titik tetap).

Dengan kata lain titik tetap tersebut dapat dituliskan ke dalam fungsi sebagai, misalkan f:x→y,x∈S, f kontinu ∃p∈S ∋ f

( )

p =p .

Maka f

( )

p =p merupakan titik tetap.

Bukti untuk teorema Titik Tetap Brouwer ini tidak diberikan, dapat dilihat pada buku ” Some Topics in Two Person Games” yang ditulis oleh T. Parthasarathy dan T.E.S. Raghavan, 1977.

Teorema 2.4.2 (Teorema Nash)

Sebarang permainan untuk dua orang (berjumlah nol atau berjumlah tidak nol) dengan sejumlah strategi yang berhingga paling sedikit mempunyai satu pasangan ekuilibrium.

Bukti :

Misal adalah nilai harapan untuk pemain 1 jika pemain 1 menggunakan strategi I , dan

(

,y

1 Ii

e

)

(

IIj

)

e₂ x, adalah nilai harapan untuk pemain 2 jika pemain 2 menggunakan strategi II.

Didefinisikan

(

∀x∈X,y∈Y

)

( )

{

e

( ) ( )

I e

}

i n

c_i x,y =max 0, _{1 i},y − ₁ x,y ,1≤ ≤

( )

{

e

(

II

)

e

( )

}

j m

d_i x,y =max 0, ₂ x, _j − ₂ x,y ,1≤ ≤

dengan n banyaknya strategi murni pemain 1 dan m banyaknya strategi murni pemain 2.

Diberikan fungsi f : S → S dengan f (x,y) =

(

x′,y′

)

dimana

( )

( )

x,y y x,

∑

=

+ + = ′

n

i i i i i

c c x x

1

1

, 1≤i<n

dan

( )

( )

∑

=

+ + = ′

m

j j j j j

d d y y

1

1 x,y

y x,

, 1≤ j<m

Fungsi f adalah suatu fungsi yang kontinu, karena jika diambil sebarang x∈X, y∈Y, f akan selalu terdefinisi dengan perubahan yang kecil dalam x dan y, akan menyebabkan perubahan kecil dalam x′ dan y′. Dengan demikian menurut teorema Titik Tetap Brouwer ada suatu titik tetap

(

x*,y*

)

dimana

f

(

x*,y*

)

=

(

x*,y*

)

(2.4.1)

(

)

( )

(

)

(

(

* *

)

* * * * * y , x y x y , x y y , x 1 * * 1 1 1 * 1 1 *

1 , 1. ,

e e e x I e x e n i i i n i i = = ≤ =

∑

∑

= =

)

Jadi untuk suatu i diperoleh c_i

(

x*,y*

)

= 0 dari persamaan (2.4.1) diperoleh

(

)

(

)

∑

= + + = _n i i i i i c c x x 1 * *

1 * *

* * y , x y , x (2.4.2)

dan untuk i dimana c_i

(

x*,y*

)

= 0, maka

(

)

0.

1 =

∑

= * * y , x n i i c

Jadi ∀i, 1≤i<n, c_i

(

x*,y*

)

= 0 berlaku e₁

(

x*,y*

) ( )

≥e₁ I_i,y* , sehingga dari sini diperoleh

(

) ( )

e X

e₁ x*,y* ≥ ₁ x,y* , ∀x∈ (2.4.3)

Demikian juga untuk ∀j, 1≤ j<m, menurut persamaan (2.3.3) jika menggunakan strategi campuran maka

(

)

(

)

(

)

(

(

* *

)

2 * * 2 2 1 * 2 1 * 2 , , . 1 , y x y x y , x x y ,

x* * * *

e e e y II e y e m j j j m j j = = ≤ =

∑

∑

= =

)

Jadi untuk suatu j, d_j

(

x*,y*

)

=0

Dari persamaan (2.4.1) diperoleh

(

)

(

)

∑

= + + = _m j j j j j d d y y 1 * *

1 * *

* * y , x y , x (2.4.4)

Jadi (∀j,1≤ j<m), d_j

(

x*,y*

)

=0 berlaku e₂

(

x*,y*

) (

≥e₂ x*,II_j

)

sehingga diperoleh

(

∀y∈Y

)

e₂

(

x*,y*

) ( )

≥e₂ x*,y (2.4.5)

Dari persamaan (2.4.3) dan persamaan (2.4.5) diperoleh

( ) (

* * *

)

y , x y

x, ₁

1 e

e ≤ dan e₂

( ) (

x*,y ≤e₂ x*,y*

)

dengan demikian berdasarkan definisi pasangan ekuilibrium untuk permainan tidak berjumlah nol maka

(

* *

)

y ,

x adalah

suatu pasangan ekuilibrium. ▄

E . Metode Swastika untuk menemukan Pasangan Ekuilibrium

Teorema Nash menyatakan bahwa paling sedikit ada satu titik ekuilibrium dalam suatu permainan. Tetapi dalam teorema tersebut tidak disebutkan cara untuk mendapatkannya. Metode untuk mencari titik ekuilibrium

(

x*,y*

)

dari permainan dua orang berjumlah tidak nol antara lain dengan metode Swastika. Metode swastika ini digunakan pada matriks hasil berordo 2 x 2 dengan langkah-langkah sebagai berikut :

1. Dimisalkan x = (x, 1-x) adalah strategi untuk pemain 1 dan y = (y,1-y) adalah strategi untuk pemain 2.

2. Hitung , yaitu nilai harapan hasil pemain i yang

berhubungan dengan strategi x dan y.

(

x,y

i

e

)

)

3. Tentukan nilai dan yang memaksimalkan untuk

semua nilai y, dan yang memaksimalkan

*

x y* e₁

(

x,y

( )

x,y 2

4.

(

x*,y*

)

merupakan titik ekuilibrium.

Contoh 2.5.1

Diberikan matriks hasil untuk permainan berjumlah tidak nol

Pemain 2

II1 II2

I1 (3,2) (2,1)

Pemain 1

I2 (0,3) (4,4)

Akan dicari hasil yang optimal untuk masing-masing pemain, yaitu titik ekuilibrium untuk permainan ini dan hasil permainan untuk setiap titik ekuilibrium.

Penyelesaian : Untuk pemain 1 Langkah 1:

Matriks hasil untuk pemain 1 adalah

A =

y 1 - y

x 3 2

Langkah 2 :

Nilai harapan hasil pemain 1 adalah

e1(x,y) = x ( 3y + 2 (1 – y)) + (1 – x) (0.y + 4 (1 – y)) = x ( 3y + 2 – 2y) + (1 – x) (4 – 4y)

= x (y + 2) + (4 – 4y – 4x + 4xy) = x (y + 2) + x (4y – 4) + (4 – 4y)

= x (5y – 2) + (4 – 4y) (2.5.1)

Langkah 3 :

Untuk mendapatkan hasil e1(x,y) yang optimal maka akan dicari titik kritisnya, yakni dengan menurunkan persamaan (2.5.1) terhadap x, sehingga diperoleh :

(

x,y ' 1

e

)

= (5y – 2) = 0 ⇒ _y=₅2 _.

Terdapat tiga kemungkinan nilai y, yaitu ₅2 5 2 5

2_, = _, >

< y y

y .

Dari persamaan (2.5.1) akan didapatkan : Jika _y<₅2 _{maka e}

1(x,y) dimaksimalkan oleh x = 0 Jika _y=₅2 _{maka e}

1(x,y) dimaksimalkan oleh 0<x<1 Jika _y>₅2 _{maka e}

1(x,y) dimaksimalkan oleh x = 1

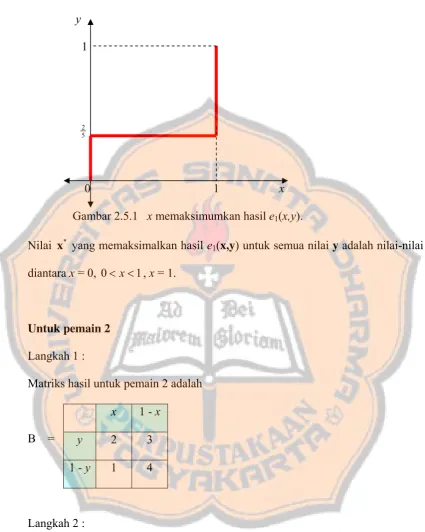
y 1

₅2

0 1 x Gambar 2.5.1 x memaksimumkan hasil e1(x,y).

Nilai x* yang memaksimalkan hasil e1(x,y) untuk semua nilai y adalah nilai-nilai diantara x = 0, 0<x<1, x = 1.

Untuk pemain 2 Langkah 1 :

Matriks hasil untuk pemain 2 adalah

B =

x 1 - x

y 2 3

1 - y 1 4

Langkah 2 :

Nilai harapan hasil pemain 2 adalah

= y (-x + 3) + (-3x + 4 + 3xy – 4y) = y (-x + 3) + y (3x – 4) + (4 – 3x)

= y (2x – 1) + (4 – 3x) (2.5.2)

Langkah 3 :

Untuk mendapatkan hasil e2(x,y) yang optimal maka akan dicari titik kritisnya, yakni dengan menurunkan persamaan (2.5.2) terhadap y, sehingga diperoleh :

(

x,y ' 2

e

) = (2x – 1) = 0

⇒_x =₂1 _.

Terdapat tiga kemungkinan nilai x, yaitu ₂1 2 1 2

1_, = _, >

< x x

x .

Dari persamaan (2.5.2) diperoleh bahwa

jika 2 1

<

x maka e2(x,y) dimaksimalkan oleh y = 0

jika 2 1

=

x maka e2(x,y) dimaksimalkan oleh 0< y<1

jika 2 1

>

x maka e2(x,y) dimaksimalkan oleh y = 1

y

1

0 ₂1 _{1 x}

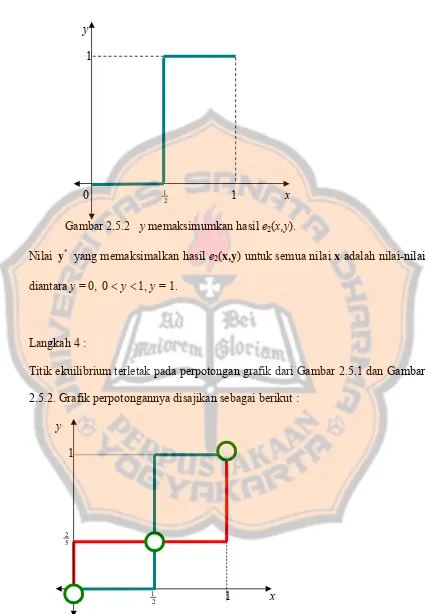
Gambar 2.5.2 y memaksimumkan hasil e2(x,y).

Nilai y* yang memaksimalkan hasil e2(x,y) untuk semua nilai x adalah nilai-nilai diantara y = 0, 0< y<1, y = 1.

Langkah 4 :

Titik ekuilibrium terletak pada perpotongan grafik dari Gambar 2.5.1 dan Gambar 2.5.2. Grafik perpotongannya disajikan sebagai berikut :

y 1

₅2

0 ₂1 _{1 x}

Dari gambar 2.5.3 diperoleh tiga buah titik potong, yaitu A(0,0), B( ₅2 2

1_{, ), C(1,1).}

Akan ditentukan nilai permainan dari titik ekuilibrium-ekuilibrium tersebut. Perhatikan kembali, dari persamaan 2.5.1 dan persamaan 2.5.2 diperoleh

(

x,y 1

e

)

)

= x (5y – 2) + (4 – 4y)

(

x,y

2

e = y (2x – 1) + (4 – 3x)

Untuk titik ekuilibrium A(0,0), yakni x=0dany=0 maka didapatkan

(

0,0

1

e

)

)

= 0 (5.0 – 2) + (4 – 4.0) = 4 .

(

0,0

2

e = 0(2.0 – 1) + (4 – 3.0) = 4 . Dengan demikian hasilnya adalah (4,4). Untuk titik ekuilibrium B( ₅2

2

1_{, ), yakni}

5 2 2

1 _dan =

= y

x maka didapatkan

( )

₅2 2 1

1 ,

e = ₂1 _(5. 5

2 _{– 2) + (4 – 4.} 5 2_{) =}

5

12 _{= 2,4 .}

( )

₅2 2 1

2 ,

e = ₅2 _(2. 2

1 _{– 1) + (4 – 3.} 2

1 _{) = 2,5 .}

Dengan demikian hasilnya adalah (2,4 ; 2,5).

Untuk titik ekuilibrium C(1,1), yakni x=1dany=1 maka didapatkan

( )

1,1

1

e = 1 (5. 1– 2) + (4 – 4.1) = 3.

(

₅2 2 1

2 ,

e

)

= 1 (2. 1 – 1) + (4 – 3. 1) = 2. Dengan demikian hasilnya adalah (3,2).

Jadi titik ekuilibrium

(

x*,y*

)

adalah (0,0),

( )

₅2 2

1_{, , (1,1) dan hasil permainannya}

masing-masing adalah (4,4), (2,4 ; 2,5), (3,2).

Dapat disimpulkan dari matriks hasil di atas bahwa hasil permainan untuk pemain 1 adalah 2,4. Akan ditunjukkan grafik untuk permainan tersebut.

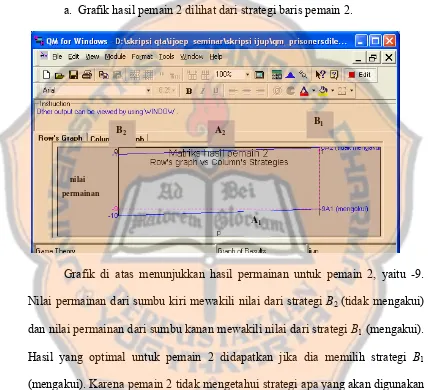
a. Grafik hasil pemain 1 dilihat dari strategi baris pemain 1.

Strategi kedua dari pemain 1

Strategi pertama dari pemain 1 Strategi kedua

dari pemain 2

nilai permainan

Strategi pertama dari pemain 2

hubungan strategi pertama dan strategi kedua pemain 1 terhadap strategi pemain 2. Pemain 1 akan memilih strategi pertama daripada memilih strategi kedua. Karena strategi pertama dari pemain 1 merupakan strategi yang memaksimumkan minimum keuntungan. Dengan peluang menggunakan strategi strategi pertama dari pemain 1 adalah 0,8 dan nilai permainan adalah 2,4.

b. Grafik hasil pemain 1 dilihat dari strategi kolom pemain 2.

Strategi kedua dari pemain 2

Strategi pertama dari pemain 2 Strategi pertama

dari pemain 1

nilai permainan

Strategi kedua dari pemain 1

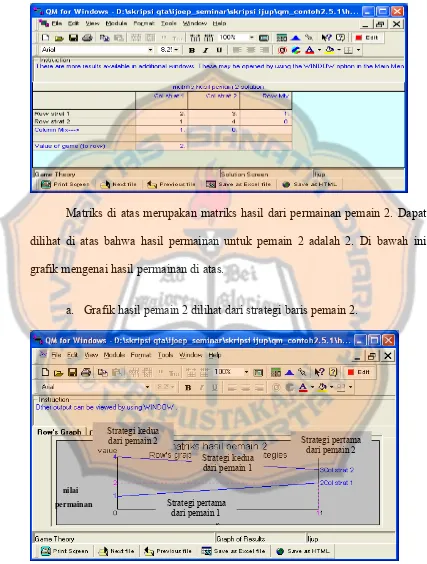
Matriks hasil pemain 2 ditunjukkan sebagai berikut :

Matriks di atas merupakan matriks hasil dari permainan pemain 2. Dapat dilihat di atas bahwa hasil permainan untuk pemain 2 adalah 2. Di bawah ini grafik mengenai hasil permainan di atas.

a. Grafik hasil pemain 2 dilihat dari strategi baris pemain 2.

Strategi kedua

dari pemain 2 Strategi pertama dari pemain 2 Strategi kedua

dari pemain 1

nilai

permainan Strategi pertama

dari pemain 1

nilai pada sumbu kanan mewakili nilai strategi pertama pemain 2. Pemain 2 memilih menggunakan strategi pertama karena akan mendapatkan hasil yang maksimal, yaitu 2. Daripada memilih strategi kedua akan mendapatkan hasil 1. Pemain 2 pasti akan memilih strategi pertama yang membuat dia meminimumkan maksimum kerugian. Dengan peluang menggunakan strategi pertama adalah 1 dan nilai permainannya adalah 2.

b. Grafik hasil pemain 2 dilihat dari strategi kolom pemain 1.

Strategi kedua dari pemain 1

Strategi pertama dari pemain2

Strategi pertama dari pemain 1

nilai permainan

Strategi kedua dari pemain 2

Contoh 2.5.2

Diberikan matriks hasil untuk permainan Prisoners Dilemma sebagai berikut : Pemain 2

II1 II2

I1 (-9,-9) (0,-10)

Pemain 1

I2 (-10,0) (-1,-1)

Dengan metode Swastika tentukan titik ekuilibrium untuk permainan ini dan hasil permainan untuk setiap titik ekuilibriumnya.

Penyelesaian : Untuk pemain 1 Langkah 1:

Matriks hasil untuk pemain 1 adalah

A =

y 1 - y

x -9 0

1 - x -10 -1

Langkah 2 :

Nilai harapan hasil pemain 1 adalah

= x (-9y) + (1-x) (-9y -1) = x (-9y) + (-9y -1 + 9xy +x) = x (-9y) + x (9y +1) + (-9y -1)

= x- 9y -1 (2.5.3)

Langkah 3 :

Untuk mendapatkan hasil e1(x,y) yang optimal maka akan dicari titik kritisnya, yakni dengan menurunkan persamaan (2.5.3) terhadap x, sehingga diperoleh :

(

x,y ' 1

e

)

= 1 .

Maka nilai x* yang memaksimalkan hasil e1(x,y) untuk semua nilai y adalah .

( )

1,0

*=

x

Digambarkan dalam grafik berikut : y

1

0 1 x Gambar 2.5.4 x memaksimumkan hasil e1(x,y).

Untuk pemain 2 Langkah 1 :

B =

x 1 - x

y -9 0

1 - y -10 -1

Langkah 2 :

Nilai harapan hasil pemain 2 adalah

e2(x,y) = y ( -9 x + 0 (1 - x)) + (1 - y) ( -10.x + (-1) (1 - x)) = y ( -9x) + (1 – y) ( -10x -1 + x)

= y (-9x) + (1 – y) (-9x -1) = y (-9x) + (-9x - 1 + 9xy + y) = y (-9x) + y (9x +1 ) + ( -9x -1)

= y - 9x -1 (2.5.4)

Langkah 3 :

Untuk mendapatkan hasil e2(x,y) yang optimal maka akan dicari titik kritisnya, yakni dengan menurunkan persamaan (2.5.4) terhadap y, sehingga diperoleh :

(

x,y ' 2

e

)

= 1

Maka Nilai y* yang memaksimalkan hasil e2(x,y) untuk semua nilai x adalah .

( )

0,1

* =

y

y 1

0 1 x Gambar 2.5.5. y memaksimumkan hasil e2(x,y).

Langkah 4 :

Titik ekuilibrium terletak pada perpotongan grafik berikut : y

1

0 1 x

Gambar 2.5.6 Metode Swastika untuk pasangan ekuilibrium.

Dari gambar 2.5.6 diperoleh sebuah titik potong, yaitu (1,1). Akan ditentukan nilai permainan dari titik ekuilibrium tersebut. Perhatikan kembali, dari persamaan 2.5.3 dan persamaan 2.5.4 diperoleh

(

x,y 1

e

)

)

= x- 9y -1

(

x,y

2

Untuk titik ekuilibrium (1,1), yakni x=1dany=1 maka didapatkan

( )

1,1

1

e = 1 -9 -1= -9 .

( )

1,1

2

e = 1-9 -1 = -9 .

Dengan demikian hasilnya adalah (-9,-9).

Jadi titik ekuilibrium

(

x*,y*

)

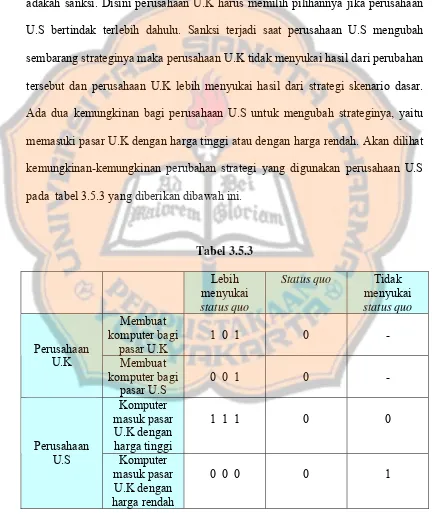
adalah (1,1) dan hasil permainannya adalah (-9,-9).

Mencari titik ekuilibrium pada permainan Prisoners Dilemma di atas menggunakan program QM.

Matriks hasil pemain 1 disajikan sebagai berikut :

a. Grafik hasil pemain 1dilihat dari strategi baris pemain 1.

A1

A2 BB2

nilai permainan

BB1

Dari grafik di atas dapat ditunjukkan bahwa nilai pemainan pada sumbu kiri mewakili nilai-nilai dari strategi (tidak mengakui) dan nilai permainan pada sumbu kanan mewakili nilai-nilai dar strategi A

2

A

1 (mengakui). Grafik di atas menunjukkan hubungan strategi A1 dan A2 terhadap strategi kolom pemain 2.

Pemain 1 akan lebih memilih A1 daripada , karena pemain 1 memilih kemungkinan terburuk, yaitu jika pemain 1 memilih A

2

A

1 maka dia akan mendapatkan hukuman penjara selama 9 tahun. Daripada memilih strategi maka akan mendapatkan hukuman penjara selama 10 tahun. Maka pemain 1 memilih strategi yang meminimumkan maksimum hukuman yang akan dia terima, yaitu memilih dihukum 9 tahun daripada 10 tahun.

2

A

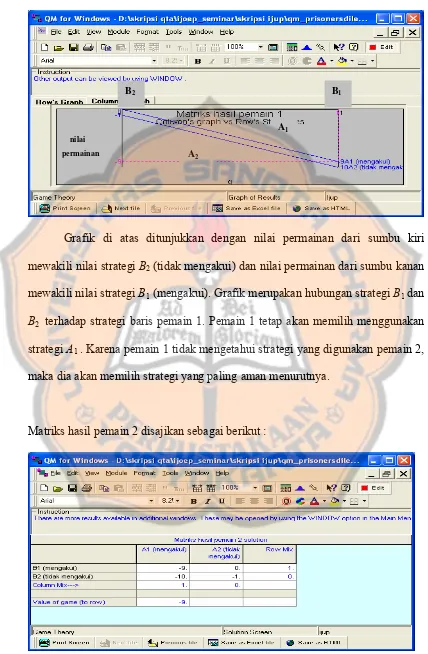
BB2 BB1

A1 nilai

permainan _A2

Grafik di atas ditunjukkan dengan nilai permainan dari sumbu kiri mewakili nilai strategi BB2 (tidak mengakui) dan nilai permainan dari sumbu kanan mewakili nilai strategi B1B (mengakui). Grafik merupakan hubungan strategi BB1 dan B2 B terhadap strategi baris pemain 1. Pemain 1 tetap akan memilih menggunakan strategi A1 . Karena pemain 1 tidak mengetahui strategi yang digunakan pemain 2, maka dia akan memilih strategi yang paling aman menurutnya.

Dari matriks di atas hasil permainan untuk pemain 2 adalah -9. Hasil permainan tersebut sesuai dengan hasil permainan pada contoh 2.2.2. Akan diperlihatkan grafik untuk pemain 2 dari permainan di atas.

a. Grafik hasil pemain 2 dilihat dari strategi baris pemain 2.

BB1

A2

BB2

nilai permainan

A1

b. Grafik hasil pemain 2 dilihat dari strategi kolom pemain 1

A2 _A

1

B B B1 nilai

permainan

B

2

Dari grafik di atas menunjukkan bahwa nilai permainan dari sumbu kiri mewakili nilai-nilai dari strategi (tidak mengakui) dan nilai permainan dari sumbu kanan mewakili nilai-nilai dari strategi (mengakui). Grafik tersebut menunjukkan hubungan strategi dan terhadap strategi baris pemain 2. Pemain 2 memilih untuk menggunakan strategi B

2

A

1

A

2

A A₁

B

1 (mengakui) daripada memilih strategi B2 B (tidak mengakui). Karena jika pemain 2 memilih BB2 (tidak mengakui) maka kemungkinan terburuknya adalah pemain 2 akan dihukum penjara selama 10 tahun. Tetapi jika dia memilih strategi B1B (mengakui) maka kemungkinan terburuknya adalah pemain 2 akan dihukum penjara selama 9 tahun.

BAB III

METAGAME TANPA KERJASAMA UNTUK 2 PEMAIN

Metagame adalah permainan dengan strategi permainan yang titik ekuilibriumnya didapat berdasarkan pada permainan yang sedang berlangsung. Permainan tanpa kerjasama untuk dua pemain adalah permainan yang melibatkan dua pemain dimana tidak ada kerjasama antara kedua pemain tersebut. Jadi metagame tanpa kerjasama untuk dua pemain adalah permainan yang melibatkan dua pemain dimana diantara para pemainnya tidak ada kerjasama dan strategi permainan yang digunakan oleh para pemain didasarkan pada permainan yang sedang berlangsung.

pemain lainnya. Dan hasil permainan yang didapatkan akan seperti dalam kenyataan.

Kesulitan pada permainan ini adalah bahwa pemain yang satu memberikan peluang kepada pemain yang lain untuk memilih fungsi reaksi yang akan digunakan sebagai strateginya, dan jika terjadi terus menerus maka fungsi reaksi yang terjadi akan sampai tak hingga banyaknya. Asumsi untuk menemukan hasil nyata yang stabil adalah masing-masing pemain memprediksi dengan tepat strategi dari para pemain lainnya, dan memilih hasil yang paling menguntungkan untuknya.

A. Metagame dan Metaekuilibria

Misalkan pemain 1 memainkan strategi campuran

(

*

)

1 * 12 * 11 *

1 x ,x .,...,xn

X = ,

pemain 2 memainkan strategi campuran X₂* =

(

x*₂₁,x₂₂* ,...,x₂*n

)

dan misalkan juga

(

* *

)

2 *

1, ,..., n

i x x x

e adalah hasil untuk pemain i jika pemain 1 memainkan strategi

campuran X₁* dan pemain 2 memainkan strategi campuran X₂*. Akan dijabarkan pengertian dari ekuilibrium dalam permainan tanpa kerjasama dengan n pemain yang telah didefinisikan dalam bab sebelumnya, yaitu definisi 2.2.8.

Misalkan pada sebuah permainan G dengan n pemain, pemain i

mempunyai kumpulan strategi murni dengan i = 1,2 ,…,n. Hasil dari sebuah permainan ditentukan dari strategi yang digunakan masing-masing pemain. Pada umumnya para pemain akan memilih strategi yang nantinya akan lebih

i

X

menguntungkan untuk dirinya sendiri. Dalam metagame strategi yang digunakan pemain akan menentukan hasil rasional pada permainan tersebut.

Definisi 3.1.2

Misalkan X_i =

(

x₁,x₂,...,x_n

)

adalah kumpulan strategi murni dari n pemain. Hasil rasional pada saat permainan sedang berlangsung untuk pemain i merupakan n

pasang strategi x₁*, x₂*,..., x_n* , dengan

(

₁*, ₂*,..., *_i,..., *_n

) (

_{i 1}*, *₂,..., _i,..., *_n)

i x x x x e x x x x

e ≥ , untuk semua .

Sekumpulan hasil rasional untuk pemain i dalam permainan G dinyatakan dengan .

i

i X

x ∈

( )

G R_i

Definisi 3.1.3

Ekuilibrium dari permainan G dengan n pemain adalah hasil rasional untuk semua pemain, yakniE

( )

G , yang memenuhi :

= .

( )

G

E R

( )

G

n

i i

I

1

=

Definisi 3.1.4

Hasil yang stabil terjadi jika pemain lawan menggunakan strategi lain, maka hal tersebut tidak akan mempengaruhi hasil permainan yang terjadi.

Untuk mempertimbangkan hasil mana yang stabil maka misalkan dipertimbangkan metagame 1G. Dalam permainan ini masing-masing pemain

kecuali pemain 1 terlebih dahulu memilih strateginya dalam permainan dasar G. Setelah pemain lain memilih strateginya barulah pemain 1 memilih strateginya dalam permainan dasar tersebut dengan mempertimbangkan strategi–strategi lawannya. Jika pemain 1 dapat memprediksi strategi–strategi pemain lain sebelum memil