MOMEN, KECONDONGAN DAN KERUNCINGAN

(1)

MOMEN, KECONDONGAN DAN

KERUNCINGAN

Oleh :

Malalina (20102512008) Febrina Bidasari (20102512018)

Mahasiswa Pasca Sarjana Universitas Sriwijaya

Rata-rata dan varians sebenarnya merupakan hal istimewa dari kelompok

ukuran lain yang disebut Momen. Dari Momen ini juga dapat diturunkan beberapa

ukuran lain.

1. MOMEN

a. Untuk Data Tunggal

Misalkan diberikan variabel x dengan harga-harga: x1, x2, x3, …, xn. Jika

A = sebuah bilangan tetap dan r = 0, 1, 2, …, n, maka momen ke-r sekitar A,

disingkat mr’, didefinisikan oleh hubungan :

(

)

n A x m

r i r

− =

'

… (1.1)

Untuk A = 0 didapat momen ke-r sekitar nol atau disingkat momen ke-r.

n x m

r i r =

'

… (1.2)

maka untuk r = 1 didapat rata-rata x

Jika A=x kita peroleh momen ke-r sekitar rata-rata, biasa disingkat mr.

(

)

n x x m

r i r

− =

Untuk r = 2, persamaan (2.3) memberikan varians s2.

Untuk membedakan apakah momen itu untuk sampel atau untuk populasi, maka

dipakai simbol :

mr dan mr’ untuk momen sampel

(2)

Jadi mr dan mr’ adalah statistik sedangkan r dan r’ merupakan parameter.

b. Untuk Data Kelompok

Jika data telah disusun dalam daftar distribusi frekuensi (data kelompok),

maka persamaan-persamaan di atas berturut-turut berbentuk :

Momen ke-r di sekitar A

(

)

n A x f m

r i i r

− =

'

Untuk A = 0 didapat momen ke-r sekitar nol atau disingkat momen ke-r.

n x f m

r i i r =

'

Jika A=x kita peroleh momen ke-r sekitar rata-rata, biasa disingkat mr.

(

)

n x x f m

r i i r

− =

Keterangan :

= f_i

n

xi= tanda kelas interval

fi= frekuensi yang sesuai dengan xi.

Dengan menggunakan persamaan diatas untuk data kelompom dapat ditulis

dengan cara coding menjadi :

=

n ci fi p

m

r r

r

.

'

Keterangan :

P = Panjang kelas,

c = Variabel coding, (c = 0, + 1, + 2, .... )

(3)

( )

_' 4

1 ' 2 2 ' 1 ' 3 ' 1 ' 4 4 3 ' 1 ' 2 ' 1 ' 3 3 2 ' 1 ' 2 2 3 6 4 2 3 m m m m m m m m m m m m m m m − + − = + − = − = Contoh :

Untuk menghitung momen disekitar rata-rata, untuk data dalam daftar distribusi

frekuensi, kita lakukan sebagai berikut:

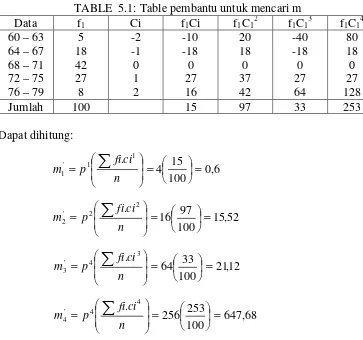
TABLE 5.1: Table pembantu untuk mencari m

Data f1 Ci f1Ci f1C12 f1C13 f1C14 60 – 63

64 – 67 68 – 71 72 – 75 76 – 79

5 18 42 27 8 -2 -1 0 1 2 -10 -18 0 27 16 20 18 0 37 42 -40 -18 0 27 64 80 18 0 27 128

Jumlah 100 15 97 33 253

Dapat dihitung: 6 , 0 100 15 4 . 1 1 '

1 = = =

n ci fi p m 52 , 15 100 97 16 . 2 2 '

2 = = =

n ci fi p m 12 , 21 100 33 64 . 3 4 '

3 = = =

n ci fi p m 68 , 647 100 253 256 . 4 4 '

4 = = =

n ci fi p

m

(4)

( )

4752 , 652 3888 , 0 872 , 55 688 , 50 68 , 647 3 6 4 384 , 6 432 , 0 936 , 27 12 , 21 2 3 16 , 15 36 , 0 52 , 15 ) 6 , 0 ( 52 , 15 4 ' 1 ' 2 2 ' 1 ' 3 ' 1 ' 4 4 3 ' 1 ' 2 ' 1 ' 3 3 2 2 ' 1 ' 2 2 = − + − = − + − = − = + − = + − = = − = − = − = m m m m m m m m m m m m m m m

Jadi Varian S2 = m2 = 15,16

2. KECONDONGAN ATAU KEMENCENGAN (SKEWNESS)

Tampilan kurva yang diperlihatkan oleh suatu distribusi data bisa saja

berbentuk simetris maupun tidak simetris. Kurva yang mencerminkan distribusi

data dikatakan simetris bila belahan kanan dan belahan sebelah kiri memiliki

bentuk dan ukuran yang sama. Sebaiknya, kurva yang menggambarkan distribusi

data dikatakan tidak simetris jika belahan sebelah kiri dan belahan sebelah kanan

tidak memiliki bentuk dan ukuran yang sama. Guna menunjukkan tingkat

simetrisitas suatu kurva yang ditampilkan dari suatu distribusi data, konsep dan

pengertian mengenai ukuran kecondongan (skewness) menjadi penting untuk dipahami.

Bentuk suatu kurva merupakan pencerminan pola distribusi data.

Karenanya, kecondongan suatu kurva dapat dilihat dari perbedaan letak antara

mean, median, dan modus. Bila disajikan dalam bentuk grafik maka akan terlihat

sebagai berikut :

Kurva Keterangan

Distribusi suatu gugusan data

dikatakan simetris bila nilai mean, median, dan modus terletak dalam suatu titik temu atau mempunyai

(5)

Condong secara Negatif

(Condong ke Kiri)

Kecondongan Penyebaran Data ke

Arah kiri.

Karena nilai mean, median, dan modus tidak sama maka bentuk kurva yang ditampilkan akan condong pada salah satu sisi kiri saja.

x Mo

Condong secara Positif

(Condong ke Kanan)

Kecondongan Penyebaran Data ke

Arah Kanan.

Karena nilai mean, median, dan modus tidak sama maka bentuk kurva yang ditampilkan akan condong pada salah satu sisi kanan saja.

x Mo

Contoh :

Tentukan bentuk Kurva dari Nilai Ujian Statistik Semester II ?

Nilai Ujian Frekuensi (f) Nilai Tengah (X) f.X

32 - 41 7 36.5 255.5

42 - 51 12 46.5 558

52 - 61 22 56.5 1243

62 - 71 12 66.5 798

72 - 81 7 76.5 535.5

60 3390

Penyelesaian :

Dari tabel diatas dilakukan perhitungan mean, median dan modus.

(6)

50 , 56 60 3390

= =

=

f fX X

Median dari data nilai ujian statistik adalah :

50 , 56 22

19 30 10 50 , 51 2

1

= − +

=

f F n p b Me

Modus dari data nilai ujian statistik adalah :

50 , 56 10 10

10 10 50 , 51

2 1

1 ₌

+ +

= + +

=

b b

b p b Mo

Dari data ujian statistik karena nilai mean, median dan modus adalah sama maka

akan membentuk kurva yang simetris yaitu :

Md x Mo= =

Untuk mengetahui bahwa kurva condong kekiri atau ke kanan dapat digunakan

metode berikut :

a. Koefisien Kemencengan Person

Karl Pearson (seorang pakar statistika ternama) telah merumuskan suatu

formula, yakni melalui apa yang dinamakan sebagai koefisien kecondongan

Pearson. Rumus untuk mengukur tingkat kecondongan distribusi data oleh Karl

Pearson ini adalah :

s Mo X PSk = −

Keterangan :

PSk = Koefisien kecondongan Person

X = Mean

(7)

s = standar deviasi

Selain melalui rumus yang lebih menekankan pada nilai-nilai modus,

dalam kondisi tertentu median dipandang sebagai ukuran nilai sentral yang lebih

mampu memberikan angka valid. Karl Pearson merumuskan kembali hubungan di

atas secara umum :

) (

3 X Md Mo

X − = −

Keterangan : Md = Median

X = Mean

Mo = Modus

Apabila rumus di atas disederhanakan dengan memperhitungkan median dan nilai

modus dari hubungan itu, maka akan menjadi :

s Md X

PSk =3( − )

Keterangan :

Md = Median

X = Mean

Mo = Modus

s = Standar Deviasi

Berkenaan dengan perhitungan koefisien kecondongan Pearson itu, ada tiga

kemungkinan yang dapat terjadi yaitu :

a. Nilai koefisien kecondongan Pearson adalah 0 maka distribusi data dalam

suatu gugusan akan membentuk pola yang simetris.

b. Nilai kecondongan Pearson nilainya lebih dari 0 maka arah kecondongan

adalah ke kanan di mana dalam hal ini data akan terkonsentrasikan pada

nilai yang rendah (X terletak di sebelah kanan Mo).

c. Sementara apabila nilai koefisien kecondongan kurang dari 0 maka arah

kecondongan adalah ke kiri di mana dalam hal ini ia akan terkonsentrasikan

pada nilai yang relatif tinggi (X terletak di sebelah kanan Mo).

(8)

Tentukan niali koefisien person dan tentuka kemencengan kurva dari data Nilai

Ujian Statistik di Universitas Borobudur Tahun 2009

Nilai Ujian Frekuensi (f)

Nilai Tengah

(X) f.X

(

X −X

)

(

X−X

)

2 f

(

X −X

)

2

31 - 40 4 35.5 142 -32 1024 4096

41 - 50 3 45.5 136.5 -22 484 1452

51 - 60 5 55.5 277.5 -12 144 720

61 - 70 8 65.5 524 -2 4 32

71 - 80 11 75.5 830.5 8 64 704

81 - 90 7 85.5 598.5 18 324 2268

91 - 100 2 95.5 191 28 784 1568

40 2700 10840

Penyelesaian :

nilai mean :

5 , 67 40 2700 = = = f fX X

Nilai standar deviasai :

(

)

2 , 16 271 40 10840 2 = = = − = n X X f s

Nilai Median :

5 , 70 8 12 40 2 1 10 5 , 60 2 1 = − + = − + = f F n p b Md

Nilai Modus :

94 , 74 4 3 3 10 5 , 70 2 1 1 ₌ + + = + + = b b b p b Mo

Nilai koefisien kecondongan Pearson :

(9)

Karena nilai koefisien kecondongan Pearson adalah negatif maka kurvanya

condong ke kiri.

b. Koefisien Kemencengan Bowley

Koefisien kemencengan Bowley berdasarkan pada hubungan kuartil-kuartil

(Q1,Q2 dan Q3) dari sebuah distribusi. Koefisien kemencengan Bowley

dirumuskan :

(

) (

)

(

3 2

) (

2 1

)

1 2 2 3

Q Q Q Q

Q Q Q Q sk_B

− + −

− − − =

Atau

) (

) 2 (

1 3

2 1 3

Q Q

Q Q Q sk_B

− − + =

Keterangan :

skb = Koefisien kemencengan Bowley

Q = Kuartil

Koefisien kemencengan Bowley sering juga disebut Kuartil Koefisien

Kemencengan.

Apabila nilai skb dihubungkan dengan kurva, didapatkan :

a. Jika Q3 - Q2 > Q2 – Q1 maka distribusi akan menceng ke kanan (Menceng

positif)

b. Jika Q3 - Q2 < Q2 – Q1 maka distribusi akan menceng ke kiri (Menceng

negatif)

c. skb positif berarti distribusi menceng ke kanan

(10)

e. skb = + 0,01 berarti distribusi yang menceng tidak berarti

(11)

Contoh :

Tentukan kemencengan kurva nilai ujian statistik universitas Borobudur Tahun

2007

31 - 40 4 35.5 142

41 - 50 3 45.5 136.5

51 - 60 5 55.5 277.5

61 - 70 8 65.5 524

71 - 80 11 75.5 830.5

81 - 90 7 85.5 598.5

91 - 100 2 95.5 191

40 2700

i = 1 maka

( )

10 4 40 1

4 = =

in

terletak dikelas ke-3

i = 2 maka

( )

20 4

40 2

4 = =

in

i = 3 maka

( )

30 4

40 3

4 = =

in

terletak di kelas ke-5

b1 = 50,5 ; b2 = 60,5 ; b1 = 70,5

p = 10

f1 = 5 ; f1 = 8 ; f1 = 11

F1 = 7 ; F1 = 12 ; F1 = 20 ;

( )

5 , 56 5

7 4 40 1

10 5 , 50

1 =

− +

=

Q

( )

5 , 70 8

12 4 40 2

10 5 , 60

2 =

− +

=

Q

( )

59 , 79 11

20 4 40 3

10 5 , 70

3 =

− +

(12)

Sehingga nilai koefisien kemencengan Bowley adalah :

(

)

2 , 0 5

, 56 59 , 79

5 , 70 2 5 , 56 59 , 79 )

(

) 2 (

1 3

2 1

3 ₌₋

− − + =

Q Q

Q Q Q skB

Karena skB negatif yaitu -0,2 maka kurva menceng kekiri dengan kemencengan

yang berarti.

c. Koefisien Kemencengan Persentil

Koefisien kemencengan persentil didasarkan atas hubungan antarpersentil

(P90, P50 dan P10) dari sebuah distribusi. Koefisien kemencengan persentil

dirumuskan :

10 50

10 50 90 2

P P

P P P skP

− + − =

Keterangan :

skP = Koefisien kemencengan Persentil

P = Persentil

Contoh :

2007

31 - 40 4 35.5 142

41 - 50 3 45.5 136.5

51 - 60 5 55.5 277.5

61 - 70 8 65.5 524

71 - 80 11 75.5 830.5

81 - 90 7 85.5 598.5

91 - 100 2 95.5 191

40 2700

(13)

n = 40

i = 10 maka

( )

4

100 40 10

100 = =

in

i = 50 maka

( )

20

100 40 50

100 = =

in

i = 90 maka

( )

36

100 40 90

4 = =

in

b10 = 30,5 ; b50 = 60,5 ; b90 = 80,5

p = 10

f10 = 4 ; f50 = 8 ; f90 = 7

F10 = 4 ; F50 = 12 ; F90 = 31

( )

5 , 30 4 4 100 40 10 10 5 , 30 10 = − + = P

( )

5 , 70 8 12 100 40 50 10 5 , 60 50 = − + = P

( )

64 , 87 7 31 100 40 90 10 5 , 80 90 = − + = P

Sehingga koefisien kemencengan persentil adalah :

(

)

5715 , 0 5 , 30 5 , 70 5 , 30 5 , 70 2 64 , 87 2 10 50 10 50

90 ₌₋

− + − = − + − = P P P P P sk_P

(14)

d. Koefisien Kemencengan Momen

Koefisien kecondongan momen atau koefisien kecondongan merupakan

perbandingan momen ketiga dengan pangkat tiga simpangan baku. Dilambangkan

3

α

, merupakan penyederhanaan dari koefisien kecondongan Pearson.

Kecondongan momen dinamakan pula koefisien kecondongan relatif(relative skewness coefficient).

Apabila nilai

α

₃ dihubungkan dengan keadaan kurva maka :

a. Nilai koefisien kecondongan momen adalah 0 maka distribusi simetris atau

normal.

b. Nilai koefisien kecondongan momen positif, distribusi data condong ke

kanan.

c. Nilai koefisien kecondongan momen negatif, arah kecondongan distribusi

data adalah ke kiri.

d. Menurut karl pearson distribusi yang memiliki nilai

α

₃ > + 0,50 adalah distribusi yang sangat menceng

e. Menurut kenney dan keeping nilai

α

₃ bervariasi antara + 2 bagi distribusi yang menceng.

Untuk mencari nilai

α

₃, dibedakan antara data tunggal dan data kelompok

a. Untuk Data Tunggal

Koefisien kemencengan momen untuk data tunggal dirumuskan :

(

)

3 3 3

3 3

1

s X X n s

M −

= =

α

Keterangan :

3

α

= koefisien kemencengan momen

Contoh :

(15)

Penyelesaian :

6 5

11 9 5 3 2

= + + + + =

X

X X −X

(

X −X

)

2

(

X −X

)

3

2 -4 16 64

3 -3 9 27

5 -1 1 1

9 3 9 27

11 5 25 125

JUMLAH 60 60

(

)

873 , 3 4 60 1

2

= =

− − =

n X X s

Sehingga koefisien momen adalah :

(

)

( )

(

3,873

)

0,2

60 5 1 1

2 3

3

3 = =

− =

s X X n α

Maka kecondongan dari data ini adalah kecondongan ke kanan (positif)

b. Untuk Data Berkelompok

Koefisien kemencengan momen untuk data kelompok dirumuskan :

(

)

3 3 3

1

s

f X X

n −

=

(16)

Contoh :

2007

Nilai Ujian Frekuensi (f)

Nilai Tengah

(X)

f.X _X ₋_X

(

)

2

X

X −

(

)

3

X

X − f

(

X −X

)

3

31 - 40 4 35.5 142

41 - 50 3 45.5 136.5

51 - 60 5 55.5 277.5

61 - 70 8 65.5 524

71 - 80 11 75.5 830.5

81 - 90 7 85.5 598.5

91 - 100 2 95.5 191

40 2700

Penyelesaian :

5 , 67 40 2700

= =

=

f fX X

(

)

5 , 8 40 2828 1

2

= =

− − =

n X X s

Sehingga Koefisien kemencengan momen adalah :

(

)

(

)

31 , 3 4

, 8

81360 40

1 1

3 3

3 =−

− = −

=

s

f X X n α

(17)

3. KERUNCINGAN ATAU KURTOSIS

Keruncingan atau kurtosisi adalah tingkat kepuncakan dari sebuah

distribusi yang biasa diambil secara relatif terhadap suatu distribusi normal.

Berdasarkan keruncingannya, kurva distribusi dapat dibedakan atas tiga

macam, yaitu :

Leptokurtik

Leptokurtik merupakan

distribusi yang memiliki puncak

relatif tinggi

Platikurtik

Platikurtik merupakan distribusi

yang memiliki puncak hampir

mendatar

Mesokurtik

Mesokurtik merupakan

distribusi yang memiliki puncak

yang tidak tinggi dan tidak

mendatar.

(18)

Bila distribusinya simetris maka distribusi mesokurtik dianggap sebagai distribusi

normal.

Untuk mengetahui keruncingan suatu distribusi, ukuran yang sering

digunakan adalah koefisien keruncingan atau koefisien kurtosisi persentil.

a. Koefisien Keruncingan

Koefisien keruncingan dilambangkan dengan α₄. Hasil perhitungan koefisien keruncingan diperoleh :

- Jika α4 <3 maka distribusi platikurtik - Jika α₄ >3 maka distribusi leptokurtik - Jika α₄ =3 maka distribusi mesokurtik

Untuk mencari nilai koefisien keruncingan, dibedakan antara data tunggal

dan data kelompok.

a. Untuk data Tunggal

(

)

4 4 4

1

s X X

n −

=

α

Contoh :

Tentukan keruncingan dari data : 2, 3, 6, 8, 11 dengan s= 3,67 dan X =6

X _X −_X

(

X − X

)

4

2 -4 256

3 -3 81

6 0 0

8 2 16

11 5 625

JUMLAH 978

Sehingga koefisien keruncingannya adalah :

(

)

(

)

(

3,67

)

1,08

978 5 1 1

4 4

4

4 = =

− =

s X X n α

Karena nilai koefisien keruncingan lebih kecil dari 3 maka distribusinya

(19)

b. Untuk data Kelompok

(

)

4 4 4

1

s

f X X

n −

=

α

Contoh :

Tentukan keruncingan dari tabel distribusi frekuensi dengan s = 3,42 berikut :

Nilai Ujian Frekuensi

(f)

Nilai

Tengah (X) X −X

(

)

4

X

X − f

(

X −X

)

4

65 - 67 2 66 -7.425 3039.3858 6078.7716

68 - 70 5 69 -4.425 383.4009 1917.0044

71 - 73 13 72 -1.425 4.1234 53.6047

74 - 76 14 75 1.575 6.1535 86.1490

77 - 79 4 78 4.575 438.0911 1752.3643

80 - 82 2 81 7.575 3292.5361 6585.0723

40 16472.9662

Penyelesaian :

(

)

(

)

(

3,42

)

3,01

9662 , 16472 40

1 1

4 4

4

4 = =

− =

s f X X n α

(20)

b. Koefisien Kurtosisi Persentil

Koefisien kurtosisi persentil dilambangkan dengan K (kappa). Untuk

distribusi normal, nilai K = 0,263. Koefisien kurtosisi Persentil dirumuskan :

(

)

10 90

1 3

2 1

P P

Q Q K

− − =

Contoh :

Tentukan koefisien kurtosisi persentil (K) dari nilai ujian statistik universitas

Borobudur Tahun 2007

31 - 40 4 35.5 142

41 - 50 3 45.5 136.5

51 - 60 5 55.5 277.5

61 - 70 8 65.5 524

71 - 80 11 75.5 830.5

81 - 90 7 85.5 598.5

91 - 100 2 95.5 191

40 2700

Penyelesaian :

( )

5 , 56 5

7 4 40 1

10 5 , 50

1 =

− +

=

Q

( )

59 , 79 11

20 4 40 3

10 5 , 70

3 =

− +

Q

( )

5 , 30 4

4 100

40 10

10 5 , 30

10 =

− +

=

(21)

( )

64 , 87 7

31 100

40 90

10 5 , 80

90 =

− +

=

P

Sehingga nilai koefisien kurtosisi persentil adalah :

(

)

(

)

2 , 0 14 , 57

09 , 23 2 1 2

1

10 90

1 3

= =

− − =

P P

Q Q K

Karena nilai K = 0,2 maka distribusinya adalah distribusi normal dan grafiknya

adalah sebagai berikut :

DAFTAR PUSTAKA

Hasan, Iqbal. 2009. Pokok-Pokok Materi Statistik 1 (Statistik Deskriptif). Jakarta:Bumi Aksara

N. Reksoatmodjo, Tedjo. 2009. Bandung:Refika Aditama.

Riduwan. 2003. Dasar-Dasar Statistika. Bandung:Alfabeta.

Sudjana. 2002. Metode Statistika. Bandung:Tarsito

Walpole, Ronald E. 1997. Pengantar Statistika Edisi Ke-3. Jakarta:PT. Gramedia Pustaka Utama.

(22)