Analisis Rangkaian Listrik

Analisis

Analisis

Analisis

Analisis

Rangkaian Listrik

Rangkaian Listrik

Rangkaian Listrik

Rangkaian Listrik

Menggunakan

Transformasi Fourier

Sudaryatno Sudirham

BAB 1

Transformasi Fourier

Kita telah mempelajari tanggapan frekuensi dari suatu rangkaian. Analisis dengan menggunakan transformasi Fourier yang akan kita pelajari berikut ini akan memperluas pemahaman kita mengenai tanggapan frekuensi, baik mengenai perilaku sinyal itu sendiri maupuan rangkaiannya. Selain dari pada itu, pada rangkaian-rangkaian tertentu dijumpai keadaan dimana model sinyal dan piranti tidak dapat dinyatakan melalui transformasi Laplace akan tetapi dapat dilakukan melalui transformasi Fourier. Topik-topik yang akan kita bahas meliputi: deret Fourier, transformasi Fourier, sifat-sifat transformasi Fourier, dan analisis rangkaian menggunakan transformasi Fourier. Dalam bab ini kita mempelajari tiga hal yang pertama, sedangkan hal yang terakhir akan kita pelajari di bab berikutnya.

Dengan mempelajari deret dan transformasi Fourier kita akan • memahami deret Fourier.

• mampu menguraikan bentuk gelombang periodik menjadi deret Fourier.

• mampu menentukan spektrum bentuk gelombang periodik.

• memahami transformasi Fourier.

• mampu mencari transformasi Fourier dari suatu fungsi t.

• mampu mencari transformasi balik dari suatu transformasi Fourier.

1.1. Deret Fourier 1.1.1. Koefisien Fourier

Kita telah melihat bahwa sinyal periodik dapat diuraikan menjadi spektrum sinyal. Penguraian suatu sinyal periodik menjadi suatu spektrum sinyal tidak lain adalah pernyataan fungsi periodik kedalam deret Fourier. Jika f(t) adalah fungsi periodik yang memenuhi persyaratan Dirichlet, maka f(t) dapat dinyatakan sebagai deret Fourier :

[

]

∑

∞ =

ω

+

ω

+

=

1 0 0 0

cos(

)

sin(

)

)

(

n n n

n

t

b

n

t

a

a

t

f

(1.1)

yang dapat kita tuliskan sebagai (lihat sub-bab 3.2)

(

)

∑

∞ =









₊

_ω

₋

_θ

+

=

1 0 2 2 0

cos(

)

)

(

n n n n

b

n

t

a

a

t

f

(1.2)

Koefisien Fourier a0, an, dan bn ditentukan dengan hubungan berikut.

∫

∫

∫

− − − > ω = > ω = = 2 / 2 / 0 0 2 / 2 / 0 0 2 / 2 / 0 0 0 0 0 0 0 0 0 ; ) sin( ) ( 2 0 ; ) cos( ) ( 2 ) ( 1 T T n T T n T T n dt t n t f T b n dt t n t f T a dt t f T a (1.3)

Hubungan (1.3) dapat diperoleh dari (1.1). Misalkan kita mencari an: kita kalikan (1.1) dengan cos(kωot) kemudian kita integrasikan antara

−To/2 sampai To/2 dan kita akan memperoleh

∑

∫

∫

∫

∫

∞ = − − − −             ω ω + ω ω + ω = ω 1 /2 2 / 0 o 2 / 2 / 0 o 2 / 2 / 0 o 2 / 2 / o o o o o o o o o ) cos( ) sin( ) cos( ) cos( ) cos( ) cos( ) ( n T T n T T n T T T T dt t k t n b dt t k t n a dt t k a dt t k t f

Dengan menggunakan kesamaan tigonometri

) sin( 2 1 ) sin( 2 1 sin cos ) cos( 2 1 ) cos( 2 1 cos cos β + α + β − α = β α β + α + β − α = β α

(

)

(

)

∑

∫

∫

∫

∫

∞ = − − − −             ω + + ω − + ω + + ω − + ω = ω 1 /2 2 / 0 o 2 / 2 / 0 o 2 / 2 / 0 o 2 / 2 / o o o o o o o o o ) ) sin(( ) ) sin(( 2 ) ) cos(( ) ) cos(( 2 ) cos( ) cos( ) ( n T T n T T n T T T T dtdt t k n t k n b dt t k n t k n a dt t k a dt t k t f

Karena integral untuk satu perioda dari fungsi sinus adalah nol, maka semua integral di ruas kanan persamaan ini bernilai nol kecuali satu yaitu

(

n k t

)

dt a n k

a T n

T

n _{− ω = =}

∫

− cos(( ) ) 2 yang terjadijika

2 2 / 2 / 0 o o

oleh karena itu

∫

− ω = /2 2 / 0 o o o ) cos( ) ( 2 T T n f t n t dt T a

Pada bentuk-bentuk gelombang yang sering kita temui, banyak diantara koefisien-koefisien Fourier yang bernilai nol. Keadaan ini ditentukan oleh kesimetrisan fungsi f(t) yang pernah kita pelajari di Bab-3; kita akan melihatnya sekali lagi dalam urain berikut ini. 1.1.2. Kesimetrisan Fungsi

Simetri Genap. Suatu fungsi dikatakan mempunyai simetri genap jika f(t) = f(−t). Salah satu contoh fungsi yang memiliki simetri genap adalah fungsi cosinus, cos(ωt) = cos(−ωt). Untuk fungsi semacam ini, dari (1.1) kita dapatkan

[

]

[

]

∑

∑

∞ = ∞ = ω − ω + = − ω + ω + = 1 0 0 0 1 0 0 0 ) sin( ) cos( ) ( dan ) sin( ) cos( ) ( n n n n n n t n b t n a a t f t n b t n a a t f

Kalau kedua fungsi ini harus sama, maka haruslah bn = 0, dan f(t) menjadi

[

]

∑

∞ = ω + = 1 0 o cos( ) ) ( n n n t a a t f (1.4)

COTOH-1.1: Tentukan deret Fourier dari bentuk gelombang deretan pulsa berikut ini.

Penyelesaian :

Bentuk gelombang ini memiliki simetri genap, amplitudo A, perioda To , lebar pulsa T.

              π π =               π π = ω ω = ω = = = = = − − − −

∫

∫

o o 2 / 2 / o o o 2 / 2 / o o o 2 / 2 o 2 / 2 / o o sin 2 sin 2 sin 2 ) cos( 2 ; 0 ; 1 T T n n A T T n n A t n n T A dt t n A T a b T AT T At Adt T a T T T T n n T T/ T T

Untuk n = 2, 4, 6, …. (genap), an = 0; an hanya mempunyai nilai untuk n = 1, 3, 5, …. (ganjil).

( )

1 cos( ) 2 ) cos( sin 2 ) ( o , 1 2 / ) 1 ( o o , 1 o o t n n A T AT t n T T n n A T AT t f ganjil n n ganjil n ω − π + = ω               π π + =

∑

∑

∞ = − ∞ = Pemahaman :

Pada bentuk gelombang yang memiliki simetri genap, bn = 0. Oleh karena itu sudut fasa harmonisa tanθn = bn/an = 0 yang berarti θn = 0o.

Simetri Ganjil. Suatu fungsi dikatakan mempunyai simetri ganjil jika f(t) = −f(−t). Contoh fungsi yang memiliki simetri ganjil adalah fungsi sinus, sin(ωt) = −sin(−ωt). Untuk fungsi semacam ini, dari (1.1) kita dapatkan

[

]

∑

∞ = ω + ω − + − = − − 1 0 0 0 cos( ) sin( ) ) ( n n n n t b n t a a t f −T/2 0 T/2 v(t) A T To

Kalau fungsi ini harus sama dengan

[

]

∑

∞ = ω + ω + = 1 0 0 0 cos( ) sin( ) ) ( n n n n t b n t a a t f maka haruslah

[

sin( )

]

) ( 0 dan 0 1 0 0

∑

∞ = ω = ⇒ = = n n n f t b n t a a (1.5)

COTOH-1.2: Carilah deret Fourier dari bentuk gelombang persegi di samping ini.

Penyelesaian:

Bentuk gelombang ini memiliki

simetri ganjil, amplitudo A, perioda To = T.

; 0 ; 0 o= an= a

(

1 cos ( ) 2cos( )

)

) cos( ) cos( 2 ) sin( ) sin( 2 2 2 / o 2 / 0 o o 2 / o 2 / 0 o π − π + π =      _{− ω + ω} ω =       ω − + ω =

∫

∫

n n n A t n t n Tn A dt t n A dt t n A T b T T T T T T n

Untuk n ganjil cos(nπ) = −1 sedangkan untuk n genap cos(nπ) = 1. Dengan demikian maka

(

)

(

1 1 2

)

0 untuk genap ganjil untuk 4 2 1 1 n n A b n n A n A b n n = − + π = π = + + π =

∑

∞ = ω π = ⇒ ganjil n t n n A t v , 1 o) sin( 4 ) ( Pemahaman:

Pada bentuk gelombang dengan semetri ganjil, an = 0. Oleh karena itu sudut fasa harmonisa tanθn = bn/an = ∞ atau θn = 90o.

v(t)

t

T A

Simetri Setengah Gelombang. Suatu fungsi dikatakan mempunyai simetri setengah gelombang jika f(t) = −f(t−To/2). Fungsi dengan

sifat ini tidak berubah bentuk dan nilainya jika diinversi kemudian digeser setengah perioda. Fungsi sinus(ωt) misalnya, jika kita kita inversikan kemudian kita geser sebesar π akan kembali menjadi sinus(ωt). Demikain pula halnya dengan fungsi-fungsi cosinus, gelombang persegi, dan gelombang segitiga.

[

]

[

]

∑

∑

∞ = ∞ = ω − − ω − − + − = π − ω − π − ω − + − = − − 1 0 0 0 1 0 0 0 o ) sin( ) 1 ( ) cos( ) 1 ( )) ( sin( )) ( cos( ) 2 / ( n n n n n n n n t n b t n a a t n b t n a a T t f

Kalau fungsi ini harus sama dengan

[

]

∑

∞ = ω + ω + = 1 0 0 0 cos( ) sin( ) ) ( n n n n t b n t a a t f

maka haruslah ao = 0 dan n harus ganjil. Hal ini berarti bahwa

fungsi ini hanya mempunyai harmonisa ganjil saja. 1.1.3. Deret Fourier Bentuk Eksponensial

Deret Fourier dalam bentuk seperti (1.1) sering disebut sebagai bentuk sinus-cosinus. Bentuk ini dapat kita ubah kedalam cosinus (bentuk sinyal standar) seperti (1.2). Sekarang bentuk (1.2) akan kita ubah ke dalam bentuk eksponensial dengan menggunakan hubungan

2 cos α − α₊ = α ej e j .

(

)

∑

∑

∑

∑

∞ = θ − ω − ∞ = θ − ω ∞ = θ − ω − θ − ω ∞ =           ₊ +           ₊ + =         ₊ + + =     _{+ ω −θ} + = 1 ) ( 2 2 1 ) ( 2 2 0 1 ) ( ) ( 2 2 0 1 0 2 2 0 0 0 0 0 2 2 2 ) cos( ) ( n t n j n n n t n j n n n t n j t n j n n n n n n n n n n e b a e b a a e e b a a t n b a a t f (1.6)

Suku ketiga (1.6) adalah penjumlahan dari n = 1 sampai n =∞. Jika penjumlahan ini kita ubah mulai dari n = −1 sampai n = −∞, dengan penyesuaian an menjadi a−n , bn menjadi b−n , dan θn menjadi θ−n, maka menurut (1.3) perubahan ini berakibat

tan ) sin( ) ( 2 ) sin( ) ( 2 ) cos( ) ( 2 ) cos( ) ( 2 2 / 2 / 0 0 2 / 2 / 0 0 2 / 2 / 0 0 2 / 2 / 0 0 0 0 0 0 0 0 0 0 n n n n n n n T T T T n n T T T T n a b a b b dt t n t f T dt t n t f T b a dt t n t f T dt t n t f T a θ − = θ ⇒ − = = θ − = ω − = ω − = = ω = ω − = − − − − − − − − − −

∫

∫

∫

∫

(1.7) Dengan (1.7) ini maka (1.6) menjadi

∑

∑

−∞ − = θ − ω ∞ = θ − ω         ₊ +         ₊ = 1 ) ( 2 2 0 ) ( 2 2 0 0 2 2 ) ( n t n j n n n t n j n n _{n n} e b a e b a t f (1.8) Suku pertama dari (1.8) merupakan penjumlahan yang kita mulai dari n = 0 untuk memasukkan a0 sebagai salah satu suku

penjumlahan ini. Dengan cara ini maka (1.8) dapat ditulis menjadi

∑

∑

+∞ −∞ = ω ∞ + −∞ = ω θ − ₌           ₊ = n t n j n t n j j n n e c e e b a t f n ( ) n ) ( 2 2 0 0 2 ) ( (1.9)

Inilah bentuk eksponensial deret Fourier, dengan cn adalah koefisien Fourier yang mungkin berupa besaran kompleks.

2 2 2 2 n n j n n n jb a e b a c = + − θ= − (1.10) 0 jika tan ; 0 jika tan dengan dan 2 1 n 1 n 2 2 >       = θ <       − = θ θ = ∠ + = − − n n n n n n n n n n n a a b a a b c b a c (1.11)

Jika an dan bn pada (1.3) kita masukkan ke (1.10) akan kita dapatkan

∫

− ω − = − = /2 2 / 0 0 0 ) ( 1 2 T T t jn n n n f t e dt T jb a c n _(1.12)

dan dengan (1.12) ini maka (1.9) menjadi

∑

_∫

∑

+∞ −∞ = ω − ω − +∞ −∞ = ω       = = n t n j T T t jn n t n j e dt e t f T e c t f /2 ( ) 2 / 0 ) ( n 0 0 0 o 0 1 ₍₎ ) ( (1.13)

Persamaan (1.11) menunjukkan bahwa 2|cn| adalah amplitudo dari harmonisa ke-n dan sudut fasa harmonisa ke-n ini adalah ∠cn. Persamaan (1.10) ataupun (1.12) dapat kita pandang sebagai pengubahan sinyal periodik f(t) menjadi suatu spektrum yang terdiri dari spektrum amplitudo dan spektrum sudut fasa seperti telah kita kenal di Bab-1. Persamaan (1.9) ataupun (1.13) memberikan f(t) apabila komposisi harmonisanya cn diketahui. Persamaan (1.12) menjadi cikal bakal transformasi Fourier, sedangkan persamaan (1.13) adalah transformasi baliknya.

COTOH-1.3: Carilah koefisien Fourier cn dari fungsi pada contoh-1.1. Penyelesaian :

(

/2

)

sin 2 1 o o o 2 / 2 / o o 2 / 2 / o o 2 / 2 / o o o o o T n T n A j e e T n A jn e T A dt e A T c T jn T jn T T t jn T T t jn n ω ω =         ₋ ω =         ω − = = ω − ω − ω − − ω −

∫

1.2. Transformasi Fourier 1.2.1. Spektrum Kontinyu

Deret Fourier, yang koefisiennya diberikan oleh (1.12) hanya berlaku untuk sinyal periodik. Sinyal-sinyal aperiodik seperti sinyal eksponensial dan sinyal anak tangga tidak dapat direpresentasikan dengan deret Fourier. Untuk menangani sinyal-sinyal demikian ini kita memerlukan transformasi Fourier dan konsep spektrum kontinyu. Sinyal aperiodik dipandang sebagai sinyal periodik dengan perioda tak-hingga.

Jika diingat bahwa ω0 = 2π/T0 , maka (1.13) menjadi

∑ ∫

∑

∫

∞ −∞ = ω − ω − ∞ −∞ = ω − ω − ω       π =       = n t jn T T t jn n t jn T T t jn e dt e t f e dt e t f T t f 0 0 0 0 0 0 0 0 ) ( 2 1 ) ( 1 ) ( 0 2 / 2 / 2 / 2 / 0 (1.14)

Kita lihat sekarang apa yang terjadi jika perioda T0 diperbesar.

Karena ω0 = 2π/T0 maka jika T0 makin besar, ω0 akan makin kecil.

Beda frekuensi antara dua harmonisa yang berturutan, yaitu

0 0 0 0 2 ) 1 ( T n n+ ω − ω =ω = π = ω ∆

juga akan makin kecil yang berarti untuk suatu selang frekuensi tertentu jumlah harmonisa semakin banyak. Oleh karena itu jika perioda sinyal T0 diperbesar menuju ∞ maka spektrum sinyal

menjadi spektrum kontinyu, ∆ω menjadi dω (pertambahan frekuensi infinitisimal), dan nω0 menjadi peubah kontinyu ω. Penjumlahan

pada (1.14) menjadi integral. Jadi dengan membuat T0 → ∞ maka

(1.14) menjadi

∫

∫ ∫

−∞∞ ω ∞ ∞ − ω ∞ ∞ − ω − _{ω ω} π = ω       π = f t e dt e d F e d t f j t j t ( ) j t 2 1 ) ( 2 1 ) ( (1.15) dengan F(ω) merupakan sebuah fungsi frekuensi yang baru, sedemikian rupa sehingga

∫

−∞∞ ω − = ω) f(t)e j tdt ( F (1.16)

dan F(ω) inilah transformasi Fourier dari f(t), yang ditulis dengan notasi

[

f(t)

]

=F(ω)

F

Proses transformasi balik dapat kita lakukan melalui persamaan (1.15). ) ( ) (_t =

F

−1 ω f

COTOH-1.4: Carilah transformasi Fourier dari bentuk gelombang pulsa di samping ini.

Penyelesaian :

Bentuk gelombang ini adalah

aperiodik yang hanya mempunyai nilai antara −T/2 dan +T/2, sedangkan untuk t yang lain nilainya nol. Oleh karena itu integrasi yang diminta oleh (1.16) cukup dilakukan antara −T/2 dan +T/2 saja. 2 / ) 2 / sin( 2 2 / ) ( 2 / 2 / 2 / 2 / 2 / 2 / T T AT j e e A e j A dt e A T j T j T T t j T T t j ω ω =         ₋ ω = ω − = = ω ω − ω − ω − − ω −

∫

F

Kita bandingkan transformasi Fourier (1.16)

∫

−∞∞ ω − = ω) f(t)e j tdt ( F

dengan koefisien Fourier

∫

− ω − = − = /2 2 / 0 0 0 ) ( 1 2 T T t jn n n n f t e dt T jb a c n (1.17) Koefisien Fourier cn merupakan spektrum sinyal periodik dengan perioda T0 yang terdiri dari spektrum amplitudo |cn| dan spektrum

−T/2 0 T/2 v(t) A

sudut fasa ∠cn, dan keduanya merupakan spektrum garis (tidak kontinyu, memiliki nilai pada frekuensi-frekuensi tertentu yang diskrit). Sementara itu transformasi Fourier F(ω) diperoleh dengan mengembangkan perioda sinyal menjadi tak-hingga guna mencakup sinyal aperiodik yang kita anggap sebagai sinyal periodik yang periodenya tak-hingga. Faktor 1/T0 pada cn dikeluarkan untuk memperoleh F(ω) yang merupakan spektrum kontinyu, baik spektrum amplitudo |F(jω)| maupun spektrum sudut fasa ∠ F(ω). COTOH-1.5: Gambarkan spektrum amplitudo dari sinyal pada

contoh 1.4. Penyelesaian : Spektrum amplitudo sinyal aperiodik ini merupakan spektrum kontinyu |F(jω)|. 2 / ) 2 / sin( ) ( T T AT ω ω = ω F Pemahaman:

Sinyal ini mempunyai simetri genap. Sudut fasa harmonisa adalah nol sehingga spektrum sudut fasa tidak digambarkan. Perhatikan pula bahwa |F(ω)| mempunyai spektrum di dua sisi, ω positif maupun negatif; nilai nol terjadi jika sin(ωT/2)=0 yaitu pada ω = ±2kπ/T (k = 1,2,3,…); nilai maksimum terjadi pada ω = 0, yaitu pada waktu nilai sin(ωT/2)/(ωT/2) = 1.

COTOH-1.6: Carilah transformasi Fourier dari f(t) = [A e−αt ] u(t) dan gambarkan spektrum amplitudo dan fasanya.

Penyelesaian : -5 0 |F(ω)| T π −2 T π −4 T π −6 T π 2 T π 4 T π 6 0 ω

0 untuk ) ( ) ( 0 ) ( 0 ) ( > α ω + α = ω + α − = = = ω ∞ ω + α − ∞ _−α+ω ∞ ∞ − ω − α −

∫

∫

j A j e A dt Ae dt e t u Ae t j t j t j t F α ω − = ω ∠ = ω θ ⇒ ω + α = ω ⇒ −1 2 2 tan ) ( ) ( | | ) ( j F A F Pemahaman:

Untuk α < 0, tidak ada transformasi Fourier-nya karena integrasi menjadi tidak konvergen.

1.3. Transformasi Balik

Pada transformasi Fourier transformasi balik sering dilakukan dengan mengaplikasikan relasi formalnya yaitu persamaan (1.15). Hal ini dapat dimengerti karena aplikasi formula tersebut relatif mudah dilakukan

COTOH-1.7: Carilah f(t) dari ) ( 2 ) (ω = πδω F Penyelesaian : 1 ) 1 )( ( ) ( 2 2 1 ) ( 2 2 1 ) ( 0 0 = ω ω δ = ω ω πδ π = ω ω πδ π =

∫

∫

∫

+ − + − α α ω ∞ ∞ − ω d d e d e t f j t j t +90o −90o θ(ω) 90 |F(ω) | ω A/α 25

Pemahaman :

Fungsi 2πδ(ω) adalah fungsi di kawasan frekuensi yang hanya mempunyai nilai di ω=0 sebesar 2π. Oleh karena itu e jωt juga hanya mempunyai nilai di ω=0 sebesar e j0t =1. Karena fungsi hanya mempunyai nilai di ω=0 maka integral dari −∞ sampai +∞ cukup dilakukan dari 0− sampai 0+, yaitu sedikit di bawah dan di atas ω=0. Contoh ini menunjukkan bahwa transformasi Fourier dari sinyal searah beramplitudo 1 adalah 2πδ(ω). COTOH-1.8: Carilah f(t) dari

) ( 2 ) (jω = πδω−α F Penyelesaian : t j t j t j t j e d e d e d e t f α α α α α α ω ∞ ∞ − ω = ω α − ω δ = ω α − ω πδ π = ω α − ω πδ π =

∫

∫

∫

+ − + − ) ( ) ( 2 2 1 ) ( 2 2 1 ) ( Pemahaman :

Fungsi 2πδ(ω−α) adalah fungsi di kawasan frekuensi yang hanya mempunyai nilai di ω=α sebesar 2π. Oleh karena itu e jωt juga hanya mempunyai nilai di ω=α sebesar ejαt. Karena fungsi hanya mempunyai nilai di ω=α maka integral dari −∞ sampai +∞ cukup dilakukan dari α− sampai α+, yaitu sedikit di bawah dan di atas ω=α.

COTOH-1.9: Carilah f(t) dari

[

( ) ( )

]

) ( ω+α − ω−α α π = ω A u u F Penyelesaian :

[

]

[ ]

t t A j e e t A jt e e A jt e A d e A d e u u A t f t j t j t j t j t j t j t j α α = − α = − α = α = ω α π π = ω α − ω − α + ω α π π = α − α α − α α α − ω ∞ ∞ − ω ∞ ∞ − ω

∫

∫

) sin( 2 2 2 1 2 1 ) ( ) ( 2 1 ) ( Pemahaman:

Dalam soal ini F(ω) mempunyai nilai pada selang −α<ω<+α oleh karena itu e jωt juga mempunyai nilai pada selang frekuensi ini juga; dengan demikian integrasi cukup dilakukan antara −α dan +α.

Hasil transformasi balik f(t) dinyatakan dalam bentuk sin(x)/x yang bernilai 1 jika x→0 dan bernilai 0 jika x→∞. Jadi f(t) mencapai nilai maksimum pada t = 0 dan menuju nol jika t menuju ∞ baik ke arah positif maupun negatif. Kurva F(ω) dan f(t) digambarkan di bawah ini.

1.2.3. Dari Transformasi Laplace ke Transformasi Fourier Untuk beberapa sinyal, terdapat hubungan sederhana antara transformasi Fourier dan transformasi Laplace. Sebagaimana kita ketahui, transformasi Laplace didefinisikan melalui (8.1) sebagai

∫

∞ − = 0 () ) (s f t e stdt F (1.18) F(ω) ω +β −β 0 f(t) A t

dengan s = σ + jω adalah peubah frekuensi kompleks. Batas bawah integrasi adalah nol, artinya fungsi f(t) haruslah kausal. Jika f(t) memenuhi persyaratan Dirichlet maka integrasi tersebut di atas akan tetap konvergen jika σ = 0, dan formulasi transformasi Laplace ini menjadi

∫

∞ − ω

=

0

(

)

)

(

s

f

t

e

j t

dt

F

(1.19)

Sementara itu untuk sinyal kausal integrasi transformasi Fourier cukup dilakukan dari nol, sehingga transformasi Fourier untuk sinyal kausal menjadi

∫

∞ − ω

=

ω

0

(

)

)

(

f

t

e

j t

dt

F

(1.20)

Bentuk (1.20) sama benar dengan (1.19), sehingga kita dapat simpulkan bahwa 0 ) ( ) ( berlaku integrasi -di dapat dan kausal ) ( sinyal untuk = σ = ω s t f F F (1.21)

Persyaratan “dapat di-integrasi” pada hubungan (1.21) dapat dipenuhi jika f(t) mempunyai durasi yang terbatas atau cepat menurun menuju nol sehingga integrasi |f(t)| dari t=0 ke t=∞ konvergen. Ini berarti bahwa pole-pole dari F(s) harus berada di sebelah kiri sumbu imajiner. Jika persyaratan-persyaratan tersebut di atas dipenuhi, pencarian transformasi balik dari F(ω) dapat pula dilakukan dengan metoda transformasi balik Laplace.

COTOH-1.10: Dengan menggunakan metoda transformasi

Laplace carilah transformasi Fourier dari fungsi-fungsi berikut (anggap α, β > 0).

[

sin

]

() ) ( c) ) ( ) ( b). ) ( ) ( a). 3 2 1 t u t e A t f t t f t u e A t f t t β = δ = = α − α − Penyelesaian:

α + ω = ω → α − = → α + = → → = −α j p s A s F t u Ae t f t 1 ) ( imag) sumbu kiri (di pole ) ( integrasi -di dapat dan kausal fungsi ) ( ) ( a). 1 1 F 1 ) ( 1 ) ( integrasi -di dapat dan kausal fungsi ) ( ) ( b). ₂ = ω → = → → δ = F s F t t f

[

]

αω + ω − β + α = β + α + ω = ω → β ± α − = → β + α + = → → β = −α 2 ) ( ) ( im) sumbu kiri (di pole ) ( ) ( integrasi -di dapat kausal, fungsi ) ( sin ) ( c). 2 2 2 2 2 2 2 3 j a j A j p s A s t u t e A t f t F F

COTOH-1.11: Carilah f(t) dari

) 4 )( 3 ( 10 ) ( + ω + ω = ω j j F Penyelesaian :

Jika kita ganti jω dengan s kita dapatkan ) 4 )( 3 ( 10 ) ( + + = s s s F

Pole dari fungsi ini adalah p1 = −3 dan p2 = −4, keduanya di

sebelah kiri sumbu imajiner.

4 10 3 10 ) ( 10 3 10 ; 10 4 10 4 3 ) 4 )( 3 ( 10 ) ( 4 2 3 1 2 1 + − + = ⇒ − = + = = + = → + + + = + + = − = − = s s s s k s k s k s k s s s s s F F

Transformasi balik dari F(ω) adalah :

[

10 10

]

( )

)

(t e 3 e 4 ut

1.4. Sifat-Sifat Transformasi Fourier 1.4.1. Kelinieran

Seperti halnya transformasi Laplace, sifat utama transformasi Fourier adalah kelinieran.

[ ]

[

]

[

₁() ₂()

]

( ) ( ) : maka ) ( ) ( dan ) ( ) ( : Jika 2 1 2 1

+ = ω + ω ω = ω = F F F F B A t Bf t Af t f t f

F

F

F

2 1 (1.22) COTOH-1.12: Carilah transformasi Fourier dari v(t) = cosβt.

Penyelesaian:

Fungsi ini adalah non-kausal; oleh karena itu metoda transformasi Laplace tidak dapat di terapkan. Fungsi cosinus ini kita tuliskan dalam bentuk eksponensial.

[

]

j t j t

[ ]

j t

[ ]

j t e e e e β − β ₌ β ₊ − β         ₊ = β

F

F

F

F

cos t 2 1 2 1 2

Dari contoh 1.8. kita ketahui bahwa

F

 ω_ej t_=2πδ(ω−β) Jadi

F

[

cosβt

]

=πδ(ω−β)+πδ(ω+β)

1.4.2. Diferensiasi

Sifat ini dinyatakan sebagai berikut ) ( ) ( _{= ω ω}       F j dt t df

F

_(1.23) Persamaan (1.15) menyatakan

(

)

) ( ) ( ) ( 2 1 ) ( 2 1 ) ( 2 1 ) ( ) ( 2 1 ) ( ω ω =       → ω ω ω π =       _{ω ω} π =       ω ω π = → ω ω π =

∫

∫

∫

∫

∞ ∞ − ω ∞ ∞ − ω ∞ ∞ − ω ∞ ∞ − ω F j dt t df d e F j d e F dt d d e F dt d dt t df d e F t f t j t j t j t j

F

1.4.3. Integrasi

Sifat ini dinyatakan sebagai berikut.

) ( ) 0 ( ) ( ) ( +π δ ω ω ω =      

∫

−∞ F F j dx x f t

F

_(1.24)

Suku kedua ruas kanan (1.24) merupakan komponen searah jika sekiranya ada. Faktor F(0) terkait dengan f(t); jika ω diganti dengan nol akan kita dapatkan

∫

−∞∞ = f(t)dt ) 0 ( F

COTOH-1.13: Carilah transformasi Fourier dari f(t) = Au(t). Penyelesaian:

Metoda transformasi Laplace tidak dapat diterapkan untuk fungsi anak tangga. Dari contoh (1.10.b) kita dapatkan bahwa

[ ]

δ(t) =1

F

_{. Karena fungsi anak tangga adalah integral dari}

fungsi impuls, kita dapat menerapkan hbungan (1.24) tersebut di atas.

[ ]

() ( ) 1 +πδ(ω) ω = δ =

∫

∞ − x dx j t u

F

t

F

1.4.4. Pembalikan

Pembalikan suatu fungsi f(t) adalah mengganti t dengan −t. Jika kita membalikkan suatu fungsi, maka urutan kejadian dalam fungsi yang baru berlawanan dengan urutan kejadian pada fungsi semula. Transformsi Fourier dari fungsi yang dibalikkan sama dengan kebalikan dari transformasi Fourier fungsi semula. Secara formal hal ini dapat dituliskan sebagai

[

()

]

( ) maka

[

( )

]

( )

Jika

F

f t =F ω

F

f −t =F −ω _(1.25) Menurut (1.16)

[

]

[

]

[

]

) ( ) ( ) ( ) ( ) ( Misalkan ; ) ( ) ( ω − = τ τ = τ τ − = τ = − → τ = − − = −

∫

∫

∫

∞ ∞ − ωτ − ∞ − ∞ ωτ ∞ ∞ − ω − F d e f d e f f t f t dt e t f t f j j t j

F

F

F

Sifat pembalikan ini dapat kita manfaatkan untuk mencari transformasi Fourier dari fungsi signum dan fungsi eksponensial dua sisi.

COTOH-1.14: Carilah transformasi Fourier dari fungsi signum dan eksponensial dua sisi breikut ini.

Penyelesaian : Contoh 1.13. memberikan

[ ]

() 1 +πδ(ω) ω = j t u

F

_maka

[

]

[

]

ω = − − = j t u t u t) () ( ) 2 sgn(

F

F

Contoh 1.10.a memberikan

[

]

ω + α = α − j t u e t () 1

F

_maka

[ ] [

]

2 2 ) ( | | 2 ) ( 1 1 ) ( ) ( ω + α α = ω − + α + ω + α = − + = −α −α− α − j j t u e t u e e t

F

t t

F

1.4.5. Komponen yata dan Imajiner dari F(ωωωω)

Pada umumnya transformasi Fourier dari f(t), F(ω), berupa fungsi kompleks yang dapat kita tuliskan sebagai

t 0 v(t) 1 −1 −u(−t) u(t) signum : sgn(t) = u(t) − u(−t) 0 t 0

eksponensial dua sisi :

e−α| t | = e−αt u(t) + e−α(−t) u(−t)

e−αt u(t) v(t)

1 e−α(−t)

ω θ ∞ ∞ − ∞ ∞ − ∞ ∞ − ω − ω = ω + ω = ω − ω = = ω

∫

∫

∫

j t j e jB A dt t s t f j dt t c t f dt e t f ) ( ) ( ) ( in ) ( os ) ( ) ( ) ( F F dengan

∫

∫

−∞∞ ∞ ∞ − ω ω =− ω = ω f t tdt B f t tdt A( ) ( )cos ; ( ) ()sin (1.26)       ω ω = ω θ ω + ω = ω − ) ( ) ( tan ) ( ; ) ( ) ( ) ( 2 2 1 A B B A F (1.27)

Jika f(t) fungsi nyata, maka dari (1.26) dan (1.27) dapat kita simpulkan bahwa

1. Komponen riil dari F(ω) merupakan fungsi genap, karena A(−ω) = A(ω).

2. Komponen imajiner F(ω) merupakan fungsi ganjil, karena B(−ω) =− B(ω).

3. |F(ω)| merupakan fungsi genap, karena |F(−ω)| = |F(ω)|. 4. Sudut fasa θ(ω) merupakan fungsi ganjil, karena θ(−ω) =−

θ(ω).

5. Kesimpulan (1) dan (2) mengakibatkan : kebalikan F(ω) adalah konjugat-nya, F(−ω) = A(ω) − jB(ω) = F*(ω) . 6. Kesimpulan (5) mengakibatkan : F(ω) × F(−ω) = F(ω) ×

F*(ω) = |F(ω)|2.

7. Jika f(t) fungsi genap, maka B(ω) = 0, yang berarti F(ω) riil. 8. Jika f(t) fungsi ganjil, maka A(ω) = 0, yang berarti F(ω)

imajiner. 1.4.6. Kesimetrisan

Sifat ini dinyatakan secara umum sebagai berikut.

[

()

]

( ) maka

[

()

]

2 ( )

Jika

F

f t =F ω

F

F t = π f −ω (1.28) Sifat ini dapat diturunkan dari formulasi transformasi balik.

∫

∫

∫

∞ ∞ − ω − ∞ ∞ − ω − ∞ ∞ − ω ω = ω − π ω ω ω = − π → ω ω = π d e t f t d e t f d e t f t j t j t j ) ( ) ( 2 : maka kan dipertukar dan Jika ) ( ) ( 2 ) ( ) ( 2 F F F 1.4.7. Pergeseran Waktu

Sifat ini dinyatakan sebagai berikut.

[

()

]

( ) maka

[

( )

]

( )

Jika

F

f t =F ω

F

f t−T =e−jωTF ω _(1.29) Sifat ini mudah diturunkan dari definisinya.

1.4.8. Pergeseran Frekuensi Sifat ini dinyatakan sebagai berikut.

[

( )

]

() maka 1

[

( )

]

()

1

Jika

F

− F ω = f t

F

− F ω−β =ejβtf t _(1.30)

Sifat ini juga mudah diturunkan dari definisinya. 1.4.9. Penskalaan

Sifat ini dinyatakan sebagai berikut.

[

]

[

]

      ω = ω = a a at f t f F F | | 1 ) ( maka ) ( ) ( Jika

F

F

_(1.31) 1.5. Ringkasan

Tabel-1.1 berikut ini memuat pasangan transformasi Fourier sedangkan sifat-sifat transformasi Fourier termuat dalam Tabel-1.2.

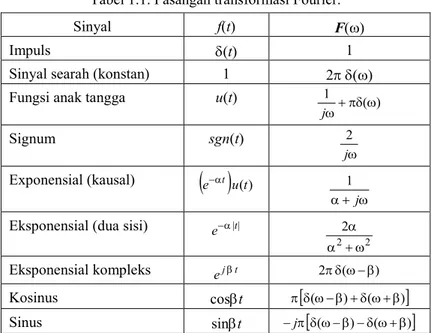
Tabel 1.1. Pasangan transformasi Fourier.

Sinyal f(t) F(ω)

Impuls δ(t) 1

Sinyal searah (konstan) 1 2πδ(ω)

Fungsi anak tangga u(t) 1 _+πδ(ω)

ω j Signum sgn(t) ω j 2 Exponensial (kausal)

( )

_e−αt _u(t) ω + α j 1

Eksponensial (dua sisi) _e−α| t|

2 2 2 ω + α α Eksponensial kompleks _ejβt 2πδ(ω−β) Kosinus cosβt π

[

δ(ω−β)+δ(ω+β)

]

Sinus sinβt −jπ

[

δ(ω−β)−δ(ω+β)

]

Tabel 1.2. Sifat-sifat transformasi Fourier.

Sifat Kawasan Waktu Kawasan Frekuensi

Sinyal f(t) F(ω) Kelinieran A f1(t) + B f2(t) AF1(ω) + BF2(ω) Diferensiasi dt t df() jωF(ω) Integrasi

_∫

∞ − t dx x f( ) ( )+π (0)δ(ω) ω ω F F j Kebalikan f (−t) F(−ω) Simetri F (t) 2π f (−ω) Pergeseran waktu f (t − T) e−jωTF₍ω₎ Pergeseran frekuensi e j β t f (t) F(ω−β)

Penskalaan _{|a| f (at) }

     ω a F

Soal-Soal

Deret Fourier Bentuk Sinus-Cosinus.

1. Tentukan deret Fourier dari gelombang segitiga berikut ini.

a).

b).

c).

d).

e).

2. Siklus pertama dari deretan pulsa dinyatakan sebagai

)

3

(

)

2

(

)

1

(

2

)

(

2

)

(

t

=

u

t

−

u

t

−

+

u

t

−

−

u

t

−

v

Gambarkan siklus pertama tersebut dan carilah koefisien Fourier-nya serta gambarkan spektrum amplitudo dan sudut fasaFourier-nya.

v 1ms t 10V −5V v t 20ms 150V v t 20ms 150V t v 10V 1ms t v 5V −5V 1ms

3. Suatu gelombang komposit dibentuk dengan menjumlahkan tegangan searah 10V dengan gelombang persegi yang amplitudo puncak ke puncak-nya 10 V. Carilah deret Fouriernya dan gambarkan spektrum amplitudonya.

Deret Fourier Bentuk Eksponensial.

4. Carilah koefisien kompleks deret Fourier bentuk gelombang berikut. a). b). c). d). e). v 1ms t 10V −5V v 20ms t 150V v 10V −5V 1ms 2ms t t v 10V 1ms t v 5V −5V 1ms

Transformasi Fourier

5. Carilah transformasi Fourier dari bentuk-bentuk gelombang berikut: a). ()

[

u(t) u(t T)

]

T At t v = − − ; b). _            ₋ −       ₊       π = 4 4 2 cos ) ( u t T u t T T t A t v c). _            ₋ −       ₊             π + = 2 2 2 cos 1 2 ) ( u t T u t T T t A t v d).

v

(

t

)

=

2

+

2

u

(

t

)

; e). v(t)=2sgn(−t)+6u(t) f). v(t)=

[

2e−2tu(t)+2sgn(t)

]

δ(t+2) g). v(t)=2e−2(t−2)u(t−2)+2e−2(t+2)u(t+2) 6. Tentukan transformasi balik dari fungsi-fungsi berikut:

a).

(

)

−α|ω|

α

π

=

ω

e

F

; b).

(

)

[

(

ω

+

β

)

−

(

ω

−

β

)

]

β

π

=

ω

A

u

u

F

c).

)

50

(

)

20

(

1000

)

(

+

ω

+

ω

=

ω

j

j

F

; d).

)

50

(

)

20

(

)

(

+

ω

+

ω

ω

=

ω

j

j

j

F

e).

)

50

(

)

20

(

)

(

2

+

ω

+

ω

ω

−

=

ω

j

j

F

; f).

)

50

(

)

20

(

1000

)

(

+

ω

+

ω

ω

=

ω

j

j

j

F

g).

)

50

(

)

50

(

500

)

(

+

ω

+

ω

−

ω

=

ω

j

j

j

F

; h).

)

50

(

)

50

(

5

)

(

+

ω

+

ω

ω

=

ω

j

j

j

F

i).

)

50

(

)

50

(

5000

)

(

+

ω

+

ω

−

ω

=

ω

j

j

j

F

; j).

2500

200

)

(

5000

)

(

2

₊

_ω

₊

ω

−

ω

δ

=

ω

j

F

k).

F

(

ω

)

=

4

π

δ

(

ω

)

+

e

−2ω; l).

ω

−

ω

δ

π

=

ω

ω −

j

e

j2

)

4

(

4

)

(

F

m).

)

2

(

)

1

(

4

)

(

4

)

(

ω

+

ω

+

ω

+

ω

δ

π

=

ω

j

j

j

F

; n).

F

(

ω

)

=

4

π

δ

(

ω

)

+

e

−2ω o).

F

(

ω

)

=

4

π

δ

(

ω

)

+

4

π

δ

(

ω

−

2

)

+

4

π

δ

(

ω

+

2

)