BAB II LANDASAN TEORI A. Hakikat Matematika - PERBEDAAN HASIL BELAJAR MATEMATIKA SISWA MELALUI PENERAPAN PENDEKATAN PENDIDIKAN MATEMATIKA REALISTIK DENGAN PENDEKATAN PEMECAHAN MASALAH MATERI KELILING DAN LUAS LINGKARAN SISWA KELAS VIII DI MTs NEGERI 6 BLI
Teks penuh
Gambar

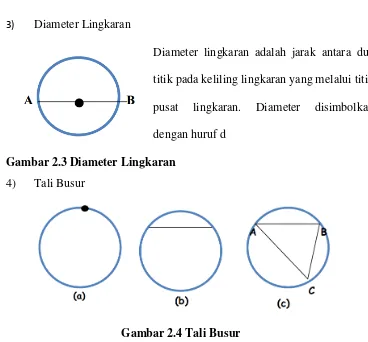
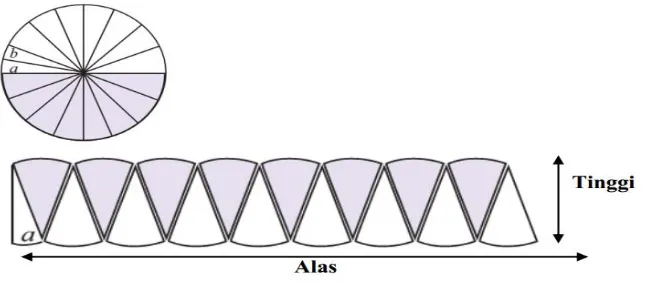
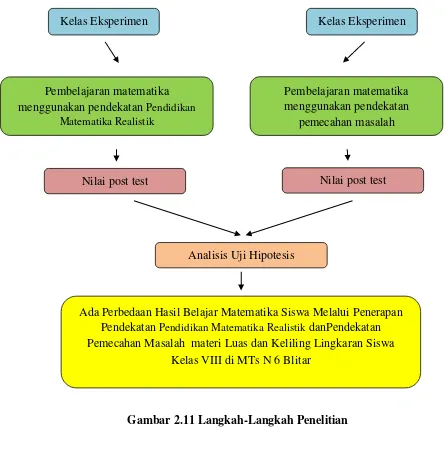
Dokumen terkait
Desain Visual Teori dan Aplikasi, T Gramedia Pustaka Utama, Yogyakarta, 2010.. Suryani,
Sejalan dengan hal tersebut dalam buku Quantum Learning dituliskan bahwa anak didik memiliki modalitas belajar yang dibedakan menjadi tiga tipe, yaitu visual,
Sumber penularan adalah pasien TB BTA positif.Pada waktu batuk atau bersin, pasien menyebarkan kuman keudara dalam bentuk percikan dahak (droplet nuclei).Sekali batuk dapat
11) Semua siswa ditugaskan untuk berkelompok dengan teman yang duduk di bangku belakangnya (berpasangan/berdua) kemudian mengerjakan tugas di halaman 34 (Ajang Pendapat)
Ketika BRR bersiap menutup kantornya, proyek portofolio mereka bisa dikategorikan sebagai berikut dalam hubungannya dengan skenario pelimpahan: proyek tahun jamak (dari IRFF,
Pemerintah berperan dalam memberikan fasilitas yang diperlukan pihak akademisi agar pengembangan “ Ecoblue ” dapat terealisasi dengan baik yang dapat mengoptimalkan kondisi Sungai
Mahasiswa Fiskom yang menggunakan kosa kata Bahasa dalam. pergaulannya saat berkomunikasi secara lisan
Sebagai uji kompetensi atau pengetahuan, guru dapat dilakukan dalam bentuk penugasan, untuk menjawab atau melengkapi pertanyaan yang terdapat dalam Tugas Mandiri