Pengantar Analisis Real Bartle and Sherbert AnalisisRealKSA

Bacaan Warga K SA

Pengantar Analisis Real

Introduction to real analy sis

Dikumpulkan dari berbagai sumber oleh: Abu Abdillah

KOMUNITAS STUDI ALKWARIZMI

PERSEMBAHAN

Untuk bahan bacaan warga KSA (Komunitas Studi Al Khwarizmi).

Pesan

Janganlah kesibukan duniamu melalaikan untuk menuntut ilmu Agama,

KATA PENGANTAR

uku ini ditulis dalam rangka pengadaan buku ajar mata kuliah

Analisis Real I dan II, yang merupakan mata kuliah wajib.

Buku ini berisi materi yang diperuntukan bagi mahasiswa

yang telah mengambil mata Kalkulus I dan Kalkulus II. Topik-topik dalam

buku ini sebenarnya sudah dikenal oleh mahasiswa yang telah mengambil

kedua mata kuliah tersebut. Hanya saja, materi pada buku ini lebih abstrak,

teoritis, dan mendalam. Materi pada buku ini merupakan materi dasar analisis

real. Analisis real merupakan alat yang esensial, baik di dalam berbagai

cabang dari matematika maupun bidang ilmu-ilmu lain, seperti fisika, kimia,

dan ekonomi. Mata kuliah Analisis I adalah gerbang menuju mata kuliah yang

lebih lanjut, baik di dalam maupun di luar jurusan Matematika. Jika mata

kuliah ini dapat dipahami dengan baik maka mahasiswa mempunyai modal

yang sangat berharga untuk memahami mata kuliah lain. Diharapkan, setelah

mempelajari materi pada buku ini, mahasiswa mempunyai kedewasaan

dalam bermatematika, yang meliputi antara lain kemampuan berpikir secara

deduktif, logis, dan runtut, serta memiliki kemampuan menganalisis masalah

dan mengomunikasikan penyelesaiannya secara akurat dan rigorous.

Buku ini terdiri dari lima bab. Bab I membahas tentang aljabar

himpunan, fungsi, dan induksi matematika. Sebagaimana kita ketahui bahwa

materi pada bab ini adalah materi penunjang pemahaman pada bab-bab

selanjutnya, maka diharapkan para pembaca dan pengajar tidak

mengabaikan penyampaian bab I ini. Bab II membahas tentang himpunan

bilangan real. Di dalamnya, dibicarakan tentang sifat aljabar (lapangan), sifat

terurut, dan sifat kelengkapan dari himpunan bilangan real. Kemudian,

dikonstruksi berdasarkan sifat terurutnya, yang disebut sebagai interval.

Dijelaskan pula tentang representasi desimal dari bilangan real dan

menggunakannya untuk membuktikan Teorema Cantor. Selanjutnya, bab III

berisi tentang barisan bilangan real, yang meliputi definisi dan sifat-sifat

barisan, Teorema Bolzano-Weierstrass, kriteria Cauchy, barisan divergen,

dan sekilas tentang deret tak hingga. Kemudian, bab IV mendiskusikan

tentang definisi limit fungsi (termasuk limit sepihak, limit di tak hingga, dan

limit tak hingga) dan sifat-sifatnya. Lalu, bab V membahas kekontinuan fungsi,

yang meliputi definisi fungsi kontinu dan sifat-sifatnya, fungsi kontinu pada

interval, kekontinuan seragam, serta fungsi monoton dan fungsi invers.

Buku ini masih dalam proses pengembangan dan tentunya masih jauh

dari sempurna. Untuk itu, penulis membuka diri terhadap saran dan kritik dari

pembaca, demi semakin baiknya buku ini sebagai buku ajar mata kuliah wajib

Analisis I.

Unaaha, April 2013

Penulis,

DAFTAR ISI

PERSEMBAHAN ... ii

KATA PENGANTAR ... iii

DAFTAR ISI ... v

BAB I PENDAHULUAN 1.1 Aljabar Himpunan ... 1

1.2 Fungsi ... 8

1.3. Induksi Matematika ... 17

BAB II HIMPUNAN BILANGAN REAL 2.1 Sifat Aljabar dari R... 27

2.2 Sifat Terurut dari R ... 29

2.3. Sifat Kelengkapan dari R ... 38

2.4. Interval ... 48

2.5 Representasi Desimal dari Bilangan Real ... 51

BAB III BARISAN BILANGAN REAL 3.1 Definisi Barisan Bilangan real ... 54

3.2 Sifat-Sifat Barisan Bilangan Real ... 57

3.3 Teorema Bolzano-Weierstrass ... 64

3.4 Kriteria Cauchy ... 65

3.5 Barisan Divergen ... 68

3.6 Deret Tak Hingga ... 71

BAB IV LIMIT FUNGSI 4.1 Titik Timbun ... 80

BAB V KEKONTINUAN FUNGSI

5.1 Definisi Fungsi Kontinu ... 89

5.2 Sifat-Sifat Fungsi Kontinu ... 92

5.3 Fungsi Kontinu pada Interval ... 94

5.4 Kekontinuan Seragam ... 97

5.5 Fungsi Monoton dan Fungsi Invers ... 100

BAB I

HIMPUNAN BILANGAN REAL

ada bab ini, kita akan membahas beberapa prasyarat yang diperlukan untuk mempelajari analisis real. Bagian 1.1 dan 1.2 kita akan mengulang sekilas tentang aljabar himpunan dan fungsi, yang keduanya merupakan perkakas penting untuk semua cabang matematika.

Pada bagian selanjutnya yakni bagian 1.3 kita akan mengulas mengenai induksi matematika. Sebagaimana kita ketahui bahwa induksi matematika berhubungan dengan sifat dasar sistem bilangan asli yang akan sering kita gunakan pada pembuktian beberapa masalah khusus dalam bab selanjutnya.

1.1 ALJABAR HIMPUNAN

Bila Amenyatakan suatu himpunan, maka untuk suatu unsur

x

kita akan menuliskannya menjadi

A

x , ■ untuk menyatakan

x

suatu unsur di A,

x

anggota A, atau

x

termuat di A, atau A memuat

x

. Selanjutnya bila kita ingin menyatakan bahwa

x

suatu unsur yang bukan di A maka dapat kita tuliskan menjadi:

A

x , ■ Selanjutnya bila A dan B keduanya adalah himpunan sehingga untuk setiap unsur xA mengakibatkan xB ( setiap unsur di A juga unsur di B), maka kita katakan A termuat di B, atau B memuat A, atau A suatu subhimpunan dari B, dan kita menuliskannya dengan:

B

A



atau

B



A

, ■

Bila

A



B

dan terdapat unsur di B yang bukan anggota A maka kita

1.1.1. Definisi Kesamaan Dua Himpunan

Dua buah himpunan A dan B dikatakan sama bila keduanya memuat unsur yang sama. Dengan kata lain untuk setiap unsur

x

anggota himpunan A

maka

x

juga merupakan anggota himpunan B, dan juga sebaliknya untuk setiap unsur y anggota himpunan B maka y juga merupakan anggota himpunan A.

Selanjutnya kedua buah himpunan A dan B dikatakan sama maka kita menuliskannya dengan:

B

A ■ Untuk menunjukkan bahwa AB , kita harus menunjukkan bahwa

B

A



dan

B



A

.

Suatu himpunan dapat ditulis dengan mendaftar anggota-anggotanya, atau dengan menyatakan sifat keanggotaannya. Kata “sifat keanggotaan” memang menimbulkan keragu-raguan, akan tetapi bila P menyatakan sifat keanggotaan (yang tak bias maknanya) maka suatu himpunan

x

yang memenuhi P akan kita tuliskan dengan cara:



x P(x)



■ Notasi diatas kita baca: “himpunan semua

x

yang memenuhi (sedemikian sehingga) P”. Bila perlu untuk menyatakan subhimpunan S yang memenuhiP, maka kita dapat menuliskannya dalam bentuk:



xS P(x)



■ Beberapa himpunan tertentu akan banyak digunakan dalam buku ini, dan akan kita tuliskan dengan penulisan standar yakni sebagai berikut:

 Himpunan bilangan asli,

N





1

,

2

,

3

,...



 Himpunan bilangan bulat

Ζ





0

,

1

,



1

,

2

,



2

,...



 Himpunan bilangan rasional





















m

,

n

,

n

0

n

m

Contoh-contoh:

1. Himpunan



xN x2 3x20



, menyatakan himpunan bilangan asli yang memenuhi persamaan kuadrat

x

2



3

x



2



0

. Karena yang memenuhi hanya x1 dan x2 , maka himpunan tersebut dapat juga dituliskan menjadi

 

1

,

2

.

2. Terkadang formula dapat pula digunakan untuk menyingkat penulisan himpunan. Sebagai contoh himpunan bilangan genap positif sering dituliskan

dengan cara



2x xN



, dari pada kita menuliskannya



yN y2x,xN



.

Operasi Himpunan

Pada bagian ini kita akan mendefinisikan aturan untuk membangun (mengkonstruksi) himpunan baru dari himpunan yang sudah ada.

1.1.2. Definisi

a. Bila A dan B keduanya adalah himpunan, maka irisan (interseksi) dari A

dan Bdituliskan dengan AB , merupakan himpunan yang unsur-unsurnya adalah anggota himpunan A dan juga merupakan anggota himpunan B.



xx A x B



B

A   _dan  ■

b. Gabungan dari himpunan A dan Badalah himpunan yang unsurnya paling tidak termuat di salah satu dari himpunan A atau B . Gabungan dari himpunan A dan Bdituliskan dengan AB.



xx A x B



B

A   _atau  ■

1.1.3. Definisi

1.1.4. Teorema

Misalkan

A,

B

dan C sebarang himpunan, maka:

a)

A



A



A

,

A



A



A

Idempoten

b)

A



B



B



A

,

A



B



B



A

Komutatif

c)



A



B





C



A





B



C

 

,

A



B





C



A





B



C



Asosiatif

d)

A





B



C

 



A



B

 



A



C



,

A





B



C

 



A



B

 



A



C



Distributif.

Bukti teorema diatas diserahkan kepada pembaca!

Dimungkinkan juga untuk menunjukkan bahwa bila



A

₁

,

A

₂

,...,

A

_n



merupakan koleksi himpunan, maka terdapat sebuah himpunan, maka terdapat sebuah himpunan A yang memuat unsur yang merupakan unsur semua himpunan A_j, j1,2,...,n ; dan terdapat sebuah himpunan B yang unsurnya paling tidak unsur dari suatu Aj, j1,2,...,n. Dengan menanggalkan kurung,

kita tuliskan dengan

n

A

A

A

A



₁



₂



...



n

B

B

B

B



1



2



...



Untuk mempersingkat penulisan, A dan B di atas sering dituliskan dengan



n

j j

A

A

1







n

j j

A

B

1



1.1.5. Definisi

Misalkan A dan B suatu himpunan, maka komplemen dari B relatif terhadap

A, dituliskan dengan A \B (baca “A minus B”) adalah himpunan yang unsur-unsurnya adalah semua unsur di A tetapi bukan anggota B. Dibeberapa buku ditulis menggunakan notasi AB atau AB.



xx A anx B



B

A\   _d  ■

Seringkali A tidak dinyatakan secara eksplisit, karena sudah dimengerti/disepakati. Dalam situasi begini A \B sering dituliskan dengan

C

 

A

.

1.1.6. Teorema

Misalkan

A

,

B

,

C

sebarang himpunan, maka

A

\

(

B



C

)



(

A

\

B

)



(

A

\

C

)

,

)

\

(

)

\

(

)

(

\

B

C

A

B

A

C

A







.

Bukti:

Kita akan membuktikan kesamaan pertama dan meninggalkan bagian kedua pada pembaca sebagai bahan latihan.

Untuk menunjukkan

A

\

(

B



C

)



(

A

\

B

)



(

A

\

C

)

, berarti yang harus

ditunjukkan adalah:

A

\

(

B



C

)



(

A

\

B

)



(

A

\

C

)

dan

)

\

(

)

\

(

)

(

\

B

C

A

B

A

C

A







 Akan ditunjukkan

A

\

(

B



C

)



(

A

\

B

)



(

A

\

C

)

Ambil sebarang

x





A

\

(

B



C

)



, maka xAdan

x





B



C



, ini berarti bahwa

x

di A tetapi

x

bukan unsur B atau C, karenanya

x

di A tetapi

x

tidak di B dan

x

di A tetapi

x

tidak di C, sehingga dapat dituliskan



A

B



x



\

dan

x





A

\

C



, hal ini berarti bahwa

x





A

\

B

 



A

\

C



,

sehingga terbuktilah bahwa

A

\

(

B



C

)



(

A

\

B

)



(

A

\

C

)

Ambil sebarang

y



(

A

\

B

)



(

A

\

C

)

, maka

y





A

\

B



dan

y





A

\

C



,

maka

y



A

tetapi

y



B

dan

y



A

tetapi

y



C

. Jadi

y



A

tetapi bukan

anggota dari B atau C . Akibatnya

y



A

dan

y





B



C



, ini berarti



A

\

(

B

C

)



y





, sehingga terbukti bahwa

A

\

(

B



C

)



(

A

\

B

)



(

A

\

C

)

.

Dari dua bukti diatas dapat disimpulkan bahwa

)

\

(

)

\

(

)

(

\

B

C

A

B

A

C

A







.

Produk (hasil kali) kartesius

Berikut ini kita definisikan produk kartesius yang akan kita gunakan pada pembahasan tentang fungsi pada bagian selanjutnya.

1.1.7. Definisi

Bila A dan B keduanya adalah himpunan-himpunan tak kosong, maka produk kartesius dari A dan Byang selanjutnya akan kita tuliskan menggunakan notasi

B

A adalah himpunan pasangan berurut

 

a,

b

dengan aA dan bB

 



a b a A anb B



B

A  ,  _d  ■

Sehingga bila

A



 

1

,

2

,

3

dan

B



 

4

,

5

, maka

           



1

,

4

,

1

,

5

,

2

,

4

,

2

,

5

,

3

,

4

,

3

,

5







B

A

Latihan 1.1.

1. Gambarkan diagram yang menyatakan masing-masing himpunan pada Teorema 1.1.4

2. Buktikan teorema 1.1.4.

3. Buktikan bahwa

A



B

jika dan hanya jika AB A.

Himpunan D ini sering disebut selisih simetris dari A dan B. Nyatakan dalam diagram.

5. Tunjukkan bahwa selisih simetris D pada soal nomor 4, juga diberikan oleh:



A

B

 

A

B



D





\



6. Jika

A



B

tunjukkan

B



A

\



A

\

B



7. Diberikan himpunan A dan B , tunjukkan bahwa AB dan A \B saling asing dan bahwa

A





A



B

 



A

\

B



.

8. Diberikan sebarang himpunan A dan B, tunjukkan

A



B



A

\



A

\

B



.

9. Bila



A

₁

,

A

₂

,...,

A

_n



suatu koleksi himpunan, dan E sebarang himpunan,

tunjukkan bahwa









n

j

j n

j

j

E

A

A

E

1

1 









, dan









n

j

j n

j

j

E

A

A

E

1 1  







.

10. Mengacu pada soal nomor 9 tunjukkan bahwa









n

j

j n

j

j

E

A

A

E

1

1 









, dan









n j j n j

j

E

A

A

E

1 1  







.

11. Mengacu pada soal nomor 9 buktikan hukum de morgan







n



j

n

j

j

j

E

A

A

E

1 1

\

\





 ,









n j j n j

j

E

A

A

E

1 1

\

\

 



Catatan bila E \A_j dituliskan dengan C

 

A_j , maka kesamaan diatas

mempunyai bentuk

 





n j j n j j

A

A

1 1  











C

C

,





 

n j j n j j

A

A

1 1  











C

C

12. Misalkan J suatu himpunan dan untuk setiap

j



J

, A_j termuat di E .

13. Bila

B

₁ dan

B

₂ subhimpunan dari B dan

B



B

₁



B

₂ tunjukkan bahwa



A

B

1

 

A

B

2



B

A











1.2 FUNGSI

Pada bagian ini kita akan membahas gagasan fundamental suatu fungsi atau pemetaan. Selanjutnya akan kita ketahui bahwa fungsi merupakan suatu jenis khusus dari himpunan, walaupun terdapat visualisasi lain yang sering lebih bersifat sugesti. Pada bagian terakhir ini kita akan banyak membahas mengenai jenis-jenis fungsi, tetapi sedikit lebih abstrak dibandingkan bagian ini.

Bagi matematikawan abad terdahulu kata “fungsi” biasanya berarti formula tertentu, seperti

 



2



3



5

x

x

x

f

yang bersesuaian dengan masing-masing bilangan real

x

dan bilangan lain

 

x

f

. Mungkin juga seseorang memunculkan kontroversi, apakah nilai mutlak

 

x x

h 

dari suatu bilangan real merupakan “fungsi sejati” atau bukan. Selain itu definisi

x diberikan pula yakni:















0

,

0

,

x

x

x

x

x

bila bila

Definisi pertama:

suatu fungsi

f

dari himpunan A ke himpunan B adalah aturan

korespodensi yang memasangkan masing-masing unsur

x

di A secara tunggal dengan unsur

f

 

x

di B.

Definisi di atas mungkin saja tidak jelas, dikarenakan tidak jelasnya makna frase “aturan korespondensi”. Untuk mengatasi hal ini kita akan mendefinisikan fungsi dengan menggunakan himpunan seperti yang telah dibahas pada bagian sebelumnya.

Berikut ini adalah definisi yang mungkin saja dapat membuat kita kehilangan kandungan intuitif dari definisi terdahulu, tetapi kita dapatkan kejelasan.

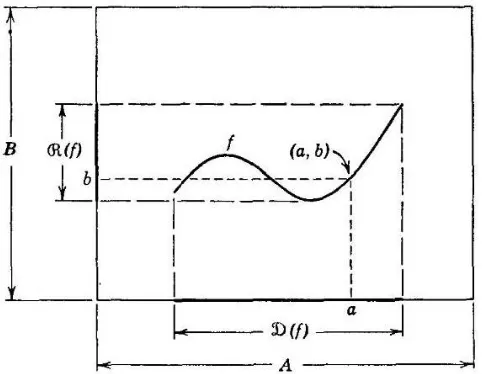
[image:15.595.190.433.463.650.2]

Ide dasar pendefinisian berikut ini adalah memikirkan gambar dari suatu fungsi; yaitu, suatu korelasi dari pasangan berurut. Bila kita perhatikan tidak setiap koleksi pasangan berurut merupakan gambar suatu fungsi, karena sekali unsur pertama dalam pasangan berurut diambil, unsur keduanya ditentukan secara tunggal.

Gambar 1.1 Gambar grafik sebuah fungsi

masing aA terdapat bB yang tunggal dengan

   

a

,

b

,

a

,

b

'



f

, maka

'

b

b . Himpunan A dari unsur-unsur pertama dari

f

disebut daerah asal

“domain” dari

f

, dan dituliskan

D

 

f

. Sedangkan unsur-unsur dari B yang

menjadi unsur kedua di

f

disebut “range” dari

f

dan dituliskan dengan

R

 

f

. Notasi

B

A

f

:



Menunjukkan bahwa

f

suatu fungsi dari A ke B ; akan sering kita

katakan bahwa

f

suatu pemetaan dari A ke B atau

f

memetakan dari A ke

dalam B. Bila

 

a

,

b



f

, sering ditulis dengan:

 

a

f

b



Pembatasan dan Perluasan Fungsi

Bila

f

suatu fungsi dengan domain

D

 

f

dan

D

₁ suatu subhimpunan

dari

D

 

f

, sehing kali bermanfaat untuk mendefinisikan fungsi baru

f

₁ dengan

domain

D

₁ dan

f

₁

   

x



f

x

untuk setiap

x



D

₁ . Fungsi

f

₁ ini disebut

pembatasan fungsi

f

pada

D

₁ . Sehingga menurut definisi 1.2.1, kita

mempunyai

 



1



1 a,b f a D

f   

Terkadang kita tuliskan f₁  f D₁ untuk menyatakan pembatasan fungsi

f

pada himpunan

D

₁.

Konstruksi yang serupa untuk gagasan perluasan. Bila suatu fungsi g

dengan domain

D

 

g

dan

D

₂



D

 

g

, maka sebarang fungsi

g

₂ dengan

domain

D

₂ sedemikian sehingga

g

₂

   

x



g

x

untuk setiap

x



D

 

g

disebut

Bayangan Langsung dan Bayangan Invers

1.2.2. Definisi

Misalkan

f

:

A



B

suatu fungsi dengan domain A dan range B . Bila E

subhimpunan A , maka bayangan langsung dari E terhadap

f

adalah

subhimpunan

f

 

E

dari A yang diberikan oleh

 

E



f

 

x

x

E



f



:



Bila H subhimpunan B, maka bayangan invers dari H terhadap

f

adalah

subhimpunan

f

1

 

H

dari A, yang diberikan oleh

 

H



x

A

f

 

x

H



f

1





:



Jadi bila diberikan himpunan

E



A

,

maka titik

y

₁



B

di bayangan langsung

 

E

f

jika dan hanya jika terdapat paling tidak sebuah titik

x

1



E

sedemikian

sehingga

y

₁



f

 

x

₁ . Secara sama bila diberikan

H



B

, titik

x

2



A

di dalam

bayangan invers

f

1

 

H

jika dan hanya jika

y



f

 

x

₂ di H.

1.2.3. Contoh

a. Misalkan

f

:

R



R

didefinisikan dengan

f

 

x



x

2 . Bayangan langsung

himpunan E



x0x2



adalah himpunan f

 

E 



y0 y4



. Bila



0 4



 y y

G , maka bayangan invers G adalah himpunan

 



2 2



1

   

 _{G x x}

f . Jadi

f

1

f

 

E



E

.

Disatu pihak kita mempunyai

f



f

1

 

G





G

. Tetapi bila H 



y1 y1



, maka kita peroleh f



f 1

 

H







x0x1



H

Pada buku ini kita akan bahas

f

1



G



H





f

1

 

G



f

1

 

H

dan meninggalkan yang sebaliknya yakni



G

H



f

 

G

f

 

H

f

1





1



1

sebagai latihan bagi pembaca.

i. Akan dibuktikan

f

1



G



H





f

1

 

G



f

1

 

H

Ambil sebarang

x



f

1



G



H



, ini berarti bahwa

f

  

x



G



H



, hal

ini mengakibatkan

f

 

x



G

dan

f

 

x



H

, sehingga ini mengakibatkan

 

G

f

x



1 dan

x



f

1

 

H

, karena itu

x





f

1

 

G



f

1

 

H



bukti selesai.

ii. Bukti sebaliknya diserahkan pada pembaca.

Sifat-sifat Fungsi

1.2.4. Definisi

Suatu fungsi

f

:

A



B

dikatakan injektif atau satu-satu bila untuk

setiap

x

1

,

x

2



A

demikian sehingga

x

1



x

2 mengakibatkan

f

   

x

1



f

x

2 . Bila

f

satu-satu, kita katakan

f

suatu injeksi.

Secara ekivalen,

f

injektif jika dan hanya jika

f

   

x

₁



f

x

₂

mengakibatkan

x

₁



x

₂ untuk setiap

x

₁

,

x

₂



A

.

1.2.5. Definisi

Suatu fungsi

f

:

A



B

dikatakan surjektif atau memetakan A pada B

bila

f

 

A



B

. Bila

f

surjektif, maka kita sebut

f

suatu surjeksi.

Secara ekivalen,

f

:

A



B

surjektif bila

R

 

f



B

, yaitu untuk setiap

B

y



terdapat xA sedemikian sehingga

f

 

x



y

.

1.2.6. Definisi

Suatu fungsi

f

:

A



B

dikatakan bijektif bila bersifat injektif dan

surjektif. Bila suatu fungsi

f

bijektif, kita sebut

f

suatu bijeksi.

Fungsi-Fungsi Invers

Bila

f

:

A



B

suatu fungsi dari A ke B , (karenanya, subhimpunan khusus dari AB ), maka pasangan berurut BA diperoleh dengan saling menukar unsur pertama dan kedua di

f

. Secara umum hasil penukaran tersebut

bukanlah fungsi. Tetapi bila

f

injektif, maka penukaran ini menghasilkan fungsi

yang disebut invers dari

f

.

1.2.7. Definisi

Misalkan

f

:

A



B

suatu fungsi injektif dengan domain A dan

R

 

f

di

B . Bila g 



 

b,a BA

 

a,b  f



, maka g suatu fungsi injektif dengan

   

g

R

f

D



dan range A. Fungsi g disebut fungsi invers dari

f

dan dituliskan

.

1



f

Dalam penulisan fungsi yang standar, fungsi

f

1 berelasi dengan

f

sebagai berikut:

x



f

1

 

y

jika dan hanya jika

y



f

 

x

.

1.2.8. Contoh

Suatu fungsi

 

1  

x x x

f dengan D

 

f 



xRx1



bersifat injektif

(buktikan

f

suatu injeksi untuk latihan pembaca). Selanjutnya kita akan peroleh

Fungsi Komposisi

Sering kita ingin mengkomposisikan dua buah fungsi dengan mencari

 

x

f

terlebih dahulu, kemudian menggunakan g untuk memperoleh

g

 

f

 

x

,

akan tetapi hal ini bisa dilakukan bila

f

 

x

ada didalam domain g. Jadi kita

harus mengasumsikan bahwa

R

 

f



D

 

g

1.2.9. Definisi

Untuk fungsi

f

:

A



B

dan

g

:

B



C

, komposisi

g



f

adalah fungsi dari A ke C yang didefinisikan dengan

g



f

 

x



g

 

f

 

x

untuk setiap xA.

1.2.10. Teorema

Bila

f

:

A



B

dan

g

:

B



C

fungsi dan H suatu subhimpunan dari C.

Maka



f g

  

1 H 



g1 f 1



 

H g1



f1

 

H



.

1.2.11. Teorema

Bila

f

:

A



B

dan

g

:

B



C

keduanya bersifat injektif, maka

komposisi

g



f

juga bersifat injektif.

(Bukti teorema diberikan sebagai latihan bagi pembaca)

Barisan

Fungsi dengan Ν sebagai domain memainkan aturan yang sangat khusus dalam analisis, yang akan kita perkenalkan daalam konsep barisan berikut ini.

1.2.12. Definisi

Suatu barisan dalam himpunan S adalah suatu fungsi yang domannya himpunan bilangan asli Ν dan rangenya termuat di S.

Untuk barisan X :ΝS , nilai X di nΝ sering ditulis dengan

x

_n

daripada

 

x

_n , dan nilainya sering kita sebut suku ke-

n

barisan tersebut. Barisan

Sebagai contoh, barisan di R yang dituliskan dengan



n

n



Ν



sama artinya dengan fungsi X :ΝR dengan X

 

n  n.

Penting sekali untuk membedakan antara barisan



x_n nΝ



dengan nilainya



xn nΝ



, yang merupakan subhimpunan dari S. Suku barisan harus

dipandang mempunyai urutan yang diinduksi dari urutan bilangan asli, sedangkan range dari barisan hanya merupakan subhimpunan dari S. Sebagai

contoh, suku-suku dari barisan



 



1

n

n



Ν



berganti-ganti 1 dan 1, tetapi range dari barisan tersebut adalah

 



1

,

1

, memuat dua unsur dari R

Latihan 1.2.

1. Misalkan AB



xR1 x1



dan subhimpunan R dari R , apakah himpunan ini fungsi?

2. Misalkan

f

fungsi fungsi pada Ryang didefinisikan dengan

f

 

x



x

2, dan



 1 0



 x R x

E dan F 



xR0 x1



tunjukkan bahwa

 

0





F

E

dan

f



E



F

  



0

. Sementara f

   

E  f F 



yR0 x1



.

Disini

f



E



F



adalah subhimpunan sejati dari

f

   

E



f

F

. Apa yang

terjadi bila 0 dibuang dari E dan F?

3. Bila E dan F seperti soal nomor 2. Tentukan E \F dan

f

   

E

\

f

F

dan

tunjukkan bahwa

f



E

\

F

    



f

E

\

f

F

salah!

4. Tunjukkan bahwa bila

f

:

A



B

dan E ,F subhimpunan dari A, maka



E

F

    

f

E

f

F

f







dan

f



E



F

    



f

E



f

F

.

5. Tunjukkan bila

f

:

A



B

, dan G , H subhimpunan dari B , maka



G

H



f

 

G

f

 

H

6. Misalkan

f

didefinisikan dengan

 

x

R

x

x

x

f







,

1

2 . Tunjukkan bahwa

f

bijektif dari R pada



y

:



1



y



1



.

7. Untuk

a

,

b



R

dengan ab, tentukan bijeksi dari A



xa xb



pada



0 1



 y y

B .

8. Tunjukkan bahwa bila

f

:

A



B

bersifat injektif dari

E



A

, maka

 



f

E



E

f

1



. Berikan suatu contoh untuk menunjukkan kesamaan tidak

dipenuhi bila

f

tidak injektif.

9. Tunjukkan bahwa bila

f

:

A



B

bersifat surjektif, dan

H



B

, maka

 



f

H



H

f

1



. Berikan satu contoh untuk menunjukkan kesamaan tidak

dipenuhi bila

f

tidak surjektif.

10. Buktikan bila

f

:

A



B

suatu injeksi, maka f 1 



  

b,a a,b R



suatu fungsi dengan domain

R

 

f

. Kemudian buktikan bahwa

f

1 injektif dan

f

invers dari

f

1.

11. Misalkan

f

:

A



B

injektif, tunjukkan bahwa

f

1

f

 

x



x

untuk setiap

 

f

D

x



dan

f



f

1

 

y



y

untuk setiap

y



R

 

f

.

12. Berikan contoh dua buah fungsi

f

:

A



B

,

f

:

A



B

dari

f

:

A



B

pada

B

A

f

:



sehingga

f

:

A



B

, tetapi

f

:

A



B

13. Buktikan teorema 1.2.10 dan 1.2.11

14. Misalkan

f ,

g

fungsi dan

g



f

 

x



x

untuk semua

x

di

D

 

f

. Tunjukkan bahwa

f

injektif dan

R

 

f



D

 

f

dan

R

   

g



D

g

.

15. Misalkan

f ,

g

fungsi dan dan

g



f

 

x



x

untuk semua

x

di

D

 

f

dan

 

y

g

1.3 INDUKSI MATEMATIKA

Induksi matematika merupakan metode pembuktian penting yang akan sering digunakan dalam buku ini. Metode ini digunakan untuk menguji kebenaran suatu pernyataan yang diberikan dalam suku-suku bilangan asli. Walaupun kegunaannya terbatas pada masalah tertentu, tetapi induksi matematika sangat dibutuhkan disemua cabang matematika. Karena banyak bukti induksi matematika sangat diperlukan disemua cabang matematika. Karena banyak bukti induksi mengikuti urutan formal argumen yang sama, kita akan sering menyebutkan “hasilnya mengikuti induksi matematika” dan meninggalkan bukti lengkapnya kepada pembaca. Dalam bagian ini kita akan membahas prinsip induksi matematika dan memberi beberapa contoh untuk mengilustrasikan bagaimana proses bukti induksi.

Kita akan mengasumsikan kebiasaan (pembaca) dengan himpunan bilangan asli



1

,

2

,

3

,...





Ν

Dengan operasi matematika penjumlahan dan perkalian seperti biasa dan dengan arti suatu bilangan kurang dari bilangan lain. Kita juga akan mengasumsikan sifat fundamental dari Ν berikut ini

1.3.1. Sifat urutan dengan baik di Ν

Setiap subhimpunan tak kosong dari Ν mempunyai unsur terkecil.

Pernyataan yang lebih detail dari sifat ini sebagai berikut: bila S sub himpunan dari Ν dan S , maka terdapat unsur mS sedemikian sehingga

k

m untuk setiap kS.

1.3.2. Prinsip Induksi Matematika

Misalkan S sub himpunan dari Ν yang mempunyai sifat: i. 1S

ii. Jika kS, maka k1S. Maka S Ν

Bukti:

Andaikan S Ν. Maka Ν\S . Karenanya berdasar sifat urutan dengan baik, maka Ν\S mempunyai unsur terkecil, sebut

m

. Karena 1S , maka m1. Karena itu m1 dengan m1 juga bilangan asli. Karena m1m dan

m

unsur terkecil di N \S, maka m1 haruslah di S.

Sekarang kita gunakan hipotesis (2) terhadap unsur k m1 di S, yang berakibat

k



1





m



1





1



m

di S . Kesimpulan ini kontradiksi dengan pernyataan bahwa

m

tidak di S . Karena

m

diperoleh dengan pengandaian

S

\

Ν tidak kosong, kita dipaksa pada kesimpulan bahwa Ν\S kosong. Karena itu kita telah buktikan bahwa S Ν.

Prinsip induksi matematika sering dinyatakan dalam kerangka sifat atay pernyataan tentang bilangan asli. Bila

P

 

n

berarti pernyataan tentang nΝ, maka

P

 

n

benar untuk beberapa nilai

n

, tetapi belum tentu benar untuk yang

lain. Sebagai contoh, bila

P

 

n

pernyataan “

n

2



n

”, maka

P

 

1

benar,

sementara

P

 

n

salah untuk semua n1, nN dalam konteks ini prinsip induksi matematika dapat dirumuskan sebagai berikut:

Untuk setiap nΝ , misalkan

P

 

n

pernyataan tentang

n

, misalkan bahwa

a)

P

 

1

benar

b) Jika

P

 

k

benar, maka

P

 

k



1

benar.

Maka

P

 

n

benar untuk semua nΝ.

Dalam kaitannya dengan versi induksi matematika terdahulu yang

Dalam (b) asumsi “jika

P

 

k

benar” disebut hipotesis induksi. Disini, kita

tidak memandang pada benar salahnya

P

 

k

, tetapi hanya pada validitas

implikasi “ jika

P

 

k

benar, maka

P

 

k



1

benar”.

1.3.3. Contoh

a. Untuk setiap nN, jumlah

n

pertama bilangan asli diberikan oleh

 

1

2 1 ...

2

1  n n n

Untuk membuktikan kesamaan ini, kita misalkan S himpunan nΝ , sehingga kesamaan tersebut benar. Kita harus membuktikan kondisi (1) dan (2) pada 1.3.2 dipenuhi.

i. Bila n1, maka kita mempunyai

 

.1.

 

1 1 2

1 1 :

1  

P , jadi

P

 

1

benar

ii. Bila

P

 

k

kita asumsikan benar yakni

 

1

. 2 1 ...

2

1  k  k k

Bila kita tambahkan pada kedua ruas dengan

 

k



1

,maka menjadi:

 

.

   

1 1

2 1 1 ...

2

1  k k  k k  k

 

1

 

1

2

1

1

...

2

1





























k

k

k

k

  

2

 

1

2 1 1 ...

2

1  k k  k k

   

1 2



2 1 1 ...

2

1  k k  k k

     

1



1 1



2 1 1 ...

2

1  k k  k k 

Dari persamaan terakhir kita ketahui bahwa karena

P

 

k

berimplikasi pada

b. Untuk setiap nΝ, jumlah kuadrat dari

n

bilangan pertama asli adalah sebagai berikut:

 



6 1 2 1 ... 2

12  2  n2  nn n

Untuk membuktikan formula diatas, maka pertama-tama kita buktikan kebenaran formula diatas untuk n1, selanjutnya jika benar untuk nk, maka akan dibuktikan benar pula untuk

n



 

k



1

i. Bila n1, maka kita mempunyai

 

 



1 6 6 6 1 1 . 2 1 1 1 1 :

1     

P , jadi

 

1

P

benar

ii. Bila

P

 

k

kita asumsikan benar yakni

 



6 1 2 1 ... 2

12  2  k2  k k k

Bila kita tambahkan pada kedua ruas dengan

 

k12,maka menjadi:

 

2

 

  

2

2 2 2 1 6 1 2 1 1 ... 2

1   k  k  k k k  k

    

  

































1

6

1

2

1

1

...

2

1

2 2

k

2

k

2

k

k

k

k

    

 



































6

6

6

1

2

1

1

...

2

1

2 2

k

2

k

2

k

k

k

k

   

   _    _     6 6 6 2 1 1 ... 2 1 2 2 2 2

2 k k k

k k k

   

   _   _     6 6 7 2 1 1 ... 2 1 2 2 2 2

2 k k

k k k

   

   _   _     6 6 7 2 1 1 ... 2 1 2 2 2 2

2 k k

k k k

    



































6

3

2

2

1

1

...

2

1

2 2

k

2

k

2

k

k

k

 

   



  







































6

1

1

2

1

1

1

1

...

2

Hasil terakhir memiliki arti bahwa

P

 

k



1

bernilai benar sebagai implikasi

dari

P

 

k

yang bernilai benar, mengikuti induksi matematika, maka validitas

formula diatas berlaku untuk setiap nΝ

c. Diberikan

a,

b

, kita akan buktikan pernyataan



a



b



adalah faktor dari

n n

b

a



untuk setiap nΝ.

Pertama-tama kita akan melihat untuk n1, maka kita ketahui bahwa pernyataan matematika bernilai benar karena



a



b



adalah faktor dari



a

1



b

1







a



b



.

Selanjutnya asumsikan bahwa pernyataan juga bernilai benar untuk nk, sehingga



a



b



adalah faktor dari



a

k



b

k



.

Selanjutnya perhatikan bahwa:



1 1



1 1











k k k k k k

b

ab

ab

a

b

a



a

k1



b

k1

 



a

a

k



b

k





b

k



a



b



Berdasarkan hipotesis maka kita ketahui bahwa



a



b



faktor dari

a



a

k



b

k



,

selain itu kita ketahui bahwa



a



b



adalah faktor dari

b

k



a



b



, sehingga

dari sini kita simpulkan bahwa



a



b



adalah faktor dari



a

k1



b

k1



. Dengan

induksi matematika dapat kita simpulkan bahwa



a



b



adalah faktor dari



n n



b

a



untuk setiap nΝ

d. Untuk setiap nΝ buktikanlah bahwa ketaksamaan berikut benar

 

1

!

2

n



n



Untuk membuktikan, pertama kita lihat untuk n1 yakni

2

1



 

1



1

!



2

bernilai benar.

Selanjutnya kita asumsikan bahwa

2

k



 

k



1

!

. Dengan menggunakan fakta

2

2k , diperoleh:

  

1

!

2

  

.

1

!

2

  

!



1

1



!

2

2

.

2

Jadi, bila ketaksamaan tersebut berlaku untuk k, maka berlaku pula untuk

1 

k . Karenanya dengan induksi matematika, kita simpulkan bahwa ketaksamaan tersebut benar untuk setiap nΝ.

e. Bila rR, r1 dan nΝ, maka

r

r

r

r

r

n n

















1

1

...

1

1 2

Ini merupakan jumlah

n

suku deret geometri. Untuk membuktikan kesamaan

diatas, kita misalkan n1, maka kita mempunyai

r

r

r









1

1

1

2

, jadi formula

diatas benar untuk n1. Selanjutnya kita asumsikan benar untuk nk ,

sehingga

r

r

r

r

r

k k

















1

1

...

1

1 2

benar. Selanjutnya pada kedua ruas

kita tambahkan

r

k1, sehingga menjadi:

1 1 1 2

1

1

...

1

  



















k k k k

r

r

r

r

r

r

r

 

 

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

k k k k k k k k









































      

1

1

1

1

1

1

1

1

1

...

1

2 2 1 1 1 1 1 2  

r

r

r

r

r

r

k k k

















  

1

1

...

1

1 1 1 2

Hasil terakhir memiliki arti formula tersebut juga berlaku untuk nk1, sehingga mengikuti prinsip induksi matematika, maka formula tersebut benar untuk setiap nΝ.

Pada sekolah menengah kita sudah diajarkan membuktikan kesamaan diatas tanpa menggunakan induksi matematika yakni:

Misalkan S_n 1rr2 ...rn

, maka   2 ... n  n1

n r r r r

rS ,



2

 

2 1



... ...

1          

 n n n

n

n rS r r r r r r r

S

 

1

1 1r S_n  rn

f. Penggunaan prinsip induksi matematika secara ceroboh dapat menghasilkan kesimpulan yang salah. Pembaca diharapkan mencari kesalahan pada “Bukti Teorema” berikut.

Bila

n

sebarang bilangan asli dan bila maksimum dari dua bilangan asli p dan q adalah

n

, maka pq. (akibatnya bila p dan q dua bilangan asli sebarang, maka pq).

Bukti:

Misalkan S sub himpunan dari bilangan asli sehingga pernyataan tersebut benar. maka 1S, karena p,q di Ν dan maksimumnya 1. Maka maksimum

1



p

dan

q



1

adalah k, karenanya

p



1



q



1

, karena kS , dari sini kita simpulkan pq. Jadi

 

k



1



S

dan kita simpulkan bahwa pernyataan tersebut benar untuk setiap nΝ.

g. Terdapat juga beberapa pernyataan yang benar untuk beberapa bilangan asli, tetapi tidak untuk semua. Sebagai contoh formula

P

 

n



n

2



n



41

memberikan bilangan prima untuk

n



1

,

2

,

3

,...,

41

. Tetapi,

P

 

1

bukan bilangan prima.

Prinsip induksi matematika memiliki bentuk dalam versi lain yang kadang-kadang sangat berguna. Sering disebut prinsip induksi kuat, walaupun sebenarnya ekivalen dengan versi terdahulu.

1.3.4. Prinsip Induksi Kuat.

Misalkan S sub himpunan Ν sedemikian hingga 1S, dan bila



1

,

2

,...,

k





S

maka

 

k



1



S

. Maka S Ν.

Latihan 1.3.

Buktikan bahwa yang berikut ini berlaku untuk semua nΝ

1.

 

1

1

1

...

3

.

2

1

2

.

1

1













n

n

n

n

2.

 

2 3 3 3 1 2 1 ... 2 1     _   

 n n n

3.

 

 

2 1 1 ... 3 2

12  2     n1  n n

4.

n

3



5

n

dapat dibagi 6

5.

5

2n



1

dapat dibagi 8

6.

5

n



4

n



1

dapat dibagi 16.

7. Buktikan bahwa jumlah pangkat tiga dari bilangan asli berurutan,

2

,

1

,

n



n



n

habis dibagi 9.

8. Buktikan bahwa

n



2

n untuk semua nΝ

9. Tentukan suatu formula untuk jumlah



2

1



2

1



1

...

5

.

3

1

3

.

1

1











n

n

Dan buktikan dugaan tersebut dengan menggunakan induksi matematika. (dugaan terhadap pernyataan matematika, sebelum dibuktikan sering disebut

“Conjecture”)

10. Tentukan suatu formula untuk jumlah

n

buah bilangan ganjil pertama



2

1



...

3

1







n



11. Buktikan variasi dari 1.3.2 berikut: misalkan S subhimpunan tak kosong dari

Ν sedemikian sehingga untuk suatu

n

₀



Ν

berlaku (a)

n

₀



S

, dan (b) bila

0 

k dan kS, maka k1S. Maka S memuat himpunan



nΝnn₀



.

12. Buktikan bahwa

2

n



n

!

Untuk setiap n4, nΝ (lihat latihan 11).

13. Buktikan bahwa

2

n



3



2

n2 untuk setiap n5, nΝ (lihat latihan 11). 14. Untuk bilangan asli yang mana

n

2



2

n ? Buktikan pernyataanmu (lihat

latihan 11)

15. Buktikan bahwa

n

n









...

1

2

1

1

1

untuk setiap nΝ.

16. Misalkan S sub himpunan dari N sedemikian sehingga (a) k



S

2

untuk setiap kN , dan (b) bila kS , dan k2 , maka k1S . Buktikan

Ν



S .

17. Misalkan barisan

 

x

_n didefinisikan sebagai berikut:

x

₁



1

,

x

₂



2

, dan



n n



n x x

x _2  _1  2

1

untuk nN. Gunakan prinsip induksi kuat 1.3.4. untuk

BAB II

HIMPUNAN BILANGAN REAL

ab ini menjelaskan tentang hal-hal yang berkaitan dengan dengan sistem bilangan real sebagai suatu sistem matematika yang memiliki sifat-sifat sebagai suatu lapangan yang terurut dan lengkap. Yang dimaksud dengan sistem bilangan real sebagai suatu lapangan di sini adalah bahwa pada himpunan semua bilangan real R yang dilengkapi dengan operasi penjumlahan dan perkalian berlaku sifat-sifat aljabar dari lapangan. Sifat terurut dari R berkaitan dengan konsep kepositifan dan ketidaksamaan antara dua bilangan real, sedangkan sifatnya yang lengkap berkaitan dengan konsep supremum atau batas atas terkecil. Teorema-teorema dasar dalam kalkulus elementer, seperti Teorema Eksistensi Titik Maksimum dan Minimum, Teorema Nilai Tengah, Teorema Rolle, Teorema Nilai Rata-Rata, dan sebagainya, didasarkan atas sifat kelengkapan dariRini. Sifat ini berkaitan erat dengan konsep limit dan kekontinuan. Dapat dikatakan bahwa sifat kelengkapan dari R

mempunyai peran yang sangat besar di dalam analisis real.

Bab ini terdiri dari beberapa sub bab. Sub bab 2.1 membahas sifat lapangan dari

R. Sub bab 2.2 menjelaskan sifat terurut dari R, dan di dalamnya dibahas juga tentang konsep nilai mutlak. Pada sub bab 2.3 didiskusikan tentang sifat kelengkapan dari R. Pada sub bab ini dibahas mengenai sifat Archimedean dan sifat kerapatan dari himpunan bilangan rasional. Selanjutnya, sub bab 2.4, menjelaskan tentang interval, sebagai suatu himpunan bagian dari R yang dikonstruksi berdasarkan sifat terurut dari R . Yang terakhir, sub bab 2.5 membahas tentang representasi desimal dari bilangan real. Pada sub bab ini, juga dipaparkan bagaimana membuktikan Teorema Cantor dengan menggunakan konsep representasi desimal dari bilangan real ini. Teorema Cantor mengatakan bahwa himpunan R merupakan himpunan yang tak terhitung (uncountable).

2.1 Sifat Aljabar dari R

Sifat 2.1 (Sifat Aljabar dari R ). Pada himpunan bilangan real R yang dilengkapi operasi penjumlahan (



) dan operasi perkalian () berlaku sifat-sifat, terhadap operasi penjumlahan :

T1. a b  b a untuk setiap

a,

b



R

T2.



a b    



c a



b c



untuk setiap

a ,

,

b

c



R

T3. Terdapat elemen 0R sedemikian sehingga 0   a a 0 a untuk setiap

R



a

T4. Terdapat elemen aR sedemikian sehingga      a a a

 

a 0 untuk setiap aR

terhadap operasi perkalian :

K1. a b  b a untuk setiap

a,

b



R

K2.

 

a b c    a b c

 

untuk setiap

a ,

,

b

c



R

K3. Terdapat elemen 1R sedemikian sehingga 1   a a 1 a untuk setiap

a฀

K4. Terdapat elemen 1/aR sedemikian sehingga

 

1/a   a a

 

1/a 1

untuk setiap aR, dan

D. a b     



c



a b a c dan



b     c



a b a c a untuk setiap

a ,

,

b

c



R

.

Terkait dengan elemen identitas 0 (terhadap operasi penjumlahan) dan 1 (terhadap operasi perkalian), kita memiliki fakta bahwa kedua elemen ini merupakan elemen yang unik atau tunggal. Selain itu, perkalian setiap elemen di

R dengan elemen 0 hasilnya adalah 0. Fakta-fakta ini, secara formal matematis, dapat direpresentasikan dalam teorema berikut ini.

Teorema 2.2.

a. Jika

z,

a



R

dan

z

 

a

a

maka z0.

b. Jika u b b dengan

u,

b



R

dan b0 maka u1.

c. a 0 0 untuk setiap aR. Bukti.

a. Berdasarkan sifat T3, T4, T2, dan hipotesis

z

 

a

a

,

 







  

 

0 0

z     z z a a        z a a a a . b. Berdasarkan sifat K1, K2, K3, dan hipotesis u b b, b0,

 





   

 

1 1/ 1/ 1/ 1

u    u u b b   u b b  b b  . c. Berdasarkan sifat K3, D, dan T3,

 

0 1 0 1 0 1

a           a a a a a a.

Berdasarkan a., diperoleh bahwa a 0 0. ■

Selain fakta di atas, kita juga memiliki fakta berikut ini.

Teorema 2.3.

a. Jika

a,

b



R

, a0, dan a b 1 maka b1/a. b. Jika a b 0 maka a0 atau b0.

Bukti.

a. Berdasarkan sifat K3, K4, K2, dan hipotesis a0, dan a b 1,

 





     

1 1/ 1/ 1 1/ 1/

b    b b a a   b a a   a  a.

b. Andaikan a0 dan b0 . Akibatnya,

   

a b 



1/ a b



1. Berdasarkan hipotesis, yaitu a b 0, dan Teorema 2.2.c., kita memiliki bahwa

Terjadi kontradiksi di sini, yaitu antara pernyataan

   

a b 



1/ a b



1 dan

   

a b 



1/ a b



0. Dengan demikian, haruslah bahwa a0 atau b0.■

Teorema 2.3.a. mengatakan bahwa eksistensi invers dari suatu elemen di R

adalah unik. Sedangkan Teorema 2.3.b. mengandung arti bahwa perkalian dua elemen tak nol di R tidaklah mungkin menghasilkan elemen nol.

Di dalam himpunan bilangan real R dikenal pula operasi lain, yaitu operasi pengurangan () dan pembagian (

:

). Jika

a,

b



R

maka operasi pengurangan didefinisikan dengan a b   : a

 

b sedangkan operasi pembagian didefinisikan dengan a b: : a

 

1/b , b0.

2.2 SIFAT TERURUT DARI R

Seperti yang telah disinggung pada pendahuluan bab ini, sifat terurut dari R

berkaitan dengan konsep kepositifan dan ketidaksamaan antara dua bilangan real. Seperti apa kedua konsep tersebut? Di sini, kita akan membahasnya. Terlebih dahulu kita akan membahas konsep kepositifannya.

Sifat 2.4 (Sifat Kepositifan). Terdapat himpunan bagian tak kosong dari R, yang dinamakan himpunan bilangan real positif

R

, yang memenuhi sifat-sifat :

a. Jika

a,

b



R

 maka

a



b



R

.

b. Jika

a,

b



R

 maka

a



b



R

.

c. Jika aR maka salah satu diantara tiga hal, yaitu

a



R

 , a0, dan







a

R

, pasti terpenuhi.

Sifat 2.4.c. disebut juga sebagai sifat Trichotomy. Sifat ini mengatakan bahwa R

dibangun oleh tiga buah himpunan yang disjoin. Tiga buah himpunan tersebut

bisa juga dituliskan dengan

R

 . Jika

a



R

 maka a0 dan

a

dikatakan sebagai bilangan real positif. Jika

a



R

 

 

0

maka a0 dan

a

dikatakan sebagai bilangan real nonnegatif. Jika

a



R

 maka a0 dan

a

dikatakan sebagai bilangan real negatif. Jika

a



R

 

 

0

maka a0 dan

a

dikatakan sebagai bilangan real nonpositif.

Penjumlahan k buah suku elemen 1 menghasilkan bilangan k . Himpunan bilangan k yang dikonstruksi dengan cara demikian disebut sebagai himpunan bilangan asli, dinotasikan dengan N. Himpunan N ini merupakan himpunan

bagian dari himpunan

R

. Himpunan ini memiliki sifat fundamental, yakni bahwa setiap himpunan bagian tak kosong dari N memiliki elemen terkecil. Sifat yang demikian disebut sebagai sifat well-ordering dari N.