Translate Bab 4 Analisis Real

(1)

Ryan Prasetya (3115111153)

Bagian 4.1. Limit Fungsi

Dalam bagian ini kami akan memperkenalkan ide penting dari limit fungsi. Ide dari fungsi f mempunyai sebuah limit L pada titik c adalah nilai f(x) mendekati L ketika x sangat dekat namun berbeda dari c. Tapi ini sangat penting untuk membuat secara teknis ide dari “dekat” dab ini berhasil dengan definisi  yang akan dijelaskan berikut.

Untuk membuat sebuah arti dari limit fungsi f pada titik c, sangat penting dijelaskan bahwa f didefinisikan pada titik dekat c. tidak harus tepat pada titik c, namun cukup dekat dengan titik c untuk membuat pembelajaran menarik. Ini adalah alasan untuk definisi berikut

4.1.1 Definisi.

Ambil A . Sebuah titik c adalah titik kumpul dari A jika untuk setiap  0 ada paling sedikit satu titik xA x, c dimana x c 

Definisi ini diartikan dengan cara lain dengan bahasa lain seperti : sebuah titik c adalah titik kumpul dari himpunan A jika setiap lingkungan- V c_( ) (c ,c) dari c memuat paling sedikit satu titik dari A yang berbeda dengan c

Catatan

Titik c mungkin saja anggota A maupun tidak, tapi bahkan jika itu ada di A, itu dihiraukan dalam menentukan apa itu merupakan titik kumpul dari A atau bukan, karena secara eksplisit kita membutuhkan ada titik di V c_( )A yang berbeda dari c untuk c menjadi titik kumpul dari A

Untuk contoh, jika A:= {1,2}, maka titik 1 bukanlah titik kumpul A, jika memilih

1 :

2

  memberikan lingkungan dari 1 yang tidak memuat titik dari A yang berbeda dengan 1. Hal yang sama juga terjadi untuk titik 2, jadi A tidak punya titik kumpul

4.1.2 Teorema

Sebuah angka c adalah titik kumpul dari subset A dari R jika dan hanya jika ada sebuah barisan (a ) di A dimana lim( )_n a_n c dan a_n c untuk setiap n

(2)

Bukti

Jika c adalah titik kumpul dari A, maka untuk sembarang n lingungan (1/n) V_1/_n( )c

memuat paling sedikit satu titik a di A yang berbeda dengan c. Maka, _n , , dan 1/

n n n

a A a c a  c n mengakibatkan lim(a_n)c

Konversnya, jika ada sebuah barisan (a di A\{c} dengan lim( )_n) a_n c, maka untuk sembarang  0ada J dunaba huja nK , maka a_nV c_( ) , olehkarenanya lingkungan-

( )

V c_ dari c memuat titik a , untuk n_n K , dimana pada A dan berbeda dengan c Terbukti

Contoh selanjutnya menegaskan bahwa sebuah titik kumpul dari sebuah himpunan bisa saja berada pada himpunan tersebut ataupun tidak

4.1.3 Contoh

(A) untuk sebuah interval terbuka A1:=(0,1), setia titik dari interval tertutup [0,1]

adalah titik kumpul dari A1. Catatan bahwa titik 0,1 adalah titik kumpul dari A1, namun tidak

berada pada A1. Semua titik pada A1 adalah titik kumpul dari A1

(b) Sebuah himpunan berhingga tidak mempunyai titik kumpul (c) Himpunan takhingga tidak mempunyai titik kumpul

(d)Himpunan A4:={1/n; n } hanya mempunyai titik 0 sebagai titik kumpul. Tidak ada

titik pada A4 yang merupakan titik kumpul dari A4

(e) Jika I:={0,1}, maka himpunan A₅: I memuat semua angka rasional di I. Mengikuti teorema 2.4.8, bahwa setiap titik di I adalah titik kumpul dari A5

Izzaty Amalia (3115111154)

Definisi Limit

Kita sekarang menyatakan definisi yang tepat dari batas fungsi f pada titik c. Penting untuk dicatat bahwa dalam definisi ini, tidaklah menjadi masalah apakah jika f pada suatu titik c atau tidak. Dalam kasus ini, kita mengecualikan c dari pertimbangan dalam penentuan batas

(3)

Diberikan AR, dan diberikan c menjadi titik kelompok A . Untuk fungsi ,

:

f AR bilangan real L menjadi limit dari f di c jika diberikan sebarang  0 yang eksis dan  0 sedemikian rupa sehingga xA dan 0  x c , then f x( ) L . Keterangan

(a). Karena nilai dari  biasanya tergantung pada , kita kadang-kadang akan menulis  

 

bukan  untuk menekankan ketergantungan ini.

(b) Ketidaksetaraan 0 x c ekuivalen dengan mengatakan xc.

Jika L adalah batas f di c, maka kita juga mengatakan bahwa f konvergen ke L di

c. kita sering menulis. lim ( ) x c L f x   atau lim x c L f  

Kita juga mengatakan bahwa "f x( ) mendekati L sebagai x mendekati c". (tapi perlu dicatat bahwa titik tidak benar-benar bergerak di mana saja.) dengan symbol

( )

f x L dengan xc juga digunakan kadang-kadang untuk mengungkapkan fakta bahwa

f memiliki batas L pada c.

Jika batas f di c tidak ada, kita mengatakan bahwa f menyimpang di c.

Hasil pertama kami adalah bahwa nilai L dari batas tersebut ditentukan unik. Keunikan ini bukan bagian dari definisi limit, tetapi harus disimpulkan.

4.1.5 Teorema

Jika f :AR dan jika c adalah titik kelompok dari A , maka f hanya dapat mempunyai 1 limit di c.

Bukti. Misalkan nomor L dan L memuaskan Definisi 4.1.4. Untuk '  0, terdapat

 

2 0

   sedemikian sehingga jika xA dan0  x c  

 

2 , maka f x( ) L  2. Juga terdapat  '

 

2 sedemikian sehingga jika xA dan 0  x c  '

 

2 , maka

( ) ' 2

f x L  . Sekarang diberikan (gak kebaca). Maka jika xA dan 0  x c , Segitiga Ketimpangan menyiratkan bahwa

( ) ( ' ( ))

(4)

' ( ) ( ( ) L') 2 2

L L  L f x  f x    

Karena  0 adalah tak tentu, kita menyimpulkan bahwa L L ' 0, sehingga LL'' Definisi limit dapat sangat baik dijelaskan dalam hal lingkungan. (Lihat Gambar ....) Kami mengamati bahwa karena





( ) ( , ) :

V c_  c  c  x x c 

ketimpangan 0  x c  setara dengan mengatakan bahwa xcdan x milik  lingkungan

( )

V c_ dari c. Demikian pula, ketimpangan f x( ) L  adalah setara dengan mengatakan bahwa f x( )milik  lingkungan V L_( ) dari L . Dengan cara ini, kita memperoleh hasil pembaca berikut harus menulis argumen rinci untuk mendirikan teorema.

Wahyu widyastuti (3115111166)

4.1.6Teorema

Misalkan f :AR , dan misalkan c adalah titik kumpul dari A, maka pernyataan

berikut adalah ekuivalen: (i). ( )

(ii). Untuk setiap lingkungan-V L( ) dari L, terdapat lingkungan-V(c) dari c sehingga jika xc merupakan titik sebarang pada V_(c)A, maka f x( ) termasuk V L_( ).

Sekarang kami berikan beberapa contoh yang mengilustrasikan aplikasi dari definisi limit.

4.1.7Contoh

a.

Untuk menjadi lebih eksplisit, misalkan f x( ) :buntuk semua xR. Kita akan buktikan

bahwa ( ) .

Jika diberikan  0, kita misalkan  : 1 (pada kenyataannya, semua  positif akan memenuhi syarat tersebut).

Dengan demikian, jika 0 |  x c| 1, maka kita dapatkan | f x( )    b| |b b| 0 . Karena  0 adalah sebarang, kita simpulkan berdasarkan Definisi 4.1.4 bahwa ( ) .(?)

(5)

b.

Misalkan g x( ) :xuntuk semua xR. Jika  0, misalkan  ( ). Maka jika

0 |  x c|  ( ), maka kita mempunyai | ( )g x    c| |x c| . Karena  0sebarang, maka kita

berkesimpulan bahwa ( ) . (?)

c.

Misalkan h x( ) :x2untuk semua xR.Kita ingin membuat selisih

2 2 2

| ( )h x c | | x c |

lebih kecil dari suatu 0yang diberikan dengan pengambilan x yang cukup dekat dengan c. Untuk itu, kita perhatikan bahwax2c2 (xc x c)(  ). Selain itu, jika

|x c | 1, maka

| | | | 1x  c  sehingga |x c| | | | | | | | |x  c x  c (2 | |c 1) |xc|--- (1)

Selain itu suku terakhir ini akan lebih kecil dari  asalkan kita mengambil

|x c | / (2 | | 1)|c  x c |. Akibatnya, jika kita memilih ( ) : inf 1, 2 | | 1c     _ _   

maka jika0 |  x c|  ( ), pertama akan berlaku bahwa|x c | 1dengan demikian (1) adalah valid. Selanjutnya, karena|x c |  / (2 | | 1)c  , maka

2 2

|x c | (2 | | 1) | c  x c |

Karena kita mempunyai pilihan  ( )0untuk sebarang pilihan dari  0, maka dengan demikian kita telah menunjukkan bahwa ( )

. (?)

d.

jika c > 0

Misalkan ( ) : 1/x  x untuk x> 0 dan misalkan c> 0. Untuk menunjukkan bahwa

( )x , kita ingin membuat selisih 1 1 1

( )x

c x c

(6)

lebih kecil dari  0yang diberikan dengan pengambilan x cukup dekat dengan c > 0. Pertama kita perhatikan bahwa

1 1 1 1

(c x) |x c| x c cx  cx 

Untuk x > 0.

Nia Puspitasari (3115111184)

Untuk . Ini digunakan untuk mendapatkan batas atas untuk syarat _{( )} yang berlaku di beberapa lingkungan c. Khususnya, jika| | , lalu . Jadi

untuk | |

Oleh karena itu, untuk nilai-nilai ini kita memiliki x.

(2) | ( ) | | |

Untuk membuat istilah terakhir kurang dari itu sudah cukup untuk mengambil | | . Dengan konsekuensi jika kita memilih

( ) * +

| ( ) | | |

Sejak kita memilih ( ) untuk sewenang-wenang pilihan dari , kita dapat menyimpulkan bahwa

e.)

misal: ( ) ( ) untuk , lalu beri sedikit manipulasi aljabar | ( ) | | |

( )

| |

(7)

Untuk mendapatkan batas dari koefisien | | kita membatasi x dari kondisi . Untuk x di dalam interval, kita mempunyai dan ( ) ( ) , jadi

| ( ) |

| |

| | Sekarang untuk , kita memilih

( ) * +

Kriteria berurutan untuk Limit

Rumus penting yang mengikuti batas dari suatu fungsi adalah urutan terminologi lmit. Karakteristik ini memperbolehkan teori dari Chapter 3 untuk digunakan dalam pembelajaran limit suatu fungsi.

Teorema 4.1.8 (Kriteria Berurutan)

Misal dan misal c menjadi titik perkumpulan dari A, maka berikut ini setara i)

ii) untuk setiap uruta ( ) di A konvergen untuk c sehingga untuk semua , sebuah urutan ( ( )) konvergen ke L.

Delpi Batubara (3115115698)

4.1.8 Teorema (Sequential Kriteria)

Misalkan f : A ~ R dan misalkan c menjadi titik kumpul di A. Kemudian, berikut ini adalah setara :

(i)

(ii) Untuk setiap barisan (xn ) di A yang konvergen ke c sehingga xn ≠c untuk setiap n є N,

barisan (f(xn)) konvergen ke L.

Bukti :

(i) → (ii). Asumsikan f memiliki limit L di c, dan andaikan (xn) adalah sebuah barisan di A

dengan ( ) dan xn ≠ c untuk semua n. Kita harus membuktikan bahwa barisan (f (xn

(8)

)) konvergen di L.

(ii) → (i). Pembuktian kontradiktif. Jika (i) tidaklah benar,ada sebuah ɛ0 sekitaran Vɛ0

sedemikian hingga berapa pun sekitaran- δ yang kita pilih, akan ada sedikitnya satu

bilangan xδ di A ∩ Vδ(c) dengan xδ≠ c sedemikian hingga (xδ) ≠Vδ(L). Sejak untuk setiap

n є N, sekitaran- (1/n) di c yang terdiri dari sebuah bilangan xn sedemikian hingga:

dan

Kita dapat menyimpulkan bahwa barisan xnkonvergen di c, tapi barisan (f (xn )) tidak

konvergen di L. Sehingga kita telah menunjukkan bahwa jika (i) tidak benar, maka (ii) juga tidak benar. Maka kesimpulannya adalah (ii) implikasi (i).

Kita akan lihat di bagian berikutnya bahwa banyak dari sifat-sifat limit fungsi dasar dapat dibentuk dengan menggunakan properti yang berhubungan untuk barisan konvergen. Sebagai contoh, kita tahu dari pekerjaan kita dengan barisan bahwa jika (xn) adalah setiap

barisan yang konvergen ke bilangan c, maka (xn2) konvergen ke c2.

Anindya Diva P. (3115126496)

4.1.10 contoh

(a)

. / tidak ada di IR.

Seperti pada contoh 4.1.7 (d) ambil φ(x) = 1/x untuk x >0. Namun, di sini kita mempertimbangkan c=0. Argumentasi di contoh 4.1.7 (d) salah jika c = 0 sejak kita tidak dapat memperoleh batas seperti pada contoh itu. Tentunya, jika kita mengambil barisan (xn)

dengan xn=1/n untuk n ϵN, lalu lim(xn) = 0, tapi φ(xn) = 1/(1/n) = n. seperti yang kita tau,

barisan (φ(xn)) = (n) tidak konvergen di R, karena tidak dibatasi. Maka, menurut teori

4.1.9(b),

(9)

Bunyi teori 4.1.9 (b): Fungsi f tidak memiliki limit di c jika dan hanya jika ada barisan (xn) di A dengan xn≠ c untuk semua n ϵ N sehingga barisan (xn) konvergen ke c tetapi barisan

(f (xn)) tidak konvergen di R.

(b)

sgn(x) tidak ada.

Ambil fungsi signum (sgn) didefinisikan sebagai

Sgn (x) = +1 untuk x > 0 0 untuk x = 0 -1 untuk x < 0

Perhatikan bahwa sgn (x) = x/|x| untuk x = 0 F (LihatGambar 4.1.2.) Kami akan menunjukkan bahwas gn tidak memiliki batas pada x = 0. Kita akan melakukan hal ini dengan menunjukkan bahwa ada barisan (xn) seperti lim (xn) = 0, tapi seperti (sgn (xn)) tidak

konvergen.

Ambil xn = ( -1 )n/n untuk n ϵ N sedemikian hingga (xn) = 0. namun, sejak

sgn(xn) = ( -1 )n untuk n ϵ N

hal tersebut seperti pada Contoh 3.4.6 (a) bahwa (sgn (xn)) tidak konvergen. Oleh karena itu

sgn(x) tidak ada.

Contoh 3.4.6 (a) berbunyi: Barisan X = ( -1 )n divergen. Sub barisan X’= (( -1 )2n )= (1,1,..) konvergen ke 1 dan sub barisan X” = (( -1 )2n-1 ) = (-1,-1,...). oleh karena itu, kita simpulkan X divergen.

(c )

sin(1/x) tidak ada di R

Ambil g (x): = sin (1 / x) untuk x ≠0 (Lihat Gambar 4.1.3.) Kami akan menunjukkan bahwa g tidak memiliki limit di c = 0, dengan memperlihatkan dua barisan (xn) dan (yn) dengan xn ≠

0 danYn ≠ 0 untuk semua n ϵ N dan seperti lim (xn) = 0 dan lim (yn) = 0, tapi seperti lim

(10)

Kita mengingat dari kalkulus bahwa sin t = 0 jika t = nπ untuk n ϵ Z, dan sin t = +1 jika t = ½ π + 2πn untuk n ϵ Z. Sekarang ambilxn = 1/nπ untuk n ϵ N sehingga lim (g(xn)) = 0.

Selain itu, ambil yn = (½ π + 2πn) -1 untuk n ϵ N. Lalu lim (yn) = 0 dan (g(yn)) = sin (½ π +

2πn) = 1 untuk semua n ϵ N, sehingga lim (g(yn)) = 1. Kita simpulkan bahwa

sin (1/x)

tidak ada.

Annisa Ramalika Hanani (3115126497)

- Latihan Bagian 4.1

1. Tentukan keadaan pada | | yang akan menjamin bahwa: (a) | |

(b) | |

(c) | | , untuk setiap (d) | | , untuk setiap

2. Tentukan keadaan pada | | yang akan menjamin bahwa: (a) |√ |

(b) |√ |

3. Misalkan c menjadi titik kumpul dari dan .

Buktikan bahwa ( ) jika dan hanya jika | ( ) | .

4. Misalkan dan .

Tunjukan ( ) jika dan hanya jika ( ) 5. Misalkan ( ) dimana , dan ( ) untuk .

(11)

Untuk setiap titik , tunjukan bahwa | ( ) | | |. Gunakan pertidaksamaan ini untuk membuktikan bahwa untuk setiap

6. Misalkan menjadi interval di , , . Tunjukan bahwa ( ) . 7. Tunjukan bahwa untuk

8. Tunjukan bahwa √ √ untuk

9. Gunakan salah satu, definisi limit atau limit “Sequential Criterion”, untuk menentukan limit berikut.

(a)

(b) (c) _{| |} (d)

10. Gunakan definisi limit untuk menunjukan bahwa. (a) ( )

(b)

11. Tunjukan bahwa limit berikut tidak ada. (a) ( )

(b) _√ ( )

(c) ( ( ))

(d) ( )

12. Misalkan fungsi memiliki limit di 0, dan . Jika didefinisikan oleh ( ) ( ) untuk , tunjukan bahwa ( ) .

13. Misalkan dan sedemikian sehingga ( ( )) .

(a) Tunjukan bahwa jika , kemudian ( ) .

(b) Tunjukan dengan contoh bahwa jika , kemudian mungkin tidak punya limit di c.

14. Misalkan didefinisikan melalui pengaturan ( ) jika adalah rasional, dan ( ) jika adalah irasional.

(a) Tunjukan bahwa memiliki limit di .

(b) Gunakan argumen “sequential” untuk menunjukan bahwa jika , kemudian tidak memiliki limit di c.

(12)

15. Misalkan , menjadi interval terbuka di , . Jika dibatasi dari ke , tunjukan bahwa memiliki limit di c jika dan hanya jika memiliki limit di c, dan limit tersebut sama.

16. Misalkan , menjadi interval tertutup di , . Jika dibatasi dari ke , tunjukan jika memiliki limit di c kemudian memiliki limit di c. Tunjukan melalui contoh bahwa tidak ada pengaruh jika memiliki limit di c kemudian memiliki limit di c.

Bagian 4.2, Teorema Limit Definisi 4.2.1

Misalkan , , dan ambil menjadi titik kumpul dari A. Kita mengatakan bahwa dibatasi pada lingkungan c jika setiap lingkungan ( ) dari c dan konstan sedemikian sehingga | ( )| untuk setiap ( ).

Dini Amalia (3115126501)

Teorema 4.2.2

Jika A  R dan f: A R mempunyai limit pada c R, maka f adalah batas beberapa sekitaran pada c.

Bukti :

Jika L , maka untuk , ada beberapa seperti jika | | , maka | ( ) | ; sejak ( digunakannya hukum 2.2.4 (a)).

Hukum 2.2.4 jika a, b  R, maka (a) || | | || | |

| ( )| | | | ( ) |

Oleh karena itu, jika ( ) , maka | ( )| | | . Jika cA, kita ambil M=| | , jika cA kita ambil M := sup {| ( )| | | ++ . Itu mengikuti bahwa jika x∊A∩ ( ), maka | ( )| . Ini menunjukkan bahwa f adalah batas sekeliling ( ) pada c.

Definisi selanjutnya adalah persamaan untuk definisi penjumlahan, pengurangan, perkalian, dan pembagian pada barisan yang diberikan dibagian 3.2 ( Teorema Limit )

(13)

Definisi 4.2.3

Misal AR dan missal f dan g menjadi fungsi yang digambarkan pada A ke R. kita gambarkan penjumlahan f+g, pengurangan f-g, dan perkalian fg pada A ke R menjadi fungsi yang diberikan oleh

(f + g)(x):=f(x) + g(x), (f - g)(x):=f(x) - g(x), (fg)(x):=f(x)g(x)

Untuk semua xA. Selanjutnya jika b R, kita gambarkan perkalian bf menjadi fungsi yang diberikan oleh

(bf)(x):=bf(x) untuk semua x  A

Akhirnya, jika h(x)≠0 untuk x  A, kita gambarkan pembagian f/h menjadi fungsi yang diberikan oleh

. / ( ) _{( )} ( ) untuk semua x  A

Teorema 4.2.4

Misal A  R, misal f dan g menjadi fungsi pada A ke R, dan misal c  R menjadi titik kumpul pada A. Selanjutnya, misal b  R.

(a) Jika , maka :

( ) , ( )

(b) Jika h : A → R, jika h(x) ≠ 0 untuk semua x ϵ A dan jika , maka

( )

Bukti

Satu bukti pada teorema ini adalah sama pada teorema 3.2.3. Sebagai alternative, itu bisa dibuktikan menggunakan teorema 3.2.3 dan 4.1.8. Untuk contoh, misal ( ) adalah sembarang barisan di A seperti

untuk n dan ( ). Itu mengikuti dari teorema 4.1.8 yaitu ( ( )) , ( ( ))

Teorema 3.2.3

(a) Misal dan menjadi barisan bilangan asli yang convergen pada x dan y, berturut-turut, dan misal . Maka barisan barisannya X + Y, X – Y, X . Y dan cX barisan ke x + y, x – y, xy, dan cx, berturut-turut.

(14)

(b) Jika konvergen ke x dan adalah barisan pada bilangan asli bukan nol yang konvergen ke z dan jika maka barisan pembagian X/Z konvergen ke x/z.

Teorema 4.1.8 ( standar contoh )

Misal dan misal c menjadi titik kumpul pada A. maka mengikuti persamaan (i)

(ii) Untuk setiap barisan ( ) di A konvergen ke c seperti untuk semua n barisan ( ( )) konvergen ke L.

Dengan kata lain, definisi 4.2.3 mengimplikasikan bahwa

( )( ) ( ) ( ) untuk n

Oleh karena itu, aplikasi dari teorema 3.2.3 menghasilkan

(( )( )) , ( ) ( )- , ( )-, ( )- Akibatnya, mengikuti dari teorema 4.1.8 bahwa

( ) (( )( ))

Bagian lain pada teorema ini terbukti di persamaan cara. Kita tinggalkan secara detail untuk pembaca.

Keterangan

(1) Kita catat bahwa, di bagian (b), asumsi penjumlahan bahwa adalah

buatan. Jika asumsi tidak benar, maka limit

Mungkin atau tidak mungkin ada. Tetapi tetap jika limit ini ada, kita tidak bisa menggunakan teorema 4.2.4 (b) untuk menghitung itu.

Teorema 4.2.4 (b)

Jika h : A → R, jika h(x) ≠ 0 untuk semua x ϵ A dan jika , maka

( )

(2) Jika A  R, dan missal menjadi fungsi pada A ke R dan misal c menjadi titik kumpul pada A. jika,

(15)

Kemudian mengikuti dari teorema 4.2.4 dengan argument induksi bahwa

Dan

Di keterangan-keterangan, kita menarik kesimpulan bahwa jika dan

n maka

( ( ))

Fahmadiyah Annissa (3115126505)

Contoh 4.2.5

(a) Beberapa dari limit di bagian 4.1 dapat dibuktikan dengan menggunakan Teorema 4.2.4. Sebagai contoh, mengikuti hasil ini bahwa , kemudian dan jika c > 0, maka

(b) ( )( )

Ikuti dari Teorema 2.4.2 bahwa

( )( ) ( ( ))( ( ))

( )( ) 5.4 (c) ( )

Jika berlaku Teorema 4.2.4 b, maka = ( )

( )

Catatan bahwa limit dengan penyebut (i.e ( ) ) tidak sama dengan 0,

maka Teorema 4.2.b berlaku. (d)

Jika diberikan f(x) = dan h(x) = 3x-6 untuk x є R maka tidak dapat digunakan teorema 4.2.4b untuk mengevaluasi ( )_{( )} karena

(16)

Bagaimanapun, jika x ≠ 2, maka

( )( )

( ) ( ) Maka dari itu

( ) ( )

Catatan bahwa fungsi ( ) mempunyai limit di x= 2 meskipun tidak ada definisinya (e) tidak terdapat di R

Tentu saja = 1 dan . Bagaimanapun, ketika H = 0, tidak dapat digunakan teorema 4.2.4b untuk mengevaluasi . Dalam faktanya, lihat contoh

4.1.10a, fungsi ( ) tidak mempunyai sebuah limit di x = 0. Kesimpulan mengikuti juga dari teorema 4.2.2 ketika fungsi( ) tidak terbatas dipersekitaran x = 0

(f) jika p adalah sebuah fungsi polynomial, maka ( ) ( ) Biarkan p menjadi fungsi polynomial di R maka

( ) untuk semua x є R. Berdasarkan Teorema 4.2.4

dan fakta bahwa , maka ( ) , _- ( ) ( ₎ ( ) ( ) = = ( )

Karena ( ) ( ) untuk setiap fungsi polynomial p (g) jika p da q adalah fungsi polynomial di R danjika q(c) ≠ 0 maka

( ) ( ) ( ) ( )

Ketika q(x) adalah sebuah fungsi polynomial, berdasarkan dari sebuah teorema di aljabar bahwa ada paling banyak bilangan terbatas bilangan real [bilangan real nol di q(x)] maka ( ) dan jika ( ), maka q(x) ≠ 0. Karenanya, jika ( ) kita dapat definisikan

( ) ( ) ( )

(17)

Jika c tidak nol di q(x), maka q (c) ≠ 0, dan mengikuti dari bagian (f) bahwa ( ) ( ) . Oleh karena itu kita dapat menerapkan teorema 4.2.4b untuk menyimpulkan bahwa ( ) ( ) ( ) ( ) ( ) ( ) Hasil berikutnya adalah analog langsung dari teorema 3.2.6

Fajar Nur Rahman (3115126506)

Teorema 4.2.6

Diberikan , misalkan suatu fungsi f : A  B (suatu fungsi f dari A memetakan ke B) dan diketahui sebagai titik tumpul pada A. Jika ( ) untuk semua , dan ada, maka

Bukti :

Memang, jika , maka itu mengacu pada teorema 4.1.8 (Teorema Kriteria Pengurutan : misalkan suatu fungsi f : A  B (suatu fungsi f dari A memetakan ke B) dan diketahui sebagai titik tumpul pada A, maka berikut ini ekuivalen dengan : (i) (ii) untuk setiap barisan (xn) pada A dan konvergen ke c sehingga xn ≠ c untuk

semua , maka barisan (f(xn)) konvergen ke L) bahwa jika (xn) adalah beberapa barisan

dari bilangan real sehingga c ≠ xn untuk semua dan jika barisan (xn) konvergen ke

c, maka barisan (f(xn)) konvergen ke L. ketika ( ) untuk semua , maka itu

mengacu pada teorema 3.2.6 (Teorema 3.2.6 : jika ( ) adalan barisan konvergen dan jika ( ) untuk semua , maka ( ) ) bahwa .

Kita dapat berargumen sebuah analogi pada Teorema Apit 3.2.7 (Diketahui bahwa

X=(xn) , Y=(yn), dan Z=(zn) adalah barisan dari bilangan real sehingga xn ≤ yn ≤ zn untuk

semua , dan terdapat lim (xn) = lim (zn). Maka Y=(yn) adalah konvergen dan lim (xn) =

lim (yn) = lim (zn)) (?). Kita tinggalkan pembuktian ini kepada pembaca.

Teorema 4.2.7

Teorema Apit 4.2.7 Diberikan , misalkan suatu fungsi f, g, h: , dan diberikan sebagai titik tumpul dari A, jika ( ) ( ) ( ) untuk semua , dan jika , maka . (?)

(18)

Misalkan ( ) untuk ( ). Sejak pertidaksamaan memenuhi untuk (kenapa?) (?), itu memenuhi bahwa ( ) _untuk

. Sehingga itu memenuhi dari teorema apit 4.2.7 bahwa .

b) .

Itu akan dibuktikan nanti (lihat pada teorema 8.4.8) (Teorema 8.4.8 : Jika ada , maka kita mempunyai : (vii) ( ) (viii) ( ) ; (ix) ( ) ; (x) ( ) ) bahwa

untuk semua

Karena ( ) , itu memenuhi dari Teorema Apit bahwa

c) .

Itu akan dibuktikan nanti (lihat pada teorema 8.4.8) (ada di bagian b teoremanya) bahwa

untuk semua

Karena . / , itu memenuhi dari Teorema Apit bahwa

d) . /

Kita tidak dapat menggunakan teorema 4.2.4 (b) (Diberikan , misalkan f dan g adalah sebuah fungsi A ke , dan terdapat sebagai titik tumpul dari A. Selanjutnya, misalkan ; (a) Jika dan , maka memenuhi : (i) ( ) (ii) ( ) (iii) ( ) (iv) . (b)

Jika ada h: A jika ( ) untuk semua , dan jika , maka . / ) untuk menyelesaikan limit ini (kenapa tidak?) (?). bagaimanapun, itu memenuhi dari pertidaksamaan (1) pada bagian (c) bahwa

( ) untuk Dan bahwa

( ) untuk

Sekarang misalkan ( ) untuk dan ( ) untuk , serta juga misalkan ( ) untuk dan ( ) untuk . Kemudian kita mempunyai ( ) ( ) ( ) untuk

(19)

Sejak itu mudah terlihat bahwa memenuhi dari Teorema Apit bahwa . /

e) . /

Kembali lagi kia tidak dapat menggunakan teorema 4.2.4(b) untuk menyelesaikan limit ini. Bagaimanapun itu akan dibuktikan nanti (lihat Teorema 8.4.8) (Teorema 8.4.8 : Jika ada , maka kita mempunyai : (vii) ( ) (viii) ( ) ; (ix) ( ) ; (x) ( ) ) bahwa

untuk dan bahwa

untuk

Kesimpulannya memenuhi (kenapa?) bahwa ( ) untuk semua

Tetapi semenjak . / ( ) kita kembalikan lagi dari

Teorema Apit bahwa . /

Lazuardi Fajar P. (3115126514) (f) 0 1 lim .sin 0 x x _x  _{  }    _{ }   Misalkan f x =

 

x.sin 1 x    

  untuk x0. Karena  1 sinz1 untuk setiap zR ,

kita mempunyai pertidaksamaan

 

1 .sin x f x x x x      _{ }  

untuk setiap xR x, 0. Karena 0

lim 0

x x  , hal ini didapat dari Teorema Apit bahwa

0

lim 0

x f  . Untuk grafiknya, lihat Gambar 5.1.3 atau sampul buku ini.

Ada beberapa hasil yang berhubungan dengan Teorema 3.2.9 dan 3.2.10; hanya saja, kami akan menjadikannya latihan. Kami menyimpulkan bagian ini dengan sebuah hasil yang, dalam beberapa arti, sebagian kebalikan dari Teorema 4.2.6.

(20)

4.2.9 Teorema

Misalkan AR , misalkan f A: R dan misalkan cR adalah sebuah gugusan titik. Jika

lim 0 , lim 0

xc f respectively xc f

 

 _  _

maka ada sebuah daerah V c_

 

dari csehingga f x

 

0, _respectively f x,

 

0_ untuk setiap x A V c x_

 

, c. Bukti. Misalkan : lim x c L f 

 dan andaikan L0. Kita ambil 1 0 2L

   pada Definisi 4.1.4, dan mendapatkan sebuah angka  0 sehingga jika 0  x c  dan xA , maka

 

1

2

f x  L L . Untuk itu (kenapa?) didapat bahwa jika x A V c x_

 

, c, maka

 

1

0 2

f x  L

Jika L0 , sebuah argumen yang sama terjadi. Latihan Bagian 4.2

12. Misalkan f R: R sedemikian hingga f x



y



 f x

 

 f y

 

untuk setiap x y, di R . Asumsikan bahwa

0 lim

x f L ada. Buktikan L0 , lalu buktikan bahwa f mempunyai

limit di setiap titik cR .

[Petunjuk: pertama, perhatikan bahwa f

 

2x  f x

   

 f x 2f x

 

untuk setiap xR

. Perhatikan juga bahwa f x

 

 f x c



 



f c

 

untuk , di x c R.]

Putri Rijkiyah (3115126519)

13. Misal , , dan sebagai titik cluster dari A. Jika ada,

14. Misal , , dan sebagai titik cluster dari A. Selain itu, asumsikan bahwa ( ) untuk semua , dan misalkan √ merupakan sebuah fungsi

(21)

yang didefinisikan untuk oleh (√ ) √ ( ). Jika ada, buktikan bahwa √ √

Bagian 4.3: beberapa perpanjangan dari konsep limit

Di bagian ini, kita akan menyajikan tiga jenis ekstensi dari gagasan tentang limit dari suatu fungsi yang sering muncul. Karena semua ide di sini erat sejajar dengan apa yang telah kami sajikan, bagian ini dapat dibaca dengan mudah.

Limit satu sisi

Ada kalanya fungsi f mungkin tidak memiliki limit pada titik c, namun limit itu ada ketika fungsi dibatasi dalam selang di satu sisi pada titik cluster c.

Contohnya, fungsi signum berdasarkan contoh 4.1.10 (b) yang diilustrasikan pada gambar 4.1.2, tidak memiliki limit ketika c=0. Namun, jika kita batasi fungsi signum pada selang ( ), fungsi itu menghasilkan limit yang bernilai 1 ketika c=0. Sama halnya saat kita batasi fungsi signum pada batas ( ), fungsi itu menghasilkan limit yang bernilai -1 ketika c=0. Ini adalah contoh dasar dari limit kanan dan kiri ketika c=0.

4.3.1 Definisi

Misal dan

i. Jika adalah titik cluster dari himpunan ( ) * + kemudian kita katakan bahwa adalah suatu limit kanan dari f pada titik c dan kita tulis:

( )

Jika diberikan ada sebuah ( ) sehingga untuk semua dengan , kemudian | ( ) |

ii. Jika adalah titik cluster dari himpunan ( ) * + kemudian kita katakan bahwa adalah suatu limit kiri dari f pada titik c dan kita tulis:

(22)

Jika diberikan ada sebuah sehingga untuk semua dengan , kemudian | ( ) |

Catatan

(1) dan dikatakan limit satu sisi dari f pada c. Mungkin saja kedua limit satu sisi itu tidak ada. Dan juga, mungkin saja salah satu darinya ada walaupun yang lain tidak ada. Sama halnya, pada kasus ( ) ( ) ketika , mereka mungkin ada dan berbeda.

(2) Jika A adalah selang dengan titik pangkal kiri c, kemudian lebih mudah terlihat bahwa mempunyai limit di c jika dan hanya jika dia mempunyai limit kanan di c. Selain itu, pada kasus ini dan limit kanan adalah sama. (situasi yang sama

muncul untuk limit kiri ketika A adalah selang dengan titik pangkal kanan c.)

Pembaca dapat menunjukkan bahwa f dapat mempunyai hanya satu limit kanan pada suatu titik (begitupun yang kiri). Ada hasil yang sesuai dengan bagian yang telah ditetapkan pada bagian 4.1 dan 4.2 untuk limit dua arah. Khususnya, keberadaan dari limit satu sisi dapat dikurangi untuk pertimbangan yang berurutan

Retno Kusuma P. (3115126523)

Theorem 4. 3. 2

Ambil A c R, jika suatu fungsi f : A → R, dan ambil c 𝞊 R menjadi titik kumpul dari A (c,∞). Lalu pernyataan- pernyataan yang equivalen :

(i)

(ii) Untuk setiap barisan ( ) itu konvergen ke c seperti 𝞊 A dan > c untuk semua n 𝞊 N, barisan (f < ) konvergen ke L.

Kita tinggalkan bukti dari hasil ini (dan rumus serta bukti dari hasil untuk batas disisi kiri) untuk pembaca. Kita tidak akan berikan jarak untuk menulis rumus dari satu sisi dari hasil lainnya di sub bab 4. 1 dan 4. 2.

Hasil berikutnya berhubungan dengan notasi dari batas fungsi ke batas satu sisi. kita tinggalkan bukti diatas sebagai latihan.

(23)

Theorem 4. 3. 3

Ambil A c R, jika suatu fungsi f : A → R, dan ambil c 𝞊 R menjadi titik kumpul dari kedua himpunan A ∩ (c, ∞) dan A ∩ (-∞, c). Lalu jika dan hanya jika

Contoh 4. 3. 4

(a) Ambil f(x) := sgn(x).

Kita lihat contoh 4. 1. 10 (b) itu sgn tidak punya limit di 0. Hal tersebut jelas bahwa ( ) ( ) Sejak limit disatu sisi berbeda, yang juga mengikuti dari theorem 4. 3. 3 bahwa sgn(x) tidak punya limit di 0.

(b) Ambil g(x) := ⁄ _{untuk x ≠ 0. ( lihat gambar 4. 3. 1.)}

1

x Gambar 4. 3. 1 Grafik dari g(x) = ⁄ _{( x ≠ 0).}

Pertama kita tunjukkan g tidak punya batas sisi kanan yang berhingga di c = 0 karena tidak dibatasi disetiap lingkungan kanan (0, δ) dari 0. Kita akan memanfaatkan ketidaksamaan

(1) 0 < t < e' . untuk t > 0,

Yang mana akan dibuktikan kemudian (lihat kesimpuan 8. l. l). itu diikuti dari (1) jika x > 0, lalu 0 < 1/x < ⁄ . Oleh karena itu, jika kita ambil x,. = 1/n, lalu g(x,.) > n untuk semua n

𝞊 N. Oleh karena itu, ⁄ _{tidak ada di R.}

Namun, ⁄ . Memang, jika x < 0 dan kita ambil t = -1/x di (1) kita memperoleh 0 < -1/x < ⁄ . Sejak x < 0, ini diimplikasikan bahwa 0 < ⁄ < -x untuk

(24)

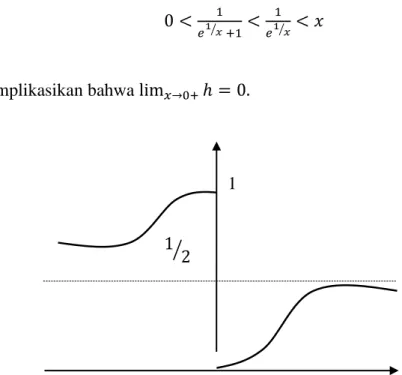
(c) Ambil h(x) := 1/( ⁄ ) untuk x ≠ 0. (lihat gambar 4. 3. 2.) Kita lihat dibagian (b) bahwa 0 < 1/x < ⁄ untuk x > 0, yang mana

_⁄

⁄

Yang mana dimplikasikan bahwa

1

⁄

Gambar 4. 3. 2. Grafik dari h(x) = 1/( ⁄ + 1) (x ≠ 0).

Riska Ramanda S. (3115126524)

Karena kita telah melihat di bagian (b) bahwa maka dari analog Teorema 4.2.4 (b) untuk batas kiri bahwa

Perhatikan bahwa untuk fungsi ini, baik batas satu sisi ada di R, tetapi mereka tidak sama.

Limit Tak Berhingga

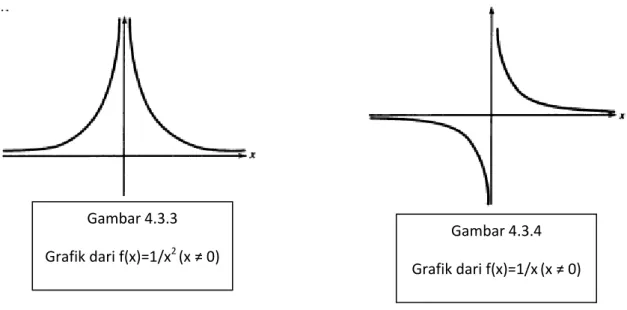
Fungsi f(x):= 1/x2 untuk x ≠ 0 (lihat gambar 4.3.3) tidak dibatasi oleh kitaran 0, sehingga tudak bisa mempunyai sebuah limit dalam arti definisi 4.14. sementara simbol ∞ (=+∞) dan -∞ tidak mewakili bilangan ril, itu terkadang berguna untuk dapat mengatakan bahwa “f(x)= 1/x2 _{menuju ∞ sebagai x}_{0”. Penggunaan +∞ tidak akan menimbulkan}

(25)

kesulitan, asalkan kita berhati-hati dan tidak pernah menafsirkan ∞ atau -∞ sebagai bilangan ril.

Definisi 4.3.5

Anggap dan anggap c R menjadi titik cluster A. (i) Kita katakan bahwa f menuju ke ∞ sebagai x c, ditulis:

Jika untuk setiap ada ( ) sehingga untuk semua | | ( )

(ii) Kita katakan bahwa f menuju -∞ sebagai x c, dan ditulis:

Jika untuk setiap ada ( ) sehingga untuk semua | | ( )

Contoh 4.3.6

(a) ( )

Untuk, jika diketahui, anggap √ . Oleh karena itu jika | | maka sehingga 1/x2 _>

(b) Misalkan g(x) := 1/x untuk x ≠ 0 (lihat gambar 4.3.4)

Gambar 4.3.3 Grafik dari f(x)=1/x2 (x ≠ 0)

Gambar 4.3.4 Grafik dari f(x)=1/x(x ≠ 0)

(26)

Fungsi g tidak menuju ∞ maupun -∞ sebagai x 0. Sebab, jika a> 0 maka g(x) < untuk semua x < 0, sehingga g tidak menuju ∞ sebagai x 0. Sama halnya, jika < 0 maka g(x) > untuk semua x > 0, sehingga g tidak menuju -∞ sebagai x 0

Sementara itu banyak dari hasil di bagian 4.1 dan 4.2 memiliki ekstensi untuk membatasi ini, tidak smeua dari mereka lakukan sejak ±∞ adalah bukan bilangan ril. Hasil berikutnya adalah analog dari Teorema Squeeze 4.2.7 (lihat juga Teorema 3.6.4)

Teorema 4.3.7

Misalkan anggap f,g: A R dan anggap C R menjadi titik cluster A. Anggap bahwa f(x) < g(x) ntuk semua

(a) Jika , maka (b) Jika , maka Bukti.

(a) Jika dan diketahui , maka ada ( ) sehingga jika

| | ( ) dan , maka f(x) > . tapi sejak f(x) < g(x) untuk semua , selanjutnya bahwa jika | | ( ) dan maka g(x) > . Sehingga .

Pembuktian (b) serupa.

Fungsi g (x) = 1 / x dipertimbangkan dalam Contoh 4.3.6 (b) menunjukkan bahwa mungkin berguna untuk mempertimbangkan satu sisi limit tak berhingga. Kami akan menentukan hanya batas kanan limit tak berhingga.

Definisi 4.3.8

Misalkan dan misalkan f : A R. jika c R adalah titik cluster dari himpunan maka kita sebut bahwa f menuju ke ∞ [berturut-turut, - ∞] sebagai x c dan kita tulis

(27)

Jika untuk setiap ada ( ) sehingga untuk semua dengan maka ( ) , ( ) -

Safrielanita Deya W. (3115126526)

Contoh 4.3.9

(a) Ambil ( ) ⁄ Kita memiliki catatan di contoh 4.3.6(b) bahwa tidak ada. Bagaimanapun, ini adalah soal yang mudah untuk membuktikan

( ) ⁄ dan ( ⁄ ) .

(b) Ini sudah ditunjukkan di contoh 4.3.4 bahwa fungsi ( ) ⁄ _{for tidak dibatasi}

dengan semua interval ( ) . Dimana limit kanan dari ⁄ _{dengan tidak ada}

dengan esensi dari Definisi 4.3.1(i) bagaimanapun, saat ⁄ ⁄ untuk sudah terlihat bahwa ⁄ _{sesuai dengan Definisi 4.3.8.}

(Definisi 4.3.1 Ambil A dan ambil .

(i) Jika adalah titik kumpul dari himpunan ( ) * + maka dapat dikatakan bahwa adalah limit kanan dari di c dan tulis

( )

jika diberikan semua terdapat sebuah ( ) sedemikian untuk semua dengan maka | ( ) | )

Limit di Tak Hingga

Ini juga diperlukan sekali untuk member definisi dari limit sebuah fungsi sebagai . Definisi sebagai adalah sama.

Definisi 4.3.10

Ambil dan ambil Andaikan ( ) untuk sebagian Kita dapat mengatakan bahwa adalah limit dari dan ditulis

( )

jika diberikan semua disana ada ( ) seperti itu untuk semua lalu | ( ) |

Pembaca harus mencatat kemiripan antara 4.3.10 dan definisi dari limit sebuah deret. Kami meninggalkan ini untuk pembaca untuk membuktikan limit dari unik sewaktu-waktu saat mereka ada. Kami juga memiliki criteria contoh untuk limit ini;

(28)

itu dapat hanya dalam keadaan . Ini dapat digunakan notasi dari limit sebuah deret divergen yang pantas

(lihat Definisi 3.6.1 Ambil (xn) sebuah deret bilangan-bilangan riil.

(i) Dapat dikatakan bahwa (xn) cenderung menuju dan tulis ( ) jika

untuk semua disana terdapat sebuah bilangan asli K(α) sedemikian jika ( ) maka

(ii) Dapat dikatakan bahwa (xn) cenderung menuju dan tulis lim( ) jika

untuk semua disana terdapat sebuah bilangan asli K(β) sedemikian jika ( ), maka

Dapat dikatakan bahwa (xn) adalah divergen dengan wajar dalam kasus kita

memiliki salah satu dari ( ) ( ) .)

Teorema 4.3.11

Ambil , ambil , dan andaikan ( ) untuk beberapa . Lalu pernyataan berikut setara:

(i)

(ii) Untuk semua deret (xn) di ( ) sedemikian bahwa lim(xn) = , deret (

(xn)) konvergen ke L.

Ditinggalkan untuk pembaca untuk membuktikan teorema ini dan untuk memformulasi dan membuktikan hasil kawan mengenai limit dengan .

Warih Pratiwi (3115126530)

Contoh 4.3.12

(a) Ambil ( ) ⁄ .

Ini soal dasar untuk membuktikan bahwa ( ) ⁄ ( ) ⁄ (Lihat Gambar 4.3.4)

(29)

(b) Ambil ( ) ⁄

Pembaca sebaiknya membuktikan bahwa ( ⁄ ) ( ⁄ ) (Lihat Gambar 4.3.3)

Satu langkah yang dilakukan ini adalah untuk membuktikan jika ⁄ ⁄ Dapat dilihat bagian (a), ini menyatakan bahwa ( ⁄ ) .

Hanya sebagai ini tepat untuk dapat dikatakan bahwa ( ) sebagai ini sesuai untuk memiliki hubungan dugaan sebagai ini dapat memperlakukan kasus dimana .

Definisi 4.3.13

Ambil , ambil , dan andaikan ( ) untuk beberapa . Dapat dikatakan bahwa cenderung untuk , - sebagai , dan ditulis

, -

.jika diberikan semua disana terdapat ( ) sedemikian untuk semua maka ( ) , ( ) -.

Seperti sebelumnya ada kriteria yang berurutan untuk limit ini.

Teorema 4.3.14

Misalkan , misalkan dan anggaplah bahwa ( ) untuk beberapa Kemudian pernyataan berikut adalah sama (equivalent):

i. ,

-

ii. Untuk setiap urutan ( ) di ( ) seperti lim( ) , kemudian lim( ( )) , ( ( )) -

(30)

Teorema 3.6.5

Misalkan ( ) dan ( ) sebagai urutan dari bilangan real positif dan anggaplah bahwa untuk beberapa , kami mempunyai

(2) ( )

Kemudian ( )= + jika dan hanya jika ( )= + Bukti. Jika (2) berlaku, terdapat seperti

, untuk semua

Maka kami memiliki . / ( ) untuk semua .

Teorema 4.3.15

Misalkan , misalkan dan anggaplah bahwa ( ) untuk beberapa

Misalkan lebih lanjut bahwa ( ) untuk semua dan untuk beberapa , kami mempunyai

( )

i. Jika maka jika dan hanya jika ii. Jika maka jika dan hanya jika

Bukti

i. Sejak hipotesis menunjukkan bahwa ada sehingga ( )_{( )} untuk setiap

Oleh karena itu kami memiliki . / ( ) ( ) ( ) ( ) untuk semua , dari kesimpulan yang didapat

bukti ii serupa

Kami menyerahkan kepada pembaca untuk merumuskan hasil analog seperti

Arum Wulandari (3115115684)

4.3.16 Contoh

(31)

misal g(x) := xn untuk x {0, ), , misal K sup{1, }. Untuk semua x > K,

kita mempunyai g (x) = xn x > . karena adalah sebarang, oleh karena itu

= .

(b) lim xn for n , n bilangan genap, and lim xn = - for n , n bilangan ganjil.

Akan kita buktikan n bilangan ganjil, n = 2k+1 dengan k = 0, 1, · · ·. Diketahui , misal

K inf{ , -1}. Untuk setiap x < K, kemudian karena (x 2)k 1, kita memiliki xn = (x 2)k x

x < .

karena adalah sebarang, oleh karena itu lim xn

= - .

(c) misalkan p: fungsi polinomial.

p(x) := anxn + an-1 xn-1 + ... + a1x + a0.

ketika = if an > 0, dan = - jika an < 0.

benar, misal g(x} := xn dan menerapkan teorema 4.3.15. karena

Oleh karena itu lim (p{x)/g(x)) =an. Since lim g = , penegasan ini mengikuti dari

teorema 4.3.15.

(d) misalkan p adalah fungsi polinomial pada bagian (c). ketika lim p = [berturutan, - ]

Jika n adalah bilangan genap [berturutan, bilangan ganjil] and an > 0.

Latihan

1. Buktikan teorema 4.3.2.

2. Berikan sebuah contoh fungsi yang memiliki batas kanan tapi tidak memiliki batas kiri pada titik

3. Misalkan . ( ) | | for Tunjukan bahwa ( ) ( )

(32)

4. Misalkan c dan misalkan f didefinisikan untuk x (c, ) dan f(x) > 0 untuk semua

x (c, ). Tunjukan bahwa jika dan hanya jika .

5. Evaluate the following limits, or show that they do not exist.

7. Misalkan f dan g memiliki limits in R as x dan f (x) g (x) untuk semua x (a, ). Buktikan bahwa

8. Misal f didefinisikan pada (0, ) untuk . Buktikan bahwa ( ) jika dan

hanya jika . /

9. Tunjukan jika f: (a, ) sedemikian sehingga ( ) dimana , ketika ( )

11. Misalkan ( ) dimanaL > 0, dan ( ) . Tunjukan bahwa

( ) ( ) . Jika L = 0, tunjukan dengan contoh bahwa kesimpulan ini mungkin gagal.

12. Cari fungsi f and g pada (0, ) sedemikian sehingga dan . dan ( ) . Dapatkah anda menemukan fungsi tersebut, dengan g(x) >

0 untuk semua x (0, ), sedemikian sehingga . /

13. Misal f dan g pada (a, ) dan misalkan dan l .Buktikan bahwa