Materi Lengkap Fungsi Eksponen dan Logar

(1)

Materi Lengkap Fungsi Eksponen dan

Logaritma

Posted On July 20, 2013 | Under Category: Fungsi Eksponen dan Logaritma advertisements

Rumus matematika yang kali ini akan saya paparkan yaitu tentang eksponen dan logaritma, pasti temen-temen sudah pernah mendengarnya, atau bahkan telah mempelajarinya disekolah.

1. Fungsi Eksponen

Bentuk an_{disebuat sebagai bentuk eksponensial atau perpangkatan, dengan a disebut basis atau}

bilangan pokok dan n disebut eksponen atau pangkat. Eksponen memiliki sifat – sifat sebagai berikut :

Bentuk umum dari fungsi eksponen yaitu y = ax_{dimana a ≥ 0 dan a ≠ 1}

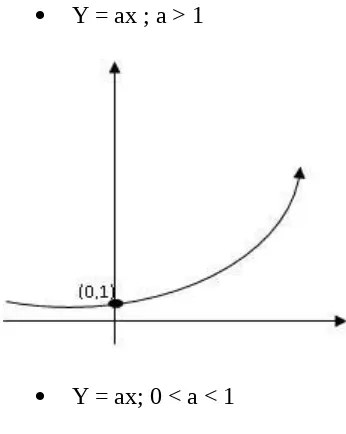
a. Grafik fungsi y = ax_{, untuk 0 < a < 1}

Mempunyai sifat-sifat sebagai berikut :

1. Terdefinisi untuk semua x Rϵ

2. Jika x mempunyai nilai kecil dan negatif maka sebaliknya y bernilai besar dan positif.

3. Jika x mempunyai nilai besar dan positif maka y mendekati nol dan positif.

(2)

Gambar Grafik Fungsinya sebagai berikut :

2. Fungsi Logaritma

Bentuk eksponen atau perpangkatan dapat kita tulis dalam bentuk logaritma. Secara umum dapat ditulis sebagai berikut :

Jika ab_{= c dengan a > 0 dan a ≠ 1 maka}a_{log c = b dalam hal ini a disebut basis atau pokok}

logaritma dan c merupakan bilangan yang dilogaritmakan. Logaritma memuliki sifat-sifat sebagai berikut :

Bentuk umum dari fungsi logaritma yaitu Jika a_{= x dengan a ≥0 dan a ≠ 1 maka y =}y a_{log x}

2.1. Grafik Fungsi y =a_{log x untuk 0 < a < 1}

contoh :

mempunyai sifat-sifat :

1. semua x > 0 terdefinisi

(3)

3. untuk x=1 maka y=o

4. untuk x > 1 maka y negatif sehingga jika nilai x semakin besar maka nilai y semakin kecil.

Berikut ini gambar grafiknya.

2.2. Grafik Fungsi y =a_{log x untuk a > 1}

contoh :

mempunyai sifat – sifat sebagai berikut :

1. untuk semua x > 0 terdefinisi

2. jika x mendekati no maka y kecil sekali dan negatif

3. untuk x=1 maka y=0

4. untuk x > 1 maka y positif sehingga jika x semakin besar maka y semakin besar.

(4)

FUNGSI, PERSAMAAN DAN PERTIDAKSAMAAN EKSPONEN, LOGARITMA

Standar Kompetensi

5. Merancang dan menggunakan model matematika program linear serta menggunakan sifat dan aturan yang berkaitan dengan barisan,deret, matriks, vektor, transformasi, fungsi eksponen, dan logaritma dalam pemecahan masalah.

Kompetensi Dasar

5.1 Menggambarkan grafiik dan menggunakan sifat- sifat fungsi eksponen dalam pemecahan masalah

5.2 Menggunakan sifat- sifat fungsi eksponen dalam penyelesaian pertidaksamaan eksponen

5.3 Menggambarkan grafik dan menggunakan sifat- sifat fungsi logaritma dalam pemecahan masalah

5.4 Menggunakan sifat- sifat fungsi eksponen dalam penyelesaian pertidaksamaan eksponen

Indikator

1. Menentukan penyelesaian persamaan eksponen

2. Menjelaskan sifat-sifat fungsi eksponen yang digunakan dalam proses penyelesaian persamaan eksponen.

3. Menentukan penyelesaian pertidaksamaan eksponen

4. Menjelaskan sifat-sifat fungsi eksponen yang digunakan dalam proses penyelesaian pertidaksamaan eksponen.

5. Menjelaskan sifat-sifat fungsi logaritma yang digunakan dalam proses penyelesaian persamaan logaritma.

6. Menentukan penyelesaian persamaan logaritma.

(5)

8. Menjelaskan sifat-sifat fungsi logaritma yang digunakan dalam proses penyelesaian pertidaksamaan logaritma

A. Tujuan Pembelajaran Peserta didik dapat

 Menjelaskan sifat-sifat fungsi eksponen yang digunakan dalam proses

penyelesaian persamaan eksponen;

 Menentukan penyelesaian persamaan eksponen;

 Menentukan penyelesaian persamaan logaritma.

 Menjelaskan sifat-sifat fungsi logaritma yang digunakan dalam proses

penyelesaian persamaan logaritma

 Menjelaskan sifat-sifat fungsi logaritma yang digunakan dalam proses

penyelesaian pertidaksamaan logaritma

 Menentukan penyelesaian pertidaksamaan logaritma

B.Materi Pembelajaran

 Fungsi dan Persamaan Eksponen

 Pertidaksamaan Eksponen

 Fungsi dan Persamaan Logaritma

(6)

(7)

(8)

(9)

(10)

(11)

GRAFIK FUNGSI EKSPONEN

Fungsi eksponen merupakan pemetaan bilangan real x ke ax dengan a > 0 dan a ≠ 1. jika a > 0 dan a ≠ 1, x Є R maka f : x ax atau f (x) = ax_{atau y = a}x_{disebut fungsi}

eksponen.

Fungsi eksponen y = f (x) = ax_{; a > 0 ; a ≠ 1 mempunyai sifatt – sifat}

( i ). Kurva terletak diatas sumbu x (definit positif)

( ii ). Memotong salib sumbu hanya di titik (0,1)

( iii ). Mempunyai asimtot datar y = 0 sumbu x)

( iv ). Monoton naik untuk a > 1

( v ). Monoton turun untuk a < a < 1.

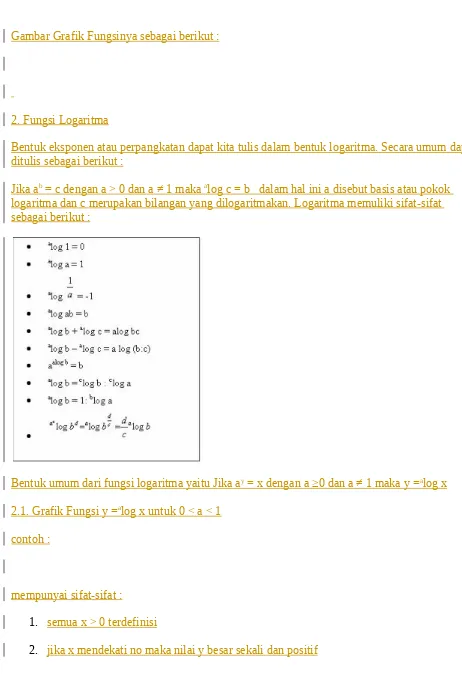
Grafik fungsi eksponen y = ax

 Y = ax ; a > 1

(12)

GRAFIK FUNGSI LOGARITMA

Secara umum fungsi logaritma dapat ditulis dengan a > 0 dan a ≠ 1. grafik dari fungsi logaritma y = a log x mempunyai sifat:

( i ). Berada disebelah kanan sumbu x; (terdefinisi untuk x > 0)

( ii ). Memotong salib sumbu di (1 , 0)

( iii ). Mempunyai asimtot tegak x (sb. Y)

( iv ). Monoton naik untuk a > 1

( v ). Monoton turun untuk 0 < a < 1.

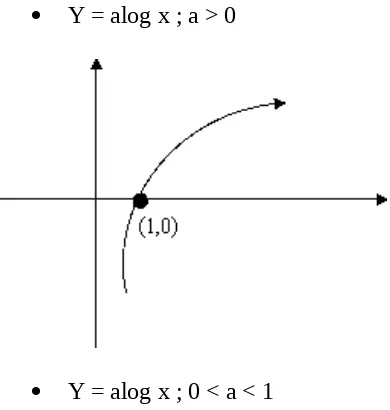
Grafik fungsi logaritma y = a log x.

 Y = alog x ; a > 0

(13)