APLIKASI COMPRESSIVE SENSING UNTUK ESTIMASI ARAH KEDATANGAN SINYAL PROPOSAL DISERTASI

APLIKASI COMPRESSIVE SENSING UNTUK

ESTIMASI ARAH KEDATANGAN SINYAL

PROPOSAL DISERTASI

diajukan untuk memenuhi syarat kelulusan Mata Kuliah EI7096:Penyusunan Proposal

Institut Teknologi Bandung

Oleh

Koredianto Usman

NIM : 33213002

(Program Studi Teknik Elektro dan Informatika)

ABSTRAK

APLIKASI COMPRESSIVE SENSING UNTUK ESTIMASI

ARAH KEDATANGAN SINYAL

Oleh

Koredianto Usman

NIM : 33213002

Proposal ini berisi tentang rencana penelitian penggunaan teknik compressive

sensing untuk pengurangan sinyal pada skema estimasi arah kedatangan sinyal.

Algoritma penentuan arah sinyal klasik secara umum terdiri dari dua skema besar yaitu skema yang berbasis maximum likelihood (Delay and Sum dan Capon) dan skema berbasis sub-space (MUSIC dan ESPRIT). Pada perkembangannya, algoritma yang berbasis sub-space memperoleh perhatian yang besar di kalangan peneliti karena kemampuan mendeteksi beberapa sumber sekaligus dengan resolusi pemisahan yang tinggi. Meski memiliki keunggulan ini, algoritma estimasi arah kedatangan berbasissub-spacememiliki permasalahan komputasi berat yang antara lain disebabkan karena proses perhitungan matriks kovariansi, analisis eigen dan

exhaustive search pada arah kedatangan. Evolusi dan modifikasi pada algoritma

berbasis sub-space umumnya berupa modifikasi pada penyederhanaan komputasi pada sisi penyederhaan dan transformasi nilai eigen dari kompleks ke real. Modifikasi ini kemudian dituangkan dalam algoritma baru seperti Root-MUSIC, Unitary MUSIC, Beamspace-MUSIC, Unitary ESPRIT, dan Beamspace ESPRIT. Perkembangan pada bidang compressive sensing membuka arah yang berbeda dalam penyederhanaan skema yaitu dengan cara pengurangan sampel. Terdapat tiga jenis teknik popular dalam teknik compressive sensing untuk estimasi arah kedatangan sinyal, yaitu teknik sparsitas waktu, sparsitas spasial, dan sparsitas sudut. Teknik sparsitas sudut menjadi fokus dalam penelitian ini karena teknik ini dapat mengestimasi arah kedatangan sinyal dengan satu sampel saja. Meski demikian, masih terdapat kekurangan dari skema ini, yaitu sensitif terhadap

noise. Perbaikan yang diusulkan adalah memperluas algoritma ini agar dapat

mengakomodasi multi-snap sampel. Hasil simulasi awal menunjukkan perbaikan akurasi estimasi pada lingkungan dengan SNR kurang dari 5 dB. Pengembangan lainnya adalah penanganan hasil estimasi yang jauh menyimpang (outliers) untuk meningkatkan akurasi lebih tinggi lagi.

Kata kunci : direction of arrival estimation, compressive sensing, convex

APLIKASI COMPRESSIVE SENSING UNTUK ESTIMASI

ARAH KEDATANGAN SINYAL

Oleh

Koredianto Usman

NIM : 33213002

(Program Studi Teknik Elektro dan Informatika)

Institut Teknologi Bandung

Menyetujui Tim Pembimbing

Tanggal 13 Mei 2014

Ketua Anggota

(Prof. Dr. Andriyan Bayu Suksmono) (Prof. Dr. Hendra Gunawan)

DAFTAR ISI

ABSTRAK i

DAFTAR ISI ii

I PENDAHULUAN 1

I.1 Latar Belakang . . . 1

I.2 Rumusan Masalah . . . 3

I.3 Tujuan . . . 3

I.4 Kontribusi dan Dampak Penelitian . . . 4

II KAJIAN LITERATUR 6 II.1 Estimasi Arah Kedatangan Sinyal . . . 6

II.1.1 Model Matematika . . . 6

II.1.2 Algoritma Klasik Estimasi arah Kedatangan . . . 8

II.2 Compressive Sensing . . . 15

II.2.1 Terminologi PadaCompressive Sensing . . . 16

II.2.2 Model Matematik . . . 19

II.3 Compressive SensingPada Estimasi Arah Kedatangan . . . 21

III METODOLOGI 23 III.1 Persiapan Data . . . 23

III.2 Persiapan Lingkungan Simulasi . . . 25

III.3 Simulasi . . . 27

III.4 Analisis Perfomansi . . . 28

III.5 Skema yang ditinjau . . . 29

V.2 Simulasi perbandingan dengan algoritma klasik . . . 34

BAB I

PENDAHULUAN

I.1

Latar Belakang

Estimasi arah kedatangan sinyal merupakan salah satu tugas yang dikerjakan radar di samping dua tugas lainnya yaitu estimasi jarak dan kecepatan objek. Dengan demikian teknik estimasi arah kedatangan memiliki usia setua usia radar. Estimasi arah kedatangan memfokuskan diri pada tugas menentukan sudut kedatangan sinyal. Pada sistem yang lebih maju, estimasi arah kedatangan sinyal disyaratkan untuk mampu mendeteksi arah kedatangan beberapa sumber sekaligus.

Pada perkembangannya, radar mula-mula dikembangkan pada kapal laut untuk keperluan mendeteksi objek penghalang di depan kapal termasuk keberadaan kapal lain yang ada di sekitar. Pada masa Perang Dunia I dan II, radar berkembang sangat pesat untuk kebutuhan pertahanan. Setelah Perang Dunia II, perkembangan radar diarahkan untuk memenuhi kebutuhan sipil seperti kelengkapan sistim monitor udara di bandara.

Memasuki era digital, teknik pengolahan sinyal berubah dari analog menjadi digital. Pada masa ini berkembang teknik estimasi arah kedatangan yang maju yang membuka jalan bagi berbagai perkembangan teknologi radar canggih pada masa kini. Beberapa aplikasi terbaru di bidang ini adalah sistem ground penetrating

radar (GPR) dan through the wall radar (TTWR). Ground penetrating radar

adalah sistem radar yang digunakan untuk mendeteksi benda di bawah permukaan tanah, sedangkanthrough the wall radaradalah teknik radar yang digunakan untuk mendeteksi benda atau manusia yang berada di balik dinding.

Teknik estimasi arah kedatangan termasuk salah satu aplikasi dariarray processing

yang memiliki sejarah yan cukup panjang. Sebagai contoh, Capon mengusulkan skema estimasi arah kedatangan sinyal pada publikasinya tahun 1969 [1]. Usulan dari Capon ini selanjutnya menjadi popular sebagai algoritma Capon atau

Minimum Variance Distortionless Respons (MVDR). Di sisi lain Applebaum

resolusi yang tinggi.

Meski memiliki resolusi yang tinggi, algoritma MUSIC memiliki kekurangan utama pada beratnya proses komputasi. Permasalahan komputasi terletak pada

eigen analysis dari matriks kovariansi kompleks serta exhaustive search pada

semua sudut kedatangan. Permasalahan ini membuat para peneliti lain berupaya untuk memodifikasi algoritma MUSIC ini untuk menghindari proses perhitungan

eigen analysis. Alternatif lainnya adalah melakukan transformasi matriks

kovariansi kompleks menjadi matriks kovariansi riil, sehingga eigen analysis

dapat dilakukan pada lingkungan bilangan riil yang lebih cepat dibandingkan dengan lingkungan bilangan kompleks. Skema modifikasi dengan transformasi ini menghasilkan algoritma varian dari MUSIC yang disebut dengan Unitary-MUSIC [4]. Transformasi yang mengubah matrik kovariansi dari kompleks menjadi riil ini dipelopori oleh Anna Lee dalam tulisannya tentang centro-hermitian matrix [5]. Penggunaannya untuk keperluan penyederhaan matrik kovariansi kompleks telah dilakukan oleh Huarng, peneliti beamforminglainnya dari Taiwan [6]. Modifikasi lain yang dilakukan adalah melakukan proyeksi matriks kovariansi pada dimensi yang lebih kecil. Skema ini kemudian menghasilkan algoritma varian lainnya yaitu Root-MUSIC [7].

Roy et al. [8] melakukan pendekatan berbeda dalam upaya mengurangi kompleksitas komputasi, bukan pada upaya untuk menyederhanakan perhitungan

eigen analysis, tapi pada sudut pandang bahwa susunan linier dapat dibagi dalam

dua sub-array identik dengan yang satu adalah pergeseran linier dari yang lain.

Dengan cara pandang ini, Roy et al. menghindari proses perhitungan exhaustive

searchyang terdapat pada algoritma MUSIC. Algoritma ini terkenal dengan nama

ESPRIT (Estimation of Signal Parameter via Rotational Invariant Techniques). Peneliti lain mengkombinasikan algoritma ESPRIT ini dengan upaya pengurangan perhitungan eigen analysis seperti halnya algoritma MUSIC, sehingga muncul varian baru dari ESPRIT yaitu Unitary ESPRIT [9] dan Beam ESPRIT [10].

Di antara penelitian tersebut, skema yang diajukan oleh Goronitsky dan Rao [14] banyak menarik perhatian dari peneliti lain. Dengan asumsi bahwa sinyal yang datang memiliki sifatsparsedalam arah kedatangan, Goronitsky dan Rao berhasil mengunakan satu sampel sinyal saja untuk mengestimasi arah kedatangan sinyal. Meski memiliki sifat yang menjanjikan ini, skema Goronitsky dan Rao memiliki kekurangan pada sensitifitas padanoise. Perbaikan dari kekurangan ini merupakan fokus dari penelitian yang diajukan ini.

I.2

Rumusan Masalah

Arah baru dari penyederhanaan komputasi dari skema estimasi arah kedatangan sinyal dilakukan dengan pengurangan sampel menggunakan teknik compressive sensing [11], [12]. Penelitian di bidang ini antara lain adalah dengan algoritma FOCUSS [14], time-spatial CS [16], dan compressive MUSIC [18]. Meskipun teknikcompressive sensingini tampak menjanjikan, namun terdapat permasalahan

inherentterhadap sampel yang sedikit yaitu ketahanan terhadapnoiseyang rendah [19]. Pada lingkungan dengan noise yang tinggi, seperti redaman sinyal akibat hujan atau sinyal melewati penghalang alam seperti hutan, akurasi estimasi arah kedatangan menurun secara signifikan. Penurunan ini berdampak pada kesalahan penentuan arah kedatangan sinyal. Perbaikan yang diusulkan pada penelitian ini adalah penggunaan skema multi-snap sampling untuk mengkompensasi pengaruh

noisetersebut. Teknikmulti-snap sampling ini lebih lanjut dapat ditingkatkan lagi akurasinya dengan teknikoutliers removal. Teknikoutliers removalmengacu pada pembuangan hasil estimasi yang jauh menyimpang dari nilai rata-rata hasil estimasi.

I.3

Tujuan

Tujuan utama dari penelitian ini adalah mencapai skema compressive sensing

1. memahami dan mensimulasikan skema-skema klasik dari estimasi arah kedatangan sinyal,

2. memahami dan mensimulasikan teknik-teknikcompressive sensing,

3. memahami dan mensimulasikan penggabungan teknik compressive sensing

dengan skema estimasi arah kedatangan sinyal,

4. memahami dan mensimulasikan pengaruhnoisedalam penggabungan teknik

compressive sensingdan skema estimasi arah kedatangan sinyal tersebut,

5. memperbaiki, memodifikasi, mengusulkan teknik compressive sensingbaru agar penerapannya pada skema estimasi arah kedatangan sinyal menghasilkan skema yang tahan terhadapnoise,

6. membandingkan kinerja skema yang dihasilkan dengan skema estimasi arah kedatangan klasik.

I.4

Kontribusi dan Dampak Penelitian

Penelitian penerapan teknik compressive sensing pada skema estimasi arah kedatangan sinyal dimaksudkan untuk mengurangi jumlah sampel yang diperlukan untuk menentukan arah kedatangan sinyal. Dengan jumlah sampel yang sedikit, maka sistem radar yang bekerja pada jaringan terdistribusi akan semakin mudah diimplementasikan. Jumlah sampel yang sedikit juga memungkinkan untuk menempatkan unit-unit radar pemantau di daerah dengan terpencil dengan

bandwidth komunikasi yang sangat terbatas. Kontribusi penelitian ini dapat

dituliskan dalam poin-poin berikut:

1. memodifikasi skema yang ada agar dapat bekerja pada lingkungan dengan

noisetinggi,

2. memperluas skema yang ada dari teknik satu sampel menjadi multi-sampel (multi snap),

3. memperluas kajian dan pengembangan dari skemacompressive sensingyang ada,

Adapun penelitian ini diharapkan memberikan dampak antara lain:

1. membuka peluang pengimplementasian skema estimasi arah kedatangan sinyal dengan jumlah sampel yang sangat sedikit,

2. membuka peluang sistem radar dengan topologi tersebar, dengan unit jauh yang hanya bertugas mengumpulkan sedikit data sehingga menghemat energi dan sumber daya,

3. membuka peluang sistem radar yang dapat bekerja denganbandwidthsempit yang biasanya terdapat di daerah-daerah terpencil.

BAB II

KAJIAN LITERATUR

Pada bagian kajian literatur ini, akan dibahas tiga macam kajian literatur yaitu kajian literatur tentang algoritma estimasi arah kedatangan sinyal, kajian literatur tentang

compressive sensing, dan kajian tentang penerapan teknik compressive sensing

untuk aplikasi estimasi arah kedatangan sinyal. Pada setiap bagian, akan dibahas literatur-literatur dari setiap skema serta literatur-literatur terkait lainnya. Sebelum pembahasan tentang kajian literatur tersebut dilakukan, landasan teori serta model matematisnya diperkenalkan terlebih dahulu.

II.1

Estimasi Arah Kedatangan Sinyal

II.1.1

Model Matematika

Skema estimasi arah kedatangan sinyal diturunkan dari model matematik dilanjutkan dengan penyederhanaan-penyederhaannya. Untuk keperluan pemodelan ini, ditinjau susunanarrayantena yang berupa elemen antena isotropis yang disusun secara linier dengan jarak konstan (Gambar II.1). Susunan antena ini disebut dengan

Uniform Linear Array(ULA). Dengan asumsi bahwa sinyal datang pada jarak yang

yang relatif jauh maka berkas sinyal yang datang pada susunan antena tersebut dapat dianggap sejajar.

a1

a2

a3

a_M d

d

Gambar II.1: Contoh Susunan ULA

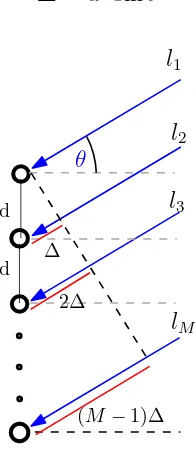
sebesar:

∆ =d·sinθ (II.1)

d

d

θ

l1

l2

l3

l_M

∆

2∆

(M−1)∆

Gambar II.2: Sistem ULA dengan satu sumber datang pada sudutθ.

Perbedaan jarak ini menyebabkan keterlambatan fasa sebesar:

ψ = 2·π

λ ·d·sinθ (II.2)

Dengan menotasikan sinyal sumber sebagai s(n) dan sinyal yang datang pada antena berturut-turut sebagai x1(n), x2(n) dan x3(n) , maka persamaan vektor

sinyal datangx(n)dapat ditulis dalam vektor menjadi:

x(n) =

   

1

e−j·2π

λ ·d·sin(θ)

e−j·2π

λ ·(N−1)·d·sin(θ)   

·s(n) (II.3)

Persamaan di atas disingkat menjadi:

x(n) =a(θ)·s(n) (II.4)

menjadi M, makasteering-vectora(θ)dapat ditulis sebagai:

a(θ) =

       1

e−j·2π

λ ·d·sin(θ) .. .

e−j·2π

λ ·(N−1)·d·sin(θ)        (II.5)

Pada kondisi terdapat beberapa sumber yang datang (k), maka persamaan sinyal sumber juga dapat digeneralisasi menjadi:

s(n) = s1(n) s2(n) · · · sk(n)

T

(II.6)

II.1.2

Algoritma Klasik Estimasi arah Kedatangan

Algoritma estimasi arah kedatangan sinyal yang dijadikan referensi pada penelitian ini adalah empat macam algoritma estimasi arah kedatangan klasik yang populer:

Algoritma Delay-and-Sum (DAS), algoritma Minimum Variance Distortionless

Response (MVDR), algoritma Multiple Signal Classification (MUSIC), dan

algoritma Estimation of Signal Parameters via Rotational Invariance Technique

(ESPRIT). Bagian selanjutnya akan mendiskusikan detail dari masing-masing algoritma tersebut.

Algoritma DAS

Algoritma estimasi arah kedatangan dengan metode delay-and-sum ini termasuk algoritma klasik dan menjadi acuan bagi perkembangan skema estimasi arah kedatangan. Metode ini dimodelkan pertama kali oleh Sidney P. Applebaum [2]. Veen [20] memformulasikan kembali skema DAS dalam kajiannya tentangversatile adaptive beamformer. Struktur dari algoritma DAS dapat dilihat pada Gambar II.3.

Pada Gambar II.3, pada setiap cabang sinyal terima xi(n), terdapat M buah tap

delay dengan bobot w1, sampai wM. Setelah melalui masing-masing bobot ini,

maka sinyal akan melewati delay D. Pada skema DAS, estimasi arah kedatangan dilakukan dengan scanning semua bobot yang mungkin dengan arah scanning

pada rentang sudut tertentu, tipikalnya adalah dari −90 sampai90derajat. Proses

scanning secara praktikal dilakukan dengan men-set nilai bobot w sama dengan

D

w₁

x₁

x_M

w_M

D

Σ

y

Gambar II.3: Skema DAS, diadaptasi dari [21]

scanningdapat dituliskan sebagai:

P(w) =

M

X

i=1

wi·xi(n) (II.7)

Arah kedatangan sinyal diestimasi sebagaibθpada nilaiwyang menyebabkanP(w)

bernilai maksimum.

b

θ

→

maxP(w)P(w) =

M

X

i=1

wi·xi(n) (II.8)

Nilaix(n)adalah vektor sinyal terima seperti yang dinyatakan pada Persamaan II.4.

Skema delay and sum ini memiliki keuntungan dalam hal kesederhanaan. Kesederhanan ini tergambar pada skema di penerima yang hanya terdiri dari proses delay dan sum. Alasan kesederhanaan juga yang menyebabkan skema

delay and sum sering menjadi pilihan implementasi untuk berbagai aplikasi,

baik radio [21] maupun audio [22]. Walau pun memiliki keuntungan pada sisi kesederhanaannya, algoritma ini memiliki kelemahan. Kelemahan ini antara lain adalah rendahnya kemampuan resolusi sinyal. Resolusi rendah berimplikasi bahwa algoritma tidak dapat mendeteksi adanya dua sinyal yang memiliki arah kedatangan yang berdekatan. Kelemahan lainnya adalah sensitifitas sinyal terhadap noisedan interferensi [23].

Algoritma MVDR

dari matriks kovariansi yang disusun dari vektor sinyal terima. Vektor sinyal terima

x(n) dikumpulkan seperti Persamaan II.4. Matriks kovariansi dari sinyal terima dihitung dengan persamaan:

Rxx =

x(n)·xH_(n)

N (II.9)

Algoritma Capon dapat dituliskan sebagai berikut:

1. hitung matriks kovariansiRxx dari vektor sinyal datangx(n)

2. Hitung invers dari matrix kovariansiRxx(R

−₁

xx)

3. bangkitkansteering vektora(θ)seperti Persamaan II.5 untuk suatu sudutθ.

4. Hitung spektrum sinyal P(θ) untuk setiap nilai θ dari 0 sampai360 derajat dengan persamaan (exhaustive search).

5. Tentukan arah kedatangan sinyal dengan mengambil nilai θ sehingga P(θ) bernilai maksimal.

Dari sisi performa, para peneliti menemukan dua kekurangan utama dari algoritma Capon yaitu komputasi yang berat dan rentan terhadap interferensi dari jammer

yang berkorelasi dengan sinyal. Komputasi yang berat dikontribusi oleh tiga hal yaitu perhitungan matriks kovariansi (langkah 1), perhitungan invers matriks kovariansi (langkah 2), dan exhaustive search (langkah 4). Perhitungan matriks kovariansi memiliki kompleksitas O(n2_{). Kompleksitas perhitungan inversi matrik}

memiliki komputasi yang berat [24]. Ada pun pengaruh interferensi terhadap algoritma Capon diteliti oleh Zoltowski [25]. Pada paper tersebut, Zoltowski menunjukkan sensitifitas dari algoritma MVDR Beamforming pada kasusmultiple

interference. Performa sistem menurun dengan drastis pada kondisi interferensi

tersebut.

Algoritma MUSIC

peneliti selama beberapa dekade. Keberhasilan algoritma ini dalam mendeteksi beberapa sumber sekaligus dengan resolusi yang sangat tinggi menjadi daya tarik utama dari algoritma ini. Algoritma MUSIC termasuk pelopor dalam penggunaan

eigen-analysis sehingga sering disebut eigen-assisted based algorithm. Basis dari algoritma ini adalah proses dekomposisi matriks kovariansi ke dalam vektor eigen

dan nilai eigen. Proses dekomposisi ini dapat dinyatakan dengan persamaan:

Rxx =U·Σ·UH (II.10)

Dimensi dari matrikRxx,Σ, danUadalahM xM, denganM adalah jumlah antena dalamarray. MatriksΣadalah matriks diagonal dengan elemen diagonal berisi nilai

eigen. Σ =       

λ1 0 · · · 0

0 λ2 · · · 0

..

. ... . .. ...

0 0 · · · λM

      

=diagλ1 λ2 · · · λM

(II.11)

Pada Persamaan II.11 di atas, terdapat R buah nilai eigen dominan (R ≤< M) yang berkorespondensi dengan R sumber sinyal yang datang [3]. Sisa nilai eigen (M-R) menyatakan nilai eigen tak dominan. Jika nilai eigen pada matrikΣdiurutkan dari yang terbesar ke yang terkecil, maka matrik U dapat dipartisi secara kolom menjadiUsdanUn. Oleh karena nilai eigen dominan dan tak dominan berturut-turut berkorespondensi dengan sinyal dannoise, maka Us danUn berturut-turut disebut

signal subspacedannoise subspace.

U =Us Un

(II.12)

Selanjutnya, oleh karena setiap kolom dalam matrikU adalah salingorthonormal,

maka inner-product dari setiap kolom pada Us dan Un bernilai nol. Dengan

mengingat bahwa steering vector pada arah kedatangan aktual adalah kombinasi linear kolom vektor padaUs, maka

a(θ)H·Un·a(θ) = 0 (II.13)

MUSIC sebagai:

P(θ) = 1

a(θ)H_·U

n·a(θ)

(II.14)

Denganθ dihitung pada semua sudut yang dipindai. Arah kedatangan ditunjukkan pada nilaiθyang memaksimalkanP(θ).

Algoritma MUSIC, dengan teori yang dijelaskan di atas, dirangkum dalam langkah-langkah berikut:

1. hitung matriks kovariansiRxx dari vektor sinyal datangx(n)

2. hitung dekomposisi eigen dariRxx seperti Persamaan II.10

3. bangkitkansteering vektora(θ)seperti Persamaan II.5 untuk suatu sudutθ.

4. hitung spektrum sinyalP(θ) seperti Persamaan II.14 untuk setiap nilaiθdari

0sampai360derajat (exhaustive search).

5. tentukan arah kedatangan sinyal dengan mengambil nilai θ sehingga P(θ) bernilai maksimal.

Analisis performa algoritma MUSIC telah banyak dilakukan oleh para peneliti (Kaveh dan Barabell [26]; Stoica and Nehorai [27]). Kaveh dan Barabell melakukan pengujian performa algoritma MUSIC dengan parameter kemampuan resolusi MUSIC dengan dua sinyal datang pada lingkungan yang memiliki

noise. Hasil simulasi menunjukkan bahwa MUSIC memiliki performa yang

buruk pada lingkungan dengan noise tinggi. Stoica dan Nehorai melakukan pengujian performansi algoritma MUSIC dengan menghitung jaraknya dengan batas minimum yang dapat dicapai dari suatu nilai estimasi yaitu Cramer-Rao

Bound (CRB). Penelitiannya menunjukkan bahwa algoritma MUSIC memiliki

performa yang hampir berimpit dengan untuk SNR yang tinggi.

Algoritma ESPRIT

Skema ESPRIT diperkenalkan oleh Roy, Paulraj, dan Kailath [8]. Skema ini mengambil pendekatan berbeda jika dibandingkan dengan algoritmaDAS,MVDR,

danMUSIC. Jika algoritmaDAS,MVDR, dan MUSICmelakukan prosesscanning

sudut pada semua kemungkinan(exhaustive search), maka algoritma ESPRIT tidak melakukan hal tersebut, melainkan memanfaatkan struktur yang disebut dengan

rotational invariantdari susunan ULA. Strukturrotational invariantadalah struktur pembagianarrayantenna menjadi 2sub-array, sedemikian rupa sehingga salah satu

sub-arrayadalah versi tergeser spasial dari sub-array lainnya.

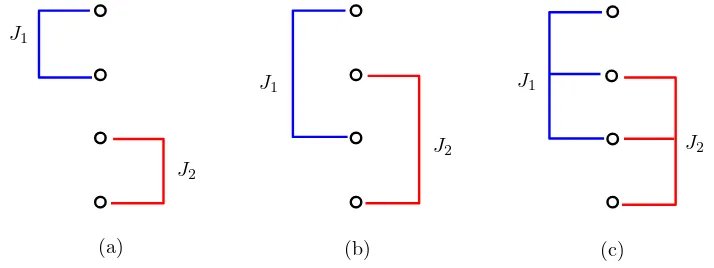
Gambar III.4 memperlihatkan contoh susunan ULA dan pengelompokannya ke dalam dua sub-array yang memenuhi sifat sifat ini. Gambar (a), (b), dan (c) menunjukkan pembagian array antena menjadi sub-array J1 dan J2. Kedua

sub-arrayadalah identik, dengan yang satu adalah pergeseran linier dari yang lain.

(a) (b) (c)

J₁

J₂

J₁

J₂

J₁

J₂

Gambar II.4: Pembagian array 4 antena menjadi dua sub-array yang bersifat

rational invariant. (a) dan (b) menunjukkan dua sub-array dengan dua antena

sedangkan (c) menunjukkan tiga antena dalamsub-array.

Sinyal yang diterima pada sub-array 1 adalah sama dengan sinyal yang diterima

dari sub-array 2 dengan perbedaan pada selisih waktu kedatangan. Dengan

memanfaatkan selisih waktu kedatangan ini, Roy et al. pada [8] berhasil merumuskan algoritma untuk memperoleh arah kedatangan sinyal. Pembagian

arrayutuh menjadi duasub-array ini dapat dinyatakan denganselection vector J. Sebagai contohselection vectorJ1danJ2pada Gambar III.4.(a) berturut-turut dapat

dinyatakan dengan:

J1 =



1 0 0 0

0 1 0 0



J2 =



0 0 1 0

0 0 0 1



 (II.16)

Seperti halnya algoritma MUSIC, algoritma ESPRIT memanfaatkan analisiseigen

dari matrik kovariansi. Pembagian nilai eigen menjadi komponen dominan dan komponen tak dominan yang berkorespondensi dengan signal subspace Us dan

noise subspace Un. Lebih lanjut, algoritma ESPRIT menghitung signal subspace

pada masing-masing sub-array. Signal subspace sub-array 1 dan sub-array 2

berturut-turut dihitung dengan

Us1 =J1·Us (II.17)

Us2 =J2·Us. (II.18)

Urutan estimasi arah kedatangan sinyal dengan algoritma ESPRIT dapat dirangkum dalam langkah-langkah berikut (langkah 1 dan adalah sama dengan langkah pada algoritma MUSIC):

1. hitung matriks kovariansiRxx dari vektor sinyal datangx(n)

2. hitung dekomposisi eigen dariRxx seperti untuk menghasilkan matrikΣdan

U

3. partisi matrikU menjadiUs dan Un sesuai dengan nilai eigen dominan dan tak dominan.

4. Tetapkanselection vectorJ1danJ2

5. Hitung sinyalsubspacedarisub-arrayJ1danJ2 (Persamaan II.17 dan II.18)

6. hitung matrikrotational invariant

Ψ =Us+1·Us2 = (UsH1·Us1)

−1

·UsH1·Us2. (II.19)

7. lakukan dekomposisi pada matrikΨdan tentukan nilai eigen dominan

8. estimasi sudut kedatangan dengan kedatangan dihitung dengan persamaan:

θi =tan

−1

im(λi)

re(λi)

Variabel λi menyatakan nilai eigen dominan ke-i dari matrikΨ, sedangkan operator im(.) dan re(.) berturut-turut menyatakan bagian imaginer dan

realdari bilangan kompleks

Modifikasi dan perbaikan algoritma ESPRIT banyak dilakukan oleh para peneliti. Sebagian besar modifikasi tersebut ditujukan untuk mengurangi atau menghindari perhitungan eigen analysis yang biasanya melibatkan perhitungan bilangan kompleks dalam dimensi yang besar, lainnya berupaya untuk menyederhanakan perhitungan yang melibatkan bilangan komplek. Xu [10] mengusulkan skema Beamspace ESPRIT yang berfokus pada upaya penyederhanaan eigen analysis. Huarng [6] memanfaatkan hasil penelitian Lee [5] tentang matrikcentro-hermitian, mengajukan transformasi unitary untuk mengubah nilai kompleks menjadi nilai riil. Hasil ini menginspirasi Martin Haardt untuk melakukan upaya penyederhanaan perhitungan bilangan kompleks dengan transformasi unitary. Hasil modifikasi ini diberi nama Unitary ESPRIT [9].

II.2

Compressive Sensing

Dalam dunia digital, diperlukan langkah digitalisasi untuk mengubah sinyal analog menjadi sinyal digital. Proses utama adalah langkah digitalisasi adalah sampling. Proses sampling adalah proses mencuplik sinyal analog secara periodik dengan suatu interval tertentu. Perioda antar sampel telah diteliti orang dan dituangkan dalam berbagai paper. Teori sampling klasik dipelopori oleh Harry Nyquist [29]. Teori ini kemudian dikembangkan pula oleh Claude Shannon yang terkenal dalam paper klasiknya [30]. Teorema sampling Nyquist-Shannon ini menyatakan bahwa

frekuensi sampling minimumharus memenuhi:

FSM = 2·fmax (II.21)

Pada Persamaan II.21,FSM adalah frekuensi sampling minimum, danfmax adalah frekuensi maksimum yang dibawa oleh sinyal informasi. Sebagai contoh, sinyal analog yang berasal dari suara manusia, memiliki frekuensi maksimum 3.400 Hz. Dengan demikian frekuensi sampling minimum yang diperlukan untuk digitalisasi adalah 6.800 sampel / detik.

yang banyak terjadi karena sinyal secara periodik harus di-sampling. Sebagai contoh, untuk suara manusia di atas, dalam satu detik terdapat 6.800 sampel. Dengan demikian dalam satu menit terdapat 60 x 6.800 sampel atau 408.000 sampel. Permasalahan redudansi terjadi jika sinyal yang disampling memiliki pola teratur.Sebagai contoh sinyal sinusoidal dengan frekuensi 1 MHz, memerlukan frekuensi sampling 2 juta sampel per detik. Di sisi lain, mensampling sinyal sinusoidal 1 menit tidak memberikan informasi tambahan dibandingkan dengan mensampling sinyal sinusoidal 1 detik.

Permasalahan teori sampling klasik ini, khususnya permasalahan kedua, yang melahirkan teori sampling baru yang disebut compressive sampling atau

compressive sensing. Compressive Sensingmengambil asumsi bahwa sinyal yang

disampling bersifat sparse. Sparse atau sparsitypada sinyal menunjukkan bahwa sinyal hanya memiliki sedikit komponen signifikan. Sisa komponen adalah nol. Sebagai contoh dari sinyal sparse adalah sinyal yang memiliki sangat sedikit nilai tak nol dan sisanya bernilai nol. Contoh lain adalah sinyal sinusoidal dan sinyal periodik (sinyal gergaji, sinyal persegi periodik, dan sebagainya). Teori

compressive sensing dimulai dengan asumsi sparsitas sinyal ini. Publikasi pionir di bidang ini antara lain adalah David L Donoho [11] dan Emmanuel Candes [12]. Sedangkan aspek teknis dan aplikasi banyak diteliti dan dikembangkan oleh Candes dan Richard Baraniuk [13]. Mengingat penelitian compressive sensing

tersebar di berbagai bidang, beberapa peneliti merangkum perkembangan dan potensi compressive sensing dalam survey paper, antara lain oleh Strohmer [31] dan pada bidang sistem komunikasi oleh Hayashi et al. [32].

II.2.1

Terminologi Pada Compressive Sensing

Sebelum membahas model matematis daricompressive sensing, maka perlu dibahas terlebih dahulu beberapa terminologi yang terkait dengan teknik CS. Terminologi ini antara lain adalah sparsitas sinyal, norm, measurement matrix, dan sifat

restricted isometric property. Terminologi-terminologi ini dijelaskan di berbagai literatur CS ([11], [12], dan [13]). Hayashi et al. meresume terminologi ini secara sistematis dalam paper survei tentang CS ([32]).

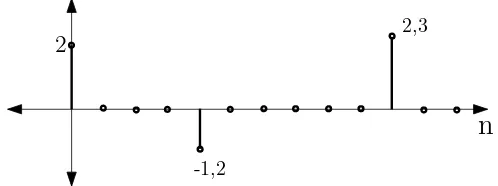
menunjukkan contoh sinyalsparsedengan tingkat sparsitas 3.

n

2

-1,2

2,3

Gambar II.5: Contoh sinyalsparsedalam domain waktu

Sinyal yang sparse dalam domain waktu dapat dilihat langsung dari plot sinyal. Banyak jenis sinyal lain yang tidak sparse dalam domain waktu, namun sparse

dalam suatu basis lain. Sebagai contoh sinyal sinusoidal, sinyal ini tidak sparse

pada domain waktu, namun sparse pada domain frekuensi. Jika sinyal x bersifat

sparsedalam basisΨ, dapat didekomposisi menjadi:

x= Ψ·xˆ (II.22)

Denganxˆadalah sinyalsparsedalam domain waktu.

Norm. Jikax(n)menyatakan sinyal pengamatan pada waktu ndari1sampaiN,

x(n) = [x1, x2,· · · , xN], makanorm orde-p(p non-negatif) darix(n) dinyatakan dengan:

|x|_p = p v u u

tN

−1

X

0

xp_{(n) (II.23)}

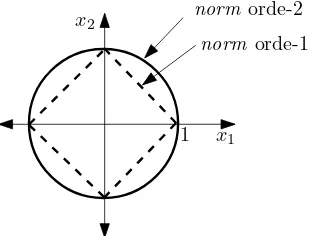
Simbol |.| menyatakan nilai absolut. Tiganormyang sering dipakai pada CS adalah

normorde-0 (l0),normorde-1 (l1), dannormorde-2 (l2).Normorde-0 menyatakan

jumlah elemen tak nol pada sinyal. Normorde-1 menyatakan jumlah absolut dari elemen tak nol pada sinyal, sedangkan norm orde-2 menyatakan jarak euclidean

yang dibentuk oleh pada sinyal. Gambar II.6 menunjukkan arti geometris dari norm orde-1 dan orde-2 dari sinyalxdengan dua elemenx1danx2.

Measurement matrix. Measurement matrix adalah terminologi penting pada

CS. Measurement matrix sering disebut juga sebagai sensing matrix. Matrik ini

berfungsi untuk mengurangi jumlah sampel sinyal semula. Jika matrik semula x

1 x₁ x₂

norm orde-2

normorde-1

Gambar II.6: Ilustrasinormorde-1 dannormorde-2.

menjadimelemen (m<n), maka diperlukan danmeasurement matrix Aberdimensi

m xn. Sinyal hasily diperoleh dengan mengalikan sinyalxdenganmeasurement matrix A.

y=A·x (II.24)

Pada Persamaan II.24, sinyalyberdimensimx1, matriksAberdimensimxn, dan matrikxberdimensinx1. Sinyalxdisebut sebagai sinyal asli dan sinyalxdisebut sinyal pengukuran.

Restricted Isometric Property - RIP. Permasalahan lain yang penting pada CS adalah memilih measurement matrix A sedemikian sehingga sinyal asli x dapat dikembalikan dari pengukuran y. Emmanuel Candes [12] menurunkan syarat dari

measurement matrix A yang disebut dengan RIP. Suatu measurement matrix A

dikatakan bersifat RIP jika memenuhi kondisi:

(1−δs)· |x|₂ ≤ |A·x|₂ ≤(1 +δs)· |x|₂ (II.25)

Denganδs adalah suatu bilangan kecil. Sifat RIP ini secara geometris menyatakan bahwanorm orde-2 dari vektor x sebelum dan setelah transfromasi tidak berubah banyak.

II.2.2

Model Matematik

Tujuan dari CS adalah melakukan sampling dari sinyal sparse x(n) sehingga diperoleh sinyal hasil sampling y(n) yang memiliki jumlah sampel yang lebih sedikit dari x(n). Pengurangan sampel ini dilakukan sedemikian sehingga dimungkinkan untuk memperoleh kembali sinyal asli x(n) melalui proses rekonstruksi. Proses sampling ini dinyatakan dengan Persamaan II.24 untuk suatu matriks compressivemeasurement matrixA.

Permasalahan rekonstruksi yang harus dipecahkan adalah, jika y(n) adalah hasil CS sertameasurement matrixA diberikan, bagaimana memperoleh kembali sinyal x(n) ini.

Algorima Penyelesaian CS.

Terdapat 2 skema utama dalam menyelesaikan masalah rekonstruksi, yaitu: basis pursuit(BP) dangreedy.

Basis Pursuit (BP). Algoritma BP banyak dikembangkan oleh kelompok Terence Tao, Justin Romberg, dan Emmanuel Candes ([33], [33], dan [34]). Permasalahan

compressive sensing seperti pada Persamaan II.24 diselesaikan secara BP dengan

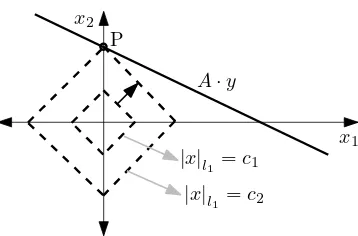
mencari kombinasi x, yang memenuhi norm orde-1 minimal. Secara matematis, konstrain penyelesaian BP dapat dituliskan sebagai:

ˆ

x_l

1 =argmin

x |x| subject to A·x=y (II.26) Penyelesaian dari Persamaan II.26 dengan BP adalah mencari semua kemungkinan nilai yang meminimalisasi|x|l1. Untuk kondisi dua dimensi (x(n) = [x1 x2]), maka

permasalahan BP dapat diilustrasikan seperti pada Gambar II.7.

Secara analitis permasalahan BP diselesaikan denganLinear Programming. Justin Romberg [35] menyelesaikan permasalahan BP dengansoftwarel1−M agic. Variasi

lain dari penyelesaian BP adalah dengan Convex Programming. Skema berbasis

convex programming ini dikembangkan oleh Stephen Boyd [36] bekerja untuk

x₁ x₂

A·y

|x|l 1 =c1 |x|l

1 =c2 P

Gambar II.7: Ilustrasi solusi CS dengan BP untuk 2 variabel

Algoritma Greedy. Skema algoritma greedy secara teori dipelopori oleh Friedman dan Stuetzle [37] dalam kajiannya tentang regression projection pursuit

sebagai penyelesaian dari persamaan linier. Mallat dan Zhang [38] selanjutnya menggunakan dasar dari projection pursuit tersebut untuk menyelesaikan persamaan linier dalam kajiannya tentang time-frequency matching pursuit. Istilah

matching pursuit dipakai oleh Mallat dan Zhang untuk menggambarkan proses

mencari basis dari sinyal. Basis ini disusun dalam suatu dictionarydengan jumlah elemen biasanya melebihi kebutuhan (over complete dictionaries). Istilah basis ini pada literatur lain disebut juga denganatom(Chen et al.[39]).

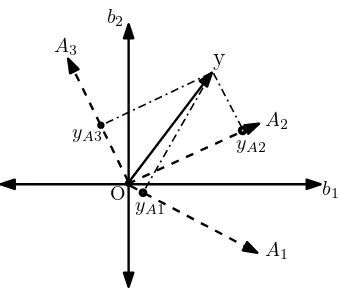
Permasalahan compressive sensing sebagai mana yang direpresentasikan pada Persamaan II.24, pada skema greedy, dipandang sebagai permasalahan kombinasi linier dari setiap kolom (basis) dari measurement matrix A, dengan kombinasi menggunakan koefisien pada x. Skema greedy melakukan langkah invers dari kombinasi linier ini. Proses inversi ini dimulai dengan mencari basis terdekat dari

A yang paling dekat dengan vektor pengukuran y. Basis terdekat diambil sebagai basis memberikan hasil proyeksiyyang terbesar. Nilai proyeksi dikalikan kembali dengan y dan dikurangkan dengan basis yang dipilih menghasilkan residu. Basis terdekat berikutnya dicari dari proyeksi residu ini ke basis tersisa. Demikian proses ini diulangi sehingga nilai residu lebih kecil dari suatu nilaithreshold. Gambar II.8 mengilustrasikan proses mencari basis ini.

Pada Gambar II.8, diasumsikan measurement matrix A sebagai A = [A1 A2 A3]

sehingga terdapat tiga basis yaitu A1, A2, A3. Proyeksi y pada A1, A2, dan A3

menghasilkanyA1, yA2, dan yA3. Pada gambar tersebut, terlihat bahwa basis yang

terpilih adalahA2, karena panjangyA2 dariO adalah yang paling besar.

A1

A2

A3

y

y_A1

y_A2

y_A3

b1

b2

O

Gambar II.8: Ilustrasi Matching Pursuit dengan tiga basis

Tropp memformulasikan skema OMP sebagai berikut:

1. inisialisasi proses dengan basisA1,A2, ...An, dan residu awalr1 =y

2. pilih basis Ai yang memaksimalkan inner product: max(< Aj, ri >) untuk semuaj

3. hitung residuriuntuk iterasi berikutnya:ri =ri−1−< A_i, r_i > ·r_i

4. ulangi langkah 2 dan 3 di atas sampai nilai residu lebih kecil dari suatu

threshold

Skema lain yang termasuk dalam kategori greedy adalah skema Focal

Underdetermined Problem Solver (FOCUSS). Algoritma ini diusulkan oleh

Goronitsky dan Rao [14] dalam kajiannya tentang solusi persamaan linear yang melibatkan teknik sparsitas. Skema FOCUSS menggunakan teknik proyeksi

pseudo-inverse sebagai ganti dari proyeksi inner product yang digunakan pada

algoritma OMP.

II.3

Compressive Sensing Pada Estimasi Arah Kedatangan

Secara umum, penerapan compressive sensing pada algoritma estimasi arah kedatangan dapat dikelompokkan berdasarkan tiga teknik, yaitu teknik sparse

spatial [15] dan [17], teknik sparse pada waktu [16], dan teknik sparse pada

sudut kedatangan [14]. Pada skema dengan tekniksparse spatial, matrik sampling

A dipilih sedemikian sehingga sinyal yang diolah oleh M buah antena penerima dikurangi menjadi K buah antena (K < M). Skema dengan teknik sparse pada waktu, matrik sampling A dipilih sedemikian sehingga sinyal yang diambil sepanjang T dikurangi menjadi R (R < T). Pendekatan dengan teknik sparse

pada sudut kedatangan bekerja dengan hanya mengambil satu sampel pengukuran, kemudian membentuk matrik pengukuranAyang tersusun dari vektor kolom yang berasal daristeering vectorpada semua arah kedatangan yang dipindai. Meskipun menggunakan asumsi yang berbeda, ketiga skema di atas memiliki prinsip kerja yang sama.

Untuk ilustrasi dan menjelaskan keberhasilan dan permasalahan yang masih ada pada algoritma compressive sensing ini, maka dilakukan simulasi algoritma

compressive sensingberbasis sparsitas sudut yang dikembangkan oleh Goronitsky

BAB III

METODOLOGI

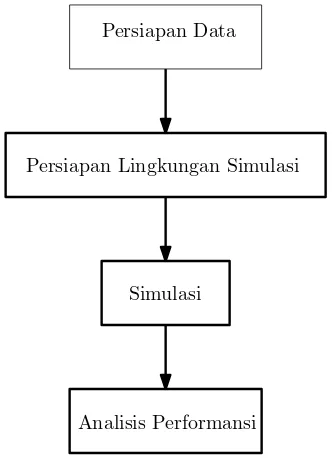
Ada pun urutan pengerjaan pada rencana penelitian ini adalah: persiapan data, persiapan lingkungan simulasi, simulasi, dan analisis performansi (Gambar III.1)

Persiapan Data

Simulasi

Analisis Performansi Persiapan Lingkungan Simulasi

Gambar III.1: Langkah pengerjaan penelitian

III.1

Persiapan Data

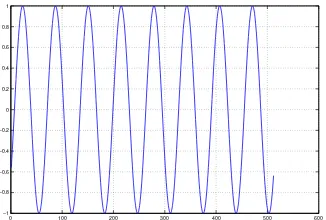
Persiapan data adalah tahapan pembangkitan data untuk simulasi. Tahapan ini terdiri dari dua tahap yaitu penyiapan data input, dan penyiapan datanoise. Pada penelitian estimasi arah kedatangan sebelumnya yaitu MUSIC [3] dan ESPRIT [8], sinyal radar yang dibangkitkan berupa sinyal sinusoidal. Sinyal sinusoidal untuk radar tersebut terdiri dari sinyal sinusoidal murni (pure sinusoid / monochrome, dan sinyal sinusoidal majemuk (composite sinusoids). Sinyal sinusoidal murni adalah sinyal yang hanya terdiri dari satu komponen sinyal sinusoidal. Sinyal sinusoidal majemuk adalah sinyal yang terdiri dari superposisi dari beberapa sinyal yang sinusoidal. Sinyal sinusoidal murni dinyatakan dengan persamaan

Sedangkan persamaan untuk sinyal sinusoidal majemuk adalah

x(n) =

N

X

i=1

sin(2·π·fi·n+φi) (III.2)

Pada Persamaan III.2, sinyal tersusun atas komposisiNbuah sinyal sinusoidal. Fasa sinyal (φi) dibangkitkan secara random dengan distribusi uniform pada interval

[0−2π]. Gambar II.2 dan II.3 memperlihatkan sinyal sinusoidal murni dan sinyal sinusoidal majemuk. Di samping penentuan fasa sinyal, penentuan frekuensi juga penting. Frekuensi sinyal ditentukan sesuai dengan kondisi aktual di lapangan. Frekuensi tipikal untuk sinyal radar adalah300 MHz.

0 100 200 300 400 500 600 −1

−0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1

Gambar III.2: Sinyal sinusoidal murni (pure sinusoid)

0 100 200 300 400 500 600

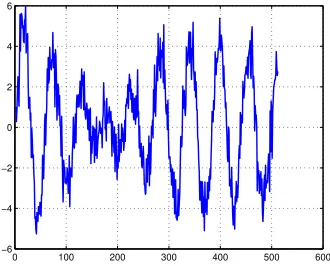
−6 −4 −2 0 2 4 6

Gambar III.3: Sinyal sinusoidal majemuk dengan 12 elemen frekuensi

Untuk noise, noisedibangkitkan untuk mengemulasi situasi pemancar, kanal, dan penerima. Oleh karena komunikasi antara pemancar dan penerima bersifat line of

sight, maka noise yang muncul di penerima adalah noise gaussian yang bersifat

Penambahan sinyal dengan noise AWGN ini diatur setelah nilai amplitudo sinyal dan nilai amplitudo noise ditetapkan. Perbandingan nilai amplitudo sinyal dan

noise ini dinyatakan dengan istilah Signal to Noise Ratio (SNR). SNR biasanya

dinyatakan dalam logaritma basis 10 yang disebutdecibel(dB).

SN R= 10·log(Ps

Pn

) (III.3)

Dengan Ps adalah daya rata-rata sinyal dan Pn adalah daya rata-rata noise. Daya sinyal dannoiseberturut-turut dinyatakan dengan:

Ps =

PN

i=1x2s(n)

N (III.4)

Pn=

PN

i=1x2n(n)

N (III.5)

Gambar III.4, memperlihatkan sinyal yang telah terkena noise AWGN. Pada gambar tersebut, SNR adalah sebesar 20 dB.

0 100 200 300 400 500 600

−6 −4 −2 0 2 4 6

Gambar III.4: Sinyal sinusoidal majemuk yang terkenanoisedengan SNR 10 dB

Pada pelaksanaan penelitian, pengaruh darinoisediselidiki dengan mengubah-ubah nilai SNR pada setiap simulasi.

III.2

Persiapan Lingkungan Simulasi

sensing. Untuk simulasi estimasi arah kedatangan klasik, persiapan simulasi akan meliputi:

• persiapansetting arrayantena

• penentuan jumlah sumber sinyal

• penentuan faktor lingkungan

Persiapan Antena . Persiapan setting array antena secara sederhana adalah menentukan jenis susunan antena dan jarak antar elemennya. Untuk seluruh simulasi, susunan antena dipilih jenis Uniform Linear Array (ULA) dengan jarak antar elemen konstanta. Mengikuti penelitian yang terdahulu, jarak antar elemen dipilih λ/2. Gambar berikut memperlihatkan asumsi array antena yang disimulasikan. Jumlah elemen antena yang terdapat dalamarrayadalah M.

a1

a2

a3

a_M d

d

Gambar III.5: Susunan ULA dengan jumlah elemenM dan jarak antar elemend.

Penentuan jumlah sumber . Penentuan jumlah sumber merupakan parameter yang penting pada simulasi. Pada kondisi satu sumber saja, permasalahan estimasi arah kedatangan sinyal hanya fungsi dari SNR noise saja. Pada kondisi beberapa sinyal yang datang, permasalahannya adalah penentuan sudut kedatangan pada masing-masing sumber merupakan fungsi darinoise, jarak sudut antara dua sinyal berdekatan, serta korelasi antar sinyal. Gambar III.6 memperlihatkan jumlah sumber satu dan beberapa. Pada Gambar III.6(b), jarak sudut antara sumber satu dan sumber dua adalah θ1 − θ2. Kemampuan dari algoritma untuk memisahkan

a1

a2

a3

a_M

a1

a2

a3

a_M

θ θ1

θ

θ

θ

θ2

(a) (b)

Gambar III.6: Sinyal yang datang ke array antena. (a). Satu sumber (b). Dua sumber dengan sudut datangθ1 danθ2

Penentuan faktor lingkungan . Faktor lingkungan ini antara lain meliputi redaman sinyal akibat propagasi dan pergeseran frekuensi akibat efek doppler akibat pergerakan sumber. Redaman sinyal akibat propagasi terjadi karena jarak yang ditempuh, serta sifat fisis media yang dilintasi. Untuk keperluan simulasi ini, media propagasi yang dilewati adalah udara bebas. Parameter fisis udara bebas adalah permitivitas (ǫ0) dan permeabilitas (µ0). Dengan asumsi ini, maka cepat rambat

gelombang di udara adalah3·108 _{meter per detik. Redaman propagasi gelombang}

mengikuti modelpath-lossyaitu:

α= 32,5 + 20·f + 20·d (III.6)

Denganαadalah redaman dalam dB,f adalah frekuensi dalam MHz, dand adalah jarak dalam kilometer. Pergeseran frekuensi dilakukan dengan mensimulasikan pergerakan objek dengan kecepatanv. Pergeseran frekuensi yang ditimbulkan oleh kecepatan ini dihitung dengan persamaan:

∆f = v

c·f0·cos(θ) (III.7)

III.3

Simulasi

Terdapat tiga skema yang akan diteliti pada penelitian ini, yaitu skemacompressive sensing berbasis sparsitas pada domain frekuensi, sparsitas pada domain spasial, dan sparsitas pada domain arah kedatangan. Ketiga skema ini telah dibahas pada bagian kajian literatur sebelumnya.

III.4

Analisis Perfomansi

Untuk menilai keberhasilan skema, maka diperlukan parameter-parameter untuk mengukur performansi dari skema-skema yang diteliti. Parameter performansi yang akan diukur adalah:

• akurasi sebagai fungsi dari SNR

• resolusi sebagai fungsi dari SNR

• akurasi sebagai fungsi dari doppler shift

• akurasi sebagai fungsi dari tingkat sparsitas frekuensi

Akurasi sebagai fungsi dari SNR. Akurasi yang dimaksud di sini adalah nilai absolut dari selisih antara sudut aktual kedatangan sinyal dengan sudut hasil estimasi skema. Untuk memperoleh hasil yang memadai, maka nilai akurasi ini perlu disimulasikan cukup banyak, dan hasil yang diambil adalah nilai rata-rata dari semua percobaan tersebut.

AK =

PNs

i=1[θ−θbi]

Ns

(III.8)

Nilai AK menyatakan akurasi,θadalah sudut aktual,θbi adalah sudut estimasi ke-i, danNs adalah jumlah eksperimen yang dilakukan. Percobaan diulangi untuk nilai SNR yang berbeda-beda.

rata-rata resolusi dari semua percobaan. Seperti halnya pada percobaan akurasi, percobaan resolusi ini dilakukan juga pada nilai SNR yang berbeda-beda.

Akurasi sebagai fungsi dari doppler shift. Pada percobaan jenis ini, sumber adalah sinyal sinusoidal murni dengan frekuensi f0 yang bergerak dengan suatu

kecepatanv. Akibat pergerakan ini, maka frekuensi sinyal bergeser dari nilai semula dengan besar bergeseran seperti yang dihitung dengan persamaan III.7. Untuk hasil yang lebih baik, nilai yang akan dilaporkan di sini adalah nilai rata-rata dari sinyal setelah dilakukan beberapa kali percobaan. Seperti halnya percobaan akurasi, pada percobaan ini, lingkungan sinyal juga dilakukan pada SNR yang berbeda-beda.

Akurasi sebagai fungsi dari tingkat sparsitas frekuensi. Pada beberapa kasus, sinyal yang dikirim bukan berupa sinyal sinusoidal murni, namun sinyal sinusoidal komposit. Ketepatan estimasi arah kedatangan sinyal merupakan fungsi dari ketepatan estimasi jumlah komponen dari frekuensi sinyal penyusunnya. Mengingat bahwa jumlah frekuensi sinyal penyusun tetap lebih sedikit dibandingkan dengan sampel sinyal, maka asumsi sparsitas sinyal di frekuensi masih tetap berlaku. Pada percobaan jenis ini, jumlah frekuensi sinyal akan divariasikan, selanjutnya setiap metoda akan diukur tingkat akurasi estimasi sudutnya. Seperti percobaan yang lain, akan diambil nilai rata-rata dari beberapa percobaan. Demikian juga lingkungan yang akan diubah-ubah tingkat SNR-nya dengan beberapa nilai yang berbeda-beda.

III.5

Skema yang ditinjau

Pada proposal ini, dari tiga skema yang dibahas di atas, skema compressive sensingberbasis sparsitas pada arah kedatangan yang akan ditinjau dan diperbaiki. Skema ini memiliki keuntungan dibandingkan dengan skema sparsitas pada ruang/spasial maupun skema sparsitas pada waktu. Keuntungan ini yaitu jumlah sampel yang ekstrim sedikit. Irina Goronitsky dan Bhaskar Rao ([14]) bahkan hanya menggunakan satu sampel saja. Skema ini dapat diilustrasikan seperti pada Gambar III.7.

Skema ini, dengan kesederhanaannya, memiliki kelemahan utama yaitu rentan terhadapnoise. Pada bagian Simulasi Awal akan ditunjukkan kelemahan skema ini secara simulasi.

a0,1

a0,2

a0,M

.. .

a1,1

a1,2

a1,M

.. .

aθx,1

aθx,2

aθx,M .. . · · · · · · · · · .. . · · · · · · · · · .. .

a360,1

a360,2

a360,M

.. .

steering vectoruntuk sudut 0

steering vectoruntuk sudutθx

0 0 .. . 1 .. . 0 x1 x2 xM .. .

Gambar III.7: Skema Compressive Sensing untuk Estimasi Arah Kedatangan dengan satu sampel sinyal

sudut. Berbeda dengan skema asalnya yang hanya menggunakan satu sudut, skema

multi-snapmenggunakan beberapasnapssinyal terima, untuk kemudian diestimasi

arah kedatangan. Hasilnya kemudian dikompilasi untuk menghasilkan estimasi arah kedatangan yang lebih akurat. Hasil simulasi dari skema multi-snap dari sparsitas sudut tersebut diperlihatkan pada bagian Simulasi Awal. Gambar III.8 memperlihatkan skemamulti-snapsparsitas sudut tersebut.

a0,1

a0,2

a0,M

.. .

a1,1

a1,2

a1,M

.. .

aθx,1

aθx,2

aθx,M .. . · · · · · · · · · .. . · · · · · · · · · .. .

a360,1

a360,2

a360,M

.. .

steering vectoruntuk sudut 0

steering vectoruntuk sudutθx

0 0 .. . 1 .. . 0 x11 x12

x1M

.. .

Maktrik indikator arah kedatangan (dicari)

Vektor pengamatan/keluaran antena 0 0 .. . 1 .. . 0 0 0 .. . 1 .. . 0 · · · · · · · · · · · · · · · · · · 0 .. . _{· · ·}

xN1

xN2

xN M

.. . · · · · · · · · · · · · Nsnapshot

Nilai 1 tidak mesti terjadi pada baris yang sama

BAB IV

TIMELINE RENCANA PENELITIAN

Penelitian ini direncanakan selesai dalam kurun waktu tiga tahun (2014-2016). Perencanaan pengerjaan dibagi per tahun. Rincian rencana penelitian untuk tahun 2014, 2015, dan 2016 dijabarkan dalam Tabel IV.1, Tabel IV.2, dan Tabel IV.3. Rencana penelitian ini dibagi menjadi tahapan-tahapan yaitu:

• Persiapan penelitian Meliputi kegiatan studistate of the art, penentuan fokus, penelitian awal dengan mensimulasikan metoda estimasi arah kedatangan yang ada serta teknik-teknik compressive sensing, merumuskan rencana kontribusi, penyusunan proposal dan ujian kualifikasi

• Pelaksanaan Penelitian Merumuskan metode yang baru, yaitu penggabungan algoritma estimasi arah kedatangan dengan compressive sensing, membandingkan dengan algoritma yang ada dan memodifikasi lebih lanjut untuk memperoleh keunggulan skema.

• Pengujian dengan simulasi

• Publikasi dan Seminar Kemajuan I, II, dan III

• Perumusan kontribusi ilmiah, penulisan disertasi dan Seminar Kemajuan IV

• Ujian disertasi.

Adapun target detail per dijabarkan dengan rincian berikut. Untuk tahun 2014, target utama adalah pada menemukan permasalahan dan proposed method.

Proposed method di sini masih bersifat tentatif, namun ditanda keberhasilan

dari proposed method ini diverifikasi dengan simulasi awal. Dua milestone yang

diharapkan dicapai pada tahun 2014 adalah Seminar Proposal dan Pengajuan Seminar I. Ada pun paper awal diharapkan dapat dikirimkan pada jurnal nasional. Untuk tahun 2015, target yang dipentingkan adalah proposed method baru, atau pematangan dari proposed method semula. Tantangan yang akan dijawab pada tahun kedua ini adalah keberhasilan untuk mengirim pada jurnal internasional dan diterima. Ada pun target yang direncanakan sehubungan dengan syarat akademik pendidikan adalah melakukan Seminar Kemajuan II serta pengajuan untuk mengikuti Seminar Kemajuan III.

dan pengirimannya mungkin masih dilakukan, jika syarat paper belum terpenuhi atau paper tahun sebelumnya tidak lolos publikasi. Sidang tertutup menjadi target penting pada tahun ketiga ini.

Tabel IV.1: Rencana Kegiatan Penelitian Tahun 2014

No Kegiatan Penelitian Bulan

ke-1 2 3 4 5 6 7 8 9 10 11 12 1 Persiapan Penelitian

2 Ujian Kualifikasi

3 Analisis Metode DoA dan CS yang ada 4 Perumusan algoritma yang ditawarkan 5 Penulisan paper dan pengajuan publikasi 6 Pengajuan Seminar Kemajuan I

Tabel IV.2: Rencana Kegiatan Penelitian Tahun 2015

No Rencana Kegiatan Bulan

ke-1 2 3 4 5 6 7 8 9 10 11 12 1 Seminar Kemajuan I

2 Formulasi Metode Baru 3 Simulasi Metode Baru 4 Penulisan Paper dan Publikasi 5 Pengajuan Seminar Kemajuan II 6 Seminar Kemajuan II

7 Perbandingan Metode Baru dengan Metode Lama 8 Simulasi komprehensif

9 Penulisan Paper dan Publikasi 10 Pengajuan Seminar Kemajuan III

Tabel IV.3: Rencana Kegiatan Penelitian Tahun 2016

No Rencana Kegiatan Bulan

ke-1 2 3 4 5 6 7 8 9 10 11 12 1 Seminar Kemajuan III

2 Penulisan Paper untuk Junal Internasional 3 Pengajuan Seminar Kemajuan IV 4 Seminar Kemajuan IV

BAB V

SIMULASI PENDAHULUAN

V.1

Simulasi dalam lingkungan berderau

Pada bagian ini akan ditunjukkan permasalahan pada skema estimasi arah kedatangan dengan teknik sparsitas sudut yang diusulkan oleh Irina dan Rao [14] (Gambar III.7). Permasalahan yang dimaksudkan di sini adalah sensitif skema terhadapnoise. Sifat sensitif terhadapnoiseini mudah diperkirakan karena menurut teori estimasi, nilai terbaik untuk mengestimasi suatu besaran adalah dari nilai rata-rata pengukuran tersebut ([19]). Dengan hanya satu sampel, maka nilai rata-rata tergantung dengan sampel itu sendiri. Untuk verikasi kelemahan ini, program simulasi dikembangkan menggunakan Matlab dengan parameter sebagai berikut:

• jumlah antena : 12

• jumlah sumber : 1

• sudut kedatangan sinyal : -30 derajat

• jarak antar antena (λ) : 0,5

• SNR (db) : variabel dari -20 sampai 20 dengan interval 5 dB.

• jumlah percobaan : 10 kali untuk setiap SNR.

Hasil simulasi berupa estimasi arah kedatangan diperlihatkan pada Gambar V.1. Pada gambar tersebut, terlihat bahwa skema sparsitas sudut memiliki kesalahan estimasi yang besar untuk SNR yang kurang dari 5 dB. Untuk membandingkan tingkat estimasi kesalahan pada tiap SNR, maka pada setiap SNR, hasil estimasi sudut kedatangan dihitung nilai standar deviasinya. Standar deviasi ini dikurvakan seperti yang tampak pada Gambar V.2.

−5 0 5 10 15 −80

−60 −40 −20 0 20 40

SNR (dB)

Sudut

Gambar V.1: Hasil estimasi sudut sebagai fungsi SNR dari skema sparsitas sudut dengan sepuluh percobaan untuk setiap SNR

V.2

Simulasi perbandingan dengan algoritma klasik

Untuk memperoleh perbandingan bagaimana sensitifitas dari skema sparsitas sudut ini dibandingkan dengan algoritma klasik dari estimasi arah kedatangan, simulasi kedua dijalankan dalam lingkungan yang sama seperti sebelumnya. Algoritma klasik yang diujicobakan adalah algoritma MVDR dan MUSIC. Sumber sinyal ada satu buah yang datang pada sudut -30 derajat. Akurasi estimasi dinyatakan dengan standard deviasi kesalahan antara sudut estimasi dengan sudut sebenarnya. Hasil perbandingan terlihat pada Gambar V.3. Pada gambar tersebut, terlihat bahwa performa dari algoritma klasik MVDR sangat superior dibandingkan dengan sparsitas sudut. Bahkan untuk SNR -10 dB, skema klasik MVDR masih memiliki kesalahan yang kurang dari 5 derajat.

V.3

Simulasi skema yang diusulkan

Selanjutnya disimulasikan skema multi-snap sparsitas sudut sebagai usulan perbaikan dari skema sparsitas sudut dengan 1 sampel saja. Skema multi-snap

−50 0 5 10 15 5

10 15 20 25

SNR

STD Error

PERFORMA COMPRESSIVE SENSING − DOA (SPARSITAS PADA SUDUT − ALGORITMA IRINA)

Gambar V.2: Standard Deviasi Error sebagai fungsi dari SNR

digunakan 20 sampel. Hasil simulasi menunjukkan adanya perbaikan performa dibandingkan dengan skema asal. Untuk SNR lebih dari 0 dB, skema ini menunjukkan tingkat akurasi yang sama baik dengan algoritma MUSIC dan MVDR. Sebagai pengembangan lebih lanjut, skema yang diusulkan ini kemudian diperbaiki lagi dengan membuang hasil estimasi outliers. Pembuangan outliers

−200 −15 −10 −5 0 5 10 15 20 5

10 15 20 25 30 35 40

SNR (dB)

Standard Deviasi Error

CS−Sparsitas Sudut MVDR

MUSIC

Gambar V.3: Perbandingan performansi skema sparsitas sudut dengan algoritma MVDR dan MUSIC

−200 −15 −10 −5 0 5 10 15 20 5

10 15 20 25 30 35 40

SNR (dB)

Standard Deviasi Error

CS−Sparsitas Sudut MVDR

MUSIC Proposed Method

Proposed Method − Outliers Removal

DAFTAR PUSTAKA

[1] J. Capon, “High-resolution frequency-wavenumber spectrum analysis,”

Proceedings of IEEE, Vol. 57, No. 8, August 1969, 1969.

[2] S. P. Applebaum, “Adaptive array,” IEEE Transactions on Antennas and Propagation, Vol. Ap-24, No. 5, September 1976, 1976.

[3] R. O. Schmidt, “Multiple emitter location and signal parameter estimation. in ieee transactions on antennas and propagation, vol. ap-34, no. 3, march 1986,” IEEE Transactions on Antennas and Propagation, Vol. Ap-24, No. 5,

September 1976, 1986.

[4] A. J. Barabell, “Improving the resolution performance of eigenstructure-based direction-finding algorithms,” Proceeding of IEEE Conference on Acoustics, Speech, and Signal Processing, 1983, 1983.

[5] A. Lee, “Centrohermitian and skew-centrohermitian matrices,” Journal of Linear Algebra and Its Applications. 29:205-210, 1980.

[6] K.-C. Huarng and C.-C. Yeh, “A unitary transformation method for angle-of-arrival estimation,”IEEE Transactions on Signal Processing, Vol. 39, No.4, April 1991, 1991.

[7] M. Pesavento, A. B. Gershman, and M. Haardt, “Unitary root-music with a real-valued eigendecomposition: A theoretical and experimental performance study,” IEEE Transactions on Signal Processing, Vol.48, No. 5, May 2000, 2000.

[8] R. Roy, A. Paulraj, and T. Kailath, “Estimation of signal parameters via rotational invariance techniques esprit.” Proceeding of IEEE Military

Communications (MILCOM) Conference - Communications, Vol.3, Oct. 1986,

1986.

[9] M. Haardt and J. Nossek, “Unitary esprit: How to obtain increased estimation accuracy with a reduced computational burden,”IEEE Transactions on Signal Processing, Vol. 43, No. 5, May 1995, 1995.

[11] D. L. Donoho, “Compressed sensing,” IEEE Transactions on Information Theory, Vol. 52, No. 4, April 2006, 2006.

[12] E. Candes, “Compressive sampling,” Proceedings of the International

Congress of Mathematicians, Madrid, Spain, 2006, 2006.

[13] R. Baraniuk, “Compressive sensing,” IEEE Signal Processing Magazine. Volume 24. July 2007, 2007.

[14] I. F. Gorodnitsky and B. D. Rao, “Sparse signal reconstruction from limited data using focuss: A re-weighted minimum norm algorithm,” IEEE Transactions on Signal Processing, Vol.45. No.3, March 1997, 1997.

[15] Y. Wang, A. Pandharipande, and G. Leus, “Compressive sampling based mvdr spectrum sensing,”Proceeding of IAPR 2010., 2010.

[16] A. C. Gurbuz and J. H. McClellan, “A compressive beamforming method,”

Proceeding of the IEEE International Conference on Acoustics, Speech and

Signal Processing, 2008., 2008.

[17] Direction Estimation Using Compressive Sampling Array Processing, 2009.

[18] J. M. Kim, O. K. Lee, and J. C. Ye, “Compressive music: Revisiting the link between compressive sensing and array signal processing,”IEEE Transaction on Information Theory, Vol. 58, No. 1, January 2012, 2012.

[19] S. M. Kay, Statistical Signal Processing - Volume 1 : Estimation Theory. Englewood Cliff, 1998.

[20] B. V. Veen and K. M. Buckley, “Beamforming: A versatile approach to spatial filtering,”IEEE ASSP Magazine, April 1988, 1988.

[21] P. Chen, X. Tian, Y. Chen, and X. Yang, “Delay and sum of beamforming on fpga,”In ICSP Proceeding 2008, 2008.

[22] Y. Zeng and R. C. Hendriks, “Distributed delay and sum beamformer for speech enhancement via randomized gossip,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, Vol. 22, No. 1, January 2014, 2014.

[23] H. Cox, R. M. Zeskind, and M. M. Owen, “Robust adaptive beamforming,”

IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. Assp-35,

[24] G. H. Golub and C. V. Loan,Matrix Computation. Johns Hopkins University Press; 3rd edition (October 15, 1996), 1996.

[25] M. Zoltowski, “On the performance analysis of the mvdr beamformer in the presence of correlated interference,”IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 36, No. 6, June 1988., 1988.

[26] M. Kaveh and A. J. Barabell, “The statistical performance of the music and the minimum-norm algorithms in resolving plane waves in noise,” IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. ASSP-34, No.

2, April 1986., 1986.

[27] P. Stoica and A. Nehorai, “Music, maximum likelihood, and cramer-rao bound,” IEEE Transactions on Acoustics Speech and Signal Processing. Vol 37. No 5.May 1989, 1989.

[28] Direction Finding with Uniform Circular Array Via Phase Mode Excitation

and Beamspace Root-MUSIC, 1992.

[29] H. Nyquist, “Certain topics in telegraph transmission theory,” Transaction of AIEE, Vol. 47, pp. 617644, Apr. 1928, 1928.

[30] C. E. Shannon, “Communication in the presence of noise,” Proceeding of Institute of Radio Engineers, Vol. 37, No. 1, Jan. 1949, 1949.

[31] T. Strohmer, “Measure what should be measured: Progress and challenges in compressive sensing,” IEEE Signal Processing Letters, Vol. 19, No. 12,

December 2012, 2012.

[32] K. Hayasi, M. Nagahara, and T. Tanaka, “A users guide to compressive sensing for communications systems,” In IEICE Transaction on Communication. Vol.E86-B. No.3. March 2013, 2013.

[33] E. Candes, J. Romberg, and T. Tao, “Robust uncertainty principles: Exact recovery from highly incomplete fourier information,”IEEE Transactions on Information Theory, February 2006, 2006.

[34] T. T. Emmanuel Candes, Justin Romberg, “Stable signal recovery from incomplete and inaccurate measurements,” Journal of Communications on Pure and Applied Mathematics, Vol.59, No.8, August 2006, 2006.

[35] J. Romberg. (2005) l1-magic. [Online]. Available:

[36] S. Boyd. (2014) Cvx: Matlab software for disciplined convex programming. [Online]. Available: http://cvxr.com/cvx/

[37] J. H. Friedman and W. Stuetzle, “Projection pursuit regression,”Journal of the American Statistical Association, Vol. 76, No. 376 (Dec., 1981), pp. 817-823, 1981.

[38] S. Mallat and Z. Zhang, “Matching pursuits with time-frequency dictionaries,”

IEEE Transactions on Signal Processing, Volume:41, Issue: 12. 1993, 1993.

[39] S. S. Chen, D. L. Donoho, and M. A. Saunders, “Atomic decomposition by basis pursuit,”SIAM Review, Society for Industrial and Applied Mathematics, Vol. 43,No. 1, pp. 129159, 2001, 2001.

[40] J. A. Tropp, “Greed is good : Algorithmic results for sparse approximation,”