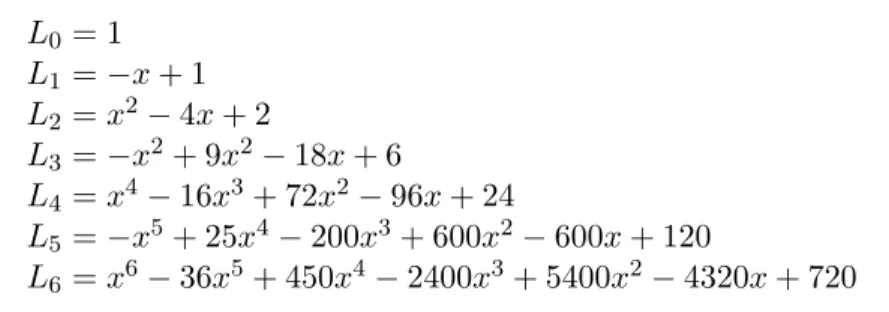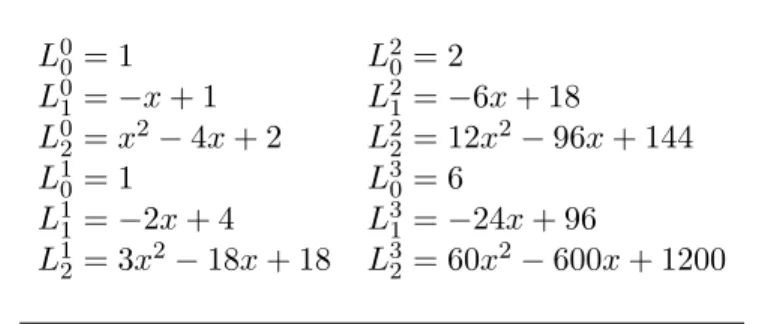Mekanika Kuantum dalam Koordinat Bola dan Atom Hidrogen

Mekanika Kuantum dalam Koordinat

Bola dan Atom Hidrogen

David J. Griffiths diterjemahkan dari

Introduction to Quantum Mechanics (Edisi 2) physics.translation@gmail.com

1

Persamaan Schr¨

odinger dalam Koordinat Bola

Bentuk umum persamaan Schr¨odinger untuk tiga dimensi dapat diperoleh secara langsung dengan mudah. Persamaan Schr¨odinger berbunyi

i~∂Ψ

∂t =HΨ; (1)

operator HamiltonanH dapat diperoleh dari 1 2mv 2_{+V =} 1 2m p 2 x+p2y+p2z +V

dengan mengikuti aturan yang sama:

px→ ~ i ∂ ∂x, py → ~ i ∂ ∂y, pz → ~ i ∂ ∂z, (2)

atau lebih singkatnya

p→ ~ i∇. (3) Sehingga i~∂Ψ ∂t =− ~2 2m∇ 2_{Ψ +VΨ, (4)} dimana ∇2 ≡ ∂ 2 ∂x2 + ∂2 ∂y2 + ∂2 ∂z2 (5)

adalahLaplacian dalam sistem koordinat kartesian.

Sekarang, energi potensialV dan fungsi gelombang Ψ adalah fungsir= (x, y, z) dant. Peluang untuk menemukan partikel di dalam elemen volume

d3r=dx dy dz adalah |Ψ(r, t)|2_d3_{r, dan normalisasinya menjadi}

Z

|Ψ|2d3r= 1, (6)

dimana integralnya diambil untuk selurung ruang. Jika potensialnya bebas (tak-gayut) waktu, maka keadaan-keadaan stasionernya adalah

Ψn(r, t) =ψn(r)e−iEnt/~, (7)

dimana fungsi gelombang spasialψn memenuhi persamaan Schr¨odinger tak-gayut waktu:

−~

2

2m∇

2_{ψ+V ψ=Eψ. (8)}

Penyelesaian umum untuk persamaan Schr¨odingergayut waktu adalah Ψ(r, t) =Xcnψn(r)e−iEnt/~, (9)

dengan cn adalah tetapan yang dapat diperoleh dari keadaan awal

fung-si gelombang, Ψ(r,0). (Jika potensialnya membolehkan keadaan-keadaan kontinyu, maka penjumlahan pada 9 berubah menjadi integral.)

1.1 Pemisahan Variabel

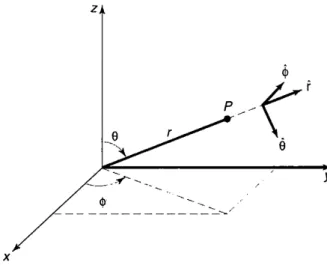
Biasanya, potensial hanya berupa fungsi jarak dari titik asal (origin). Pada kasus tersebut digunakan koordinat bola, (r, θ, φ) (lihat Gambar 1). Di dalam koordinat bola, Laplacian memiliki bentuk

∇2 = 1 r2 ∂ ∂r r2 ∂ ∂r + 1 r2_sinθ ∂ ∂θ sinθ ∂ ∂θ + 1 r2_sin2_θ ∂2 ∂φ2 . (10) Sehingga, persamaan Schr¨odinger dalam koordinat bola menjadi

−~ 2 2m 1 r2 ∂ ∂r r2∂ψ ∂r + 1 r2_sinθ ∂ ∂θ sinθ∂ψ ∂θ + 1 r2_sin2_θ ∂2ψ ∂φ2 +V ψ=Eψ. (11) Kita mulai mencari dengan bentuk penyelesaian yang dapat dipisahkan menjadi perkalian dari:

ψ(r, θ, φ) =R(r)Y(θ, φ). (12) Mensubstitusikan ke Persamaan 11, maka kita dapatkan

−~ 2 2m Y r2 ∂ ∂r r2∂R ∂r + R r2_sinθ ∂ ∂θ sinθ∂Y ∂θ + R r2_sin2_θ ∂2Y ∂φ2 +V RY =ERY.

Membaginya denganRY dan mengalikannya dengan−2mr2/~2:

1 R d dr r2dR dr −2mr 2 ~2 [V(r) −E] +1 Y 1 sinθ ∂ ∂θ sinθ∂Y ∂θ + 1 sin2θ ∂2Y ∂φ2 = 0.

Suku-suku yang ada pada kurung kurawal pertama hanya bergantung pada

r, sedangkan sisanya hanya bergantung pada θ dan φ, sehingga keduanya harus sama dengan suatu bilangan. Untuk alasan yang akan muncul kemu-dian, saya akan menuliskan “tetapan pemisahan” ini dalam bentukl(l+ 1):

1 R d dr r2dR dr −2mr 2 ~2 [V(r) −E] =l(l+ 1); (13) 1 Y 1 sinθ ∂ ∂θ sinθ∂Y ∂θ + 1 sin2θ ∂2Y ∂φ2 =−l(l+ 1). (14)

1.2 Persamaan Anguler

Persamaan 14 menentukan kebergantunganψ padaθdan φ; dengan meng-alikan kedua ruas dengan Y sin2θ, maka ia menjadi:

sinθ ∂ ∂θ sinθ∂Y ∂θ +∂ 2_Y ∂φ2 =−l(l+ 1) sin 2_{θ Y. (15)}

Mungkin Anda bisa mengenali persamaan ini—ia adalah penyelesaian untuk persamaan Laplace dalam elektrodinamika klasik. Seperti biasanya, kita mencoba pemisahan variabel:

Y(θ, φ) = Θ(θ),Φ(φ). (16)

Dengan mensubstitusikan pemisahan variabel ini dan membaginya dengan ΘΦ, kita dapatkan: 1 Θ sinθ d dθ sinθdΘ dθ +l(l+ 1) sin2θ + 1 Φ d2Φ dφ2 = 0.

Suku pertama hanya fungsiθdan suku kedua hanya fungsiφ, jadi keduanya harus sama dengan suatu bilangan. Kali ini saya akan menggunakan tetapan pemisahanm2_: 1 Θ sinθ d dθ sinθdΘ dθ +l(l+ 1) sin2θ=m2 (17) 1 Φ d2_Φ dφ2 =−m 2 ₍₁₈₎

Persamaan φmudah untuk diselesaikan:

d2Φ

dφ2 =−m

2_{Φ⇒Φ(φ) =e}imφ_{. (19)}

[Sebenarnya ada dua penyelesaian: exp(imφ) dan exp(−imφ), tetapi ki-ta akan menyerki-takan penyelesaian kedua dengan cara membolehkanm-nya bernilai negatif. Kemudian, dimungkinkan juga ada suatu tetapan di depan penyelesaian ini, tetapi tetapan ini akan kita masukkan ke Θ. Secara tidak sengaja, dalam elektrodinamika kita menuliskan fungsi azimut (Φ) dalam bentuk sinus dan kosinus, daripada bentuk eksponensial, hal ini karena po-tensial listrik harus bernilai riil. Di dalam mekanika kuantum tidak ada batasan semacam ini dan bentuk eksponensial lebih mudah untuk dikerjak-an.] Sekarang, ketikaφberputar sejauh 2π, kita kembali ke titik yang sama di ruang tersebut (Lihat Gambar 1), sehingga kita mensyaratkan bahwa

Dengan kata lain, exp[im(φ+ 2π)] = exp(imφ), atau exp(2πim) = 1. Maka dari sinim harus berupa bilangan bulat:

m= 0,±1,±2,· · · . (21) Persamaan θ, sinθ d dθ sinθdΘ dθ +l(l+ 1) sin2θ−m2Θ = 0. (22)

tidak begitu sederhana. Penyelesaiannya adalah

Θ(θ) =AP_lm(cosθ), (23)

dimanaP_lm adalah fungsi Legendre sekawan, didefinisikan dengan

P_lm(x)≡(1−x2)|m|/2 d dx |m| Pl(x). (24)

dan Pl(x) adalah polinomial Legendre ke-l, yang didefinisikan

menggu-nakanrumus Rodrigues:

Pl(x)≡ 1 2l_l! d dx l (x2−1)l. (25) Sebagai contoh, P0(x) = 1, P1(x) = 1 2 d dx(x 2_{−1) =x,} P2(x) = 1 4·2 d dx 2 (x2−1)2= 1 2(3x 2_−1),

dan seterusnya. Beberapa polinomial Legendre yang pertama diberikan pa-da Tabel 1. Seperti yang diisyaratkan oleh namanya,Pl(x) merupakan

po-linomial x (berderajat l), dan bersifat fungsi genap atau ganjil bergantung terhadap paritasl. Tetapi, secara umum P_lm(x) bukanlah polinomial—jika

m ganjil ia memiliki faktor√1−x2_:

P₂0(x) = 1 2(3x 2_{−1), P}1 2(x) = (1−x2)1/2 d dx 1 2(3x 2₋₁₎ = 3xp1−x2_. P₂2= (1−x2) d dx 2 1 2(3x 2₋₁₎ = 3(1−x2),

Tabel 1: Beberapa polinomial Legendre yang pertama,Pl(x). P0= 1 P1=x P2= 1₂(3x2−1) P3= 1₂(5x3−3x) P4= 1₈(35x4−30x2+ 3) P5= 1₈(63x5−70x3+ 15x)

dll. (Di sisi lain, apa yangkitaperlukan adalahP_lm(cosθ), dan√1−cos2_θ=

sinθ, sehinggaP_lm(cosθ) selalu berupa polinomial cosθ, dikalikan dengan— jika m bernilai ganjil—sinθ. Beberapa fungsi Legendre cosθsekawan dibe-rikan pada Tabel 2)

Perhatikan bahwa l harus bilangan bulat bukan ganjil agar rumus Ro-drigues menjadi masuk akal; selain itu, jika |m| > l, maka Persamaan 24 mengatakan P_lm = 0. Maka, untuk sebarang l, ada (2l+ 1) nilai m yang mungkin:

l= 0,1,2,· · · ; m=−l,−l+ 1,· · · ,−1,0,1,· · · , l−1, l. (26)

Tapi tunggu! Persamaan 22 adalah persamaan diferensial orde dua: Ia harus mempunyaiduapenyelesaian yang saling bebas linier, untuk sebarang nilai l dan m. Dimana penyelesaian yang lainnya? Jawab: Tentu saja

ada, sebagai penyelesaian matematis bagi persamaan ini, tetapi ia tidak dapat diterimasecara fisis karena nilainya menjadi tak-berhingga saatθ= 0 dan/atau θ=π.

Tabel 2: Beberapa fungsi Legendre sekawan, P_lm(cosθ).

P₀0= 1 P₂0= 1₂(3 cos2θ−1)

P₁1= sinθ P₃3= 15 sinθ(1−cos2θ)

P₁0= cosθ P₃2= 15 sin2θcosθ P₂2= 3 sin2θ P₃2= 3₂sinθ(5 cos2θ−1)

Sekarang elemen volum dalam koordinat bola adalah

d3r=r2sinθdr dθ dφ, (27) sehingga keadaan normalisasinya (Persamaan 6) menjadi

Z |ψ|2r2sinθdr dθ dφ= Z |R|2r2dr Z |Y|2sinθ dθ dφ= 1.

Lebih memudahkan jika kita menormalisasiR dan Y secara terpisah: Z ∞ 0 |R|2_r2 _{dr= 1 dan} Z 2π 0 Z π 0 |Y|2_{sinθ dθ dφ= 1. (28)}

Fungsi gelombang anguler yang ternormalisasi disebut sebagai harmonik bola (spherical harmonics):

Y_lm(θ, φ) = s (2l+ 1) 4π (l− |m|)! (l+|m|)!e imφ_Pm l (cosθ). (29)

dimana= (−1)m untukm≥0 dan= 1 untuk m≤0. Seperti yang akan kita buktikan nanti, penyelesaian-penyelesaian ini secara otomatis bersifat ortogonal, sehingga Z 2π 0 Z π 0 [Y_lm(θ, φ)]∗[Y_l0m0(θ, φ)] sinθ dθ dφ=δ_ll0δ_mm0. (30) Pada Tabel 3, saya menuliskan beberapa harmonik bola yang pertama. Un-tuk alasan historis,ldisebutbilangan kuantum azimut, danmbilangan kuantum magnetik.

Tabel 3: Beberapa harmonik bola yang pertama, Y_lm(θ, φ).

Y₀0= _4π1 1/2 Y₂±2= _32π151/2sin2θe±2iφ Y₁0= _4π3 1/2

cosθ Y₃0 = _16π7 1/2

(5 cos3θ−3 cosθ)

Y₁±1=∓ _8π3 1/2

sinθe±iφ Y₃±1=∓ _64π21 1/2

sinθ(5 cos2θ−1)e±iφ Y₂0= _16π5 1/2

(3 cos2θ−1) Y₃±2= _32π151/2

sin2θcosθe±2iφ Y₂±1=∓ _8π151/2

sinθcosθe±iφ Y₃±3=∓ _64π35 1/2

1.3 Persamaan Radial

Perhatikan bahwa bagian anguler dari fungsi gelombang,Y(θ, φ), selalu sa-ma untuk semua potensial yang bentuknya simetri bola. Bentuk sebenarnya dari potensial,V(r), hanya mempengaruhi bagian radial dari fungsi gelom-bang,R(r), yang ditentukan oleh Persamaan 13:

d dr r2dR dr −2mr 2 ~2 [V(r) −E]R=l(l+ 1)R. (31)

persamaan ini menjadi sederhana jika kita ganti variabelnya: Misalkan

u(r)≡rR(r), (32) sehinggaR=u/r, dR dr = 1 r2 r du dr , d dr r2dR dr =rd 2_u dr2, dan sehingga −~ 2 2m d2u dr2 + V + ~ 2 2m l(l+ 1) r2 u=Eu. (33)

Ini disebut persamaan radial; persamaan ini identik bentuknya dengan persamaan Schr¨odinger berdimensi satu, kecuali bahwa potensial efek-tifnya, Vef=V + ~ 2 2m l(l+ 1) r2 , (34)

memiliki suku tambahan yang disebut suku sentrifugal, (~2/2m)[l(l +

1)/r2]. Potensial ini memiliki kecenderungan untuk melemparkan partikel keluar (menjauhi titik asal), sama seperti gaya-(pseudo) sentrifugal dalam mekanika klasik. Sementara itu, keadaan normalisasinya (Persamaan 28) menjadi

Z ∞

0

|u|2_{dr= 1. (35)}

Itulah yang bisa kita capai sejauh ini sampai diketahui bentuk spesifik po-tensialnya,V(r).

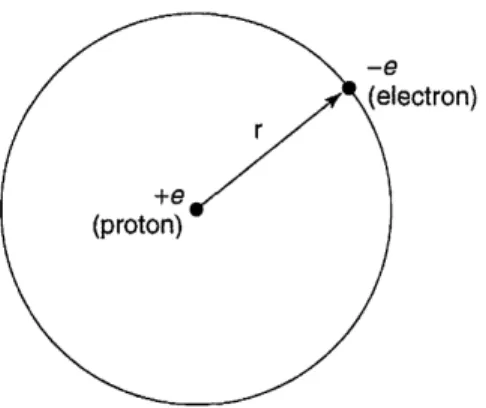
Gambar 2: Atom hidrogen.

2

Atom Hidrogen

Atom hidrogen tersusun atas proton yang berat dan dapat dianggap tak-bergerak (kita akan menggunakannnya sebagai titik asal), bermuatane, de-ngan sebuah elektron yang jauh lebih ride-ngan (bermuatan−e) yang mengor-bit di sekitarnya, terikat oleh gaya tarikan muatan yang saling berlawanan (Lihat Gambar 2). Dari hukum Coulomb, energi potensial (dalam satuan SI) adalah V(r) =− e 2 4π0 1 r, (36)

dan persamaan radialnya (Persamaan 33) berbunyi

−~ 2 2m d2u dr2 + − e 2 4π0 1 r + ~2 2m l(l+ 1) r2 u=Eu. (37)

Permasalahan kita adalah menyelesaikan persamaan ini sebagai u(r), dan menentukan energi-energi yang diperbolehkan, E. Atom hidrogen adalah contoh kasus yang sangat penting dan saya tidak akan memberikan pada Anda penyelesaiannya saja—kita akan menyelesaikannya secara mendetail, melalui metode yang kita gunakan pada penyelesaian analitik osilator har-monik. Secara tidak sengaja, potensial Coulomb (Persamaan 37) membo-lehkan keadaankontinyu (untukE >0), dapat digunakan untuk menjelask-an hamburmenjelask-an elektron-proton, maupun keadamenjelask-anterikat yang diskrit, tetapi kita akan membatasi perhatian kita pada hal yang terakhir disebutkan.

2.1 Fungsi Gelombang Radial

Tugas pertama kita adalah merapikan notasi yang digunakan. Misalkan

κ≡ √

−2mE

~ . (38)

(Untuk keadaan terikat,Ebernilai negatif, sehinggaκadalah bilanganriil.) Membagi Persamaan 37 denganE, kita dapatkan

−1 κ2 d2u dr2 = 1− me 2 2π0~2κ 1 κr + l(l+ 1) (κr)2 u.

Persamaan ini mengisyaratkan kita untuk memperkenalkan

ρ≡κr, dan ρ0 ≡ me2 2π0~2κ, (39) sehingga d2u dρ2 = 1−ρ0 ρ + l(l+ 1) ρ2 u. (40)

Berikutnya kita menguji bentuk asimtotik penyelesaiannya. Saat ρ → ∞, maka suku yang konstan yang ada di dalam kurung menjadi lebih do-minan, sehingga (kira-kira)

d2u dρ2 =u.

Penyelesaian umumnya adalah

u(ρ) =Ae−ρ+Beρ, (41) tetapi eρ nilainya menuju tak berhingga (saat ρ → ∞, sehingga B = 0. Terbukti,

u(ρ)∼Ae−ρ, (42)

untuk ρ besar. Di sisi lain, saat ρ → 0 suku sentrifugalnya menjadi lebih dominan; maka kira-kira:

d2u dρ2 =

l(l+ 1)

Penyelesaian umumnya adalah

u(ρ) =Cρl+1+Dρ−l.

tetapiρ−l menuju tak-berhingga (saat ρ→0), jadi D= 0. Sehingga

u(ρ)∼Cρl+1, (43)

untukρ kecil.

Langkah berikutnya adalah “menguliti” perilaku asimtotik, dengan mem-perkenalkan fungsi baruv(ρ):

u(ρ) =ρl+1e−ρv(ρ). (44) dengan harapan bahwa v(ρ) akan menjadi lebih sederhana daripada u(ρ). Isyarat yang pertama tidak begitu melegakan

du dρ =ρ l_e−ρ (l+ 1−ρ)v+ρdv dρ , dan d2u dρ2 =ρ l_e−ρ −2l−2 +ρ+l(l+ 1) ρ v+ 2(l+ 1−ρ)dv dρ +ρ d2v dρ2 .

dinyatakan dalamv(ρ), maka persamaan radial (Persamaan 40) berbunyi

ρd 2_v

dρ2 + 2(l+ 1−ρ) dv

dρ + [ρ0−2(l+ 1)]v= 0. (45)

Akhirnya, kita mengasumsikan penyelesaiannya,v(ρ), dapat diungkapk-an dalam bentuk deret pdiungkapk-angkat dariρ:

v(ρ) =

∞

X

j=0

cjρj. (46)

Satu-satunya yang menjadi masalah kita adalah menentukan koefisien - ko-efisiennya (c0, c1, c2,· · ·). Dengan menurunkan suku demi suku:

dv dρ = ∞ X j=0 jcjρj−1= ∞ X j=0 (j+ 1)cj+1ρj.

[Pada penjumlahan yang kedua, saya mengubah “indeks boneka”: j →j+1. Jika hal ini menyulitkan Anda, tuliskan beberapa suku pertama secara eks-plisit, danperiksalah. Anda mungkin tahu bahwa penjumlahannya seharus-nya dimulai dari j = −1, tetapi faktor (j+ 1) membuang suku tersebut, sehingga kita bisa memulainya dari nol.] Menurunkan sekali lagi,

d2v dρ2 = ∞ X j=0 j(j+ 1)cj+1ρj−1.

Memasukkan kedua turunan ini ke Persamaan 45, maka kita dapatkan

∞ X j=0 j(j+ 1)cj+1ρj+ 2(l+ 1) ∞ X j=0 (j+ 1)cj+1ρj −2 ∞ X j=0 jcjρj+ [ρ0−2(l+ 1)] ∞ X j=0 cjρj = 0

Dengan menyamakan koefisien dari pangkat yang sama diperoleh

j(j+ 1)cj+1+ 2(l+ 1)(j+ 1)cj+1−2jcj+ [ρ−2(l+ 1)]cj = 0, atau cj+1= 2(j+l+ 1)−ρ0 (j+ 1)(j+ 2l+ 2) cj. (47)

Rumus rekursi ini menentukan koefisien-koefisien tersebut, dan sehingga fungsi v(ρ): Kita mulai denganc0 (ini berarti menjadikan semuanya

konst-an), dan Persamaan 47 memberikan c1; masukkan kembali, kita dapatkan c2, dan seterusnya.

Sekarang mari kita lihat bagaimana bentuk koefisiennya untuk nilai j

yang besar (hal ini berkaitan dengan nilai ρ yang besar, dimana pangkat yang lebih tinggi lebih mendominasi). Di daerah ini rumus rekursinya ber-bunyi cj+1 ∼= 2j j(j+ 1)cj = 2 j+ 1cj.

Untuk sementara, kita misalkan rumus ini sifatnyaeksak. Maka

cj =

2j

jadi v(ρ) =c0 ∞ X j=0 2j j!ρ j _=c 0e2ρ, dan sehingga u(ρ) =c0ρl+1eρ, (49)

yang nilainya menjadi tak-berhingga saatρ-nya besar. Bentuk eksponensial positif jelas adalah perilaku asimtotik yang tidak kita inginkan, di Persa-maan 41. Hanya ada satu jalan keluar dari dilema semacam ini: Deretnya harus dihilangkan. Harus ada bilangan bulat maksimum, jmaks, sedemikian

rupa sehingga

c(jmaks+1)= 0, (50)

(dan suku yang diatasnya secara otomatis koefisiennya hilang). Terbukti (Persamaan 47)

2(jmaks+l+ 1)−ρ0 = 0.

Dengan mendefinisikan

n≡jmaks+l+ 1 (51)

(kemudian disebut bilangan kuantum utama), kita dapatkan

ρ0 = 2n. (52)

Tetapiρ0 menentukan E (Persamaan 38 dan 39): E =−~ 2_κ2 2m =− me2 8π22 0~2ρ20 , (53)

jadi energi yang diperbolehkan adalah

En=− " m 2~2 e2 4π0 2# 1 n2 = E1 n2, n= 1,2,3,· · ·. (54)

Ini adalahrumus Bohryang sangat terkenal—hasil yang paling penting di mekanika kuantum. Bohr mendapatkannya pada 1913 menggunakan cam-puran antara fisika klasik yang tidak dapat diaplikasikan dengan teori ku-antum awal yang primitif (persamaan Schr¨odinger baru muncul pada 1924).

Dengan menggabungkan Persamaan 39 dan 52, maka dapat kita ketahui bahwa κ= me2 4π0~2 1 n = 1 an, (55) dimana a≡ 4π0~ 2 me2 = 0,529×10 −10 _{m (56)}

adalah yang disebut sebagai jari-jari Bohr. Kemudian (dari Persamaan 39 lagi) dapat diketahui bahwa

ρ= r

an. (57)

Fungsi gelombang spasial untuk atom hidrogen ditandai dengan tiga bilang-an kubilang-antum (n, l,dan m):

ψnlm(r, θ, φ) =Rnl(r)Ylm(θ, φ), (58)

dimana (kembali Persamaan 32 dan 44)

Rnl(r) =

1

rρ

l+1_e−ρ_{v(ρ), (59)}

dan v(ρ) merupakan polinomial ρ berderajat jmaks =n−l−1, yang

koefi-siennya ditentukan oleh rumus rekursi

cj+1=

2(j+l+ 1−n)

(j+ 1)(j+ 2l+ 2)cj. (60)

Keadaan dasar (yaitu kedaan dengan energi paling rendah) adalah kasus dimana n = 1, dengan memasukkan nila-nilai tetapan fisis yang di-perbolehkan, maka kita dapatkan:

E1=− " m 2~2 e2 4π0 2# =−13,6 eV. (61)

Terbukti bahwaenergi ikat atom hidrogen (jumlah energi yang Anda bu-tuhkan untuk melepaskan elektron yang berada pada keadaan dasar untuk mengionisasi atom tersebut) adalah 13,6 eV. Persamaan 51 memaksal= 0, sehinggam= 0 (lihat Persamaan 26), jadi

Rumus rekursi memotong polinomialnya setelah suku pertama (Persamaan 60 denganj= 0 memberikanc1 = 0), jadiv(ρ) bernilai konstan (c0), dan

R10(r) = c0

ae

−r/a_{. (63)}

Dengan menormalisasinya, sesuai dengan Persamaan 28: Z ∞ 0 |R10|2r2dr= |c0|2 a2 Z ∞ 0 e−2r/ar2dr=|c0|2 a 4 = 1, jadic0 = 2 √

a. Sementara,Y₀0= 1/√4π, maka keadaan dasar atom hidrogen adalah ψ100(r, θ, φ) = 1 √ πa2e −r/a_{. (64)}

Jikan= 2, energinya adalah

E2=

−13,6 eV

4 =−3,4 eV, (65)

ini adalah keadaan tereksitasi pertama—atau sering disebut, keadaan per-tama saja. Karena kita bisa mendapatkan energi yang sama dengan l= 0 (untuk kasus m= 0) maupun dengan l = 1 (denganm =−1,0, atau +1); terbukti bahwa empat keadaan yang berbeda memiliki energi yang sama. Jikal= 0, maka rumus rekursi (Persamaan 60) memberikan

c1 =−c0 (menggunakanj= 0), dan c2 = 0 (menggunakan j= 1),

jadiv(ρ) =c0(1−ρ), sehingga R20(r) = c0 2a 1− r 2a e−r/2a. (66)

[Perhatikan bahwa koefisien ekspansi {cj} benar-benar berbeda untuk

bi-langan kuantumndanlyang berbeda.] Jikal= 1 rumus rekursi menghapus suku-suku deretnya setelah satu suku, sehinggav(ρ) menjadi hanya berupa tetapan, maka kita dapatkan

R21(r) = c0

4a2re

−r/2a_{. (67)}

(Pada tiap kasus di atas, tetapanc0 dapat diperoleh melalui normalisasi.)

Untuk sebarang n, nilai l yang mungkin (sesuai dengan Persamaan 51) adalah

Tabel 4: Beberapa polinomial Laguerre, Lq(x), yang pertama L0 = 1 L1 =−x+ 1 L2 =x2−4x+ 2 L3 =−x2+ 9x2−18x+ 6 L4 =x4−16x3+ 72x2−96x+ 24 L5 =−x5+ 25x4−200x3+ 600x2−600x+ 120 L6 =x6−36x5+ 450x4−2400x3+ 5400x2−4320x+ 720

dan untuk setiaplada (2l+ 1) nilai myang mungkin (Persamaan 26), jadi total kemerosotan (degenerasi) tingkat energi En adalah

d(n) =

n−1

X

l=0

(2l+ 1) =n2. (69)

Polinomial v(ρ) (didefinisikan menggunakan rumus rekursi, Persamaan 60) adalah fungsi yang sangat dikenal matematikawan, terlepas dari proses nor-malisasi, polinomial ini dapat dituliskan sebagai

v(ρ) =L2l+1_n−l−1(2ρ), (70) dimana Lp_q−p(x)≡(−1)p d dx p Lq(x) (71)

adalahpolinomial Laguerre sekawan, dan

Lq(x)≡ex d dx q e−xxq (72)

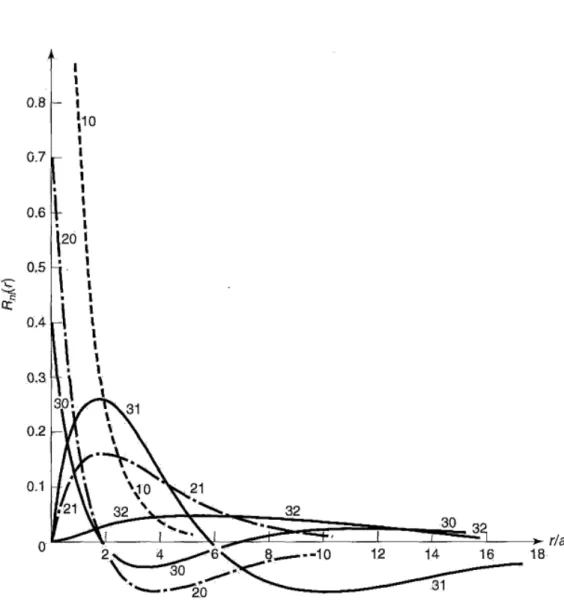
adalah polinomial Laguerre ke-q. (Beberapa polinomial Laguerre yang pertama dituliskan pada Tabel 4, sedangkan beberapa polinomial Laguerre sekawannya diberikan pada Tabel 5. Kemudian beberapa fungsi gelombang radial yang pertama diberikan pada Tabel 6, dan digambarkan pada Gambar 3.) Fungsi gelombang atom hidrogen yang ternormalisasi adalah

ψnlm= s 2 na 3 (n−l−1)! 2n[(n+l)!]3e −r/na 2r na l h L2l+1_n−l−1(2r/na)iY_lm(θ, φ). (73)

Tabel 5: Beberapa polinomial Laguerre sekawan, Lp_q−p(x) L0₀ = 1 L2₀= 2 L0₁ =−x+ 1 L2₁=−6x+ 18 L0 2 =x2−4x+ 2 L22= 12x2−96x+ 144 L1₀ = 1 L3₀= 6 L1₁ =−2x+ 4 L3₁=−24x+ 96 L1₂ = 3x2−18x+ 18 L3₂= 60x2−600x+ 1200

Persamaan ini tidak kelihatan cantik, tetapi jangan protes—persamaan ini-merupakan salah satu dari beberapa sistem realistis yang dapat diselesaikan dalam bentuk eksak. Perhatian bahwa meskipun fungsi gelombang ber-gantung pada ketiga bilangan kuantum, namun energinya (Persamaan 54) hanya ditentukan oleh n saja. Hal ini merupakan keanehan dari potensi-al Coulomb; pada potensipotensi-al sumur bola, Anda ingat bahwa energinya juga berhantung pada l. Fungsi gelombang untuk atom hidrogen bersifat saling ortogonal:

Z

ψ_nlm∗ ψn0_l0_m0r2sinθdr dθ dφ=δ_nn0δ_ll0δ_mm0. (74)

Sifat ini diperoleh dari ortogonalitas harmonik bola (Persamaan 30) dan (untuk n 6=n0) dari fakta bahwa mereka adalah swafungsi (eigenfunction) dariH dengan swanilai (eigenvalue) yang berbeda.

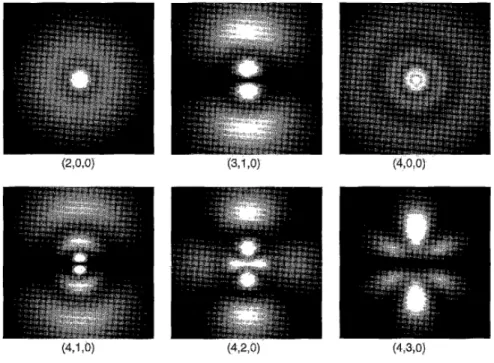
Menggambarkan fungsi gelombang atom hidrogen tidaklah mudah. Para kimiawan lebih suka untuk menggambarkan “kerapatan”, dimana kecerahan awan berbanding lurus dengan|ψ|2_{(Gambar 4). Gambaran yang lebih}

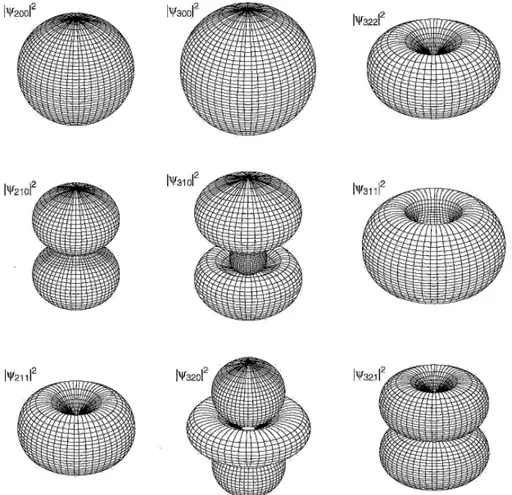
kuan-titatif (tetapi mungkin lebih sulit untuk dibaca) adalah permukaan dengan rapat peluang yang konstan (permukaan untuk nilai |ψ|2 _{konstan, Gambar}

5)

2.2 Spektrum Hidrogen

Pada prinsipnya, jika Anda meletakkan atom hidrogen pada keadaan stasio-nerψnlm, maka ia harus berada pada keadaan itu selamanya. Namun, jika

Anda sedikit mengusiknya (dengan tumbukan dengan atom lain, atau de-ngan menyinarinya dede-ngan cahaya), maka elektron akan mengalamitransisi

Tabel 6: beberapa fungsi gelombang radial, Rnl(r), yang pertama

untuk atom Hidrogen.

R10= 2a−3/2exp (−r/a) R20= √1₂a−3/2 1− 1_2ar exp (−r/2a) R21= √1₂₄a−3/2_arexp (−r/2a) R30= √2₂₇a−3/2 1−2 3 r a+ 2 27 r a 2 exp (−r/3a) R31= ₂₇8√₆a−3/2 1−1_6ar _r a exp (−r/3a) R32= ₈₁√3₃₀a−3/2 _ar 2 exp (−r/3a) R40= 1₄a−3/2 1−3₄r_a+1_{8 a}r2− ₁₉₂1 _ar3 exp (−r/4a) R41= √ 5 16√3a −3/2₁₋ 1 4 r a + 1 80 r a 2 _r a exp (−r/4a) R42= ₆₄1√₅a−3/2 1−₁₂1 r_{a r} a 2 exp (−r/4a) R43= ₇₆₈1√₃₅a−3/2 r_a 3 exp (−r/4a)

bergerak ke keadaan energi yang lebih tinggi, atau denganmelepaskan ener-gi (biasanya berupa radiasi elektromagnetik) dan bergerak turun ke keadaan yang lebih rendah. Pada kenyataannya gangguan semacam iniselalu hadir. Transisi (atau terkadanag disebut “lompatan kuantum”) secara konstan te-rus terjadi, dan hasilnya adalah hidrogen yang selalu melepaskan cahaya (foton), yang energinya berkaitan denganselisih energi antara keadaan awal dan keadaan akhir:

Eγ =Ei−Ef =−13,6 eV 1 n2 i − 1 n2 f ! . (75)

Sekarang, menurut rumus Planck, energi foton berbanding lurus de-ngan frekuensinya:

Sementara itu,panjang gelombanya diberikan olehλ=c/ν, jadi 1 λ =R 1 n2_i − 1 n2_f ! , (77) dimana R≡ m 4π~3 e2 4π0 2 = 1,097×107 m−1 (78)

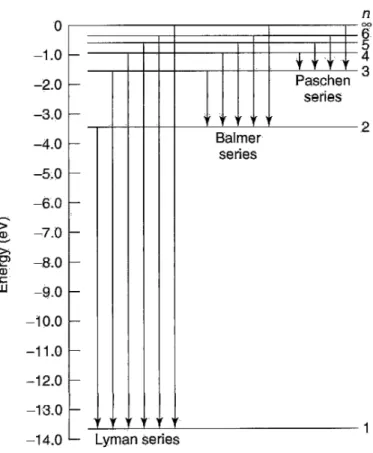
yang dikenal sebagai tetapan Rydberg. Persamaan 77 adalah rumus Rydberg untuk spektrum hidrogen, rumus ini ditemukan secara empiris pada abad kesembilanbelas dan merupakan capaian terbesar dari teori Bohr adalah kemampuannya untuk cocok dengan hasil ini—dan untuk menghi-tungR sebagai tetapan alam yang fundamental. Transisi ke keadaan dasar (nf = 1) berada pada daerah ultraviolet, yang dikenal oleh para

spektrosko-pis sebagaideret Lyman. Transisi ke keadaan tereksitasi pertama (nf = 2)

jatuh di daerah cahaya tampak dan membentukderet Balmer. Transisi ke

nf = 3 (deret Paschen) berada pada daerah inframerah; dan seterusnya

(Gambar 6). (Pada suhu kamar, sebagian besar atom hidrogen berada pada keadaan dasar, untuk mendapatkan spektrum emisi Anda harus mengum-pulkan atom-atom hidrogen yang berada pada keadaan tereksitasi, biasanya hal ini dilakukan dengan melewatkan lucutan listrik di dalam gas hidrogen.)

Gambar 3: Grafik beberapa fungsi gelombang radial, Rnl(r),

Gambar 4: Plot kerapatan untuk fungsi gelombang hidrogen

(n, l, m). Bayangkan setiap plot diputar terhadap sumbu z (ver-tikal).

Gambar 5: Permukaan |ψ|2 _{yang konstan untuk beberapa fungsi}