KOOPERATIF TIPE THINK PAIR SHARE (TPS) TERHADAP
KEMAMPUAN KOMUNIKASI MATEMATIS SISWA
(Kuasi Eksperimen di SMPN 3 Tangerang Selatan)
Skripsi
Diajukan Kepada Fakultas Ilmu Tarbiyah dan Keguruan
Untuk Memenuhi Persyaratan Memperoleh Gelar Sarjana Pendidikan (S.Pd)
Oleh:
SITI MARYAM NOER AZIZAH NIM : 106017000551
JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS ILMU TARBIYAH DAN KEGURUAN
UNIVERSITAS ISLAM NEGERI SYARIF HIDAYATULLAH
i
Kemampuan Komunikasi Matematis Siswa”. Skripsi Jurusan Pendidikan Matematika, Fakultas Ilmu Tarbiyah dan Keguruan, Universitas Islam Negeri Syarif Hidayatullah Jakarta, 2011.
Tujuan penelitian ini adalah untuk mengetahui pengaruh penerapan model pembelajaran kooperatif tipe Think Pair Share terhadap kemampuan komunikasi matematis siswa. Metode yang digunakan dalam penelitian ini adalah metode kuasi eksperimen dengan rancangan penelitian two group randomized subject posttest only. Penelitian ini dilakukan di SMPN 3 Tangerang Selatan tahun ajaran 2010/2011. Teknik pengambilan sampel dalam penelitian ini menggunakan cluster random sampling.
Instrumen yang digunakan untuk mengumpulkan data pada penelitian ini adalah tes essay yang sesuai dengan indikator komunikasi matematis pada materi himpunan. Tes yang diberikan terdiri dari 6 soal bentuk uraian.
Hasil penelitian menunjukkan bahwa rata-rata kemampuan komunikasi matematis siswa yang diajarkan dengan pembelajaran kooperatif tipe Think Pair Share adalah sebesar 64,75, sedangkan rata-rata kemampuan komunikasi matematis siswa yang diajarkan dengan pembelajaran konvensional adalah sebesar 55,25. Berdasarkan perhitungan uji-t, diperoleh thitung = 2,93 dan ttabel sebesar 1,67 dengan taraf signifikansi (α) = 0,05 dan derajat kebebasan 78. Karena thitung > ttabel, maka
rata-rata kemampuan komunikasi matematis siswa yang diajarkan dengan model pembelajaran kooperatif tipe Think Pair Share lebih tinggi daripada rata-rata kemampuan komunikasi matematis siswa yang diajarkan dengan pembelajaran konvensional. Dengan demikian, terdapat pengaruh yang signifikan penerapan model pembelajaran kooperatif tipe Think Pair Share (TPS) terhadap kemampuan komunikasi matematis siswa.
ii
SITI MARYAM NOER AZIZAH (106017000551). “The Effect of Cooperative Learning Think Pair Share (TPS) Type to Students Mathematical Communication”. Skripsi for Mathematic Education Department, Faculty of Tarbiyah and Teachers Training, Syarif Hidayatullah State Islamic University Jakarta, 2011.
The purpose of the research is to know the effect of cooperative learning Think Pair Share type to students mathematical communication. The method of the research is quasi eksperiment with two group randomized subject posttest only design. The research was conducted at SMPN 3 Tangerang Selatan for academic year 2010/2011. The technique of the research is cluster random sampling.
The instrument used to collect data in this research is essay test, which is based on indicator of mathematical communication at the subject of set. Tests consisted of 6 questions in essay.
The result of research revealed that the mean score of the students who are taught by cooperative learning Think Pair Share (TPS) type is 64,75, whereas the mean score of the students who are taught by conventional learning is 55,25. Based on hypothesis testing, found that tvalue = 2,93 and ttable = 1,67 at significant level 0,05
and degree of freedom 78. Cause tvalue is higher than ttable, than the students who
are taught by cooperative learning Think Pair Share (TPS) type have mean score of matematics communication higher than the students who are taught by conventional learning. So that, there’s significant effect of cooperative learning Think Pair Share (TPS) type to students mathematical communication .
iii
Alhamdulillah, puji syukur penulis panjatkan kehadirat Allah SWT yang telah memberikan rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan
skripsi ini. Shalawat dan salam semoga senantiasa tercurahkan kepada Nabi
Muhammad SAW, keluarga, sahabat dan para pengikutnya yang senantiasa
mengikuti ajarannya sampai akhir zaman.
Skripsi ini disusun untuk melengkapi salah satu persyaratan dalam
memperoleh gelar sarjana pendidikan pada program studi pendidikan matematika.
Skripsi ini disusun berdasarkan hasil penelitian di SMPN 3 Tangerang Selatan.
Penulis menyadari masih banyak kekurangan dan hambatan dalam penulisan
skripsi ini. Hal ini dikarenakan keterbatasan pengetahuan dan pengalaman penulis,
namun berkat dorongan dan bantuan dari berbagai pihak maka hambatan tersebut
dapat terselesaikan dengan baik.
Oleh karena itu, pada kesempatan kali ini penulis menyampaikan terima
kasih yang sebesar-besarnya kepada semua pihak yang telah membantu dan
memberikan moril dan materil, sehingga skripsi ini dapat selesai. Ucapan terima
kasih penulis sampaikan kepada:
1. Prof. Dr. Dede Rosyada, MA., Dekan Fakultas Ilmu Tarbiyah dan Keguruan
UIN Syarif Hidayatullah Jakarta.
2. Ibu Maifalinda Fatra, M.Pd., Ketua Jurusan Pendidikan Matematika Fakultas
Ilmu Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta.
3. Bapak Otong Suhyanto, M.Si., Sekretaris Jurusan Pendidikan Matematika
Fakultas Ilmu Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta.
4. Bapak Drs. H. M. Ali Hamzah, M.Pd., Dosen Pembimbing I yang penuh
kesabaran dan keikhlasan dalam membimbing penulis selama ini.
5. Ibu Lia Kurniawati, M.Pd., Dosen pembimbing II yang telah memberikan
bimbingan, arahan dan semangat kepada penulis selama menyusun skripsi ini.
6. Seluruh Dosen Jurusan Pendidikan Matematika UIN Syarif Hidayatullah
iv
berikan mendapatkan keberkahan dari Allah SWT.
7. Staff Jurusan Pendidikan Matematika UIN Syarif Hidayatullah Jakarta yang
telah memberi kemudahan dalam pembuatan surat-surat serta sertifikat.
8. Pimpinan dan staff Perpustakaan Umum dan Perpustakaan Fakultas Ilmu
Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta yang telah membantu
penulis dalam menyediakan serta memberikan pinjaman literatur yang
dibutuhkan.
9. Bapak Mulyono, SE. M.Pd. dan Bapak Drs. Sholeh Fathoni, Kepala Sekolah
dan Wakil Kepala Sekolah Bidang Kurikulum SMPN 3 Tangerang Selatan
yang telah memberikan kesempatan untuk penelitian kepada penulis. Serta Ibu
Rd. Lendra, S.Pd. dan Ibu Wiwit Turtinowati, S.Pd., guru matematika yang
telah membantu penulis dalam penelitian skripsi ini.
10.Siswa dan siswi SMPN 3 Tangerang Selatan, khususnya kelas 7.2 dan 7.6
yang telah kooperatif dalam penelitian ini.
11.Teristimewa untuk kedua orangtuaku tercinta, ayahanda M. Abdul Aziz dan
Ibunda Siti Rohana yang tiada hentinya mencurahkan kasih sayang, selalu
mendoakan, serta memberikan dukungan moril dan materil kepada penulis.
Adik - adikku tersayang M. Akbarullah Al-Aziz dan Siti Sarah Nurul Aziz
yang telah memberi dukungan moril serta doanya kepada penulis.
12.Sahabat-sahabat seperjuanganku di bangku kuliah Titin Nurhayati, Latifah,
Siti Mariam, Nita Suantika Zainul, Luk Luk Maknun, serta seluruh
teman-teman Pendidikan Matematika angkatan 2006 khususnya kelas B. Terima
kasih atas kebersamaan kalian selama ini, dengan kehadiran dan canda tawa
yang selalu menghiasi hari-hari penulis.
13.Seluruh sahabat kos Naeli Zakiah, Musyrifatul Khairiyah, Lisnawati, Iyke
Navy Samudra, Ela Yulia, Hafizah, Rahmawati, untuk semua canda tawa dan
motivasinya. Serta semua pihak yang telah membantu yang tidak bisa
disebutkan satu persatu, terima kasih untuk semuanya.
Penulis menyadari bahwa penulisan skripsi ini masih jauh dari
v
Jakarta, Februari 2011
Penulis
vi
ABSTRAK ... i
KATA PENGANTAR ... iii
DAFTAR ISI ... vi
DAFTAR TABEL ... viii
DAFTAR GAMBAR ... ix
DAFTAR BAGAN ... x
DAFTAR LAMPIRAN ... xi
BAB I PENDAHULUAN A. Latar belakang masalah ... 1
B. Identifikasi Masalah ... 6
C. Pembatasan Masalah ... 7
D. Perumusan Masalah ... 7
E. Tujuan Penelitian ... ... 7
F. Manfaat Penelitian ... ... 8
BAB II LANDASAN TEORI, KERANGKA BERPIKIR DAN PENGAJUAN HIPOTESIS A. Landasan Teori ... 9
1. Kemampuan Komunikasi Matematis ... 9
a. Pembelajaran Matematika ... 9
b. Kemampuan Komunikasi Matematis ... 15
c. Indikator Kemampuan Komunikasi Matematis ... 22
2. Model Pembelajaran Kooperatif tipe Think Pair Share (TPS) ... 24
a. Model Pembelajaran Kooperatif ... 24
b. Pembelajaran Kooperatif tipe Think Pair Share (TPS) ... 27
c. Keunggulan dan Kelemahan Model Pembelajaran Kooperatif tipe Think Pair Share (TPS) ... 29
3. Pembelajaran Konvensional ... 30
vii
A. Tempat dan Waktu Penelitian ... 37
B. Metode dan Desain Penelitian ... 37
C. Populasi dan Teknik Pengambilan Sampel Penelitian ... 38
D. Instrumen Penelitian ... 39
E. Teknik Pengumpulan Data ... 42
F. Teknik Analisis Data ... 42
G. Hipotesis Statistik ... 46
BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. Deskripsi Data ... 47
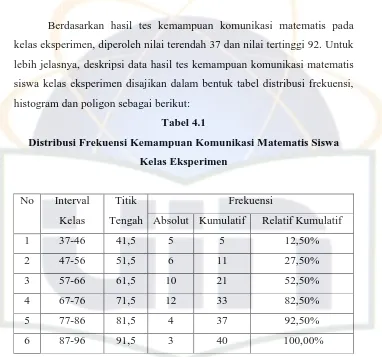
1. Kemampuan Komunikasi Matematis Siswa Kelompok Eksperimen ... 47
2. Kemampuan Komunikasi Matematis Siswa Kelompok KontroL ... 49
B. Hasil Pengujian Prasyarat Analisis ... 53
1. Uji Normalitas ... 53
2. Uji Homogenitas ... 54
C. Pengujian Hipotesis dan Pembahasan ... 55
1. Pengujian Hipotesis Penelitian... 55
2. Pembahasan Hasil Penelitian ... 56
D. Keterbatasan Penelitian ... 65
BAB V KESIMPULAN DAN SARAN A. Kesimpulan ... 66
B. Saran ... 66
viii
Tabel 3.1 : Jadwal Penelitian ... 37
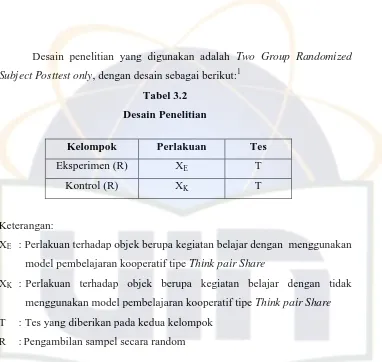
Tabel 3.2 : Desain Penelitian ... 38
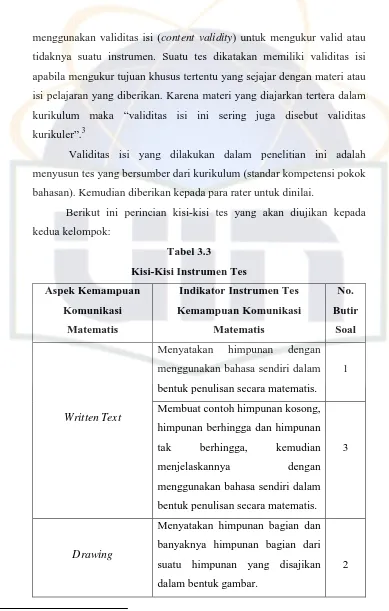
Tabel 3.3 : Kisi-Kisi Instrumen Tes ... 40
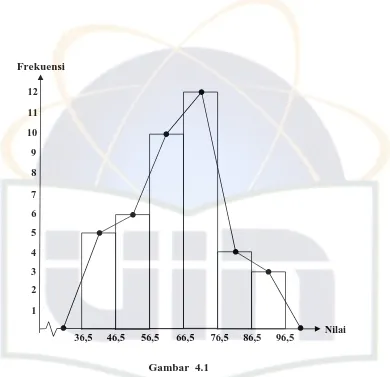
Tabel 4.1 : Distribusi Frekuensi Kemampuan Komunikasi Matematis Siswa Kelas Eksperimen ... 48
Tabel 4.2 : Distribusi Frekuensi Kemampuan Komunikasi Matematis Siswa Kelas Kontrol ... 50
Tabel 4.3 : Statistik Deskriptif Hasil Penelitian ... 52
Tabel 4.4 : Rekapitulasi Hasil Perhitungan Uji Normalitas ... 54
Tabel 4.5 : Rekapitulasi Hasil Perhitungan Uji Homogenitas ... 55
Tabel 4.6 : Rekapitulasi Hasil Perhitungan Uji Hipotesis ... 56
ix
Siswa Kelas Eksperimen ... 49
Gambar 4.2 : Grafik Histogram dan Poligon Kemampuan Komunikasi Matematis
Siswa Kelas Kontrol ... 51
Gambar 4.3 : Hasil Tes Akhir Siswa Kelas Eksperimen (Aspek Written Text) ... 59
Gambar 4.4 : Hasil Tes Akhir Siswa Kelas Kontrol (Aspek Written Text) ... 60
Gambar 4.5 : Hasil Tes Akhir Siswa Kelas Eksperimen (Aspek Drawing) ... 61
Gambar 4.6 : Hasil Tes Akhir Siswa Kelas Kontrol (Aspek Drawing) ... 62
Gambar 4.7 : Hasil Tes Akhir Siswa Kelas Eksperimen (Aspek Mathematical
Expression) ... 63 Gambar 4.8 : Hasil Tes Akhir Siswa Kelas Kontrol (Aspek Mathematical
[image:10.612.133.534.65.460.2]x
xi
Lampiran 2 : RPP Kelas Kontrol ... 92
Lampiran 3 : Lembar Kerja Siswa ... 109
Lampiran 4 : Penilaian Validitas Isi Instumen Kemampuan Komunikasi Matematis Oleh Panelis (Rater) ... 142
Lampiran 5 : Hasil Penilaian Validitas Isi oleh Para Rater ... 147
Lampiran 6 : Reliabilitas Interrater ... 148
Lampiran 7 : Soal Instrumen Tes ... 150
Lampiran 8 : Kriteria Penskoran ... 152
Lampiran 9 : Daftar Nilai Post Test Siswa ... 157
Lampiran 10 : Distribusi Frekuensi Kelompok Eksperimen ... 159
Lampiran 11 : Distribusi Frekuensi Kelompok Kontrol ... 163
Lampiran 12 : Perhitungan Uji Normalitas Kelas Eksperimen ... 167
Lampiran 13 : Perhitungan Uji Normalitas Kelas Kontrol ... 168
Lampiran 14 : Perhitungan Uji Homogenitas ... 169
1
PENDAHULUAN
A.
Latar Belakang Masalah
Pendidikan pada dasarnya merupakan suatu upaya untuk memberikan
pengetahuan, wawasan, keterampilan, dan keahlian tertentu kepada manusia
untuk mengembangkan bakat serta kepribadian mereka. Pendidikan juga
merupakan aktivitas manusia yang penting dan tidak dapat dipisahkan dari
kehidupan manusia, mulai dari manusia dilahirkan sampai akhir hayatnya.
Tujuan yang ingin dicapai dari proses pendidikan tersebut adalah
pengabdian kepada Allah, hal ini sejalan dengan tujuan penciptaan manusia
yang ditegaskan oleh Al-Quran dalam surat Al-Dzariyat 56:
ِ ْا ُ ْ ََ َ َو ِنْوُ ُْ َِ ِإ َ ِْ اَو
) ت را ا : ٥٦ (
Artinya: ”Dan Aku tidak menciptakan jin dan manusia melainkan agar
mereka beribadah kepada-Ku.”
Tujuan tersebut sejalan dengan tujuan hidup manusia, yaitu
semata-mata untuk beribadah kepada Allah swt. Dalam hal ini pendidikan harus
memungkinkan manusia memahami dan menghayati tentang Tuhannya
sedemikian rupa, sehingga semua ibadahnya dilakukan dengan penuh
penghayatan dan kekhusu’an kepada-Nya.
Sejalan dengan itu, UUD 1945 pasal 31 ayat 1 mengamanatkan
kepada Pemerintah untuk mengusahakan dan menyelenggarakan satu
pendidikan nasional yang mampu meningkatkan keimanan dan ketakwaan
kepada Tuhan Yang Maha Esa, serta akhlak mulia dalam rangka
mencerdaskan kehidupan bangsa. Hal ini senada dengan yang tertuang dalam
UU RI No. 20 tahun 2003 tentang fungsi dan tujuan pendidikan nasional
BAB II Pasal 3 yang berbunyi:
beriman dan bertaqwa terhadap Tuhan Yang Maha Esa, berahklak mulia, sehat, berilmu, cakap, kreatif, mandiri dan mejadi warga negara yang demokratis serta bertanggung jawab.1
Untuk mewujudkan tujuan pendidikan tersebut, maka
diselenggarakanlah rangkaian kependidikan. Diantaranya pendidikan formal
seperti sekolah, mulai dari tingkat kanak-kanak, sekolah dasar, sekolah
menengah sampai perguruan tinggi. Dalam keseluruhan proses pendidikan di
sekolah, kegiatan belajar dan pembelajaran merupakan kegiatan yang paling
pokok. Hal ini berarti bahwa berhasil tidaknya pencapaian tujuan pendidikan
banyak bergantung kepada bagaimana proses belajar dan pembelajaran di
sekolah.
Di sekolah, proses belajar dan pembelajaran meliputi berbagai bidang
ilmu pengetahuan diantaranya ilmu agama, sains, sosial, bahasa dan
matematika. Dalam sistem pendidikan, matematika merupakan bidang studi
yang menduduki peranan penting. Hal ini dapat dilihat dengan adanya jam
pelajaran matematika di sekolah yang lebih banyak di banding dengan jam
mata pelajaran lainnya. Selain itu, matematika merupakan mata pelajaran
yang diberikan di semua jenjang pendidikan mulai dari pendidikan dasar,
pendidikan menengah, dan sebagian di perguruan tinggi (PT). Tidak seperti
halnya mata pelajaran lain yang hanya diberikan pada jenjang tertentu.
Bertolak dari pentingnya peranan matematika dalam pendidikan,
maka matematika perlu diajarkan. Cockroft mengemukakan bahwa
matematika perlu diajarkan karena (1) selalu digunakan dalam segala segi
kehidupan; (2) semua bidang studi memerlukan keterampilan matematika
yang sesuai; (3) merupakan sarana komunikasi yang kuat, singkat, dan jelas;
(4) dapat digunakan untuk menyajikan informasi dalam berbagai cara; (5)
meningkatkan kemampuan berpikir logis, ketelitian, dan kesadaran
1
keruangan; dan (6) memberikan kepuasan terhadap usaha memecahkan
masalah yang menantang.2
Atas dasar pentingnya peranan matematika dalam pendidikan, maka
sampai batas tertentu matematika hendaknya dapat dikuasai oleh setiap
individu. Namun, dibalik pentingnya peranan yang dimiliki matematika,
matematika juga merupakan momok yang masih ditakuti oleh sebagian besar
siswa. Banyak siswa di setiap jenjang pendidikan menganggap matematika
sebagai pelajaran yang sulit dan sering menimbulkan berbagai masalah yang
sulit untuk dipecahkan, sehingga berdampak pada rendahnya prestasi belajar
siswa.
Prestasi belajar matematika siswa yang secara umum belum
menggembirakan tersebut dapat dilihat dari hasil UN SMP 2010 dengan
angka kelulusan yang mengalami penurunan cukup signifikan dibanding UN
2009, yaitu dari 95,05 % menjadi 90,27 % atau dari 3.605.163 siswa yang
mengikuti UN sebanyak 350.798 (9,73 %) siswa tidak lulus dan harus
mengikuti UN ulang.3 Dari empat mata pelajaran yang diujikan dalam UN
yaitu Bahasa Indonesia, Bahasa Inggris, Matematika dan Ilmu Pengetahuan
Alam, umumnya siswa yang tidak lulus dikarenakan nilai mata pelajaran
matematika yang tidak mencapai standar kelulusan.
Rendahnya prestasi belajar matematika bukan hanya disebabkan
karena matematika yang sulit, melainkan disebabkan oleh beberapa faktor
yang meliputi berbagai hal seperti siswa itu sendiri, guru, metode
pembelajaran, maupun lingkungan belajar yang saling berhubungan satu
sama lain. Faktor dari siswa itu sendiri adalah kurangnya pemahaman konsep
siswa terhadap materi yang diajarkan. Selain itu, faktor lain yang dapat
mempengaruhi rendahnya prestasi belajar siswa adalah adanya
2
Mulyono Abdurrahman, Pendidikan Bagi Anak Berkesulitan Belajar, (Jakarta: PT. Rineka Cipta, 2003), h. 253.
3
anggapan/asumsi yang keliru dari guru-guru yang menganggap bahwa
pengetahuan itu dapat dipindahkan secara utuh dari pikiran guru ke pikiran
siswa. Dengan adanya asumsi tersebut, guru memfokuskan pembelajaran
matematika pada upaya penuangan pengetahuan tentang matematika
sebanyak mungkin kepada siswa. Akan tetapi, dalam perkembangan seperti
sekarang ini, guru dituntut agar tugas dan peranannya tidak lagi sebagai
pemberi informasi melainkan sebagai pendorong belajar agar siswa dapat
mengkonstruksi sendiri pengetahuannya melalui berbagai aktifitas seperti
komunikasi matematis.
Kemampuan komunikasi matematis merupakan salah satu
kemampuan berpikir tingkat tinggi yang dikembangkan dalam pembelajaran
matematika. Kemampuan komunikasi matematis adalah kemampuan
mengkomunikasikan gagasan atau ide-ide matematik kedalam bentuk simbol,
tabel, grafik, atau diagram dan sebaliknya, untuk memperjelas keadaan atau
masalah serta pemecahannya.
Kemampuan komunikasi perlu diperhatikan dalam pembelajaran
matematika sebab kemampuan komunikasi sangat diperlukan dalam
menghadapi berbagai masalah, khususnya masalah yang berhubungan dengan
kehidupan sehari-hari. Dengan berkomunikasi, siswa dapat lebih memahami
simbol-simbol dan informasi yang ada di dalam pelajaran tersebut. Ironisnya
dalam pelaksanaan pembelajaran matematika di sekolah, jarang sekali siswa
diberi kesempatan untuk mengkomunikasikan ide-idenya. Hal ini berdampak
pada rendahnya kemampuan komunikasi matematis siswa.
Laporan TIMSS menyebutkan bahwa kemampuan siswa Indonesia
dalam komunikasi matematis sangat jauh di bawah negara-negara lain.
Sebagai contoh, untuk permasalahan matematik yang menyangkut
kemampuan komunikasi matematis, siswa Indonesia yang berhasil menjawab
dan Taiwan yang mencapai lebih dari 50%.4 Sejalan dengan hal tersebut,
Rohaeti dan Wihatma dalam Priyambodo menyatakan bahwa “rata-rata
kemampuan komunikasi matematis siswa berada dalam kualifikasi kurang”.5
Rendahnya kemampuan komunikasi matematis tidak terlepas dari
proses pembelajaran. Pembelajaran matematika masih banyak menggunakan
rumus-rumus yang sudah baku. Hal ini menyebabkan proses pembelajaran
masih cenderung pasif dan peserta didik kurang kreatif. Siswa yang tidak
dilibatkan untuk aktif dalam pembelajaran, dapat menyebabkan siswa sulit
untuk berekplorasi, berkreatifitas terhadap ide-ide yang mereka miliki
khususnya ide-ide matematika. Proses pembelajaran seperti ini menjadikan
siswa tidak komunikatif dan tidak mempunyai keterampilan dalam
mengembangkan dirinya.
Atas dasar permasalahan tersebut maka kemampuan komunikasi
matematis siswa harus ditingkatkan. Peningkatan kemampuan komunikasi
matematis siswa dapat dilakukan dengan mengadakan perubahan-perubahan
dalam pembelajaran. Dalam hal ini, perlu dirancang suatu pembelajaran yang
membiasakan siswa untuk mengkonstruksi pemikirannya baik dengan guru,
teman maupun terhadap materi matematika itu sendiri. Salah satu cara yang
dapat dilakukan untuk meningkatkan kemampuan komunikasi matematis
siswa adalah dengan menerapkan model pembelajaran yang tepat.
Model pembelajaran yang sebaiknya diterapkan adalah model
pembelajaran yang memberikan kesempatan kepada siswa untuk
mengkonstruksi pengetahuannya sendiri sehingga siswa lebih mudah untuk
memahami konsep-konsep yang diajarkan dan mengkomunikasikan
ide-idenya dalam bentuk lisan maupun tulisan. Salah satu alternatif untuk
mendukung hal tersebut adalah dengan menerapkan model pembelajaran
4
Andri Setiawan, Pembelajaran Berbasis Masalah untuk Meningkatkan Kemampuan Komunikasi dan Pemecahan Masalah Matematik Siswa Sekolah Menengah Pertama, (Bandung: Tesis UPI, Tidak Diterbitkan, 2008), h. 8.
5
kooperatif. Model pembelajaran kooperatif merupakan model pembelajaran
yang memungkinkan siswa untuk berinteraksi satu sama lain, baik interaksi
dengan sesama siswa maupun dengan guru.
Model pembelajaran kooperatif memiliki beberapa tipe. Salah satu
tipe model pembelajaran kooperatif yang dapat mendorong partisipasi aktif
siswa di dalam kelas adalah model pembelajaran kooperatif tipe
think-pair-share. Think-Pair-Share merupakan jenis pembelajaran kooperatif yang dirancang untuk mempengaruhi pola interaksi siswa serta memberikan
kesempatan kepada setiap siswa untuk menunjukkan pertisipasinya kepada
orang lain. Think-Pair-Share juga merupakan salah satu metode pembelajaran dengan kelompok kecil. Jumlah anggota kelompok yang hanya
terdiri dari 2 orang (berpasangan) dapat mengoptimalkan peran aktif setiap
siswa dalam kelompoknya serta memudahkan siswa untuk saling bekerja
sama dalam menuangkan dan mendiskusikan gagasan-gagasan matematika
yang dimilikinya baik dalam bentuk lisan maupun tulisan.
Berdasarkan latar belakang yang telah paparkan tersebut, penulis
merasa tertarik untuk melakukan penelitian secara teoritik dan praktik
dengan judul Pengaruh Penerapan Model Pembelajaran Kooperatif Tipe
Think Pair Share (TPS) Terhadap Kemampuan Komunikasi Matematis
Siswa.
B.
Identifikasi Masalah
Berdasarkan latar belakang terjadinya masalah yang telah dipaparkan,
penulis mengidentifikasi masalah sebagai berikut:
1. Kemampuan komunikasi matematis siswa yang masih rendah.
2. Siswa masih menganggap matematika sebagai mata pelajaran yang sulit
dan menakutkan.
3. Kemampuan pemahaman siswa terhadap konsep-konsep matematika
yang masih kurang.
C.
Pembatasan Masalah
Berdasarkan identifikasi masalah yang telah diuraikan, terdapat
berbagai masalah yang harus dihadapi. Sehingga pembatasan masalah dalam
penelitian ini sebagai berikut:
1. Masalah difokuskan pada pengaruh model pembelajaran kooperatif tipe
Think Pair Share terhadap kemampuan komunikasi matematis siswa. 2. Kemampuan komunikasi matematis siswa yang dimaksud adalah
kemampuan komunikasi matematis dalam bentuk tertulis, yang meliputi
written text, drawing, dan mathematical expression.
3. Penelitian dilakukan di SMPN 3 Tangerang Selatan kelas VII semester 2
tahun ajaran 2010/2011, pada pokok bahasan himpunan.
D.
Perumusan Masalah
Atas dasar identifikasi dan pembatasan masalah yang telah diuraikan,
maka penulis merumuskan masalah dalam penelitian sebagai berikut:
1. Bagaimana kemampuan komunikasi matematis siswa yang diajarkan
dengan model pembelajaran kooperatif tipe Think Pair Share dan pembelajaran konvensional?
2. Apakah terdapat pengaruh penerapan model pembelajaran kooperatif tipe
Think Pair Share terhadap kemampuan komunikasi matematis siswa?
E.
Tujuan Penelitian
Berdasarkan perumusan masalah yang diuraikan sebelumnya, maka
yang menjadi tujuan dalam penelitian ini adalah:
1. Mengetahui kemampuan komunikasi matematis siswa yang diajarkan
dengan model pembelajaran kooperatif tipe Think Pair Share dan pembelajaran konvensional.
2. Membandingkan kemampuan komunikasi matematis siswa yang
Think Pair Share dengan kemampuan komunikasi matematis siswa yang diajarkan dengan pembelajaran konvensional.
F.
Manfaat Penelitian
Manfaat penelitian yang dilakukan, diantaranya:
1. Bagi penulis, sebagai pedoman sekaligus menambah pengetahuan
tentang strategi mengajar mata pelajaran matematika dalam
mempersiapkan diri menjadi seorang pendidik profesional.
2. Bagi guru, agar dapat dijadikan sebagai salah satu alternatif dalam
memilih variasi yang dapat diterapkan dalam pembelajaran matematika
untuk meningkatkan kemampuan komunikasi matematis siswa serta
menjadikan proses belajar-mengajar menjadi lebih efektif, efisien dan
bermakna.
3. Bagi siswa, agar dapat meningkatkan kemampuan komunikasi matematis
dan meningkatkan kemampuan bersosialisasi dalam kelompok belajar
matematika.
4. Bagi sekolah yang di teliti, agar dapat meningkatkan mutu pendidikan di
sekolah tersebut.
5. Bagi pembaca, agar dapat dijadikan suatu kajian yang menarik untuk
9
LANDASAN TEORI, KERANGKA BERPIKIR
DAN PENGAJUAN HIPOTESIS
A.
Landasan Teori
1. Kemampuan Komunikasi Matematis a. Pembelajaran Matematika
Belajar merupakan suatu kegiatan yang tidak terpisahkan dari
kehidupan manusia. Untuk memenuhi kebutuhan dan sekaligus
mengembangkan dirinya, manusia telah melakukan kegiatan belajar
sejak dilahirkan. Hal ini sesuai dengan hadits yang diriwayatkan oleh
Rasulullah yang mewajibkan manusia untuk belajar semenjak dari
ayunan sampai liang lahat.
Belajar adalah tahapan perubahan seluruh tingkah laku individu
yang relatif menetap sebagai hasil interaksi dengan lingkungan yang
melibatkan proses kognitif.1 Perubahan-perubahan yang dihasilkan
akibat proses belajar merupakan hasil pengalaman yang dilakukan
dengan sadar dan bukan kebetulan karena melibatkan kognitif
seseorang. Dalam hal ini, seseorang yang belajar menyadari adanya
perubahan dalam dirinya. Perubahan yang diakibatkan oleh mabuk, gila
dan sebagainya tidak dapat dikatakan belajar karena individu yang
bersangkutan tidak menyadarinya.
Lebih dari sekedar melibatkan kemampuan kognitif, proses
belajar juga melibatkan kemampuan afektif (sikap) dan psikomotorik
(keterampilan) yang dimiliki seseorang. Hal ini dimaksudkan agar
perubahan akibat proses belajar bersifat positif dan berguna sehingga
lebih baik dari yang sebelumnya. Hal ini senada dengan yang
dikemukakan oleh Djamarah dalam bukunya Psikologi Belajar yang
1
mengatakan bahwa “belajar adalah serangkaian kegiatan jiwa raga
untuk memperoleh perubahan tingkah laku sebagai hasil dari
pengalaman individu dalam interaksi dengan lingkungannya yang
menyangkut kognitif, afektif, dan psikomotorik”.2
Mengenai pengertian belajar, lebih lanjut Yamin
mengemukakan bahwa belajar adalah “perubahan perilaku seseorang
akibat pengalaman yang ia dapat melalui pengamatan, pendengaran,
membaca dan meniru”.3 Dengan demikian, dapat dikatakan bahwa
perubahan yang terjadi pada proses belajar tidak hanya diperoleh
melalui proses interaksi atau pengalaman saja, melainkan melalui
proses latihan yang meliputi pengamatan, pendengaran, membaca dan
meniru.
Berdasarkan beberapa definisi belajar yang diutarakan oleh
beberapa ahli tersebut, secara umum belajar dapat didefinisikan sebagai
tahapan perubahan seluruh tingkah laku individu yang relatif menetap
untuk mencapai pribadi yang lebih baik sebagai hasil pengalaman dan
interaksi dengan lingkungan yang melibatkan kemampuan kognitif,
afektif dan psikomotorik.
Pembelajaran adalah segala upaya yang dilakukan oleh pendidik
agar terjadi proses belajar pada diri peserta didik.4 Hal senada juga
dikemukakan oleh Muhaimin (dalam Riyanto) yang mengatakan bahwa
“pembelajaran adalah upaya membelajarkan siswa untuk belajar”.5
Dalam hal ini kegiatan pembelajaran tidak berarti jika tidak
menghasilkan kegiatan belajar pada para peserta didiknya. Sehingga
kegiatan pembelajaran akan melibatkan peserta didik untuk
mempelajari sesuatu dengan cara yang efektif dan efisien.
2
Syaiful Bahri Djamarah, Psikologi Belajar, (Jakarta: PT. Rineka Cipta, 2008), h. 13.
3
Martinis Yamin, Strategi Pembelajaran Berbasis Kompetensi, (Jakarta: PT. Gaung Persada Press, 2005), h. 99.
4
Bambang Warsita, Teknologi Pembelajaran, Landasan dan Aplikasinya, (Jakarta: Rineka Cipta, 2008), h. 85.
5
Menurut Fontana (dalam Suherman) pembelajaran merupakan
upaya penataan lingkungan yang memberi nuansa agar program belajar
tumbuh dan berkembang secara optimal.6 Dengan demikian proses
pembelajaran bersifat eksternal yang sengaja direncanakan dan bersifat
rekayasa perilaku. Untuk itu, agar kegiatan pembelajaran menjadi
bermakna bagi peserta didik, maka harus diciptakan lingkungan yang
nyaman dan memberikan rasa aman bagi peserta didik.
Pembelajaran juga dapat diartikan sebagai proses belajar
mengajar, karena pada dasarnya pembelajaran merupakan interaksi
antara pendidik dalam mengajar (theaching) dan peserta didik dalam
belajar (learning).7 Implikasi dari pengertian tersebut adalah dalam
mencapai tujuan pembelajaran melibatkan unsur-unsur manusiawi yang
satu sama lain saling bersinergi.
Berdasarkan pengertian-pengertian yang telah dikemukakan,
dapat disimpulkan bahwa pembelajaran adalah suatu proses yang
disengaja atau upaya yang dirancang oleh pendidik dengan tujuan untuk
menciptakan suasana lingkungan (kelas/sekolah) yang memungkinkan
siswa melakukan kegiatan belajar, serta terjadinya interaksi optimal
antara guru dengan siswa serta antara siswa dengan siswa.
Matematika berasal dari perkataan latin mathematica yang mulanya diambil dari perkataan mathematike yang berarti relating to learning. Perkataan itu mempunyai asal katanya mathema yang berarti pengetahuan atau ilmu (knowledge, science). Kata mathematike berhubungan erat dengan kata lainnya yang hampir sama, yaitu
mathenein yang artinya belajar (berpikir). Jadi, berdasarkan asal katanya, maka perkataan matematika berarti ilmu pengetahuan yang
didapat dengan berpikir (bernalar). 8
6
Erman Suherman, dkk, Strategi Pembelajaran Matematika Kontemporer, (Bandung: JICA UPI, 2003), h. 7.
7
Oemar Hamalik, Kurikulum dan Pengajaran, (Jakarta: Bumi Aksara, 2009), h. 57.
8
Matematika merupakan salah satu mata pelajaran yang
mempelajari tentang bilangan-bilangan dengan operasinya dan dengan
aturan tertentu. Matematika sangat berkaitan dengan simbol-simbol,
konsep-konsep, pola bilangan dan sebagainya, yang semuanya
menyertakan logika dan pola pikir untuk bisa menganalisa dan dapat
dibuat kesimpulan. Seperti yang dikemukakan oleh James dan James
bahwa “matematika adalah ilmu tentang logika mengenai bentuk,
susunan, besaran, dan konsep-konsep yang berhubungan satu dengan
yang lainnya dengan jumlah yang banyak yang terbagi ke dalam tiga
bidang, yaitu aljabar, analisis, dan geometri”.9
Terdapat beberapa definisi lain mengenai matematika, Paling
mendefinisikan matematika sebagai “suatu cara untuk menemukan
jawaban, menggunakan informasi, menggunakan pengetahuan tentang
bentuk dan ukuran, serta menggunakan pengetahuan tentang
menghitung dan memikirkan dalam diri manusia itu sendiri dalam
melihat dan menggunakan hubungan-hubungan.”10 Sedangkan Hudoyo
mengatakan bahwa “matematika berkenaan dengan ide-ide,
struktur-struktur dan hubungan-hubungan yang diatur menurut urutan yang
logis”.11
Berdasarkan definisi-definisi yang telah dipaparkan dapat
disimpulkan bahwa yang dimaksud dengan matematika adalah ilmu
pengetahuan mengenai logika, bentuk, susunan, besaran dan konsep
yang saling berhubungan satu sama lain dan diatur secara logis, dimana
konsep-konsep yang baru didasarkan pada konsep-konsep terdahulu
yang telah diterima kebenarannya. Matematika merupakan ilmu yang
diperoleh melalui penalaran. Dalam hal ini konsep-konsep yang ada
dalam matematika dibuktikan kebenarannya secara deduktif. Selain itu
9
Erman Suherman, dkk, Strategi Pembelajaran..., h. 16.
10
Mulyono Abdurrahman, Pendidikan Bagi Anak Berkesulitan Belajar, (Jakarta: PT. Rineka Cipta, 2003), h. 252.
11
matematika juga dapat digunakan sebagai cara untuk menyelesaikan
permasalahan-permasalahan dalam kehidupan.
Matematika yang diajarkan di Pendidikan Dasar dan Pendidikan
Menengah disebut matematika sekolah.12 Matematika sekolah
merupakan bagian dari matematika yang dipilih berdasarkan atau
berorientasi kepada kepentingan pendidikan dan perkembangan IPTEK
sehingga tidak terlepas dari karakteristik matematika.
Matematika sekolah berkaitan dengan peserta didik yang
menjalani proses perkembangan kognitif dan emosional
masing-masing. Secara khusus dapat dikatakan bahwa dalam matematika
sekolah perlu memperhatikan aspek teori psikologi khususnya teori
psikologi perkembangan. Peserta didik memerlukan tahapan belajar
sesuai dengan perkembangan jiwa dan kognitifnya. Potensi yang ada
dalam diri anak berkembang dari tingkat rendah ke tingkat yang tinggi,
dari sederhana ke kompleks, dan dari konkrit menuju abstrak.
Matematika sekolah mempunyai peranan yang sangat penting
bagi semua komponen yang meliputi siswa, warga negara, negara dan
matematika itu sendiri. Bagi siswa, matematika sekolah berperan
sebagai bekal pengetahuan, pembetukan sikap dan pola pikirnya. Bagi
negara dan warga negaranya, matematika sekolah berperan bagi
perkembangan negara dan agar warga negaranya dapat hidup layak.
Sedangkan bagi matematika sendiri, matematika sekolah berperan
dalam rangka melestarikan dan mengembangkannya.
Pada pelaksanaannya, pembelajaran matematika di sekolah tidak
bisa terlepas dari sifat-sifat matematika yang abstrak dan sifat
perkembangan intelektual siswa yang diajar. Oleh karena itu, kita perlu
memperhatikan beberapa sifat atau karakteristik pembelajaran
matematika di sekolah. Menurut Erman Suherman, dkk dalam buku
yang berjudul “Strategi Pembelajaran Matematika Kontemporer”,
12
beberapa karakteristik matematika di sekolah diantaranya adalah bahwa
pembelajaran matematika adalah berjenjang, mengikuti metoda spiral,
menekankan pola pikir deduktif, serta menganut kebenaran
konsistensi.13
Karakteristik pembelajaran matematika yang menyatakan
pembelajaran matematika adalah berjenjang dimaksudkan bahwa materi
matematika diajarkan secara bertahap. Dimulai dari mengajarkan hal
yang konkrit dilanjutkan ke hal yang abstrak. Dalam pembelajaran
matematika harus dilakukan tahap demi tahap, dimulai dengan hal yang
sederhana ke hal yang kompleks. Siswa tidak mungkin mempelajari
konsep yang tinggi sebelum dia menguasai konsep yang lebih rendah,
karenanya matematika diajarkan dari konsep yang mudah menuju
konsep yang lebih sukar.
Selain diajarkan secara bertahap, pembelajaran matematika juga
mengikuti metoda spiral. Dalam mengajarkan konsep yang baru, perlu
dikaitkan dengan konsep yang telah dimiliki siswa sebelumnya,
sekaligus untuk mengingatkannya kembali. Pengulangan konsep
dengan cara memperluas dan memperdalam diperlukan dalam
pembelajaran matematika. Metoda spiral yang dimaksud di sini adalah
mengajarkan konsep dengan pengulangan atau perluasan dengan
adanya peningkatan. Jadi, spiral yang dimaksud adalah spiral naik,
bukan spiral datar.
Sifat pembelajaran matematika selanjutnya adalah menekankan
pola pikir deduktif. Matematika merupakan ilmu deduktif. Namun
demikian, dalam mengajarkannya perlu disesuaikan dengan kondisi
siswa. Misalnya, sesuai dengan perkembangan intelektual siswa di
SMP, maka dalam pembelajaran matematika tidak sepenuhnya
menggunakan pendekatan secara deduktif, melainkan dikombinasikan
dengan induktif. Seperti dalam pengenalan himpunan, siswa tidak
13
langsung diberikan definisi himpunan tersebut, tetapi diawali dengan
memberikan beberapa contoh kumpulan/kelompok yang di antaranya
ada yang merupakan himpunan. Sehingga dari contoh-contoh tersebut
siswa dapat membedakan antara himpunan dengan bukan himpunan.
Pembelajaran matematika juga menganut kebenaran konsistensi
yang didasarkan kepada kebenaran-kebenaran terdahulu yang telah
diterima. Kebenaran dalam matematika diperoleh secara deduktif.
Walaupun dimulai dengan pembuktian secara induktif, tetapi
selanjutnya harus bisa dibuktikan secara deduktif dengan cara
pengandaian.
Pada proses pembelajaran matematika, hendaknya guru
memberikan kesempatan kepada siswa untuk turut serta dalam
membangun sendiri pemahaman mengenai suatu konsep. Selain itu
guru juga harus memberikan kesempatan kepada siswa untuk
menggungkapkan pendapatnya mengenai konsep yang telah diperoleh
sehingga siswa dapat mengembangkan kemampuan komunikasi
matematisnya sesuai dengan yang diharapkan.
b. Kemampuan Komunikasi Matematis
Komunikasi merupakan hal yang sangat penting bagi manusia.
Untuk kelangsungan hidup manusia dari hari ke hari, manusia tidak
pernah terlepas dari komunikasi. Pada dasarnya komunikasi dapat
terjadi dalam berbagai konteks kehidupan termasuk dunia pendidikan.
Komunikasi dalam dunia pendidikan terjadi baik antara pendidik dan
peserta didik, maupun antara sesama peserta didik.
Komunikasi berasal dari bahasa latin “communis” atau dalam
bahasa inggrisnya “commun” yang artinya sama. Suwardi (dalam
Rohim) menyatakan bahwa “apabila kita berkomunikasi (to
untuk menimbulkan kesamaan”.14 Dalam hal ini, komunikasi dapat
terjadi apabila ada kesamaan antara penyampai pesan dan orang yang
menerima pesan.
Komunikasi merupakan cara berbagi gagasan dan
mengklarifikasi pemahaman, sehingga melalui komunikasi
gagasan-gagasan direfleksikan, diperbaiki, didiskusikan, dan diubah.15 Dalam
proses komunikasi, ide-ide yang diperoleh tidak semuanya dapat
diterima begitu saja. Beberapa ide tersebut ada yang mengalami
perbaikan dan perubahan melalui proses diskusi, sebelum akhirnya
ide-ide tersebut diterima dan kemudian digunakan.
Menurut Carl I. Hovland, komunikasi adalah “the process by
whichan individuals (the communicator) transmits stimuli (usually verbal symbols) to modify the behavior of other indivisuals (communicant)” yang berarti: “proses dimana seseorang (komunikator) menyampaikan perangsang-perangsang (biasanya lambang-lambang
dalam bentuk kata-kata) untuk merubah tingkah laku orang-orang lain
(komunikan)”.16 Hal yang senada dikemukakan oleh Effendy,
menurutnya “komunikasi adalah proses penyampaian pesan oleh
komunikator kepada komunikan melalui media yang menimbulkan
efek”.17
Proses komunikasi dikatakan berhasil apabila tujuannya yakni
terciptanya keadaan “saling mengerti” antara pihak pemberi pesan dan
pihak penerima pesan akan ide yang dikomunikasikan. Untuk mencapai
keberhasilan tersebut, proses komunikasi bergantung pada berbagai
faktor yang meliputi komunikator (pengirim pesan), pesan yang
14
Syaiful Rohim, Teori Komunikasi (Perspektif, Ragam dan Aplikasi), (Jakarta: Rineka Cipta, 2009), h. 8.
15
Wahyudin, Pembelajaran dan Model-model Pembelajaran, (Jakarta: CV. Ipa Abong, 2008), Seri-1, h. 38.
16Roudhonah, Ilmu Komunikasi, (Jakarta: Lembaga Penelitian UIN Jakarta, 2007), h. 20. 17
disampaikan, komunikan (penerima pesan), konteks dan sistem
penyampaian pesan.18
Keberhasilan proses komunikasi tidak hanya melibatkan
pengirim dan penerima pesan saja. Isi pesan yang sesuai dengan
kebutuhan penerima pesan, keadaan yang kondusif (nyaman,
menyenangkan, aman dan menantang) pada saat menyampaikan pesan,
serta metode dan media yang digunakan dalam menyampaikan pesan
juga merupakan faktor yang menunjang dan menentukan keberhasilan
komunikasi.
Berdasarkan beberapa definisi komunikasi yang telah
dikemukakan dapat disimpulkan bahwa komunikasi adalah proses
penyampaian, pemberitahuan, dan penerimaan ide-ide dari seseorang
(komunikator) kepada orang lain (komunikan) melalui media yang
menimbulkan efek; baik berupa lisan, tulisan, maupun gerakan, dimana
melalui komunikasi ide-ide direfleksikan, diperbaiki dan didiskusikan
sehingga ide-ide yang disampaikan memiliki kesamaan makna diantara
keduanya.
Komunikasi merupakan kemampuan penting dalam pendidikan
matematika, karena pembelajaran matematika pada umumnya terfokus
pada pengkomunikasian. Kemampuan komunikasi matematis adalah
menempatkan matematika sebagai alat untuk mempresentasikan dan
menyelesaikan berbagai masalah dalam kehidupan.19 Dengan demikian
komunikasi matematis merupakan hal yang sangat penting dalam
pembelajaran matematika di sekolah, karena selain sebagai kemampuan
yang harus dimiliki oleh setiap siswa, komunikasi matematis juga
merupakan sebuah alat yang dapat digunakan untuk menyelesaikan
permasalahan-permasalahan khususnya permasalahan matematika.
18
Igak Wardani, Dasar-dasar Komunikasi dan Keterampilan Dasar Mengajar, (Jakarta: Universitas Terbuka, 2001),h. 5-7.
19
Mengenai komunikasi matematis, Greenes dan Schulman
(dalam Satriawati) mengutarakan bahwa:
“komunikasi matematik merupakan: 1) kekuatan sentral bagi siswa dalam merumuskan konsep dan strategi matematik, 2) modal keberhasilan bagi siswa terhadap pendekatan dan penyelesaian dalam eksplorasi dan investigasi matematik, 3) wadah bagi siswa dalam berkomunikasi dengan temannya untuk memperoleh informasi, membagi pikiran, dan penemuan, curah pendapat, menilai dan mempertajam ide untuk meyakinkan yang lain.” 20
Dalam hal ini komunikasi matematis selain sebagai alat dalam
merumuskan konsep dan menyelesaikan permasalahan matematika,
juga sebagai sarana bagi siswa untuk saling bertukar informasi dan
ide-ide matematika sehingga konsep-konsep yang dirumuskan dapat
diyakini kebenarannya oleh semua pihak.
Aryan mengemukakan bahwa “kemampuan komunikasi dalam
matematika mengandung arti kemampuan siswa untuk berkomunikasi
dalam matematika yang meliputi penggunaan keahlian membaca,
menulis, menyimak, menelaah, menginterpretasi, dan mengevaluasi ide,
simbol, istilah, serta informasi matematika”.21 Ketika siswa
memperoleh konsep atau informasi matematika yang diberikan oleh
guru melalui proses menyimak yang kemudian mencatat ide penting
dari konsep yang disampaikan tersebut, atau siswa memperoleh konsep
tersebut secara sendiri melalui bacaan yang ditelaah dan kemudian
diinterpretasikannya, maka pada saat tersebut berlangsung proses
komunikasi dalam pembelajaran matematika.
Menurut Ernest (dalam Kadir dan Sumarna) komunikasi
matematis terdiri dari dua jenis, yakni tulisan (non-verbal) dan lisan
(verbal).22 Komunikasi matematis dalam bentuk tulisan adalah
20
Algoritma, Volume 1 No.1, (Jakarta: CeMED Jurusan Pendidikan Matematika UIN Jakarta, 2006), h. 109.
21
Bambang Aryan, Komunikasi dalam Matematika, dari http://rbaryans.wordpress.com/2007/05/30/komunikasi-dalam-matematika/, (14 Juli 2010, 15:20).
22
kemampuan dan keterampilan siswa menggunakan kosa kata, notasi
dan struktur matematika untuk menyatakan hubungan dan gagasan serta
memahaminya dalam memecahkan masalah. Sedangkan komunikasi
lisan tercermin melalui intensitas keterlibatan siswa dalam kelompok
kecil selama berlangsungnya proses pembelajaran.
Kedua jenis komunikasi matematis (tulisan dan lisan)
memainkan peranan yang penting dalam interaksi sosial siswa di kelas
matematika. Guru yang membiasakan siswa mampu
mengkomunikasikan ide melalui bahasa lisan dan tulisan ini dapat
membantu meningkatkan kemampuan komunikasi matematis siswa
sesuai standar komunikasi matematis yang ditetapkan.
Standar Isi (SI) yang terdapat pada Kurikulum Tingkat Satuan
Pendidikan (KTSP) menguraikan bahwa komunikasi matematis
merupakan salah satu kemampuan yang harus dimiliki oleh siswa selain
kemampuan pemahaman konsep, kemampuan penalaran, kemampuan
pemecahan masalah dan kemampuan koneksi matematis.23 Berdasarkan
hal tersebut, seorang siswa dikatakan mampu dalam komunikasi secara
matematis apabila ia mampu mengkomunikasikan gagasan matematik
dengan simbol, tabel, diagram atau media lain untuk memperjelas
keadaan atau masalah.
Sejumlah ahli mengemukakan bahwa kemampuan komunikasi
matematis merupakan salah satu kemampuan yang perlu
ditumbuhkembangkan di kalangan siswa. Menurut Baroody, ada dua
alasan penting mengapa kemampuan komunikasi dalam pembelajaran
matematika perlu ditumbuhkembangkan di kalangan siswa, yaitu:
mathematics as language (matematika sebagai bahasa) dan mathematics learning as social activity (matematika sebagai aktifitas sosial dalam pembelajaran).24
23Sri Wardhani, Analisis SI dan SKL Mata Pelajaran Matematika SMP/MTs untuk
Optimalisasi Tujuan Mata Pelajaran Matematika, (Yogyakarta: PPPPTK Matematika, 2008), h. 8.
24
Alasan yang menyatakan matematika sebagai bahasa
dimaksudkan bahwa matematika tidak hanya sekedar alat bantu
berpikir, menemukan pola, atau menyelesaikan masalah, namun
matematika merupakan alat yang tak terhingga nilainya untuk
mengkomunikasikan berbagai ide dengan jelas, tepat dan ringkas.
Sedangkan matematika sebagai aktifitas sosial dalam pembelajaran
maksudnya bahwa matematika sebagai wahana interaksi, baik interaksi
antar sesama siswa maupun antar guru dan siswa.
Selain mengemukakan tentang pentingnya
menumbuhkembangkan kemampuan komunikasi di kalangan siswa,
Baroody juga mengemukakan bahwa pembelajaran harus dapat
membantu siswa mengkomunikasikan ide matematika melalui lima
aspek komunikasi yang meliputi:25
1) Representasi (representing), yang diartikan sebagai kemampuan
siswa dalam mengungkapkan ide kedalam bentuk-bentuk visual.
2) Mendengar (listening), adalah aktifitas mendengarkan saat guru
ataupun siswa lain sedang berbicara.
3) Membaca (Reading), adalah aktifitas membaca teks secara aktif
dan mengelaborasi untuk mencari jawaban atas
pertanyaan-pertanyaan yang telah disusun, kemudian membuat catatan-catatan
kecil dari teks tersebut.
4) Diskusi (discussing), adalah aktifitas siswa dalam
mengkomunikasikan hasil yang diperoleh dari proses membaca.
Melalui diskusi dan saling interaksi yang dijalin oleh siswa dalam
bentuk kelompok, akan terbina suasana ketergantungan yang positif
antar anggota kelompok yang akhirnya akan dicapai suatu
pemahaman bersama.
25
5) Menulis (writing), adalah kegiatan yang dilakukan dengan sadar
untuk mengungkapkan dan merefleksikan pikiran/ide kedalam
bentuk tulisan.
Kemampuan komunikasi matematis yang dikembangkan di
tiap-tiap tingkat kelas memiliki karakteristik yang berbeda. Di
tingkat-tingkat kelas 5-8, pelajaran matematika hendaknya meliputi
kesempatan-kesempatan untuk berkomunikasi sehingga siswa
mampu:26
1) memodelkan situasi-situasi menggunakan metode lisan, tertulis, konkret, gambar, grafik dan aljabar.
2) merefleksikan dan memperjelas pemikiran mereka tentang ide-ide dan situasi-situasi matematis.
3) membangun pemahaman umum mengenai ide-ide matematis, termasuk peranan definisi-definisi.
4) menggunakan keahlian membaca, menulis dan memandang untuk menginterpretasikan dan mengevaluasi ide-ide matematis.
5) mendiskusikan ide-ide matematis serta membuat dugaan dan argumen yang meyakinkan.
6) mengapresiasi nilai notasi matematis dan peranannya dalam pembangunan ide-ide matematis.
Untuk meningkatkan kemampuan komunikasi matematis siswa
di tingkat-tingkat kelas tersebut, NCTM menyarankan agar komunikasi
difokuskan pada tugas-tugas matematika yang bermakna. Guru
seharusnya mengidentifikasi dan menggunakan tugas-tugas yang
berkaitan penting dengan ide matematika, dapat diselesaikan dengan
berbagai metode, memenuhi banyak contoh, dan memberikan
kesempatan kepada siswa untuk mengartikan, menyelidiki, dan
melakukan perkiraan/dugaan.27
26
Wahyudin, Pembelajaran dan Model-model Pembelajaran, (Jakarta: CV. Ipa Abong, 2008), Seri-1, h.64.
27
Dalam mengembangkan kemampuan komunikasi matematis di
kalangan siswa, terdapat beberapa faktor yang perlu diperhatikan,
antara lain:28
1) Pengetahuan prasyarat (Prior knowledge). Pengetahuan prasyarat merupakan pengetahuan yang telah dimiliki siswa sebagai hasil dari proses belajar sebelumnya. Hasil belajar yang diperoleh siswa bervariasi sesuai dengan kemampuan siswa itu sendiri. Jenis kemampuan yang dimiliki siswa sangat menentukan hasil pembelajaran selanjutnya.
2) Kemampuan membaca, diskusi, dan menulis. Dalam komunikasi matematis, kemampuan membaca, diskusi, dan menulis dapat membantu siswa memperjelas pemikiran dan dapat mempertajam pemahaman. Diskusi dan menulis adalah dua aspek penting dari komunikasi untuk semua tingkatan kelas.
3) Pemahaman matematik (Mathematical knowledge).
Merujuk pada pengertian komunikasi matematis di atas, dapat
disimpulkan bahwa yang dimaksud dengan kemampuan komunikasi
matematis adalah kemampuan siswa dalam mengekspresikan atau
menyampaikan ide-ide matematika (mathematical thinking) mereka
dengan bahasa matematika secara benar, baik dalam bentuk lisan,
tulisan, gambar, grafik, maupun simbol, dimana dengan kemampuan
komunikasi matematis yang dimiliki, siswa dapat menyelesaikan
permasalahan-permasalahan dalam kehidupan khususnya
permasalahan-permasalahan yang menuntut untuk diselesaikan secara
matematis.
c. Indikator Kemampuan Komunikasi Matematis
Ada beberapa indikator dalam kemampuan komunikasi
matematis yang dapat dicermati. Standar kurikulum NCTM tentang
komunikasi matematis, menyatakan bahwa indikator kemampuan
komunikasi matematis dapat dilihat dari:29
28Algoritma, Volume 1 No.1, ..., h. 111. 29
1) Kemampuan mengekspresikan ide-ide matematis melalui lisan, tulisan dan mendemonstrasikannya serta menggambarkannya secara visual.
2) Kemampuan memahami, menginterpretasikan dan mengevaluasi ide-ide matematis baik secara lisan, tulisan maupun dalam bentuk visual lainnya.
3) Kemampuan dalam menggunakan istilah-istilah, notasi-notasi matematika dan struktur-strukturnya untuk menyajikan ide-ide, menggambarkan hubungan-hubungan dengan model-model situasi.
Sumarmo mengemukakan bahwa indikator kemampuan
komunikasi matematis siswa meliputi:30
1) Menghubungkan benda nyata, gambar dan diagram kedalam idea matematika.
2) Menjelaskan idea, situasi dan relasi matematika, secara lisan/tulisan dengan benda nyata, grafik dan aljabar.
3) Menyatakan peristiwa sehari-hari dalam bahasa/simbol matematika.
4) Mendengarkan, berdiskusi dan menulis tentang matematika.
5) Membaca dengan pemahaman suatu prosentase matematika tertulis.
6) Membuat konjektur, mengurus argumen, merumuskan definisi dan generalisasi.
7) Menjelaskan dan membuat pertanyaan matematika yang telah dipelajari.
Sebagaimana yang telah diuraikan sebelumnya bahwa
kemampuan komunikasi matematis meliputi kemampuan komunikasi
lisan dan tulisan. Untuk melihat kemampuan komunikasi tertulis, Ross
mengemukakan sebagai berikut:31
1) Menggambarkan situasi masalah dan menyatakan solusi masalah menggunakan gambar, bagan tabel dan secara aljabar.
2) Menyatakan hasil dalam bentuk tertulis.
3) Menggunakan representasi menyeluruh untuk menyatakan konsep matematika dan solusinya.
4) Membuat situasi matematika dengan menyediakan ide dan keterangan dalam bentuk tertulis.
30Prosiding Seminar Nasional Matematika, Permasalahan Matematika dan Pendidikan
Matematika Terkini, (Bandung: UPI, 2007), h. 71.
31
Adapun indikator kemampuan komunikasi matematis yang
dikemukakan oleh Satriawati, yaitu:32
1) Written Text, yaitu memberikan jawaban dengan menggunakan bahasa sendiri, membuat model situasi atau persoalan menggunakan lisan, tulisan, konkret, grafik dan aljabar, menjelaskan dan membuat pertanyaan tentang matematika yang telah dipelajari, mendengarkan, mendiskusikan, dan menulis tentang matematika, membuat konjektur, menyusun argumen dan generalisasi.
2) Drawing, yaitu merefleksikan benda-benda nyata, gambar dan diagram ke dalam ide-ide matematika.
3) Mathematical Expression, yaitu mengekspresikan konsep matematika dengan menyatakan peristiwa sehari-hari dalam bahasa atau simbol matematika.
Berdasarkan uraian-uraian yang telah dikemukakan, dapat
disimpulkan bahwa kemampuan komunikasi matematis yang akan
digunakan dalam penelitian ini adalah kemampuan komunikasi
matematis dalam bentuk tertulis yang meliputi written text, drawing dan
mathematical expression.
2. Model Pembelajaran Kooperatif tipe Think Pair Share (TPS) a. Model Pembelajaran Kooperatif
Pembelajaran kooperatif adalah sebuah bentuk dari strategi
mengajar yang di desain untuk mendukung kerjasama di dalam
kelompok dan interaksi diantara siswa. Strategi ini dibuat untuk
mengurangi kompetisi yang ditemukan di banyak ruang kelas, yang
dapat menimbulkan “siapa yang menang dan siapa yang kalah” dan
dapat meningkatkan motivasi siswa untuk saling membantu dengan
tujuan yang sama.
Pembelajaran kooperatif adalah pembelajaran yang merujuk
pada berbagai macam metode pengajaran dimana para siswa bekerja
dalam kelompok-kelompok kecil untuk saling membantu satu sama
32
lainnya dalam mempelajari materi pelajaran”.33 Berdasarkan uraian
tersebut dapat dikatakan bahwa pembelajaran kooperatif tertuang dalam
wadah kelompok. Dalam masing-masing kelompok tersebut para siswa
saling bekerjasama. Kerjasama yang dijalin oleh setiap siswa tidak
hanya dalam menyelesaikan tugas yang diberikan oleh guru, melainkan
lebih kompleks lagi dengan saling bekerjasama dalam memahami
materi yang telah disampaikan dengan cara tutor sebaya. Dengan
demikian, dalam pembelajaran kooperatif siswa dijadikan sebagai
sumber belajar, selain guru, buku maupun sumber belajar lainnya.
Banyak para ahli yang mendefinisikan pembelajaran kooperatif,
diantaranya Wena mendefinisikan pembelajaran kooperatif sebagai
“sistem pembelajaran yang berusaha memanfaatkan teman sejawat
(teman lain) sebagai sumber belajar, disamping guru dan sumber belajar
yang lain”.34 Sedangkan Trianto mengemukakan bahwa “pembelajaran
kooperatif adalah pembelajaran yang memerlukan kerjasama antar
siswa dan saling ketergantungan dalam struktur pencapaian tugas,
tujuan, dan penghargaan”.35
Berdasarkan definisi-definisi diatas, dapat disimpulkan bahwa
pembelajaran kooperatif adalah suatu variasi pembelajaran dimana
siswa belajar, bekerja, dan berinteraksi di dalam kelompok-kelompok
kecil untuk mencapai tujuan bersama dengan memanfaatkan sesama
siswa sebagai sumber belajar, selain guru maupun sumber belajar
lainnya.
Pembelajaran kooperatif tidak hanya sekedar belajar kelompok,
sistem pembelajaran kooperatif bisa didefinisikan sebagai kerja/belajar
33
Robert E. Slavin, Cooperative Learning-Teori, Riset, dan Praktik, (Bandung: Nusa Media, 2005), h. 4.
34
Made Wena, Strategi Pembelajaran Inovatif Kontemporer, (Jakarta: PT. Bumi Aksara, 2009), h. 190.
35
kelompok yang terstruktur. Sebagai kelompok belajar yang terstruktur,
pembelajaran kooperatif memiliki unsur-unsur dasar sebagai berikut:36
1) Para siswa harus memiliki persepsi bahwa mereka “tenggelam atau berenang bersama”.
2) Para siswa harus memiliki tanggung jawab terhadap siswa atau peserta didik lain dalam kelompoknya, selain tanggung jawab terhadap diri sendiri dalam mempelajari materi yang dihadapi. 3) Para siswa harus berpandangan bahwa mereka semua memiliki
tujuan yang sama.
4) Para siswa membagi tugas dan berbagi tanggung jawab di antara para anggota kelompok.
5) Para siswa diberikan satu evaluasi atau penghargaan yang akan ikut berpengaruh terhadap evaluasi kelompok.
6) Para siswa berbagi kepemimpinan sementara mereka memperoleh keterampilan bekerja sama selama belajar.
7) Setiap siswa akan diminta mempertanggungjawabkan secara individual materi yang ditangani dalam kelompok kooperatif.
Pada hakikatnya, pembelajaran kooperatif sama dengan kerja
kelompok. Oleh sebab itu, banyak guru yang mengatakan tidak ada
sesuatu yang aneh dalam pembelajaran kooperatif, karena mereka
menganggap telah terbiasa menggunakannya. Walaupun pembelajaran
kooperatif terjadi dalam bentuk kelompok, tetapi tidak setiap kerja
kelompok dikatakan pembelajaran kooperatif.
Bennet menyatakan ada lima unsur dasar yang dapat
membedakan pembelajaran kooperatif dengan kerja kelompok, yaitu:37
1) Positive Interdependence, yaitu hubungan timbal balik yang didasari adanya kepentingan yang sama, atau perasaan diantara
anggota kelompok di mana keberhasilan seseorang merupakan
keberhasilan yang lain pula atau sebaliknya.
2) Interaction Face to face, yaitu interaksi yang langsung terjadi antar siswa tanpa adanya perantara. Tidak adanya penonjolan kekuatan
individu, yang ada hanya pola interaksi dan perubahan yang
36Isjoni, Cooperative Learning (Efektifitas Pembelajaran kelompok), (Bandung: Alfabeta,
2009), h. 13-14.
37
bersifat verbal diantara siswa yang ditingkatkan oleh adanya saling
hubungan timbal balik yang bersifat positif. Sehingga dapat
mempengaruhi hasil pendidikan dan pengajaran.
3) Adanya tanggung jawab pribadi mengenai materi palajaran dalam
anggota kelompok.
4) Membutuhkan keluwesan, yaitu menciptakan hubungan antar
pribadi, mengembangkan kemampuan kelompok, dan memelihara
hubungan kerja yang efektif.
5) Meningkatkan keterampilan bekerja sama dalam memecahkan
masalah (proses kelompok).
Apabila unsur-unsur dasar tersebut dilaksanakan oleh siswa
dalam pembelajaran maka siswa dapat meraih academic skill, social skill, dan interpersonal skill yang baik.
b. Pembelajaran Kooperatif tipe Think Pair Share (TPS)
Think-Pair-Share (berpikir, berpasangan, berbagi) merupakan salah satu jenis pembelajaran kooperatif yang dikembangkan oleh Frank
Lyman dan koleganya di Universitas Maryland. Menurutnya
think-pair-share merupakan suatu cara yang efektif untuk membuat variasi pola suasana diskusi kelas.38 Think-Pair-Share (TPS) atau berpikir berpasangan berbagi ini merupakan jenis pembelajaran kooperatif yang
dirancang untuk mempengaruhi pola interaksi siswa. Interaksi dalam
hal ini meliputi interaksi antar sesama siswa maupun antara siswa
dengan guru.
Think-Pair-Share memberikan kepada siswa waktu untuk berpikir dan merespon serta saling membantu satu sama lain. Dalam hal
ini siswa memiliki waktu lebih banyak untuk memikirkan jawaban atas
pertanyaan/permasalahan yang diajukan oleh guru, siswa diberi
kesempatan untuk menanggapi jawaban yang dikemukakan oleh sesama
38
temannya, serta siswa dipercaya untuk membantu temannya dalam
berbagai kesempatan, baik itu dalam menyelesaikan tugas maupun
dalam memahami materi pelajaran.
Adapun langkah-langkah yang ada dalam think-pair-share adalah sebagai berikut:39
1) Berpikir (Thinking)
Guru mengajukan suatu pertanyaan atau permasalahan yang
dikaitkan dengan materi pelajaran yang sedang dipelajari.
Selanjutnya guru meminta siswa menggunakan waktu beberapa
menit untuk memikirkan jawaban atas pertanyaan atau
permasalahan tersebut secara individu. Dalam tahap ini siswa perlu
dijelaskan bahwa berbicara atau mengerjakan bukan bagian dari
berpikir.
2) Berpasangan (Pairing)
Guru meminta siswa untuk berpasangan dan mendiskusikan apa
yang telah mereka peroleh dari proses berpikir (thinking)
sebelumnya. Interaksi yang dilakukan oleh siswa selama proses ini
dapat menyatukan jawaban yang dimiliki oleh masing-masing
siswa jika yang diajukan adalah suatu pertanyaan, dan dapat
menyatukan ide/gagasan apabila yang diajukan adalah suatu
masalah khusus yang diidentifikasi.
3) Berbagi (Sharing)
Pada tahap ini guru meminta pasangan-pasangan yang telah
dibentuk untuk membagikan hasil diskusinya kepada seluruh kelas.
Secara bergiliran masing-masing kelompok (pasangan)
mendapatkan kesempatan untuk melaporkan hasil diskusi tersebut
di depan kelas. Tahap ini berakhir sampai hampir sebagian dari
seluruh kelompok (pasangan) mendapat kesempatan melaporkan.
39
Berdasarkan uraian diatas, langkah-langkah pembelajaran
kooperatif tipe think-pair-share memiliki 3 tahapan yang meliputi tahap
berpikir (thinking), berpasangan (pairing), dan berbagi (sharing).
Ketiga tahap ini harus dilakukan secara sempurna, apabila tidak
dilakukan secara sempurna maka pembelajaran kooperatif tipe think-pair-share ini tidak akan mencapai hasil yang diharapkan.
c. Keunggulan dan Kelemahan Model Pembelajaran Kooperatif tipe Think Pair Share (TPS)
Jika dibandingkan dengan pembelajaran yang masih bersifat
konvensional, pembelajaran kooperatif tipe think-pair-share memiliki beberapa keunggulan. Keunggulan dari think-pair-share ini diantaranya: dapat memberikan kesempatan kepada siswa untuk bekerja
sendiri serta bekerjasama dengan orang lain, dapat mengoptimalkan
partisipasi siswa selama proses pembelajaran, dan dapat digunakan
dalam semua mata pelajaran pada semua tingkat usia anak didik.40
Selain memiliki keunggulan, pembelajaran kooperatif tipe
think-pair-share juga memiliki kekurangan. Kekurangan dari metode ini adalah sangat sulit diterapkan di sekolah yang rata-rata kemampuan
siswanya rendah. Selain itu, terbatasnya waktu yang tersedia dan
banyaknya jumlah kelompok yang terbentuk ditiap kelas menyebabkan
pembelajaran kooperatif tipe think-pair-share ini tidak efektif untuk diterapkan. Dalam hal ini guru harus pintar mengalokasikan waktu yang
tersedia dan adil dalam mendistribusikan kesempatan kepada setiap
kelompok (pasangan).
Setelah mengetahui keunggulan dan kelemahan yang terdapat
pada pembelajaran kooperatif tipe think-pair-share, baik siswa maupun
guru harus lebih menguasai aturan-aturan yang ada dalam pembelajaran
kooperatif tipe think-pair-share ini. Dengan begitu pembelajaran
40
kooperatif tipe think-pair-share dapat dilaksanakan dengan maksimal dan menjadikan suasana belajar yang menyenangkan.
3. Pembelajaran Konvensional
Pembelajaran konvensional merupakan suatu istilah dalam
pembelajaran yang lazim diterapkan dalam pembelajaran matematika.
Pembelajaran konvensional ini merupakan pembelajaran yang banyak di
kritik, namun banyak disukai oleh guru-guru karena pada dasarnya
pembelajaran konvensional mudah untuk diajarkan kepada siswa.
Pembelajaran konvensional yang dimaksud dalam penelitian ini
adalah pembelajaran secara klasikal dimana pada prosesnya lebih berpusat
pada guru41 atau instruktur. Pada proses pembelajaran ini keaktifan siswa
kurang optimal. Dalam pelaksanaannya, pembelajaran ini menitikberatkan
pada metode ceramah dan tanya jawab.
Metode ceramah merupakan suatu cara menyajikan pelajaran
melalui penuturan secara lisan atau penjelasan langsung kepada
sekelompok siswa.42 Pembelajaran ini cenderung membuat siswa pasif
dalam belajar, karena komunikasi yang digunakan oleh guru dalam
interaksinya dengan siswa adalah komunikasi satu arah. Siswa hanya
mendengar dan mencatat hal-hal apa yang disampaikan oleh guru. Dalam
hal ini guru seolah-olah bertugas memindahkan atau mentransfer
pengetahuan yang dimilikinya kepada siswa.
Ceramah sebagai metode pengajaran mempunyai beberapa
kelebihan, yaitu:43
a. Ceramah merupakan metode yang ’murah’ dan ’mudah’ untuk
dilakukan.
b. Ceramah dapat menyajikan materi pelajaran yang luas.
41
Erman Suherman, dkk, Strategi Pembelajaran..., h. 255.
42
Wina Sanjaya, Strategi Pembelajaran Berorientasi Standar Proses Pendidikan, (Jakarta: Kencana, 2008), h. 147.
43