SISWA
Skripsi
Diajukan untuk Memenuhi Persyaratan Mencapai Gelar Sarjana Pendidikan
Oleh
Puji Syafitri Rahmawati
NIM 109017000059
JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS ILMU TARBIYAH DAN KEGURUAN
UNIVERSITAS ISLAM NEGERI SYARIF HIDAYATULLAH
LEMBAR PENGESAIHN PEMBIMBING
SKRIPSI
Skripsi berjudul Pengaruh Pendekatan Probtem
Salrizg
TerhadapKemampuan Representasi Matematis Siswa disusun
oleh
Paji
SyafitriRahmawati
NIM.
109017000059, Jurusan Pendidikan Matematika, Fakultas Ilmu Tartiyah dan Keguruan, Universitas Islam Negeri lyarif Hidayatullah Jakarta. Telah melalui bimbingan dan dinyatakan sah , sebagai karya ilmiah yang berhak untuk diujikan pada siding munaqasah sesuai ketentuan yang ditetapkap oleh fakultas.Yang Mengesahkan,
Jakarta,5)nd
2015lcbruai
Pembimbing II Pembimbing I
I
4L,tfu"'
U
Dr, Gelar Dwirahayu
NIP. I 9790601 200,604 2 004 NtP. 19820528 201
l0I
2 0l Ii
PUJI SYAFITRI RAHMAWATI (109017000059), “Pengaruh Pendekatan Problem Solving Terhadap Kemampuan Representasi Matematis Siswa”, Fakultas
Ilmu Tarbiyah dan Keguruan, Universitas Islam Negeri Syarif Hidayatullah Jakarta, Januari 2015.
Tujuan penelitian ini adalah untuk menganalisis perbedaan kemampuan representasi matematis siswa yang diajarkan dengan pendekatan problem solving dan pendekatan konvensional, serta menganalisis kemampuan representasi matematis siswa yang diajarkan dengan pendekatan problem solving. Penelitian ini dilakukan di SMP Negeri 32 Bekasi Tahun Ajaran 2014/2015. Metode yang digunakan pada penelitian ini adalah metode eksperimen kuasi dengan desain penelitian Randomized Posttest-Only Control Group Design yang melibatkan 76 siswa sebagai sampel. Penentuan sampel menggunakan teknik cluster random sampling. Pengumpulan data setelah perlakuan menggunakan tes kemampuan representasi matematis siswa.
Hasil penelitian mengungkapkan bahwa kemampuan representasi matematis siswa yang diajarkan dengan pendekatan problem solving lebih tinggi dibandingkan dengan kemampuan representasi matematis siswa yang diajarkan dengan pendekatan konvensional. Hal ini dapat dilihat dari nilai rata-rata hasil tes kemampuan representasi matematis siswa yang diajarkan dengan pendekatan problem solving
sebesar 67,13 dan nilai rata-rata kemampuan representasi matematis siswa yang diajarkan dengan pendekatan konvensional sebesar 57,45 (thitung > ttabel = 2,73 > 1,66).
Kesimpulan dari hasil penelitian ini adalah bahwa kemampuan representasi matematis siswa yang diajarkan dengan menggunakan pendekatan problem solving
lebih tinggi dibandingkan dengan kemampuan representasi matematis siswa yang diajarkan dengan menggunakan pendekatan konvensional.
ii
PUJI SYAFITRI RAHMAWATI (109017000059), “Impact of Problem Solving Approach toward Students’ Mathematical Representation Skills”. Paper of Major of Mathematics Education, Faculty of Tarbiyah and Teaching Learning, Stated Islamic University of Syarif Hidayatullah Jakarta, January 2015.
The purpose of this research is to analyze differences in students’ mathematical representation skills being taught by using a problem solving approach from the students’ mathematical skills being taught conventional approach, and to
analyze students’ mathematical representation skills who are taught by using problem solving approach. This research was conducted at SMP Negeri 32 Bekasi for 2014/2015 Academic Year. The method used in this research is a quasi experimental method with randomized posttest-only control group design involving 76 students as the samples. The samples withdrawal technique is by using cluster random sampling technique. Collecting data after treatment uses a students’ mathematical representation skills test.
The result of research reveals that the students’ mathematical representation skills being taught by using a problem solving approach was higher than the students’ mathematical representation skills being taught by using conventional approach. This result can be looked from that mean value of the students’ mathematical representation skills test who taught by using problem solving approach is 67,13 and that mean value of students’ mathematical representation skills being taught by using conventional approach is 57,45 (t-count > t-table = 2,73 > 1,66). The conclusion of this research is that the students’ mathematical representation skills being taught by
using a problem solving approach was higher than the students’ mathematical
representation skills being taught by using conventional approach.
iii
Alhamdulillah segala puji kehadirat Allah SWT. yang telah melimpahkan
rahmat, karunia, nikmat islam, nikmat iman, nikmat sehat yang berlimpah kepada
kita semua. Shalawat serta salam juga tidak lupa dicurahkan kepada Nabi
Muhammad SAW serta pengikutnya yang telah membawa kita dari jaman gelap
gulita ke jaman terang benderang seperti sekarang ini.
Dalam masa penyusunan skripsi, penulis tidak memungkiri bahwa tidak
sedikit duka dan luka yang dialami. Namun berkat kerja keras, usaha, kesabaran
dan doa, serta kesungguhan hati dan dorongan-dorongan positif baik secara
langsung maupun tidak langsung dari banyak pihak membuat penulis akhirnya
dapat menyelesaikan skripsi ini. Oleh sebab itu, penulis mengucapkan banyak
terima kasih kepada:
1. Bapak Prof. Dr. Ahmad Thib Raya, MA, Dekan Fakultas Ilmu Tarbiyah dan
Keguruan UIN Syarif Hidayatullah Jakarta
2. Bapak Dr. Kadir, M.Pd, Ketua Jurusan Pendidikan Matematika Fakultas Ilmu
Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta
3. Bapak Abdul Muin, S.Si, M.Pd, Sekretaris Jurusan Pendidikan Matematika
Fakultas Ilmu Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta
4. Bapak Otong Suhyanto, M.Si., Dosen Penasehat Akademik Pendidikan
Matematika Fakultas Ilmu Tarbiyah dan Keguruan UIN Syarif Hidayatullah
Jakarta yang selalu memperhatikan mahasiswa-mahasiswa didiknya, termasuk
penulis.
5. Ibu Dr. Gelar Dwirahayu, Dosen Pembimbing I, dan Ibu Eva Musyrifah, M.si,
Dosen Pembimbing II, yang telah memberikan waktu, bimbingan, arahan,
motivasi, dan semangat dalam membimbing penulis selama ini. Terlepas dari
segala perbaikan dan kebaikan, semoga Ibu selalu berada dalam
kemuliaan-Nya.
6. Seluruh Dosen Jurusan Pendidikan Matematika UIN Syarif Hidayatullah
penulis menjalani masa perkuliahan. Semoga ilmu-ilmu yang Bapak dan Ibu
berikan mendapatkan keberkahan dari Allah SWT.
7. Para Staf Fakultas Tarbiyah dan Keguruan dan Para Staf Jurusan Pendidikan
Matematika yang senantiasa memberikan kemudahan pada penulis dalam hal
pembuatan surat-surat dan sertifikat. Pimpinan dan Staf Perpustakaan Umum
dan Perpustakaan Fakultas Ilmu Tarbiyah dan Keguruan UIN Syarif
Hidayatullah Jakarta yang telah membantu penulis dalam menyediakan serta
memberikan pinjaman literatur yang dibutuhkan.
8. Bapak H. Syamsuri, S.Pd, Kepala Sekolah SMP Negeri 32 Bekasi, yang telah
memberikan ijin kepada penulis untuk melakukan penelitian. Para dewan guru,
khususnya Ibu Fanny Febriyanti, S.Pd, selaku guru mata pelajaran matematika
yang telah membantu penulis pada saat melakukan penelitian. Seluruh siswa
SMP Negeri 32 Bekasi, khususnya siswa kelas 8.3 dan 8.1.
9. Keluarga tercinta. Mamah Ai Rustini dan Papah Asep Suratman yang selalu
memberikan semangat-semangat positif di saat penulis merasa down, dukungan moril dan materil, serta doa yang tidak pernah terputus demi
kelancaran, kemudahan, dan kesuksesan penulis dalam menyelesaikan skripsi
ini. Kakak tercinta Gama Ufiz Arfakhsyadz, Rina Nur Fitriyani, serta Adik
Martina Fauziyah yang selalu memberikan kasih sayang yang berlimpah,
kebahagiaan dan masukan-masukan yang sangat berarti dalam penyusunan
skripsi ini. Tidak lupa juga untuk keponakan tercinta, terlucu, terimut dan
tertampan, Umar Faiz Abdullah, yang selalu menjadi mood-booster, memberikan keceriaan, penghilang rasa lelah dan sedih bagi penulis. Semoga
mamah, papah, kakak-kakak, adik, dan Umar tampan selalu berada dalam
lindungan-Nya dan diberikan kemudahan dan kelancaran dalam segala hal
oleh Allah SWT.
10.Yang terkasih, Muchtar, S.Pd, yang selalu ada disaat penulis membutuhkan
saran dan masukan, tempat curhat, teman mengobrol, memberikan banyak
kasih sayang, penghilang rasa jenuh dan lelah, dan selalu memberikan
lindungan-Nya, dan diberikan kemudahan kelancaran dalam segala hal oleh
Allah SWT.
11.Keluarga keduaku, Anak Kosan Keche Badai. Ichamy Beruang Banchi
Gembhul, Hestyschon Masha Desriyanto, Arya Pimpim, Qisty Dora, Mamih
Indah, Imute, Elaphe, Nyai Dijah, Atu, Iva, dan Ipit, serta adik-adik kosan
yang sedang berjuang bersama-sama penulis dalam penyusunan skripsi yang
selalu memberikan semangat dan kasih sayang yang berlimpah, menemani
penulis dalam menyusun skripsi, bertukar saran dan masukan dalam
penyusunan skripsi, dan membuat hari-hari penulis lebih berwarna.
12.Teman-teman seperjuangan mahasiswa Jurusan PMTK kelas A, B, dan C angkatan 2009. Semoga kalian selalu sehat wal’afiat dan selalu dalam lindungan-Nya.
Ucapan terimakasih juga ditujukan kepada pihak-pihak yang namanya
belum bisa disebutkan satu per satu. Penulis hanya dapat memohon dan berdoa
semoga bantuan-bantuan, masukan-masukan, semangat-semangat yang kalian
berikan menjadi pintu datangnya ridho yang diberikan Allah SWT di dunia dan akhirat. Aamiin Ya Rabbal’alamiin.
Demikianlah, walaupun penulis sudah berupaya menyusun skripsi ini
dengan sebaik-baiknya, akan tetapi tetap saja penulis merasa masih terdapat
banyak kesalahan di dalam skripsi ini. Oleh karena itu, penulis dengan senang hati
akan menerima kritik dan saran yang membangun dari siapa saja yang membaca
skripsi ini.
Penulis berharap skripsi ini dapat memberikan manfaat sebesar-besarnya
bagi penulis pribadi dan para pembaca umumnya.
Jakarta, Februari 2015
iv
ABSTRAK ... i
ABSTRACT ... ii
KATA PENGANTAR ... iii
DAFTAR ISI ... iv
DAFTAR TABEL ... vii
DAFTAR GAMBAR ... viii
DAFTAR LAMPIRAN ... x
BAB I PENDAHULUAN ... 1
A. Latar Belakang Masalah ... 1
B. Identifikasi Masalah ... 7
C. Pembatasan Masalah... 8
D. Perumusan Masalah ... 8
E. Tujuan Penelitian ... 8
F. Manfaat Penelitian ... 8
BAB II KAJIAN TEORI DAN PENGAJUAN HIPOTESIS ... 10
A. Deskripsi Teoretik ... 10
1. Kemampuan Representasi Matematis ... 10
a. Representasi Eksternal ... 13
b. Representasi Internal ... 13
2. Pendekatan Problem Solving ... 18
a. Pengertian Pendekatan Problem Solving ... 18
b. Tahap Pendekatan Problem Solving ... 21
c. Hubungan Pendekatan Problem Solving dengan Kemampuan Representasi Matematis ... 23
B. Hasil Penelitian yang Relevan ... 26
C. Kerangka Berpikir ... 27
BAB III METODOLOGI PENELITIAN ... 31
A. Tempat dan Waktu Penelitian ... 31
B. Metode dan Desain Penelitian ... 31
C. Populasi dan Teknik Pengambilan Sampel ... 32
D. Instrumen Penelitian ... 32
1. Uji Validitas ... 35
2. Uji Reliabilitas ... 36
3. Uji Indeks Kesukaran ... 37
4. Uji Daya Pembeda ... 38
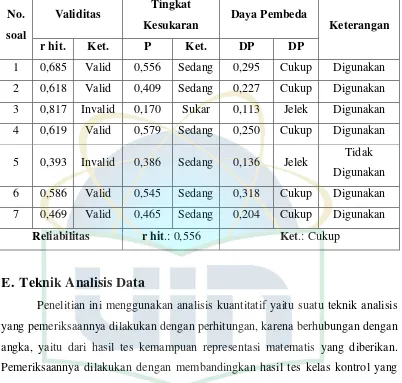
E. Teknik Analisis Data ... 39
1. Uji Normalitas ... 40
2. Uji Homogenitas ... 41
3. Uji Hipotesis ... 41
BAB IV HASIL PENELITIAN DAN PEMBAHASAN ... 44
A. Deskripsi Data ... 44
1. Kemampuan Representasi Matematis Siswa ... 44
a. Kelas Eksperimen ... 44
b. Kelas Kontrol ... 46
c. Perbandingan Kemampuan Representasi Matematis Kelas Eksperimen dan Kelas Kontrol ... 49
2. Kemampuan Representasi Matematis Siswa Berdasarkan Indikator Representasi ... 51
a. Kelas Eksperimen ... 51
b. Kelas Kontrol ... 53
c. Perbandingan Kemampuan Representasi Matematis Kelas Eksperimen dan Kelas Kontrol Berdasarkan Indikator Representasi ... 54
B. Pengujian Persyaratan Hipotesis ... 56
1. Uji Normalitas ... 56
a. Uji Normalitas Kelas Eksperimen ... 56
2. Uji Homogenitas ... 57
C. Pengujian Hipotesis ... 58
D. Pembahasan Hasil Penelitian ... 59
1. Proses Pembelajaran Kelas Eksperimen dan Kelas Kontrol .... 60
2. Analisis Kemampuan Representasi Matematis ... 65
a. Indikator Visual ... 65
b. Indikator Persamaan/Ekspresi Matematis ... 67
c. Indikator Kata-Kata/Teks Tertulis ... 69
E. Keterbatasan Penelitian ... 73
BAB V KESIMPULAN DAN SARAN ... 75
A. Kesimpulan ... 75
B. Saran ... 75
DAFTAR PUSTAKA ... 77
vii
Tabel 2.1 Indikator Kemampuan Representasi ... 17
Tabel 3.1 Rancangan Desain Penelitian ... 31
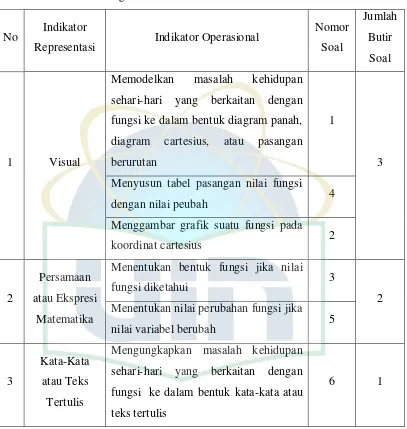
Tabel 3.2 Kisi-Kisi Instrumen Tes Kemampuan Representasi Matematis ... 33
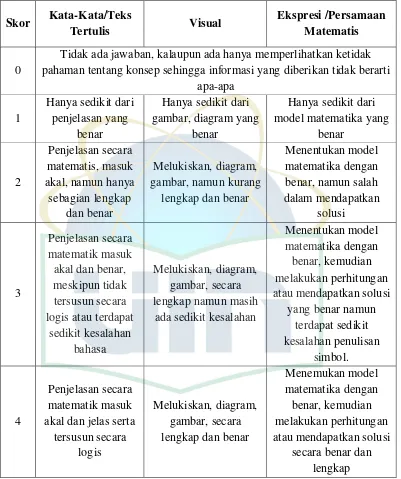
Tabel 3.3 Pedoman Penskoran Tes Kemampuan Representasi Matematis Materi Relasi Fungsi ... 34
Tabel 3.4 Derajat Reliabilitas ... 36
Tabel 3.5 Klasifikasi Indeks Kesukaran Soal ... 37
Tabel 3.6 Klasifikasi Daya Pembeda Soal ... 38
Tabel 3.7 Rekapitulasi Hasil Uji Validitas, Daya Pembeda, Taraf Kesukaran, dan Reliabitas ... 39
Tabel 4.1 Distribusi Frekuensi Kemampuan Representasi Matematis Siswa pada Kelompok Eksperimen ... 45
Tabel 4.2 Distribusi Frekuensi Kemampuan Representasi Matematis Siswa pada Kelompok Kontrol ... 47
Tabel 4.3 Perbandingan Nilai Kemampuan Representasi Matematis Siswa Kelompok Eksperimen dengan Kelompok Kontrol ... 49
Tabel 4.4 Data Kemampuan Representasi Matematis Siswa Per Indikator Kelompok Eksperimen ... 52
Tabel 4.5 Data Kemampuan Representasi Matematis Siswa Per Indikator Kelompok Kontrol ... 53
Tabel 4.6 Perbandingan Kemampuan Representasi Matematis Kelompok Eksperimen dan Kelompok Kontrol Berdasarkan Indikator Representasi ... 54
Tabel 4.7 Hasil Perhitungan Uji Normalitas Data Kelompok Eksperimen dan Kelompok Kontrol ... 57
Tabel 4.8 Hasil Uji Homogenitas Kelompok Eksperimen dan Kelompok Kontrol ... 57
viii
Gambar 1.1 Hasil Jawaban Siswa yang Diteliti ... 4
Gambar 2.1 Contoh Representasi Usia oleh Anak ... 12
Gambar 2.2 Hubungan Timbal Balik Antara Representasi Eksternal dan
Representasi Internal ... 15
Gambar 2.3 Five Different Representations of Mathematical Ideas.
Translation Between and Within Each Can Help Develop New Concepts ... 16
Gambar 2.4 Kerangka Pemecahan Masalah Matematika ... 24
Gambar 2.5 Kerangka Berpikir Penelitian ... 29
Gambar 4.1 Histogram Distribusi Frekuensi Kumulatif Hasil Tes
Kemampuan Representasi Matematis Siswa Kelompok
Eksperimen ... 46
Gambar 4.2 Histogram Distribusi Frekuensi Kumulatif Hasil Tes
Kemampuan Representasi Matematis Siswa Kelompok
Kontrol ... 48
Gambar 4.3 Kurva Perbandingan Nilai Kemampuan Representasi Matematis
Siswa pada Kelompok Eksperimen dan Kelompok Kontrol ... 50
Gambar 4.4 Persentase Kemampuan Representasi Matematis Siswa
Kelompok Eksperimen dan Kontrol Berdasarkan Indikator ... 55
Gambar 4.5 Kurva Uji Perbedaan Data Kelompok Eksperimen dan
Kelompok Kontrol ... 59
Gambar 4.6 Proses Understand pada Pendekatan Problem Solving ... 61 Gambar 4.7 Proses Plan dan Carry Out pada Pendekatan Problem Solving . 62 Gambar 4.8 Proses Conclusion pada Pendekatan Problem Solving ... 63
Gambar 4.9 Suasana Belajar pada Kelas 8.3 Sebagai Kelompok Eksperimen:
(a) Siswa Duduk Bersama Kelompoknya, dan (b) Siswa
Berdiskusi dalam Menyelesaikan LKS yang Diberikan ... 64
Gambar 4.11 Jawaban Siswa Kelompok Kontrol pada Indikator Visual ... 66
Gambar 4.12 Jawaban Siswa Kelompok Eksperimen pada Indikator
Persamaan/Ekspresi Matematis ... 68
Gambar 4.13 Jawaban Siswa Kelompok Kontrol pada Indikator
Persamaan/Ekspresi Matematis ... 68
Gambar 4.14 Jawaban Siswa Kelompok Eksperimen pada Indikator
Kata-Kata/Teks Tertulis ... 70
Gambar 4.15 Jawaban Siswa Kelompok Kontrol pada Indikator
x
Lampiran 1 RPP Eksperimen ... 81
Lampiran 2 RPP Kontrol ... 93
Lampiran 3 LKS Eksperimen ... 102
Lampiran 4 Pedoman Penskoran Kemampuan Representasi Matematis ... 120
Lampiran 5 Kisi-Kisi Tes Kemampuan Representasi Matematis ... 121
Lampiran 6 Instrumen Tes Kemampuan Representasi Matematis ... 122
Lampiran 7 Kunci Jawaban Instrumen Tes Kemampuan Representasi Matematis ... 124
Lampiran 8 Hasil Ujicoba Instrumen Tes Kemampuan Representasi Matematis ... 128
Lampiran 9 Hasil Uji Validitas Instrumen ... 129
Lampiran 10 Perhitungan Uji Validitas Instrumen ... 130
Lampiran 11 Hasil Uji Reliabilitas Instrumen ... 131
Lampiran 12 Perhitungan Uji Reliabilitas Instrumen ... 132
Lampiran 13 Hasil Uji Taraf Kesukaran Instrumen ... 133
Lampiran 14 Perhitungan Uji Taraf Kesukaran Instrumen ... 134
Lampiran 15 Hasil Uji Daya Beda Instrumen ... 145
Lampiran 16 Perhitungan Uji Daya Beda Instrumen ... 136
Lampiran 17 Hasil Tes Kemampuan Representasi Matematis Kelompok Eksperimen ... 137
Lampiran 18 Hasil Tes Kemampuan Representasi Matematis Kelompok Kontrol ... 139
Lampiran 19 Perhitungan Daftar Distribusi Frekuensi, Mean, Median, Modus, Varians, Simpangan Baku, Kemiringan dan Kurtosis Kelompok Eksperimen ... 141
Lampiran 21 Perhitungan Data Kemampuan Representasi Matematis Siswa
Kelompok Eksperimen Berdasarkan Indikator Representasi ... 147
Lampiran 22 Perhitungan Data Kemampuan Representasi Matematis Siswa Kelompok Kontrol Berdasarkan Indikator Representasi ... 148
Lampiran 23 Perhitungan Uji Normalitas Kelompok Eksperimen ... 149
Lampiran 24 Perhitungan Uji Normalitas Kelompok Kontrol ... 151
Lampiran 25 Perhitungan Uji Homogenitas ... 153
Lampiran 26 Perhitungan Uji Hipotesis Statistik ... 154
Lampiran 27 Tabel Nilai Koefisien Korelasi (r) Product Moment dari Pearson 156 Lampiran 28 Tabel Chi-Square ... 158
Lampiran 29 Tabel Nilai Kritis Distribusi f ... 159
1
PENDAHULUAN
A.
Latar Belakang Masalah
Matematika berperan sangat penting di dunia ini. Peranan ini dapat dilihat
pada berbagai sektor kehidupan manusia, seperti komputasi, transportasi,
komunikasi, ekonomi/perdagangan dan pengembangan ilmu pengetahuan dan
teknologi. Matematika sudah diperkenalkan oleh ilmuan-ilmuan terdahulu dan
terus-menerus berkembang pesat sejalan dengan perkembangan jaman hingga saat
ini. Keberhasilan dan kemajuan teknologi yang mengubah dunia semakin canggih
pun tidak lepas dari peranan matematika.
Mata pelajaran matematika diberikan pada setiap jenjang pendidikan dari
mulai penghitungan sederahana sampai bentuk yang kompleks. Sasaran dalam
pembelajaran matematika diantaranya adalah mengembangkan kemampuan siswa
dalam berpikir matematis. Hal ini sejalan dengan yang dikatakan oleh Johnson
dan Rising dalam bukunya bahwa matematika adalah pola berpikir, pola
mengorganisasikan, pembuktian yang logik, matematika itu adalah bahasa yang
menggunakan istilah yang didefinisikan dengan cermat, jelas, dan akurat,
representasinya dengan simbol dan padat, lebih berupa bahasa simbol mengenai
ide daripada mengenal bunyi.1 Oleh karena itu, siswa yang merupakan sumber
daya manusia melalui pembelajaran matematika dapat meningkatkan kualitasnya
dengan memiliki kemampuan berpikir yang logis, cermat, kritis, sistematis, dan
rasional.
Boole berpendapat bahwa itu matematika adalah ide-ide tentang jumlah
dan kuantitas.2 Sementara Ruseffendi berpendapat bahwa matematika lebih
menekankan kegiatan dalam dunia rasio (penalaran), bukan menekankan dari hasil
1
Erman Suherman, dkk., Common Text Book Strategi Pembelajaran Matematika Kontemporer , (Bandung: JICA-UPI, 2001), h. 19.
2
Marsigit, Sejarah dan Filsafat Matematika, 18 Maret 2014, pkl. 15.00, h. 3,
eksperimen atau hasil observasi matematika terbentuk karena pikiran-pikiran
manusia, yang berhubungan dengan ide, proses, dan penalaran.3
Menurut berbagai pandangan di atas, dapat disimpulkan bahwa
matematika adalah kegiatan berpikir matematis yang terbentuk oleh
pikiran-pikiran manusia dan berhubungan dengan ide, proses, dan penalaran.
Kemampuan berpikir matematis tidak sekedar menyampaikan berbagai
informasi seperti aturan, definisi, dan prosedur untuk dihafal oleh siswa
tetapi guru harus melibatkan siswa secara aktif dalam proses belajar
mengajar. Keaktifan siswa dalam pembelajaran matematika akan membantu
memperkuat pemahaman mereka tentang konsep-konsep matematika. Hal ini
sesuai dengan prinsip konstruktivisme bahwa siswa membangun pemahaman
matematikanya sendiri baik secara personal atau sosial, pemahaman tersebut tidak
dapat berpindah dari guru ke siswa, kecuali ada keaktifan dari siswa untuk
bernalar, siswa aktif untuk mengkonstruksi terus menerus sehingga pemahaman
yang berbeda-beda dapat dibentuk menjadi pemahaman yang baru, guru hanya
sebagai pemberi sarana atau situasi agar proses kontruksi siswa berjalan dengan
baik. Akan tetapi keaktifan siswa kurang dikembangkan oleh guru dalam proses
pembelajaran, siswa seringkali menerima ilmu matematika secara pasif dari guru
dan selalu menghapal rumus sehingga kemampuan berpikir matematis tidak
terbentuk dan berkembang sebagaimana yang diharapkan.
Untuk berpikir secara matematis, siswa harus dapat mengemukakan ide-ide
matematikanya dalam berbagai cara. Hal inilah yang disebut dengan representasi.
Pengembangan kemampuan berpikir secara matematis diperlukan untuk lebih
memahami konsep-konsep dan dapat digunakan dalam standar kemampuan dalam
belajar. National Council of Teachers of Mathematics menyebutkan bahwa dalam
belajar matematika siswa dituntut untuk memiliki kemampuan: pemahaman,
pemecahan masalah, komunikasi, koneksi matematika, dan merepresentasikan
3
Hakikat Matematika dan Pembelajaran Matematika di SD, 07 November 2013, pkl.
ide-ide.4 Dengan demikian, kemampuan representasi merupakan hal penting
dalam pembelajaran matematika.
Kemampuan representasi dapat meningkatkan dan memperkaya
pengetahuan matematika siswa karena dapat digunakan dalam memecahkan
berbagai masalah di kehidupan nyata. Hal ini sejalan degan teori yang disebutkan
oleh Villegas et al. yang berpendapat bahwa “representation systems fulfill certain requirements for complexity, interrelationship and power of symbolization and abstraction; mastering them broadens and enriches human intelligence, in that they are useful instruments for modeling reality and practical tools for solving different problems in real life.” 5 Artinya, sistem representasi memenuhi
persyaratan tertentu untuk kompleksitas, keterkaitan dan kekuatan simbolisasi dan
abstraksi; menguasai memperluas dan memperkaya kecerdasan manusia, dalam
arti bahwa mereka adalah instrument yang berguna untuk pemodelan realitas dan
alat-alat praktis untuk memecahkan masalah yang berebda dalam kehidupan nyata.
Oleh karena itu, kemampuan representasi dianggap sangat penting dalam
keberhasilan pembelajaran matematika.
Kemampuan representasi merupakan salah satu kemampuan yang
mempunyai keterkaitan dengan pemahaman matematis. Representasi merupakan
hal terpenting dalam mengkonstruksi ide dan pemahaman siswa terkait dengan
konsep-konsep matematika. Dengan adanya representasi, siswa dapat memberikan
informasi tentang pendapatnya mengenai suatu konteks atau ide matematika. Oleh
karena itu, kemampuan representasi sangatlah dibutuhkan siswa untuk menunjang
pemahaman siswa dalam proses pembelajaran dan dalam pemecahan masalah
matematika.
Setiap siswa mempunyai cara yang berbeda-beda dalam membangun
pengetahuannya. Dalam hal ini, sangat memungkinkan bagi siswa untuk mencoba
berbagai representasi dalam memahami suatu konsep. Menurut Neria dan Amit
4
Hani Handayani, “Pengaruh Pembelajaran Kontekstual Terhadap Kemampuan Pemahaman dan Representasi Matematis Siswa Sekolah Dasar”, Tesis pada Pascasarjana UPI Bandung, Bandung, 2013, h. 1, tidak dipublikasikan.
5
Sebagaimana dinyatakan Brenner bahwa proses pemecahan masalah yang sukses
bergantung kepada keterampilan merepresentasi masalah seperti mengkonstruksi
dan menggunakan representasi matematik di dalam kata-kata, grafik, tabel, dan
persamaan-persamaan, penyelesaian dan manipulasi simbol.6
Georgia DeClark, seorang guru taman kanak-kanak, mengadakan sebuah
penelitian dengan memberikan sebuah pertanyaan ”Ada berapa banyak kaki di rumah kalian?” kepada tiga siswa taman kanak-kanak dan meminta mereka untuk menjawab dengan menggambarkannya pada sebuah kertas. 7 Ketiga siswa tersebut
memberikan jawaban yang berbeda-beda mengenai pertanyaan yang diberikan.
Gambar 1.1 Hasil Jawaban Siswa yang Diteliti8
Siswa A memberikan jawaban dengan menggambarkan seluruh bagian
tubuh anggota keluarganya, siswa B memberikan jawaban hanya dengan
menggambarkan banyaknya kaki seluruh anggota keluarganya, sedangkan siswa
C hanya membuat garis-garis sebanyak 8 garis. Pertanyaan yang diberikan oleh
peneliti tersebut termasuk ke dalam pertanyaan untuk mengetahui kemampuan
representasi siswa. Kemampuan representasi siswa A tidak hanya dalam bentuk
pengetahuan angka, tetapi pengetahuan ilmiah tentang anggota tubuh dan
pengetahuan sosial tentang nama-nama anggota keluarganya. Siswa B memiliki
cukup pengetahuan ilmiah, tetapi hanya menggambarkan bagian tubuh yang
6 Kartini, “Peranan Representasi dalam Pembelajaran Matematika”,
Prosiding pada Seminar Nasional Matematika dan Pendidikan Matematika Jurusan Pendidikan Matematika FMIPA UNY, 2009, hh. 361-362.
7
Gerald Goldin & Nina Shteingold, Systems of Representations and the Development of Mathematical Concepts dalam Albert A. Cuoco (ed), The Roles of Representation in School Mathematics 2001 Yearbook, (NCTM, 2001), h. 33.
8
memang ditanyakan. Sedangkan siswa C kemampuan representasinya merupakan
tipe representasi yang mana pengetahuan logika matematikanya belum dominan.
Meskipun kemampuan representasi matematis merupakan hal yang sangat
penting dalam pembelajaran matematika, namun pada kenyataannya masih
banyak guru yang mengesampingkan kemampuan representasi matematis siswa.
Padahal dengan kemampuan representasi matematis yang baik, siswa akan lebih
mudah memahami konsep yang sedang dipelajarinya. Hal ini sejalan dengan
pendapat Hudiono yang menyatakan bahwa menurut guru, representasi matematis
berupa grafik, tabel, dan gambar hanya merupakan pelengkap pembelajaran saja
dan guru jarang memperhatikan perkembangan kemampuan representasi
matematis siswa.9
Sebuah penelitian yang dilakukan oleh TIMSS (Trends in International Mathematics and Science Study) pada tahun 2011, menunjukkan bahwa
peringkat matematik siswa SMP kelas VIII di Indonesia menduduki peringkat
ke-38 dari 48 negara yang ikut serta dengan skor rata-rata 386. Skor rata-rata
tersebut termasuk kedalam kategori rendah, masih jauh dari kategori sedang
yang memerlukan skor 500. Salah satu kemampuan yang diteliti ialah siswa dapat
mengidentifikasi ekspresi aljabar yang koresponden dengan situasi sederhana dan
menambahkan ekspresi aljabar.10 Kemampuan tersebut merupakan salah satu
kemampuan representasi dan jika dilihat dari skor rata-rata yang diperoleh,
membuktikan bahwa kemampuan representasi siswa kelas VIII Indonesia masih
rendah. Selain itu, hasil penelitian yang telah dilakukan Ummu Aiman di salah
satu Sekolah Menengah Pertama Negeri di Jakarta menyatakan bahwa rata-rata
kemampuan representasi matematis siswa kelas VIII yang diajarkan dengan
pembelajaran konvensional adalah 54,14, sedangkan nilai rata-rata gabungan
9
Bambang Hudiono, “Peran Pembelajaran Diskursus Multi Representasi Terhadap Pengembangan Kemampuan Matematik dan Daya Representasi pada Siswa SLTP”, Disertasi pada Sekolah Pascasarjana UPI, Bandung: 2005, h. 4, tidak dipublikasikan.
10
kelas kontrol dan kelas eksperimen adalah 59,54.11 Karena kemampuan
representasi matematis yang masih rendah, maka dalam pembelajaran
matematika di kelas, kemampuan representasi matematis merupakan salah satu
kemampuan yang perlu ditingkatkan. Pentingnya kemampuan representasi dalam
pembelajaran matematika sudah banyak dibuktikan oleh peneliti-peneliti
sebelumnya, seperti penelitian Kalathil & Sherin, Neria & Amit, Gagatsis & Elia,
Elia, Michaelidou, N, et al., Amit dan Fried, Harries & Barmby, Hwang, dkk, dan
lain-lain.12
Berdasarkan uraian tersebut, perlu adanya suatu usaha untuk
meningkatkan kemampuan representasi matematis. Terdapat banyak pendekatan
pembelajaran yang telah dirumuskan oleh para ahli untuk membantu
meningkatkan kemampuan representasi dalam pembelajaran matematika. Salah
satu pendekatan yang dipandang dapat memfasilitasi dalam meningkatkan
kemampuan representasi matematis siswa adalah pendekatan problem solving. Pendekatan problem solving merupakan suatu pendekatan yang membantu siswa untuk menggunakan pengetahuan dan keterampilan yang sudah dimiliki
untuk diterapkan ke dalam pemecahan masalah yang tidak rutin. Suherman
menyatakan bahwa pendekatan pembelajaran matematika merupakan upaya yang
ditempuh guru dalam melaksanakan pembelajaran agar konsep matematika yang
disajikan bisa beradaptasi dengan siswa.13 Artinya, konsep matematika yang
diberikan dapat disatukan dengan konsep matematika yang telah dimiliki siswa
sehingga membentuk konsep baru yang lebih bermakna dan dapat membangun
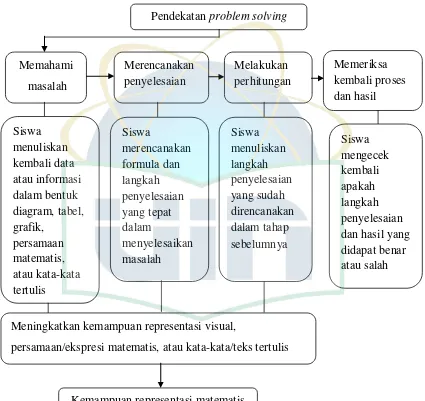
pengertian baru dalam pikiran siswa. Pendekatan problem solving yang diadopsi dari G. Polya ada 4 tahap, yaitu: (1) Memahami masalah, (2) Merencanakan
penyelesaian, (3) Melakukan perhitungan (melaksanakan rencana), (4) Memeriksa
11 Ummu Aiman, “Pendekatan Pembelajaran Model Eliciting Activities (MEAs) Terhadap
Kemampuan Representasi Matematis Siswa”, Skripsi pada UIN Syarif Hidayatullah Jakarta, Jakarta, 2013, h. 48, tidak dipublikasikan.
12Kartini, “Peranan Representasi dalam Pembelajaran Matematika”,
Prosiding Seminar Nasional Matematika dan Pendidikan Matematika Jurusan Pendidikan Matematika FMIPA UNY, 2009, h. 367.
13
kembali proses dan hasil. Hal ini sejalan dengan pendapat dari Tatang Herman
yang mengatakan bahwa pendekatan problem solving dalam belajar matematika akan melatih siswa untuk berpikir efektif dan strategis dalam menyelesaikan
permasalahan.14 Dalam prosesnya, siswa diminta untuk mengemukakan ide dalam
berbagai cara dan menentukan cara yang paling tepat untuk menyelesaikan
permasalahan. Kemampuan representasi diperlukan dalam proses ini karena siswa
diminta memilih satu dari sekian formula penyelesaian yang dikemukakan. Jadi
dapat disimpulkan bahwa pendekatan problem solving dapat melatih siswa mengembangkan kemampuan berpikir matematis khususnya kemampuan
representasi.
Sebagai upaya untuk menjawab permasalahan mengenai rendahnya
kemampuan representasi matematis siswa dan latar belakang masalah yang
diuraikan di atas, maka peneliti terdorong untuk melakukan penelitian dengan
judul ”Pengaruh Pendekatan Problem Solving terhadap Kemampuan Representasi Matematis Siswa”.
B.
Identifikasi Masalah
Berdasarkan uraian dari latar belakang masalah yang telah dikemukakan,
maka timbul pernyataan yang mendasari penelitian ini, antara lain:
1. Kesempatan siswa mengemukakan ide-ide matematika mereka kurang
diberikan oleh guru dikarenakan beberapa siswa mempelajari matematika
hanya dengan menghapal rumus, bukan dengan menganalisa setiap soal
yang diberikan.
2. Keaktifan siswa kurang dikembangkan oleh guru dalam proses
pembelajaran dikarenakan siswa seringkali menerima ilmu secara satu
arah yaitu dari guru ke siswa.
3. Kemampuan representasi matematis siswa masih dikesampingkan oleh
banyak guru dikarenakan guru menganggap representasi matematis hanya
merupakan pelengkap pembelajaran saja.
14 Tatang Herman, “Tren Pembelajaran Matematika pada Era Informasi Global”, 31
4. Kemampuan representasi matematis siswa masih tergolong rendah. Hal ini
sesuai dengan hasil penelitian peneliti terdahulu mengenai kemampuan
representasi matematis siswa, dimana nilai rata-rata siswa yang diajar
dengan pembelajaran konvensional yaitu 54,14 dan rata-rata gabungannya
59,54
C.
Pembatasan Masalah
Agar penelitian terarah dan tidak terjadi penyimpangan yang tidak
diharapkan, maka peneliti memberikan batas sebagai berikut:
1. Penelitian ini menggunakan pendekatan problem solving yang mengadopsi teori G. Polya yang dilakukan dengan kegiatan memahami, merencanakan,
melakukan perhitungan, dan memeriksa kembali proses dan hasil.
2. Penelitian ini akan meneliti kemampuan representasi matematis siswa
hanya pada aspek kemampuan representasi eksternal matematis.
D.
Perumusan Masalah
Berdasarkan identifikasi masalah dan pembatasan penelitian, maka masalah
yang akan diteliti yaitu:
Apakah terdapat pengaruh pendekatan problem solving terhadap kemampuan representasi matematis siswa?
E.
Tujuan Penelitian
Berdasarkan perumusan masalah di atas, tujuan dari penelitian ini yaitu:
Untuk menganalisis kemampuan representasi matematis siswa yang
diajarkan dengan menggunakan pendekatan problem solving.
F.
Manfaat Penelitian
Apabila penelitian ini menunjukkan bahwa penggunaan pendekatan
problem solving dapat memberikan hasil yang signifikan terhadap kemampuan representasi siswa, maka diharapkan dapat memberikan manfaat, yaitu:
2. Bagi siswa, membantu siswa mengembangkan kemampuan representasi
matematisnya dengan menggunakan pendekatan problem solving.
3. Bagi peneliti selanjutnya, penelitian ini diharapkan dapat dijadikan suatu
kajian untuk mengadakan penelitian lanjutan yang berhubungan dengan
10
A.
Deskripsi Teoretik
1. Kemampuan Representasi Matematis
NCTM menetapkan lima standar kemampuan matematis yang harus
dimiliki oleh siswa, yaitu kemampuan pemecahan masalah (problem solving), kemampuan komunikasi (communication), kemampuan koneksi (connection), kemampuan penalaran (reasoning), dan kemampuan representasi (representation).1 Hal tersebut memperlihatkan bahwa kemampuan representasi merupakan salah satu standar kemampuan yang harus ada dalam proses
pembelajaran matematika. Jones menambahkan bahwa terdapat 3 alasan yang
mendasari representasi sebagai salah satu standar proses yaitu: 2
1. Kelancaran dalam melakukan translasi diantara berbagai jenis
representasi yang berbeda merupakan kemampuan dasar yang perlu
dimiliki siswa untuk membangun suatu konsep dan berpikir matematis.
2. Ide-ide matematis yang disajikan guru melalui berbagai representasi
akan memberikan pengaruh yang sangat besar terhadap siswa dalam
mempelajari matematika.
3. Siswa membutuhkan latihan dalam membangun representasinya
sendiri sehingga memiliki kemampuan dan pemahaman konsep yang
baik dan fleksibel yang dapat digunakan dalam pemecahan masalah.
Fadillah mengungkapkan bahwa representasi adalah ungkapan-ungkapan
dari ide matematis yang ditampilkan siswa sebagai model atau bentuk pengganti
dari suatu situasi masalah yang digunakan untuk menemukan solusi dari suatu
1 Leo A. Effendi, “Pembelajaran Matematika dengan Metode Penemuan Terbimbing
untuk Meningkatkan Kemampuan Representasi dan Pemecahan Masalah Matematis Siswa SMP”, Jurnal Penelitian Pendidikan, Vol. 13, No. 2, 2012, h. 2.
2
masalah yang sedang dihadapinya sebagai hasil dari interpretasi pikirannya.3
Kemudian Gerald Goldin menyatakan, “a representation is a configuration that can represent something else in some manner. For example, a word can represent a real-life object, a numeral can represent the cardinality of a set, or
the same numeral can represent a position on a number line”.4 Hal ini dapat diartikan bahwa representasi adalah sebuah konfigurasi yang dapat mewakili
sesuatu dalam beberapa cara. Contohnya, sebuah kata dapat mewakili objek
kehidupan nyata, sebuah angka dapat mewakili kardinalitas himpunan, atau urutan
angka yang sama dapat mewakili posisi pada garis bilangan. Dan juga menurut
Hutagaol, representasi menunjuk pada proses ataupun hasil (produk) dalam
tindakan-tindakan yang dilakukan untuk menangkap suatu konsep hubungan
matematis di dalam suatu bentuk matematika itu sendiri.5 Artinya, ide matematika
yang dicerna siswa diproses sedemikian rupa dan menuangkannya dalam bentuk
konkrit sehingga memahami bahwa ada keterkaitan antara ide matematika dengan
bentuk matematikanya. Dari beberapa pernyataan di atas, dapat disimpulkan
bahwa representasi adalah proses atau hasil dari berfikir efektif tentang ide-ide
matematika yang dituangkan dalam bentuk konkrit sehingga dapat ditemukan
adanya keterkaitan hubungan antara konsep matematika dengan bentuk
matematikanya.
Cai, Lane dan Jakabcsin menyatakan bahwa representasi merupakan cara
yang digunakan seseorang untuk mengemukakan jawaban atau gagasan matematis
yang bersangkutan. 6 Misalnya, seorang anak diberi pertanyaan “berapakah
3
Devi Aryanti, Zubaidah, dan Asep Nursangaji, Kemampuan Representasi Matematis Menurut Tingkat Kemampuan Siswa pada Materi Segi Empat di SMP, 23 Desember 2013, pkl. 20:55, (http://jurnal.untan.ac.id/index.php/jpdpb/article/download/812/pdf).
4
Gerald Goldin, Representation in Mathematical Learning and Problem Solving, dalam Lyn D. English (ed.), Handbook of International Research in Mathematics Education, (New Jersey: Lawrence Erlbaum Associates, Inc., Publisher, 2002), h. 208.
5 Kartini Hutagaol, “Pembelajaran Kontekstual untuk Meningkatkan Kemampuan
Representasi Matematis Siswa Sekolah Menengah Pertama”, Jurnal Ilmiah Program Studi Matematika STKIP Siliwangi Bandung, Vol 2, No.1, 2013, h. 91.
6
usiamu?” oleh gurunya, anak tersebut menggambarkan atau menuliskan usia lima tahun seperti pada Gambar 2.1 berikut:
Gambar 2.1 Contoh Representasi Usia oleh Anak
Saat ditanya “mengapa bentuk angka lima seperti itu?”, anak bisa saja
terdiam karena memang dari awal mengenal angka, dia dikenalkan dengan angka lima yang berbentuk “5”, terlepas anak belum mempelajari konsep bilangan.
Representasi yang dimunculkan oleh siswa adalah ungkapan-ungkapan
dari gagasan-gagasan atau ide-ide matematika yang ditampilkan siswa dalam
upaya untuk mencari solusi dari permasalahan yang sedang dihadapi. Standar
representasi NCTM menyebutkan bahwa, program pembelajaran matematika dari
pra-taman kanak-kanak sampai kelas 12, harus memungkinkan siswa untuk:7
1. Membuat dan menggunakan representasi untuk mengorganisir,
mencatat dan mengkomunikasikan ide-ide matematika.
2. Memilih, menerapkan dan menerjemahkan representasi matematik
untuk memecahkan masalah.
3. Menggunakan representasi untuk memodelkan dan
menginterpretasikan kejadian fisik, sosial ataupun matematika.
Dari penuturan NCTM dan Jones di atas, representasi merupakan standar
proses yang harus dikuasai sebelum sekolah sampai kelas 12 karena kemampuan
representasi yang dilatih sejak dini dapat membantu memperdalam pemahaman
konsep sehingga dapat membantu dalam pemecahan masalah. Representasi
merupakan salah satu penunjang terbentuknya kemampuan matematis. Selain itu,
representasi juga dapat membuat siswa mengkomunikasikan informasi kepada
7
Miriam Amit, “Multiple Representations in 8THGrade Algebra Lessons: Are Learners
Really Getting It”, Proceedings of the 29th Conference of International Grup For The Psychology
guru tentang bagaimana cara berpikir siswa mengenai suatu konteks atau ide-ide
matematika. Oleh karena itu, guru harus dapat menemukan cara mengembangkan
kemampuan representasi siswa dalam pembelajaran matematika.
Representasi dibagi menjadi dua bagian, yaitu representasi eksternal dan
representasi internal.
a. Representasi Eksternal
Gerald Goldin dan Nina Shteingold mendeskripsikan representasi eksternal
sebagian besar meliputi: (1) notasi dan bentuk, (2) menunjukkan hubungan secara
visual atau spasial, (3) huruf dan kalimat, (4) tulisan atau lisan.8 Sementara
jenis-jenis representasi eksternal menurut Ostad adalah konkret, konkret,
semi-tanda, dan tanda.9 Konkret meliputi benda nyata, semi-konkret meliputi gambar
dari benda nyata, semi-tanda meliputi benda nyata dengan satu propertinya (misal
garis-garis atau titik-titik sejumlah benda yang direpresentasikan), dan tanda
meliputi simbol arbitrer (berubah-ubah) dan konvensional (lima, 5, V, dll). Jadi,
representasi eksternal adalah cara menyampaikan ide atau konsep matematika ke
dalam bentuk nyata/konkret baik berupa benda-benda maupun tulisan atau lisan.
Hiebert dan Carpenter menyatakan bahwa komunikasi matematik adalah bagian
dari representasi eksternal (bahasa lisan, simbol tertulis, gambar atau objek fisik),
sedangkan untuk berpikir tentang pemahaman matematis bagian dari representasi
internal.10
b. Representasi Internal
Sistem internal, sebaliknya, termasuk membangun simbolisasi pribadi
siswa dan penugasan arti notasi matematika, serta bahasa alami mereka, citra
visual dan representasi spasial, strategi pemecahan masalah mereka dan heuristik,
8
Gerald Goldin dan Nina Shteingold, System of Representations and the Development of Mathematical Concept, dalam Albert A. Cuoco (ed), The Roles of Representation in School Mathematics 2001 Yearbook, (NCTM, 2001), hh. 4-5.
9
Snorre A. Ostad, Memahami dan Menangani Bilangan, 23 Desember 2013, pkl.
21:17,h.3,(http://www.idp-europe.org/docs/uio_upi_inclusion_book/13-Memahami_dan_Menangan_Bilangan.pdf).
10
dan (sangat penting) mereka mempengaruhi dalam kaitannya dengan
matematika.11 Representasi internal memiliki: 12
1. Sistem lisan yang berhubungan dengan kalimat, yang meliputi
kemampuan berbahasa alami - kemampuan menyusun kalimat, asosiasi
verbal, serta tata bahasa dan kalimat;
2. Sistem imagistic, termasuk visual - berhubungan dengan ruang, tactile - berhubungan dengan keindahan (gestur tangan dan bahasa tubuh), dan pendengaran - kode berirama;
3. Sistem notasi formal, termasuk konfigurasi internal yang sesuai untuk
dipelajari, sistem simbol konvensional dalam matematika (penomoran,
notasi aljabar, dll) dan aturan untuk memanipulasinya,
4. Sistem perencanaan, pemantauan, kontrol dan eksekutif yang
memandu pemecahan masalah, strategis termasuk berpikir, heuristics,
dan banyak dari apa yang sering disebut sebagai kemampuan
metakognitif,
5. Sistem afektif yang tidak hanya meliputi emosi “global” yang terkait
dengan keyakinan dan sikap yang relatif stabil, tetapi juga perubahan
keadaan perasaan “lokal” yang terjadi selama pembelajaran
matematika dan pemecahan masalah.
Jadi, representasi internal merupakan sistem membangun simbolisasi
matematika dalam diri untuk digambarkan menjadi bentuk representasi eksternal.
Representasi internal tidak dapat diamati secara langsung dengan menggunakan
indera penglihatan karena berlangsung secara mental dalam otak. Akan tetapi,
baik atau tidaknya kemampuan representasi internal dapat dilihat dari kemampuan
representasi eksternalnya. Sesuai dengan hal tersebut Ostad menyatakan bahwa
bentuk representasi eksternal (materi fisik, gambar, simbol, dll) yang
dipergunakan oleh siswa menentukan cara siswa merepresentasikan pengetahuan
matematikanya secara internal. Sebaliknya, cara siswa menangani atau membuat
representasi eksternal dapat mengungkapkan bagaimana siswa telah
11
Gerald Goldin dan Nina Shteingold, op. cit., h. 2.
12
merepresentasikan informasi tersebut secara internal. 13 Dengan kata lain, ada
hubungan timbal-balik antara representasi eksternal dan representasi internal
dalam diri seseorang dalam memecahkan masalah seperti yang ditunjukkan pada
Gambar 2.2 berikut:
Gambar 2.2 Hubungan Timbal-Balik Antara Representasi Eksternal dan Representasi Internal
Mayer mengkaitkan kemampuan representasi seseorang berdasarkan
proses kognisi yang terjadi pada memori kerja. Menurut Mayer, terdapat tiga
unsur representasi yang saling berkaitan, yaitu visual, verbal dan referensi.14
Kemampuan representasi visual (gambar atau grafik) adalah kemampuan
menerjemahkan masalah matematik menjadi tabel, gambar, ataupun grafik.
Kemampuan representasi verbal adalah kemampuan menerjemahkan hal-hal yang
diselidiki dan hubungannya dengan masalah matematika yang dihadapi kedalam
kata-kata atau bahasa. Kemampuan referensi dimaksudkan sebagai kemampuan
menerjemahkan masalah yang bersumber dari dunia nyata dan hal yang sifatnya
konkret kedalam representasi rumus aritmatika.
Lesh, Post & Behr mendeskripsikan sistem representasi dalam lima tipe,
yaitu: picture, written symbols, oral language, real-world situations, dan
manipulative models yang semuanya saling berinteraksi satu sama lain.Hubungan
tipe-tipe representasi yang terkait satu sama lain tersebut dapat dilihat pada
Gambar 2.3 sebagai berikut:
13
Snorre A. Ostad, op. cit., h. 4.
14
Gambar 2.3 Five Different Representations of Mathematical Ideas. Translations Between and Within Each Can Help Develop New Concepts.15
Konsep representasi menurut NCTM, Mayer, dan Lesh et.al dapat
dikaitkan satu sama lain. Poin pertama dalam standar representasi menurut NCTM
yaitu, membuat dan menggunakan representasi untuk mengorganisir, mencatat
dan mengkomunikasikan ide-ide matematika, termasuk ke dalam representasi
visual dan verbal yang disebutkan oleh Mayer. Poin kedua, yaitu memilih,
menerapkan dan menerjemahkan representasi matematik untuk memecahkan
masalah, dapat berupa representasi visual, verbal dan referensi menurut Mayer.
Poin ketiga, yaitu menggunakan representasi untuk memodelkan dan
menginterpretasikan kejadian fisik, sosial ataupun matematika, termasuk
representasi referensi menurut Mayer. Ketiga unsur representasi yang
dikemukakan oleh Mayer, dijabarkan kembali oleh Lesh, Posh & Behr.
Representasi visual mencakup gambar, model manipulatif dan simbol-simbol
15
tertulis. Representasi verbal mencakup bahasa lisan. Sementara representasi
referensi mencakup situasi dunia nyata (real-world situations).
Selanjutnya, Mudzakir dalam penelitiannya mengelompokkan representasi
matematis ke dalam tiga ragam representasi yang utama, yaitu 1) representasi
visual berupa diagram, grafik, atau tabel, dan gambar; 2) Persamaan atau ekspresi
matematika; dan 3) Kata-kata atau teks tertulis. Adapun indikatornya adalah
sebagai berikut: 16
Tabel 2.1 Indikator Kemampuan Representasi
No Representasi Bentuk-Bentuk Operasional
[image:34.595.109.519.278.618.2]1 Representasi visual a. Diagram, tabel, atau
grafik
Menyajikan kembali data atau informasi dari suatu representasi ke representasi diagram, grafik, atau tabel
Menggunakan representasi visual untuk menyelesaikan masalah
b. Gambar Membuat gambar pola-pola geometri
Membuat gambar untuk memperjelas masalah dan memfasilitasi penyelesaiannya
2 Persamaan atau ekspresi matematis
Menyatakan masalah dalam bentuk persamaan atau model matematis
Membuat konjektur dari suatu pola bilangan Menyelesaikan masalah dengan melibatkan
ekspresi matematis 3 Kata-kata atau teks
tertulis
Membuat situasi masalah berdasarkan data atau representasi yang diberikan
Menuliskan interpretasi dari suatu representasi Menuliskan langkah-langkah penyelesaian
masalah matematika dengan kata-kata Menyusun cerita yang sesuai dengan suatu
representasi yang disajikan
Menjawab soal dengan menggunakan kata-kata atau teks tertulis
Berdasarkan uraian mengenai representasi matematis di atas, kemampuan
representasi matematis adalah kemampuan menyatakan ide matematis dalam
bentuk diagram, grafik, tabel, persamaan matematis, dan kata-kata tertulis.
16
Adapun indikator-indikator kemampuan representasi matematis siswa
yang digunakan dalam penelitian ini adalah:
1) Representasi visual dalam bentuk diagram, tabel, atau grafik meliputi:
a. Menyajikan kembali data atau informasi dari suatu representasi ke
representasi diagram, grafik, atau tabel.
2) Representasi berupa persamaan atau ekspresi matematis meliputi:
a. Menyatakan masalah dalam bentuk persamaan atau model matematis
3) Representasi berupa kata-kata atau teks tertulis meliputi:
a. Menyusun cerita yang sesuai dengan suatu representasi yang disajikan
2. Pendekatan Problem Solving
a. Pengertian Pendekatan Problem Solving
Sebagian besar ahli mengatakan bahwa masalah merupakan hal yang harus
dijawab atau direspon. Masalah atau problem menurut Hayes merupakan
kesenjangan antara keadaan sekarang dengan tujuan yang ingin dicapai, sementara
kita tidak mengetahui apa yang harus dikerjakan untuk mencapai tujuan
tersebut.17Kemudian Krulik dan Jesse Rudnick menyatakan bahwa “problem is a situation, quantitative or otherwise, that confronts an individual or group of individuals, that requires resolution, and for which the individual sees no
apparent or obvious means or path to obtaining a solution”.18 Artinya, masalah merupakan situasi, kuantitatif atau sebaliknya, yang dihadapi oleh individu atau
sekelompok individu, yang memerlukan pemecahan, dan yang mana individu
melihat maksud yang tidak nyata atau jelas atau jalur untuk memperoleh solusi.
Jadi, masalah merupakan situasi yang membingungkan atau sulit yang
menghendaki untuk dikerjakan atau memerlukan pemecahan masalah.
Dalam kehidupan sehari-hari, kita dihadapi dengan berbagai macam
masalah, tidak terkecuali dalam matematika. Grouws menyatakan masalah dalam
17
Marzuki, Perbedaan Kemampuan Pemecahan Masalah dan Komunikasi Matematika Antara Siswa yang Diberi Pembelajaran Berbasis Masalah dengan Pembelajaran Langsung,Tesis pada Pascasarjana Universitas Negeri Medan, Medan, 2012, h. 22, tidak dipublikasikan.
18
matematika adalah segala sesuatu yang menghendaki untuk dikerjakan.19 Hal ini
berarti bahwa permasalahan-permasalahan yang terdapat dalam matematika
bertujuan untuk menguji kemampuan yang dimiliki siswa dan jika dapat
diselesaikan dengan baik dan benar maka siswa dapat memahami konsep yang
terkait dengan permasalahan tersebut dan secara tidak langsung kemampuan yang
dimiliki siswa juga dapat berkembang.
Pemecahan masalah pada dasarnya adalah proses yang ditempuh oleh
seseorang untuk menyelesaikan masalah yang dihadapinya sampai masalah itu
tidak lagi menjadi masalah baginya.20 Sementara Polya mengartikan pemecahan
masalah sebagai satu usaha mencari jalan keluar dari satu kesulitan guna
mencapai satu tujuan yang tidak begitu mudah segera untuk dicapai, sedangkan
menurut Utari mengatakan bahwa pemecahan masalah dapat berupa menciptakan
ide baru, menemukan teknik atau produk baru.21 Jadi, kegiatan memecahkan
masalah harus dilakukan sedemikian rupa dengan menggunakan pendekatan
pembelajaran dan mengerahkan kemampuan-kemampuan matematis yang dimiliki
siswa sehingga masalah yang ada dapat menjadi pemahaman yang baru dan
menyatu dengan pemahaman yang sudah didapat sebelumnya dan memunculkan
kesimpulan baru dalam memahami konsep matematika.
Sumardyono berpendapat bahwa problem solving sebagai tujuan merupakan pembelajaran tentang bagaimana menyelesaikan masalah22 Kurniawati
pun berpendapat bahwa pemecahan masalah merupakan bagian dari kurikulum
matematika yang sangat penting karena dalam proses pembelajaran maupun
penyelesaian, siswa dimungkinkan memperoleh pengalaman menggunakan
pengetahuan serta keterampilan yang sudah dimiliki untuk diterapkan pada
19
Sukowiyono, Tri Atmojo K., Imam Sujadi, Proses Berpikir Siswa Kelas VII Sekolah Menengah Pertama dalam Memecahkan Masalah Matematika Materi Pokok Bangun Datar Berdasarkan Perspektif Gender, 10 April 2014, pkl. 21:35, h. 327, (portalgaruda.org/download_article.php?article=106940&val=4039 ).
20Nyimas Aisyah, “Pendekatan Pemecahan Masalah Matematika”, 18 Maret 2014, pkl.
11:43,h.3,(http://staff.uny.ac.id/sites/default/files/PengembanganPembelajaranMatematika_UNIT_ 5_0.pdf).
21
Muhammad Zainal Abidin, “Teori Pemecahan Masalah Polya dalam Pembelajaran Matematika”, 19 Maret 2014, pkl. 01:21, h. 9,(http://masbied.files.wordpress.com/2011/05/modul-matematika-teori-belajar-polya.pdf).
22 Durrotul Falahah, “Pembelajaran Matematika Melalui Pendekatan
pemecahan masalah yang bersifat tidak rutin.23 Yang dimaksud masalah tidak
rutin adalah masalah yang penyelesaiannya tidak seperti yang biasa dihadapi
dalam proses belajar. Biasanya masalah tidak rutin ini bersifat lebih kompleks dan
dalam menyelesaikannya diperlukan pemikiran yang mendalam dan beberapa
konsep yang saling berkaitan.
Pendekatan pembelajaran dapat diartikan sebagai titik tolak atau sudut
pandang kita terhadap proses pembelajaran, yang merujuk pada pandangan
tentang terjadinya suatu proses yang sifatnya masih sangat umum, di dalamnya
mewadahi, menginsiprasi, menguatkan, dan melatari metode pembelajaran dengan
cakupan teoretis tertentu.24 Pendekatan, menurut T. Raka Joni, menunjukkan cara
umum dalam memandang permasalahan atau objek kajian, sehingga berdampak,
ibarat seorang yang memakai kacamata dengan warna tertentu di dalam
memandang alam sekitar.25 Dari dua pernyataan tersebut, dapat disimpulkan
bahwa pendekatan pembelajaran merupakan latar suatu pembelajaran yang
bersifat umum yang di dalamnya terdapat segala strategi, model atau metode yang
dilakukan oleh guru dalam memfasilitasi siswa untuk menyelesaikan masalah.
Pemecahan masalah sebagai suatu pendekatan pembelajaran, yang
digunakan untuk menemukan kembali (reinvention) dan memahami materi, konsep, dan prinsip matematika.26 Pendekatan pemecahan masalah merupakan
fokus dalam pembelajaran matematika. Pemecahan masalah mencakup masalah
tertutup dengan solusi tunggal, masalah terbuka dengan solusi tidak tunggal, dan
masalah dengan berbagai cara penyelesaian.27 Dari dua pernyataan di atas, dapat
23 Lia Kurniawati, “Pembelajaran dengan Pendekatan Pemecahan Masalah untuk
Meningkatkan Kemampuan Pemahaman dan Penalaran Matematik Siswa SMP”, ALGORITMA Jurnal Matematika dan Pendidikan Matematika, Vol. 1 No. 1, Juni 2006, h. 82.
24 Nelly Nurmelly, “Pendekatan, Model Dan Strategi, dalam Model Pembelajaran”, 18
Maret 2014, pkl. 16:05, h. 1,(http://sumsel.kemenag.go.id/file/file/TULISAN/seiq1331701491.pdf).
25
Milan Rianto (ed), Pendekatan, Strategi, dan Metode Pembelajaran, (Malang: Depdiknas, 2006), h. 4.
26
Muhammad Kholidi, Upaya Meningkatkan Kemampuan Koneksi dan Pemecahan Masalah Siswa SMA Melalui Pendekatan Pembelajaran Kooperatif, Tesis dari Universitas Negeri Medan, 2011, h. 5, tidak diterbitkan.
27 Endang Sulistyowati, “Pemecahan Masalah dalam Pembelajaran Matematika SD/MI”,
disimpulkan bahwa pendekatan problem solving merupakan fokus yang digunakan dalam pembelajaran matematika yang proses penyelesaiannya
melibatkan berbagai masalah baik terbuka maupun tertutup yang bertujuan untuk
menemukan kembali, memahami materi, konsep dan prinsip matematika.
Pendekatan problem solving merupakan pendekatan pembelajaran dalam menyelesaikan permasalahan non-rutin yang dilakukan melalui kegiatan
memahami masalah, merencanakan penyelesaian masalah, melaksanakan
perencanaan penyelesaian masalah, dan memeriksa kembali masalah yang sudah
diselesaikan.
b. Tahap Pendekatan Problem Solving
Dalam problem solving, terdapat beberapa tahapan dalam proses pembelajarannya. Gagne menyatakan dalam problem solving (pemecahan masalah) terdiri dari lima langkah yang harus dilakukan, yaitu:
1. Menyajikan masalah dalam bentuk yang lebih jelas;
2. Menyatakan masalah dalam bentuk yang lebih operasional;
3. Menyusun hipotesis-hipotesis alternatif dan prosedur kerja yang
diperkirakan baik;
4. Mengetes hipotesis dan melakukan kerja untuk memperoleh hasilnya;
5. Mengecek kembali hasil yang sudah diperoleh.28
Sedangkan John Dewey, dalam buku How we think membahas secara ringkas lima langkah pemecahan masalah, langkah-langkah tersebut adalah:
1. Mengenali adanya masalah
2. Mengidentifikasi masalah
3. Memanfaatkan pengalaman-pengalaman sebelumnya
4. Menguji hipotesis-hipotesis atau kemungkinan-kemungkinan
penyelesaian secara berurutan
5. Mengevaluasi penyelesaian-penyelesaian dan menarik kesimpulan
berdasarkan bukti.29
28
Erman Suherman dkk., Common Text Book: Strategi Pembelajaran Matematika Kontemporer, (Bandung: JICA – UPI, 2001), h. 36.
29
Selain itu, Polya dalam bukunya menyatakan bahwa fase pemecahan
masalah terdiri dari 4 fase, di antaranya:
1. Memahami masalah, menemukan secara pasti apa yang menjadi pokok
permasalahan.
2. Merencanakan penyelesaian, melihat bagaimana bermacam-macam
item dapat terhubung, bagaimana hal yang tidak diketahui terhubung oleh data, untuk memperoleh ide dari solusi.
3. Melakukan perhitungan.
4. Memeriksa kembali proses dan hasil, ditinjau lalu didiskusikan.30
Dari berbagai tahapan problem solving (pemecahan masalah) yang diuraikan di atas, pada hakekatnya tidak ada perbedaan yang mendasar. Oleh
karena itu, tahapan pemecahan masalah yang digunakan dalam penelitian ini
memakai tahapan yang dikemukakan oleh Polya. Karena, tahapan pembelajaran
problem solving yang dinyatakan oleh George Polya terlihat lebih sederhana daripada tahapan dari Gagne dan John Dewey.
Tahapan pertama dan kedua milik Gagne, yaitu menyajikan masalah
dalam bentuk yang lebih jelas dan menyatakan masalah dalam bentuk yang lebih
operasional dipersingkat menjadi tahapan memahami masalah oleh Polya. Begitu
juga dengan tahapan mengenali adanya masalah dan mengidentifikasi masalah
yang dikemukakan oleh John Dewey, yaitu dipersingkat menjadi tahapan
memahami masalah oleh Polya. Selain tahapan-tahapan tersebut, tahapan lainnya
yang dikemukakan oleh ketiga ahli tidak ada perbedaan. Adapun gambaran umum
tahapan pemecahan masalah menurut Polya seperti berikut:
a. Tahap memahami masalah
Langkah pertama adalah membaca soalnya dan meyakinkan diri bahwa
soal tersebut benar-benar dipahami. Buatlah pertanyaan dalam diri sebagai
berikut :
- Apa yang diinginkan oleh soal?
- Data apa yang diketahui di dalam soal?
30
- Apakah syarat yang diberikan cukup, tidak cukup, atau berlebihan?
b. Tahap merencanakan penyelesaian
Langkah kedua adalah mencari hubungan antara informasi yang diberikan
dengan yang tidak diketahui yang memungkinkan anda untuk memghitung
variabel yang tidak diketahui. Buatlah pertanyaan dalam diri sebagai berikut:
- Apakah kamu pernah menemukan permasalahan yang sama atau
berkaitan?
- Dapatkah kamu menggunakan jawaban atau metode yang sama
dari permasalahan yang pernah didapat? Dapatkah dibuat langkah
penyelesaiannya?
- Jika tidak ada, dapatkah kamu merumuskan dan memecahkan
masalah yang terkait dan menggunakan hasilnya?
c. Tahap melakukan perhitungan (melaksanakan rencana)
Dalam melaksanakan rencana yang tertuang pada tahap kedua, kita harus
memeriksa tiap langkah dalam rencana dan menuliskannya secara detail untuk
memastikan bahwa tiap langkah sudah benar. Sebuah persamaan tidaklah cukup!
d. Tahap memeriksa kembali proses dan hasil
- Dapatkah kamu memeriksa hasil dari setiap langkah
penyelesaiannya? Apakah benar atau salah? Apakah kamu
menggunakan semua data yang ada?
- Apakah kamu memenuhi semua syarat yang diberikan?
- Apakah ada solusi lain untuk memecahkan permasalahan yang
diberikan?
- Dapatkah hasil yang diperoleh digunakan pada permasalahan yang
lain?
c. Hubungan Pendekatan Problem Solving dengan Kemampuan Representasi Matematis
Problem solving merupakan pusat pembelajaran matematika. Hal ini melibatkan akuisisi dan penerapan konsep-konsep matematika dan keterampilan
dalam berbagai macam situasi, termasuk non-rutin, masalah terbuka dan
bergantung pada lima komponen yang saling berkaitan, yaitu konsep (concepts), keahlian (skills), proses (processes), sikap (attitudes) dan metakognisi (metacognition) seperti yang terlihat pada gambar berikut:
Gambar 2.4 Kerangka Pemecahan Masalah Matematika31
Berdasarkan Gambar 2.4 di atas, maka gambaran umum tentang kerangka
pemecahan masalah matematika adalah sebagai berikut:
a. Konsep
Konsep matematika meliputi numerik, aljabar, geometri, statistik,
probabilitas, analisis. Siswa harus mengembangkan dan mengeksplorasi ide-ide
matematika secara mendalam dan melihat bahwa matematika terintegrasi secara
keseluruhan, tidak hanya terisolasi menjadi potongan-potongan pengetahuan.
Siswa harus diberikan pengetahuan yang bervariasi agar pengetahuan yang sudah
didapat bisa lebih berkembang lagi. Kegunaan manipulasi, soal-soal latihan, dan
teknologi dapat menjadi bagian dalam pembelajaran siswa untuk mengembangkan
ide-ide matematika sehingga membentuk konsep baru.
b. Keahlian
Keahlian matematika meliputi penghitungan numerik, manipulasi aljabar,
visualisasi spasial, analisis data, pengukuran, penggunaan alat/media matematika
31
dan perkiraan (estimation). Pengembangan keahlian pada siswa sangat penting dalam pembelajaran dan penerapannya dalam matematika. Meskipun siswa harus
kompeten dalam berbagai keahlian, penekanan yang terlalu berlebihan tanpa
memahami prinsip-prinsip dasar matematika harus dihindari. Keahlian yang
termasuk penggunaan teknologi secara tepat membutuhkan penggunaan keahlian
berpikir dan heuristik dalam proses pengembangan keahlian.
c. Proses
Proses dalam matematika meliputi penalaran, komunikasi dan koneksi,
kemampuan berpikir dan heuristik, aplikasi dan memodelkan. Keahlian berpikir
merupakan keahlian yang digunakan dalam proses berpikir seperti mengklarifikasi,
membandingkan, menganalisis bagian atau keseluruhan, mengidentifikasi
pola-pola dan hubungan, induksi, deduksi, dan visualisasi spasial. Salah satu contoh
heuristik ialah untuk memberikan sebuah representasi dalam bentuk tabel,
diagram, menggunakan persamaan, dan lain-lain.
d. Sikap
Sikap merupakan aspek afektif yang meliputi:
1. Mempercayai matematika dan kegunaannya
2. Tertarik dan menikmati dalam mempelajari matematika
3. Percaya diri dalam menggunakan matematika
4. Tekun dalam memecahkan masalah
Sikap siswa dalam matematika membuat matematika menjadi
menyenangkan, lebih berarti, dan relatif lebih lama menanamkan sikap positif
terhadap mata pelajaran matematika. Perhatian harus diberikan dalam setiap
pembelajaran agar terbentuk kepercayaan diri dan mengembangkan apresiasi
dalam mata pelajaran matematika.
e. Metakognitif
dan menggunakan strategi pemecahan masalah. Hal ini meliputi monitoring
pemikiran sendiri, dan pembelajaran pengendalian diri. 32
Dalam bagian proses matematika, terdapat keahlian berpikir dan heuristik
yang salah satu contohnya yaitu memberikan sebuah representasi dalam bentuk
diagram, tabel, persamaan matematika, dan lain-lain. Selain itu, dalam pendekatan
problem solving, terdapat beberapa strategi yang mungkin diperkenalkan kepada siswa, salah satunya adalah strategi membuat diagram atau gambar. Hal ini
membantu siswa untuk mengungkapkan informasi yang terkandung dalam
masalah sehingga hubungan antar komponen dalam permasalahan tersebut dapat
terlihat dengan jelas. Membuat gambar atau diagram adalah salah satu contoh
representasi visual. Dengan demikian dapat disimpulkan bahwa dalam problem solving memerlukan kemampuan representasi dalam prosesnya.
B.
Hasil Penelitian yang Relevan
a. Anwar Bey & Asriani (2013) dengan judul penelitian “Penerapan
Pembelajaran Problem Solving untuk Meningkatkan Aktivitas dan Hasil Belajar Matematika pada Materi SPLDV”. Penelitian ini bertujuan untuk
meningkatkan aktivitas dan hasil belajar matematika siswa kelas VIIIC
SMP Negeri 2 Kulisusu melalui penerapan pembelajaran problem solving
pada materi Sistem Persamaan Linier Dua Variabel (SPLDV) selama dua
siklus. Hasil dari penelitian ini dapat disimpulkan bahwa pendekatan
problem solving dapat