KEISOMORFISMAAN GEOMETRI AFFIN

BAB I PENDAHULUAN

1.1 Latar Belakang

Geometri Affin adalah bentuk khusus dari geometri insidensi yang di dalamnya memuat kesejajaran dan merupakan bagian khusus dari geometri Euclide. Geometri Affin terbentuk berdasarkan aksioma Affin. Aksioma Affin berupa aksioma kesejajaran. Karena geometri Affin sangat berkaitan erat dengan geometri insidensi, maka perlu juga dilakukan analisis mengenai geometri insidensi. Geometri insidensi memiliki aksioma-aksioma yang mengakibatkan terbentuknya geometri Affin, sehingga perlu adanya pengkajian mendalam tentang geometri insidensi.

Salah satu hal yang menjadi masalah dasar dalam geometri Affin adalah adanya sifat yang isomorfis pada geometri Affin. Dua geometri yang isomorfis akan memiliki kesamaan sifat dan memiliki pemetaan tepat satu-satu dari G ke G’ dari geometri Affin, dimana G merupakan suatu bentuk geometri Affin, sedangkan G’ merupakan suatu bentuk geometri

Affin yang lain. Bentuk dari geometri Affin berupa ruang yang memuat garis dan bidang yang mengandung aksioma kesejajaran.

1.2 Tujuan Penelitian

Tujuan dilakukannya penelitian tentang geometri Affin adalah sebagai berikut: 1. Memeriksa apakah terdapat keisomorfismaan di dalam geometri Affin.

2. Menganalisis bahwa terdapat suatu bentuk geometri yang sifatnya berlaku dalam geometri Affin dan sifatnya berlaku juga dalam geometri insidensi.

1.3 Manfaat Penelitian

Manfaat dari penelitian ini adalah sebagai berikut :

1. Bertambahnya pengetahuan tentang konsep geometri khususnya geometri Affin. 2. Bertambahnya informasi tentang ke-isomorfismaaan geometri.

3. Bertambahnya informasi tentang keterkaitan ilmu geometri tentang geometri Affin dengan ilmu struktur aljabar tentang keisomorfismaan.

4. Mengenal aksioma-aksioma yang membentuk geometri Affin.

Bab II TINJAUAN PUSTAKA

2.1 Konsep Dasar Geometri Affin ( Rawuh, 2009)

Aksioma-aksioma yang membentuk geometri Affin disebut dengan aksioma playfair

yaitu aksioma yang menyatakan bahwa melalui suatu titik yang terletak di luar suatu garis dapat ditarik tepat satu garis yang sejajar dengan garis yang diketahui. Sedangkan , aksioma-aksioma dalam geometri Affin antara lain:

1. Kesejajaran dua bidang dan garis 2. Ketransversalan garis

3. Terdapat perlintasan garis dan bidang 4. Relasi searah antara dua bidang

2.1.1 Kesejajaran Dua Bidang dan Garis Definisi Kesejajaran Geometri Affin

Kesejajaran dalam geometri Affin adalah suatu relasi ekuivalensi yang memenuhi sifat-sifat sebagai berikut :

2. Refleksi, yaitu setiap garis a//a.

3. Simetrik, yaitu jika garis a //b, maka garis b //a.

4. Transitif, yaitu jika garis a //b dan garis b //c, maka garis a //c.

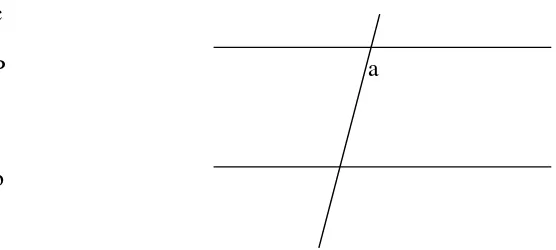
Misalkan garis a sejajar dengan garis b, jika garis c memotong garis a, maka c juga memotong garis b.

Bukti :

Andaikan c memotong a di titik P dan andaikan c\\b. Ini berarti bahwa melalui P ada dua garis yaitu a dan c yang sejajar dengan garis b. Hal ini berlawanan dengan aksioma kesejajaran. Jadi haruslah c memotong garis b.

c

P a

b

Gambar 1.1 Suatu garis yang melintasi dua garis yang sejajar

Akibat 2.1.1

1. Jika garis a \\b dan c\\a, maka garis c\\b. 2. Jika garis a\\b, b\\c maka a=c atau a\\c.

Definisi pusat kesejajaran yang tak kolinier adalah sebagai berikut:

1. Empat titik A,B,C, dan D yang tidak segaris dikatakan membentuk suatu jajaran genjang jika

AB sejajar DC dan BC sejajar AD.

2. A,B,C, dan D adalah titik sudut jajaran genjang tersebut. Segmen-segmen AB, BC,CD, dan

Definisi Kesejajaran Garis

1. Jika garis a // b , maka garis a searah dengan garis b. 2. Dua garis l dan m dinamakan sejajar (ditulis l//m) apabila

 l dan m termuat dalam satu bidang dan

 l dan m tidak memiliki titik sekutu Akibatnya

Apabila l//m maka l dan m termuat dalam satu bidang. Bukti

Menurut definisi kesejajaran garis, andaikan terdapat suatu bidang V yang memuat l dan m. Andaikan bidang V’ juga memuat l dan m, dan titik �, maka V’ dan V memuat l dan titik A, maka V’ = V. Jadi, hanya ada satu (unik) bidang yang memuat dua garis yang sejajar.

Teorema 1

Jika bidang V terdapat dua garis berpotongan yang sejajar dengan bidang W maka V\\W. Teorema 2

Jika titik A pada bidang V dan A tidak pada bidang W dan jika pada V ada dua garis melalui A sejajar dengan garis-garis pada W, maka V\\W.

Bukti:

Andaikan l dan m garis pada V yang sejajar dengan garis-garis pada W, karena l tidak pada W, sehingga l\\W. Begitu pula karena m\\W, sehingga V\\W.

Teorema 3

Jika dua garis berbeda saling sejajar, maka keduanya terletak pada tepat satu bidang. Teorema4

Jika dua buah garis koplanar dan keduanya tegak lurus terhadap suatu garis yang sama, maka keduanya saling sejajar.

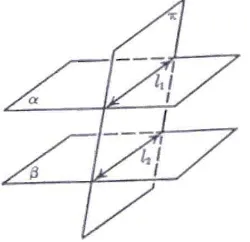
Jika suatu bidang memotong dua buah bidang yang saling sejajar, maka perpotongannya adalah dua buah garis yang saling sejajar seperti gambar berikut ini

Gambar 1.2 Suatu bidang yang melintasi dua bidang yang sejajar

Teorema 6

Jika suatu garis tegak lurus terhadap salah satu bidang dari dua bidang yang saling sejajar, maka garis tersebut tegak lurus terhadap bidang yang kedua.

Teorema7

Jika dua bidang yang setiap bidangnya tegak lurus terhadap suatu garis yang sama, maka kedua bidang tersebut saling sejajar.

Teorema 8

Jika dua garis tegak lurus terhadap suatu bidang yang sama, maka kedua garis tersebut saling sejajar.

Teorema 9

Dua bidang yang saling sejajar, maka keduanya berjarak sama.

Definisi Garis Searah

Kesearahan garis merupakan perluasan kesejajaran dan juga merupakan relasi ekuivalensi, maka berlaku :

i. Jika a searah b maka b searah a

ii. Jika a searah b dan b searah c, maka garis a searah c.

Definisi Relasi Equivalensi Geometri

Andaikan S suatu himpunan dan R suatu relasi dalam S x S yang ditulis sebagai a R b untuk a S dan b S relasi R, maka berlaku:

i. aRa ( sifat refleksif) untuk setiap a S

ii. Apabila aRb maka bRa (sifat simetri) untuk setiap a, b S. iii. Apabila aRb dan bRa maka aRc untuk setiap a, b, c S.

Definisi Kesejajaran Dua Bidang

Dua bidang yang berbeda pada suatu bidang dan juga suatu garis, dikatakan saling sejajar, jika keduanya tidak berpotongan.

Gambar 1.3 Bentuk bidang yang sejajar

2.1.2 Ketransversalan Garis

Definisi Ketransversalan Garis yaitu:

Jika garis l dan m sebidang, maka terdapat tiga kemungkinan yaitu: (1) l\\ m

(3) l \\ m atau l = m

Hubungan antara kesejajaran dan perlintasan dituangkan dalam teorema berikut Teorema 1:

Apabila sebuah bidang terdapat sebuah garis transversal dengan satu dari dua garis sejajar, maka akan transversal dengan garis yang lainnya.

Akibatnya

1. a lint b jika dan hanya jika perpotongan antara a dan b adalah sebuah titik.

2. jika a dan b dua garis yang sebidang (coplanar) maka ada tiga kemungkinan,yaitu (i) a sejajar b

(ii) a lint b (iii) a=b Teorema 2

Apabila terdapat garis pada suatu bidang melintasi salah satu dari dua garis yang sejajar, maka garis tersebut akan melintasi garis yang lain.

2.1.3 Perlintasan Garis dan Bidang

Definisi perlintasan bidang adalah sebagai berikut:

Bidang V dikatakan melintasi bidang W, ditulis V lint W apabila terdapat perpotongan V dan W berupa garis.

Konsep kesejajaran dari perlintasan garis dan bidang adalah sebagai berikut: 1. Apabila g dan V tidak memiliki titik potong maka, g\\V atau V\\g.

2. Apabila garis g dan bidang V bertemu pada suatu titik maka, garis g lint(melintasi) V atau V lint(melintasi) g.

3. Apabila V∩W =∅ (himpunan kosong), maka terdapat bidang V \\W.

Sebuah model geometri insidensi adalah sebuah sistem(S1, S2 ,S3) yang terdiri atas tiga himpunan tertentu S1, S2, S3. Anggota-anggota himpunan tersebut masing-masing dinamakan titik, garis,dan bidang yang memenuhi aksioma insidensi.

Aksioma insidensi terdiri dari

Garis mengandung paling sedikit dua titik

1. Paling banyak satu garis mengandung dua titik yang berlainan

2. Bidang mengandung paling sedikit tiga titik yang tak segaris(tak kolinier) 3. Tiga titik berlainan yang tak segaris terkandung dalam cukup satu bidang

4. Apabila sebuah bidang memuat dua titik berlainan dari sebuah garis, maka bidang itu akan memuat setiap titik pada garis tersebut (garis terletak dalam bidang itu ).

5. Apabila dua bidang bersekutu pada sebuah titik maka kedua bidang itu akan bersekutu pada titik kedua yang lain.

Jadi, sebuah himpunan titik-titik bersama dengan himpunan bagian seperti garis dan bidang yang memenuhi aksioma 1 sampai 6 disebut geometri insidensi. Karena, suatu geometri dibentuk berdasarkan aksioma yang berlaku dalam geometri-geometri tersebut maka dapat dikatakan bahwa geometri insidensi didasari oleh aksioma insidensi. Dalam geometri selain aksioma diperlukan juga unsur-unsur tak terdefinisi. Untuk suatu geometri diperlukan unsur tak terdefinisi sebagai berikut.

1. Titik

2. Garis( Himpunan titik-titik) 3. Bidang (himpunan titik-titik)

Teorema 11

Definisi Garis

Suatu garis yang mengandung titik A dan titik B yang berbeda disebut garis AB. Teorema 12

Apabila titik A tidak pada garis BC maka titik A, B, dan C berlainan dan tidak kolinier. Bukti:

a) Bukti garis A, B, C berlainan.

Menurut ketentuan ≠ . Andaikan A = B, karena (B pada garis BC), maka . Hal ini berlawanan dengan yang diketahui sehingga pengumpamaan A = B adalah tidak benar. Maka haruslah ≠ . begitu pula dengan cara yang sama dapat dibuktikan ≠ . Jadi A, B, C berlainan.

a) Bukti garis A,B C kolinier.

Untuk membuktikan titik A, B, C tak segaris. Andaikan A, B, C segaris. Akan ditunjukkan adanya kontradiksi. Andaikan titik A, B, C segaris maka ada garis g yang memuat A, B, dan C. Karena g memuat b dan C dan ≠ maka g = BC, hal ini berlawanan dengan yang diketahui bahwa tidak pada garis BC. Sehingga pengandaian bahwa A, B, C segaris mengakibatkan kontradiksi. Ini berarti A, B, C tak segaris (tidak kolinier).

Teorema 13

Suatu garis dan suatu titik yang tidak pada garis itu termuat dalam tepat satu bidang. Bukti

memuat garis g dan titik A. Jadi V’ memuat pula B dan C. Ini berarti V’ memuat A, B, dan C. Menurut aksioma 4 bahwa V’ = V. Jadi V adalah satu-satunya bidang yang memuat g dan A.

Karena jika ada bidang lain yang memuat A, B dan C bidang tersebut akan sama dengan bidang V.

Definisi Garis dan Bidang

1. Andaikan � (titik A tidak pada garis g), bidang yang memuat garis g dan titik A dapat ditulis dengan gA.

2. Andaikan titik A, B, dan C berlainan dan tak kolinier, bidang yang memuat A, B, dan C dapat ditulis dengan ABC.

2.3 Ke-Isomorfismaan

Definisi isomorf adalah suatu padanan(korespondensi) satu-satu antara suatu himpunan S dan himpunan S’ adalah suatu padanan a _{a’ (dibaca a sepadan dengan a’ atau}

a’ sepadan dengan a) antara unsur-unsur S dan unsur-unsur S’ sedemikian hingga tiap unsur a dalam S sepadan dengan unsur tunggal a’ dalam S’ dan sebaliknya tiap unsur b’ dalam S’ adalah padanan unsur tunggal b dalam S sehingga b’b.

Bidang G1 dan G2 disebut isomorfis jika ada sebuah fungsi bijektif (satu-ke-satu dan

onto) dari V1 ke V2 dengan sifat bahwa a bertetangga dengan b pada G1 jika dan hanya jika

f(a) bertetangga dengan f(b) pada G2, untuk seluruh a dan b pada V1.

Dua geometri affin G dan G’ yang isomorf, memiliki struktur yang sama. Jika G1,

G2, G3 tiga geometri affin, maka berlaku suatu relasi keequivalenan sebagai berikut: 1. G1≅ G1( sifat reflektif)

3. Jika G1≅G2,G2≅G3, maka G1≅ G3( Transitif)

Keterangan ≅ adalah simbol isomorf. Beberapa teorema:

 Jika f : GG’ suatu isomorfisma, e dan e’ masing-masing adalah unsur kesatuan G dan G’, maka f(e)=e’.

 Jika f : GG’ suatu isomorfisma dan f(a) = a’, aG, a’G’, maka f(a-1_)=[f(a)]-1_.

 Jika f : GG’ suatu isomorfisma dan order elemen a adalah n, maka order f(a) juga adalah n.

 Relasi isomorfisma dalam himpunan grup adalah relasi ekuivalen

Definisi (Rawuh, 2009)

Dua geometri G dan G’ disebut isomorf apabila ada tiga padanan satu-satu yaitu antara

titik-titik, antara garis-garis, dan antara bidang-bidang. PP’, gg’, dan VV’ ( dibaca: titik P sepadan P’, garis g sepadan g’, dan bidang V sepadan V’) dengan sifat:

i) P g dan P’ g’

BAB III METODE PENELITIAN 3.1 Waktu dan Tempat Penelitian

Penelitian ini dilakukan pada semester ganjil tahun ajaran 2012-2013 bertempat di Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam.

3.2 Metode Penelitian

Metode yang digunakan dalam penelitian ini adalah studi pustaka yaitu dengan mempelajari buku-buku penunjang dan Journal. Sedangkan, langkah-langkah yang dilakukan dalam penelitian ini adalah:

1. Mengidentifikasi masalah menggunakan buku dan Journal

2. Mengidentifikasi masalah dengan menggunakan teorema-teorema yang ada 3. Menentukan titik-titik, garis-garis, dan bidang-bidang yang sepadan. 4. Menentukan apakah bidang termasuk dalam geometri Insidensi.

5. Menyelidiki apakah bidang yang terbentuk sesuai dengan teorema-teorema geometri Affin.

BAB V KESIMPULAN DAN SARAN

5.1 Kesimpulan

Dari hasil penelitian yang telah dilakukan diperoleh kesimpulan sebagai berikut: 1. Terbukti bahwa dalam geometri Affin terdapat keisomorfismaan.

2. Terdapat suatu bentuk geometri yang sifatnya berlaku dalam geometri Affin dan sifatnya berlaku juga dalam geometri insidensi.

3. Hal-hal yang membentuk geometri Affin, yaitu kesejajaran dan kesepadanan antata titik dengan garis, titik dengan bidang, dan garis dengan bidang.

1.2 Saran

PERNYATAAN

Yang bertanda tangan di bawah ini: Nama : Pratiwi Handayani

NPM : 0817031045

Jurusan : Matematika

Fakultas : MIPA

Dengan ini Saya menyatakan bahwa dalam skripsi ini tidak terdapat karya yang pernah diajukan untuk memperoleh gelar kesarjanaan di suatu perguruan tinggi dan sepanjang pengetahuan Saya juga tidak terdapat karya atau pendapat yang pernah ditulis atau diterbitkan oleh orang lain, kecuali yang secara tertulis diacu dalam naskah dan disebutkan dalam daftar pustaka.

Apabila ternyata kelak dikemudian hari terbukti ada ketidakbenaran dalam pernyataan Saya diatas, maka Saya akan bertanggung jawab sepenuhnya.

Bandar Lampung, Desember 2013

iv

SANWACANA

Alhamdulillah, puji syukur penulis panjatkan kepada Allah SWT yang telah melim-pahkan karunia, rahmat, dan ridho-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul “Keisomorfismaan Geometri Affin”. Shalawat serta salam senantiasa tercurah kepada Rasulullah Muhammad SAW, keluarga, sahabat, serta umatnya yang senantiasa istiqomah di jalan-Nya.

Pada kesempatan ini, penulis menyampaikan ucapan terima kasih kepada:

1. Bapak Dr. Muslim Ansori, sebagai pembimbing utama atas kesediaan dan kesabarannya memberikan bimbingan, saran, dan motivasi dalam proses penyusunan skripsi ini.

2. Ibu Dorrah Azis, M.Si., sebagai pembimbing pembantu atas kesediaan dan kesabarannya memberikan bimbingan, saran, dan motivasi dalam proses penyusunan skripsi ini.

3. Bapak Agus Sutrisno, M.Si., sebagai dosen penguji yang telah memberikan saran dan kritik dalam penyusunan skripsi ini.

iv

6. Ibu Fitriani, M. Si., sebagai Pembimbing Akademik, atas kesediaan dan kesabarannya memberikan bimbingan, saran, dan motivasi dalam proses penyelesaian kuliah dan penyusunan skripsi ini.

6. Seluruh dosen dan staf di Jurusan Matematika MIPA Matematika Unila atas bantuan dan curahan ilmunya.

7. Teristimewa untuk Bapak, Ibu dan saudara-saudaraku tercinta.

8. Teman-teman seperjuangan Matematika ‘08 terkhusus kepada Marlina, Anggun, Herlisa, Diah, Nurul, Ririn, Mira yang telah banyak membantu. Semoga persahabatan ini selalu terjalin.

11. Saudara-saudariku tercinta di ROIS 2010/2011, di BIROHMAH khususnya presidium dan juga para pimpinan yang solid terimakasih motivasi dan perhatian kalian semua.

12. Semua pihak yang telah membantu dalam menyelesaikan skripsi ini.

Akhirnya penulis berharap semoga skripsi ini dapat bermanfaat bagi penulis khusus-nya dan pembaca pada umumkhusus-nya.

Bandar Lampung, Januari 2013 Penulis,

ABSTRAK

KEISOMORFISMAAN GEOMETRI AFFIN

Oleh Pratiwi Handayani

Kesejajaran dari unsur-unsur tak terdefinisi akan membentuk geometri Affin yang isomorfis. Dugaan sementara geometri Affin memiliki sifat kesejajaran, sehingga kemungkinan besar bahwa terdapat keisomorfismaan pada geometri Affin. Hal yang akan dijadikan sebagai pokok pembahasan adalah tentang adanya kebenaran yang nyata dari suatu bidang-bidang yang sejajar.Metode yang digunakan adalah dengan gambar dan juga contoh. Metode kontradiksi, juga dijadikan sebagai solusi penyelesaian masalah.

RIWAYAT HIDUP

Penulis dilahirkan di Tegal Ombo pada tanggal 5 Maret 1991, anak pertama dari tiga bersaudara pasangan Bapak Jumangin dan Ibu Rostiyowati.

Pendidikan di Sekolah Dasar Negeri 1 Seputih Banyak diselesaikan pada tahun 2002; Sekolah Lanjut Tengah Pertama Negeri 1 Seputih Banyak diselesaikan pada tahun 2005; Sekolah Menegah Umum Negeri 1 Seputih Banyak diselesaikan pada tahun 2008. Pada tahun yang sama penulis terdaftar sebagai mahasiswa di jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Univeritas Lampung melalui Seleksi Nasional Masuk Peguruan Tinggi Negeri (SNMPTN).

Selama kuliah, penulis aktif di beberapa organisasi kemahasiswaan yaitu HIMATIKA sebagai anggota muda (2008-2009), ROIS FMIPA sebagai Sekretaris Biro Kesekretariatan(2010-2011), BIROHMAH sebagai Sekretaris Bidang Keputrian(2011-2012). Penulis juga mengikuti Komunitas Setia Lampung (2012-2013) dan Komunitas Lingkar Anak Muda(2012-2013). Penulis melaksanakan Kerja Praktek pada tahun 2011

Kupersembahkan untuk Ibunda dan Bapak Tercinta

Para Aktivis Dakwah Kampus

Man Jadda Wa Jadda

Dan bahwasanya seorang manusia tiada memperoleh

selain apa yang telah diusahakannya

(An-Najm : 39)

Hidup adalah perjalanan yang memiliki dua rasa:

manis dan getir; lapang dan sesak; suka dan duka;

nikmat dan musibah.

(Salim A. Fillah)