Kajian Teoritik Tingkat Energi Osilator Anharmonik Dengan Potensial Kuartik

LAMPIRAN A

OSILATOR HARMONIK

Persamaan Schrodinger untuk Osilator Harmonik dapat dinyatakan sebagai

berikut:

�2_�

��2

+ (α

– y

2

)Ψ = 0

(A.1)

Dengan y =

(

1_ħ

√��

)

1/2

α

= 2�

ħ

�

�

�

=

2�

ℎ�

dimana v = 1

2�� �

� Merupakan frekuensi Osilator harmonik.

Bentuk Asimtotik �∞ dari fungsi gelombang.

Kita mulai dengan mencari bentuk asimtotik yang harus dimiliki Ψ ketika y

→±∞. Jika fungsi Ψ menyatakan partikel sebenarnya yang terlokalisasi dalam

ruang, harganya harus mendekati nol ketika y mendekati tak terhingga agar

∫_−∞∞ IΨI2dy menjadi terhingga, bukan nol.

Kita tuliskan kembali persamaan (A.1) sebagai berikut:

�2_�

��2

- (y

2

-

α) Ψ = 0

�2_�

��2

= (y

2

-

α) Ψ

�2_�/��2

(y2 −α) Ψ

= 1

Ketika y → ∞, y2≫ �, sehingga:

lim

y →∞�

2_�/��2

Fungsi Ψ∞ yang memenuhi persamaan (A.2) adalah: Ψ∞ = �−�2/2

Karena:

lim

y →∞�

2_� ∞

��2

=

lim

y →∞

(

y 2

- 1

)

�

−�2/2

=

y2

�

−�2/2(A.3)

Persamaan (A.3) merupakan bentuk Asimtotik Ψ yang diperlukan.

Persamaan Diferensial untuk fungsi f(y)

Kita dapat menuliskan fungsi gelombang osilator harmonik sebagai berikut:

Ψ = f(y)

�

∞

= f(y)

�

−�

2_/2

(A.4)

Dengan f(y) fungsi dari y yang harus dicari. Dengan memasukkan persamaan

(A.4) dan (A.1) maka kita peroleh:

�2_�

��2

– 2y

��

��

+(α

-1) f = 0

(A.5)

Ini merupakan persamaan diferensial yang harus di penuhi oleh f.

Pengembangan deret pangkat f(y)

Prosedur yang di gunakan untuk menyelesaikan persamaan diferensial (A.5) ialah

menganggap bahwa f(y) dapat diuraikan dalam deret pangkat y, yaitu:

f(y) =

A

0

+ A

1

y + A

2

y

2

+

�3�

3

+

⋯

=

∑

∞�=1

�

�

�

� (A.6)

kemudian menentukan harga koefisien An. Diferensial f menghasilkan

:

��

��

= A

1

+ 2A

2

y + 3A

3

y

2

+ … =

�

∞_�

��

_�

�

�−1

=1

y

��

��

= A

1

y+ 2A

2

y

2

+ 3A

3

y

3

+ … =

∑

∞_�=1

��

_�

�

�(A.7)

Turunan kedua dari f terhadap y adalah:

�2_�

��2

= 1.2 A

2

+ 2.3A

3

y + 3.4A

4

y

2

+ … =

�

∞_�

n(n

−

1)

�

_�

�

�−2

=2

Yang sama dengan:

�2_�

��2

=

�

(n + 2)(n + 1)

�

�+2

�

�

∞

�=0 (A.8)

Rumus rekursi untuk koefisien An

Dengan mensubstitusikan persamaan (A.6) dan persamaan (A.8) kedalam

persamaan (A.5), maka kita peroleh:

�

[(n + 2)(n + 1)

�

_�+2

−

(2

�

+ 1

− �

)

∞

�=0

A

n

]y

n

= 0

(A.9)

Supaya persamaan ini berlaku untuk setiap y, kuantitas dalam tanda kurung harus

0 untuk setiap harga n, sehingga kita dapatkan persyaratan:

(n+2)(n+1)A

n+2

= (2n+1-

α)A

n

Rumus rekursi:

A

_{n+2 =} 2�+1−∝

(�+2)(�+1)

A

n(A.10)

Rumus rekursi ini memungkinkan kita untuk mencari koefisien A2, A3, A4, ……...

dinyatakan dalam A0 dan A1. Karena persamaan (1.5) merupakan persamaan

diferensial orde kedua, maka penyelesaiannya memiliki dua konstanta sembarang,

disini konstanta itu adalah A0 dan A1. Mulai dari A0 kita dapatkan deret koefisien

Persyaratan yang harus dipenuhi f(y)

Ketika y → ∞; hanya jika Ψ →0 ketika y → ∞, Ψ merupakan fungsi gelombang yang dapat diterima secara fisis. Karena f(y) dikalikan dengan �−�2/2, Ψ memenuhi persyaratan diatas jika:

lim y →∞f(y)

<

�

−�2_/2

Pengembangan deret pangkat fungsi gelombang asimtotik �_∞

Cara yang memadai untuk membandingkan perilaku asimtotik dari f(y) dan

�−�2_/2

ialah menyatakannya dalam deret pangkat (f sudah dalam bentuk deret

pangkat) dan memeriksa rasio antara koefisien deret yang berurutan ketika n →

∞. Dari rumus rekursi persamaan (A.10) kita dapat menyatakan bahwa:

lim

y →∞�_��+2

�

=

2

� (A.11)

Karena

�

�

= 1 + z +

� 2

2!

+

�3

3!

+ …..

Kita dapat menyatakan ��2/2 dalam deret pangkat sebagai berikut:

�

�2_/2

= 1 +

� 2

2

+

�4

22_{. 2!}

+

�6

23 _.3!

+ ……

=

∑

1

2�/2_{. �}� 2�!

∞

�=0,2,4,…

y

n

=

∑∞_{�=0,2,4,… ���}� (A.12)

Rasio antara koefisien yang berurutan dari yn dalam persamaan (A.11) adalah:

��+2

��

=

2�/2 . ��₂�! 2�

+2 2 . ��+2

2 �!

=

2

�/2 _{. �}� 2�!

2 . 2�/2 _{. �}� 2 + 1� (

� 2)!

=

1

2 (�

=

1

�+2

Dalam limit n → ∞, rasio ini menjadi:

lim

n →∞ �_��+2

�

=

1

�(A.13)

Jadi koefisien yang berurutan An dalam deret untuk f berkurang lebih lambat dari

deret pangkat �−�2/2 alih alih lebih cepat, ini berarti f(y) �−�2/2 tidak menuju nol ketika y → ∞.

Jika deret f berakhir pada harga n tertentu, sehingga koefisien An menjadi

nol untuk harga n yang lebih tinggi dari harga tertentu itu, maka � akan menuju nol ketika y → ∞ karena faktor �−�2/2. Dengan kata lain, jika f suatu polynomial dengan suku terhingga alih alih deret tak-terhingga, maka f dapat diterima.

Dari rumus rekursi:

A

n+2 =

2�+1−∝ (�+2)(�+1)

A

n

Jelaslah bahwa jika:

∝

=

2n+1

(A.14)

Untuk setiap harga n, maka An+2 =An+4

=

An+6

= … = 0.

Persamaan (A.14) menentukan suatu deretan koefisien saja, yaitu deretan n genap

mulai dengan A0 atau deretan n ganjil mulai dengan A1. Jika n genap , maka A1= 0

dan hanya pangkat y genap muncul dalam polynomial, jika n ganjil, maka A0= 0

dan hanya pangkat y ganjil muncul.

Rumus tingkat energy yang dihasilkan

Persyaratan

∝

=

2n+1

merupakan syarat perlu dan cukup supaya fungsi gelombang persamaan (A.1) memiliki solusi yang memenuhi berbagai

Dari persamaan

α

= 2�

ħ

�

�

�

=

2�

ℎ�

,

kita peroleh nilai

α

sebagai berikut:

α =

2�

ℎ�

= 2n+1

En

=

(n +

1

2) hv dimana n = 0,1,2,3,4,5,… (A.15)

Jadi energy sebuah osilator harmonik terkuantisasi dengan langkah hv.

Kita lihat untuk n= 0

Maka:

E0 =

1

2 hv (A.16)

Yang menyatakan energy terendah yang dapat dimiliki oleh osilator tersebut.

Harga ini disebut energy titik nol karena sebuah osilator harmonik dalam keadaan

setimbang dengan sekelilingnya akan mendekati E=E0 dan bukan E=0.

Untuk setiap pilihan parameter

α

n terdapat fungsi gelombang yang berbeda

��. Setiap fungsi terdiri dari suatu polinom ��(y) disebut sebagai Polinom

hermite, yang y-nya berpangkat genap atau ganjil, faktor eksponensial �−�2/2, dan sebuah koefisien numerik diperlukan untuk memenuhi syarat normalisasi:

∫ ∣_−∞∞ �� ∣2 dx = 1 dimana n = 0,1,2,3,4,5,… (A.17)

Rumus umum fungsi gelombang Osilator Harmonik ke n adalah sebagai

berikut:

�

_�

= (

2��

ħ

)

1/4

Enam polinom hermite

�

_�

(y)

yang pertama di daftarkan dalam table berikut:

n

�

_�

(y)

∝� Tingkat Energi ke-n (En)

0 1 1 1

2hv

1 2y 3 3

2hv

2 4y2 – 2 5 5

2hv

3 8y3 – 12y 7 7

2hv

4 16y4 – 48y2 + 12 9 9

2hv

5 32y5 – 160y3 + 120y 11 11

LAMPIRAN B

POLINOMIAL HERMITE

Dalam bahasan ini akan dibahas bagaimana mencari solusi umum

polynomial Hermite yang diberikan dalam bentuk persamaan sebagai berikut:

y’’ – pxMy’ + prxM-1y = 0, (B.1)

Dimana nilai p≠ 0, dan r adalah bilangan bulat positif. Untuk M = 1, p = 2, dan r adalah sebuah bilangan bulat positif sehingga persamaan (B.1) menjadi persamaan

Hermite dan memiliki solusi yang sering dikenal dengan nama Polinomial

Hermite. Bagaimana jika p ≠ 0, apakah persamaan (B.1) memiliki solusi polynomial, M adalah bilangan bulat positif yang lebih besar dari satu dan r

adalah bilangan bulat positif.

Terdapat sebuah solusi polynomial untuk persamaan (B.1) berderajat r jika

dan hanya jika:

r = k(M+1) (B.2)

Atau

r = k(M+1) +1 (B.3)

untuk suatu k = 0,1,2,3,4,5,…

selanjutnya, ada beberapa kasus terdapat satu (hingga untuk konstanta perkalian)

solusi polynomial yang selalu berderajat r yang memiliki (k+1) suku dengan

selisih derajat (M+1),yakni jika satu suku berderajat b, maka satu suku tertinggi

berikutnya menjadi berderajat b+M+1.

Pembuktian:

Kita substitusikan bentuk persamaan:

kepada persamaan (B.1) yang didefenisikan dengan manipulasi rumus:

a2 = a3 = … = am = 0 (B.5)

sehingga diperoleh:

an+M+1 = �

(�−�)�_�

(_�+�+1)(�+�) n = 1,2,3,4,5,… (B.6)

kita turunkan persamaan (B.4) sebanyak dua kali:

y’ = ∑∞_�=1�_���−1 (B.7)

y’’ = ∑∞_�=2�(� −1)�_���−2 (B.8)

substitusikan persamaan (B.7) dan persamaan (B.8) kepada persamaan (B.1)

sehingga kita peroleh:

∑_�∞=2�(� −1)�_���−2 - p xM∑∞�=1�����−1 + pr xM-1∑∞�=0���� = 0

Atau,

∑_�∞=2�(� −1)�_���−2 - p ∑�∞=1�����+�−1 + pr ∑∞�=0����+�−1 = 0 (B.9)

Kita substitusikan nilai n = 0,1,2,3,…, n, n+M+1 ke persamaan (B.9) menjadi:

2.1a2 + 3.2a3x + 4.3a4 x2 + … + (n+M+1)(n+M)an+M+1 xn+M-1 + …

- pa1xM – 2pa2xM+1 – 3pa3xM+2- … - pnanxn+M-1 - …

+ pra0xM-1 + pra1xM + pra2xM+1 + … +pranxn+M-1 + … = 0

Kita pisahkan persamaan berdasarkan koefisien yang sama, sehingga diperoleh:

2a2 - pxMa1 + pra0 xM-1 = 0 Untuk koefisien x

6a3x - 2 pxMa2 + pr xM-1 a1x = 0 Untuk koefisien x (B.10)

Melalui manipulasi rumus, a2 = a3 = … = aM = 0 dengan n = 2, 3 , … maka akan

(n+M+1)(n+M) an+M+1 – pnan + pran = 0

(n+M+1)(n+M) an+M+1 = pnan - pran

(n+M+1)(n+M) an+M+1 = (pn – pr) an

an+M+1 =

p(n−r)a (�+�+1)(�+�)

sehingga diperoleh rumus rekursi untuk mencari solusi persamaan Polinomial

Hermite sebagai berikut:

an+M+1 =

p(n−r)a

(�+�+1)(�+�) dengan n = 0,1,2,3,4,… (B.11)

kita misalkan terdapat solusi Polinomial berderajat r. jika r = 1, maka r =

0(M+1)+1.

Jika r ≥2, maka r ≥ M+1 dengan persamaan (B.4) ketika ar = 0 maka ar-(M+1) = 0 juga. Jika r-(M+1) ≤ �, maka persamaan (B.4) memaksa r-(M+1) setara dengan 0 ataupun 1. Sebaliknya dapat dilanjutkan dengan mengurangkan r dengan

kelipatan (M+1) hingga bilangan bulat k diperoleh sedemikian sehingga:

r – k(M+1) = 0,1 (B.12)

untuk r – (M+1) = 0, r dikurangi dengan kelipatan (M+1), (2M+2, …, (kM+2)

sehingga diperoleh:

r – (M+1) = 0

r – (2M+2) = 0

r – (3M+3) = 0

.

.

.

r – (kM+k) = 0

r – k(M+1) = 0

r = k(M+1).

Untuk r – (M+1) = 1, r dikurangi dengan kelipatan (M+1), (2M+2), …, (kM+k)

r – (M+1) = 1

r – (2M+2) = 1

r – (3M+3) = 1

.

.

.

r – (kM+k) = 1

r – k(M+1) = 1

r = k(M+1)+1

maka persamaan (B.4) memiliki r – (M+1) sama untuk 0 atau 1

r – k(M+1) = 0 atau 1 (B.13)

dengan demikian ditentukan persamaan (B.2) dan persamaan (B.3), sebaliknya,

jika

r = k(M+1) untuk semua k, maka dapat dinyatakan dari persamaan (B.5) bahwa

ketika n = r = k(M+1), diperoleh an+M+1 = 0.

Oleh sebab itu al(M+1) = 0 untuk semua l≥ �+ 1. selanjutnya, dengan menggunakan persamaan (B.4) disertai dengan persamaan (B.5) diperoleh ai+l(M+1)

= 0, untuk semua 2 ≤ � ≤ � dan � ≥ �.

Kemudian dapat disimpulkan bahwa jika ai+l(M+1) = 0, untuk semua l ≥ �, harus ditetapkan nilai a = 0 dan kita gunakan persamaan (B.5). Jika a≠ 0, persamaan (B.5) kembali mengimplikasikan bahwa ar = ak(M+1) dan karena itu y(x)

merupakan sebuah polynomial berderajat r.

Kemudian dapat disimpulkan bahwa jika a ≠0, maka y(x) bukan sebuah polynomial. Dengan demikian didapat a0 sedemikian sehingga ar = 1, dan disini

dapat dilihat bahwa solusi polynomial adalah tunggal hingga konstanta perkalian

a0. Pertimbangan yang sama dapat diterapkan pada kasus r = k(M+1)+1. Solusi

polinomialnya tunggal hingga konstanta perkaliannya a1.

r = k(M+1) maka derajat terendah dari solusinya adalah a0, jika r = k(M+1)+1

maka derajat terendah dari solusinya adalah: a1x. catatan jika r = k(M+1), maka

pilihannya adalah a1 = 0. Jika r = k(M+1)+1, maka pilihannya adalah a0 = 0.

Pembuktiannya:

Analisa dari r = k(M+1) dalam rumus rekursi persamaan (B.6) diikuti

pengurangan rumus (k-1).

k dikurangi dengan kelipatan (k-1), (k-2), … , (k-k) sehingga diperoleh:

arxxr = ak(M+1) xk(M+1)

a(k-1) (M+1)x(k-1) (M+1)

.

.

.

a(M+1) x(M+1)

a0.

Jika r = k(M+1) maka derajat terendah dari solusi polynomial adalah a0 sama, jika

r = k(M+1)+1 maka derajat terendahnya adalah a1x.

Catatan: jika r = k(M+1), maka pilihannya adalah a1 = 0. Jika r = k(M+1)+1, maka

LAMPIRAN C

DERET PANGKAT

Bentuk umum deret pangkat.

Deret pangkat merupakan perkembangan dari deret kompleks biasa. Secara

prinsip, deret pangkat adalah deret kompleks yang memiliki bentuk pangkat dari

(z – z0).

Suatu deret takhingga dengan bentuk:

∑ ���� = ∑∞�=0���� = �0 + �1� + �2�2 + �3�3 + … + ���� + …

(C.1)

Dimana �_� konstan disebut deret pangkat dalam x. sesuai itu, maka diperoleh deret takhingga dengan bentuk:

∑ ��(� − �0)� = �0 + �1(� − �0) + �2(� − �0)2 + �3(� − �0)3 + … + ��(� −

�0)� + … (C.2)

Bentuk umum deret pangkat adalah sebagai berikut:

∑∞�=0�� . (z-z0)n (C.3)

Dengan z adalah peubah kompleks (complex variable) dan koefisien an. deret ini

memiliki titik pusat z0 dan jari jari konvergensi dengan symbol �. kedua hal ini adalah parameter dalam deret pangkat.

Ada 2 cara untuk mencari � adalah sebagai berikut: 1. Formula Cauchy-Hadamard, yaitu: lim_{�→∞∣�}∣��∣

�+1∣ = � 2. lim_�→∞ ∣��∣

∣��∣

1

�

Setelah kita memperoleh nilai �, maka ada 3 sifat dari deret pangkat tersebut berdasarkan nilai � yang dimiliki, yaitu:

1. Jika � = 0, maka deret diatas konvergen hanya pada titik z0, dan divergen pada titik yang lain.

2. Jika 0 < � < ∞, maka deret diatas pasti konvergen mutlak untuk semua nilai z dengan ∣ � − �₀ ∣< � dan divergen untuk semua nilai z dengan

∣ � − �0 ∣>�. Lalu bagaimana dengan ∣ � − �0 ∣= �? itu bisa konvergen,

bisa juga divergen.

3. Jika �= ∞, maka deret diatas konvergen mutlak untuk semua nilai z. artinya deret tersebut tidak pernah divergen.

Latihan soal.

Soal 1.Jika diketahui deret pangkat sebagai berikut:

∑ 1

(1+�)�

∞

�=0 (�+ 2− �)�, tentukanlah pusat dan jari jari konvergensi.Dan

periksa juga apakah deretnya merupakan konvergen atau divergen pada

jari- jari konvergensinya.

Penyelesaian:

∑ 1

(1+�)� ∞

�=0 (�+ 2− �)� ; dari bentuk deret disamping kita bisa melihat bahwa:

z0 = -2 + i. dengan demikian maka an =

1

(1+�)� maka jari – jari konvergensinya:

lim_�→∞ 1 (1+�)�

1 (1+�)�+1

� = lim �→∞

(1+�)�+1 (1+�)�

= lim

�→∞ (1+i)

= 1 + i

Jari jari konvergensi � = ∣1+i∣ = �(1)2_{+ (1)}2 _{= √2}

Kesimpulan sementara yang dapat diambil adalah:

Deret ∑ 1

(1+�)� ∞

�=0 (�+ 2− �)�, pasti konvergen pada semua z dengan

Dan deret tersebut pasti juga divergen pada semua z di ∣z + 2 - i∣>√2. Lalu bagaimana dengan lingkaran tepat pada jari jari √2?? Kita harus melakukan test lagi dengan cara melakukan substitusi (z + 2 - i) = √2 ke dalam deret diatas. Sehingga deret diatas menjadi:

∑ 1

(1+�)� (√2) � ∞

�=0 atau dapat dituliskan:

∑ 2�2

(1+�)� .

Sekarang kita anggap deret diatas menjadi sebuah deret baru. Lalu kita periksa

apakah deret itu konvergen atau tidak. Jika konvergen, maka deret semula dalam

soal 1 ini konvergen pada lingkaran (z + 2 - i) = √2 . Untuk memeriksa deret ∑ 2

�

2

(1+�)� apakah konvergen atau tidak;

∑ 2�2

(1+�)�dapat ditulis menjadi ∑( √2 1+�)

� _{→ tampak, jika n → ∞ maka deret ini makin}

besar: berarti deret ini Divergen.

Dengan demikian, kesimpulannya ialah deret dalam soal 1 ini,

∑ 1

(1+�)� ∞

�=0 (�+ 2− �)�konvergen pada cakram terbuka ∣z + 2 - i∣<√2.

Soal 2.Jika diketahui deret pangkat sebagai berikut:

∑ 2� . (�+1)� (2�−1) ∞

�=1 , tentukanlah pusat dan jari jari konvergensi.Dan periksa juga

apakah deretnya merupakan konvergen atau divergen pada jari- jari

konvergensinya.

Penyelesaian:

�2�₍₂ . (_{� −}�+ 1)₁₎ �

∞

�=1

Dari bentuk diatas, maka pusatnya z0 = -1. Dan an=

2� (2�−1).

Maka jari jari konvergensi:

lim_�→∞ 2� 2(�+1) ∗

(2(�+1)−1)

(2�−1) = lim�→∞ 2� (2�+2) ∗

(2�+1) (2�−1) =

Maka deret diatas pasti konvergen untuk semua z pada cakram terbuka ∣z+1∣< 1. Untuk mengetahui sifat deret tersebut, pada lingkaran ∣z+1∣ = 1, kita substitusi nilai ini ke dalam deret diatas, sehingga terbentuk sebuah deret baru:

∑2� .(1)� (2�−1) = ∑

2� 2�−1

TIPS:

Kita perhatikan pangkat tertinggi dari n untuk pembilang dan penyebut. Ternyata

sama, yaitu 1. Maka, bila kita memakai uji rasio untuk deret ini, kita akan

mendapat bahwa harga limitnya sama dengan 1.

Itu artinya, kita tetap tidak dapat menentukan apakah konvergen atau

divergen.Maka kita jangan memakai uji rasio.

Kita periksa deret tersebut dengan cara sebagai berikut:

lim_�→∞ 2� (2�−1) =

2

2 = 1 →≠ 0.

Maka deret ∑ 2�

2�−1 bersifat divergen.

Dengan demikian deret semula dalam soal ini hanya konvergen pada cakram

LAMPIRAN D

OSILATOR ANHARMONIK

Persamaan Schrodinger digunakan untuk menggambarkan berbagai macam sistem

mekanika kuantum, walaupun sebenarnya tidak dapat diselesaikan kecuali untuk

beberapa model sederhana. Persamaan Schrodinger ini biasanya menggunakan

persamaan linear dua variable yang diselesaikan dengan menggunakan metode

ekspansi deret pangkat persamaan diferensial, atau menggunakan operator tangga

dalam mekanika kuantum. Pada osilator anharmonik, persamaan fungsi

gelombang schrodinger yang digunakan adalah sebagai berikut:

−_��ħ�Ψ’’(x) + Ax4Ψ(x) = E Ψ(x) (D.1)

Untuk memecahkan persamaan ini dalam satu dimensi, pertama kita

menggunakan persamaan diferensial orde dua, kemuadian dilanjutkan dengan

metode deret pangkat.

4.1. Persamaan Awal

Pertama kita perkenalkan persamaan linear dua variable sebagai berikut:

y’’ – 2xy’ + (2n +x2 – x4)y = 0 (D.2)

ini bukan merupakan adjoint nya, melainkan untuk mempermudah

memperkenalkan serangkaian fungsi abnormal (�_�) sebagai berikut:

�� = �−�2/2. y(x) (D.3)

Dengan mensubstitusikan persamaan (D.3) ke dalam persamaan (D.2), maka akan

diperoleh persamaan diferensial untuk �_� sebagai berikut:

Persamaan (D.4) ini merupakan persamaan diferensial untuk osilator anharmonik

mekanika kuantum dengan energy potensial V(x) = Ax4.

4.2. Solusi Analitik

Dengan menggunakan metode deret pangkat, kita memperoleh solusi dari

persamaan (D.2) sebagai berikut:

y(x) = xk (�₀ + �₁� + �₂x2 + �₃x3 + …)

y(x) = ∑∞_�=0�_���+� , a0≠ 0 (D.5)

dimana eksponen k dan koefisien koefisien am sudah ditentukan. Dengan

menurunkan persamaan (D.5) sebanyak dua kali, maka kita peroleh:

��

�� = ∑∞�=0�� (�+�)��+�−1, �2_�

��2 = ∑ �� (�+�)(�+� −1)��

+�−2 ∞

�=0 (D.6)

Dengan mensubstitusikan persamaan (D.6) kedalam persamaan (D.2) maka kita

peroleh:

∑∞�=0�� (�+�)(�+� −1)��+�−2 – 2∑∞�=0�� (�+�)��+� +

2n∑∞_�=0�_���+� + ∑_�∞₌₀�_���+�+2 - ∑∞_�=0�_���+�+4 = 0 (D.7)

Pangkat x terendah pada persamaan (D.7) adalah: xk-2, untuk m=0 pada

penjumlahan pertama. Keunikan dari deret pangkat memerlukan penghilangan

koefisien yang menghasilkan:

�0k(k-1) = 0

Dimana �₀ ≠ 0.

Jika �₀ = 1, maka kita peroleh:

persamaan (D.8) ini merupakan persamaan indisial yang menghasilkan nilai k-0

atau k-1.

Jika kita tinjau kembali persamaan (D.7) dan menetapkan m = j+2 pada

penjumlaham yang pertama, kemudian m = j,m = j, m = j-2, m = j-4 berturut turut

pada penjumlahan kedua, ketiga, keempat dan kelima maka kita peroleh:

aj+2 (k+j+2)(k+j+1) – 2aj (k+j-n)+aj-2 – aj-4 = 0

a

j+2

=

��−4−��−2+ 2�� (�+� −�)

(�+�+2)(�+�+1) (D.9)

dengan menggunakan cara yang sama pada persamaan (D.8) untuk k = 0 dan j =

bilangan genap, kita peroleh:

a2 = �0

2! 2(-n)

a4 = �0

4! [-2! + 2

2

(-n)(2-n)]

a6 = �0

6! [4! – 4!

2! 2(-n) – 2

2

(4-n) + 23 (-n)(2-n)(4-n)]

dan untuk k = 1 dan j = bilangan genap, kita peroleh:

a2 = �0

3! 2(1-n)

a4 = �0

5! [-3! + 2

2

(1-n)(3-n)]

Pada kasus k = 0, semua nilai koefisiennya kita masukkan kedalam persamaan

(D.5), maka kita peroleh:

ygenap = a0 [1+

1

2! (2(-n))x

2 + 1

4! (-2! + 2

2

(-n)(2-n))x4 + 1

6!(4! – 4!

2! 2(-n) – 2

2

(4-n) +

23(-n)(2-n)(4-n))x6 + …] (D.10)

melalui persamaan (D.10), kita tentukan Polynomial Hermite untuk n = genap

dan menghasilkan beragam parameter sebagai berikut:

ygenap = a0 [1+

1

2! (2(-n))x

2 + 1

4!(2

2

(-n)(2-n))x4 + 1

6!(2

3

(-n)(2-n)(4-n))x6 + …] + a0

[−2!

4! x

4 + 1

6! (4! – 4!

2! 2(-n) – 2

2

dengan cara yang sama kita juga dapat menetukan Polinomial Hermite untuk n =

ganjil dan k = 1 sebagai berikut:

yganjil = a0 [x +

1

3!(2(1-n))x

3 + 1

5!( 2

2

(1-n)(3-n))x5 + 1

7!(2

3

(1-n)(3-n)(5-n))x7 + …] +

a0 [-

3! 5!x

5 + 1

7!(5! – 5!

3! 2(1-n) – 3!2(5-n))x

7

+ …] (D.12)

Tanda kurung siku pertama dari ruas kanan ygenap dan yganjil hanya menunjukkan

bentuk dari polynomial hermite yang kemudian kita masukkan nilainya kedalam

persamaan (D.3).

Maka untuk n = genap kita peroleh:

��(x) = �−�2/2 {Hn(x) + �0�4 [- 2! 4! +

1 6! (4! –

4!

2! 2(-n) – 2

2

(4-n)) x2 + …]} (D.13)

Untuk n = ganjil kita peroleh:

��(x) = �−�

2_/2

{Hn(x) + �0�5 [- 3! 5! +

1 7! (5! –

5!

3! 2(1-n) – 3!2 (5-n)) x

2

+…]}(D.14)

4.3. Fungsi fungsi gelombang dan tingkat tingkat energi

Persamaan fungsi gelombang Schrodinger dengan energy potensial V(x) = Ax4,

Dituliskan sebagai berikut:

−_��ħ�Ψ’’(x) + Ax4 Ψ(x) = E Ψ(x), dimana m = massa partikel dan E = energy total.

Dengan mengggunakan kuantitas tidak berdimensi sebagai berikut:

x = αz dimana ∝6 ₌ 2��

ħ2 (D.15)

λ = 2��_ħ2_�2 = E(

2� ħ2 )

2/3

(A)1/3 (D.16)

τ = 1 2� 2�� � ( � � )

1/4г(1/4)

г(3/4) (D.17)

Dengan [Ψ(z) = Ψ(x/α) = ѱ(x)], maka persamaan (D.1) menjadi:

�2_ѱ

��2 + (λ – x 4

) ѱ(x) = 0 (D.18)

Persamaan (D.18) ini merupakan persamaan (D.4) dengan λ = 2n+1. Maka untuk n = genap kita peroleh:

Ѱn(x) = K�−� 2_/2

{Hn(x) + a0x4 [-

2! 4! +

1 6!(4! –

4!

2! 2(-n) – 2

2

(4-n))x2 + …]} (D.19)

Untuk n = ganjil kita peroleh:

Ѱn(x) = K�−� 2_/2

{Hn(x) + a0x5 [-

3! 5! +

1 7!(5! –

5!

3! 2(1-n) – 3!2(5-n))x

2

+ …]} (D.20)

Persamaan (D.19) dan persamaan (D.20) merupakan fungsi fungsi gelombang

Osilator Anharmonik mekanika kuantum untuk genap Ѱ 0, Ѱ2,… dan ganjil Ѱ 1, Ѱ3,…

Dengan menggunakan persamaan (D.16) dan persamaan (D.17) dan diketahui

nilai г(1/4) = 4.(1

4)! = 4 dan г(3/4) = � √2

4 maka kita peroleh Energi:

En = (�

4)

3/4

. г(1/4)

√2�г(3/4)ħ�

En = (2n+1)3/4 .

4

�√2�ħ� (D.21)

Untuk Energy tingkat dasar dengan n = 0 adalah:

E0 = 4

�√2� ħ� = 0,5079ħ�≅ 1

LAMPIRAN E

FUNGSI GAMMA (г)

DEFENISI:

1. Merupakan salah satu fungsi khusus yang biasanya disajikan dalam

pembahasan kalkulus tingkat lanjut

2. Dalam aplikasinya fungsi Gamma ini digunakan untuk membantu

menyelesaikan integral-integral khusus yangsulit dalam pemecahannya

dan banyak digunakan dalammenyelesaikan permasalahan di bidang fisika

maupunteknik.

3. Pada dasarnya dapat didefinisikan pada bidang real dankompleks dengan

beberapa syarat tertentu.

Fungsi gamma dinyatakan oleh г (x)yang didefenisikan sebagai berikut ini:

Г(x) = ∫ �∞ �−1�−�

0 �� (E.1)

x dan r adalah bilangan real.

Rumus ini merupakan integral yang konvergen untuk x > 0.

Rumus rekursif untuk fungsi gamma adalah:

г(x+1) = xг(x) (E.2)

melalui persamaan (E.2) dapat ditentukan harga г(x) untuk semua x>0 bila nilai

nilai untuk 1≤ � ≤2.

Jika x adalah bilangan bulat maka: г(x+1) = x!

jika di kombinasikan persamaan (E.1) dan persamaan (E.2) maka diperoleh

Г(x) = г(x+1)

� (E.3)

Sifat dasar fungsi gamma real

a. Г(x) tidak terdefenisi untuk setiap x = 0 atau bilangan bulat negatif

Pembuktian:

Dari persamaan (E.1) dengan x = 0, diperoleh:

Г(0) = ∫ �∞ −1_�−�

0 ��

Bukti tersebut merupakan integral divergen sehingga Г(0) tidak terdefinisi.

Untuk x = n bilangan bulat negatif dan dengan mensubstitusikan x kedalam

persamaan (E.3), maka diperoleh:

Г(n) = Г(0)

�(_�+1)(�+2)…(−2)(−1) (E.4)

Karena Г(0) tidak terdefinisi, maka Г(n) tidak terdefenisi pula untuk n bilangan

bulat negatif.

n! ~√2���.�−� (E.5)

LAMPIRAN F

PERIODE OSILATOR NONLINEAR

Sebuah partikel dengan massa m yang pada hakekatnya berosilasi secara

nonlinear dibawah pengaruh fungsi energi potensial memberikan:

V(x) = Axn (F.1)

(Dimana A adalah konstanta positif dan n adalah sebuah bilangan bulat genap

yang lebih besar atau sama dengan 4).

Sistem ini, tentu saja konservatif, sehingga diperoleh:

1 2�ẋ

2_{+ �(�) =� (F.2)}

Dimana total Energi selalu konstan positif sehingga persamaan (K.2) dapat

dituliskan sebagai berikut:

��= ±(� 2�)

1 2 . ��

�1−�(�)

�

(F.3)

Untuk memperoleh nilai periode osilasi maka persamaan (K.3) kita integrasikan

sehingga diperoleh:

T = 4(� 2�)

1/2_∫ ��

�1−���/� �

0 (F.4)

Dimana A adalah Amplitudo osilasi yang berhubungan dengan nilai Energi total

E= bAn lalu substitusikan nilai x = (� �)

1

� .���

2

Sehingga persamaan (F.4) menjadi:

T = 8

� . ( � 2�)

1 2 . ( �

�)

1

�∫�/2���2��−1���

0 (F.6)

Setelah mengintegrasikan persamaan (K.6), maka diperoleh T dalam bentuk yang

lebih ssederhana sebagai berikut ini:

T = 4

(

�� 2

)

1/2

. (

�1−�/2

�

)

1/�

.

г(

1 �+1)

г( 1_�+₂ 1)(F.7)

Dimana pada persamaan (K.7) ini kita menggunakan bentuk identitas dari fungsi gamma (г) sebagai berikut ini:

Г(z+1) = z г(z) (F.8)

Jika kita substitusi syarat syarat dari amplitude untuk total energi, maka diperoleh

bentuk periode sebagai berikut ini:

�= 2√2� . г( 1 �+1)

г(1_�+₂ 1)

.

�

1−�/2

�

�

�(F.9)

Dengan n > 0

Persamaan (F.9) ini merupakan periode osilasi dari osilator yang terdapat

dalam energy potensial pada persamaan (F.1).dalam persamaan ini, n tidak perlu

harus merupakan bilangan bulat. Persamaan (F.9) menunjukkan bahwa periode

dan frekuensi osilasi tidak bergantung pada amplitude dan energi total nya hanya

jika n = 2 (merupakan osilator harmonik sederhana).

Dalam hal ini, dengan b = k/2 maka persamaan (F.9) mengurangi nilai

periode osilasi sistem massa pegas, T = 2л ��_� . meskipun setiap osilator linear memiliki sebuah periode yang tidak bergantung amplitude, namun itu tidak benar.

LAMPIRAN G

LISTING PROGRAM MATLAB FUNGSI GELOMBANG

OSILATOR ANHARMONIK

clear;

clc;

disp('Plot Grafik');

disp('---');

xMin=input('masukkan x minimum = ');

xMax=input('masukkan x maksimum = ');

x=xMin:0.1:xMax;

y1=zeros(1, length(x));

y2=zeros(1, length(x));

y3=zeros(1, length(x));

y4=zeros(1, length(x));

y5=zeros(1, length(x));

y6=zeros(1, length(x));

for i=1:length(y1)

y1(i)=2.7^-(x(i)^2/2)*(1+(x(i)^4)*(faktorial(2)/faktorial(4)+(1/faktorial(6))*(faktorial(4)(fakt

orial(4)/faktorial(2))*2*0-2^2*(4-2))*x(i)^2));

end

y2(i)=2.7^-(x(i)^2/2)*(2*x(i)+(x(i)^5)*(faktorial(3)/faktorial(5)+(1/faktorial(1))*(faktorial(5)

(faktorial(5)/faktorial(3))*2*(1-1)-faktorial(3)*2*(5-1))*x(i)^2));

end

for i=1:length(y3)

y3(i)=2.7^-(x(i)^2/2)*(((4*x(i)^2)2)+(x(i)^4)*(faktorial(2)/faktorial(4)+(1/faktorial(6))*(fakt

orial(4)(faktorial(4)/faktorial(2))*2*(-2)-2^2*(4-2))*x(i)^2));

end

for i=1:length(y4)

y4(i)=2.7^-(x(i)^2/2)*((8*x(i)^3-12*x(i))+(x(i)^5)*(-

faktorial(3)/faktorial(5)+(1/faktorial(1))*(faktorial(5)-(faktorial(5)/faktorial(3))*2*(1-3) faktorial(3)*2*(5-3))*x(i)^2));

end

for i=1:length(y5)

y5(i)=2.7^-(x(i)^2/2)*((16*x(i)^4-48*x(i)^2+12)+(x(i)^4)*(-

faktorial(2)/faktorial(4)+(1/faktorial(6))*(faktorial(4)-(faktorial(4)/faktorial(2))*2*(-4)-2^2*(4-4))*x(i)^2));

end

for i=1:length(y6)

y6(i)=2.7^-(x(i)^2/2)*((32*x(i)^5-160*x(i)^3+120*x(i))+(x(i)^5)*(-

faktorial(3)/faktorial(5)+(1/faktorial(1))*(faktorial(5)-(faktorial(5)/faktorial(3))*2*(1-5)-faktorial(3)*2*(5-5))*x(i)^2));

end

subplot(3,2,1)

title('Grafik n=0')

subplot(3,2,2)

plot(x,y2)

title('Grafik n=1')

subplot(3,2,3)

plot(x,y3)

title('Grafik n=2')

subplot(3,2,4)

plot(x,y4)

title('Grafik n=3')

subplot(3,2,5)

plot(x,y5)

title('Grafik n=4')

subplot(3,2,6)

plot(x,y6)

LAMPIRAN H

LAMPIRAN I

LAMPIRAN J

Daftar Pustaka

Beiser, Arthur.1987. Konsep Fisika Modern.Edisi Keempat. Jakarta: Penerbit

Erlangga

Eisberg, R, dan Resnick, R, 1970, Quantum Physics, Jhon wiley & Sons,New

York,California.

Fitri, Sari Rachma dkk.Makassar Fisika Dasar ii. 2012. Balikpapan: universitas

Balikpapan press.

Giancoli, Douglas C. 2001. Fisika. Edisi Kelima Jilid 1. Erlangga. Jakarta.

J. Arfken, Mathematical Methods for Physicists, Third Edition Academic Press,

Harcourt Brace Jovanovich, Publisher (1985) p. 564

Krane, Kenneth. 1992. Fisika Modern. Jakarta: Penerbit Universitas Indonesia

(UI Press)

Nicolaide, Andre. 2012. General Theory of the Electromagnetic Field.

Transilvania University Press. Braşov, Romania.

P.M. Morse, H. Feshbach, Methods of Theoritical Physics, Mc Graw-Hill Book

Company(1993)

P . Mohazzabi, Am.J.Phys. 72, 492(2004)

Ruwanto, Bambang. Fisika II. 2007. Yogyakarta: Yudhi Tira.

Said. L, M. Fisika Dasar I. 2007. Makassar.UIN press.

Sugiyarni, Anik. 2010. Mekanika Kuantum. Universitas Sebelas Maret. Surakarta.

Stolze,Joachim dan Dieter, 2007, Quantum Computing, University Of Dartmond,

Institute Of Physics,Weinheim,Germany

Suwana, Wayan. Osilator harmonic. Pendidikn Fisika universitas lampung

S. James, Single Variable Calculus, Early Transcendental. Fourth Edition. New

York: Brooks/Cole Publishing Company, 1999

Tjia,M.O.1999. Mekanika Kuantum. Bandung: Penerbit ITB

Halaman: 80-84

Wiley and Sons Ltd Singh,Kamal,2006, Element Of Quantum Mechanics,

S.Chand & Company LTD

Zettili, Nouredine.2009. Quantum Mechanics Concepts and Applications. John

BAB 3

METODOLOGI PENELITIAN

3.1. Tempat Penelitian

Tempat dilakukannya penelitian dengan judul: “Kajian Teoritik Osilator

Anharmonik dengan Potensial Kuartik” adalah:

1. Perpustakaan Umum USU

2. Perpustakaan LIDA FMIPA USU

3. Laboratorium Fisika Komputasi FMIPA USU

3.2. Waktu Penelitian

Penelitian ini akan dilakukan pada Januari 2016 – Juni 2016.

NO Nama

kegiatan

Januari

2016

Februari

2016

Maret

2016

April

2016

Mei

2016

Juni

2016

1 Studi

literatur

2 Seminar

proposal

3 Pengolahan

Data

4 Analisa

Data

5 Seminar

hasil

6 Meja Hijau/

3.3. Rancangan Penelitian

Adapun rancangan penelitian judul “Kajian Teoritik Tingkat Energi Osilator

Anharmonik dengan Potensial Kuartik” adalah sebagai berikut:

1. Menyelesaikan persoalan Fisika dengan persamaan diferensial orde kedua

yang mengarah kepada persamaan diferensial Osilator Anharmonik

Mekanika kuantum.

2. Mengembangkan solusi analitis berdasarkan metode deret pangkat dan

kemudian dilanjutkan dengan Polinomial Hermite.

3. Menggunakan koefisien dalam deret pangkat yang dihasilkan untuk

memperkenalkan fungsi gelombang dan tingkat energi Osilator

[image:36.595.89.486.127.699.2]

3.4.

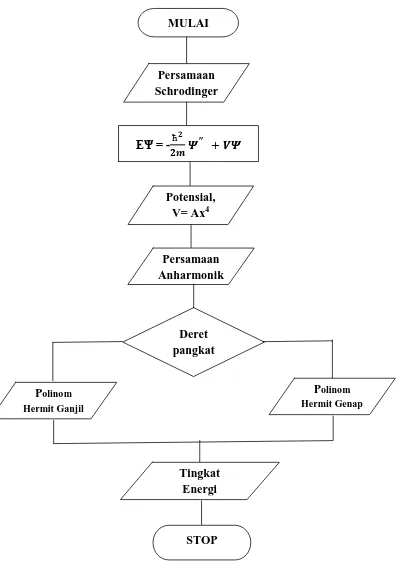
Diagram Alir Penelitian

Gambar 3.1.Diagram Alir Kajian Teoritik Tingkat Energi Osilator Anharmonik

dengan Potensial Kuartik.

MULAI

Persamaan Schrodinger

EΨ = -ħ

�

���′′ +��

Potensial, V= Ax4

Persamaan Anharmonik

Deret pangkat

Polinom Hermit Ganjil

Polinom Hermit Genap

Tingkat Energi

BAB 4

HASIL DAN PEMBAHASAN

4.1. Persamaan Awal

Persamaan Schrodinger untuk osilator anharmonik adalah sebagai berikut:

−_��ħ�Ψ’’(x) + Ax4Ψ(x) = E Ψ(x) (4.1)

Persamaan (4.1) ini dikalikan dengan [−2�

ħ2 ], sehingga diperoleh:

−_��ħ�Ψ’’(x) + Ax4Ψ(x) - E Ψ(x) = 0

Ψ’’(x)- 2�

ħ2 (��

4_{) Ψ(x) +}2�

ħ2 (�) Ψ(x) = 0

Ψ’’(x)- 2�

ħ2 [��

4_{+ �]} Ψ(_{x) = 0}

Ψ’’(x)+ 2_ħ�₂ [� − ��4] Ψ(x) = 0 (4.2)

Persamaan (4.2) merupakan persamaan linear dua variabel yang dapat dituliskan

bentuknya sebagai berikut ini:

�′′ _{− 2��}′ _{+ (2�+�}2_{− �}4_{)�= 0 (4.3)}

Dimana persamaan (4.3) ini bukan merupakan adjoin dari persamaan (4.2)

melainkan hanya untuk mempermudah memperkenalkan serangkaian fungsi �_�

berikut ini:

�� = �−� 2_/2

Persamaan (4.4) ini dikalikan dengan ��2/2 �_�, maka akan diperoleh:

(�_� ) (��2/2 �_�) = �−�2/2 y(x) (��2/2 �_�)

y(x) = ��2/2 �_� (4.5)

Turunan pertama untuk persamaan (4.5) adalah sebagai berikut:

�′_{(�) = ��}�2_/2

�� + ��2/2 ��′

�′_{(�) = �}�2_/2

(��_� + �_�′)

(4.6)

Turunan kedua untuk persamaan (4.5) adalah sebagai berikut:

�′′_{(�) = ��}�2_/2

��� +��2/2 �� + ��2/2 ���′ + ���2/2 ��′ +��2/2 ��′′

= �2��2/2 �_� + 2���2/2 �_�′ + ��2/2 �_� + ��2/2 �_�′′

= �2��2/2 �_� + ��2/2 �_� + 2���2/2 �_�′ + ��2/2 �_�′′

= ��2/2�_� (�2+ 1) + 2���2/2 �_�′ + ��2/2 �_�′′

�′′_{(�) = �}�2_/2

{ �_� (�2+ 1) + 2��_�′ + �_�′′} (4.7)

Lalu kita substitusi persamaan (4.5), persamaan (4.6), persamaan (4.7) kedalam

persamaan persamaan (4.3) maka akan diperoleh:

�′′ _{− 2��}′ _{+ (2�+�}2_{− �}4_{)�= 0}

��2_/2

{ �_� (�2+ 1) + 2��_�′ + �_�′′} – 2x { ��2/2 (��_� + �_�′)} + (2�+�2−

�4_){��2/2 _�

�} = 0

��2_/2

{ (�2+ 1) �_� + 2��_�′ + �_�′′} – 2x2�_� − 2��_�′ + 2��_� +�2�_� −

�4_�

� } = 0

�2_�

��′′ + 2��� + �� − �4�� = 0

��′′ + (2�+ 1 − �4) �� = 0 (4.8)

Persamaan (4.8) ini merupakan persamaan diferensial untuk osilator anharmonik

pada mekanika kuantum dengan energi potensial, V(x) = Ax4.

4.2 Solusi Analitik

Prosedur baku untuk memecahkan persamaan diferensial seperti persamaan (4.3)

adalah dengan menganggap bahwa y(x) dapat diuraikan dengan deret pangkat x

sebagai berikut:

y(x) = xk (�₀ + �₁� + �₂x2 + �₃x3 + …)

y(x) = ∑∞_�=0�_���+� , a0≠ 0 (4.9)

Turunan pertama dari y(x) adalah:

�′_{(�) =∑ �}

� (�+�)��+�−1 ∞

�=0 (4.10)

Turunan kedua dari y(x) adalah:

�′′_{(�)∑ �}

� (�+�)(�+� −1)��+�−2 ∞

�=0 (4.11)

Kemudian kita substitusikan kembali persamaan (4.9), persamaan (4.10),

persamaan (4.11) ke dalam persamaan (4.3) sehingga akan diperoleh:

�′′ _{− 2��}′ _{+ (2�+�}2_{− �}4_{)�= 0}

∑∞�=0�� (�+�)(�+� −1)��+�−2 - 2x {∑�∞=0�� (�+�)��+�−1} + (2�+�2− �4)∑∞_�=0�_���+� = 0

∑∞�=0�� (�+�)(�+� −1)��+�−2 – 2∑∞�=0�� (�+�)��+� +

Dari persamaan (4.12) ini, kita substitusi;

m = j + 2 untuk penjumlahan pertama

m = j untuk penjumlahan kedua

m = j untuk penjumlahan ketiga

m = j - 2 untuk penjumlahan keempat

m = j – 4 untuk penjumlahan kelima

Sehingga akan diperoleh:

∑∞�=0��+2 (�+�+ 2)(�+�+ 2−1)��+�+2−2 – 2∑∞�=0�� (�+�)��+� +

2n∑∞_�=0�_���+� + ∑�∞=0�_�−2��+�−2+2− ∑∞�=0��−4��+�−4+4 = 0

∑∞�=0��+2 (�+�+ 2)(�+� −1)��+� – 2∑∞�=0�� (�+�)��+� +

2n∑∞_�=0�_���+� + ∑_�∞=0�_�−2��+� − ∑∞_�=0��−4��+� = 0

∑∞�=0[�_�+2 (�+�+ 2)(�+�+ 1)– 2��(�+�)+ 2n�� + ��−2− �� −4]��+� = 0

∑∞�=0[�_�+2 (�+�+ 2)(�+�+ 1)–2��(�+�-n)+ �� −2− ��−4]��+� = 0 (4.13)

Supaya persamaan (4.13) ini berlaku untuk setiap x, maka kuantitas dalam tanda

kurung harus nol untuk setiap harga n, sehingga kita dapatkan persyaratan sebagai

berikut:

��+2 (�+�+ 2)(�+�+ 1) – 2��(�+� - n)+ ��−2− �� −4 = 0

��+2 (�+�+ 2)(�+�+ 1) = 2��(�+� - n)−�� −2+ �� −4

��+2 =

��−4−��−2+ 2�� (�+� −�)

(�+�+2)(�+�+1) (4.14)

Persamaan (4.14) adalah merupakan rumus rekursi untuk koefisien �_�.

Rumus rekursi ini memungkinkan kita untuk mencari koefisien �2, �3, �4, �5, …

Tetapi sebelumnya kita perhatikan persamaan (4.12), pangkat terendah dari x

Penjumlahan pertama dipilih karena hanya pada penjumlahan pertama yang dapat

menghasilkan 2 nilai k yang berfungsi untuk memperoleh fungsi genap dan fungsi

ganjil dalam rumus rekursi.

Kita substitusi nilai m = 0 pada penjumlahan pertama persamaan (4.12) maka

diperoleh:

��(�+�)(�+�+ 1) = 0 �0(�)(� −1) = 0

Sehingga kita peroleh nilai :

k = 0 untuk jgenap

k = 1 untuk jganjil.

• untuk k = 0 dan jgenap dimulai dari 0, 2, 4, … pada persamaan (4.14) kita peroleh:

Rumus dasar: �_�+2 = ��−4−��−2+ 2�� (�+� −�)

(�+�+2)(�+�+1)

j = 0

→

a2 =

�−4−�−2+ 2�0 (−�)

(2.1)

= 2�0 (−�)

2!

a2 = �0

2! 2(-n)

j = 2

→

a4 =

�−2−�0+ 2�2 (2−�)

(4.3)

;

kita substitusi nilai a2, sehingga di peroleh:

= −�0+2 �

�0

2! . 2(−�)�(2−�)

4! 1

2

x 2

2

a4 = �_4!0 [-2! + 22 (-n)(2-n)]

j = 4

→

a6 =�

0−�2+ 2�4 (4−�)

(4.5)

;

kita substitusi nilai a2 dan nilai a3, diperoleh:

= �0−

�0

2! . 2(−�)+ 2

�0

4! [−2!+ 2

2_{(−�)(2−�)](4−�)}

6! . _4!1

.

4! 4!

a6 =�0

6! [4! – 4!

2! 2(-n) – 2

2

Catatan:

Nilai a terendah yang diijinkan adalah a0 (nilai a negative dianggap tidak ada)

karena dari persamaan awal: ∑∞_�=0�_�(�+�)(�+� −1) …dst, nilai a terkecil

adalah a0.

Kemudian nilai koefisien �2, �4, �6 ini kita substitusikan kedalam persamaan

(4.9) sehingga diperoleh:

y(x) = ∑∞_�=0�_���+�

ygenap = (�0�� + �2��+2 + �4x�+4 + �6x�+6 + …)

untuk k = 0, diperoleh:

ygenap = (�0 + �2�2 + �4x4 + �6x6 + …)

ygenap = �0 + �_2!0 2(-n) �2 + �_4!0 [-2! + 22 (-n)(2-n)] x4 + �_6!0 [4! – 4!

2! 2(-n) – 2

2

(4-n) +

23 (-n)(2-n)(4-n)] x6 + …)

ygenap = a0 [1+

1

2! (2(-n))x

2 + 1

4! (-2! + 2

2

(-n)(2-n))x4 + 1

6!(4! – 4!

2! 2(-n) – 2

2

(4-n) +

23(-n)(2-n)(4-n))x6 + …] (4.15)

Melalui persamaan (4.15) kita akan memperoleh beragam parameter yang disebut

dengan Polinomial Hermite untuk n = genap sebagai berikut:

ygenap = a0 [1+

1

2! (2(-n))x

2 + 1

4!(2

2

(-n)(2-n))x4 + 1

6!(2

3

(-n)(2-n)(4-n))x6 + …] +

a0 [−

2! 4! x

4 + 1

6! (4! – 4!

2! 2(-n) – 2

2

(4-n))x6 + …] (4.16)

Tanda kurung siku pertama pada persamaan (4.16) merupakan bentuk Polinomial

Hermite untuk n = genap, maka diperoleh bentuk sederhana persamaan (4.16)

adalah sebagai berikut:

ygenap= {Hn(x) + �0�4 [- 2! 4! +

1 6! (4! –

4!

2! 2(-n) – 2

2

(4-n)) x2 + …]}

Kemudian nilai y(x) untuk genap kita subtitusikan kedalam persamaan (4.4)

��(x) = �−�2/2 {Hn(x) + �0�4 [- 2! 4! +

1 6! (4! –

4!

2! 2(-n) – 2

2

(4-n)) x2 + …]} (4.17)

• untuk k = 1 dan jganjil dimulai dari 1, 2, 3, … pada persamaan (4.14) kita peroleh:

j = 1

→

a3 = �0

3! 2(1-n)

j = 3

→

a5 = �0

5! [-3! + 2

2

(1-n)(3-n)]

Kemudian nilai koefisien �₃, �₅, ini kita substitusikan kedalam persamaan (4.9)

sehingga diperoleh:

y(x) = ∑∞_�=0�_���+�

yganjil = (�1��+2 + �3��+4 +… )

untuk k = 1, diperoleh:

ygenap = (�1�3 + �3�5 + … )

Dengan melakukan cara yang sama seperti mencari ygenap kita juga dapat

menentukan Polinomial Hermite untuk n = ganjil dan k = 1 sebagai berikut:

yganjil = a0 [x +

1

3!(2(1-n))x

3 + 1

5!( 2

2

(1-n)(3-n))x5 + 1

7!(2

3

(1-n)(3-n)(5-n))x7 + …] +

a0 [-

3! 5!x

5

+ 1

7!(5! – 5!

3! 2(1-n) – 3!2(5-n))x

7

+ …]

(4.18)

Tanda kurung siku pertama pada persamaan (4.18) merupakan bentuk Polinomial

Hermite untuk n = ganjil, maka diperoleh bentuk sederhana persamaan (4.18)

adalah sebagai berikut:

yganjil= {Hn(x) + a0 [-

3! 5!x

5 + 1

7!(5! – 5!

3! 2(1-n) – 3!2(5-n))x

7 + …]

Kemudian nilai y(x) untuk ganjil kita subtitusikan kedalam persamaan (4.4)

sehingga diperoleh persamaan baru sebagai berikut:

��(x) = �−�2/2 {Hn(x) + �0�5 [- 3! 5! +

1 7! (5! –

5!

3! 2(1-n) – 3!2 (5-n)) x

2

4.3. Fungsi fungsi gelombang Osilator Anharmonik

Persamaan fungsi gelombang Schrodinger untuk Osilator Anharmonik dengan

energi potensial V(x) = Ax4, dituliskan sebagai berikut:

−_��ħ�Ψ’’(z) + Az4Ψ(z) = E Ψ(z) (4.20)

Dimana m adalah massa partikel dan E adalah energi total.

Dengan Ψ(z) = Ψ(x/α) = ѱ(x), maka bentuk persamaan (4.20) ini menjadi:

−_��ħ� �2ѱ(x)

��2 + Az

4_{ѱ(x) = E ѱ(x)}

−_��ħ� �2_��ѱ(x)2 + Az

4_ѱ(x)

- E ѱ(x) = 0

Untuk mempermudah solusi, kita sederhanakan persamaan (4.20) dengan

memperkenalkan kuantitas yang disingkat sebagai berikut ini:

x = αz dimana ∝6 ₌ 2��

ħ2 (4.21)

λ = 2��

ħ2_�2 = E(

2�

ħ2 )

2/3

(A)-1/3 (4.22)

Persamaan (4.20) kita kalikan dengan (−2�

ħ ) sehingga diperoleh: �2_ѱ(x)

��2 + ��

ħ� (E - Az

4

) ѱ(x) = 0

�2_ѱ(x) ��2 +

��

ħ� (E - A �4

∝4) ѱ(x) = 0 �2_ѱ(x)

��2 + ( ���

ħ� - ���

ħ� �4

∝4 ) ѱ(x) = 0 �2_ѱ(x)

��2 + ( ���

ħ� - ∝6 �4

∝4 ) ѱ(x) = 0

�2_ѱ(x) ��2 + (

���

Berdasarkan nilai λ pada persamaan (4.22) dan mengalikan [∝2

∝2] kedalam persamaan (4.23), maka diperoleh:

�2_ѱ(x) ��2 + (

��� ħ�_∝2 . ∝

2 _{- ∝}2 _�4 ₎ ѱ(x) = 0

�2_ѱ(x)

��2 + ( λ∝

2 _{- ∝}2 _�4 _{) ѱ(x) = 0}

�2_ѱ(x) ��2 + ∝

2 _{( λ -�}4 _{) ѱ(x) = 0 (4.24)}

Untuk α = 1, maka persamaan (4.24) menjadi:

�2_ѱ(x)

��2 + ( λ -�

4 ₎ ѱ(x) = 0 (4.25)

Persamaan (4.25) ini memiliki bentuk yang sama dengan Persamaan (4.8) yang

merupakan persamaan diferensial untuk osilator anharmonik pada mekanika

kuantum dengan energi potensial, V(x) = Ax4.

Persamaan (4.25) merupakan kelipatan dari persamaan (4.8), sehingga diperoleh

hubungan:

Ѱn(x) = K ��(x) (4.26)

Jika kita substitusi nilai �_�(x) pada persamaan (4.17) ke dalam persamaan (4.26),

maka kita peroleh fungsi gelombang Osilator Anharmonik untuk n = genap

sebagai berikut:

Ѱn(x) = K�−�

2_/2

{Hn(x) + a0x4 [-

2! 4! +

1 6!(4! –

4!

2! 2(-n) – 2

2

(4-n))x2 + …]} (4.27)

Dengan menggumakan Matlab, grafik persamaan fungsi gelombang persamaan

Kemudian kita substitusi nilai �_�(x) pada persamaan (4.19) ke dalam persamaan

(4.26), maka kita peroleh fungsi gelombang Osilator Anharmonik untuk n = ganjil

sebagai berikut:

Ѱn(x) = K�−�

2_/2

{Hn(x) + a0x5 [-

3! 5! +

1 7!(5! –

5!

3! 2(1-n) – 3!2(5-n))x

2

+ …]} (4.28)

Dengan menggumakan Matlab, grafik persamaan fungsi gelombang persamaan

4.4. Tingkat tingkat energi Osilator Anharmonik

Berdasarkan periode gerak partikel klasik [lihat persamaan (F.7) pada lampiran F]

yang sesuai dengan energi potansial V(x) = Axn = Ax4 dalam Osilator Nonlinear

dapat dituliskan sebagai berikut ini:

T = 4

(

��

2

)

1/2

. (

�1−�/2

�

)

1/�

.

г(

1

�+1) г(1

�+

1 2)

(4.29)

T = 4

(

��

2

)

1/2

. (

�1−4/2

�

)

1/4

.

г(1₄+1)

г(1₄+1₂)

T = (16�� 2 )

1/2

.

(�)−1/4

(�)1/4

.

1 4г(

1 4)

г(3

4)

T = (8��)1/2

.

(�)−

1/4

(�)1/4

.

1 4

.

г(1₄)

г(3₄)

T = (8��_� )1/2

.

(�)

1/4

(�)1/4

.

1 4

.

г(1

4)

г(3

4)

T = (4.2��

� )1/2

.

(�)1/4 (�)1/4

.

1 4

.

г(1

4)

г(3₄)

T = 2(2��

� )1/2

.

(�)1/4 (�)1/4

.

1 4

.

г(1₄)

г(3

4)

T =1

2

(

2��

�

)

1/2

. (

�

�

)

1/4

.

г(

1 4)

г(3

4)

T =1

2

�

2��

�

. (

� �

)

1/4

.

г(

1 4)

г(3

4)

(4.30)

Melalui persamaan (4.30) ini, kita dapat menentukan A sebagai berikut ini:

T =1

2

�

2��

�

.

�1/4

�1/4

.

г(1

4)

г(3₄)

�

1/4

=

1 2

.

√2��

�1/2

.

�1/4

�

.

г(1

4)

г(3

4)

�

1/4

=

1 2

.

√2��

�1/2

.

�1/4

�

.

г(1

4)

г(3

4)

�

1/4

=

1 2

.

√2��

�1/4

.

1

�

.

г(1₄)

Kemudian kita cari nilai A dengan menggunakan persamaan (4.22) sebagai

berikut:

λ = E (2�

ħ2 )

2/3 (A)-1/3

(A)1/3 = �

� . (

2�

ħ2)

2/3

Ruas kiri dan ruas kanan dikali dengan pangkat 3, maka diperoleh:

A =�

3

�3

. (

2�

ħ2

)

2

(4.32)

Nilai A pada persamaan (4.32) ini kita substitusikan kedalam persamaan (4.31),

sehingga diperoleh:

�

1/4

=

1 2

.

√2��

�1/4

.

1

�

.

г(1₄)

г(3₄)

[

�

3

�3

. (

2�

ħ2

)

2

]

1/4

=

1

2

.

√2��

�1/4

.

1

�

.

г(1

4)

г(3

4)

�3/4

�3/4

. (

2�

ħ2

)

1/2

=

1

2

.

√2��

�1/4

.

1

�

.

г(1

4)

г(3₄)

,

dimana: �=

2�

�

→ �

=

2�

�

�

3/4

=

1 2

.

�

3/4

. (

ħ2 2�

)

1/2

.

√2�� �1/4

.

1 2� �

.

г( 1 4)

г(3₄)

�

3/4

.

�

1/4

=

1 2

.

�

3/4

. (

ħ2 2�

)

1/2

.

√

2

��

.

�

2�

.

г(1

4)

г(3

4)

�

=

�

3/4

4

.

ħ

. �

2

��

2

�

.

�

√�

2

.

г

(

1

4

)

г

(

3

4

)

=

�

3/4

43/4. 41/4

.

ħ

.

� √�

.

г(1₄)

г(3₄)

�

= (

�

4

)

3/4

.

ħ

.

�

√2�

.

г(1

4)

г(3

4)

�

�

= (

₄ �

)

3 4

.

г�

1 4�

Kemudian dengan mengetahui bahwa nilai г(1/4) = 4 dan г(3/4) = �√2

4 , maka kita

peroleh energi E menjadi:

�� =

(

�₄

)

3/4

.

г(1

4)

√2� . г(3

4)

. ħ�

=�

3/4

43/4

.

4

√2� .�√2

4

. ħ�

=

�

3/4

.

4

1/4

√2� .�√2

4

.

ħ_�

=

�

3/4

.

4

1/4

√2�

.

4

�√2

.

ħ�

=

�

3/4

.

4.4

1/4

�√2�√2

.

ħ�

=

�

3/4

.

4 . 4

1/4

�√2� . 41/4

.

ħ�

�� =

�

3/4

.

4

�√2�

.

ħ� (4.34)

Dengan mensubstitusikan nilai λ = 2n+1 [lihat persamaan (4.8)

→

persamaan

diferensial untuk osilator anharmonik pada mekanika kuantum dengan energi

potensial, V(x) = Ax4]kedalam Persamaan (4.31) ini, maka diperoleh tingkat

tingkat Energi untuk Osilator Anharmonik sebagai berikut:

�� = (2�+ 1)3/4

.

_�√4_2�

.

ħ� (4.35)

Untuk Energi tingkat dasar dengan:

n = 0, diperoleh:

E0 = (2.0 + 1)3/4 _. 4

�√2�ħ�

= 0,5079ħ�≅ 1

Untuk n = 1, diperoleh:

E1 = (2.1 + 1)3/4 _{. 0,5}ħ�

= 2,28 . 0,5ħ�

E1 = 1,14ħ� (4.37)

Untuk n = 2, diperoleh:

E2 = (2.2 + 2)3/4 _{. 0,5}ħ�

= 3,34 . 0,5ħ�

E2 = 1,67ħ� (4.38)

Untuk n = 3, diperoleh:

E3 = (2.3 + 2)3/4 _{. 0,5}ħ�

= 4,3 . 0,5ħ�

E3 = 2,35ħ� (4.39)

BAB 5

KESIMPULAN DAN SARAN

5.1.

Kesimpulan

1. Tingkat Energi dasar untuk Osilator Anharmonik dan Osilator Harmonik

adalah sama

2. Tingkat Energi Osilator Anharmonik lebih kecil daripada Tingkat Energi

Osilator Harmonik

3. Perbedaan Tingkat Energi untuk Osilator Anharmonik dan Osilator

Harmonik adalah sebagai berikut:

Energy Osilator Harmonik Osilator Anharmonik ∆E

E0 0,5 ħ� 0,5 ħ� 0

E1 1,5 ħ� 1,14 ħ� 0,36 ħ�

E2 2,5 ħ� 1,67 ħ� 0,83 ħ�

E3 3,5 ħ� 2,35 ħ� 1,15 ħ�

4. Perbedaan tingkat energi (∆E) antara Osilator Harmonik dengan Osilator

Anharmonik diakibatkan oleh adanya gangguan pada sistem Osilator

Anharmonik.

5.2.

Saran

1. Sebaiknya peneliti selanjutnya mengkaji secara teoritik Tingkat energi

Osilator Anharmonik dengan menggunakan Potensial Morse

2. Sebaiknya peneliti selanjutnya mengkaji secara teoritik tingkat energi

Osilator Harmonik Teredam dan menganalisis perbedaannya dengan

BAB 2

TINJAUAN PUSTAKA

2.1. Mekanika Kuantum

2.1.1. Sejarah Awal Mekanika Kuantum

Dasar dimulainya periode mekanika kuantum adalah ketika mekanika

klasik tidak bisa menjelaskan gejala-gejala fisika yang bersifat mikroskofis dan

bergerak dengan kecepatan yang mendekati kecepatan cahaya. Oleh karena itu,

gejala fisika tersebut ternyata hanya ada satu kumpulan, dan mekanika kuantum

mengungkapkan usaha kita yang terbaik sampai saat ini untuk merumuskannya.

Perkembangan teori atom menunjukkan adanya perubahan konsep susunan atom

dan reaksi kimia antaratom.Kelemahan model atom yang dikemukakan

Rutherford disempurnakan olehNiels Henrik David Bohr.Bohr mengemukakan

gagasannya tentang penggunaan tingkat energi elektron pada struktur atom.Model

ini kemudian dikenal dengan model atom Rutherford-Bohr.Tingkat energi

elektron digunakan untuk menerangkan terjadinya spektrum atom yang dihasilkan

oleh atom yang mengeluarkan energi berupa radiasi cahaya.

Setiap memasuki pemahaman dunia atom, ilmuan mengalami kesulitan

yang luar biasa.Teori-teori mapan tidak berdaya, bahasa yang digunakan

mengalami kebuntuan, bahkan imajinasi terhadap dunia atom dipengaruhi

pandangan emosional. Pengalaman ini dilukiskan Heisenberg: “Saya ingat

pembicaraan saya dengan Bohr yang berlangsung selama berjam-jam hingga larut

malam dan mengakhirinya dengan putus asa; dan ketika perbincangan itu berakhir

saya berjalan-jalan sendirian di taman terdekat dan mengulangi pertanyaan pada

diri saya sendiri berkali-kali: Mungkinkah alam itu absurd sebagaimana yang

tampak pada kita dalam eksperimen-eksperimen atom ini?” (Fritjof Capra, 2000)

Situasi psikologis Heisenberg, pada akhirnya merupakan salah satu kata

kunci dalam perkembangan revolusioner dunia atom.Benda/materi yang diamati

tidak terlepas dari pengalaman pengamat.benda/materi bukan lagi sebagai objek

benda/materi sendiri yang berbicara dan mempunyai keinginan sesuai fungsi dan

kedudukannya dalam suatu benda/materi.Sub-atom bukan ‘benda’ tetapi,

merupakan kesalinghubungan dalam membentuk jaringan dinamis yang terpola.

Sub-subatom merupakan jaring-jaring pembentuk dasar materi yang merubah

pandangan manusia selama ini yang memandang sub atom sebagai blok-blok

bangunan dasar pembentuk materi.

Meminjam istilah Kuhn, mekanika kuantum merupakan paradigma sains

revolusioner pada awal abad 20.Lahirnya mekanika kuantum, tidak terlepas dari

perkembangan-perkembangan teori, terutama teori atom.Mekanika kuantum,

bukan untuk menghapus teori dan hukum sebelumnya, melainkan Mekanika

kuantum tidak lebih untuk merevisi dan menambal pandangan manusia terhadap

dunia, terutama dunia mikrokosmik.Bisa jadi, sebenarnya hukum-hukum yang

berlaku bagi dunia telah tersedia dan berlaku bagi setiap fenomena alam, tetapi

pengalaman manusialah yang terbatas.Oleh sebab itu, sampai disini kita harus

sadar dan meyakini bahwa sifat sains itu sangat tentatif.

Mengapa teori kuantum merupakan babak baru cara memandang alam?

Vladimir Horowitz pernah mengatakan bahwa “mozart terlalu mudah untuk

pemula, tetapi terlalu sulit untuk para ahli”. Hal yang sama juga berlaku untuk

teori kuantum. Secara sederhana teori kuantum menyatakan bahwa “partikel pada

tingkat sub atomik tidak tunduk pada hukum fisika klasik”.“Entitas seperti

elektron dapat berwujud [exist] sebagai dua benda berbeda secara simultan

materi atau energi, tergantung pada cara pengukurannya”. (Paul Strathern, 2002)

Kerangka mendasar melakukan penalaran dalam sains adalah berpikir dengan

metoda induksi.Apabila melakukan penalaran dengan metoda ini, maka

pengamatan terhadap wajah alam fisik dilakukan melalui premis-premis yang

khusus tentang materi-materi kecil atau mikro bahan alam fisik yang kasat

mata.Hukum-hukum sains klasik yang telah terpancang lama, ternyata terlihat

kelemahannya ketika berhadapan dengan fenomena mikrokosmik.

Gary Zukaf (2003) memberikan pengertian secara etimologis dari

mekanika kuantum.‘Kuantum’ merupakan ukuran kuantitas sesuatu, besarnya

tertentu.‘Mekanika’ adalah kajian atau ilmu tentang gerak.Jadi, mekanika

mengatakan bahwa alam semesta terdiri atas bagian-bagian yang sangat kecil

yang disebut kuanta [quanta, bentuk jamak dari quantum], dan mekanika kuantum

adalah kajian atau ilmu yang mempelajari fenomena ini.

2.1.2. Perkembangan Mekanika Kuantum

Pada tahun 1905, Albert Einstein berhasil menjelaskan efek foto listrik

dengan didasari oleh pendapat Planck lima tahun sebelumnya dengan

mempostulatkan bahwa cahaya atau lebih khususnya radiasi elektromagenetik

dapat dibagi dalam paket-paket tertentu yang disebut kuanta dan berada dalam

ruang. Energi berhasil menjelaskan bahwa untuk membuat elektron terpancar dari

permukaan logam diperlukan cahaya yang menumbuk.Cahaya tersebut harus

memiliki frekuensi melebih frekuensi ambang dari logam tersebut.Efek foto listrik

ini tidak bergantung pada intensitas cahaya yang ditembakkan seperti pandangan

mekanika klasik tetapi hanya bergantung pada frekuensinya saja.Walaupun

cahaya lemah ditembakkan tetapi memiliki frekuensi yang melebihi frekuensi

ambang ternyata ada elektron yang dipancarkan.

Pernyataan Einstein bahwa cahaya teradiasikan dalam bentuk paket-paket

energi yang kemudian disebut kuanta dinyatakan dalam jurnal kuantum yang

berjudul "On a heuristic viewpoint concerning the emission and transformation of

light" pada bulan Maret 1905.Pernyataan tersebut disebut-sebut sebagai

pernyataan yang paling revolusioner yang ditulis oleh fisikawan pada abad ke-20.

Paket-paket energi yang pada masa itu disebut dengan kuanta kemudian disebut

oleh foton, sebuah istilah yang dikemukakan oleh Gilbert & Lewis pada tahun

1926.Ide bahwa tiap foton harus terdiri dari energi dalam bentuk kuanta

merupakan sebuah kemajuan.Hal tersebut dengan efektif merubah paradigma

ilmuwan fisika pada saat itu yang sebelumnya menjelaskan teori gelombang.Ide

tersebut telah mampu menjelaskan banyak gejala fisika pada waktu itu.

2.1.3. Eksperimen-Eksperimen Yang Mendasari Perkembangan Mekanika

Kuantum

Berikut ini adalah eksperimen–eksperimen yang mendasari perkembangan

1. Thomas Young dengan eksperimen celah ganda mendemonstrasikan sifat

gelombang cahaya pada tahun 1805,

2. Henri Becquerel menemukan radioaktivitas pada tahun 1896,

3. J.J. Thompson dengan eksperimen sinar katoda menemuka elektron pada

tahun 1897,

4. Studi radiasi benda hitam antara 1850 sampai 1900 yang dijelaskan tanpa

menggunakan konsep mekanika kuantum,

5. Einstein menjelaskan efek foto listrik pada tahun 1905 dengan

menggunakan konsep foton dan partikel cahaya dengan energi

terkuantisasi,

6. Robert Milikan menunjukan bahwa arus listrik bersifat seperti kuanta

dengan menggunakan eksperimen tetes minyak pada tahun 1909,

7. Ernest Rutherford mengungkapkan model atom pudding yaitu massa dan <