Bab 5 Teorema Pythagoras
Teks penuh
Gambar


Garis besar
Dokumen terkait
Teorema29: (MSc Teorema) :Jika sisi miring dan sebuah sudut lancip dari sebuah segitiga sama dan membangun dengan bagian-bagian yang sama dari segitiga siku-siku
Pada sebuah segitiga siku-siku, kuadrat sisi miring (sisi di depan sudut sikusiku) sama dengan jumlah kuadrat sisi-sisi yang lain.. Pembuktian dari
Suatu segitiga siku-siku yang selalu berlaku: Luas persegi pada sisi miring (hipotenusa) sama dengan jumlah luas persegi pada sisi yang lain (sisi siku-sikunya)1. Teori
Teorema Pythagoras berbunyi bahwa “kuadrat sisi miring dari suatu segitiga siku-siku sama dengan jumlah kuadrat sisi-sisi yang lainnya“. Dengan sisi miring adalah sisi
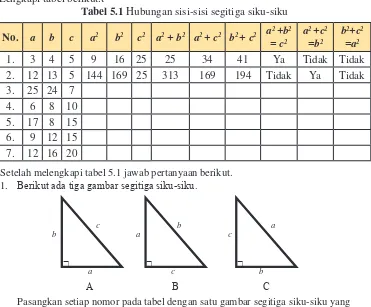
Dalam teorema pythagoras dapat dibuat pernyataan yang merupakan kebalikannya. Untuk selanjutnya kita akan menyelidiki apakah pernyataan kebalikan teorema Pythagoras
Modul 1 Kelas VIII Teorema Pythagoras 8 3 Segitiga tumpul: a, b, c adalah sisi segitiga dengan sisi terpanjang c Jika c2 > a2 + b2, maka segitiga tersebut tumpul Contoh: Selidikilah
Peradaban kuno tersebut bisa membangun bangunan, seperti piramida, yang juga menggunakan pengetahuan relasi antar sisi-sisi segitiga siku-siku tersebut atau kita kenal sebagai teorema
Teorema ini menyatakan bahwa dalam segitiga siku-siku, jumlah kuadrat panjang dua sisi yang membentuk sudut siku-siku sama dengan kuadrat panjang sisi miringnya hipotenusa.. Sisi siku –