BAB 9
PERSAMAAN DIFERENSIAL PARSIIL
Kebanyakan permasalahan dalam ilmu pengetahuan dan teknologi dapat dipresentasikan dalam bentuk persamaan diferensial parsiil. Persamaan tersebut merupakan laju perubahan terhadap dua atau lebih variabel bebas yang biasanya adalah waktu dan jarak (ruang). Bentuk umum persamaan diferensial parsiil order 2 dan dua dimensi adalah:
0 2 2 2 2 2 = + ϕ + ∂ ϕ ∂ + ∂ ϕ ∂ + ∂ ϕ ∂ + ∂ ∂ ϕ ∂ + ∂ ϕ ∂ f g y e x d y c x y b x a (9.1)
dengan a, b, c, d, e, f dan g merupakan fungsi dari variabel x dan y dan variabel tidak bebas ϕ.
Persamaan diferensial parsiil dapat dibedakan menjadi 3 tipe yaitu: 1) Persamaan Ellips jika : b2 – 4ac < 0
2) Persamaan Parabola jika : b2 – 4ac = 0
3) Persamaan Hiperbola jika : b2 – 4ac > 0
Persamaan parabola biasanya merupakan persamaan yang tergantung pada waktu (tidak permanen). Penyelesaian persamaan tersebut memerlukan kondisi awal dan batas. Persamaan ellips biasanya berhubungan dengan masalah keseimbangan atau kondisi permanen (tidak tergantung waktu), dan penyelesaiannya memerlukan kondisi batas di sekeliling daerah tinjauan. Persamaan hiperbola biasanya berhubungan dengan getaran, atau permasalahan di mana terjadi ketidak-kontinuean dalam kecepatan, tekanan dan rapat massa. Penyelesaian dari persamaan hiperbola mirip dengan penyelesaian persamaan parabola, yang menghitung nilai ϕ untuk nilai x dan t yang diberikan.
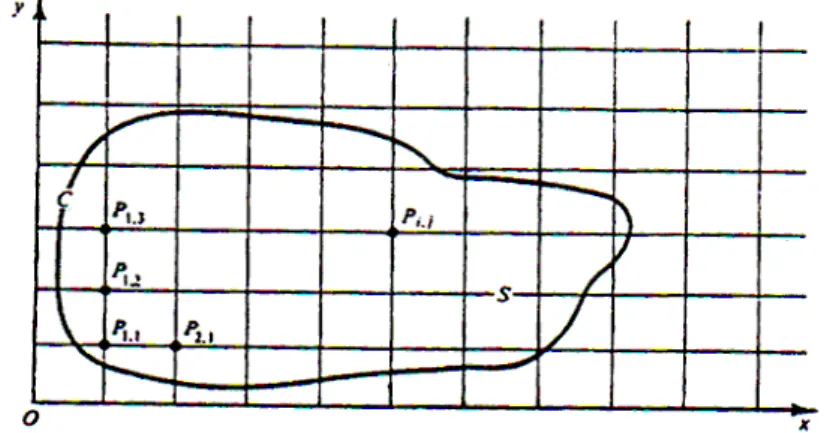
Penyelesaian persamaan diferensial parsiil dengan kondisi awal dan batas dapat diselesaikan dengan metode beda hingga. Untuk itu dibuat jaringan titik hitungan pada daerah tinjauan. Sebagai contoh penyelesaian persamaan ellips pada daerah S yang dibatasi oleh kurve C seperti tampak pada Gambar 9.1. Daerah tinjauan S dibagi menjadi sejumlah pias (titik hitungan P) dengan jarak antara pias adalah ∆x dan ∆y. Kondisi di mana variabel tidak bebas (ϕ) harus memenuhi di sekeliling kurve C disebut dengan kondisi batas. Penyelesaian persamaan diferensial merupakan perkiraan dari nilai ϕ pada titik-titik hitungan P11, P12, …, Pij, … Perkiraan dilakukan dengan mengganti turunan dari persamaan
diferensial parsiil dengan menggunakan perkiraan beda hingga.
9.1 Beberapa Bentuk Persamaan Diferensial Parsiil
Berikut ini diberikan beberapa bentuk persamaan diferensial parsiil.
a) Persamaan Ellips
Persamaan yang termasuk dalam tipe ini adalah persamaan Poisson:
0 2 2 2 2 = + ∂ ∂ + ∂ ∂ g y x ϕ ϕ (9.2) dan persamaan Laplace:
0 2 2 2 2 = ∂ ∂ + ∂ ∂ y x ϕ ϕ (9.3) b) Persamaan Parabola
Permasalahan yang mengandung waktu sebagai variabel bebas biasanya termasuk dalam persamaan parabola. Persamaan parabola yang paling sederhana adalah perambatan panas dan difusi polutan, yang mempunyai bentuk:
2 2 x T K t T ∂ ∂ = ∂ ∂
Dalam persamaan perambatan panas, T (temperatur), K (koefisien konduktivitas), serta variabel t (waktu) dan x (jarak).
c) Persamaan Hiperbola
Persamaan hiperbola yang paling sederhana adalah persamaan gelombang yang mempunyai bentuk berikut:
2 2 2 2 2 x y C t y ∂ ∂ = ∂ ∂ (9.4)
dengan y adalah perpindahan fluktuasi pada jarak x dari ujung tali yang bergetar yang mempunyai panjang L sesudah waktu t.
9.2 Perkiraan Diferensial Dengan Beda Hingga
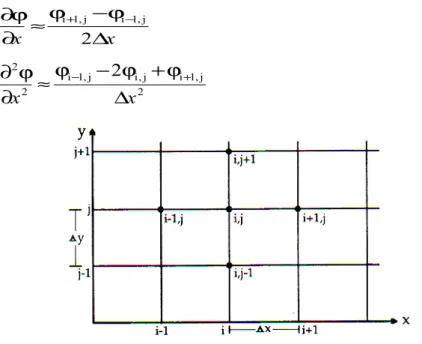
Gambar 9.2, adalah jaringan titik hitungan pada bidang x-y yang dapat dibagi menjadi sejumlah pias segi empat dengan sisi ∆x dan ∆y. Panjang pias dalam arah x adalah ∆x
dan dalam arah y adalah ∆y. Dengan menggunakan jaringan titik hitungan pada Gambar 9.2, semua diferensial ditulis pada titik hitungan (i,j). bentuk turunan pertama dan kedua didekati oleh:
x x ∆ ϕ − ϕ ≈ ∂ ϕ ∂ i+1,j i,j (9.5a) x x ∆ ϕ − ϕ ≈ ∂ ϕ ∂ i,j i−1,j (9.6a)
x x ∆ ϕ − ϕ ≈ ∂ ϕ ∂ + − 2 j , 1 i j , 1 i (9.7a) 2 j , 1 i j , i j , 1 i 2 2 2 x x ∆ ϕ + ϕ − ϕ ≈ ∂ ϕ ∂ − + (9.8a)
Gambar 9.2. Jaringan titik hitungan dalam bidang x-y
Bentuk Persamaan (9.5a), (9.6a) dan (9.7a) disebut dengan diferensial maju, mundur dan terpusat. Diferensial terhadap y juga dapat ditulis dalam bentuk seperti di atas, yaitu : y y ∆ ϕ − ϕ ≈ ∂ ϕ ∂ i,j+1 i,j (9.5b) y y ∆ ϕ − ϕ ≈ ∂ ϕ ∂ i,j i,j−1 (9.6b) y y ∆ ϕ − ϕ ≈ ∂ ϕ ∂ + − 2 1 j , i 1 j , i (9.7b) 2 1 j , i j , i 1 j , i 2 2 2 y y ∆ ϕ + ϕ − ϕ ≈ ∂ ϕ ∂ − + (9.8b)
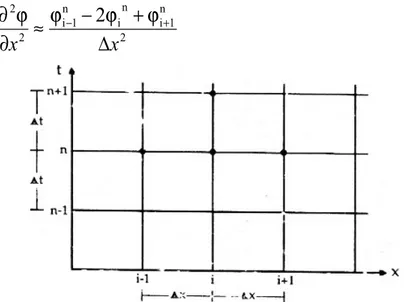
Bentuk diferensial melintang dapat didekati dengan : y x y x ∆∆ ϕ + ϕ − ϕ − ϕ ≈ ∂ ∂ ϕ ∂ + + − + + − − − 4 1 j , 1 i 1 j , 1 i 1 j , 1 i 1 j , 1 i 2 (9.9) Untuk persamaan yang mengandung variabel x dan t, perkiraan beda hingga dilakukan dengan membuat jaringan titik hitungan pada bidang x-t (Gambar 9.3), yang dibagi dalam sejumlah pias dengan interval ruang dan waktu adalah ∆x dan ∆t. Bentuk turunan pertama dan kedua terhadap waktu dan ruang adalah :
t t ∆ ϕ − ϕ ≈ ∂ ϕ ∂ + n i 1 n i (9.10)
2 n 1 i n i n 1 i 2 2
2
x
x
∆
ϕ
+
ϕ
−
ϕ
≈
∂
ϕ
∂
− + (9.11)Gambar 9.3. Jaringan titik hitungan dalam bidang x-t
Dalam bentuk beda hingga di atas superskrip n dan n+1 menunjukkan nilai ϕ pada waktu n dan n+1. Penulisan n sebagai superskrip, yang menunjukkan waktu, untuk membedakan dengan subskrip untuk i, j dan k yang menunjukkan notasi ruang.
9.3 Penyelesaian Persamaan Parabola
Penyelesaian persamaan tipe parabola dengan menggunakan metode beda hingga dapat dibedakan menjadi dua metode (skema) dasar, yaitu skema eksplisit dan skema implisit. Pada skema eksplisit, variabel (temperature) pada suatu titik dihitung secara langsung dari variabel di beberapa titik disekitarnya pada waktu sebelumnya, yang sudah diketahui nilainya. Dengan metode ini, penurunan persamaan diferensial parsiil ke dalam bentuk beda hingga adalah mudah. Namun kendala utamanya adalah kemungkinan terjadinya ketidakstabilan hitungan, apabila digunakan langkah waktu yang besar. Dalam skema implisit, untuk menghitung variabel di suatu titik perlu dibuat suatu sistem persamaan yang mengandung variabel di titik tersebut dan titik-titik di sekitarnya pada waktu yang sama.
Salah satu metode yang paling banyak digunakan untuk menyelesaikan masalah ini adalah metode sapuan ganda dari Choleski. Berdasarkan kedua skema dasar tersebut telah dikembangkan skema lainnya, seperti skema Crank-Nicholson, Preissman, Leap Frog, dan sebagainya. Skema Crank-Nicholson merupakan pengembangan dari skema eksplisit dan implisit. Skema Preissman merupakan pengembangan dari skema implisit, sedang skema Leap Frog adalah pengembangan dari skema eksplisit. Dalam bab ini, selain skema eksplisit dan implisit juga akan dipelajari skema Crank-Nicholson. Penjelasan lebih rinci dari ketiga skema tersebut diberikan berikut ini.
1) Skema Eksplisit
Metode beda hingga skema ekplisit banyak digunakan dalam penyelesaian persamaan parsiil. Skema ini sangat sederhana dan mudah untuk memahaminya. Penggunaan skema tersebut untuk menurunkan persamaan diferensial parsiil menjadi persamaan beda hingga juga mudah. Namun skema ini mempunyai kelemahan, yaitu langkah waktu ∆t dibatasi berdasarkan bilangan Courant yaitu dimana nilai dari Cr = (U ∆t) / ∆x≤1. Apabila nilai Cr>1 maka hitungan menjadi
tidak stabil. Penggunaan langkah waktu ∆t yang kecil tersebut menyebabkan prosedur dan waktu hitungan menjadi sangat panjang dan lama.
a) Bentuk skema eksplisit
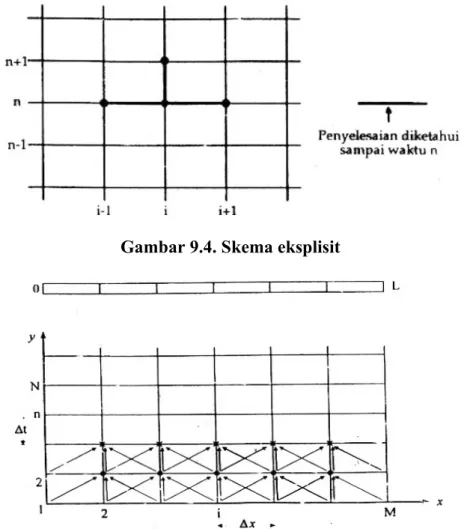
Pada skema eksplisit, variabel pada waktu n + 1 dihitung berdasarkan variabel pada waktu n yang sudah diketahui (Gambar 9.4). Dengan menggunakan skema seperti yang ditunjukkan pada Gambar 9.4, fungsi variabel (temperature) T (x,t) dan turunannya dalam ruang dan waktu didekati oleh bentuk berikut:
Gambar 9.4. Skema eksplisit
Gambar 9.5. Langkah-langkah hitungan dengan skema eksplisit
b) Stabilitas skema eksplisit
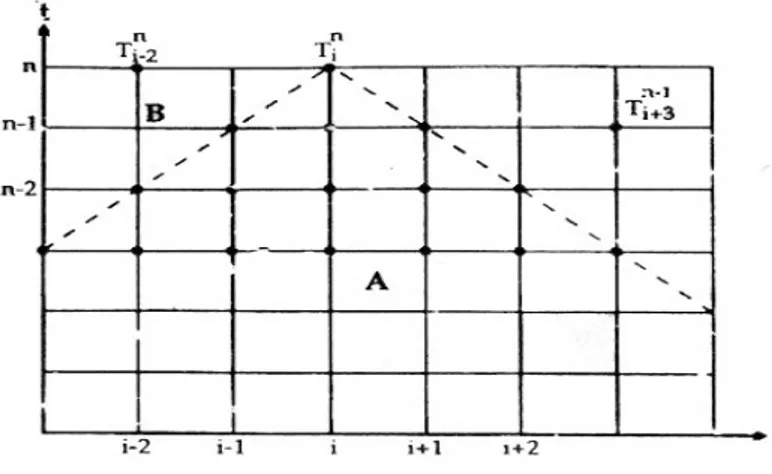
Seperti yang ditunjukkan pada Gambar (9.6), dalam skema eksplisit, n i
T tergantung pada tiga titik sebelumnya yaitu: 1
1 1 1 1−, − +− − in n i n i T danT T
Ketiga titik ini juga hanya tergantung pada 5 titik pada waktu sebelumnya. Bidang ketergantungan dari penyelesaian numerik (bidang A) lebih kecil dari pada bidang ketergantungan penyelesaian analitik (A+B). Misalnya penyelesaian analisis dari Ti tergantung di antaranya pada titik n
i T−2 dan 1 3 − +n i
T , sedang pada hitungan numerik tidak tergantung pada titik-titik tersebut. Keadaan ini dapat menyebabkan ketidak stabilan dari skema tersebut, yang berupa terjadinya amplifikasi hasil hitungan dari kondisi awal.
Gambar 9.6. Stabilitas numerik
2) Skema Implisit
Gambar 9.7, menunjukkan jaringan titik hitungan dari skema implisit.
Gambar 9.7. Skema implisit
3) Skema Crank-Nicholson
Dalam sub bab ini akan dijelaskan salah satu pengembangan dari skema eksplisit dan implisit, yaitu skema Crank-Nicholson.