SELISIH 2
TESIS
Oleh
HARI SUMARDI 127021003/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
SELISIH 2
T E S I S
Diajukan Sebagai Salah Satu Syarat
Untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh
HARI SUMARDI 127021003/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
SELISIH 2 Nama Mahasiswa : Hari Sumardi Nomor Pokok : 127021003
Program Studi : Magister Matematika
Menyetujui, Komisi Pembimbing
(Prof. Dr. Saib Suwilo, M.Sc) (Dr. Mardiningsih, M.Si)
Ketua Anggota
Ketua Program Studi Dekan
(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Saib Suwilo, M.Sc
Anggota : 1. Dr. Mardiningsih, M.Si
EKSPONEN LOKAL MASUK DUA CYCLE DWIWARNA DENGAN PANJANG SELISIH 2
TESIS
Saya mengakui bahwa tesis ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing dituliskan sumbernya.
Medan, 4 Juni 2014 Penulis,
Sebuah digraph dwiwarna D adalah sebuah digraph dimana setiap arc atau busur berarahnya di warnai dengan menggunakan satu dari dua warna dalam hal ini warna yang digunakan adalah merah atau biru. Sebuah (h, k)-jalan adalah sebuah jalan yang menggunakanhbuah busur berwarna merah dan k buah busur berwarna biru. Sebuah digraph dwiwarna D(2) dengan n verteks{v1, v2, . . . , v
n}
dikatakan primitif bila terdapat bilangan-bilangan bulat tak negatif h dan k se-hingga untuk setiap pasangan verteksvi dan vj di D(2) terdapat (h, k)-jalan dari
vi ke vj dan dari vj ke vi. Eksponen dari sebuah digraph dwiwarna, dinotasikan
exp(D(2)), adalah bilangan bulat positif h+k terkecil atas semua bilangan bulat tak negatif h dan k yang demikian. Eksponen lokal masuk dari sebuah verteks vℓ di D(2), dinotasikan expin(D(2), vℓ), adalah bilangan bulat positif s′ +t′ yang
terkecil atas semua bilangan bulat tak negatif s′ dan t′ sehingga untuk setiap
verteks vi, i = 1,2, . . . , n di D(2) terdapat (s′, t′)-jalan dari vi ke vℓ. Dari hasil
utama dapat disimpulkan bahwa expin(D(2), v
t) = expin(D(2), v1)+d(v1, vt) untuk
semuat = 1,2,· · · , n.
A two colored digraph D is a digraph each of whose arcs is colored by either red or blue. An(h, k)-walk in a two-colored digraph is a walk of lengh h+k consisting of h red arcs and k blue arcs. A two-colored digraph D(2) consisting of n vertex {v1, v2, . . . , vn} is primitive provided that there are nonnegative integers h and k such that for each pair of vertices vi and vj there exists an (h, k)-walk from vi to
vj and from vj tovi. The exponent of a vertex v in D(2), denoted exp(D(2)), is the smallest positive integer h+k over all nonnegative integers h and k such that for each vertex uin D(2) there is an (h, k)-walk fromutov. The inner local exponent
of a vertex vℓ inD(2), denoted expin(D(2), vℓ), is the smallest positive integer s′+t′ over all nonnegative integers s′ and t′ such that for each vertex vi, i = 1,2, . . . , n inD(2) there is an(s′, t′)-walk fromv
i tovℓ. From the main result we can conclude
that expin(D(2), v
t) =expin(D(2), v1) +d(v1, vt) for all t= 1,2,· · · , n.
Dengan rendah hati penulis ucapkan segala puji dan syukur kehadirat Allah SWT atas berkat dan rahmatNya sehingga penulis dapat menyelesaikan studi Program Magister Matematika pada FMIPA USU. Tesis ini merupakan salah satu syarat penyelesaian studi pada Program Studi Magister Matematika FMIPA USU.
Pada kesempatan ini penulis mengucapkan terimakasih yang sebesarbesarnya kepada:
Bapak Prof. Dr. dr. Syahril Pasaribu, DTM&H. M.Sc. (CTM), Sp.A (K) selaku Rektor Universitas Sumatera Utara yang memberi kesempatan kepada penulis untuk menempuh pendidikan di Universitas Sumatera Utara.
Bapak Dr. Sutarman, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
Bapak Prof. Dr. Herman Mawengkang, selaku Ketua Program Studi Magister Matematika FMIPA Universitas Sumatera Utara.
Bapak Prof. Dr. Saib Suwilo, M.Sc, selaku Sekretaris Program Studi Magister Matematika FMIPA USU dan selaku Pembimbing Utama yang telah banyak memberikan bimbingan dan arahan serta motivasi kepada penulis dalam penulisan tesis ini.
Ibu Dr. Mardiningsih, M.Si, selaku Pembimbing Kedua yang juga telah banyak memberikan bimbingan kepada penulis dalam penulisan tesis ini.
Bapak Prof. Dr. Opim Salim S, M.Sc, dan Bapak Prof. Dr. Tulus, M.Si, selaku penguji tesis ini.
Para Dosen Program Studi Magister Matematika FMIPA USU yang telah membekali ilmu pengetahuan kepada penulis selama perkuliahan hingga selesai.
Sumarno, danTri Wahyu Sumaryonoserta segenap keluarga yang senantiasa memberi dukungan dan Doa kepada penulis dalam menyelesaikan perkuliahan ini. Tidak lupa rekan-rekan Mahasiswa program studi Magister Matematika FMIPA USU tahun 2012, atas kerjasama dan hubungan yang baik selama perkuliahaan, semoga persahabatan yang kita jalin abadi.
Akhir kata penulis ucapkan, kiranya kekurangan yang ada pada penulisan tesis ini dapat disempurnakan bagi pihak yang memerlukan karena penulis sebagai manusia yang tidak sempurna memiliki keterbatasan dalam menyelesaikan tesis ini.
Medan, Juni 2014 Penulis,
Halaman
PERNYATAAN i
ABSTRAK ii
ABSTRACT iii
KATA PENGANTAR iv
RIWAYAT HIDUP vi
DAFTAR ISI vii
DAFTAR GAMBAR ix
BAB 1 PENDAHULUAN 1
1.1. Latar Belakang 1
1.2. Perumusan Masalah 4
1.3. Tujuan Penelitian 4
1.4. Manfaat Penelitian 4
1.5. Metodologi Penelitian 4
BAB 2 DIGRAPH 6
2.1. Dua Cycle 6
2.2. Primitifitas 8
2.3. Matriks Ketetanggaan 11
2.4. Eksponen 12
2.5. Eksponen Lokal Digraph 14
BAB 3 DIGRAPH DWIWARNA 16
3.1. Dua Cycle Dwiwarna 16
3.2. Primitifitas Digraph Dwiwarna 18
3.5. Eksponen 22
3.6. Eksponen Lokal 27
3.7. Batas Bawah dan Atas dari Eksponen Lokal Masuk 29
3.7..1 Batas bawah eksponen lokal masuk 29
3.7..2 Batas atas eksponen lokal masuk 31
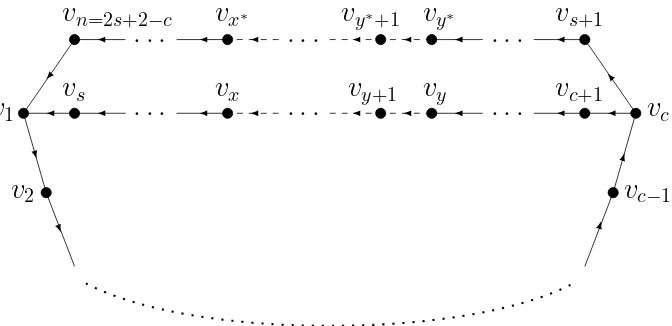
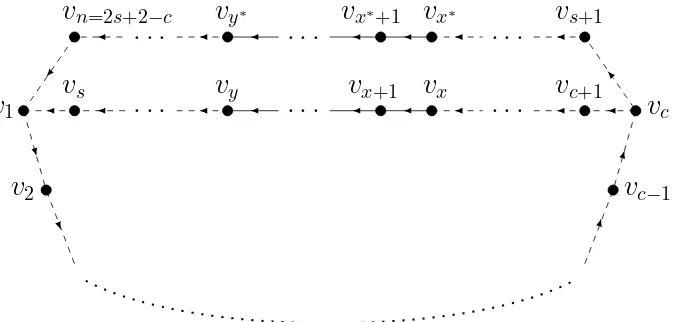
BAB 4 EKSPONEN LOKAL MASUK DUACYCLE DWIWARNA SELISIH
DUA 32
BAB 5 KESIMPULAN DAN SARAN 79
5.1. Kesimpulan 79
5.2. Saran 79
Nomor Judul Halaman
2.1 Representasi digraph 6
2.2 (a) Dua cycle berpotongan, (b) dua cycle bersinggungan pada sebuah busur berarah, dan (c) duacycle bersinggungan pada satu
verteks 8
2.3 (a) Digraph terhubung kuat, dan (b) digraph tak terhubung kuat 9
3.1 Representasi digraph dwiwarna 16
3.2 Dua cycle dwiwarna 17
4.1 Dua cycle dwiwarna 32
4.2 Path merah mempunyai verteks awal yang sama 33
4.3 Path biru mempunyai verteks awal yang sama 39
4.4 Verteks awal path biru tidak sama 45
Sebuah digraph dwiwarna D adalah sebuah digraph dimana setiap arc atau busur berarahnya di warnai dengan menggunakan satu dari dua warna dalam hal ini warna yang digunakan adalah merah atau biru. Sebuah (h, k)-jalan adalah sebuah jalan yang menggunakanhbuah busur berwarna merah dan k buah busur berwarna biru. Sebuah digraph dwiwarna D(2) dengan n verteks{v1, v2, . . . , v
n}
dikatakan primitif bila terdapat bilangan-bilangan bulat tak negatif h dan k se-hingga untuk setiap pasangan verteksvi dan vj di D(2) terdapat (h, k)-jalan dari
vi ke vj dan dari vj ke vi. Eksponen dari sebuah digraph dwiwarna, dinotasikan
exp(D(2)), adalah bilangan bulat positif h+k terkecil atas semua bilangan bulat tak negatif h dan k yang demikian. Eksponen lokal masuk dari sebuah verteks vℓ di D(2), dinotasikan expin(D(2), vℓ), adalah bilangan bulat positif s′ +t′ yang
terkecil atas semua bilangan bulat tak negatif s′ dan t′ sehingga untuk setiap
verteks vi, i = 1,2, . . . , n di D(2) terdapat (s′, t′)-jalan dari vi ke vℓ. Dari hasil
utama dapat disimpulkan bahwa expin(D(2), v
t) = expin(D(2), v1)+d(v1, vt) untuk
semuat = 1,2,· · · , n.
A two colored digraph D is a digraph each of whose arcs is colored by either red or blue. An(h, k)-walk in a two-colored digraph is a walk of lengh h+k consisting of h red arcs and k blue arcs. A two-colored digraph D(2) consisting of n vertex {v1, v2, . . . , vn} is primitive provided that there are nonnegative integers h and k such that for each pair of vertices vi and vj there exists an (h, k)-walk from vi to
vj and from vj tovi. The exponent of a vertex v in D(2), denoted exp(D(2)), is the smallest positive integer h+k over all nonnegative integers h and k such that for each vertex uin D(2) there is an (h, k)-walk fromutov. The inner local exponent
of a vertex vℓ inD(2), denoted expin(D(2), vℓ), is the smallest positive integer s′+t′ over all nonnegative integers s′ and t′ such that for each vertex vi, i = 1,2, . . . , n inD(2) there is an(s′, t′)-walk fromv
i tovℓ. From the main result we can conclude
that expin(D(2), v
t) =expin(D(2), v1) +d(v1, vt) for all t= 1,2,· · · , n.
1.1. Latar Belakang
Sebuah graph G adalah sebuah objek yang terdiri atas sekumpulan titik yang disebut verteks dan garis yang menghubungkan dua buah verteks yang disebut sisi atau edge. Pada graphGterdapat pengulangan setiap pasangan verteks (u, v) dan (v, u) yang dapat ditulis dengan (u, v). Sebuah graph dikatakan terhubung apabila terdapat bilangan bulat positifk, sehingga untuk pasangan verteksudan v terdapat jalan dengan panjang k dari verteksu ke v dan dari v ke u. Sebuah graphGadalah primitif jika dan hanya jikaGterhubung danGmemuat sedikitnya satu cycle ganjil, dimana cycle ganjil adalah cycle dengan panjang ganjil (Bo, 2003). Eksponen graph Gadalah bilangan bulat positif terkecilk sehingga untuk setiap pasangan verteks u dan v di G terdapat jalan dengan panjang k yang menghubungkan u dan v ditulis exp(G).
Andaikan G adalah sebuah graph atas n verteks {v1, v2, . . . , vn}. Sebuah
matriks ketetanggaan dari graph G adalah sebuah matriks bujursangkar A yang berordon. MatriksAadalah primitif jika setiap entriAm >0, dan bilangan bulat
positif terkecilm disebut eksponen dari graph G ditulis exp(G).
Konsep dari graph primitif digunakan dalam berbagai hal, diantaranya pada jaringan Google dan Automata. Penerapan graph pada Google yaitu keterhubung-an keterhubung-antara suatu web dengketerhubung-an kata kunci yketerhubung-ang dimasukkketerhubung-an. Dengketerhubung-an kata kunci yketerhubung-ang dimasukkan, maka Google akan mencari kata-kata pada web-web yang ada yang berkaitan dengan kata kunci tersebut. Kata-kata kunci dan web yang berkaitan membentuk sebuah graph. Page dan Brin (Langville dan Meyer, 2006) meng-ungkapkan bahwa graph Google harus primitif karena bila tidak primitif maka pencarian tidak akan berhasil. Selanjutnya Langville dan Meyer (2006) menam-bahkan graph Google harus berupa matriks bujursangkar S dengan Sm >0, dan
m >0. Dari pendapat Langville dan Meyer, graph Google adalah primitif karena semua entri dari Sm adalah positif. Penggunaan graph primitif berikutnya yaitu
Digraph atau graph berarah merupakan bagian dari teori graph. Seperti halnya graph, sebuah digraphDadalah sebuah objek yang terdiri atas sekumpul-an titik ysekumpul-ang disebut sebagai verteks dsekumpul-an garis berarah ysekumpul-ang menghubungksekumpul-an dua buah verteks di D yang disebut sebagai busur atau arc. Suatu digraph D dikatakan terhubung kuat apabila untuk setiap pasangan verteksu dan verteksv atau (u, v) di D terdapat jalan dari verteksu ke verteks v dan dari verteks v ke verteksu. Sebuah digraphD dikatakan primitif jika dan hanya jikaD terhubung kuat dan pembagi persekutuan terbesar dari panjang cycle-cycle di D adalah 1 (Brualdi dan Ryser, 1991). Brualdi dan Ryser (1991) menambahkan suatu di-graph D adalah primitif jika dan hanya jika terdapat bilangan bulat positif k sedemikian sehingga untuk setiap pasangan verteks (u, v) di D terdapat jalan dengan panjang k. Bilangan bulat positif k bervariasi dan nilai terkecil dari k disebut sebagai ekponen dari digraph D dan ditulis dengan exp(D). Bo (2003) mendefinisikan exp(D; u, v) sebagai bilangan bulat positif terkecil k sedemikian sehingga terdapat jalan dengan panjangmdari verteksuke verteksvuntuk setiap m≥ k dan exp(D) = maxu,v∈V(D)exp(D; u, v).
Penelitian tentang digraph primitif telah banyak dilakukan (Brualdi dan Ryser, 1991). Secara khusus Wielandt (Schneider, 2003) memberi penjelasan tentang digraph primitif D dengan n verteks. Wielandt memperlihatkan bahwa jikaA adalah primitif maka A(n−1)2
+1 >0 dan exp(D) = (n−1)2 + 1, dimanaA merupakan sebuah matriks ketetanggaan dari digraphDdengan ordon. Kirkland (1997) tentang kasus hamiltonian pada digraph primitif D atas n verteks yang terdiri dari 2 cycle dengan n ≥ 3 dan memperlihatkan bahwa exp(D) = ⌊[(n − 1)2 + 1]/2⌋ + 2. Penelitian tentang digraph primitif terus berkembang hingga sampai kepada kelas digraph dwiwarna.
Penelitian tentang eksponen dari digraph dwiwarna dimulai oleh Shader dan Suwilo (2003). Mereka memperlihatkan bahwa bila D adalah digraph dwiwarna primitif atas n verteks, maka 2-eksponen terbesar dari D terletak pada interval [1
2(n
3−5n2),3 2n
3+n2−n]. Lee dan Yang (2005) memperlihatkan untuk digraph dwiwarna primitif dengan duacycle dengan panjang (n−1) dan (n−2), eksponen terbesarnya terletak diantara [2n2−8n+ 7, 2n2−5n+ 3]. Gao dan Shao (2005) memperlihatkan bila digraph dwiwarna D terdiri dari dua cycle dengan selisih satu, exp(D) = 2n2 −3n + 1. Suwilo (2009) memerlihatkan digraph dwiwarna primitif yang asimetrik yang terdiri atas n verteks dan terdapat cycle s dengan s≤n, eksponennya terletak antara [(n2−1)/2,3n2+ 2n−2] ketika n ganjil dan [n2/2,3n2+ 2n−2] ketikangenap. Suwilo (2012) memperlihatkan untuk digraph dwiwarna primitif yang terdiri dari duacycle yaituC1 dan C2, ekponen dari D(2) adalah exp(D(2)) =ℓ(C1)ℓ
r+ℓ(C2)ℓb.
Lebih lanjut Gao dan Shao (2009) mengembangkan konsep eksponen lokal dari digraph ke eksponen lokal dari digraph dwiwarna. Eksponen lokal keluar dari sebuah verteks vi pada sebuah digraph dwiwarna D(2), expout(D(2), vi), adalah
bilangan bulat positif terkecils+tsehingga untuk setiap verteksvj,j = 1,2, . . . , n
di D(2) terdapat jalan dari v
i ke vj yang terdiri atas s busur merah dan t busur
biru. Eksponen lokal keluar dari beberapa kelas-kelas tertentu digraph dwiwarna yang terdiri atas duacycle telah dibicarakan dalam literatur Gao dan Shao (2009), Suwilo (2011), Syahmarani dan Suwilo (2012). Namun demikian, eksponen lokal untuk kelas digraph dari duacycle secara umum belum terdapat dalam literatur. Digraph dwiwarna dua cycle adalah semua digraph dwiwarna yang terdiri atas dua cycle, baik bersinggungan maupun berpotongan.
Sejalan dengan ekponen lokal keluar, pada penelitian ini difokuskan pada eksponen lokal masuk. Eksponen lokal masuk dari sebuah verteks vi di D(2),
dinotasikan expin(D(2), v
i), didefinisikan sebagai bilangan bulat positif terkecil
s′ +t′ sehingga untuk setiap verteks v
k, k = 1,2, . . . , n di D(2) terdapat sebuah
jalan dari verteks vk menuju ke verteks vi yang terdiri atas s′ busur merah dan
t′ busur biru. Bila R dan B masing-masing adalah matriks ketetanggaan merah
dan biru dari digraph dwiwarnaD(2), maka eksponen lokal masuk dari verteksv
i,
i= 1,2, . . . , n dapat dipandang sebagai persoalan optimisasi expin(D(2), vi) = min
s′,t′,≥0{s
′
+t′ : (R, B)(s′,t′)(:, i)>0} dimana (R, B)(s′,t′)
(:, i) adalah kolom kei dari (R, B)(s′,t′)
Hasil-hasil dari penelitian ini penting bagi penentuan batas bawah bagi
reset treshold untuk automata tersinkronkan. Sebuah automata atas n state {v1, v2, . . . , vn} dan dua alpabet{a, b}dikatakan tersinskronkan apabila terdapat
sebuah state u sehingga untuk setiap state vi dapat bergerak ke state u dengan
menggunakan sebuah barisan yang terdiri darihalpabetadan kalpabetb. Reset tresholddari sebuah automataA, dinotasikan dengan rt(A), adalah bilangan bulat terkecilh+k sehingga A adalah tersinkronkan. BilaD(2) adalah representasi di-graph dwiwarna dari automataAdengan dua alpabet, maka expin(D(2))≤rt(A).
1.2. Perumusan Masalah
Penelitian tentang eksponen digraph sampai ke eksponen digraph dwiwarna telah dilakukan sejak tahun 1997. Penelitian yang telah dilakukan membahas tentang eksponen dan eksponen lokal keluar. Namun penelitian tentang eksponen lokal masuk pada digraph dwiwarna khusus untuk kelas digraph dwiwarna dengan dua
cycle belum dibicarakan dalam literatur.
1.3. Tujuan Penelitian
Tujuan dari penelitian ini adalah menentukan nilai dari expin(D(2), v
i) bila D(2)
adalah digraph dwiwarna primitif atasn verteks yang terdiri atas tepat duacycle
dengan panjang selisih dua.
1.4. Manfaat Penelitian
Penelitian ini memberikan teori baru tentang eksponen lokal masuk dari digraph dwiwarna atasn verteks yang terdiri tepat atas duacycle dengan panjang selisih dua.
1.5. Metodologi Penelitian
Metodologi penelitian yang dilakukan adalah bersifat literatur dengan langkah-langkah sebagai berikut:
1. Menggambar digraph dwiwarna primitif yang terdiri atas dua buah cycle
2. Membuat matriks ketetanggaan dari masing-masing warna yaitu merah R dan biruB.
3. Dengan menggunakan code program yang ditulis dengan MATLAB akan ditentukan kandidat bagi bilangan-bilangan tak negatif s′ dan t′ sehingga
expin(D(2), vℓ) =s′ +t′.
Hal ini dilakukan dengan menghitung hasil kali (h, k)-Hurwitz dari matriks ketetanggaan R dan B secara rekursif.
4. Dengan s′ dan t′ yang sudah ditemukan pada proses komputasi di atas,
langkah selanjutnya adalah menentukan batas bawah dan batas atas bagi vektorx dalam persamaan-persamaan diopanthin
Mx+
r(pj,ℓ)
b(pj,ℓ)
=hst′′
i
.
Batas bawah bagi x dilakukan dengan membandingkan panjang path dari vj, j = 1,2, . . . , n, ke vℓ dan cycle dari vℓ kevℓ. Yakni dengan menentukan
nilai x dari persamaan
Mx+
r(pj,ℓ)
b(pj,ℓ)
=hst′′
i
dan My=hst′′
i
.
Batas atas dilakukan dengan membuktikan bahwa sistem persamaan
Mx+
r(pj,ℓ)
b(pj,ℓ)
=hst′′
i
, j = 1,2, . . . , n
mempunyai solusi tak negatif untuk semua verteks vj dan untuk beberapa
path pj,ℓ dari vj ke vℓ.
5. Mempelajari hubungan setiap gambar dengan nilai eksponen lokal masuk (s′+t′) sehingga diperoleh kesimpulan.
6. Membuat teorema baru yang berkaitan dengan permasalahan yang diangkat.
Pada bab ini akan dijelaskan teori-teori dasar tentang digraph yang meliputi de-finisi dua cycle, primitifitas dari digraph, eksponen, dan lokal eksponen. Dengan demikian, akan mempermudah peneliti dalam menjelaskan teori digraph dwiwar-na pada bab berikutnya.
2.1. Dua Cycle
Digraph atau graph berarah adalah sekumpulan titik-titik atau verteks yang di-hubungkan oleh busur berarah atau arc. Berikut ini definisi yang diungkapkan oleh Suwilo (2001).
Definisi 2.1. Sebuah graph berarah (directed graph) atau digraph Dadalah him-punan hingga dan tak kosong V = {1,2, . . . , n} yang unsur-unsurnya disebut dengan verteks, bersama dengan himpunanEyang merupakan pasangan-pasangan verteks di D yang unsur-unsurnya disebut dengan arc.
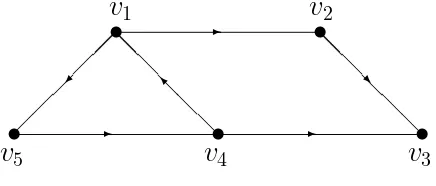
Representasi dari sebuah digraph D dapat dilihat pada contoh berikut. Contoh 2.1. Representasi dari digraph dengan 5 buah verteks.
v
1v
2v
3v
4v
5•
•
•
❅•
•
❅ ❅ ❅ ❅ ❅
❅ ❅ ❅ ❅ ❅ ❅ ✲
✠ ❘
■
✲ ✲
Gambar 2.1 Representasi digraph
Dari Gambar 2.1 terdapat himpunanV yakniV ={v1, v2, v3, v4, v5}dan terdapat himpunan busur E yakniE ={(1,2),(1,5),(2,3),(4,1),(4,3),(5,4)}.
Andaikan digraph D terdiri atas n verteks vj = v1, v2, . . . , n, didefinisikan
derajat masuk (In Degree) yaitu banyaknya busur berarah yang menujuvj
berarah yang keluar dari vj dinotasikan sebagai od(vj). Pada Contoh 2.1 terlihat
yang memiliki derajat masuk yaitu v2, v3, v4, v5, id(v2) = 1 karena hanya terda-pat satu busur berarah yang menuju v2, id(v3) = 2, id(v4) = 2, dan id(v5) = 1. Serta yang memiliki derajat keluar yaituv1, v2, v4, v5, od(v1) = 3 karena terdapat tiga busur berarah yang keluar (meninggalkan) v1, od(v2) = 1, od(v4) = 1, dan od(v5) = 1.
Pada digraph D terdapat path, cycle dan walk. Sebuah path atau lintasan sederhana dari verteksuke verteksv adalah sebuah lintasan dimana tidak terjadi pengulangan satu atau lebih verteks dari u ke v. Sebuah lintasan dari verteks u ke verteks v disebut cycle apabila verteks awal dan ujungnya sama atau dapat ditulis u = v. sebuah lintasan dari verteks u ke verteks v disebut walk apabila terdapat pengulangan satu atau beberapa verteks dari u kev.
Suatu jalan w merupakan jalan yang menghubungkan dua buah verteksu dan v di digraph D. Panjang jalan w dinotasikan dengan ℓ(w) yaitu banyaknya
arc atau busur berarah yang dilalui bila bergerak dari verteks u ke verteks v. Dalam hal ini jalan dapat berupa path, cycle ataupun walk.
Pada Contoh 2.1 dapat ditemukan beberapa path, cycle, dan walk yaitu:
1. Terdapat dua buah path dari verteks 1 ke verteks 3, yaitu v1 → v2 → v3 dengan panjang ℓ(v1, v3) = 2 dan v1 → v5 → v4 → v3 dengan panjang ℓ(v1, v3) = 3.
2. Terdapat sebuah path dari verteks 1 ke verteks 2, yaitu v1 → v2 dengan panjang ℓ(v1, v2) = 1.
3. Terdapat sebuah path dari verteks 1 ke verteks 4, yaituv1 →v5→v4dengan panjang ℓ(v1, v4) = 2.
4. Terdapat cycle dari verteks 1 ke verteks 1, v1 → v5 → v4 → v1 dengan panjang ℓ(v1, v1) = 3.
5. Terdapat walk dari verteks 1 ke verteks 3, v1 → v5 → v4 → v1 → v2 → v3 dengan panjang 5.
Dua cycle didefinisikan sebagai sebuah digraph D yang terdiri tepat dua
cycle yang bersinggungan dapat bersinggungan pada sebuah busur berarah atau pada salah satu verteks di D. Representasi duacycle dapat dilihat pada Contoh 2.2.
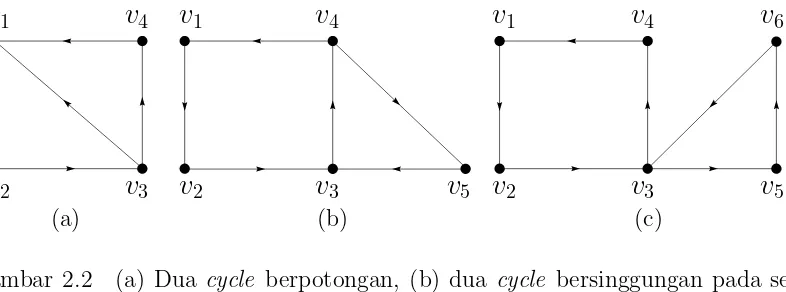
Contoh 2.2. Representasi dari dua cycle
(a) (b) (c)
v
1v
2v
3v
4v
1v
2v
3v
4v
5v
1v
2v
3v
4v
5v
6Gambar 2.2 (a) Dua cycle berpotongan, (b) dua cycle bersinggungan pada se-buah busur berarah, dan (c) dua cycle bersinggungan pada satu verteks
Pada Gambar 2.2 (a) melukiskan dua cycle yaitu dari v1 → v2 → v3 → v1 dengan panjang 3 dan dari v1 →v2 →v3 →v4 →v1 dengan panjang 4. Gambar 2.2 (b) melukiskan dua cycle yaitu dari v3 → v4 → v5 → v3 dengan panjang 3 dan dari v1 →v2 →v3 →v4 →v1 dengan panjang 4. Gambar 2.2 (c) melukiskan dua cycle yaitu dari v3 →v5 → v6 →v3 dengan panjang 3 dan dari v1 → v2 → v3 →v4 →v1 dengan panjang 4.
2.2. Primitifitas
adanya jalan dari verteks 1 ke verteks 3 yaitu 1→3, namun tidak terdapat jalan dari verteks 3 ke verteks 1, sehingga merupakan digraph yang tidak terhubung kuat. Proposisi berikut memperlihatkan hubungan antara terhubung kuat dengan verteks-verteks pada cycle.
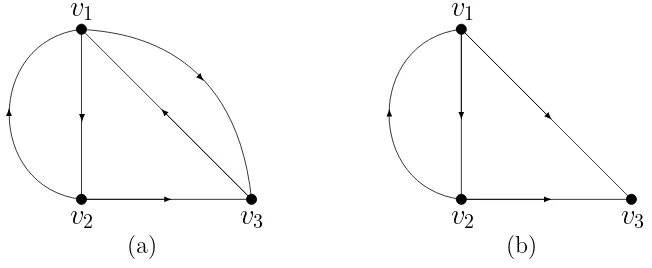
(a) (b)
v
1v
2v
3❄ ✻
❘
v
1v
2v
3Gambar 2.3 (a) Digraph terhubung kuat, dan (b) digraph tak terhubung kuat
Proposisi 2.2. Andaikan D adalah suatu digraph terhubung kuat maka setiap verteks terletak pada cycle.
Bukti. Andaikan digraphDterdiri atasnverteks{v1, v2, . . . , vn}. Ambil sebarang
verteks u dan v di D, karena D terhubung kuat, maka terdapat sebuah lintasan sederhana (path) dari verteks u ke verteks v dan dari verteks v ke verteks u. Sehingga gabungan dua buah path tersebutu→ · · · →v → · · · →umembentuk sebuah cycle di D. Akibatnya, verteksudan v terletak padacycle.
Suatu digraph D yang terhubung kuat dikatakan primitif apabila untuk dua buah verteks u dan v di D terdapat jalan dari u ke v dan dari v ke u dengan panjang k. Nilai k digunakan untuk perhitungan eksponen dari digraph D. Bilangan bulat positif terkecilk disebut eksponen dari digraph D dan ditulis dengan exp(D).
AndaikanDadalah digraph yang terhubung kuat. Misalkan terdapat sebuah verteks tertentu x di D. Untuk dua buah verteks u dan v di D terdapat jalan wxu yaitu jalan dari verteksx ke verteksu dan jalan wxv yaitu jalan dari verteks
x ke verteks v. Jika ℓ(wxu) = ℓ(wxv), maka verteks u dan v dikatakan ekivalen
diilustrasikan sebagai:
y →w xwxu
→ u
dan jalan wyv yaitu jalan dari verteks y ke verteks v, wyv dapat diilustrasikan
sebagai:
y→w xwxv
→ v.
Karenau dan v ekivalen, ini berakibat jalan dariy ke udan dari y kev memiliki panjang yang sama dimana w merupakan jalan dari y kex.
Andaikan C = {C1, C2, . . . , Cr} adalah himpunan semua cycle-cycle di D.
Misalkan ℓ(C) adalah matriks baris dengan kolom ke-idimanai= 1,2, . . . ,r, dan entri-entri dari ℓ(C) adalah panjang cycle Ci (ℓ(Ci)), yakni
ℓ(C) ={ℓ(C1), ℓ(C2), . . . , ℓ(Cr)}
dan misalkanm= gcd(ℓ(C1), ℓ(C2), . . . , ℓ(Cr)). Definisikan H sebagai sebuah
sub-grup dari sub-grup bilangan bulatZ, dimanaH dibangun oleh himpunanℓ(C). Yakni H =hℓ(C1), ℓ(C2), . . . , ℓ(Cr)i. KarenaZadalah sebuah grup siklik, demikian juga
halnya dengan H. AkibatnyaH dibangun oleh sebuah bilangan bulat, dalam hal iniH = gcd(ℓ(C1), ℓ(C2), . . . , ℓ(Cr)).
AndaikanDadalah digraph imprimitif dengan indeks imprimitifitask, maka k = gcd(ℓ(C1), ℓ(C2), . . . , ℓ(Cr)). Suatu digraph adalah primitif jika k = 1 dan
imprimitif jika k > 1. Teorema berikut menjelaskan tentang imprimitifitas dari digraph D.
Teorema 2.3. Andaikan D adalah sebuah digraph terhubung kuat. D adalah primitif jika dan hanya jika pembagi persekutuan terbesar dari panjang cycle-cycle di D adalah 1.
Bukti. Andaikan digraphDadalah primitif. Maka untuk setiap pasangan verteks u dan v di D, u ∼ v, Karena ℓ(wuv) ∈ H untuk setiap pasangan verteks u dan
v di D dan setiap jalan (wuv) dari u ke v maka u ∼ v. Di ambil jalan dengan
panjang 1, maka 1 ∈ H, karena H = hgcd(ℓ(c1), ℓ(c2), . . . , ℓ(ct)i maka pembagi
persekutuan terbesar dari panjang cycle-cycle di D adalah 1.
Sebaliknya, andaikan pembagi persekutuan terbesar dari panjangcycle-cycle
D dan setiap jalan wuv dari u kev diD diperolehℓ(wuv)∈H. Sehingga
masing-masing pasangan verteks di D adalah ekivalen. Akibatnya digraph D adalah primitif.
Contoh 2.3. Pada Gambar 2.3 (a), sebuah dua cycle dengan panjang 3 dari v1 → v2 → v3 → v1 dan dengan panjang 4 dari v1 → v2 → v3 → v4 → v1. Gcd(3,4) = 1, sehingga duacycle tersebut adalah primitif.
2.3. Matriks Ketetanggaan
Andaikan D(2) adalah sebuah digraph atas n verteks {v1, v2, . . . , v
n}. Sebuah
matriks ketetanggaan A = (aij) dari D adalah sebuah sebuah matriks
bujur-sangkar berordo n yang didefinisikan sebagai berikut.
aij =
(
1, jika terdapat busur berarah dari verteks i ke verteksj, 0, jika sebaliknya
dimana i, j = 1,2, . . . , n.
Berikut ini diberikan contoh matriks ketetanggaan dari sebuah digraph.
Contoh 2.4. Dari Gambar 2.3 (a) dan (b), matriks ketetanggaannya adalah
A=
0 1 1
1 0 1
1 0 0
B =
0 1 1
1 0 1
0 0 0
.
Sebuah matriks ketetanggaan A dari sebuah digraph D dikatakan primitif, jika terdapat bilangan bulat positif k sehingga seluruh entri dari Ak adalah posi-tif. Hal ini sesuai dengan pendapat Wielandt (Schneider, 2002), yaitu sebuah matriks tak negatif A dikatakan primitif jika Ak >0. Pada Contoh 2.3, matriks ketetanggaan A adalah matriks ketetanggaan dari digraph primitif, hal ini dapat dilihat bahwa
A1 =A=
0 1 1
1 0 1
1 0 0
.
Dengan mengambil bilangan bulat positifk yang lebih dari 1 diperoleh
A2 =
2 0 1
1 1 1
0 1 1
, A
3=
1 2 2
2 1 2
2 0 1
, A
4 =
4 1 3
3 2 3
1 2 2
, A
5=
4 4 5
5 3 5
4 1 3
Untuk nilai k > 5, Ak >0. Sehingga disimpulkan seluruh entri pada Ak dengan
k ≥4 adalah positif.
Matriks B adalah matriks dari digraph yang tak terhubung kuat sehingga tidak primitif. Andaikan B adalah primitif maka untuk bilangan bulat positif k, Bk > 0. Bila primitif, maka untuk nilai k yang besar, seluruh entri Bk adalah
positif. Diambilk = 30 sehingga diperoleh
B30=
1 0 1
0 1 1
0 0 0
.
Untuk bilangan bulat positif k > 30, entri dari Bk hanya berada pada interval
[0,1]. Karena masih terdapat entri yang bernilai 0, mengakibatkan digraph D dengan matriks ketetanggaan B tidak primitif.
2.4. Eksponen
Eksponen dari digraph D didefinisikan sebagai bilangan bulat positif terkecil k sehingga untuk setiap pasangan verteksudanvdiDterdapat jalan dariukevdan dariv keudengan panjangk. Eksponen dari digraph tersebut dinotasikan dengan exp(D). Dalam hal ini, eksponen hanya ada bila digraphD adalah primitif. Contoh 2.5. Dari Gambar 2.3 (a), akan diperlihatkan bahwa nilai eksponennya adalah 4 yaitu dengan memperlihatkan semua kemungkinan jalan dengan panjang 1, jalan dengan panjang 2, jalan dengan panjang 3, dan jalan dengan panjang 4.
1. Jalan dengan panjang 1,yaitu
v1 →v2, v1 →v3, v2 →v1, v2→v3, v3 →v1
Karena tidak terdapat jalan yang panjangnya 1 dari v1 ke v1, v2 ke v2, v3 ke v2, dan v3 ke v3 maka 1 bukanlah eksponennya.
2. Jalan dengan panjang 2, yaitu
v1 →v2 →v3 v2→ v1 →v2 v3 →v1 →v3 v1 →v2 →v1 v2→ v1 →v3
v2 →v3 →v1 v3→ v1 →v2
3. Jalan dengan panjang 3, yaitu
v1 →v2 →v3→ v1 v2 →v3 →v1 →v2 v3 →v1 →v2 →v1 v1 →v3 →v1→ v2 v2 →v3 →v1 →v3 v3 →v1 →v2 →v3 v1 →v2 →v1→ v3 v2 →v1 →v2 →v1
Karena tidak terdapat jalan yang panjangnya 3 dariv3 kev2 maka 3 bukan-lah eksponennya.
4. Jalan dengan panjang 4, yaitu
v1 →v2 →v1→ v2 →v1 v2 →v1 →v2 →v1 →v3 v1 →v2 →v3→ v1 →v2 v3 →v1 →v2 →v3 →v1 v1 →v2 →v3→ v1 →v3 v3 →v1 →v2 →v1 →v2 v2 →v3 →v1→ v2 →v1 v3 →v1 →v2 →v1 →v3 v2 →v1 →v3→ v1 →v2
Karena terdapat jalan yang panjangnya 4 dari setiap pasangan verteks (u, v) maka eksponen dari digraph tersebut adalah 4.
Eksponen suatu digraphDdapat dicari dengan menggunakan perpangkatan dari matriks ketetanggaanA. Brualdi dan Ryser (1991), menyatakan bahwa entri (i, j) dari Ak merupakan banyaknya jalan dari verteksv
i kevj dengan panjang k.
Berikut ini diperlihatkan hubungan antara suatu digraph dengan matriks kete-tanggaannya.
Proposisi 2.4. Andaikan A adalah suatu matriks ketetanggaan dari digraph D. Entri (i, j)dari Ak menyatakan banyaknya jalan dari v
i ke vj yang panjangnya k di D.
Bukti. Akan dibuktikan dengan induksi pada k. Jika k = 1 maka setiap entri a1
ij dari A1 menyatakan banyaknya jalan dari vi ke vj yang panjangnya satu.
Asumsikan setiap entri ak
ij dari Ak menyatakan banyaknya jalan dari vi ke vj
yang panjangnya adalah k diD, untuk k ≥1.
Akan diperlihatkan akij+1 adalah banyaknya jalan dari vi ke vj yang
pan-jangnya k+ 1, untuk k ≥ 1. Perhatikan setiap jalan dari vi ke vj di D dengan
panjang k untukℓ = 1,2, . . . , n dan dilanjutkan dengan busur berarah darivℓ ke
vj, sehingga akiℓaℓj menyatakan jalan dengan panjang k + 1 dari vi ke vj di D.
Andaikan tidak terdapat jalan yang panjang k dari vi ke vℓ di D, maka akiℓ = 0
sedemikian sehingga ak
iℓaℓj = 0. Ini berarti tidak terdapat jalan dengan panjang
k+ 1 dari vi kevj yang melaluivℓ diDsehingga banyaknya jalan dengan panjang
k+ 1 dari vi ke vj di Dadalah:
aki1a1j +aki2a2j+· · ·+akinanj = n
X
ℓ=1
akiℓaℓj.
KarenaAk+1 =AkA diperolehlah
akij+1 =
n
X
ℓ=1
akiℓaℓj.
Hal ini berakibat akij+1 adalah benar menyatakan banyaknya jalan dari vi ke vj
dengan panjangk+1 diD. Jadi, setiap entri (i, j) dari Akmenyatakan banyaknya
jalan dengan panjang k dari vi kevj.
Dengan menggunakan Proposisi 2.4 akan dicari eksponen dari Contoh 2.3 (a). Dari subbab 2.3 sebelumnya telah diketahui bahwa matriks ketetanggaan
A =
0 1 1
1 0 1
1 0 0
. Nilai dari A
4 =
4 1 3
3 2 3
1 2 2
dan A
5 =
4 4 5
5 3 5
4 1 3
. Karena setiap
entri dariAk>0 dipenuhi olehk ≥4 dan dari definisi eksponen adalah bilangan
positif terkecilk sehingga eksponen dari digraph tersebut adalah 4.
2.5. Eksponen Lokal Digraph
Andaikan D adalah sebuah digraph primitif atas n verteks V ={v1, v2, . . . , vn}.
Untuk vi ∈ V di D, eksponen lokal dari verteks vi di D adalah bilangan bulat
positif terkecilℓ sehingga untuk setiap verteksvj dimanaj = 1,2, . . . , nterdapat
jalan dari verteksvi ke verteks vj di D dengan panjang ℓ. Eksponen verteks vi
disebut juga sebagai eksponen lokal keluar dari verteksvi dan dinotasikan dengan
expout(vi, D).
AndaikanDadalah digraph primitif yang terdiri darinverteks. Jika verteks-verteks di Dadalah (v1, v2, . . . , vn) sedemikian hingga
Contoh 2.6. Dari Gambar 2.3 (a), akan dicari eksponen lokal dari setiap verteks di D berdasarkan Proposisi 2.4 yaitu dengan melihat entri ak
ij dari Ak, dimana
semua entri pada baris ke-i harus bernilai positif. Matriks ketetanggaan dari Gambar 2.3 (a) adalah
A=
0 1 1
1 0 1
1 0 0
.
Nilai dariA2=
2 0 1
1 1 1
0 1 1
, padaA
2 terlihat baris ke-2 memiliki entri yang positif,
sehingga expout(v2, D) = 2. Untuk A3 =
1 2 2
2 1 2
2 0 1
, pada A
3 terlihat baris ke-1
dan ke-2 memiliki entri-entri yang positif, maka expout(v1, D) = 3. Selanjutnya A4 =
4 1 3
3 2 3
1 2 2
, pada A
4 terlihat setiap baris memiliki entri-entri yang positif,
sehingga expout(v3, D) = 4.
Pada bab ini akan dijelaskan teori-teori dasar tentang digraph dwiwarna yang meliputi definisi duacycle dwiwarna, primitifitas dari digraph dwiwarna, eksponen digraph dwiwarna, dan lokal eksponen dari digraph dwiwarna. Dengan demikian, akan mempermudah peneliti dalam hal pembahasan hasil utama pada bab berikut-nya.
3.1. Dua Cycle Dwiwarna
Suatu digraph dwiwarna D(2) adalah sebuah digraph D yang setiap busurnya diwarnai dengan dua buah warna. Dalam hal ini warna yang dipakai adalah merah atau biru, tetapi tidak keduanya. Digraph dwiwarna dapat direpresentasikan dengan garis tak putus sebagai busur merah dan garis putus-putus sebagai busur biru.
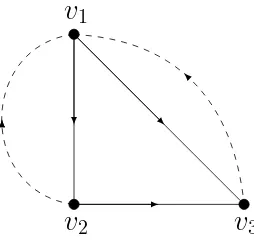
Contoh 3.1. Representasi dari digraph dwiwarna dengan 3 buah verteks.
v
1v
2v
3■
Gambar 3.1 Representasi digraph dwiwarna
Dari Gambar 3.1 tersebut dapat dilihat bahwa terdapat 3 buah garis tak putus sebagai busur merah yaitu busur v1 −→r v2, v1 −→r v3, dan busur v2 −→r v3, kemudian terdapat 2 buah garis yang putus-putus sebagai busur biru yaituv3
b
99K v1 dan v2
b
99Kv1.
[image:31.612.262.389.427.548.2]r(w) +b(w) dan vektor
r(w) b(w)
adalah komposisi dari jalan w (Syahmarani dan Suwilo, 2012).
Dari Gambar 3.1 dapat ditemukan beberapa path, cycle, dan walk yaitu:
1. Terdapat cycle dari verteks 1 ke verteks 1, v1 −→r v299Kb v1 yaitu 1 busur
merah dan 1 busur biru dengan komposisi h11i.
2. Terdapat cycle dari verteks 1 ke verteks 1, v1 −→r v3 99Kb v1 yaitu 1 busur
merah dan 1 busur biru dengan komposisi h11i.
3. Terdapat cycle dari verteks 1 ke verteks 1, v1 −→r v2 −→r v3 99Kb v1 yaitu 2
busur merah dan 1 busur biru dengan komposisi h21i.
4. Terdapat walk dari verteks 1 ke verteks 3, v1 −→r v2 −→r v3 99Kb v1 −→r v3
yaitu 3 busur merah dan 1 busur biru dengan komposisi h31i.
5. Terdapat path dari verteks 3 ke verteks 1,v3 99Kb v1 yaitu hanya satu busur
biru dengan komposisi h01i.
Duacycle dwiwarna adalah sebuah digraphD(2) yang terdiri tepat duacycle dengan masing-masing busur berarah diwarnai dengan dua buah warna, merah atau biru. Seperti halnya dua cycle pada Bab 2, dua cycle dwiwarna juga dapat berpotongan maupun bersinggungan. Representasi dua cycle dwiwarna dapat dilihat pada Contoh 3.2.
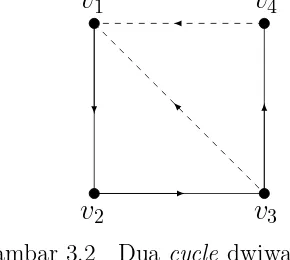
Contoh 3.2. Representasi dua cycle dwiwarna dengan 4 buah verteks
v
1v
2v
3v
4Gambar 3.2 Dua cycle dwiwarna
Pada Gambar 3.2 terlihat digraph dwiwarna memiliki dua buahcycle yaitu dari v1 −→r v2 −→r v3 99Kb v1 dengan komposisi
h2
1
i
dan dari v1 −→r v2 −→r v3−→r v4 99Kb v1 dengan komposisi
h3
1
i
[image:32.612.245.390.527.657.2]3.2. Primitifitas Digraph Dwiwarna
Seperti halnya digraph, sebuah digraph dwiwarnaD(2) dengan mengabaikan war-na dari busur-busurnya dikatakan terhubung kuat bila untuk setiap pasangan verteks (u, v) di D(2) terdapat jalan dari u ke v dan jalan dari v ke u. Untuk menentukan suatu digraph dwiwarna terhubung kuat atau tidak, dapat dilihat pada Gambar 3.1. Pada gambar tersebut, cukup ditunjukkan adanya jalan yang menghubungkan verteks 2 dengan verteks 3, karena terlihat adanya jalan dengan panjang satu yang menghubungkan verteks 1 dengan 2, verteks 2 dengan verteks 1, verteks 1 dengan verteks 3, dan verteks 3 dengan 1. Dari verteks 2 ke verteks 3 yaitu v2 −→r v3, dan dari verteks 3 ke verteks 2 yaitu v399Kb v1 −→r v2 danv2
b
99Kv1
r
−→ v3. Sehingga digraph dwiwarna tersebut dapat dikatakan terhubung kuat. Sebuah digraph dwiwarna terhubung kuat dikatakan primitif bila terdapat bilangan bulat tak negatifh dank sehingga untuk setiap pasangan verteksudan v di D(2) terdapat sebuah (h, k)-jalan dari u kev (Fornasini dan Valcher, 1997).
Andaikan D(2) adalah sebuah digraph dwiwarna terhubung kuat. Misalkan C = {c1, c2, . . . , ct} adalah himpunan semua cycle diD(2). Sebuah matriks cycle
dari D(2) adalah sebuah matriks 2×t dalam bentuk M =
r(c1) r(c2) · · · r(ct)
b(c1) b(c2) · · · b(ct)
.
Yakni sebuah matriks dimana kolom ke-idengan i= 1,2, . . . t dari matriks terse-but merupakan komposisi warna dari cycle ci. Content dari matriks cycle M
didefinisikan 0 bila rank dari M adalah 1, dan content dari M adalah pembagi persekutuan terbesar dari determinan submatriks 2×2 dari M bila rank(M) = 2 (Suwilo, 2011). Fornasini dan Valcher (1997) memberikan karakteristik untuk digraph dwiwarna primitif seperti pada Teorema 3.1 berikut.
Teorema 3.1. Misalkan D(2) adalah digraph dwiwarna yang terhubung kuat
de-ngan sedikitnya satu busur berarah dari setiap warna. Digraph dwiwarna D(2)
adalah primitif jika dan hanya jika content matriks cycle D(2) adalah 1.
Bukti. AndaikanD(2) adalah sebuah digraph dwiwarna primitif. MakaD(2) mem-punyai persisnya satu dari kelas 2-imprimitif. Oleh sebab itu, setiap pasangan verteksudanv adalah 2-ekivalen. Karena merupakan 2-ekivalen, maka untuk se-tiap verteksudan v dan setiap jalanwuv dari ukev,
r(wuv)
b(wuv)
memiliki rank 2, D(2) memiliki sedikitnya 1 busur merah dan sedikitnya 1 busur biru. Maka h10i, h01i ∈ hMi. Karenanya hMi = Z2. Misalkan S adalah bentuk normal Smith dari M, maka S = UMV untuk beberapa matriks unimodular U danV. KarenanyahSi=Z2, dan content dariSadalah 1. Teorema Cauchy-Binet menjamin bahwa content dari M adalah 1.
Sebaliknya, asumsikan content dari M adalah 1. Terdapat bilangan bulat ai dan bi, i= 1,2, . . . , c sedemikian sehingga
h1
0
i
=
c
X
i=1 ai
r(Ci)
b(Ci)
, dan h01i =
c
X
i=1 bi
r(Ci)
b(Ci)
.
Oleh sebab itu, h10i, h01i ∈ hMi dan hMi = Z2. Ini menjamin untuk setiap pasangan verteks u dan v dan setiap jalan wuv dari u ke v
r(wuv)
b(wuv)
∈ hMi. Karenanyaudanv adalah 2-ekivalen, dan disimpulkanD(2) adalah 2-primitif. Contoh 3.3. Dari Gambar 3.1, digraph dwiwarna yang terdiri dari tiga buah
cycle dan matrikscycle dari digraph dwiwarna tersebut berbentuk
M =h2 1 11 1 1i.
Submatriksnya adalah M1 = h2 11 1i, M2 = h2 11 1i, dan M3 = h1 11 1i. Dikare-nakan det(M1) = det(M2) = 1, hal ini mengakibatkan pembagi persekutuan terbesar dari determinan submatriksnya akan bernilai 1. Dengan demikian di-graph dwiwarna tersebut adalah primitif.
Duacycle dwiwarna yang terhubung kuat dikatakan primitif jika determinan dari matrikscycle diD(2)adalah 1. Proposisi 3.2 memperlihatkan primitifitas dari dua cycle dwiwarna dengan selisih 2.
Proposisi 3.2. AndaikanD(2) adalah digraph dwiwarna primitif yang terdiri atas dua cycle C1 dan C2 yang panjangnya s dan s+ 2. D(2) adalah primitif jika dan
hanya jika matriks cyclenya berbentuk
M =
(s+ 1)/2 (s+ 3)/2 (s−1)/2 (s+ 1)/2
.
dimana 0≤a ≤sdan 0≤b≤s+2. KetikaD(2)adalah primitif dan det(M) =±1 maka s(b−a)−2a = ±1. Andaikan det(M) = 1, s(b−a) = 2a+ 1 ≤ 2s+ 1. Oleh karena itu, 0 < b−a≤ 2. Jika b−a = 2, maka s(b−a) = 2a+ 1 menjadi 2s = 2a+ 1, ini mustahil karena s dan a keduanya merupakan bilangan bulat. Oleh sebab itu, dipilihlahb−a = 1 sehingga diperoleha= (s−1)/2,b= (s+ 1)/2 dan matrikscycle M berbentuk
M =
(s+ 1)/2 (s+ 3)/2 (s−1)/2 (s+ 1)/2
.
Selanjutnya andaikan det(M) =−1 maka s(b−a) = 2a−1≤2s−1. Oleh karena itub−a≤1. Jika nilai b−a≤0 maka 2a ≤1, dan hanya dipenuhi untuk a = 0. Untuk 0≤b ≤ s+ 2 dan a= 0 tidak akan diperoleh det(M) =−1. Oleh karena itu haruslah b−a = 1 sehingga diperoleha= (s+ 1)/2,b = (s+ 3)/2 dan matriks cycle M berbentuk
M =
(s−1)/2 (s+ 1)/2 (s+ 1)/2 (s+ 3)/2
.
Dengan menukar posisi cycle dari matriks cycle M dapat diasumsikan bahwa matriks cycle dari D(2) berbentuk M =
(s+ 1)/2 (s+ 3)/2 (s−1)/2 (s+ 1)/2
. Sebaliknya, andaikan matrikscyclenya dari D(2) berbentuk
M =
(s+ 1)/2 (s+ 3)/2 (s−1)/2 (s+ 1)/2
.
Determinan dari matrikscycle M, det(M) = 1, sehingga matriks cycle M memi-liki rank 2. Ini berakibat content dari matriks cycle M adalah 1. Teorema 3.1 menjamin bahwa D(2) adalah digraph dwiwarna primitif.
3.3. Matriks Ketetanggaan
AndaikanD(2) adalah sebuah digraph dwiwarna yang terdiri atasnverteks{v1, v2, . . . , vn}. Matriks ketetanggaan dari digraph dwiwarna dibedakan menjadi dua
yaitu matriks ketetanggaan merah dan matriks ketetanggaan biru. Sebuah matriks ketetanggaan merah R = (rij) dari D(2) adalah sebuah sebuah matriks
bujur-sangkar berordo n yang didefinisikan sebagai berikut.
rij =
(
Matriks ketetanggaan biru dari D(2) adalah matriks B = (b
ij) yang entrinya
didefinisikan sebagai
bij =
(
1, jika terdapat busur biru dari verteks i ke verteksj, 0, jika sebaliknya.
Perhatikan bahwa matriks ketetanggaan A dari digraph D merupakan penjum-lahan dari matriks ketetanggaan merah dan biru, A=R+B.
Contoh 3.4. Dari Gambar 3.1, matrik ketetanggaan merah dan birunya adalah
R =
0 1 1
0 0 1
0 0 0
dan B =
0 0 0
1 0 0
1 0 0
.
3.4. Hurwitz Product
Definisi 3.3. Untuk bilangan bulat tak negatif h dan k, (h, k)-hurwitz product, didefinisikan(R, B)(h,k) dariR danB adalah jumlah semua matriks dari perkalian R sebanyak h kali dan B sebanyak k kali.
Fornasini dan Valcher (1997) menemukan hubungan antara (h, k)-jalan pada digraph dwiwarna dan hasil kali khusus dari matriks ketetanggaan. Untuk matriks tak negatif R dan B dan bilangan bulat tak negatif h dan k, perkalian (h, k )-Hurwitz dari matriks R dan B, dinotasikan (R, B)(h,k), adalah jumlahan dari semua hasil kali matriks yang terdiri dari h buah matriksR dan k buah matriks B. Sebagai contoh (R, B)(2,1) = R2B +RBR+BR2, dan (R, B)(3,2) =R3B2+ R2BRB+R2B2R+RBR2B+RBRBR+RB2R2+BR3B+BR2BR+BRBR2+ B2R3.Secara umum hasil kali (h, k)-Hurwitz dari matriksR dan B dapat didefi-nisikan secara rekursif sebagai berikut:
(R, B)(h,0) =Rh untuk semua h≥0,
(R, B)(0,k)=Bk untuk semua k≥0,
(R, B)(h,k)=R(R, B)(h−1,k)+B(R, B)(h,k−1) untuk semua h, k ≥1.
Contoh 3.5. Dari matriks ketetanggaan merah dan biru pada Contoh 3.4 yaitu
R =
0 1 1
0 0 1
0 0 0
danB =
0 0 0
1 0 0
1 0 0
, akan dicari hurwirz product (R, B)
2,1sebagai
berikut
(R, B)(2,1) =R2B+RBR+BR2 =
1 2 2
0 1 2
0 0 1
3.5. Eksponen
Andaikan D(2) adalah digraph dwiwarna primitif atas n verteks, untuk setiap dua buah verteks u dan v di D(2) terdapat jalan dari u ke v dan dari v ke u dengan komposisi h buah merah dan k buah biru, bilangan bulat positif terkecil h+k disebut sebagai eksponen dari digraph dwiwarna dan dinotasikan dengan exp(D(2)).
Contoh 3.6. Dari Gambar 3.1, untuk setiap verteks u dan v terdapat jalan terpendek yang sama panjangnya dari u kev yaitu:
v1 −→r v2 −→r v3 99Kb v1 −→r v2
b
99Kv1 −→r v2
b
99Kv1.
v1 −→r v2 99Kb v1 −→r v2
b
99Kv1 −→r v2
b
99Kv1 −→r v2.
v1 −→r v3 99Kb v1 −→r v3
b
99Kv1 −→r v3
b
99Kv1 −→r v3.
v2 −→r v3 99Kb v1 −→r v2 −→r v3
b
99Kv1 −→r v2
b
99Kv1.
v2 −→r v3 99Kb v1 −→r v2
b
99Kv1 −→r v2
b
99Kv1 −→r v2.
v2 99Kb v1 −→r v2
b
99Kv1 −→r v2
b
99Kv1 −→r v2 −→r v3.
v3 99Kb v1 −→r v2 −→r v3
b
99Kv1 −→r v2 −→r v3
b
99Kv1.
v3 99Kb v1 −→r v2 −→r v3
b
99Kv1 −→r v3
b
99Kv1 −→r v2.
v3 99Kb v1 −→r v2 −→r v3
b
99Kv1 −→r v3
b
99Kv1 −→r v3.
Dari Contoh 3.6 diperoleh jalan terpendek untuk setiap verteks u ke verteks v memiliki panjang 7 dengan komposisi h43i, sehingga eksponen dari digraph dwi-warna tersebut adalah 7.
Eksponen dari sebuah digraph dwiwarna D(2) dapat juga dicari menggu-nakan Hurwitz product. Dengan menggumenggu-nakan induksi atas hdan k dapat diper-lihatkan bahwa bilaR dan B masing-masing adalah matriks ketetanggaan merah dan biru dari digraph dwiwarna D(2), maka entri (i, j) dari matriks (R, B)(h,k) adalah banyaknya jalan (h, k) dari verteksvi ke verteksvj. Lemma berikut
mem-perlihatkan hubungan antara matriks ketetanggaan merah dan biru pada digraph dwiwarna yang diungkapkan Suwilo (2001).
Bukti. Akan dibuktikan dengan induksi pada h+k, jika h+k = 1 maka h = 0 dan k = 1 atauh= 1 dan k = 0. Jikah= 0 maka entri (i, j) dari (R, B)(0,1)=B adalah sebuah jalan dengan komposisi h01i di D(2). Jika k = 0 maka entri (i, j) dari (R, B)(1,0)=M adalah sebuah jalan dengan komposisi h1
0
i
di D(2).
Andaikan Lemma ini benar untuk semua bilangan bulat tak negatif h′ dan
k′ dengan h′+k′ ≤h+k akan diperlihatkan untuk h+k+ 1 adalah benar. Dari
definisi hasil kali (h, k)-Hurwitz
(R, B)(h+1,k)=R(R, B)(h,k)+B(R, B)(h+1,k−1).
Oleh hipotesis induksi, entri (i, j) padaR(R, B)(h,k) menyatakan jalan dari verteks i ke verteksj yang dimulai dari sebuah busur merah kemudian diikuti oleh jalan (h, k), dan entri (i, j) pada B(R, B)(h+1,k−1) menyatakan jalan dari verteks i ke verteks j yang dimulai dari sebuah busur biru kemudian diikuti oleh jalan (h+ 1, k−1). Jadi entri (i, j) dari (R, B)(h+1,k) adalah panjang jalan (h+ 1, k) dari verteksike verteksj. Oleh karena itu entri (i, j) dari (R, B)(h,k)adalah banyaknya jalan (h, k) dari verteks i ke verteksj di D(2).
Sebuah pasangan matriks bujursangkar berordon, (R, B), dikatakan primitif asalkan terdapat bilangan bulat tak negatif h dan k sehingga entri (i, j) dari (R, B)(h,k) adalah positif.
Contoh 3.7.Dengan menggunakan Lemma 3.4, akan diperlihatkan bahwa matriks ketetanggaan merah dan biru pada Contoh 3.4 merupakan matriks primitif untuk bilangan bulat tak negatif h dan k, serta dicari eksponen dari bilangan h dan k yang diperoleh.
1. Jika h+k= 1, maka
(R, B)(1,0) = R=
0 1 1
0 0 1
0 0 0
.
(R, B)(0,1) = B =
0 0 0
1 0 0
1 0 0
2. Jika h+k= 2, maka
(R, B)(2,0) = R2 =
0 0 1
0 0 0
0 0 0
.
(R, B)(1,1) = RB+BR=
2 0 0
1 1 1
0 1 1
.
(R, B)(0,2) = B2 =
0 0 0
0 0 0
0 0 0
.
3. Jika h+k= 3, maka
(R, B)(3,0) = R3 =
0 0 0
0 0 0
0 0 0
.
(R, B)(2,1) = R(R, B)(1,1)+BR2 =
1 2 2
0 1 2
0 0 1
.
(R, B)(1,2) = R(R, B)(0,2)+B(R, B)(1,1)=
0 0 0
2 0 0
2 0 0
.
(R, B)(0,3) = B3 =
0 0 0
0 0 0
0 0 0
.
4. Jika h+k= 4, maka
(R, B)(4,0) = R4 =
0 0 0
0 0 0
0 0 0
.
(R, B)(3,1) = R(R, B)(2,1)+BR3 =
0 1 3
0 0 1
0 0 0
.
(R, B)(2,2) = R(R, B)(1,2)+B(R, B)(2,1)=
4 0 0
3 2 2
1 2 2
(R, B)(1,3) = RB3 +B(R, B)(1,2) =
0 0 0
0 0 0
0 0 0
.
(R, B)(0,4) = B4 =
0 0 0
0 0 0
0 0 0
.
5. Jika h+k= 5, maka
(R, B)(5,0) = R5 =
0 0 0
0 0 0
0 0 0
.
(R, B)(4,1) = R(R, B)(3,1)+BR4 =
0 0 1
0 0 0
0 0 0
.
(R, B)(3,2) = R(R, B)(2,2)+B(R, B)(3,1)=
4 4 4
1 3 5
0 1 3
.
(R, B)(2,3) = R(R, B)(1,3)+B(R, B)(2,2)=
0 0 0
4 0 0
4 0 0
.
(R, B)(1,4) = RB4 +B(R, B)(1,3) =
0 0 0
0 0 0
0 0 0
.
(R, B)(0,5) = B5 =
0 0 0
0 0 0
0 0 0
.
6. Jika h+k= 6, maka
(R, B)(6,0) = R6 =
0 0 0
0 0 0
0 0 0
.
(R, B)(5,1) = R(R, B)(4,1)+BR5 =
0 0 0
0 0 0
0 0 0
.
(R, B)(4,2) = R(R, B)(3,2)+B(R, B)(4,1)=
1 4 8
0 1 4
0 0 1
(R, B)(3,3) = R(R, B)(2,3)+B(R, B)(3,2)=
8 0 0
8 4 4
4 4 4
.
(R, B)(2,4) = R(R, B)(1,4)+B(R, B)(2,3)=
0 0 0
0 0 0
0 0 0
.
(R, B)(1,5) = RB5 +B(R, B)(1,4) =
0 0 0
0 0 0
0 0 0
.
(R, B)(0,6) = B6 =
0 0 0
0 0 0
0 0 0
.
7. Jika h+k= 7, maka
(R, B)(7,0) = R7 =
0 0 0
0 0 0
0 0 0
.
(R, B)(6,1) = R(R, B)(5,1)+BR6 =
0 0 0
0 0 0
0 0 0
.
(R, B)(5,2) = R(R, B)(4,2)+B(R, B)(5,1)=
0 1 5
0 0 1
0 0 0
.
(R, B)(4,3) = R(R, B)(3,3)+B(R, B)(4,2)=
12 8 8
5 8 12
1 4 8
.
Dari hasil di atas, terdapat jalan dari setiap verteksuke verteksvdan dari verteks v ke verteksudengan panjang 7 dengan komposisi h43i yang keseluruhan entrinya adalah positif, sehingga (R, B)(h,k) merupakan matriks primitif dan eksponen dari digraph dwiwarna tersebut adalah 7 yang terdiri dari 4 busur merah dan 3 busur biru.
Shader dan Suwilo (2003) memberikan cara lain untuk menentukan eksponen dari digraph dwiwarna dengan menggunakan pendekatan sistem persamaan dio-phantin. Perhatikan bahwa setiap jalan dari verteksvidanvjpada sebuah digraph
dapat didekomposisi menjadi sebuah path darivi kevj dan beberapa buahcycle.
bulat terkecilh+k atas semua bilangan bulat tak negatifhdank sehingga sistem persamaan
Mx+
r(pi,j)
b(pi,j)
=hhki (3.1)
mempunyai solusi tak negatif untuk semua pasangan verteks (vi, vj) dan beberapa
path pi,j dari vi kevj.
3.6. Eksponen Lokal
Pada tahun 2009, Gao dan Shao memperkenalkan konsep eksponen lokal sebagai berikut. Andaikan D(2) adalah sebuah digraph dwiwarna primitif. Eksponen dari sebuah verteksudiDadalah bilangan bulat positif terkecils+t atas semua bilangan bulat tak negatifsdantsehingga untuk setiap verteksvdiD(2) terdapat (s, t)-jalan dari u ke v. Eksponen verteks u disebut juga sebagai eksponen lokal keluar dari verteksu dan dinotasikan dengan expout(u, D(2)).
Sebagaimana halnya dengan eksponen dari digraph, eksponen lokal dari sebuah verteks u dapat ditentukan dengan menggunakan dua cara. Pertama, Andaikan D(2) adalah sebuah digraph dwiwarna atas n verteks {v1, v2, . . . , v
n}.
Bila R dan B masing-masing adalah matriks ketetanggaan merah dan biru dari digraph dwiwarnaD(2), maka eksponen lokal dari verteksv
ℓadalah bilangan bulat
positif terkecils+t atas semua bilangan bulat tak negatifs dan t sehingga baris ke ℓ dari matriks (R, B)(s,t) mempunyai entri positif.
Contoh 3.8. Pada Contoh 3.7, terdapat baris keℓ dari matriks (R, B)(s,t) mem-punyai entri positif. (R, B)(1,1) =
2 0 0
1 1 1
0 1 1
, baris ke-2 dari matriks ini adalah
positif dengan s = 1 dan t = 1 sehingga expout(v2, D(2)) = 2. (R, B)(2,1) =
1 2 2
0 1 2
0 0 1
, baris ke-1 dari matriks ini adalah positif dengan s = 2 dan t = 1
sehingga expout(v1, D(2)) = 3. (R, B)(2,2) =
4 0 0
3 2 2
1 2 2
, baris ke-3 dari matriks
ini adalah positif dengan s= 2 dan t= 2, sehingga expout(v3, D(2)) = 4.
Kedua, untuk verteksvℓyang sudah ditetapkan, misalkanpℓ,j adalah sebuah
verteks vℓ adalah bilangan bulat positif terkecil s+t atas semua bilangan bulat
tak negatif s dan t sehingga persamaan 3.1 dapat diubah menjadi Mx+
r(pℓ,j)
b(pℓ,j)
=hsti, j = 1,2, . . . n (3.2) mempunyai solusi tak negatif untuk semua verteks vj dan untuk beberapa path
pℓ,j dari vℓ ke vj.
Gao dan Shao (2009) menentukan eksponen lokal keluar dari verteks-verteks pada graph dwiwarna tipe Wiedlant. Suwilo (2011) menentukan eksponen lokal keluar dari verteks-verteks pada digraph ministrong ekstremal dwiwarna. Selan-jutnya, Syahmarani dan Suwilo (2012) menentukan eksponen lokal keluar dari digraph Hamilton atas n verteks dengan cycle terkecil berukuran n−2.
Perhatikan bahwa konsep eksponen lokal yang didefinisikan oleh Gao dan Shao (2009) hanya memperhatikan jalan-jalan dengan komposisi sama yang ber-asal dari satu verteks tertentu dan menuju ke semua verteks lainnya. Pada peneli-tian ini didefinisikan konsep eksponen lokal dari sebuah verteks dengan mem-perhatikan jalan-jalan dengan komposisi sama yang berasal dari semua verteks dan menuju ke satu verteks tertentu. Eksponen lokal masuk (expin) dari sebuah verteksvℓ adalah bilangan bulat positif terkecils′+t′ atas semua bilangan bulat
tak negatifs′ dan t′ sehingga untuk setiap verteksv
j diD(2) terdapat (s′, t′)-jalan
dari verteksvj menuju ke verteks vℓ.
Bila R dan B masing-masing merupakan matriks ketetanggaan merah dan biru dari digraph dwiwarnaD(2), maka eksponen lokal masuk dari sebuah verteks vℓ adalah bilangan bulat positif terkecil s′ +t′ atas semua bilangan bulat tak
negatif s′ dan t′ sehingga kolom ke ℓ dari matriks (R, B)(s′,t′)
mempunyai entri positif. Misalkanpj,ℓ adalah sebuah path dari verteksvj,j = 1,2, . . . , nke verteks
vℓ. Eksponen lokal masuk dari verteks vℓ adalah bilangan bulat posiitif terkecil
s′ +t′ atas semua bilangan bulat tak negatif s′ dan t′ sehingga persamaan (3.2)
dapat dimodifikasi menjadi
Mx+
r(pj,ℓ)
b(pj,ℓ)
=hst′′
i
, j = 1,2, . . . n (3.3) mempunyai solusi tak negatif untuk semua verteks vj dan untuk beberapa path
Contoh 3.9. Pada Contoh 3.7, terdapat kolom keℓ dari matriks (R, B)(s′,t′)
yang
mempunyai entri positif. (R, B)(2,1) =
1 2 2
0 1 2
0 0 1
, setiap entri pada kolom ke-3
adalah positif dengans′ = 2 dant′ = 1, sehingga expin(v3, D(2)) = 3. (R, B)(2,2) =
4 0 0
3 2 2
1 2 2
setiap entri pada kolom ke-1 adalah positif dengan s
′ = 2 dan t′ = 2
sehingga expin(v1, D(2)) = 4. (R, B)(3,2) =
4 4 4
1 3 5
0 1 3
, setiap entri pada kolom
ke-2 adalah positif dengan s′ = 3 dan t′ = 2, sehingga expin(v2, D(2)) = 5.
3.7. Batas Bawah dan Atas dari Eksponen Lokal Masuk
Andaikan D(2) adalah digraph dwiwarna primitif yang terdiri atas dua cycle C1 danC2. Karena memiliki dua cycle maka matrikscycle dari D(2) berbentukM =
r(c1) r(c2) b(c1) b(c2)
. Dari matriks M tersebut dapat dipilih banyaknya busur merah dan busur biru pada cycle C1 dan C2 sehingga det(M) = 1. Dapat diasumsikan bahwa eksponen lokal masuk pada verteksvk diperoleh dari sebuah jalan (h, ℓ).
Pencarian batas atas dan batas bawah merupakan syarat cukup untuk mencari nilai eksponen lokal masuk dari digraph dwiwarna.
3.7..1 Batas bawah eksponen lokal masuk
Batas bawah dari eksponen lokal masuk digraph dwiwarna yang terdiri atas dua
cycle C1 dan C2 dapat dilihat pada Lemma 3.5 Berikut.
Lemma 3.5. Andaikan D(2) adalah digraph dwiwarna terhubung kuat yang
ter-diri atas dua cycle C1 dan C2 dengan sedikitnya satu busur pada setiap warna. Misalkanvk adalah sebuah verteks diD(2) dan misalkan q1 dan q2 adalah bilangan bulat taknegatif sedemikian sehingga
hh
ℓ
i
=Mhq1q2i. (3.4)
Maka
hq1
q2
i
≥M−1
r(pj,k)
b(pj,k)
(3.5)
Bukti. Andaikan vk adalah verteks di D(2) dengan k = 1,2, . . . , n. Misalkan pj,k
adalah path dari verteks vj ke vk dengan j = 1,2, . . . , n. Catatan bahwa setiap
walk dapat didekomposisikan sebagai path dancycle. Jikapj,k merupakan sebuah
path terbuka, maka untuk bilangan tak negatif dari vektorx diperoleh
hh
ℓ
i
=Mx+
r(pj,k)
b(pj,k)
. (3.6)
Karena D(2) adalah digraph dwiwarna primitif, maka M adalah sebuah matriks invertibel sehingga M mempunyai invers. Dengan mempertimbangkan
hh
ℓ
i
=Mhq1q2i dan persamaan (3.6), diperoleh
hh
ℓ
i
= Mx+
r(pj,k)
b(pj,k)
Mhq1q2i = Mx+
r(pj,k)
b(pj,k)
x = hq1q2i−M−1
r(pj,k)
b(pj,k)
.
Karena vektor x ≥ 0 kita simpulkan x = hq1q2i−M−1
r(pj,k)
b(pj,k)
≥ 0. Sehingga
hq1
q2
i
≥M−1
r(pj,k)
b(pj,k)
untuk beberapa pathpj,k dari vj kevk.
Dari sistem (3.5) untuk setiap j = 1,2, . . . , n diperoleh
hq1
q2
i
≥ M−1
r(pjk)
b(pjk)
=
b(C2) −r(C2)
−b(C1) r(C1) br((ppjkjk))
=
b(C2)r(pjk)−r(C2)b(pjk)
r(C1)b(pjk)−b(C1)r(pjk)
(3.7)
untuk beberapa path pjk dari verteksvj ke verteks vk.
Selanjutnya dengan menggunakan sistem (3.4) dan (3.7) diperoleh
hh
ℓ
i
=Mhq1q2i ≥ M
b(C2)r(pjk)−r(C2)b(pjk)
r(C1)b(pjk)−b(C1)r(pjk)
=
r(C1)(b(C2)r(pjk)−r(C2)b(pjk))
b(C1)(b(C2)r(pjk)−r(C2)b(pjk))
+
r(C2)(r(C1)b(pjk)−b(C1)r(pjk))
b(C2)(r(C1)b(pjk)−b(C1)r(pjk))
Dengan menggunakan nilaih danℓ diperolehlah batas bawah dari eksponen lokal masuk yaitu
expin(vk, D(2)) = h+ℓ
≥ (r(C1) +b(C1))(b(C2)r(pjk)−r(C2)b(pjk))
+(r(C2) +b(C2))(r(C1)b(pjk)−b(C1)r(pjk))
= ℓ(C1)(b(C2)r(pjk)−r(C2)b(pjk)) +
ℓ(C2)(r(C1)b(pjk)−b(C1)r(pjk)). (3.8)
3.7..2 Batas atas eksponen lokal masuk
Batas atas dari eksponen lokal masuk digraph dwiwarna yang terdiri atas dua
cycle C1 dan C2 dapat dilihat pada Lemma 3.6 Berikut.
Lemma 3.6. Andaikan D(2) adalah sebuah digraph dwiwarna primitif atas n
verteksv1, v2, v3, . . . , vn. Misalkanv adalah sebuah verteks diD(2) dengan eksponen
lokal masukexpin(vk, D(2))≤expin(v, D(2))+d(v, vk)dimanad(v, vk)adalah jarak dari verteks v ke vk.
Bukti. Andaikan eksponen lokal masuk di verteks v dihasilkan dari sebuah jalan (s, t). Lalu untuk setiap verteksj = 1,2, . . . , nterd