BAB II LANDASAN TEORI A. Sistem Bilangan Real - BAB II DWI LIYANTI MTK'13

BAB II

LANDASAN TEORI

A. Sistem Bilangan Real

Sistem bilangan real 𝑅 adalah himpunan bilangan real yang disertai dengan operasi penjumlahan dan perkalian sehingga memenuhi aksioma tertentu. Pada sistemnya diperlakukan tiga aksioma, yang dikenal sebagai aksioma lapangan, urutan dan kelengkapan.

1. Aksioma Lapangan

Aksioma ini mengatur tentang ketertutupan terhadap operasi penjumlahan dan perkalian, sifat komutatif, assosiatif dan distributif, terdapatnya unsur 0 dan 1, serta terdapatnya unsur invers terhadap penjumlahan dan perkalian. Dari operasi dasar ini didefinisikan operasi pengurangan dan pembagian.

Pada 𝑅 didefinisikan operasi penjumlahan dan perkalian (jumlah dan hasil kali bilangan real a dan b ditulis a + b dan ab) yang memenuhi sifat – sifat berikut :

a. Sifat tertutup terhadap penjumlahan dan perkalian yaitu jika ∀𝑎,𝑏 ∈ 𝑅 maka 𝑎+𝑏 ∈ 𝑅 dan𝑎𝑏 ∈ 𝑅.

b. Sifat komutatif terhadap penjumlahan dan perkalian yaitu jika

c. Sifat assosiatif terhadap penjumlahan dan perkalian yaitu jika

∀𝑎,𝑏,𝑐 ∈ 𝑅 maka 𝑎+𝑏 +𝑐 =𝑎+ (𝑏+𝑐) dan 𝑎𝑏 𝑐=𝑎(𝑏𝑐). d. Adanya unsur kesatuan terhadap penjumlahan dan perkalian yaitu jika

terdapat 0 dan 1 ∈ 𝑅 dan 0≠ 1 sehingga 𝑎+ 0 =𝑎 dan 𝑎. 1 =𝑎 untuk setiap 𝑎 ∈ 𝑅. Bilangan 0 dinamakan unsur kesatuan terhadap penjumlahan dan 1 unsur kesatuan terhadap perkalian.

e. Adanya unsur negatif atau invers terhadap penjumlahan yaitu jika

∀𝑎 ∈ 𝑅 maka terdapat −𝑎 ∈ 𝑅 sehingga +(– 𝑎) = 0 . Bilangan real –

a dinamakan negatif atau lawan dari a.

f. Adanya unsur lawan atau invers terhadap perkalian, jika ∀𝑎 ∈ 𝑅 ,

𝑎 ≠0 maka terdapat 𝑎−1 ∈ 𝑅 sehingga 𝑎𝑎−1 = 1 . Bilangan real

𝑎−1 _{dinamakan kebalikan dari 𝑎.}

g. Sifat distributif, yaitu jika ∀𝑎,𝑏,𝑐 ∈ 𝑅 maka 𝑎 𝑏+𝑐 =𝑎𝑏+𝑏𝑐. (Martono, 1999) Operasi pengurangan dan pembagian pada himpunan bilangan real didefinisikan sebagai berikut

Definisi II.A.1

Diberikan 𝑎 dan 𝑏 bilangan real

a. Pengurangan dari 𝑎 dan 𝑏, hasilnya disebut selisih dari a dan b ditulis

𝑎 − 𝑏, didefinisikan sebagai bilangan real 𝑎+ (−𝑎)

b. Pembagian dari a dan b, hasilnya disebut hasil bagi dari a dan b,

𝑏 ≠0 ditulis 𝑎

2. Aksioma Urutan

Aksioma ini mengatur tentang pemunculan bilangan positif dan negatif. Berdasarkan ini, setiap bilangan real dapat diurutkan dari kecil sampai besar. Dari aksioma ini diturunkan berbagai sifat yang mendasari penyelesaian suatu pertidaksamaan, kemudian dirancang konsep nilai mutlak sebagai ukuran jarak dua bilangan real dan merupakan suatu alat untuk menyelesaikan pertidaksamaan yang berkaitan dengan limit.

(Martono, 1999) Pada 𝑅 terdapat suatu himpunan bagian yang unsurnya dinamakan bilangan positif yang memenuhi aksioma berikut:

a. Jika 𝑎 ∈ 𝑅 maka 𝑎 = 0 atau a bilangan positif jika 𝑎 > 0 atau –a positif bila 𝑎 < 0

b. Jumlah dan hasil kali dua bilangan positif adalah bilangan positif. Definisi II.A.2

Diberikan a dan b bilangan real

a. Bilangan a dikatakan lebih besar dari b, ditulis 𝑎>𝑏, jika𝑎 − 𝑏 bilangan positif.

b. Bilangan a dikatakan lebih kecil dari b, ditulis 𝑎< 𝑏, jika 𝑏 − 𝑎 bilangan positif.

c. Lambang ≤(lebih kecil atau sama dengan ) dan ≥(lebih besar atau sama dengan) menyatakan relasi 𝑎 ≤ 𝑏 jika 𝑎< 𝑏 atau 𝑎 =𝑏 dan

d. Pernyataan yang dihubungkan dengan tanda <, >,≤,≥ dinamakan pertidaksamaan.

e. Bilangan real a dikatakan negatif jika –a adalah bilangan positif 3. Aksioma Kelengkapan

Aksioma kelengkapan pada Sistem bilangan Real menyatakan bahwa setiap himpunan bagian tak kosong dari 𝑅 yang terbatas ke atas selalu mempunyai batas atas terkecil. Aksioma ini mengakibatkan bahwa setiap himpunan bagian tak kosong dari 𝑅 yang terbatas ke bawah selalu mempunyai batas bawah terbesar.

(Martono, 1999)

Pada aksioma ini meliputi batas atas, batas bawah, batas atas terkecil dan batas bawah terbesar.

a. Batas Atas dan Batas Bawah himpunan terurut

Sebelum mempelajari batas atas dan batas bawah himpunan terurut, maka terlebih dahulu akan didefinisikan suatu himpunan terurut sebagai berikut.

Definisi II.A.3.a.1).

Diberikan himpunan . Suatu urutan pada himpunan 𝑆 adalah suatu relasi dua sifat berikut :

1) ∀𝑥 ,𝑦 ∈ 𝑆 maka tepat satu pernyataan berikut benar : 𝑥>𝑦 atau

𝑥= 𝑦 atau 𝑥< 𝑦

Contoh II.A.3.a.1).:

𝑅 = himpunan semua bilangan real merupakan himpunan terurut. Di bawah ini didefinisikan pengertian konsep batas suatu himpunan terurut.

Definisi II.A.3.a.2).

Diberikan 𝑆 himpunan terurut, 𝑆 ≠ ∅ dan 𝐸 ⊂ 𝑆

1) Himpunan 𝐸 dikatakan terbatas ke atas jika terdapat 𝑝 ∈ 𝑆 sehingga𝑥 ≤ 𝑝 untuk ∀𝑥 ∈ 𝐸, 𝑝 dinamakan batas atas himpunan

𝐸.

2) Himpunan 𝐸 dikatakan terbatas ke bawah jika terdapat 𝑞 ∈ 𝑆 sehingga 𝑥 ≥ 𝑞 untuk∀𝑥 ∈ 𝐸, 𝑞 dinamakan batas bawah himpunan 𝐸.

3) Himpunan 𝐸 dikatakan terbatas jika 𝐸 terbatas ke atas dan terbatas ke bawah.

(Soemantri,1988 )

Contoh II.A.3.a.2).:

Diberikan himpunan 𝐸 ⊂ 𝑅 dengan 𝐸 = {−1, 0 , 1 , 2 , 3 }. Selidiki apakah 𝐸 terbatas !

Jawab :

𝐸 terbatas ke atas karena ∃𝑝= 3 ∈ 𝑅 → ∀𝑥 ∈ 𝐸 ,𝑥 ≤3 dan 𝐸 terbatas ke bawah karena ∃𝑞 =−1∈ 𝑅 → ∀𝑥 ∈ 𝐸 ,𝑥 ≥ −1. Karena

b. Batas atas terkecil dan batas bawah terbesar himpunan terurut

Suatu himpunan terurut yang terbatas ke atas memiliki batas atas terkecil dan himpunan terurut yang terbatas ke bawah memiliki suatu batas bawah terbesar. Adapun pengertian dari batas atas terkecil dan batas bawah terbesar sebagai berikut.

Definisi II.A.3.b.1).

Diberikan 𝑆 suatu himpunan terurut dengan 𝑆 ≠0 ,𝐸 ⊂ 𝑆 dan 𝐸 terbatas ke atas. Jika ∃𝑏 ∈ 𝑆 yang memenuhi sifat berikut :

1) 𝑏 adalah suatu batas atas 𝐸 2) Jika 𝑟 ≥ 𝑏 maka 𝑟 batas atas 𝐸

maka 𝑏 dikatakan batas atas terkecil (Supremum) dari 𝐸 ditulis

𝑏= sup𝑆

Definisi II.A.3.b.2).

Diberikan 𝑆 suatu himpunan terurut dengan 𝑆 ≠0 ,𝐸 ⊂ 𝑆 dan 𝐸 terbatas ke bawah. Jika ∃𝑎 ∈ 𝑆 yang memenuhi sifat berikut :

1) 𝑎 adalah suatu batas bawah 𝐸 2) Jika 𝑟 ≤ 𝑎 maka 𝑟 batas bawah 𝐸

maka 𝑎 dikatakan batas bawah terbesar (infimum) dari 𝐸 ditulis

𝑎 = inf𝑆

Contoh II.A.3.b.1).:

{𝑞 ∈ 𝑅dan𝑝 ≤ −1} , sehingga −1 merupakan batas bawah terbesar atau Inf 𝐸 =−1.

c. Sifat batas atas terkecil dan batas bawah terbesar himpunan

terurut

Adapun pengertian himpunan terurut dengan sifat batas atas terkecil dan sifat batas bawah terbesar didefinisikan sebagai berikut. Definisi II.A.3.c.1).

Himpunan terurut 𝑆 dikatakan mempunyai sifat batas atas terkecil (s.b.a.t) jika setiap himpunan 𝐸 ⊂ 𝑆 yang tidak kosong dan terbatas ke atas mempunyai Supremum.

Definisi II.A.3.c.1).

Himpunan terurut 𝑆 dikatakan mempunyai sifat batas bawah terbesar (s.b.b.t) jika setiap himpunan 𝐸 ⊂ 𝑆 yang tidak kosong dan terbatas ke bawah mempunyai Infimum.

(Soemantri,1988 )

Contoh II.A.3. :

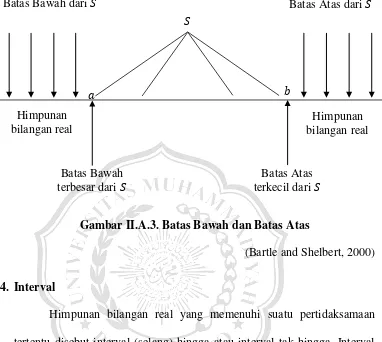
Ilustrasi gambar himpunan tersebut adalah sebagai berikut.

Gambar II.A.3. Batas Bawah dan Batas Atas

(Bartle and Shelbert, 2000) 4. Interval

Himpunan bilangan real yang memenuhi suatu pertidaksamaan tertentu disebut interval (selang) hingga atau interval tak hingga. Interval hingga adalah himpunan bagian dari 𝑅 yang terbatas ke atas dan ke bawah, sedangkan interval tak hingga tidak terbatas ke atas atau ke bawah.

Jika terdapat dua bilangan real 𝑎 dan 𝑏, dengan 𝑎 <𝑏, maka berturut– turut dapat ditulis sebagai berikut :

1. 𝑎,𝑏 = {𝑥 ∈ 𝑅 𝑎< 𝑥<𝑏}

2. [𝑎,𝑏] = {𝑥 ∈ 𝑅 𝑎 ≤ 𝑥 ≤ 𝑏}

3. (𝑎,𝑏] = {𝑥 ∈ 𝑅 𝑎< 𝑥 ≤ 𝑏}

4. [𝑎,𝑏) = {𝑥 ∈ 𝑅 𝑎 ≤ 𝑥 <𝑏}

5. 𝑎,∞ = {𝑥 ∈ 𝑅 𝑥> 𝑎}

Batas Bawah dari 𝑆 Batas Atas dari 𝑆

Himpunan bilangan real

Himpunan bilangan real

Batas Bawah terbesar dari 𝑆

Batas Atas terkecil dari 𝑆

𝑏 𝑎

6. [𝑎,∞) = {𝑥 ∈ 𝑅 𝑥 ≥ 𝑎} 7. −∞,𝑏 = {𝑥 ∈ 𝑅 𝑥< 𝑏}

8. (−∞,𝑏] = {𝑥 ∈ 𝑅 𝑥 ≤ 𝑏}

9. −∞,∞ =𝑅

(Martono, 1999) Interval 𝑎,𝑏 dinamakan interval terbuka karena tidak memuat kedua titik ujung. Sedangkan Interval [𝑎,𝑏] dinamakan interval tertutup karena memuat kedua titik ujung.

(Lipschutz, 1989)

Interval setengah terbuka atau setengah tertutup berbentuk [𝑎,𝑏) atau 𝑎,𝑏 ditentukan oleh 𝑎 dan 𝑏, interval [𝑎,𝑏) memuat titik ujung di 𝑎 sedangkan interval 𝑎,𝑏 memuat titik ujung di 𝑏.

(Bartle and Shelbert, 2000)

B. Sistem bilangan real yang diperluas

Sistem bilangan real diperluas terdiri dari sistem bilangan real dan dua lambang +∞ dan −∞. Urutan dalam 𝑅 tetap dipertahankan seperti sebelum diperluas dan didefinisikan −∞< 𝑥< +∞ untuk ∀𝑥 ∈ 𝑅. Sistem bilangan real diperluas diberi lambang 𝑅∗ 𝑅∗= 𝑅 ∪ −∞, +∞ .

supremum di dalam 𝑅∗yaitu +∞. Demikian juga himpunan bilangan real yang tidak kosong dan tidak terbatas ke bawah mempunyai infimum dalam

𝑅∗ _{yaitu −∞ .}

(Soemantri, 1988)

C. Topologi Dalam Ruang Metrik

Sebelum dibahas mengenai topologi dalam ruang metrik yang meliputi himpunan terbuka dan himpunan tertutup, terlebih dahulu diberikan definisi ruang metrik.

1. Ruang Metrik

Definisi II.C.1.

Diberikan himpunan 𝑋 yang tidak kosong, yang elemen – elemennya disebut titik. Didefinisikan fungsi bernilai real nonnegatif 𝑑 pada 𝑋×𝑋 (𝑑 fungsi dua variabel dengan variabel-variabel pada 𝑋) sebagai berikut. Untuk ∀𝑥,𝑦,𝑧 ∈ 𝑋 :

1) 𝑑 𝑥,𝑦 ≥0

2) 𝑑 𝑥,𝑦 = 0, jika hanya jika 𝑥=𝑦 3) 𝑑 𝑥,𝑦 =𝑑(𝑦,𝑥)

4) 𝑑 𝑥,𝑦 ≤ 𝑑 𝑥,𝑧 +𝑑(𝑧,𝑦)

Fungsi 𝑑 yang memenuhi keempat fungsi di atas disebut fungsi jarak atau metrik pada 𝑋. Nilai 𝑑(𝑥,𝑦) dinamakan jarak dari 𝑥 ke 𝑦. (𝑋,𝑑) disebut ruang metrik karena dilengkapi 𝑋 dengan fungsi 𝑑.

Contoh II.C.1. :

Jawab :

Ambil sebarang ,𝑦,𝑧 ∈ 𝑅 , maka : 1) 𝑑 𝑥,𝑦 = 𝑥 − 𝑦 > 0 untuk 𝑥 ≠ 𝑦

2) (⇨)𝑑 𝑥,𝑦 = 𝑥 − 𝑦 = 0⇨ 𝑥 − 𝑦= 0 ⇨ 𝑥= 𝑦

⇦ 𝑥=𝑦 ⇨ 𝑥 − 𝑦= 0⇨ 𝑥 − 𝑦 = 0 = 0 ⇨ 𝑑 𝑥,𝑦 = 0

3) 𝑑 𝑥,𝑦 = 𝑥 − 𝑦 = −(− 𝑥 − 𝑦 )

= −1(−𝑥+𝑦)

= −1 𝑦 − 𝑥

= −1 (𝑦 − 𝑥) = 1 𝑦 − 𝑥 = 𝑦 − 𝑥 =𝑑 𝑦,𝑥

4) 𝑑 𝑥,𝑦 = 𝑥 − 𝑦 = 𝑥 − 𝑧+𝑧 − 𝑦 = 𝑥 − 𝑧 + (𝑧 − 𝑦)

≤ 𝑥 − 𝑧 + 𝑧 − 𝑦 = 𝑑 𝑥,𝑧 +𝑑(𝑧,𝑦)

Jadi (𝑅,𝑑) merupakan ruang metrik

2. Persekitaran, Titik Limit dan Titik Interior

Apabila 𝑋,𝑑 ruang metrik, himpunan 𝐸 ⊂ 𝑋 dan titik 𝑝 ∈ 𝑋, maka bagian berikut ini dibahas mengenai persekitaran, titik limit dan titik interior. Adapun pengertian dari persekitaran, titik limit dan titik interior berturut – turut sebagai berikut.

Definisi II.C.2.a.

Definisi II.C.2.b.

Persekitaran 𝑝 memuat titik 𝑞 ∈ 𝐸 dan 𝑞 ≠ 𝑝. Dari definisi titik limit dapat disimpulkan bahwa

1) 𝑝 adalah titik limit himpunan 𝐸 jika dan hanya jika : (∀𝑟> 0,𝑁_𝑟(𝑝)∩ 𝐸 −{𝑝}≠ ∅

2) 𝑞 bukan titik limit himpunan 𝐸 jika dan hanya jika :

(∃𝑟> 0,𝑁_𝑟 𝑞 ∩ 𝐸 − 𝑞 =∅.

Himpunan semua titik limit 𝐸 dinotasikan 𝐸′. Contoh II.C.2.b.:

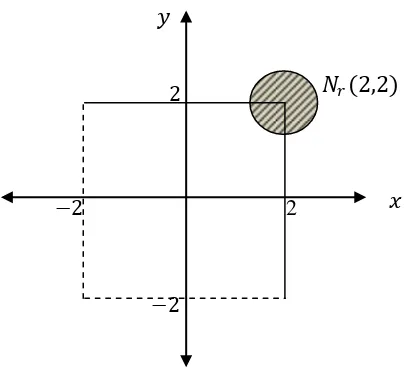
Diberikan himpunan 𝐸 = { 𝑥,𝑦 −2 <𝑥 ≤2 dan −2 < 𝑦 ≤2}

dengan 𝐸 ∈ 𝑅2 dilengkapi metrik usual

𝑑 𝑥,𝑦 = (𝑥₁− 𝑦₁)2_{+ (}𝑥

2− 𝑦2)2. Apakah titik 𝐾(2,2) dan

𝐿 −5₂,9

4 merupakan titik limit 𝐸? Jawab :

𝐾 2,2 merupakan titik limit 𝐸, karena (∀𝑟> 0,𝑁_𝑟(2,2)∩ 𝐸 −{2,2}≠ ∅

Gambar II.C.2.b.1). Persekitaran titik (𝟐,𝟐) dengan radius r

𝑥 𝑦

−2 −2

2

2

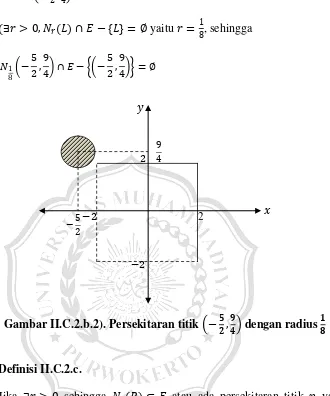
Titik 𝐿 −5

Gambar II.C.2.b.2). Persekitaran titik −𝟓

Untuk 𝑟> 3→ 𝑁_𝑟 2 = (2− 𝑟, 2 +𝑟) ⊄ 𝐴

∀𝑟> 0,𝑁_𝑟 2 ⊄ 𝐴 jadi 2 bukan titik interior himpunan 𝐴.

3. Himpunan Terbuka dan Himpunan Tertutup

Setelah mempelajari definisi dari titik interior dan titik limit diberikan definisi dari himpunan terbuka dan himpunan tertutup sebagai berikut.

Definisi II.C.3.a.

Dinamakan himpunan terbuka jika setiap anggota 𝐸 merupakan titik Interior himpunan 𝐸. Jadi, 𝐸 terbuka jika 𝐸𝑜 =𝐸.

Contoh II.C.3.a.

Jika pada 𝑅 didefinisikan metrik diskrit 𝑑 𝑥,𝑦 = 1 ,𝑥 ≠ 𝑦

0 ,𝑥=𝑦 dan

himpunan 𝐸 ⊆ 𝑅, dengan 𝐸 = {𝑥 ∈ 𝑅 0≤ 𝑥 ≤1}. Buktikan bahwa himpunan 𝐸 terbuka !

Jawab :

Ambil 𝑟=1 2

Untuk 𝑥 ∈ 𝐸,𝑁1 2 𝑥

= 𝑥 ⊂ 𝐸

Untuk 𝑥 ∉ 𝐸,𝑁1 2 𝑥

= 𝑥 ⊄ 𝐸

Jadi ∀𝑥 ∈ 𝐸, ∃𝑟=1

Definisi II.C.3.b.

Dinamakan himpunan tertutup jika himpunan 𝐸 memuat semua titik limitnya.

(Soemantri,1988) Contoh II.C.3.b.:

Jika pada 𝑅 didefinisikan metrik diskrit 𝑑 𝑥,𝑦 = 1 ,𝑥 ≠ 𝑦 0 ,𝑥= 𝑦 dan himpunan 𝐹 ⊆ 𝑅, dengan 𝐹 = {1, 3, 4}. Selidiki apakah himpunan 𝐹 tertutup!

Jawab : Ambil 𝑟= 1

𝑁1 1 ∩ 𝐹 −{1} = 1 ∩ 1, 3, 4 − 1 = 1 − 1 = ∅

𝑁1 3 ∩ 𝐹 −{3} = 3 ∩ 1, 3, 4 − 3 = 3 − 3 = ∅

𝑁1(4)∩ 𝐹 −{4} = 4 ∩ 1, 3, 4 − 4 = 4 − 4 = ∅

Jadi ∀𝑥 ∈ 𝐹,∃𝑟 = 1→ 𝑁1 𝑥 ∩ 𝐹 −{𝑥} =∅

Untuk∀𝑥 ∉ 𝐹, ambil 𝑟= 1→ 𝑁₁ 𝑥 ∩ 𝐹 − 𝑥 = 𝑥 ∩ 𝐹 − 𝑥 =∅ − 𝑥 =∅

Jadi 𝐹′ =∅

Karena ∅ merupakan himpunan bagian dari sembarang himpunan berakibat 𝐹′ ⊂ 𝐹. Terbukti bahwa himpunan 𝐹 tertutup.

Teorema II.C.3.c.

Untuk sebarang ruang metrik, himpunan 𝐸 terbuka jika dan hanya jika

Untuk sebarang ruang metrik, himpunan 𝐸 tertutup jika dan hanya jika

𝐸𝑐 _terbuka.

Teorema II.C.3.d.

Jawab :

𝒢= { 0,2 , 1,3 , 1,5 , 2,6 , 2,8 }

𝐺1∪ 𝐺2∪ 𝐺3∪ 𝐺4∪ 𝐺5 = (0,8)

Karena𝐴 ⊂ 𝐺_𝑖 5

𝑖∈1

sehingga𝒢liput terbuka 𝐴

Contoh II.C.3.c.2.

Jika 𝐴 ⊂ 𝑅 dilengkapi metrik baku 𝐴= 1, 2, 3, 4, 5, 6 apakah 𝒢 liput terbuka 𝐴 jika = 0,3 , 1,5 , 2,7 ?

Jawab :

𝒢= 0,3 , 1,5 , 2,7

𝐺1 = 0,3 → terbuka

𝐺2 = [1,5) → tidak terbuka

𝐺2 = 2,7 → tidak terbuka

Karena ada anggota 𝒢 yang tidak terbuka maka 𝒢 bukan merupakan liput terbuka.

4. Ukuran Himpunan

Sebelum mempelajari definisi ukuran dari suatu himpunan, terlebih dahulu diberikan definisi ukuran dari suatu interval.

Definisi II.C.4.a.

Ukuran interval terbuka (𝑎,𝑏) dinyatakan dengan 𝜇 𝑎,𝑏 dan didefinisikan sebagai berikut 𝜇 𝑎,𝑏 =𝑏 − 𝑎.

Ukuran interval terbuka (𝑎,∞) atau (−∞,𝑏) atau (−∞,∞) didefinisikan sebagai berikut 𝜇 𝑎,∞ =𝜇 −∞,𝑏 =𝜇 −∞,∞ = ∞.

Definisi II.C.4.b.

𝜇 ∅ = 0, 𝐸= himpunan terbuka tak terbatas sehingga 𝜇(𝐸) =∞. Definisi II.C.4.c.

Panjang suatu interval I dengan lambangℓ 𝐼 , didefinisikan sebagai selisih antara titik ujung – ujungnya. Ukuran dari suatu himpunan E diberi notasi 𝜇(E).

1) Jika I suatu interval maka 𝜇(𝐼) adalahℓ 𝐼 , dengan ℓ 𝐼 ≥ 0 untuk semua interval I.

2) Jika himpunan 𝐸₁ ⊆ 𝐸₂ maka 𝜇(𝐸1) ≤ 𝜇(𝐸2).

3) Diberikan 𝐸 ⊆ 𝑅 dan diambil 𝑥₀ sebarang, 𝑥₀ ∈ 𝑅, didefinisikan

𝐸+𝑥₀ = {𝑥+ 𝑥₀ 𝑥 ∈ 𝐸} maka 𝜇(𝐸+𝑥₀) adalah𝜇 𝐸 .

(Gordon, 1994) Definisi II.C.4.d.

ℓ 𝐼 = ℓ 𝐼_𝑖 ∞

𝑖=1

Terdapat dua ukuran di dalam suatu himpunan yaitu ukuran luar dan ukuran dalam. Definisi dari kedua ukuran tersebut sebagai berikut.

1) Ukuran Luar

Definisi II.C.4.1).

Diberikan himpunan 𝐸 ⊆ 𝑅. Ukuran luar 𝐸 diberi notasi 𝜇∗(𝐸) yang didefinisikan sebagai berikut:𝜇∗ 𝐸 = Inf {𝜇 𝑂 :𝐸 ⊆ 𝑂 dan 𝑂 himpunan terbuka}

2) Ukuran Dalam

Definisi II.C.4.2).

Diberikan himpunan 𝐸 ⊆ 𝑅. Ukuran dalam 𝐸 diberikan notasi

𝜇∗(𝐸) didefinisikan sebagai berikut: 𝜇∗ 𝐸 = Sup{ 𝜇 𝐾 :𝐸 ⊆ 𝐾

dan 𝐾 himpunan tertutup}

Dari definisi diatas jelas bahwa 𝜇_∗ 𝐸 ≤ 𝜇∗ 𝐸 untuk himpunan 𝐸 dan jika 𝐴 ⊆ 𝐵 maka 𝜇_∗ 𝐴 ≤ 𝜇∗ 𝐵 .

5. Himpunan terukur

Di bawah ini akan diberikan definisi dari himpunan yang terukur. Definisi II.C.5.

Suatu himpunan 𝐸 ⊆ 𝑅 dikatakan terukur jika ukuran luar sama dengan ukuran dalam atau 𝜇∗ 𝐸 =𝜇_∗ 𝐸 .

D. Fungsi

Diberikan himpunan 𝐴,𝐵 ⊆ 𝑅, fungsi 𝑓:𝐴 → 𝐵 adalah suatu aturan yang mengaitkan setiap unsur 𝑥 ∈ 𝐴 dengan tepat satu unsur 𝑦 ∈ 𝐵. Unsur 𝑦 yang berkaitan dengan unsur 𝑥 ini diberi lambang 𝑦= 𝑓(𝑥), yang dinamakan aturan fungsi. Lambang 𝑦= 𝑓 𝑥 ,𝑥 ∈ 𝐴 menyatakan sebuah fungsi dengan aturan 𝑦 =𝑓 𝑥 yang terdefinisi pada himpunan 𝐴. Selanjutnya 𝑥 dinamakan peubah bebas, dan 𝑦 yang nilainya bergantung dari 𝑥 dinamakan peubah tak bebas.

Apabila terdapat suatu fungsi 𝑦 =𝑓 𝑥 ,𝑥 ∈ 𝐴, maka daerah asal fungsi 𝑓 adalah himpunan 𝐴, ditulis 𝐷_𝑓 =𝐴dan daerah nilai fungsi 𝑓 adalah himpunan 𝑅_𝑓 = {𝑓(𝑥) 𝑥 ∈ 𝐴 =𝐷_𝑓}. Unsur 𝑓 𝑥 ∈ 𝐵dinamakan nilai fungsi

𝑓 di 𝑥. Jika yang diketahui hanya 𝑦= 𝑓 𝑥 maka daerah asal dan daerah nilai fungsi 𝑓 adalah 𝐷_𝑓 = {𝑥 ∈ 𝑅 𝑓(𝑥) ∈ 𝑅}dan 𝑅_𝑓 = {𝑥 ∈ 𝑅 𝑥 ∈ 𝐷_𝑓} dengan 𝐷_𝑓 merupakan daerah asal alamiah (Natural Domain) dari fungsi 𝑓 dan 𝑅_𝑓 merupakan daerah nilai dari fungsi 𝑓. Daerah asal dan daerah nilai fungsi di atas merupakan himpunan bagian dari 𝑅. Fungsi tersebut dinamakan fungsi dengan peubah real dan bernilai real, disingkat fungsi real.

Gambar II.D.1. Fungsi 𝒇 𝒙

𝐷𝑓 𝑅𝑓

𝑓

𝑥

𝑓(𝑥)

𝑓

𝑓

𝑥 _𝑓(𝑥)

𝑅

𝐷𝑓 𝑅𝑓

1. Fungsi Terbatas

Di bawah ini akan diberikan definisi dari fungsi yang terbatas sebagai berikut.

Definisi II.D.1.

Fungsi 𝑓 dikatakan terbatas jika ∃𝑀 > 0 ,∀𝑥 ∈ 𝐷_𝑓 dengan

𝑓(𝑥) ≤ 𝑀.

Dari ingkaran definisi tersebut dapat di simpulkan bahwa Fungsi

𝑓 dikatakan tidak terbatas jika ∀𝑀 > 0 ,∃𝑥_𝑜 ∈ 𝐷_𝑓 dengan

𝑓(𝑥) >𝑀.

(Martono,1999 )

Contoh II.D.1 :

a. Fungsi 𝑓 𝑥 = cos 𝑥 terbatas karena 𝑓(𝑥) = cos𝑥 ≤1 untuk

∀𝑥 ∈ 𝐷𝑓 dan 𝐷𝑓 ⊆ 𝑅.

b. Fungsi 𝑓 𝑥 = 𝑥+ 1 tidak terbatas pada interval 0,∞ karena untuk 𝑀 > 0, terdapat

𝑥

₀

=

2𝑀

> 0

sehingga

𝑓 𝑥0 = 𝑓 2𝑀 = 2𝑀+ 1 >𝑀.

2. Limit fungsi

Limit suatu fungsi merupakan konsep dasar diferensial dan integral. Pada bagian ini dibahas mengenai pengertian limit fungsi. Definisi II.D.2.a.

lim

dan lim

𝑥→4𝑓(𝑥)= 4

3. Fungsi kontinu

a. Fungsi kontinu di suatu titik

Suatu fungsi terdefinisi pada selang terbuka yang memuat suatu titik dengan daerah asal fungsi himpunan sebarang yang memuat suatu titik dimana limit fungsi tidak diketahui, maka kekontinuan fungsinya didefinisikan sebagai berikut.

Definisi II.D.3.a.

Fungsi 𝑓 dikatakan kontinu di 𝑐 ∈ 𝐷_𝑓 jika

∀𝜀> 0 ∃𝛿 > 0∍ 𝑥 − 𝑐 < 𝛿 ⇨ 𝑓 𝑥 − 𝑓(𝑐) < 𝜀

(Martono,1999 ) Contoh II.D.3.a. :

Selidiki apakah 𝑓 𝑥 = 2𝑥+ 5 kontinu di 𝑥= 3 Jawab :

Ambil sebarang 𝜀> 0 diselidiki apakah ∀𝜀> 0 ∃𝛿 > 0 sedemikian sehingga 𝑥 −3 < 𝛿 berlaku 𝑓 𝑥 − 𝑓(𝑐) <𝜀.

𝑓 𝑥 − 𝑓 𝑐 = 2𝑥+ 5− 2.3 + 5 = 2𝑥 −6 = 2 𝑥 −3 < 𝜀

Untuk 𝑥 −3 < 𝛿 ⇨2 𝑥 −3 < 2𝛿 sehingga

𝑓 𝑥 − 𝑓(𝑐) =2 𝑥 −3 < 2𝛿 untuk ∀𝜀 > 0 agar

𝑓 𝑥 − 𝑓(𝑐) < 𝜀 , maka dapat dipilih 𝜀= 2𝛿 atau

𝛿

=

ε

2

Jadi untuk ∀𝜀> 0 ∃ε

2> 0 sehingga untuk 𝑥 −3 <𝛿 berlaku

Suatu fungsi terdefinisi pada selang terbuka yang memuat suatu titik, kekontinuan fungsinya di titik itu dapat didefinisikan dengan limit fungsi. Berdasarkan Definisi II.D.3.a. dapat dikatakan bahwa fungsi 𝑓 𝑥 kontinu di 𝑥= 𝑐 jika :

1. 𝑓 𝑥 harus ada, yaitu didefinisikan di 𝑥= 𝑐 2. lim

𝑥→𝑐𝑓 𝑥 ada 3. lim

𝑥→𝑐𝑓 𝑥 =𝑓 𝑐

b. Kontinu Kiri dan Kanan

Sejalan dengan konsep limit kiri dan limit kanan, maka didefinisikan fungsi kontinu kiri dan kontinu kanan di satu titik sebagai berikut.

Definisi II.D.3.b.

Diberikan fungsi 𝑓 terdefinisi pada interval 𝑎,𝑐 . Fungsi 𝑓

dikatakan kontinu kiri di 𝑐 jika lim

𝑥→𝑐−𝑓 𝑥 =𝑓(𝑐).

Diberikan fungsi 𝑓 terdefinisi pada interval [𝑐,𝑏). Fungsi 𝑓

dikatakan kontinu kanan di 𝑐 jika lim

𝑥→𝑐+𝑓 𝑥 =𝑓(𝑐).

c. Fungsi kontinu pada suatu interval

Kekontinuan suatu fungsi dapat didefinisikan pada interval terbuka dan interval tertutup. Terdapat sembilan interval yang mungkin, yaitu 𝑎,𝑏 , 𝑎,𝑏 , 𝑎,𝑏 , 𝑎,𝑏 , 𝑎,∞ , 𝑎,∞ , −∞,𝑏 ,

Definisi II.D.3.c.1).

Fungsi 𝑓 dikatakan kontinu pada interval terbuka 𝑎,𝑏 jika fungsi 𝑓 kontinu di setiap titik (𝑎,𝑏).

Definisi II.E.3.c.2).

Fungsi 𝑓 dikatakan kontinu pada interval tertutup [𝑎,𝑏] jika fungsi 𝑓 kontinu pada interval terbuka (𝑎,𝑏), kontinu kanan di 𝑎 dan kontinu kiri di 𝑏.

(Martono,1999 ) Contoh II.D.3.c.

Selidiki apakah fungsi 𝑓 𝑥 =1_𝑥 kontinu pada [1,∞)? Jawab :

Akan dibuktikan bahwa 𝑓 kontinu pada interval (1,∞), dan kontinu kanan di 1. Berdasarkan Definisi II.D.3.b. dan Definisi

II.D.3.c. diperoleh: lim

𝑥→1+𝑓 𝑥 = lim_𝑥→1

1

𝑥=

1

1= 1 =𝑓 1 = 𝑓(𝑥)

Jadi, 𝑓 kontinu pada 𝐷_𝑓 = 1,∞ . 4. Differensial atau Turunan

Di bawah ini akan diberikan definisi dari Differensial atau Turunan sebagai berikut.

Definisi II.D.4.

= lim

𝑥→12𝑥+ 5 = 2.1 + 5 = 7

Karena 𝑓₋′ 1 =𝑓₊′(1) maka 𝑓 mempunyai turunan di 𝑥= 1 dengan

𝑓′_{(1) = 7}

5. Fungsi Naik dan Fungsi Turun

Pada bagian ini dibahas mengenai definisi dari fungsi naik, fungsi turun, fungsi naik monoton dan fungsi turun monoton.

Definisi II.D.5.a.

Fungsi 𝑓:𝐼 → 𝑅 dikatakan naik pada interval 𝐼 jika 𝑥₁ < 𝑥₂ maka

𝑓 𝑥1 < 𝑓 𝑥2 , ∀𝑥1,𝑥2 ∈ 𝐼

Fungsi𝑓:𝐼 → 𝑅dikatakan turun pada interval 𝐼 jika 𝑥₁ < 𝑥2 maka

𝑓 𝑥1 > 𝑓 𝑥2 ,∀𝑥1,𝑥2 ∈ 𝐼

Definisi II.D.5.b.

Fungsi 𝑓: (𝑎,𝑏) → 𝑅 dikatakan naik monoton pada (𝑎,𝑏) jika

𝑎 <𝑥1 < 𝑥2 < 𝑏 maka 𝑓 𝑥1 ≤ 𝑓 𝑥2 ,∀𝑥1,𝑥2 ∈ (𝑎,𝑏)

Fungsi 𝑓:𝐼 → 𝑅 turun monoton pada (𝑎,𝑏) jika 𝑎 <𝑥1 < 𝑥2 < 𝑏 maka

𝑓 𝑥1 ≥ 𝑓 𝑥2 ,∀𝑥1,𝑥2 ∈(𝑎,𝑏)

(Martono, 1999)

Contoh II.D.5.a.

Diberikan fungsi 𝑓 𝑥 = 2𝑥+ 3.

Selidiki apakah 𝑓 𝑥 fungsi naik atau fungsi turun! Jawab :

Ambil 𝑥₁ <𝑥2

⇒2𝑥1+ 3 < 2𝑥2+ 3

⇒ 𝑓(𝑥₁) <𝑓(𝑥₂)

Jadi, 𝑓(𝑥) merupakan fungsi naik Contoh II.D.5.b.

Diberikan fungsi 𝑓 𝑥 = −2𝑥+ 3.

Selidiki apakah 𝑓 𝑥 fungsi naik atau fungsi turun! Jawab :

Ambil 𝑥₁ <𝑥2

𝑥1 < 𝑥2 ⇒ −2𝑥1 > −2𝑥2

⇒ −2𝑥1+ 3 >−2𝑥2 + 3

⇒ 𝑓(𝑥1) >𝑓(𝑥2)

Jadi, 𝑓(𝑥) merupakan fungsi turun 6. Fungsi terukur

Di bawah ini akan diberikan definisi dari fungsi terukur sebagai berikut.

Definisi II.D.6.a.

Suatu𝑓:𝐸 → 𝑅 adalah terukur jika 𝐸 adalah himpunan terukur dan untuk setiap 𝑟 ∈ 𝑅, himpunan 𝑥 ∈ 𝐸 𝑓 𝑥 >𝑟 adalah terukur.

Teorema II.D.6.b.

Diberikan 𝐸 himpunan terukur dan jika 𝑓:𝐸 → 𝑅kontinu hampir dimana–mana pada 𝐸, maka 𝑓 terukur.

7. Pendekatan Derivatif (Approximate Derivative)

Di bawah ini akan diberikan definisi dari pendekatan derivatif sebagai berikut.

Definisi II.D.7.

Suatu fungsi terukur 𝑓 dikatakan mempunyai pendekatan derivatif atas

𝐹𝑎𝑝 pada 𝑥0 jika 𝐹𝑎𝑝 𝑥0 = ap- lim_𝑥→𝑥

0

sup 𝑓 𝑥 − 𝑓 𝑥0

𝑥 − 𝑥0

ada Dan juga untuk pendekatan derivatif bawah

𝐹𝑎𝑝 pada 𝑥0 jika 𝐹𝑎𝑝 𝑥0 = ap- lim_𝑥→𝑥

0

inf 𝑓 𝑥 − 𝑓 𝑥0

𝑥 − 𝑥0

ada

Definisi II.D.7.

Suatu fungsi terukur 𝑓 mempunyai suatu pendekatan derivatif di 𝑥₀ atau

𝐹′𝑎𝑝 𝑥0 jika 𝐹𝑎𝑝 𝑥0 = 𝐹𝑎𝑝 𝑥0

Adapun sifat – sifat dari pendekatan derivatif adalah sebagai berikut. a. 𝐹_𝑎𝑝(𝑓) ≤ 𝐹_𝑎𝑝(𝑓)

b. 𝐹_𝑎𝑝 −𝑓 = −𝐹_𝑎𝑝(𝑓)

c. 𝐹_𝑎𝑝 𝑓₁ +𝑓2 ≥ 𝐹𝑎𝑝(𝑓1) +𝐹𝑎𝑝(𝑓2) d. 𝐹_𝑎𝑝 𝑓₁+𝑓2 ≥ 𝐹𝑎𝑝(𝑓1) +𝐹𝑎𝑝(𝑓2)

8. Fungsi kontinu mutlak

Di dalam definisi fungsi kontinu mutlak terdapat interval yang tidak saling tumpang tindih. Adapun definisi dari interval yang tidak saling tumpang tindih sebagai berikut.

Definisi II.D.8.a.

Dua interval 𝐼 dan 𝐽 di dalam 𝑅 dikatakan tidak saling tumpang tindih jika irisan antara interior masing-masing interval kosong, 𝐼𝑜 𝐽𝑜 =∅. Jika tidak demikian 𝐼 dan 𝐽 dikatakan saling tumpang tindih.

Contoh II.D.8.a.:

Diketahui interval 𝐼= 1,2 dan 𝐽= [2,3]. Apakah interval 𝐼 dan 𝐽 merupakan interval tidak tumpang tindih?

Jawab :

Jika 𝐼= 1,2 maka 𝐼𝑜 = (1,2) dan 𝐽= [2,3] maka 𝐽𝑜 = (2,3). Sehingga menurut Definisi II.D.8.a. maka 𝐼𝑜 𝐽𝑜 = 1,2 2,3 =∅.

Berikut adalah definisi dari fungsi kontinu mutlak atau yang lebih dikenal dengan AC (absolutely continuous) dan fungsi kontinu mutlak teritlak (generalized absolutely continuous) atau ACG.

Definisi II.D.8.b.

Suatu fungsi F dikatakan kontinu mutlak (absolutely continuous) atau AC pada [𝑎,𝑏] jika untuk ∀𝜀> 0 terdapat 𝛿> 0 sehingga jika

Definisi II.D.8.c.

Suatu fungsi F dikatakan kontinu mutlak teritlak (generalized absolutely continuous) atau ACG pada [𝑎,𝑏] jika [𝑎,𝑏] merupakan gabungan sejumlah himpunan terbatas 𝑋_𝑘,𝑘= 1,2,… …, pada setiap fungsi F

adalah AC.

(Gordon, 1994) 9. Sifat hampir dimana-mana

Di bawah ini akan diberikan definisi dari sifat hampir dimana – mana sebagai berikut.

Definisi II.D.9.

Suatu fungsi dikatakan mempunyai sifat 𝑃 pada 𝐸 hampir dimana – mana jika fungsi tersebut bersifat P pada 𝐸 kecuali untuk himpunan 𝐴 ⊆ 𝐸 dan

𝜇 𝐴 = 0. Contoh II.D.9. :

Suatu 𝑓:𝐸 → 𝑅 dan 𝑔:𝐸 → 𝑅 adalah sama atau 𝑓 =𝑔 hampir dimana – mana pada 𝐸 jika dan hanya jika 𝑓 𝑥 =𝑔(𝑥) untuk ∀𝑥 ∈ 𝐸 − 𝐴 dengan

𝜇 𝐴 = 0 dan 𝑓(𝑥)≠ 𝑓(𝑔) untuk 𝑓:𝐸 → 𝑅 untuk ∀𝐴 ⊆ 𝐸 dengan

𝜇 𝐴 = 0.

E. Integral

dinamakan anti turunan (integral) atau fungsi primitif dari fungsi f pada interval I.

(Martono, 1999)

Integral terdiri dari integral tak tentu dan integral tentu. Integral

tersebut terletak pada batasnya, dimana Integral tentu memiliki batas atas dan batas bawah.

Pada bagian ini dibahas mengenai sifat – sifat yang berlaku pada integral tentu.

Jikal 𝑓 𝑥 dan 𝑔 𝑥 adalah fungsi kontinu maka: 1. ∫ 𝑓 𝑥 𝑑𝑥_𝑎𝑎 = 0

2. ∫ 𝑓 𝑥 𝑑𝑥_𝑎𝑏 = − ∫ 𝑓 𝑥 𝑑𝑥_𝑏𝑎

3. ∫ 𝑘𝑓 𝑥 𝑑𝑥_𝑎𝑏 =𝑘 ∫ 𝑓 𝑥 𝑑𝑥_𝑎𝑏 , dengan 𝑘 konstanta 4. ∫_𝑎𝑏[𝑓 𝑥 ±𝑔 𝑥 ]𝑑𝑥=∫ 𝑓 𝑥 𝑑𝑥_𝑎𝑏 ±∫ 𝑔 𝑥 𝑑𝑥_𝑎𝑏

5. ∫ 𝑓 𝑥 𝑑𝑥_𝑎𝑐 = ∫ 𝑓 𝑥 𝑑𝑥_𝑎𝑏 +∫ 𝑓 𝑥 𝑑𝑥_𝑏𝑐 , dengan 𝑎< 𝑏<𝑐

(Purcell,1984)

F. Integral Khintchine