BAB II KAJIAN TEORI A. Sistem Bilangan Real - BAB II NURWIYATI MTK'13

(1)

BAB II KAJIAN TEORI

A. Sistem Bilangan Real

Sistem bilangan real Radalah himpunan bilangan real yang disertai dengan operasi penjumlahan dan perkalian sehingga memenuhi aksioma tertentu (Martono, 1999). Sistem bilangan real dinotasikan dengan R. Untuk lebih lanjut akan dimulai dengan mengangkat sifat dasar dari bilangan real. Definisi II.A.1

Sistem bilangan real Radalah suatu sistem aljabar yang terhadap operasi jumlahan (+) dan operasi perkalian ( . ) mempunyai sifat – sifat sebagai berikut

1. Rmerupakan grup komutatif terhadap operasi jumlahan (+) 2. R

 

0 merupakan grup komutatif terhadap operasi perkalian ( . ) 3. Untuk setiap x,y,zRberlaku x.(yz) x.yx.z

(Darmawijaya, 2006) Definisi II.A.2

Harga mutlak xRditulis xdan didefinisikan sebagai berikut: 𝑥 = 𝑥,𝑥 ≥0

−𝑥,𝑥 < 0 1. Untuk setiap bilangan real x berlaku

(2)

c.  x x x

d. _x2 _ _x2 _ _x2

2. Untuk setiap bilangan real x dan y berlaku a. x  y xyx2  y2

b. xy  yx

3. Jika a0, maka

a. _x _a_a_x_a_x2 _a2

b. x axaatau xax2 a2

4. Ketaksamaan segitiga. Untuk setiap bilangan real x dan yberlaku a. xy  x  y

b. xy  x  y

c. x  y  x y

d. x  y  xy

5. Untuk setiap bilangan real x dan y berlaku a. xy  x y

b.  ,y0

y x y x

(Martono, 1999) Contoh:

Jika x 2 , buktikan

3 5 4 2

3 2

2 2

  

 

x x

(3)

Penyelesaian:

Karena penyebut bentuk pecahannya definit positif dengan



1



3 3

Ini mengakibatkan

3

Dengan menggunakan sifat nilai mutlak dan pertaksamaan, diperoleh 2

Dengan menggunakan hasil di atas,

(4)

B. Himpunan

Himpunan merupakan konsep dasar dari semua cabang matematika. Setiap cabang matematika berkaitan erat dan termasuk di dalam (menjadi bagian) teori himpunan. Pada bagian ini akan dibahas mengenai himpunan terbatas, himpunan bilangan real, serta himpunan terbuka dan tertutup.

Himpunan adalah kumpulan obyek yang mempunyai syarat tertentu dan jelas. Obyek – obyek dalam kumpulan itu dapat berupa benda konkrit atau benda abstrak, seperti: bilangan, abjad, orang, sungai, negara. Obyek – obyek ini disebut anggota atau elemen dari himpunan itu.

(Theresia, 1989) Contoh:

a. Kumpulan orang kaya

Kumpulan ini bukan suatu himpunan. Tetapi kumpulan orang yang kekayaannya melebihi satu trilyun rupiah adalah suatu himpunan.

b. Kumpulan negara – negara Asia Tenggara Kumpulan ini merupakan suatu himpunan.

1. Himpunan Terbatas

Di bawah ini akan dibahas lebih lanjut mengenai definisi urutan, himpunan terurut dan himpunan terbatas.

Definisi II.B.1.1

(5)

i. Jika xSdan ySmaka satu dan hanya satu diantara tiga pernyataan berikut yang benar

y

x atau x yatau y x

ii. Jika x,y,zS, dan jika x ydan yz, maka xz

(Soemantri, 2000) Definisi II.B.1.2

Jika pada suatu himpunan S telah didefinisikan suatu urutan, maka S

dinamakan himpunan terurut.

a. Himpunan ARdan Adikatakan terbatas ke atas (upper bound) jika ada bilangan nyata k sehingga berlaku ak, untuk setiap aA; k disebut batas atas (upper bound) himpunan A. b. Himpunan ARdan Adikatakan terbatas ke bawah (lower

bound) jika ada bilangan nyata l sehingga berlaku l a, untuk setiap aA; l disebut batas bawah (lower bound) himpunan A. c. Himpunan ARdan Adikatakan terbatas (bounded) jika A

terbatas ke atas dan terbatas ke bawah.

(Darmawijaya, 2006) Contoh:

R

(6)

Penyelesaian:

A x

p    

 8 , 8 terbatas ke atas. 8 merupakan batas atas A.

A x

q    

 3 , 3 terbatas ke bawah. 3 merupakan batas bawah A.

A

 terbatas.

Jika S suatu himpunan terurut, dan AS. Himpunan A terbatas ke atas dan terdapat suatu elemen pS_{yang memenuhi sifat}– sifat berikut

a. p adalah suatu batas atas A

b. jika u < p maka u bukan batas atas A

maka elemen p ini disebut batas atas terkecil atau supremum himpunan A dan diberikan notasi pSupA

Jika S suatu himpunan terurut, dan AS. Himpunan A terbatas ke bawah dan terdapat suatu elemen qSyang memenuhi sifat – sifat berikut:

Gambar II.1 Anggota Himpunan A

(7)

a. q adalah suatu bawah atas A

b. jika v > q maka v bukan bawah atas A

maka elemen q ini disebut batas atas terkecil atau infimum himpunan

A dan diberikan notasi q = inf A.

Contoh:



1,2,5,8,9





F

F terbatas ke atas, karena 9R sehingga xF,x9 . Batas atas F

tidak tunggal. pR,p9 merupakan batas atas F. Karena 9 merupakan batas atas paling kecil, maka 9 = Sup𝐹.

F juga terbatas ke bawah, karena  1R sehingga xF,x1. Batas batas F juga tidak tunggal. qR,q1 merupakan batas bawah

F. Karena –1 merupakan batas bawah paling besar, maka −1 = Inf𝐹.

2. Himpunan Bilangan Real

Himpunan bilangan real yang memenuhi suatu pertaksamaan tertentu dikenal sebagai selang (interval) hingga dan selang tak hingga. Selang hingga adalah himpunan bagian dari R yang terbatas di atas dan di bawah, sedangkan selang tak hingga tidak terbatas di atas atau tidak terbatas di bawah. Di bawah ini diberikan definisi selang sebagai himpunan titik dan gambarnya pada garis bilangan.

(8)

c. (a,b]



xR:axb



disebut selang tertutup di kanan atau selang terbuka di kiri.

d. [a,b)



xR:axb



disebut selang tertutup di kiri atau selang terbuka di kanan.

Untuk selang tak hingga diperlukan lambang dan, yang memenuhi relasi urutan xuntuk setiap bilangan real x. Berdasarkan ini lambang digunakan untuk sesuatu yang lebih kecil dari setiap bilangan real (membesar tanpa batas) dan lambang digunakan untuk sesuatu yang lebih kecil dari setiap bilangan real (mengecil tanpa batas).

a. (a,){xR:xa}disebut selang terbuka

b. [a,){xR:xa}disebut selang tertutup di kiri atau terbuka di kanan

c. (,b){xR:xb} disebut selang terbuka

d. (,b]{xR:xb} disebut selang tertutup di kanan atau di terbuka di kiri

e. (,)R

(Martono, 1999)

3. Himpunan Terbuka dan Tertutup

(9)

Ruang metrik



X,d



adalah himpunan tak kosong X yang elemen – elemennya disebut titik yang diperlengkapi dengan fungsi bernilai real d yang didefinisikan pada XXsedemikian sehingga untuk setiap x, y dan z di dalam X, dipenuhi:

a. d

 

x,y 0;

b. d

 

x,y 0, jika dan hanya jika x y; c. d

   

x,y d y,x ;

d. d

     

x,y d x,z d z,y .

Fungsi d yang memenuhi keempat sifat di atas dinamakan jarak atau metrik pada X.

Diberikan



X,d



_{ruang metrik. Jika} pX dan r 0, maka himpunan N_r

 

p 



xX:d

 

x,p r



disebut persekitaran (neighborhood) titik p dengan jari – jari r.

Diberikan



X,d



ruang metrik, himpunan A X dan titik pX . a. p disebut titik limit (limit point, cluster point) himpunan A jika

(10)

b. p disebut titik dalam (interior point) himpunan A jika ada bilangan r0sehingga N_r

 

p  A.

Diberikan ruang metrik



X,d



.

a. Himpunan A X merupakan himpunan terbuka jika setiap anggota A merupakan titik dalam A.

b. Himpunan A X merupakan himpunan tertutup jika A memuat semua titik limitnya.

(Soemantri, 2000)

C. Fungsi

Sebuah fungsi f adalah suatu aturan padanan yang menghubungkan tiap obyek x dalam satu himpunan, yang disebut daerah asal, dengan sebuah nilai f (x) dari himpunan kedua. Pada bagian ini dibicarakan mengenai fungsi komposisi, fungsi aljabar, fungsi transenden dan fungsi terbatas.

(Varberg, dkk, 1993) Definisi II.C

Diberikan A,B Rfungsi f :AB_{adalah suatu aturan yang} mengaitkan setiap unsur xA dengan tepat satu unsur yB. Unsur y

(11)

Terdapat suatu fungsi y f(x),xA, maka daerah asal fungsi f adalah himpunan A, ditulis ADf, dan daerah nilai fungsi f adalah himpunan

} :

) (

{ f

f f x x A D

R    . Unsur f(x)Bdinamakan nilai fungsi f di x. Jika diketahui hanya y  f(x), maka daerah asal dan daerah nilai fungsi

f adalah Df {xR: f(x)R}dan Rf {f(x):xA Df}

1. Fungsi Komposisi Definisi II.C.1.1

Fungsi komposisi dari g dan f (f dilanjutkan g), ditulis g f adalah suatu fungsi yang daerah asalnya himpunan bagian dari Df dan

aturannya ditentukan oleh (g f)(x)g(f(x)). Daerah asal dan daerah nilai fungsi g f adalah Dgf {xDf : f(x)Dg}dan

} ),

( :

{ g f

f

g y R y g t t R

R     

R R

f

D

f

R

x f(x)

Gambar II.2 Diagram Panah Fungsi

 

x

f y 

R R

f

R

f

D

) (x f

(12)

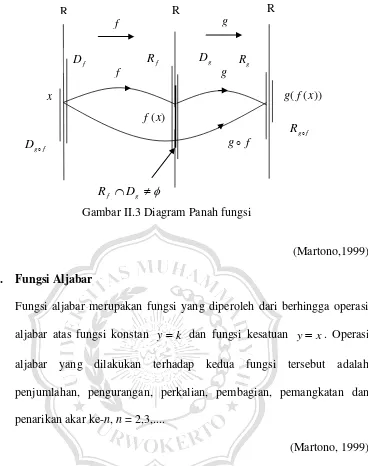
(Martono,1999) 2. Fungsi Aljabar

Fungsi aljabar merupakan fungsi yang diperoleh dari berhingga operasi aljabar atas fungsi konstan yk dan fungsi kesatuan y x. Operasi aljabar yang dilakukan terhadap kedua fungsi tersebut adalah penjumlahan, pengurangan, perkalian, pembagian, pemangkatan dan penarikan akar ke-n, n = 2,3,....

(Martono, 1999) Fungsi linear, fungsi kuadrat, fungsi pecahan linear atau kuadrat, dan fungsi trigonometri semuanya merupakan fungsi aljabar.

3. Fungsi Transenden

Fungsi transenden merupakan fungsi yang tidak dapat dinyatakan sebagai sejumlah berhingga operasi aljabar atas fungsi konstan y = k dan fungsi kesatuan y = x.

(Martono,1999)

f

D

x

) (x f

f g

f

R Dg R_g

)) ( (f x g

f g

f g

D 

f g

R _

 

 g

f D

R

Gambar II.3 Diagram Panah fungsi f

(13)

Fungsi transenden terdiri dari fungsi – fungsi berikut: a. Fungsi eksponensial, didefinisikan oleh x

a

y , untuk a0dan 1



a , xR.

Jika a = e, maka x

e

y  _{fungsi tersebut yang disebut sebagai fungsi} eksponen natural.

b. Fungsi logaritma, dinyatakan oleh yalogxxay,a1& x > 0. Jika a = e, maka yelogxy lnx fungsi tersebut yang disebut sebagai fungsi logaritma natural.

c. Fungsi trigonometri 1) y f(x)sinx 2) y f(x)cosx 3) y f(x)tanx 4) y f(x)cotx 5) y f(x)cscx 6) y f(x)secx

d. Fungsi invers trigonometri

1)

2 2

, sin

sin 1      

 

x x

y y x

2)

2 0

, cos

cos 1    

 

x x y

y x

3)

2 2

, tan

tan 1     

 

x x

y y x

4)

2 & 0

, sec

sec 1     

 

x x

x y

(14)

e. Fungsi Hiperbolik

1)

2 sinh

x x

e e x



 

2)

2 cosh

x x

e e x



 

3)

x x x

cosh sinh tanh 

4)

x x x

sinh cosh coth 

5) 𝑠𝑒𝑐ℎ

x

cosh 1



6) csch𝑥

x

sinh 1



(Varberg, dkk, 2010) 4. Fungsi Terbatas

Definisi II.C.4.1

Fungsi f dikatakan terbatas jika terdapat M > 0 sehingga f(x) M

untuk setiap xDf

(Martono, 1999) Definisi II.C.4.2

Fungsi f dikatakan tidak terbatas jika untuk sebarang M > 0 terdapat

f

D

(15)

Contoh:

a. Fungsi f(x)sinx terbatas karena f(x)  sinx 1untuk setiap

f

D x .

b. Fungsi

x x

f( ) 1 tidak terbatas pada selang (0,)karena untuk

sebarang M 0, terdapat 0

2 1

0  

M

x sehingga

M M M

f x

f   

    

 2

2 1 )

( 0 .

D. Limit

Di bawah ini akan dijelaskan lebih lanjut mengenai limit fungsi di R,

2

R dan n

R .

1. Limit Fungsi di R

Definisi II.D.1.1

Diberikan fungsi f terdefinisi pada selang terbuka I yang memuat c, kecuali mungkin di c sendiri. Limit fungsi f di c adalah L (ditulis

L x f

c

x ( )

lim atau f(x)L bila xc) jika  0

 

        

 0 0 x c f(x) L .

(16)

Definisi II.D.1.2

Diberikan fungsi f terdefinisi pada selang (c,b), limit kanan fungsi f

di c adalah L ( f x L

(Martono, 1999) Contoh:

(17)

Sifat – sifat Limit Fungsi a. Ketunggalan limit

Jika f x L

b. Operasi aljabar pada limit

Jika f x L

c. Limit fungsi sederhana

a) k k k

(18)

2. Limit Fungsi di R2

Fungsi f adalah fungsi dua variabel dengan domain D maka dapat dikatakan bahwa limit dari f(x,y)L dan ditulis _{   }f

 

x y L

b a y

x,lim , , 

jika untuk setiap  0 terdapat  0 sedemikian sehingga

 

x y L 

f , _bilamana

 

x,y D dan 0

   

x,y  a,b _dengan

   



 

2



2

,

,y a b x a y b

x     

(Varberg, dkk, 2003) 3. Limit Fungsi di Rn

Definisi yang diungkapkan untuk limit fungsi di R dan di R2_tersebut

sedemikian sehingga dapat diperluas untuk fungsi tiga peubah atau lebih. Secara umum, jika z f



x1,x2,x3,...,xn



adalah fungsi n-variabel

dengan domain D maka dapat dikatakan bahwa limit dari



x x x x



L

f 1, 2, 3,..., _n  dan ditulis _ _  f x x xn L x

x x x x

x n n



 ( , ,..., )

lim 1 2

,..., , ,...,

, ' '

2 ' 1 2

1





 ' '

3 ' 2 ' 1 2

1, ,..., , , ,..,

0 x x x_n x x x x_n

(19)

E. Kekontinuan

Bila suatu fungsi terdefinisi pada selang terbuka yang memuat suatu titik, kekontinuan fungsinya di titik itu dapat didefinisikan dengan limit fungsi. Di bawah ini akan dipaparkan kekontinuan di R, R2dan n

R . 1. Kekontinuan di _R

Definisi II.E.1.1

Fungsi f terdefinisi pada satu interval terbuka yang memuat c. Dikatakan bahwa f kontinu di c jika lim f(x) f(c)

c

x  . Jadi fungsi f

dikatakan kontinu disuatu titik c jika dan hanya jika: a. lim f(x)

c

x ada

b. f(c)ada (yakni, c berada dalam daerah asal f ), dan c. lim f(x) f(c)

c

x 

(Varberg, dkk, 2010) Definisi II.E.1.2

Fungsi f adalah kontinu kanan pada a jika lim f(x) f(a)

a

x   dan

kontinu kiri pada b jika lim f(x) f(b)

a

x   . Fungsi f kontinu pada

sebuah interval terbuka jika f kontinu pada setiap titik pada interval tersebut. Serta kontinu pada sebuah interval tertutup [a,b] jika kontinu pada (a,b), kontinu kanan pada a, dan kontinu kiri pada b.

(20)

2. Kekontinuan di R2

DefinisiII.E.2.1

Fungsi f(x,y)_{dikatakan kontinu dititik} (a,b)D,DR2_jika

   x,ylima,b f(x,y) f(a,b). Fungsi f dikatakan kontinu pada domain

D jika f kontinu di setiap titik (a,b) dalam D.

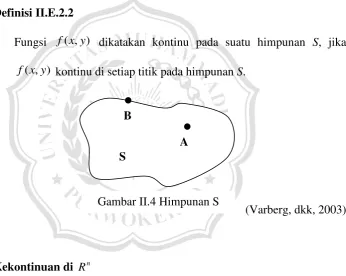
(Varberg, dkk, 2003) DefinisiII.E.2.2

Fungsi f(x,y)_{dikatakan kontinu pada suatu himpunan} _S_{, jika}

) , (x y

f _{kontinu di setiap titik pada himpunan}S.

(Varberg, dkk, 2003)

3. Kekontinuan di Rn

Fungsi z  f



x1,x2,x3,...,xn



, kontinu di titik



, ,...,



,

' ' 2 '

1 x x D

x n 

n

R D

jika _ _ _ _



2' '



' 1 2

1 ,..., , ,...,

, lim ' ' ( , ,..., ) , ,..., 2

' 1 2

1

n n

x x x x x x

x x x f x x x f

n n



 . Fungsi f dikatakan

kontinu pada domain D jika f kontinu di setiap titik



2' '



'

1,x ,...,xn

x _dalam

D.

(Varberg, dkk, 2003) B

A S

(21)

F. Turunan

Pada bagian kali ini akan dibahas lebih lanjut mengenai turunan di R, turunan di n

R . 1. Turunan di _R

Definisi II.F.1.1

Jika fungsi f terdefinisi pada suatu selang terbuka I yang memuat

(Martono, 1999)

Jika fungsi f terdefinisi pada selang (a,c]. Turunan kiri dari fungsi f

di titik c, ditulis f’(c) didefinisikan sebagai

(22)

Jika fungsi f terdefinisi pada selang [c,b). Turunan kanan dari fungsi

f di titik c, ditulis f'(c) dan didefinisikan sebagai

(Martono, 1999) Definisi II.F.1.4

Jika fungsi f terdefinisi pada selang terbuka I yang memuat c, maka fungsi f terdiferensialkan di c f_'(c) f_'(c)

(23)

Teorema II.F.1.5

a. Aturan pencarian turunan

Jika y f(x), turunan f dapat dinyatakan dengan tiga notasi (notasi

f dan g adalah fungsi yang terdiferensialkan 5)



f g

  

' x  f'

 

x g'

 

x

(24)

7)

   

f.g ' x  f

       

x g' x g x f' x

8)

) (

) ( ' ) ( ) ( ) ( ' ) (

' ₂

x g

x g x f x g x f x g

f 

      

(Varberg, dkk, 2000) b. Turunan fungsi trigonometri

Di bawah ini diberikan turunan pertama untuk fungsi trigonometri. 1) f(x)sinx f'(x)cosx

2) f(x)cosx f'(x)sinx 3) f(x)tanx f'(x)sec2 x 4) f(x)cotx f'(x)csc2x 5) f(x)secx f'(x)secxtanx 6) f(x)cscx f'(x)cscxcotx

(Martono,1999) c. Turunan fungsi invers

Definisi II.F.1.c

Jika fungsi f kontinu dan satu – satu pada selang I Df dengan

aturan y  f(x),xIdan inversnya adalah x f 1(y),yR_f. Jika fungsi f terdiferensialkan pada I dengan f'(x)0pada I, maka fungsi 1

f _{juga terdiferensialkan pada} R_f dan aturan

turunannya ditentukan oleh

) ( '

1 ))' ( ( 1

x f y

f  atau

dy dx dx dy _ 1

(25)

d. Turunan fungsi komposisi Definisi II.F.1.d

Jika y f

 

u dan u g

 

x . Jika g terdiferensiasikan di x dan f

terdiferensiasikan di u g

 

x , maka fungsi komposisi f g yang didefinisikan oleh (f g)(x) f(g(x)), adalah terdiferensiasikan di x dan (f g)'(x) f'(g(x))g'(x)atau

dx du du dy dx dy

 .

e. Turunan fungsi logaritma

1) Turunan fungsi logaritma alami dapat dituliskan sebagai berikut:

x x f x x

f( )ln  '( ) 1

2) Turunan fungsi logaritma dapat dituliskan sebagai berikut:

a x x f x x

f a

ln 1 . 1 ) ( ' log

)

(   

f. Turunan fungsi eksponensial

1) Turunan fungsi eksponen alami dapat dituliskan sebagai berikut:

x x

e x f e x

f( )  '( )

2) Turunan fungsi eksponen dapat dituliskan sebagai berikut:

1 , ln )

( ' )

(x a  f x a a a

f x x

(26)

g. Turunan tingkat tinggi

Operasi diferensiasi mengambil sebuah fungsi f dan menghasilkan sebuah fungsi baru f'. Jika f' didiferensiasi menghasilkan fungsi

''

f (f dua aksen) dan disebut turunan kedua dari f. Dan boleh didiferensiasi yang menghasilkan f' '' yang disebut turunan ketiga dari f. Turunan keempat dinyatakan dengan f (4), turunan kelima dinyatakan (5)

f dan seterusnya.

(Varberg, dkk, 2000) Contoh:

8 7 4 2 )

(  3 2  

x x x x

f , maka

7 8 6 ) (

' x  x2  x f

8 12 ) (

'' x  x f

12 ) ( '' ' x  f

0

) 4 ( 

f

Karena turunan fungsi nol adalah nol, maka turunan keempat dan semua turunan tingkat yang lebih tinggi (higher-order derivative)

dari f akan nol.

2. Turunan di n

R

(27)

bidang dengan sebuah bilangan real (unik) dari f

 

x,y . Himpunan D

disebut daerah asal (domain) suatu fungsi. Jika tidak dinyatakan secara spesifik, D dapat dinyatakan sebagai daerah asal alami (natural domain), yaitu himpunan seluruh titik

 

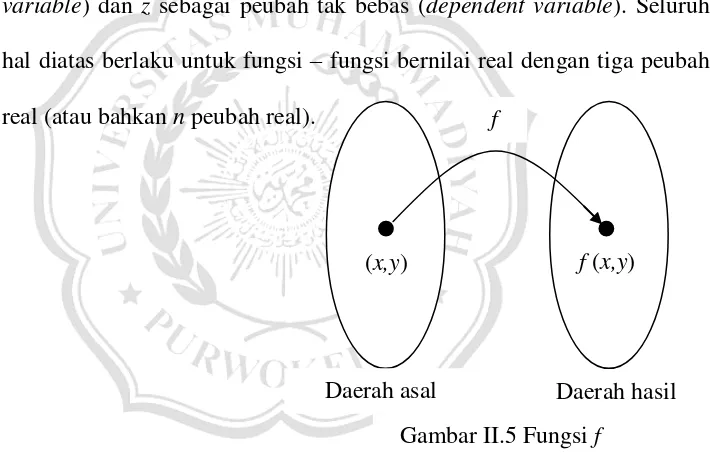
x,y pada suatu bidang dimana fungsi tersebut masuk akal dan menghasilkan nilai bilangan real. Daerah hasil (range) dari sebuah fungsi adalah himpunan dari nilai – nilainya. Jika

 

x y f

z , , maka x dan y disebut sebagai peubah bebas (independent variable) dan z sebagai peubah tak bebas (dependent variable). Seluruh hal diatas berlaku untuk fungsi – fungsi bernilai real dengan tiga peubah real (atau bahkan n peubah real).

Jika f adalah fungsi dengan dua peubah x dan y. Jika y dijaga agar tetap konstan, misal y y0 maka f(x,y0)adalah fungsi dengan

(x,y) f (x,y) (x,y)

f

(28)

peubah tunggal x. Turunannya di x x₀ disebut turunan parsial f

(29)

Demikian pula, turunan parsial f terhadap x₂di



' '



dan dituliskan

sebagai

dituliskan sebagai

(30)

 

2 3

 

2 menghasilkan empat buah turunan parsial kedua (second partial derivative) dari f.

Contoh:

Tentukan empat turunan parsial kedua dari

(31)

2 secara analogis, dan notasi penulisannya juga serupa. Jika f adalah fungsi dengan dua peubah x dan y, maka turunan parsial ketiga f diperoleh

G. Integral

(32)

Keterkaitan antara dua integral ini dikenal sebagai Teorema Dasar Kalkulus yang salah satunya adalah turunan dari bentuk integral tertentu dengan peubah di limit atasnya. Di bawah ini akan dijelaskan lebih lanjut mengenai integral tak tentu dan integral tentu.

1. Integral Tak Tentu Definisi II.G.1.1

Ambil fungsi h yang didefinisikan pada selang I dengan definisi I

x x g x f x

h( ) ( ) ( ), 

maka h'(x) f'(x)g'(x),xI

karena f'(x) g'(x) untuk xI berakibat

0 ) ( ' ) ( ' ) ( ' ) ( ' ) (

' x  f x g x  g x g x  h

Jadi, h'(x)0,xI

(33)

c x g x

f  

 ( ) ( )

I x c x g x

f    

 ( ) ( ) , .█

Jika f merupakan anti turunan khusus dari f pada selang I maka setiap anti turunan dari f pada I diberikan oleh F

 

x c dengan c

sembarang konstanta. Bukti:

Ambil G sembarang anti turunan dari f pada I maka

 

x f x x I

G'  ( ),  ... (1)

Karena F merupakan anti turunan khusus dari f pada I maka

 

x f x x I

F'  ( ),  ... (2)

dari (1) dan (2) diperoleh:

 

x F x x I G'  '( ), 

x atau

 



F x



f

 

x dx

(34)

Teorema II.G.1.4 maka akan ditunjukkan





Untuk integral pada fungsi trigonometri adalah sebagai berikut: a.



sinxdxcosxc

(35)

d.



csc2 xdxcotxc e.



secxtanxdxsecxc

g(x)dx Bukti:

f dan g mempunyai anti turunan. c

x

F( ) anti turunan dari f, jadi



f(x)dx F(x)c,



F(x) c



f(x)

d  

c x

G( ) anti turunan dari g, jadi



g(x)dxG(x)c,



G(x) c



g(x)

d  

a.



kf(x)dxk



f(x)dx

 











 



dx kc x kF d dx

c x F k

d  _ 

0 ) (

' 

kF x

 



F x



f

 

x dx d

x

kf 

 ( ),

(36)

b.





f(x)g(x)



dx



f(x)dx



g(x)dx

 







 





 



dx

c x G x F d dx

c x G d c x F

d    _  2

 

x G x F'( ) '



 

x g x

f 

 ( )

Dengan kata lain,

 







 





 



_



f(x)g x dx F x c  G x c  f(x)dx g(x)dx.█

Diberikan g fungsi yang dapat didiferensialkan dan daerah hasil (nilai) dari g adalah selang I. Jika f fungsi yang didefinisikan pada I

dan F anti turunan dari f pada I, maka

 



g x

  



g x dx



F



g

 

x



c

x

  



g x



dx

d

' .

 

 







F g x c



F



g

 

x

  



g x



dx d

' . '

 

 



g x

  

g x f . '



(37)

Jika g suatu fungsi yang dapat terdiferensiasi dan f suatu bilangan

rasional yang bukan -1, maka



 



 





c r

x g dx x g x g

r r

 

 



' ( )₁

1

.

Bukti:

Jika u = g (x) adalah fungsi yang dapat didiferensiasi dan r suatu bilangan rasional



r 1



maka,

u D u r

u

D r _x

r

x .

1

1       



atau



 





g

 

x



g

 

x r

x g

D r

r

x . '

1

1     

 



.█

2. Integral Tentu

Jika f didefinisikan pada interval tertutup [a,b]. Fungsi ini bisa bernilai positif atau negatif pada interval tersebut dan bahkan tidak perlu kontinu. Misalkan suatu partisi P membagi interval [a,b] menjadi n

interval bagian (tidak perlu sama panjang) dengan menggunakan titik – titik ax₀ x₁ x₂ ...x_n_₁ x_n b dan misalkan xi xi xi1.

Pada setiap bagian interval



xi1xi



, dengan mengambil sebuah titik

sebarang titik xi (mungkin saja titik ujung) yang disebut sebagai titik

sampel untuk interval bagian ke-i.

(38)

interval tertutup [a,b]. Jika



 

terintegrasikan pada [a,b]. Suatu jumlah Riemann ditafsirkan sebagai sebuah jumlah aljabar dari luas-luas.

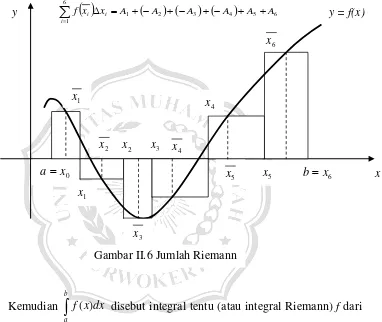
Kemudian



b

a

dx x

f( ) disebut integral tentu (atau integral Riemann) f dari

a ke b, kemudian diberikan oleh





 

Jika f kontinu (karenanya terintegrasikan) pada [a,b] dan diberikan

F adalah sebarang anti – turunan dari f pada [a,b], maka,

Gambar II.6 Jumlah Riemann

(39)

Bukti:

Karena fungsi F dan G kontinu pada interval tertutup [a,b], didapatkan F(a) = G(a) + c dan F(b) = G(b) + c. Jadi F(x) = G(x) + c

pada interval tertutup [a,b].

Karena 





b

a

dt t f a

G( ) ( ) 0, maka F(a)G(a)c0cc.

Karena itu,  







  



b

a

dt t f b G c c b G a F b

F( ) ( ) ( ) ( ) ( ) .█

a. Integral lipat dua atas persegi panjang

Jika R adalah sebuah persegi panjang dengan sisi – sisi sejajar dengan sumbu koordinat R{(x,y):a xb,c yd}. Bentuk partisi P dari R dalam pengertian membentuk garis – garis sejajar dengan sumbu x dan sumbu y (Gambar II.7).

Gambar II.7 Daerah R



 

x,y :a xb,c yd



 

xk,yk

c d

a b

x

y z

k

R

(40)

Pembuatan partisi ini membagi R menjadi persegi panjang yang lebih kecil sebanyak n, kemudian menotasikannya dengan Rk, k =

1,2,3,...,n. Misalkan xkdan ykadalah panjang sisi – sisi Rk dan

misalkan Ak xkykadalah luasnya. Pada Rkambil sebuah titik

contoh



xk,y_k



dan bentuk jumlah Riemann







n

k

k k k y A

x f

1

) ,

( yang

berhubungan (jika f(x,y)0) dengan jumlah volume n kotak (Gambar II.8).

Dengan membuat partisi tersebut semakin kecil sedemikian rupa sehingga seluruh Rk juga mengecil, akan menuntun ke konsep yang

dikehendaki. Dengan ketentuan tambahan bahwa aturan partisi P, dilambangkan dengan P adalah diagonal terpanjang dari sub persegi panjang dalam partisi tersebut.

(Varberg, dkk, 2003) Gambar II.8 Permukaan z = f (x,y)

) , (x y f z

Volume =

k k k y A

x

f( , )

c d

a b

x

y z

k

R

(41)

Definisi II.G.2.a

Jika f adalah fungsi dengan dua peubah yang didefinisikan pada

sebuah persegi panjang tertutup R. Jika







(Varberg, dkk, 2003) Sifat – sifat integral lipat dua

Jika f (x,y) dan g (x,y) kontinu dan kR maka 1) Integral lipat dua bersifat linear, yaitu

(42)





R R

dA y x g dA y x

f( , ) ( , )

(Varberg,dkk, 2003) b. Integral lipat dua atas daerah bukan persegi panjang

Definisi II.G.2.b

Suatu himpunan S yang tertutup dan terbatas pada bidang. S

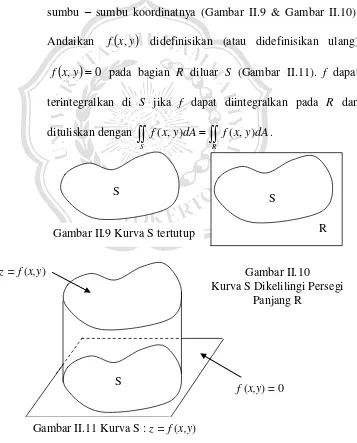
dikelilingi dengan persegi panjang R dengan sisi – sisi sejajar sumbu – sumbu koordinatnya (Gambar II.9 & Gambar II.10). Andaikan f

 

x,y didefinisikan (atau didefinisikan ulang)

 

x,y 0

f pada bagian R diluar S (Gambar II.11). f dapat terintegralkan di S jika f dapat diintegralkan pada R dan dituliskan dengan







R S

dA y x f dA y x

f( , ) ( , ) .

(Varberg, dkk, 2003) S

R

Gambar II.10

Kurva S Dikelilingi Persegi Panjang R

S

Gambar II.9 Kurva S tertutup

S

z = f (x,y)

f (x,y) = 0

(43)

c. Perhitungan Integral lipat dua atas persegi panjang

Himpunan dengan batas – batas melengkung bisa menjadi sangat rumit. Untuk tujuan yang akan dicapai, akan cukup memadai jika menggunakan himpunan sederhana-x dan himpunan sederhana-y

(dan gabungan terhingga dari himpunan – himpunan tersebut). Sebuah himpunan S dikatakan sederhana y jika himpunan tersebut sederhana pada arah y, artinya bahwa sebuah garis pada arah ini memotong S dalam selang tunggal (atau titik atau tidak sama sekali). Jadi, sebuah himpunan S disebut sederhana-y (y-simple) (Gambar II.12) jika terdapat fungsi ₁ dan fungsi ₂ pada [a,b] sedemikian rupa sehingga

 



x y x y x a x b



S  , :₁  ₂ ,  

Suatu himpunan S dikatakan sederhana-x (x-simple) (Gambar II.13) jika terdapat fungsi ₁ dan fungsi ₂ pada [c,d] sedemikian rupa sehingga

   

 



x y y x x c y d



S , :₁  ₂ ,  

y

0 x

0 x

Gambar II.15 Kurva Bukan Sederhana-x atau Sederhana-y S

1

S

2

S

(46)

koordinat Cartesius (koordinat siku – siku). Sehingga dapat diharapkan bahwa integral lipat dua atas daerah yang tertutup oleh kurva-kurva seperti itu akan mudah dihitung dengan menggunakan koordinat kutub.

Misalkan R mempunyai bentuk seperti yang digambarkan pada Gambar II.17, yang disebut dengan persegi panjang kutub (polar rectangle). Misal z f

 

x,y menentukan sebuah permukaan atas R

dan andaikan f kontinu dan tak negatif. Maka volume V benda padat di bawah permukaan ini dan di atas R (Gambar II.18) dapat dinyatakan dengan





R

dA y x f

V ( , ) ... (1)

Di dalam koordinat kutub, persegi panjang kutub R mempunyai bentuk R



 

r, :arb,  



. Untuk menghitung volumenya yaitu menggunakan koordinat kutub.

R



 

b r 

a r 

  

0 Sumbu Kutub

Gambar II.17 Persegi Panjang Kutub

R

x

y z

 

,

) ,

(x y F r f

z  

(47)

R dibagi – bagi menjadi partisi – partisi yang lebih kecil berbentuk persegi panjang kutub R1,R2,....,Rndengan menggunakan

kisi kutub (polar grid), dan misalkan rkdan kmenyatakan

Saat menggunakan limit sebagai aturan pembagian partisi yang mendekati nol, maka akan memperoleh volume yang sebenarnya. Limit ini adalah sebuah integral lipat dua.



Dari (1) dan (2) diperoleh

 fungsi – fungsi kontinu dengan tanda sebarang.

(Varberg, dkk, 2003) R

(48)

H. Integral Kurzweil-Henstock

Pendefinisian integral Kurzweil – Henstock diawali dengan pendefinisian partisi - fine.

Definisi II.H.1

 

   

 

 

 u  



  merupakan indikasi bahwa  adalah partisi - fine.

(Yee, 2000)

Teorema II.H.2 (Causin’s Lemma)

 

c,d yaitu

 

2 ,d c

, maka _







_

2 , c d

c dan _ 



c d



,d_

2

juga tidak mempunyai partisi - fine.

Ambil setengah dari interval

 

c,d yang tidak mempunyai partisi – partisi - fine sebut



c₁,d₁



. Selanjutnya, ambil setengah dari interval



c₁,d₁



 

 

(49)

yang tidak mempunyai partisi - fine. Proses dilanjutkan sampai diperoleh interval bersarang



cn,dn



dengan  







2 0

n n

n c d c

d .

Pastilah terdapat titik C yang berada pada interval



cn,dn



untuk setiap n.

Karena 

 

c 0, maka terdapat suatu bilangan N sedemikian hingga untuk nNberlaku d_n c_n 

 

c , Pertidaksamaan tersebut menunjukkan bahwa  



Cn u1C v1 dn



maka 

 min





₁

   

 ,₂ 





untuk setiap

 

a,b



 , maka partisi - fine juga merupakan partisi -ifine dengan

i=1,2. Bukti:

 

a,b R sehingga untuk setiap partisi - fine

 



,u,v



  pada

 

a, berlaku b





 



f I , dengan



f  f

 

 vu





(Yee, 2000)

Teorema II.H.5 (Teorema Kekonvergenan Monoton) Diberikan

i. Barisan



f_k

 

x



adalah monoton untuk hampir semua

n

R J

x  .

ii. Fungsi fk adalah terintegral Kurzweil-Henstock dan barisan

     



J k

f adalah terbatas, dengan kata lain untuk beberapa K

semua kN.

iii. f_k f

k 

(51)

Maka f terintegral Kurzweil-Henstock pada J dan



 

J k k J

f

f lim ... (1)

Bukti:

Diasumsikan bahwa

 

fk adalah barisan naik, fk 0 dan f . Barisan

     



B

A k

f merupakan barisan monoton dan terbatas. Limit kanan dari (1) ada,

dan dinotasikan dengan L. Diberikan , dapat diperoleh N dimana

3



 



f L

J N

x

f    k 

3 1

(2)

dari Lemma Henstock ada ukuran n pada n

R dimana

 













k K

k i i k

i

f K x f

2 .

3 (3)

dimana partisi bagian  





x_i,K_i



;i1,...,r



merupakan  -fine. Dan

 

dari sebelumnya

 

selanjutnya diestimasikan perbedaan diantara (5) dan (6), dengan kata lain

(53)

 



 

 

 



    

 



 

3 2

3 L

f K

x f K

x f

i i i

K x k i

i x k i

i

Dengan kata lain

 



 

 

 



     

 



 



L f

K x f K

x f

i i i

K x k i

i x k i

i

3 2

3 █

I. Himpunan Terukur

Terdapat dua ukuran di dalam suatu himpunan yaitu ukuran luar dan ukuran dalam. Definisi dari kedua ukuran tersebut sebagai berikut.

1. Ukuran luar Definisi II.I.1

Diberikan himpunan E R. Ukuran luar E diberi notasi *

 

(54)

3. Himpunan Terukur

Di bawah ini akan diberikan definisi dari himpunan yang terukur. Definisi II.I.3

Suatu himpunan E R dikatakan terukur jika ukuran luar sama dengan ukuran dalam atau *

 

E _*

 

E

(Royden, 1968)

J. Fungsi Terukur

Sebelum dibahas lebih lanjut mengenai fungsi terukur, terlebih dahulu akan dibahas mengenai definisi fungsi hampir dimana – mana.

Definisi II.J.1

Suatu fungsi dikatakan mempunyai sifat P pada E hampir dimana – mana jika fungsi tersebut bersifat P hampir dimana – mana kecuali untuk himpunan AEdan 

 

A 0.

Contoh:

Suatu fungsi f :ERdan g:ER adalah hampir dimana – mana pada E jika dan hanya jika f

   

x  g x untuk xEA dengan

 

A 0

(55)

Definisi II.J.2

Suatu fungsi f :E R adalah terukur jika E adalah himpunan terukur dan untuk setiap rR, himpunan



xE| f

 

x r



adalah terukur.

(Gordon, 1994)

Teorema II.J.3

Diberikan E himpunan terukur dan jika f :ER kontinu hampir dimana – mana pada E, maka f terukur.

Bukti:

Diberikan B himpunan diskontinu pada E. Jika 

 

B 0, semua subset B

adalah terukur. Misalkan rRdan diperoleh

 



xE| f x r







xEB| f

 

x r







xB| f

 

x r



. Maka akan

dibuktikan bahwa himpunan C



xBB| f

 

x r



adalah terukur. Jika f kontinu pada setiap titik pada C, untuk xC terdapat x 0 sedemikian sehingga f

 

t r dimana t



zE: zx _z



. Misalkan







C x

x

x z z U



 

 :  , maka U himpunan terukur dan berakibat



E B



U

(56)

K. Teorema Tonelli

J didefinisikan sebagai interval pada n

R _denganJ  AB, A adalah interval pada l

R dan B adalah interval pada m

R , nlm. Teorema II.K.1 ( Teorema Tonelli )

1. f terukur pada J

f terintegral Kurzweil-Henstock pada J.

Untuk g  f , berakibat: Akibat II.K.2

Jika f terukur,

Akibat II.K.3