BAB 2 LANDASAN TEORI 2.1 Sejarah Analisis Jalur - Penerapan Analisis Jalur Dalam Menentukan Faktor Yang Mempengaruhi Tingkat Kemiskinan Di Provinsi Sumatera Utara Tahun 2010

BAB 2

LANDASAN TEORI

2.1 Sejarah Analisis Jalur

Analisis jalur yang dikenal dengan path analysis dikembangkan pertama tahun 1920-an oleh seorang ahli genetika yaitu Sewall Wright (Joreskog & Sorbom, 1996; Johnson & Wichern, 1992).Teknik analisis jalur sebenarnya merupakan pengembangan korelasi yang diurai menjadi beberapa interpretasi akibat yang ditimbulkannya.Lebih lanjut, analisis jalur mempunyai kedekatan dengan regresi berganda. Dengan kata lain, regresi berganda merupakan bentuk khusus dari analisis jalur. Teknik ini juga dikenal sebagai model sebab akbat (causing modeling).Penamaan ini didasarkan pada alasan bahwa analisis jalur

memungkinkan pengguna dapat menguji proposisi teoritis mengenai hubungan sebab akibat tanpa memanipulasi variabel-variabel.Memanipulasi variabel maksudnya ialah memberikan perlakuan (treatment) terhadap variabel-variabel tertentu dalam pengukurannya (Sarwono, 2007).

2.2 Pengertian Analisis Jalur

(significance) hubungan sebab akibat hipotetikal dalam seperangkat variabel (Paul Webley, 1997).

David Garson dari North carolina State University mendefenisikan analisis jalur sebagai model perluasan regresi yang digunakan untuk menguji keselaransan matriks korelasi dengan dua atau lebih model hubungan sebab akibat yang dibandingan oleh peneliti. Modelnya digambarkan dalam bentuk gambar lingkaran dan panah dimana anak panah tunggal menunjukkan sebagai penyebab. Regresi dikenakan pada masing-masing variabel dalam suatu model sebagai variabel tergantung (pemberi respons) sedang yang lain sebagai penyebab. Pembobotan regresi diprediksikan dalam suatu model yang dibandingkan dengan matriks korelasi yang diobservasi untuk semua variabel dan dilakukan juga perhitungan uji keselaran statistik (David Garson, 2003).

Analisis jalur juga diartikan oleh Bohrnstedt (1974 dalam Riduwan dan

Engkos Achmad Kuncoro, 2008) bahwa “A technique for estimating the effect’s a

set of independent variables has on a dependent variable from a set of observed

correlations, given a set of hyphotesized causal asymetric relation among the

variables”. Sedangkan tujuan utama analisis jalur menurut Maruyama (1998

dalam riduwan dan Engkos Kuncoro, 2008) adalah “ A method of measuring the direct influence along each separate path in such a system and thus of finding the

degree to which variation of a given effect is determined by each particular cause.

The method depend on the combination of knowledge of the degree of correlation

among the variables in a system which such knowledge as may possesed of the

Jadi, model analisis jalur digunakan untuk menganalisis pola hubungan antar variabel dengan tujuan unutk mengetahui pengaruh langsung maupun tidak langsung seperangkat variabel bebas terhadap variabel terikat.Model analisis jalur yang dibicarakan adalah pola hubungan sebab akibat. Oleh karena itu rumusan masalah penelitian dalam kerangka analisis jalur hanya berkisar pada apakah variabel bebas (X1,X2,...,Xk) berpengaruh terhadap variabel Y, atau berapa besar

pengaruh kausal langsung, kausal tidak langsung, kausal total maupun simultan seperangkat variabel bebas (X1,X2,...,Xk) berpengaruh terhadap variabel Y.

(Riduwan dan Engkos Kuncoro, 2008).

2.2.1 Manfaat Analisis Jalur

Menurut Riduwan dan Engkos Kuncoro (2008), manfaat model analisis jalur adalah untuk:

1. Penjelasan (explanation) terhadap fenomena yang dipelajari atau permasalahan yang diteliti.

2. Prediksi nilai variabel endogen berdasarkan nilai variabel eksogen.

3. Faktor dominan yaitu penentu variabel eksogen mana yang berpengaruh dominan terhdap variabel endogen, juga untuk mekanisme pengaruh jalur-jalur variabel eksogen terhadap variabel endogen.

4. Pengujian model dengan menggunakan teori trimming baik untuk uji reabilitas dari konsep yang sudah ada maupun konsep baru.

2.2.2 Asumsi-asumsi Analisis Jalur

Asumsi yang mendasari analisis jalur sebagai berikut::

2. Tidak adanya adivity, yaitu tidak ada efek-efek interaksi. Semua variabel residual tidak boleh berinteraksi dengan salah satu variabel dalam model yang diteliti.

3. Sistem aliran kausal hanya satu arah (rekursif) artinya tidak ada arah kausalitas terbalik non-rekursif (reciprocal).

4. Variabel terikat minimal dalam bentuk skala ukur interval dan ratio. 5. Sampling bersifat probability sampling sehingga memungkinkan seluruh

anggota populasi memiliki peluang yang sama untuk dipilih menjadi anggota sampiling.

6. Observed variabel diukur tanpa kesalahan (instrumen valid dan reliable) artinya variabel yang diteliti dapat diobservasi secara langsung.

7. Model yang dianalisis dispesifikasikan berdasarkan teori atau konsep yang relevan, artinya model yang dikaji atau diuji dibangun berdasarkan kerangka teoritis tertentu yang mampu menjelaskan hubungan kausalitas antar variabel.

2.2.3 Beberapa Istilah Dalam Analisis Jalur

Beberapa istilah yang dikenal dalam analisis jalur aalah sebagai berikut: 1. Model Jalur

variabel endogenus masing-masing.Anak panah ganda menunjukkan korelasi antara pasangan variabel-variabel exogenus.

2. Variabel exogenus

Variabel exogenus adalah semua variabel yang tidak ada penyebab-penyebab eksplisitnya atau dalam diagram tidak ada anak-anak panah yang menuju ke arahnya, selain pada bagian kesalahan pengukuran. Jika antara variabel exogenus dikorelasikan maka korelasi tersebut ditunjukkan dengan anak panah berkepala dua yang menghubungkan variabel-variabel tersebut.

3. Variabel endogenus

Variabel endogenus ialah variabel yang mempunyai anak panah-anak panah menuju ke variabel tersebut.Variabel yang termasuk didalamnya mencakup semua variabel perantara dan tergantung.Variabel perantara endogenus mempunyai anak panah yang menuju ke arahnya dan dari arah variabel tersebut dalam suatu model diagram jalur.Adapun variabel tergantung hanya mempunyai anak panah yang menuju ke arahnya.

4. Koefisien jalur/pembobotan jalur

Koefisien jalur adalah koefisien regresi standar atau disebut „beta‟ yang

terhadap variabel lain dalam suatu modeljalur tertentu yang mengontrol dua variabel lain sebelumnya dengan menggunakan data yang sudah distandarkan atau matriks korelasi sebagai masukan.

5. Direct effect

Direct effect ialah pengaruh langsung yang dapat dilihat dari koefisien

jalur dari satu variabel ke variabel lainnya. 6. Indirect effect

Indirect effect ialah urutan jalur melalui satu atau lebih variabel

perantara.

2.2.4 Model Anlisis jalur

Ada beberapa model jalur mulai dari yang paling sederhana smpai dengan yang lebih rumit, diantaranya diterangkan di bawh ini:

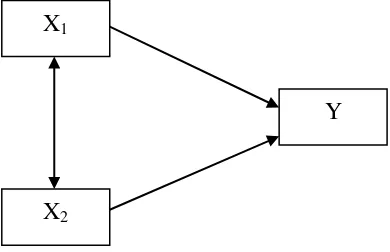
1. Model Regresi Berganda

Model ini merupakan pengembangan regresi berganda dengan menggunakan dua variabel exogenous, yaitu X1 dan X2 dengan satu

variabel endogenous Y. Model digambarkan sebagai berikut:

Gambar 2.1 Model Regresi Berganda X1

X2

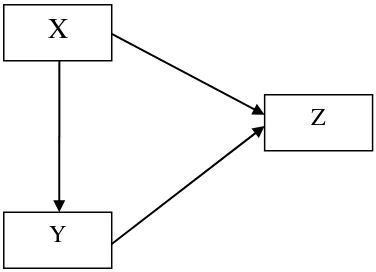
2. Model Mediasi

Model mediasi atau perantara dimana variabel Y memodifikasi pengaruh variabel X terhadap variabel Z. Model ini digambarkan sebagai berikut:

Gambar 2.2 Model Mediasi

3. Model Kombinasi Regresi Berganda dan Mediasi

Model ini merupakan kombinasi antara model regresi berganda dan mediasi, yaitu variabel X berpengaruh terhadap variabel Z secara langsung dan tidak langsung mempengaruhi variabel Z melalui variabel Y. Model digambarkan sebagai berikut:

Gambar 2.3 Model Kombinasi Regresi Berganda dan Mediasi 4. Model Kompleks

Model ini merupakan model yang lebih kompleks, yaitu variabel X1 secara

langsung mempengaruhi Y2 dan melalui variabel X2 secara tidak langsung

Z

Y X

X

Y

mempengaruhi Y2, sementara variabel Y2 juga dipengaruhi oleh variabel

Y1. Model digambarkan sebagai berikut:

Gambar 2.4 Model Kompleks

5. Model Rekursif dan Non Rekursif

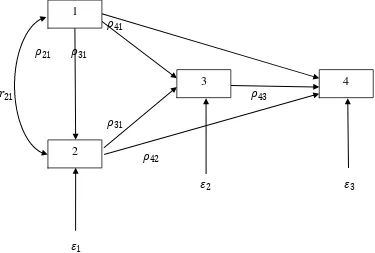
Dari sisi pandang arah sebab akibat, ada dua tipe model jalur, yaitu rekursif dan non rekursif. Model rekursif ialah jika semua anak panah menuju satu arah seperti gambar berikut:

𝜌41

𝜌21 𝜌31

𝑟21 𝜌43

𝜌31

𝜌42

𝜀2 𝜀3

𝜀1

Gambar 2.5 Model Rekursif X1

Y1

X2

Y2

1

3 4

Model sebelumnya dapat diterangkan sebagai berikut:

a. Anak panah menuju satu arah, yaitu dari 1 ke 2, 3, dan 4; dari 2 ke 3 dan dari 3 menuju ke 4. Tidak ada arah yang terbalik, misalnya dari 4 ke 1 b. Hanya terdapat satu variabel exogenous, yaitu 1 dan tiga variabel

endogenous, yaitu 2, 3, dan 4. Masing-masing variabel endogenous

diterangkan oleh variabel 1 dan error (𝜀1,𝜀2, dan 𝜀3).

c. Satu variabel endogenous dapat menjadi penyebab variabel endogenous lainnya, tetapi bukan ke variabel exogenous.

Model non recursif terjadi jika arah anak panah tidak searah atau terjadi arah yang terbalik (looping), misalnya dari 4 ke 3 atau dari 3 ke 1 dan 2, atau bersifat sebab akibat (reciprocal cause).

6. Model Trimming

Model Trimming adalah model yang digunakan untuk memperbaiki suatu model struktur analisis jalur dengan cara mengeluarkan dari model variabel bebas yang koefisien jalurnya tidak signifikan. Jadi, model trimming terjadi ketika koefisien jalur diuji secara keseluruhan ternyata

ada variabel yang tidak signifikan.Walaupun ada satu, dua, atau lebih variabel yang tidak signifikan, tentu perlu memperbaiki model struktur analisis jalur yang telah dihipotesiskan (Riduwan dan Engkos Achmad Kuncoro, 2008). Model variabel bebas dikatakan signifikan apabila nilai

probabilitasnya (Sig) ≤0,05.

2.2.5 Diagram Jalur dan Persamaan Struktural

Pada saat akan melakukan analisis jalur, disarankan untuk terlebih dahulu menggambarkan secara diagramatik struktur hubungan kausal antara variabel penyebab dengan variabel akibat. Diagram ini disebut diagram jalur (Path Diagram), dan bentuknya ditentukan oleh proposisi teoritik yang berasal dari

kerangka pikir tertentu.

X1 X2

𝜀

Gambar 2.6 Diagram Jalur Yang Menyatakan Hubungan Kausal dari X1

Sebagai Penyebab ke X2 Sebagai Akibat

di mana:

X1 adalah variabel eksogenus (exogenous variable) untuk itu selanjutnya variabel

penyebab disebut sebagai variabel eksogenus. X2 adalah endogenus (endogenous

variable), sebagai akibat dan ε adalah variabel residu ( residual variable), yang

merupakan gabungan dari: (1) Variabel lain, di luar X1, yang mungkin

mempengaruhi X2 dan telah teridentifikasi oleh teori, tetapi tidak dimasukkan

dalam model. (2) Variabel lain, di luar X2, yang mungkin mempengaruhi X2 tetapi

belum teridentifikasi oleh teori. (3) Kekeliruan pengukuran (error of measurement), dan (4) Komponen yang sifatnya tidak menentu (random

component).

Gambar 2.6 merupakan diagram jalur yang paling sederhana yang menyatakan bahwa X2 dipengaruhi secara langsung oleh X1, tetapi di luar X2,

masih banyak penyebab lain yang dalam penelitian yang sedang dilakukan tidak

diukur. Penyebab lain itu dinyatakan oleh ε. Persamaan struktural yang dimiliki

arah menggambarkan pengaruh langsung dari variabel eksogenus terhadap variabel endogenus.

X1

X2 X4

X3 ε

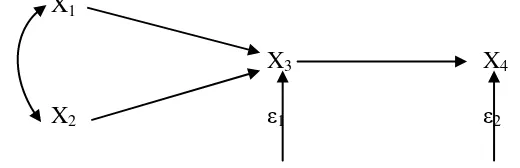
Gambar 2.7 Diagram Jalur Yang Menyatakan Hubungan Kausal dari X1,

X2,X3, dan X4

Gambar 2.7 menunjukkan bahwa diagram jalur tersebut terdapat tiga buah variabel eksogen, yaitu X1, X2, dan X3, sebuah variabel endogen (X4) serta sebuah variabel residu ε. Pada diagram di atas juga mengisyaratkan bahwa hubungan

antara X1 dengan X4, X2 dengan X4 dan X3 dengan X4 adalah hubungan kausal,

sedangkan hubungan antara X1 dengan X2, X2 dengan X3 dan X1 dengan X3

masing-masing adalah hubungan korelasional. Perhatikan panah dua arah, panah tersebut menyatakan hubungan korelasional. Bentuk persamaan strukturalnya

adalah: X4 =

ρ

X4.X1. X1 +

ρ

X4.X2. X2 +

ρ

X4.X3.X3 + ε

X1

X3 X4

X2 ε1 ε2

Gambar 2.8 Hubungan Kausal dari X1, X2, danX3 ke X4

Perhatikan bahwa pada gambar 2.8 di atas, terdapat dua buah sub-struktur.Pertama, sub-struktur yang menyatakan hubungan kausal dari X1 dan X2

ke X3, sertakedua sub-struktur yang mengisyaratkan hubungan kausal dari X3 ke

dan X4 =

ρ

X4.X3 .X3 +ε2 .Pada sub-struktur pertama X1 dan X2merupakan variabel

eksogen, X4 sebagai variabel endogen dan ε1 sebagai variabel residu.Pada

sub-struktur kedua, X3 merupakan variabel eksogen, X4 sebagai variabel endogen dan ε2 sebagai variabel residu.

2.2.6 Koefisien Jalur

Besarnya pengaruh langsung dari suatu variabel eksogenus terhadap variabel endogen tertentu, dinyatakan oleh besarnya nilai numeric koefisien jalur (path coefficient) dari eksogenus ke endogen.

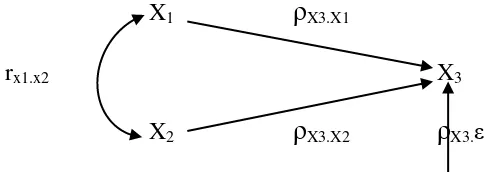
X1

ρ

X3.X1

rx1.x2 X3

X2

ρ

X3.X2

ρ

X3.ε

Gambar 2.9 Hubungan Kausal dari X1dan X2 ke X3

Hubungan antara X1 dan X2 adalah hubungan korelasional. Intensitas keeratan

hubungan tersebut dinyatakan oleh besarnya koefisien korelasirx1.x2 .Hubungan X1

dan X2, ke X3 adalah hubungan kausal.Besarnya nilai numerik koefisien

jalur

ρ

X3.X1 dan

ρ

X3.X2.Koefisien jalur

ρ

X3.εmenggambarkan besarnya pengaruh

langsung variabel residu (implicit exogenous variable) terhadap X3.

Langkah kerja yang dilakukan untuk menghitung koefisien jalur adalah:

diagram jalur, sehingga bisa tampak jelas variabel apa saja yang merupakan variabel eksogen dan apa yang menjadi variabel endogennya. 2. Menghitung matriks korelasi antar variabel.

𝑟𝑣𝑎𝑟𝑖𝑎𝑏𝑒𝑙 =

Formula untuk menghitung koefisien korelasi yang dicari adalah menggunakanProduct Moment Coeffisient dari Karl Pearson. Alasan penggunaan teknik koefisien korelasi dari Karl Pearson adalah karena variabel-variabel yang hendak dicari korelasinya memiliki skala pengukuran interval. Rumus:



3. Identifikasi sub-struktur dan persamaan yang akan dihitung koefisien jalurnya. Misalkan dalam sub-struktur yang telah diidentifikasi terdapat k buah variabel eksogen, dan sebuah (selalu hanya sebuah) variabel endogen

X_u yang dinyatakan dengan persamaan :

Kemudian hitung matriks korelasi antar variabel eksogen yang menyusun

4. Menghitung matriks invers korelasi eksogen, dengan rumus:

𝑟𝑒𝑘𝑠𝑜𝑔𝑒𝑛−1 =

2.2.7 Besarnya Variabel Eksogen Terhadap Variabel Endogen

Pengaruh yang diterima oleh sebuah variabel endogen dari dua atau lebih variabel eksogen, dapat secara sendiri-sendiri maupun secara bersama-sama.Pengaruh secara sendiri-sendiri (parsial), bisa berupa pengaruh langsung, bisa juga berupa pengaruh tidak langsung, yaitu melalui variabel eksogen yang lainnya.

Menghitung besarnya pengaruh langsung, pengaruh tidak langsung serta pengaruh total variabel eksogen terhadap variabel endogen secara parsial, dapat dilakukan dengan rumus:

1. Besarnya pengaruh langsung variabel eksogen Xuterhadap variabel

2. Besarnya pengaruh tidak langsung variabel eksogenus Xu terhadap

variabel endogenus Xk melalui hubungan korelasi dari variabel Xi =

𝜌𝑥𝑘𝑥𝑢

𝑥

𝑟𝑥𝑖𝑥𝑢

𝑥

𝜌𝑥𝑘𝑥𝑖

3.

Besarnya pengaruh tidak langsung variabel Xu terhadap variabel Ximelalui

variabel Xk = 𝜌_{𝑥𝑘𝑥𝑢}

𝑥

𝜌_{𝑥𝑖𝑥𝑘}

4. Besarnya pengaruh total adalah pengaruh lansung dijumlahkan dengan variabel tidak langsung.

5. Besarnya pengaruh simultan variabel eksogen terhadap variabel endogen adalah:

terhadap X_u atau besarnya pengaruh variabel eksogen secara

bersama-sama (gabungan) terhadap variabel endogen.

b.

𝜌

_{𝑥𝑢𝑥𝑖} adalah koefisien jalur ke-i, 𝑖 = 1, 2,…,𝑘

c.

𝑟

_{𝑥𝑢𝑥𝑘} adalah koefiesien korelasi variabel eksogen Xk dengan variabel

endogen Xu.

2.2.8 Pengujian Koefisien Jalur

perbedaan besarnya pengaruh masing-masing variabel eksogen terhadap variabel endogen, dapat dilakukan dengan langkah-langkah sebagai berikut:

1. Nyatakan hipotesis statistik (hipotesis operasional) yang akan diuji.

Ho :𝜌𝑥_𝑢𝑥_𝑘= 0 , Artinya tidak terdapat pengaruh variabel eksogen Xk

terhadap variabel endogen Xu.

H1 :𝜌𝑥_𝑢𝑥_𝑘 ≠ 0 , Artinya tidak terdapat pengaruh variabel eksogenus Xk

terhadap variabel endogenus Xu.

2. Gunakan statistik Uji yang tepat, yaitu: 1. Untuk menguji setiap koefisien jalur

𝑡

=

𝜌

𝑥𝑢𝑥𝑘

(1− 2

) ,..., ,

( 1 2 k u x x x

x

R 𝐶_𝑖𝑖

𝑛−𝑘−1

di mana:

i = 1, 2, …, k

𝑘

= Banyaknya variabel eksogen yang dalam sub-struktur

yang diuji.

𝑡

= Mengikuti tabel distribusi t , dengan derajat kebebasan

nk1

Kriteria Pengujian : Ditolak Ho jika nilai

𝑡

hitung lebih besar dari nilai

𝑡

tabel (𝑡0 >𝑡_{𝑡𝑎𝑏𝑒𝑙} ) dan sebaliknya

𝐹 =

𝑛 − 𝑘 −1 2

) ,..., ,

( 1 2 k u x x x

x R

𝑘 (1− 2

) ,..., ,

( 1 2 k u x x x

x R

di mana:

i = 1, 2, …, k

𝑘

= Banyaknya variabel eksogen yang dalam sub-struktur

yang diuji.

F = Mengikuti tabel distribusi F, dengan dk = (V1 ,V2) dengan

F_α(k, n – k – 1 )

Kriteria pengujian: Ditolak HO jika nilai F hitung lebih besar dari F

tabel atau 𝐹0 >𝐹𝑡𝑎𝑏𝑒𝑙.

2.3 Kemiskinan

Kemiskinan adalah keadaan dimana terjadi ketidakmampuan untuk memenuhi kebutuhan dasar seperti makanan, pakaian, tempat berlindung, pendidikan, dan kesehatan. Kemiskinan dapat disebabkan oleh kelangkaan alat pemenuh kebutuhan dasar, ataupun sulitnya akses terhadap pendidikan dan pekerjaan ( http://Wikipedia.com). Secara garis besar ada dua cara orang memandang kemiskinan, sebagian orang memandang kemiskinan adalah suatu proses sedangkan sebagian lagi memandang kemiskinan sebagai suatu akibat atau fenomena dalam suatu masyarakat (Dillon,1999:19).

sebagai salah satu akibat dari kegagalan kelembagaan pasar (bebas) dalam mengalokasikan sumber daya yang terbatas secara adil kepada seluruh anggota masyarakat. Paham ini mengemukakan konsep tentang kemiskinan relatif atau sering pula dikenal sebagai kemiskinan struktural.

Pandangan tentang kemiskinan sebagai suatu fenomena atau gelaja dari suatu masyarakat menghasilkan suatu konsep kemiskinan absolut, sejalan dengan konsep absolut ini, maka Bank Dunia mendefenisikan kemiskinan sebagai ketidakmampuan suatu individu untuk memenuhi kebutuhan dasarnya atau dengan kata lain prespektif dari garis absolut berada dibawah garis kemiskinan (poverty line). Garis kemiskinan adalah suatu ukuran yang menyatakan besarnya pengeluaran untuk memenuhi kebutuhan dasar minimum makanan dan kebutuhan non makanan, atau standar yang menyatakan batas seseorang dikatakan miskin bila dipandang dari sudut konsumsi. Garis kemiskinan digunakan untuk mengetahui batas seseorang dikatakan miskin atau tidak, sehingga garis kemiskinan dapat digunakan untuk mengukur dan menentukan jumlah kemiskinan.

Kemiskinan relatif menggambarkan tingkat kesejahteraan ekonomi seseorang (kelompok orang) yang relatif jauh dibawah kondisi ekonomi anggota masyarakat (kelompok) yang lain didalam suatu lingkungan masyarakat tertentu. Kemiskinan yang menimpa sekelompok masyarakat berhubungan dengan status sosial ekonomi dan potensi wilayahnya dikategorikan didalam faktor sosial ekonomi antara lain beberapa faktor yang berasal dari dalam diri masyarakat sendiri dan cenderung melekat pada dirinya seperti tingkat pendidikan dan keterampiloan yang rendah, tingkat kesehatan yang rendah dan produktivitas yang rendah. Yang dimaksud dengan potensi wilayah adalah faktor-faktor yang berasal dari luar seperti potensi alamiah, teknologi dan lain-lain. Kedua faktor tersebut menentukan aksesbilitas masyarakat miskin dalam memanfaatkan peluang-peluang ekonomi dalam menunjang kehidupannya.

Menurut Hadiwegono dan Pakpahan (1993:25) faktor-faktor yang menjadi penyebab timbulnya kemiskinan antara lain:

1. Sumber daya alam yang rendah.

2. Teknologi dan unsur penduduknya yang rendah. 3. Sumber daya manusia yang rendah.

4. Sarana dan prasarana termasuk kelembagaan yang belum baik.

relatif (Murni Daulay, 2009).Dengan demikian pertumbuhan ekonomi merupakan syarat bagi pengurangan kemiskinan.

Menurut Nugraheni, pengukuran akan pertumbuhan ekonomi memerlukan alat ukur yang tepat. Salah satunya adalah Produk Regional Bruto (PDRB).PDRB merupakan jumlah barang jasa akhir yang dihasilkan oleh suatu perekonomian dalam satu tahun dan dinyatakan dalam harga pasar. Baik PDB ( Produk Domestik Bruto) atau PDRB merupakan ukuran yang sifatnya global dan bukan merupakan alat ukur pertumbuhan ekonomi yang tepat karena belum mencerminkan kesejahteraan penduduk yang sesungguhnya, padahal sesungguhnya kesejahteraan harus dinikmati oleh setiap penduduk di negara atau daerah yang bersangkutan.

Menurut Nelson dan Leibstein (dikutip dari Sadono Sukirno, 1983) terdapat pengaruh langsung antara pertambahan penduduk terhadap tingkat kesejahteraan masyarakat. Nelson dan Leibstein menunjukkan bahwa pertumbuhan penduduk yang pesat di negara berkembang menyebabkan tingkat kesejahteraan masyarakat tidak mengalami perbaikan yang berarti dan dalam jangka panjang akan mengalami penurunan kesejahteraan serta meningkatkan jumlah penduduk miskin.

ini sering timbul terutama di negara yang tingkat perkembangan ekonominya masih rendah.

Salah satu faktor yang mempengaruhi kemiskinan adalah jumlah penduduk yang menganggur. Penganggur adalah orang yang tidak bekerja sama sekali atau bekerja kurang dari dua hari selama seminggu sebelum pencacahan dan berusaha memperoleh pekerjaan. Menurut Sadono Sukirno (1997) pengangguran adalah seseorang yang digolongkan dalam angkatan kerja, yang secara aktif sedang mencari pekerjaan pada suatu tingkat upah tertentu, tetapi tidak dapat meperoleh pekerjaan yang diinginkan.Pengangguran merupakan salah satu masalah ekonomi khususnya ekonomi makro.Masalah pengangguran yang menyebabkan tingkat pendapatan nasional dan tingkat kemakmuran masyarakat tidak mencapai potensinya yang maksimal.

Faktor lain yang mempengaruhi tingkat kemiskinan adalah pendidikan, pendidikan merupakan komponen penting dan vital terhadap pembangunan terutama dalam meningkatkan pertumbuhan ekonomi yang keduanya merupakan input bagi total produksi (Todaro, 2003) pendidikan juga berfungsi meningkatkan produktivitas. Selain dari itu kemampuan untuk menyerap teknologi memerlukan peningkatan kualitas sumber daya manusia.Oleh karena itu, pembangunan pendidikan merupakan prioritas pertama bagi setiap pemerintahan negara berkembang.Program pembangunan pendidikan yang dikembangkan cukup beragam, dimulai dari pemberantasan buta huruf, pendidikan keterampilan, sampai pengembangan pendidikan tinggi.