5_Fungsi - fungsi Kontinu

Analisis Real _- Fungsi-funpi Kontinu

5

FUNGST-FUNGSI

KONTINU

5.1

Fungsi-fungsi Kontinu

Pada bagian

ini

akan dibahas mengenai perilaku dau sifat-sifat yang

dimiliki oleh sekelompok fungsi yang sangat berperan dalam Analisis Real yaitu fungsi-fungsi kontinu. Kekontinuan fungsi merupakan salah satu topik inti dalam

Analisis Real.

Istilah kontinu sudah dipokenalkan sejak jaman Isaac Newton

(

1642-1747) yang mengaitkan dengan

grafik

kurva yang

tak

terputus. Tetapi pengungkapmnya masih belum tepat. Kerrudian pada tahun 1817 Bernhard

Bolzano

,lan

tahun 1821 Augustin Louis Cauchy mengidentifikasi bahwa

kekontinuan sebagai suatu

sifd

yang sangat berarti dari fungsi dan mencoba

membuat definisi yang lebih tepat. Tetapi pendefinisiannya dikaitkan dengan konsep

limit.

Oleh kaena

itu

pada tahun 1870

Karl

Weierstrass mencoba menyempumakan pengertian atau ide/gagasan mengenai kekontinuan ini.

Bagian pertama, pada uraian

di

bawah

ini,

dibahas mengenai

kekontinuan fungsi

di

satu

titik

dan kekontinuan fungsi pada suatu himpunan.

Selanjutqa

diperlihatkan kombinasi

dri

fungsi-fungsi

kontinu

yallg

mengftasilkan fungsi baru yang juga kontinu. Selain itu terdapat suatu sifat yang mendasar dan penting, bahwa suatu fungsi

png

kontinu pada suatu interval tertutup terbatas mempunyai nilai maksimum dan minimum. Demikian pula akan

dituqiukkan, bahwa untuk suatu firngsi kontinu, jika diberikan sebarang dua nilai

fungsi itu, maka terdapat suatu titik pada daerah asalnya sehingga nilai fungsi di titik itu merupakan nilai pertengahan dari dua nilai fungsi yang diberikan. Sifat-sifat seperti yang diuraikan di atas tidak dimiliki oleh fungsi-fungsi secara umun.

Pada bagian selanjutnya, diperkenalkan istilah kekontinuan serag:rm dengan beberapa aplikasiny4

salah

satu

diantaranya adalah mernbuat

aproksimasi firngsi kontinu dengan menggunakan fungsi-firngsi elementer (misalnya fungsi polinom).

Pada bagian terakhir, dibahas mengenai kaitan antara kekontinuan,

kernonotonan dan fungsi invers.

5.1.1

Definisi

Misallan

Ac

R,fungsi

f

:A+

Rserta

c

e

A

Fungsif

disebut kontinu di titik c jika dan hanya

jika

untuk setiap

e>

0 terdapat

6>

0, sehinggajikax €

A

dan

lx-.1

.6,

maka

_l(*)

_-(.)

I

.

".

Jika fungsi f tidak kontinu di c, dikatakan bahwa fungsi f diskontinu di c. Seperti halnya dengan definisi limit, definisi kekontinuan

di

satu

titik

dapat diformulasi dengan menggunakan notasi/istilah lingkungar-L seperti diungkapkan dalmr teorema di bawah ini.

r21 Kosim Ruhneta _-

hrDikMa

UPI 2006

An ulisis Real _- Fangsi'f*ngsi Kontinu

5.1,2

Teorcma

Statu fungsi

f

: A -+ R lantinu di titik

ce

A

_iika

dan hanya

_iika

di-berilran sebarang linglatngan-e

%(f(c)

dari f(c\ terdapat lingkungan-E

Y6(c) dari c, sehingga

jika x e

A

^

Vs(c), maka f(x)

e

Y"(f(c)) atau

dengan kata

lain

(A.t

%(c))

q

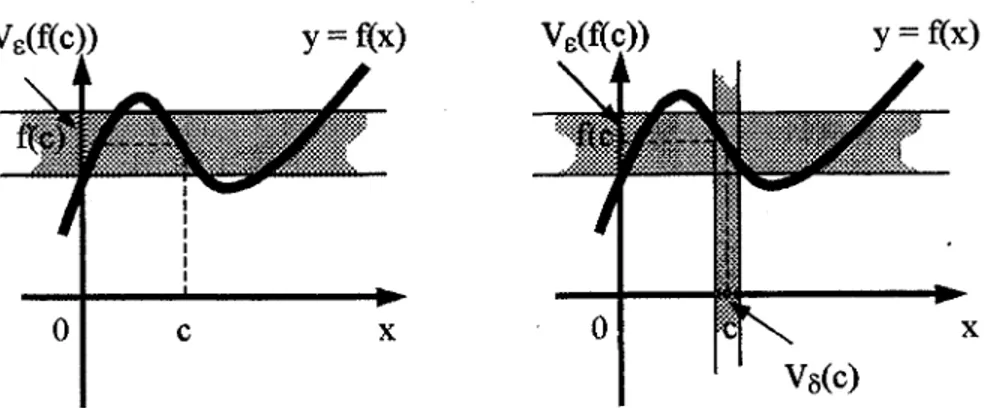
V*((c))

Ilustrasi dari teorema di atas dapat dilihat pada gambar di bawah ini.

Gambar5.I.l

Lingkungan

%(f(c)

menentukan lingkungan Vs(c)

Catatan:

(1) Jika c e A dan c titik limit dari

A

maka dengan membandingkan definisi 4.1.4 dan definisi 5.1.1, dapat dikatakan bahwa, fungsi

f

kontinu

di

c

jika

dan hanya

jika

f(c) = limf(x)

x-+c

Jadi, jika c titik limit dari

,\

maka tiga kondisi berikut harus dipenuhi supaya

funggsi f kontinu di c:

(i)

f

terdefinisi di c (f(c) nilainya ada)

(ii)

limit dari f di c ada

(

i

m

f(x)

ada di R)

x->c

(iii) nilai di (i) dan (ii) harus sama (f(c)

:

I i

m

f(x))

x-)c

(2) Jika

c e

A

dan

c

bukan

titik

limit

dari

A

maka

terdapat suatu

lingkungan-6 Vs(c) daric sehinggaAnVs (c)

=c.

Jadi

jikac

e Adan c bukan

titik

limit dari A "secara otomatis" fiurgsi

f

kontinu di

c.

Ini

menjadi kurang menarik, sehingga kondisi (1) dipandang sebagai suatu

karakteristik untuk kekontinuan fungsi dititik c.

Dengan sedikit modifikasi dari bul$i teorerna lfunit fungsi 4.1.8, berikut ini diberikan teorema kriteria barisan untuk menguji kekontinuan fungsi di satu

titik.

y:

(x)

Anatitis Real

-

Fanpi'fungsi Kontka

5.1.3

Krtteria barisan

untuk Kekontinuan

Suatu _fimgsi

f

: A' -+ R kontinu

di

titik c e

L

j ika dan

_lgya

i ika untuk

setiapbaisant*"la,Ayangkotwergenlrea,barisan(f(x"))konvergen

ket(c).

Berikut

ini

teorema yang merupakar triteria kediskontinuan sebagai suatu konnsekuensi

d*

;;e;ta

-o

ua, -(

uu"ai"gt*

dengan kriteria divergensi

4.1.9 (a) dengm L = (c) ).

5.1.4

Kriteria

Kediskontinuan

MisalkanAcR,f:A+R'danceAFungsifdiskontinudititikc

iika dnl

norryo'ii*o'i)a'yi

io'"

baisan (xJ ai A'yang konvergen ke "c,

tetapi barisan (f(c)) tidak k'onvergen kc _f(c)'

Iika semua pembahasan

di

aus mengeryr,\e'koryinual suatu fungsi di satu titik, maka berikut ini akan rlibahas mengenai kekontinuan fungsi pada suatu

himpunar.

_..

_- _r^

Secara sederhana, suatu fungsi disebut kontinu pada suatu himpunan

jika

dan

nada himmrnan

itu-

Secara formal

il*v"

jin"

firngsi itu kontinu di setiap

titik

pada

hi-pllq'P'

_.l

kekontinuann,"g'ipuau'"utoht-p,*-rlinyaakmolehddrnisiberikutini'

5.1.5

Definisi

MisaltanesR,danf:A-+R.FungsifkontinupadaA'iikadanhanya

fungsif kontinu di setiap

titikx

e A'

5.1.6

Contoh

I.

Fungsi konsan f(x)

:

b

kontinu pada R

Pada contoh

+.t.1

(a) dapat dilihat bahwa'

jika

c e

R'

maka

lim

f(x)=b.

x-tc

Krcna

f(c) = b, maka I i m f(x) =

f(c)'

Jadi fungsi f kontinu di

x->c

setiaptitikcdiRBerdasrkaudefinisi5.l'5diatas,makafungsif

kontinu Pada

R

2.

Fungsi

d*gu,

aturaxr g(x) = x kontinu pada R'

Parla

cont&

4.1.7

(b)

dapat dilihat bahwa'

jika

c e

R'

maka

lim

g(x):c.

x-)c

Karena g(c) = c, maka I i

m

g(x) = g(c)' Jadi fungsi g kontinu di

x-)c

Analhis Real

_-

Fangsi-fungsi Kontinu

setiap titik c di R. Berdasarkan ddrnisi 5.1.5 di atas, maka fungsi g

kontinu pada R.

3.

Fungsi dengan atur:m

h(x):

x2 kontinu pada R.

Pada contoh a.I.7 (c) dapat dilihat, jika c e R, maka I i

m

h(x)

:

62.

x-)c

Karena h(c)

:

c2, maka I i m h(x)

:

h(c). Jadi fungsi h kontinu di

x-)C

setiap titik c di R. Bqdasarkan definisi 5.1.5 di atas, maka fungsi h

kontinu pada R.

4.

Fungsi

f

terdefinisi pada R dengan atuan:

r/*\

_

_{[ t}

iika

x

bilanganrasional

r\^''

_-

|

o

_lita

x

bilangan irrasional

Fungsi dengan aturan seperti di aas disebut/angsi Diichlet. Fungsi Dirichlet di_skontinu di setiap titik di R.

Sebagai bukti, jika c bilangan rasional, misalkan ( x, ) suatu baiisan

bilangan irasional yang konvergen

ke

c (

teorema kepadatan

menjamin keberadaan barisan seperti ini

_).

Karqa f(x,)

=

0 untuk

setiap

n

e

N, diperoleh lim

(""):0,

sedangkan f(c)

:

1. Oleh

karena itu fungsi f diskontinu di setiap bilangan rasional c.

Di sisi laiq

jika

b bilangan irasional, misalkan ( y" ₎ suatu barism

bilangau rasional yang konvergen ke

b.

Karena f(yo)

=

1 untuk

setiap

n e

N,

diperoleh lim

(f(y,) =

1, sedangkan

(b)

=

O.

Oleh karEra

itu

fungsi

f

diskontinu

di

setiap bilangan irasional

b.

Jadi

ftssinpulannya funggsi f diskontinu di setiap titik di R.

5. Misalkan _{A = {} x e R I x > 0

}.

Untuk setiap bilmgm irasional x > 0

definisikan h(x)

=

g.

Untuk bilangan rasional di A dengan bentuk

rnln, dimana bilangan

asli

m,

dan

n

tidak mempunyai faktor

posekutuan kecuali 1, definisikan h(nr/n)

:

l/n

(

kadang-kadang

tlidefinisikan juga h(0) = 1).

Fungsi h kontinu disetiap bilangan irasional di

,\

dan diskontinu di setiap bilangan rasional di

A

Sebagai bukti, misalkan a > 0 bilangm rasional sembarang, dan ( x" ₎

suatu barisan bilangan irasional di A yang konvergen ke

a.

Kaena lim (h(x") = 0, sedangkan h(a) > 0, maka h diskontinu di

a.

Di sisi

lain,

misalkm

b

bilangan irasional senrbrang

dan

a >

0. Berdasarkan sifat Archimedes terdapat bilangan asli

ne

sehingga

l/no <

e.

Terdapat hanya sejumlah hingga bilangan rasional dengan penyebut lebih kecil dari no pada interval (b

_-

1, b + 1). ( Mengapa?). Oleh karena

itu

6 > 0 dapat dipilih cukup kecil sehingga lingkungan

O

- 6, b - 6) tidak memuat bilangan rasional dengan penyebut _lebih

kecil dari no.

Jika!*

-bl<6,

x

e

An makalnf.>

_-fiOil.e.

Jadi dengan demikian ftngsi h kontinu di bilangan inasional b.

Analitis Real

-

Fnngsi-fu ngsli Kontinu

5.1.7

Bahan

Diskusi

1.

Buktikm teorema 5.1.3 tenAng kritoia barisan untuk

kekontinuau-2.

MisalkanAc

R

dan

f

:

A+

R

kontinudititikc

e

A.

Tunjukkanbahwa untuk setiap e > 0, terd4at suatu lingkungan-8 vo (c) sehingga jika x, y

e A

n

vs (c) maka

_{lfu) -}

f0)

I < e.

3.

\disalkan

f

:

R

+

R

kontinu di c

dan(c)

>

0.

Tunjukl€n, bahwatodapat suatu lingkungm$ Vs (c) sehinggajika x e Vs (c), maka

(x)

> 0'

5.{.8

Latihan

1.

l4isalkan a < b <

c.

Misalkan pula frrngsi f kontinu pada _[q b], dan fungsi g

kontinu pada _[b,

o]

serta

f(b):

g(b). Definisikan h pada [a, c] oleh h(x) =

(x)unhrkxe[a,b]danh(x)=g(x)untukx€(b,c].Buktikanbahwa

h kontinu pada _[a c].

2.

Jika x e R, didefinisikan I x

]

adalah bilangan bulat terbesar yang lebih kecil

atau sma dengan x. Fungsi x

+

[ x

]

disebut fungsi bilangal bulat terbesar' Tentukanlah

titlt-titit

kekontinuan dari fungsi-fungsi di bawah ini:

(a)

(x)=[x]

O)

g(x):xlxl

(c)

h(x)=

[sinx]

(d) k(x)= [

Ux]

3.

Mirutt*

Ac

&

dsrf

:

A+

R

kontinu

dititik

c

e

A

Turi,kkm, untuk

setiap

e > 0 terdapat lingkungm$ %(c)

d6i

s 5ehingga jika x,

y e

An

yrlst,maka

_l(*)

_-r0)l

.r.

4.Misalkanf:R-+Rkontinudicdanf(c)>0'Tunjukkan,terdapat

lingkungan-S %(c) dari c sehingga jika x e V6(c), maka

(x)

> 0'

5.

Misalkan A

c

B

c &

f

: B

+

R dan g adalah restriksi dari f pada A ( g(x)

:

(x)

untuk setiap x e

A).

(a) Jikafkonyinu di c e A" tunjukkan bahwa g kontinu di

c-G)

r*j,'tt-

dengan contoh bahwa jika g kontinu di c, maka ini tidak perlu

mermgakibatkar

f

kontinu di

c.

o

6.

Misalkan

f

:

R

+

R

kontinu pada R dan f(r) =

0

untuk setiap bilangan

rasional r. Buktikan, bahwa

(x)

= 0 untuk setiap x e R'

7.

Misalkan A

=

(0, @) dan k: A -+ R didefinisikan sebagai berikut, untuk

x

e

d

x

irrasional didefinisikan k(x) = 0, dan untuk

x

e

A

x

rasional dengan bentuk m/n dengan m,

n

bilangan asli, m dan

n

tidak mempunyai faktor

sekutu kecuali

t,

Aaennisltan k(D =

n.

Buktikan, bahwa k tak terbatas pada setiap interval di

A

Tunj r kkan pula bahwa k diskontinu di sebarang titik dali

A

8.

Misalkm

f

: (0,1) _-+ R terbatas tetapi limimya di x = 0 tidak ada Tunjukkan,

terdapat dua barisan

(x")

dan

(yJ di

(0,1) dengan masing-masing limitrya 0 teapilim

((xJ)

dan lim ( f(y") masing-masing ada tetapi tidak sama.

125

Analisis Real

_-

Fungsi-fungsi Kontinu

5.2

Kombinasi Fungsi-fungsi Kontinu

Misalkan

A c R, f

dan

g

masing-masing adalah fungsi yang

didefinisikan pada A ke R ssta b e

R.

Jumlah, selisih, hasilkali, dan kelipatan

fungsi yang boturut-turut dinyaakan oleh

f

+

g

f

-

g, fg, dan

bg

pada bab terdatrulu telah diddrnisikan. Demikian pul4 jika h:

A

+

R sehingga h(x)

*

0

untuk semua

x €

A

telah didefinisikan hasil bagi fungsi yang dinyatakan oleh flh.

Di

bawah

ini

diperlihatkan suatu teorema yang berkaitan dengan penddnisian di atas. Jika diperhatikan, teorema ini serupa dengan tgorema 4.2.4

pada bab 4 mengenai limitfungsi.

52.1

Teorcma

Misalkan A

c

R,

f dan g masing-masingfungsi dari Ake R serta cr e R.

Jika c e

_d

f dan g kontinu di o, maka :

(a)

f + g, f

_-

g,fg, dan

af

kontinu di c

(b)

Jika

h:

A-+

Rkontinu

dic

e Adanh(x) + 0untuk setiap x

e

d

maka flh kontinu di c

Bukti:

(a)

Jika

c e

A

bukan

titik limit

dari

_A

maka secara 'ootomatis" kesimpulan terbukti. Oleh karena itu misalkan c adalah titik limit dari A.

Karena f, dan g kontinu di c, maka '

lim(x)

=

(c)

dan

limg(x)=g(c)

x-)c

x-+c

Berdasarkan teorema I .2.4 (a), maka:

tim

(f+

gXx):

limf(x) + lim

g(x):(c)

+ g(c) = (f + gxc)

x-+c

x-+c

x-)c

Oleh karena itu f + g kontinu di c.

Dengan cara yang serupa, untuk yang

lainnya

silakan penrbaca mernbuktikan sendiri sebagai latihan.

(b)

Karena c € A, makah(c)

*

0. Teapi karenah(c;

:1i-

h(x), dan

x

-+c

berdasarkan teorerna 4.2.4 (b) diperoleh:

(flexc) = f(c/h(c) =

lim

(x)Aim _.F(x) =

lim

( flhXx) oleh karena itu flh kontinu di

c.

x

_-)

c

x

-)

c

x

-)

c

Teorema

berikut

ini

merupakan konsekwensi

dari

teorema 5.2.1, digunakan untuk setiap

titik

dari himpunan

A

Secaa formal, teorema tersebut

dinyaakan sebagai berikut:

Analitis Real

-

Ftngsi-fingsi

Kofiiw

5.2.2

Teorema

Jika

Ae

R'

dan f, gmasing-masing fungsi yang kontinu dari A ke R' serta b eRmaka:

(a) Fungsi-fui6,

*

E, f

-

E, fg' danbf masing-masing kontinu

pada

A

@)

Jikah:

e'+

yiintto"

pia"

ldanh(x)*0

untukxe

A"maka fungsi hasilb agi flh lwntimr Pada A

Catatan: Jikarp:

A+R,

Ar

=

{

x e

AIQ(X)

t0 }'

makahasilbagiflrp didefinnisikan pada hinopunan Ar

oleh:

_,,*\

igqXrl

= 1x/9(x)

untukxeAr

""""""(-')

Jika

I

kontinnu di

titik;A; ,*urortri

9r

dari a pada Ar iugakontinu di

ceAr

Berdasarkan teorema 5.2.1 (b) digunakan pada

gr'

maka flrpr fontinu di

c e

A

Karcna (f/q)(x)

=

(Agt)l;i;*i

x e-er' .mata flrp kontinu

di c e Ar

Dengan.*u.r.*pu,'i*

tdan.q.

kontinu ppada

A

maka fimesi

f/o

yang

aiAehnisitan pada At, kontinu pada A1

5.2.3

Gontoh

1.

Jika P suatu firngsi

untuksetiaPxeR,

= I i mp(x)

oolinom sehingga p(x) = aoxo +

a"-tx"-t

*

'."'

*

a1x* 8o

';}.l1*d^iri*

rii"it untuk tungsi polinim vaitu p(c)

x-+c

untuk sembarang c €

&

maka fungsi polinim p kontinu pada R

2.

Jika p da q masing-masing fuirgsi polinom pada R' maka terdapat sejumlah hinggatl,r,...,

*'rt*-'t*;d;tiq'

Jikax

#

{ cr1'

"''cuo}

makaq(x) +

0

sehinggu Ouput OiJtn'isikan firngsirasional ryang dinlatakan

oleh:

r(x)

=p(x/q(x),

untukx

4

{ ct'1,

"',

cr.' _}

Oleh karena itu diPeroleh:

R(c) = P(c)/q(o) =

sehingga fungsi rasional

r

kontinu di c'

Karena

,

.*uu*og"tl*g*

r*"r

yang bukan merupakan akar dari

q,

dapat

disimpulkan

bah;;;;i;;d

r-kontinu

di

setiap bilargan real vang

merupakan domainnYa.

3,

Akan ditunjukkan bahwa fungsi sinus kontinu pada R'

Untuk setiaP x,

r,,

jrt rtruti,

(buktiuntuk

lsinrl

<

lzl

silahtan

lim

P(x/q(x)=limr(x)

x-)c

x

->c

dan I cos

,l

<l

penrbaca membuktikan sendiri )

An alisis Real * Fun gsi-fangsi Kontinu

sin x

_-sin

y =

2

sin(ll2(x-y))

ms (1/2(x

+y).

Oleh lkarena iitu, jika c G

R,

diperoleh:

lsin*-sincl

<

z.ll2lx-.1.t

=

l*-.

I

Dari sini dapat disimpulkan fuagsi sinus kontinu di c ( mengapa? _). Karcna c sembarang, maka firngsi sinus kontinu pada

R

Untuk sela4juhy4 silahkan pembaca membuktikan sendiri, bahwa fungsi

kosinus kontinu pada

Rl

Demikian

pula

untuk fungsi-fungsi tangen,

cotangm, secan dan cosecan masing-masing kontinu pada domainnya ( ingat,

tan x

=

sin x/ cos x _).

5,2.4

Teorema

MisallanAcR, f

_:A+R

dq

lfl

aiar@"itikanoleh:

I

rl

r*l

=

l(*)

|

,untuk x e A

(r)

Jika f kontinu di titikc e Aa matm

ltl

lantinu at c

(ii)

Jika f lCIntinu pada Aemata

ltl

*rntin

pada

A

Bukti:

Ini merupakan konsekuensi dari bahan diskusi 4.2.10 _Q)

5.2.5

Teorema

MisalkanAc R,

f

: A -+

R

dm(x)

>

0,

untuk setiap x e

A

Misalkanpula

{f

didefinisikanoleh:

({0(*)

=

{(r),

x e

A

(r)

Jika f

kantinudititikce

ly

mata.,lf

kantinudic

(ii)

Jika f trontinu pada A, matra ,l

f

trontinu pada

A

Bukti:

Ini merupakan konsekuensi dari bahan diskusi 4.2.10 (4)

Komposisi dari Fungsi-fungsi Kontinu

Di

bawah

ini

diberikan suatu teorema mengenai kekontinuan fungsi komposisi dari dua buah fungsi yang dibaikan yang masing-masing kontinu. Secara formal teorema tersebut dinyatakan sebagai berikut:

5,2.6

Teorcma

Misalkan A, B

cR,

f

:

A-+R

dang:

B+R

masing-masingadalah fungsi sehingga

(A)

c

B.

Jikaf kontinu di c e

\

dan gkontinu

dib:f(c)

_{eB ,}

mala knmposisi

gof:A-+R

kontinudic.

Analisis Real

_-

Fan gsi-fanpi Konthu Buliti:

Misalkan V"(gO)) adalah sembarang lingkungan+ dari

g(b)'

Karena g kontinu di b

:

f(c), maka terdapat suatu lingkungan-8

dai

b yaitu

%O)

atau

Vs(f(c) sehingga

jikay

e B

n

V6@) maka g(v) e v"(g(b))'

"""

_:""(*)

Karerla f kontinu di c, maka untuk lingkungan

%(f(c)

di atas, terdapat

lingkungan-y

dari

c

yaitu Vr(c) sehingga

jika

x e

A

n

Vr(c)

_'

maka

r1x) e VoG(c)).

Selmjutnya,karemf(x)eBmakaf(x)eBnvo(f(c))'Berdasarkan(*) ini mengakibatkan (g o _D(x)

:

g(x))

e %(g(b)).

-Karena

%(g(b))

sembarang lingkungan-e dari

g@)

maka

(g o

0

kontinu di c.

52.7

Teorcma

MisalkanA, B E

R,

f

: A

+

R kontinupada Adan

g:B

+R

kontinu padaB

Jikat(A)c.Bmatrafungsilramposlsigof:A+RkontinupadaA.

Bukti:

Teorema di atas merupakan akibat dari teorema 5.2.6,iikafi'rngsi f dan g

berturut-turut kontinu di setiap titik dari A dat B'

Teorema

5.2.6

dan

5.2.7

sangat bennanfaat dalam menentukan bahwa

suatu fungsi tertentu adalah kontinu iebagaimana dipolihatkan pada contoh

berikut dibawah

ini.

Kedua teorema

di

atas sering digunakan dalam banyak

situasi

fli

mana

jika

digunakan dengan definisi kekontinuan secara langsung akan menjadi sulit.

5.2.8

Gontoh

1.

Misalkang(x)=

lxl,

x e R.

Dengan menggunakan ketidaksarnaan,segitiga akan diperoleh:

I g(*)

-

g(c)l

<

I

*

-"1

untuk setiap x, c e R'

Oleh karena itu g kontinudi c e

R

(mengapa?)

Jika

f

: A

+

R

sembarang fungsi yang kontinu

pp+

A,

maka berdasarkan teorema

5.2.7

akan mengakibatkan

g

o

f = lfl

kontinu pada

A.

Ini

merupakm juga sebuahbukti lain dari teorcma5'2'4'

2.

Misallkanh(x)={x,

untuk

x

>0

Dari teorema

brisan

3.2.10 dm teore,ma

5.1.3

maka diperoleh bahwa h

kontinu di sebarang c > 0.

Jikaf:A+RkontinupadaAdanjika(x)>0untuksetiapxed

maka dari teorema 5.2.7 ;kandiperoleh hasil bahwa h o

f =

{

f

kontinu pada

A

Ini

merupakan sebuah bukti lain dari teorema 5'2'5

Analhis Reol

_-

Fungsi-fungsi Kontinu Misalkan s(x)

:

sin x untuk x e R.

Dalam contoh 5.2.3

_Q)

terlihat bahwa s kontinu pada R.

Jika

f

: A -+

R

kontinu pada

A

maka bardasarkan teorema 5.2.7, fungsi

s o

f

kontinu pada

A.

Secara khusus, jika

(x)

=

llx

_,

uutuk x

* 0,

maka

fungsi g(x) = sin (1/x) kontinu di setiap titik c

*

0

52.9

Bahan

Diskusi

1.

Misalkan

f,g

masing-masing didefinisikan padaR dan

ceR.

Misalkan Pulal

im

f(x)

=b

dan gkontinu di b.

x

-+c

Tunjukkan, bahwa I i m (g o 0(x)

:

gO)

x

-)c

Bandingkan dengan teorema

5.2.7

dan soal latihan 5.2.10

(4),

apa yang dapat dikomentari dari hasil ini?

2.

Misalkan

f,

g

masing-masing kontinu dari R ke

R,

dan

(r) :

g(r) untuk

-

_{setiap bilangan rasional}

_r.

Benarkah pernlataan bahwa f(x)

=

g(x)

untuk

setiap x e R.

3.

MisalLan

{

g

:

R

+

R masing-masing kontinu di titik

c,

dan h(x)

=

sup

{

f(x), g(x)

_}

untuk

x

e

R.

Tunjukkan bahwa h(x)

=

%(f(x)

+

g(x)) +

yrlf$)

_-

g(x)

|

untuk setiq x e

R.

Gunakan ini untuk menunjukkan bahwa h kontinu di c.

4.

Misalkan g : R -+

R

mernenuhi hubungan g(x + y) = g(x)g(y) untuk setiap

x, y di

R.

Tunjukkan, jika g kontinu di x =

0,

maka g kontinu di setiap

titik

dari

R.

Juga tuqfukkan,

jika

g(a)

:

0 untuk suatu

a

e

R,

maka g(x)

:

0 untuksetiapxeR.

5.2.10

Latihan

1.

Tunjukkanbahwajikaf

:A+

Rkontinupada

Ac

R,

n e

N,

makafungsi f " yang didefinisikan oleh f "(x)

:

(f(x))" untuk x e

A,

kontinu pada

A

2.

Berikan contoh suatu fungsi

f

dan

g

keduaqa diskontinu di

titik c

e

R

sehingga:

(a) jurnlah f +

g

kontinu di c. (b) hasil

kdi

fg kontinu di c.

3.

Misalkan x

-+

_{[ x}

_]

menyatakan fungsi bilangan bulat terbesar ( lihat soal

latihan 5.1.S (2) _). Tentukan titik-titik kekontinuan dari firngsi f(x) = x - [

*]

,

xeR.

Anolisis Real * Fungsi-fanpi Kontinu

4.

Misalkan firngsi g diddlrisikan pda R oleh g(1) = 0, dan g(x) = 2 jika x

*

1'

Misalkan pula f(x) = x

*

I

untrksetiap x e R'

Tunjukkan I i

m

(g o _0G)

*

G o 0(0). Mengapatidak berte,ntangan dengan

x

+0

teorcma5.2.6?

5.

Berikan contoh suatu fungsi

f

_{: [0,}

l]

+

R

yang diskontinu di setiap titik dari

[0, 1] tetapi

lfl

tontinu Pada [0,

ll.

6.

Misalkan h : R

+

R kontinu pada R dan menrenuhi

h(rrtlr)

= 0 untuk setiap m e

Z,n

e

N.

Tunjul&ao, bahwah(x):0 untuk setiap x e R'

?.

Misalkanf:R+R

kontinupadaR,

danmisalkanP={xe

n I (x)>0}'

Jika c e P, tunjukkan, bahwa terdapat suatu lingkungan Vo(c)

c

P'

g.

_Jikafdang

keduanyakontinupad4&

danmisalkanS=txen

I

f(x)

> g(x) _). Jika (s,)

c

S dan lim (s") = s, tunjukkaq bahwa s

e

S'

9.

Suatu fungsi

f

:

R

+ R

disebut *additivd'

jika

dan hanya

jlta

_frram

f(x + y) = _rtx) + f(y) untuk setiap x,

y

di

R

Buktikan, jika f kontinu di suat, titik xo, maka f kontinu di seti4 titik dari R.

10.

Misalkan

f

suatu fungsi additive kontinu pada

R'

Jika c =

(l),

tunjul&an f(x)

:

cx untuk setiap

x

e

R.

( Peunjuk Terlebih dahulu, tunj'rkkan bahhwa

jika r bilangan rasional, maka

(r)

= cr. ).

5.3

Kekontinuan Fungsi

pada

lnterval

Fungsi-firngsi yang kontinu pada interval

,

nnempunyai sejumlah

sifat-sifat yang sangat

perti"g

yaog tiaak

dimiliki

oleh fungsi-fungsi kontinu

u**"yrl

paaa _{Uanasan Ai Ui*uU ini, akan} dibahas beberapa sifat-sifat penting

itu dengan beberapa aPlikasinYa.

5.3.1

Definisi

suatu _fungsi

f

: A

+ R

disebut terbatas pada

Aiika

dan hanya

_iika

terdapat suatu bilangan realM> 0 sehingga

l(x)

I < M

_,

untuk setiap

xeA

Dengan perkataan lain, suatu firngsi terbatas pada suatu himpunan

jika

rangenya (dieralr,hasil) terbatas dalam

R.

Ilntuk mengatakan bahwa suatu fungsi

At

terlaEs pada himpunan ymg diberikan adalah dengan mengatakan bahwa

An alisis Real _- Fungsi-fungsi Kontina

tidak terdapat bilangan yang menjadi batas untuk rangenya Secara matematis

formal, suatu fungsi tak terbatas

p@

himpunan A

jika

diberikan sernbarang M >

0,

terdapat titik xr.,r e A sehingga

l(x)

I > M.

Sebagai contoh, fungsi

f

yang diddefinisikan pada interval A

=

(0, oo)

oleh

f(x) =

l/x

adalah tak terbaas pada Ao sebab untuk setiap M > 0 terdapat

(dapatdiammbil)xua:

l/(M+

l)

sehinggaf(xy):l/xu=M+ I

>M.

Contoh

ini menunjulkan bahwa fungsi kontinu tidak perlu terbatas.

Pada teorema di bawah ini, ditunjukkan bahwa suatu fungsi kontinu pada suatu interval totentu perlu terbatas.

5.3.2

Teorcma Keterbatasan

Jikal=[a"bl

interval tertutup terbatas danf

:I->R

kontinupadal,

malu _fungsi f terbatas padaI. Bukti:

Andaikan fungsi f ak terbatas pada I.

Ini

berarti untuk sembarang

n e

N,

terdappat Karena

I

terbatas,

maka

barisan

X

=

(*")

x,eI

sehingga

lr(*Jl

to.

terbatas. Menurut

teorema Bolzano-Weierstrass

(untuk barisan) terdapat baisan bagian

X'

:

(x-)

dri

X

yang konvergen ke suatu bilangan

x.

Kemudian, karena

I

tertutup dan unsur-unsur

dri

X'

tedetak

pada

I,

maka

x

e

I

(torema barisan dalam Bab

3).

Karena f kontinu di

x

e

I, maka

baisan

(

(&")

₎

konvergen ke

(x).

Oleh karena itu barisan (

(x*)

₎

haruslah terbatas. Tetapi ini konfiadiksi dengan

I

fG-)

_l,

+

>

r

untuk

r

e N.

Jadi pengandaian ftakterbatas padaladalah salah, yangbenaradatah fterbatas

padaI.

Dapatlah pembaca memberikan beberapa contoh, bahwa invers dari

teorema di atas belum tentu berlaku.

Teorcma Maksimum-Minimum

Sebelum sampaibpada t@rema mengenai maksimum-minimum, di bawah

ini

terlebih dahulu diberikan definisi yang menerangkan pengertian maksimum mutlak dan minimum mutlak.

5.3.3

Definisi

Misalkan A

_{c &}

dan

f

: A -+ R. Fungsi

_f

disebut mempunyai malaimum

mutlak pada Ajika dan hanya

jika

terdapat suatu

titikx*

e Asehingga

(x*)

> f(x), untuk setiap x e A.

Fungsi

f

disebut mempunyai minimum mutlak pada A

jika

dan hanya

jika

terdapat suatu titik x. e A sehingga

(x.)

< f(x) , untuk setiap x e A Titik

x*

adalah titik nalaimum mutlak untuk

f

pada

A

dan

titik

x-adalah titik minimum mutlak untukf pada A"

jika

masing-masing

titik

ada.

An alisis Reol

-

FungsLfangsl Kontina

Perlu dicaUt bahwa suatu ftngsi kontinu pada

_A

tidak perlu memrpunyai

maksimum atau minimum mutlak pada

A

Sebagai contoh, f(x)

: l/x

tidak

mempunyai maksimum mutlak dan minimun mutlak pada himpunan/interval A = ( 0, co

)

( lihat gambar 2.3.1). Fungsi f tidak merrpunyai maksimummutlak

oada

A:

( 0. co

)

krena f tak tobatas di atas pada

A

dan tidak m€muat titik 0

:

_{inf {}

_{f(D [}

_*

_e A

_].

Fungsi di atas juga tidak mempunyai maksimum mutlak dan minimum mutlak.jika dibatasi pada himpunan

(0,

l),

teapi firngsi itu

mempunyai maksiiltum mutlak

dm

minimum mutlak

bila

dibatasi pada

ni^p**

tr,

z].

selanjunya fungsi

(x)

=

l/x

mempunyai rnaksimum mutlak

tetapi tidakme,mpunyai minimum mutlak bila dibatasi pada himpunan _[1'

*

₎

dT

tiAui

...p*ya

-atsi*r*

mutlak it41 minimum mutlak bila dibatasi pada

(1, .o _).

Jika suatu fungsi fungsi mempunyai titik maksimum mutlak, maka

titik

ini tidak perlu

nik

(tuigeal).iebagaicontoh fungsi g(x) = x2 yan di4efial5ikan

untukx

e

A=

_[-1,

I

_]

merrpunyaiduatitikx=-l

danx=

-l

yangmasing-masing muupakan

titit

matsimum mutlak pada

A

dan titik x = 0

-di mana

titik

itu meiupakan titik minimum mutlak pada A ( lihat gmbar

5.3.2).

Suatu contoh

khusus/&sdms yaitu ftngsi konstan h(x) =

l,

setiap titik x e R merupakan

titik

maksimummutlak dan minimum mutlak dai h

Gambar 5.3.1 Fungsi

f(x):

l/x

(x>o)

Gambar 5.3.2 Fungsi g(x) = 12

r

l*l

<

t;

5.3.4

Teorcma

Maksimum-minimum

Jikal=

[ a, b

]

interval tertutup terbatas danf

:l

-+

R

kontinu padaI, malraf mempinyai mataimum mutlalc dan minimum mutlak'

Bukti:

Misalkan f(D

:

_{{ f(x) I}

x e

I

_}.

Menurutteorema

5'3'2,

f(D

terbatas pada

R.

Selaniutrya, misalkan s* = sup

(D

dan

s.

= inf f(f)' Akan tlitunjukkan, terdQat titik x+ dan titik

x'

di I sehingga

s* =

f(x*)

dm

s,

=

f(x,).

Analisis Real _- Fungsi-fangsi Kontinu

Karena

s*

= sup

(D,

_iika n e

N,

maka s* -

l/n

bukan batas atas dari

F(t). Akibahya terdryatbilangan x" e

I

sehingga :

s*-iln<f(x")Ss*,rmhrksetiapneN

...

...,(1) Karena

I

terbatas, maka barisan

X

:

(x")

terbatas. Dengan mengggunakan

teorema Bolzano-Weiersrass

(

Analisis

Real

1),

terdapat barisan bagian

X'

=

(x*)

dari

X

yang konvergen ke suatu bilangan

x*.

Kemudian, katena

uruilHmsur dari

X'

terletak pada

I

₌

_[a,

b],

maka menurut teor€ma barisan

(Analisis Real

l),

x+

e I.

Selar{utnya, karena

f

kontinu

di

x*,

maka

lim f(x*) =

(x*).

Dari (1) diperoletr:

s* -

l/n

<f(x*)

S

s*,

untuk setiap

r

e N

Berdasarkan teorema

Apit

dalam

barisan,

dapat

disimpulkan, bahwa

lim

(f(u)

= s*. Oleh karena

itq

diperoleh:

f(x*) = lim (

(x*)

₎

-

s+ = sup f@

sehingga x+ perupakan titik maksimum mmutlak dari f pada I.

Di

bawah

ini

dibberikan suatu

teorema

yang bermanfaat untuk

menentukan lokasi/letak akm-akar

dai

suatu fungsi kontinu atau menemukan

solusi dari persamaan dengm bentuk f(x) =

0,

di mana f merupakan firngsi yang

kontinu. Pmbuktian teoremanya, diserahkan kepada pembaca sebagai latihan.

5.3.5

Teorema

(

_{MengenaiLokasi Akar}

₎

Misalkan

I =

_[a,

bl

dan

f : I

-+

R

_fungsi

kontinu

padn

I.

Jikaf(a) < 0

<f@)

atau

jika f(a)>

0>f(b),

makn terdapat bilangan

c e (a,

b)

sehingga f(c) = 0.

Generalisasi dari teorerna

di

atas dapat diungkapkan dengan teorema yang dinlatakan sebagai berikut.

5.3.6

Teorema Nilai

Pertengahan

dari Bolzano

Misallan I suatu interval dan

f

: I -+ R fungsi kontinu pada

I.

Jika a,b

el

dan

k

e

R

memenuhi f(a)

<k

<f(b),

maka terdapat

titikc

e

I

antara a danb sehingga (c) = k.

Bukti:

Misalkan a<

b

dan g(x) =

(x)

_-k.

Diperoleh g(a) < 0 < gO).

Menurut teorema

5.3.5

terdapat

titik

c

dengan

a

<

c

<

b

sehingga g(c) = (c)

_-

k

:

0 atau dengan ungkapan lain

(c)

= ft.

Jikab

<a,

misalkanh(x)

=k-(x)

sehinggah(b)

< 0

<h(a).

Berdasarkan teorema

5.3.5,

terdapat

c

denganb

<c <a

sehingga

0=h(c)=k-(c).

Akibatnya

(c)

= k.

An alisi s Real

_-

Fangsi-fungsi Kontku

5.3.7

Akibat

Misatkanl= _[q bJ intental tertutup terbatas danf

:l-+R

kontinu pada

l.Jil(ak

eRmemenuhi:

Inff(I) <k<suPf([),

malea terdapat bilangm c

el

sehingga (c) = k Bukti:

Benlasarkau teorr€,ma Maksimum-Minimum

2.3.4,

t€rdapat

c'

dan c*

dil

sehingga:

Infru):(c.)

<

k

<

f(c*)

=

suPf(!.

Grnakan selanjutrya-teorenna Bolzano 2.3.7

dM

terbuktilah apa yang akan

dibuktikan.

Teorema yang akan dinyahkan berikut

di

bawah ini, mengungkapkan

bahwa peta dari

iot.*a

tertutup terbatas oleh suatu fungsi yang kontinu akan

*"*pui*

interval tertutup tertitas pula. Titik+itik ujung dari interval peta

ilt

**rputr,

nilai

minimum mutlak-dan

nilai

maksimum mutlak dari frrngsi

kontinu itu.

5.3.8

Teorcma

Jika

I

intterval tertutup terbatas dan

f

:

I

-+ R l<ontina pada

I,

maka

f(t) = {

f(x)

I x e

I

_J

merupakan intertal tertutup tterbatas'

Bulrti:

\dlsalkan m

:

inf

fCI

dan

M

:

suP

f0.

Akibatnya

(D

c [q

M]' Selanjueya,

jika

k e

[q M ,

k

sembarang, maka menurut teore'ma 5'3'7 ( Akibat

₎

terdapat titik c e

I

sehingga f(c) =

k.

oleh karena

itu k

e

I(D

dan inimenunjul&anbahwa

tqM

cf(D.

Jadi

(t)

= [m,M.

Perhafian!

1.

Jika I

:

_[a,

b]

suatu interval dan

f:

I -+ R kontinu pada

I,

telah ditunjukkan

bahwa f(I) adatah interval

_[q

Mi.

Ilhati-hati, bahwa f(D

+

_t (a), f(b)

I

( lihat gambar _{5'3'3 )'}

Z.

Peta dari intterval terbuka oleh suatu funsi korrtinu belum tentu interval

terbuka

lagi.

Sebagai

ontoh,

jika

(x)

=

ll(*

+

1)

,

I1

:

(-1,

1),

maka

f(Ir)

=

_QlL,ll,

ini bukan interval terbuka

3.

Peta dari interval tertutup tak terbatas belum tentu interval tertutup' Contohnya, untuk

f(x) =

Il(*

+

1), jika

Iz = _[0, oo) makaf(Iz)

=

(0, U, ini bukan interval tertutup ( lihat gambar 5.3.4).

Gambar 5.3.3

f(D

=

[no,M]

Analhis Real

_-

Fangsi-fangsi Konlinu

Gambar5.3.4 Grafikf(x):171*z+

1)(x

e R

5.3.9

Teorcma

(

Pengawetan lnterval

₎

Jika

I

suatu

interval

dan

f

:

I

-+

R

kontinu

pada 1,

merupakan interval.

maka f@

5.3.10

Bahan

Diskusi

1.

Misalkan f kontinu pada _{interval [0,} 1] ke

R.

jika

f(0)

=

f(1),

tunjrrkkan

terdapat c

e

_{[0, Yzl} sehingga

(c)

=

f(c + YS. Interpretasi soal ini adalah:

bahwa

pada

setiap

waktu

terdappat

dua

tempat

yang

antipodal

(

bedawanan/bertolak belakang) di khatulistiwa

di

permuk6sa $t

mi

yang

mempunlai suhu ymg _{sama ).}

Untuk me,njawab soal ini: Tentukan g(x) =

(x) -

t(x + Y)

2.

Misalkan

I-

_[0,

nl2l danf : I+R

dide]Erdsikan oleh

f(x)

=

sup

_{

x2, cos

x

}.

Tunjullcan todapat titik minimum mutlak xo

€

I

untuk f. Tuqiukkan pul4 bahwa xe su?tu solusi dari ppersam&m cos

x =

x'.

3.

Susun suatu pembuktian lengkap dan formal dari eorrema 5.3.9.

5.3.11

Latihan

1. Misalkan I =

_[q

b]

rlan

f

:

I

-+ Rfungsi kontinu sehingga(x)>

0

untuk

setiap x di

I.

Buktikan terdapat suatu bilangan

o >

0

sehingga

f(x)

> cr,

untuksetiapxel

Misalkan I = [a,

b]

dan

f :I -+R,

g:I

_-+R

masing-masingkontinuppadal

.

Tunjukkanbahwahimpunan E = { x e

t

I f(x) = g(x)

_}

mempunyai sifat: Jika (x") _S

E

dan xn

J

Xo, maka xe

€

E

2.

An alisis Real

_-

Fungsi-funpi Konrina

3.

fiisalkan

I:[qbl

danf

:I-+nf.u"gsikontinSpa4al

sehingga untuk

setiap x di

I

todapatydi

I

sehingga

lfo)l

< Ul(Dl.

Buktkanterdapat suatu titik

c

di

I

sehingga (c) = 0

4.

Tut$t'kkan setiap polinom yang berderajat

ganjil

dengan koefisien real mempunyai paling sedikit satu akarreal.

S.

Tunjukkam p-oli"i* p(x) = sa

+

7x3

-

9

mempunyai paling sedikit dua akar

real.

6.

Tunjr t'kan persaruun x = cos

x

mempunyai solusi dalam interval _10, %xl

7.

Misalkan

I

= [a, b] dan

f:.I

-+ R kontinu pada

I

serta

(a)

<

0,

f(b) > 0'

DidefinisikanW={

xell(x)<0},

danmisalkan

w

=

supW. Buktikan bahwa f(w) = 0.

8.

Misalkan f :

R+R

kontinupadaR dan

lim

(x)

= 0

dan

lim

f(x)

:

0

Buktikan bahwa

r

t.tutur'p?au?

au,

-.*#***rurri-o*

uot' minimumpadaR

9.

Misalkan

f:R+R

kontinupadaR dan

pe

R.

TunjukkanjikaxoeR

sehingga f(xo) <

_P,

-aka terdapat suatu lingkunganS dari xo yaitu Vo(xo)

sehingga (x)

<

_F

untuk setiap x € V6(xo).

10.

Jika

f

:

_[0, 1] -+

R

kontinu dan hanya me,mpunyai nilai rasional, maka

tunjukkan bahwa f merupakan firngsi kkonstan.

5.4

Kekontinuan

Seragam

Misalkan

Ac

R, dan

f

:

A+R.

Defnisi

2.l.l

manyatakanbahwa pernyataan berikut ekuivale,n;

(1)

fkontinu di setiap titik u e A

@

jikaditberikan

t>

0 dapu e

d

terdqat6>

0 sehinggauntuk setiap x e

A, l*-ul

<6maka

l(x)-(u)l

<e

Dalam

hal

ini

nilai

S tergantung dari

nilai e

dan letak

u

_fang

diambil.

Tergantung dari u mempunyai

ati

bahwa mungkin nilai f berubah cepat di dekat titik tertentu dan mungkin berubah lmrbat di dekat titik yang lainrya ( contoh:

(x)=sin(l/x);x>o).

Untuk selanjutnya, akan dibahas firngsi-fungsi dengan kondisi bahwa 6 >

0

dapat d-ipilih sehingga tidak tergantung

dri

titik u e A ( hmya tergantung dari

e

).

Sebagai mntoh" jika f(x) = 2x untuk setiap x e R, maka lf(x)

-

(u)

|

:

2x-2u

=

2lx-ol.

Ot"nt&arenaitudapatdipilih

6=el2

untuksetiape> 0

yang diboikan dm u e R.

Di sisi lain, jika g(x) ₌

l/a

x > 0, maka :

lrir.>-iir>l

=

l(r-xyuxl

=.I/ux

l,*-ul

...

(-)

Jikadiaurbil

6=inf

{%i,yro'e},

*aiadari

lx-ol

.6

diperoleh

l*-ol.

Z

u

sehinnesayzu<x<312u. Olehkmenaitu

l/x

<2h.

Iadi (+) menjadi:

I _e(*)

-

g(u)l

=

l1u-x,;ruxl

=

i/*

l'*-rl

<ztri

lr-ol

.

ztt%u's=E

An alhit Re al

_-

F un gs i-fu n gs i K ont in u

Di sini terlihat bahwa 6 yang diambil nilainya tergantung dari e dan u.

Situasi di atas dapat ditampilkaa dengan ilustasi di bawah

ini.

Ilustasi

ini

memperlihatkan bahwa untuk suatu e

>

0, pemilihan 6 yang berbeda untuk

titik

u

yang berbeda. Jika

u

mendekati nol, maka nilai 6 yarg diambil juga

mendekati nol.

%(2)

_Gambar5.4.l

g(x):

l/x,

x)0

Gambar5.4.2 g(x)=

l/x,

x>

0

5.4.1

Definisi

Misalknn

Ac

&

f

:A-+

R. Fungsif disebutkontinu seragampada A, jika dan hyya

j

_lka untuk setiap e > 0, terdapal 6 > 0 sehingga _iika x, y

ed

l*-yl

<6,maka

_{lf(x)-f(y)l<e.}

Definisi di atas, dapat diartikan bahwa'Jika

f

kontinu seragam pada

L

maka

f

kontinu pada setiap titik dari

A".

Secara unnum, konvers dari pernyataan

ini

tidak berlaku

(

misalnya untuk g(x)

= l/x,

x

>

0

_).

Ini

berguna untuk

memformulasikan suatu kondisi

ymg

ekuivalen dengan pemyataan

f

tidak kontinu seragam pada

_A

seperti yang dinyatakan

di

bawah

ini

(

buktinya

diserrahkan kepada pembaca sebagai ktihan).

5.4.2

Kriteria Kekontinuan Tidak

Seragam

Misalkan

Ac

&

f

:A-+k.

Pernyatoanbeilatt ehtivalen:

(l)

f tidak kontinu seragam pada At

Q)

Terdapat suatu en>

0

sehingga untuk setiap

6>

0

terdapat x, u e

A

l*-ol

<6rctapi

_{l(*)-(o)l>"0.}

Q)

Terdapat suatu en> 0 dan dua barisan (x") dan (u") pada Adengan

lim(x"-u,)

=

0,

tetapi

lrt*,,1-(Ul

>eo untukserrapn e N.

Kriteria ini dapat digunakan untuk menunjukkan bahwa g(x) =

l/x

tidak kontinuseragamnada

={

x

eRl x>0},

Amhil(.r-):(l/q)dan

dan

An olicis Real _- Fungsi-fungsi Kontkt

(u,)= (

l/(n+

1) _). Lim

(xo-u,)

= 0, tetapi I g(*") -g(u")

|

=

ln-1n+

1) | = 1

untuk setiap n e N. (adi dapat diambil s4=yr).

Di

bawah

ini

diberikan suatu teorema

yang

berkaitan dengan

kekontinuan seragam suatu frmgsi pada suatu interval tertutup t€6atas I.

5.4.3

Teorema

Kekontinuan

Seriagam

Jika

I

suatu interval tertutup terbattas dan

f

:

I

+

R

lcontinu pada I,

malra f kontinu seragam pada l. Bukti:

Andaikan

f

tidak kontinu semgam pada I.

maka tadapat Eo > 0 dan dua barisan

(x,)

dan (uJ <

l/n

dan

l(*J

_-

(u") I > eo untuk setiap n e N.

Berdasarkan twrelrlra 5.4.2,

padal

sehinggga

l*"-*l

Karena

I

terbatas, maka barisan

(x)

terbatas. Dengan menggunakan teore,ma Bolzano-Weierstrass, terdapat barisan bagian

(&,k)

dari

(x")

yang

konvergen ke suatu unsur z. Kemudian

_,

karena

I

tertutup,

maka

z terletak pada I.

Selanjutnya, dari ketidaksanuumlo*

_{- rl <}

lo*

_{- x*l}

+

lr* - ,l

maka dapat {isimpulkan bahwa barisan bagian

(u*)

dm (uJ juga konvergen kez.

Jika

f

kontinu

di titik

z,

mak kedua barisan

(

(x*)

)

dan

(

f(u*)

₎ konvergen ke

f(z).

Tetapi ini bertenungan dengan

lffr"l

_-

_fu")

I

> eo untuk

setiap

n

e

N. (mengapa?). Jadi peng;andaian di atas adalah salah, yang benar adalah fkontinu seragam pada I.

Fungsi

Lipschitz

Jika suatu fungsi kontinu seragam pada suatu himpunan yang bukan

interval tertutup terbatas, maka kadang-kadang didapat

kesulian

dalam menentukan kekontinuan seragamnya. Meskipun demikian, teorema

png

akan

dinyatakan

di

bawah

ini,

menjamin

k*ontinuan

seragam fungsi tersebut. Sebelumnya di berikan definisi mengenai fungsi ymg mmenuhi suatu kondisi

tertentu yang selanjutnya disebut fungsi Lipschitz.

5.4.4

Definisi

Misalkan

A

c R, f :A+R.

Fungsif

disebutfungsi Lipschitz

(memenuhi kondisi Lipschitz) pada A

jika

dan hanya

jika

terdapat lanstantaK> 0

sehingga

lq*>-f<">

lsf

I *

-ul,

untuksetiapx, u

eA

Untuk

A

: t

dan

I

suatu interval, fungsi Lipschiitz seperti yang

didefinisikan di atas dapat diinterpretasikan secara geometris sebagai berikut.

Analisis Real _- Fungsi-fungsi Kontinu

Jika kondisi Lipschitz dipenuhi, maka I ( f(x)

-

(u)

)(x -

u)

I

<

K,

x, u

€

I,

x

*

u. Nilai

( f(x)

_-

f(u)

_{/(x -}

u) adalah gradien dari ruas ggaris yang menghubungkan

titik

( x,

(x)

)

dan (u,

(u)

).

Jadi fungsi

f

memenuhi kondisi

Lipschitz

jika

dan

hanya

jika

gradien

dari

semua

ruas

gds

yang menghubungkan dua titik dari _$afik

y:

(x)

atas

I

terbatas oleh K.

5.4.5

Teorcma

Jilcaf : A -+

R

suatufungsi Lipschrtz, makafkontinu seragatn pada At

Bukti:

Misalkan e > 0 diberikan sembarang. Ambil6 = e/I(.

Jika x, u e A dan I x - o I

.

6

maka I f(x)

-(o)

I <

r

I

*

- o

I

.

K.6 = K.eA( = e.

Jadi flrngsi fkontinu seragam pada

A

5.4.6

Contoh

l.

Jika f(x) =

*

padaA:

[ 0, b

_],

maka :

l(*)-r("ll

=

I

*'-o'l

=

l**

ul

l*-"1

0,bl

Dengan demikian firngsi f meme,nuhi kondisi LipschiE dengm K = 2b > 0. Oleh krena itu fungsi kontinu seragam pada A = [ 0, b ].

Catatan: Fungsi f tidak kontinu seragam pada _[ 0,

o

_] ( mengapa? _).

2.

Tidak setiap firngsi kontinu sercgam merupakan fungsi Lipschitz. Misalkan g(x)

: {x,

untuk x e _[ 0, 2 _].

Karena g kontinu pada interval tertutup terbatas

_I

A,

2l,

maka g kontinu seragam

pada[0,2].

Selanjutnya perhatikan pemyataim :

Terdapat K > 0 sehingga I gC) -g(u) | < K I x - u

l,

*,

u e _[ 0, 2

]

... .... ( * ₎

Ambil x e [ 0,

2f,

x*

0 dan u = 0, maka :

)

K>0selalutodapat

Selanjutnya, akan ditunjukkan bahwa untuk setiap

x e

_[0,2],

x*0sehingga(**)

tidakberlah.

Untuk

0<K<1,

terdapatx:l

e[0,2]

sehinggaf

l{*l

=K.1=K<1

UntukK>

1,terdapat

x:Ll4*

e

_[0,2] sehinggaf

|{*|=K.|l2K=Yz<|

Ini

artinya bahwa pernyataan

(

*

₎

adalah salah yang benm adalah tidak

terdapat K > 0ymg _{*smenrrhi lg(x)}

-e(u)ls

fl*

-

rl,

*,

u

e

_[ 0, 2 ]. Dengan d€xnikian fungsi g bukan ftngsi Lipschitz.

Analirts Reo, _- FangsLfangsi Kontinu

3.

Teorema Kekontinuan Seragam dan teorema

5.4.5

kadang-kadang dapat

digabungkan untuk menentukan kekontinuan seragam suatu fungsi pada

suduhiryrman.

Misalkan g(x)

: {x,

x

e

[ 0,

o).

Fungsi g kontinu seragam pada interval I = [ 0, 2

],

sebagaimana ditunjukkan

pada contoh 2.

Jika

J:

_I

l,

@

_),

maka'r4tuk x e J, diperoleh

I g(x) -e(u)

l:l!*

- {+ |

:

_l*

_-ulll{*

+

{"1

Jadi fungsi g merupakan fungsi Lipschitz

pfu I

(

dengan

K=

Y.),

dan

dengan menggunakan teorema 5.4.5, dapat disimpulkan bahwa fungsi g

kontinu seragampada J.

KamaA=Ir;Jdandenganmengambil6-inf

_{

1, _{&(s), &(e)}

}

makag kontinu s€ragam pada

A

Bukti detail untuk

ini

diserahkan pada pembaca sebagai latrhan.

Teorcma Perluasan

Kontinu

Telah diperlihatkan contoh dirnana suatr ftngsi yang kontinu mungkin

tidakkontinuseragam(f(x)

=

l/x,

x

e

_{(0,1 )).}

Disisilain,

dengan

menggmakan teorema kekontinuan, suatu fungsi 5ang kontinu pada interval

tertutup terbatas selalu kontinu seragam pada interval tersebut.

Sekarang mungkin muncul pertanyaan: "Dengan kondisi bagaimana suatu frmgsi kontinu seragam pada suatu interval terbuka?"

Jawaban atas pertanyam

di

atas dapat dinyatakan sebagai teorema berikut di

bawah ini

5.4.7

Teorcma

Jilraf : A

+

R

kontinu seragam padahimpunan

Ac

R, dan (xn)suatu barisan Cauchy pada A,, maleo (f(x")) merupakan barisan Cauclry pada R.

Bukti:

Misalkan

(n)

barisan Cauchy pada

A

dan misalkan e > 0 diberikan. Karena f kontinu seragrm pada

d

maka dapat dipilih 6 > 0 se.hingga jika x, u €

Amernenuhi

[*-ul

<61,

maka

_l(rl-f(u)l

<e.

Karena (x,)

bmisan Cauchy, maka terdapat H e

N

sehingga I

*,

- **

I

.

a

uotot setiap n,

m >

H.

Ini

mmgakibatkan

l(*J

_-

f(uJ

I

< e. Oleh karena itu

d4at

disimpulkan bahwa barisan ( f(x") ₎ adalah barisan Cauchy.

Untuk fungsi

f

dengan persanuran f(x)

:

lix

,

tidak kontinu seragam

pada

( 0, 1

_).

Barisan yang diberikan oleh xo = 1/n di ( 0,

I

₎ adalah barisan

Cauchy, teapi barisan ( (x")

)

= ( n

₎

bukan barisan Cauchy.

Analhis Real

_-

Fangsi-fangsi Kontinu

5.4.8

Teorcma

Perluasan

Kontinu

Suatu _fungsi

f

adolah kontina seragam pada interval (a, b)

_iika

dan

hanya j i ka fiin gs i f i ni dap at di defi ni s i kan di t i ti k uiung a dan b s ehi ng ga

fungsi perluasan dari f kontinu.pada

lubl

Bukti:

(e

₎

Ini adalah trivial ( teorema 5.4.3 ₎

(= )

Misalkar

f

kontinu seragam pada

(a

b).

Akar ditunjukkan

bagaimana

f

dipoluas untuk

titik a

( serupa untuk titik

b).

Caranya adalah dengan menunjuli&an

bahwa 1i

m

f(*)

=

L

ada ( dengm menggunakan kriteria barisan ).

x-)a

Misalkan

(x")

suatu barisan di (a,

b)

yang konvergen ke

a.

Ini berarti barisan

1x")

adalah barisan

Cauchy

dan

dengan menggunakan

teorern

5.4.7

mengakibatkan barisan ( f(x") ) juga barisan Cauchy. Oleh kharena itu barisan ( f(x") ) konvergan. Misalkan lim (

f(x)

)

:

L.

jika

(u")

sembarang barisan lain yang konvergen ke a maka lim ( u"

_-

xo ₎ = a

_-

a

:

0.

Karena f kontinu seragrun, diperoleh:

Lim((u"))=

lim(f(u")

-

(x"))

+

lim((""))

=0+L=L

Jadi untuk setiap barisan (x") di (q b) yang konvergen ke q maka barisan (

(x")

₎ konvergen ke

L,

dan ini artinya

lim

(x)

=

L

x

-+a

Dengan mmendefinisikan

(a)

: L,

maka

f

kontinu

di

a.

Dengan cara yang serupa,

dmikian pula untuk b, yaitu dengan mengambil fO)

: lim

f(x)

x-+b

Oleh kmena itu perluasan f pada _[a"

_b]

kontinu pada _[a, b].

Karena

lim

sin (1/x

₎

tidak ada maka berdasarkan teorema di atas ( 5.4.8 ₎

x+0

dapat disimpulkan bahwa flmgsi

(D

:

sin

(1/x)

tidak kontinu seragam pada (0,

_bl,

untuk setiap b > 0.

Di sisi lain, karena

lim

x sin (1/x

):

0 maka fungsi g(x) = x sin (1/x) adalah

x-+0

kontinu seragam pada (0,

bl

untuk setiap b > 0

5.4.9

Bahan

Diskusi

1.

Gunakan kriteria kontinu tidak seragam 5.4.2 untuk menunjukkan bahwa

fungsi di bawah ini tidak kontinu seragam pada himpunan yang diberikan.

(a)

(x)

= X'

_,

A=[0,.o).

O)

g(x) = sin (1/x)

_,

B

= ( 0, co _).

Analfuis Real- Fungsi-funpi Kontinu

2.

Buktikan,

jika

f

dan

g

masing-masing kontinu seragam pada

R,

maka konnposisi fungsi f o g kontinu seragam pada R.

3.

Misalkan

Ac

R dan f :

A+

Rmempunyai sifat-sifat sebagai berikut:

"Untuk setiap e > 0,terdapat suatu fungsi g; :

A

+

R sehingga g" kontinu seragampadaA aan

l(x)

- g"(x)

_|

<

e

untuk seti4 x e

A

Buktikar bahwa

fkontinu seragam pada

A

5.4.10latihan

1.

Tunjrrkkan bahwa firngsi

f(x)

=

l/x

kontinu seragam pada himpunan

A = [u, .o

),

di mana a konstanta positif.

2.

Tunjulkan bahwa fungsi

f(x)

=

1/x2 kontinu seragam pada himpunan A = [1, o

),

tetryi tidak kontinu seragam pada B

:

(0, oo _).

3.

Tunjukkan bahwa firngsi

f(x)

: ll(*

+

1) untuk

xeR

kontinu seragam pada R.

4.

Tunj,lkkan, jika

f

dan g kontinu seragampadaAc

R,

makaf + g kontinu seragam pada

A

5.

Tuqi,kkan, jika

f

dan g kontinu seragan pada A

c

R,

dan jika keduanya terbatas pada

_A

maka perkalian fg kontinu seragam pada

A

6.

Jika f(x) = x dan g(x) = sin x , tunjukkan f dan g keduanya kontinu seragam pada R, tetapi perkalian fg tidak kontinu seragam pada R

7.

Jrkafkontinu seragampada A

c

R,

Oan

l(x)

I

>t,

0

untuk setiap x e

_d

tunjukkm, bahwa

l/f

kontinu seragampada

A

8.

Bultikan jika f kontinu seragam pada suatu himpunan bagian A dari R yang terbatas, maka fterbatas pada A.

9.

Tuqinlrk6, jika

_f

kontinu pada _[0,

o

₎

dan kontinu seragam pada _[a,

o

₎ untuk suatukonst nta positif a, maka f kontinu seragam pada _[0,

o

_).

10. Suatu fungsi f: R -+ R disebut periodik pada R jika terdapat bilangan p > 0 sehingga

(x

+ p) =

(x)

untuk setiap

x

e

R.

Buktikan, bahwa fungsi periodik yang kontinu pada R terbatas dan kontinu seragam pada R.

143 Kosim Ryhnana. _- JarDihMd UPI 2A06

An alisis Reol * Fun pi-fangsi Kontinu

5.5

Fungsi Monoton

dan

Fungsi lnvers

Pada bagian

ini

akan dibahas kaitan antara kekontinum suatu ftngsi dengan sifat-sifat kemonotonan fungsi inr, dilanjutkan kaitan antaxa kekontinuan

suatu ftngsi dengan keberadaan fimsi invasnya.

5.5.1

Definisi

MisalkanA-cR,

f:A+R.

(i).

Fungsi f disebut naik pada Aiika dan hanyaiika untuk setiap x1, x2 e

A

dan Xr

(xz

maluf(x) <

f(xz).

(i)

Fungsi f disebut naik lwat pada

Aiika

dan hanyaiika untuk setiap

xt,Y,ze A'dan Xt

(xz

nakaf(x) <

(xr).

(iiD

Fungsi f disebut turun pada Aiika dan hanya jika untuk setiap x1,

x2 c A dan

xt

<*

mala

(xr)

>

f(xz).

(rO

Fungsi f disebut turun kuat pada A jika dan hmya jika untuk setiap

X1, x2 € Adan

xr

<r"2 maka

(xr)

>

(x).

(v)

Fungsi

f

disebut monoton pada

Aiikn

dan hanya

jika

salah satu

dipenuhi: _fungsi f naik ataufungsi f turun pada

A-(vr)

Fungsi

f

disebut monoton kuat pada A,iika dan hanyaiika salah

satu dipenuhi: _fungsi f naik htat atau _fungsi f turun htat pada A*

Catatan:

(1)

Jikaf : A

+

R

naik pada Amaka g =

-f

turun pada

A

dan

jikah

:

A+

R turunpada Amaka s = -

h

naik pada

A

(2)

Fungsi monoton tidak perlu kontinu. Sebagai contoh,

(x):

0 untuk x

e

[0,

1l

dan

(x)

= 1 untukx e (1, 21. Fungsi fnaikpada [0,

2]

meskipundi

x:

1

fungsi ftidak kontinu.

Teorema

di

bawatr

ini

menunjukkan bahwa

ftngsi

monotton selalu mempunyai kedua

limit

ssepihanya

di

setiap

tittik

yang bukan

titik

ullung dai domainnya.

5.5.2

Teorcma

Misallanlc\

I interval danf : I

-+R

adalahnaikpadal.

Jika c titikyang bukan merupalean titik ujung dari I, mala

(r) Lim

f(x)

:

sup _{ f(x)

lx

e I,

x<c

_}

x-+c-(ii)

lim (D :

inf{f(x)

lxeI,x>c}

+

x-+c

Bukti:

(r)

Misalkanxel,x(c.

Karena f naik pada I, maka f(x) < f(c).

Selanjutrya, definisikan

A=

_{{ f(x) lx}

e

I,

x<c

}.

Aterbatasdiatasolehf(c), danmisalkan sup

A=

sup _{

f(x)

| x e I,

x<c

}

=L.

Kemudian,misalkane> 0

diberikan sernbarane.

Ansllsk Real

_-

Failgsi-fungsi Koninu

Berdasarka4 teorema supremum ( Analisis Real 1) maka

L

-

e

bukan batas atas

driA

Olehkarcnaitu,terdapaty"e

I, yu<c

sehingga

L-

e

< f(yJ <

t''

Ambil6"=c-y"

>0.

Iika

0<c-y<ft,

makay"<y<c.

Karenafnaik,

maka:

L-e

<

f(YJ

<

f$)

<

L+

s

Olehkaenaitu

lf[y)-Ll<s jika0<c-y<6"

,

Kar€nae>0 s€mbarang maka

lim

-(r)

=

L=

sup

{(x)

lxe

I,x<c}

x-)c

(ii)

Dengan qua yang serupa, bukti secara detail diserahkan kepada pembaca sebagai latihan.

Teorema

di

bawah

ini

merupakan akibat dari teorema 5.5.2

di

atas,

memberikan suatu kriteria untuk bekontinuan

di

suatu

titik

yang bukan merupakar titik ujung suatu int€rval yang menjadi domainnya da'i suatu fungsi

naik.

5.5.3

Akibat

Misalkan

Ic

R

suatuintervaldanf

:I

-+Radalahftngsinaikpada I.

Jika c e

I

bukan titik ujung dari

I,

maka pernyataatr berikut ekuivalen:

(r)

f

kontinu di o

(ii) lim (*):

(c)

_{= lim}

(x)

x-)c-

x-+c*

(iil)

sup{f(x)

lxeI,x<c}:

f(c)

= inf{f(x)

lxeI,x>c}

untuk buktinya diserahkan kepada pe,mbaca

(

gunakan teorema 5.5'2

dm 4.3.3 ).

Misalkan

I

suatu interval dan

f

:

I

-+ R suatu fungsi naik pada

I.

Jika a

titik ujung kiri dari

I,

dapat ditunjukkan bahwa: fkontinu di a jika dan hanya

jika

f(a) = I i

1

_x->a

.

1?

Dengan cara serupa, untuk suatu titik ujung kanan b untuk fungsu turun.

Iika?: I -+

R

naik pada

I

dan c bukan titik ujung dari

I,

didefinisikan loncatan

f

di

c

('Jump" f di c _{) yaug dinyatakan} oleh

j(c)

dan

i(c)

=

li

m

f(x)

-

li

m f(x)

(

lihat gambar _{5'5'1 )}

+

x-+a

x-+a

Berdasarkan leorema 5.5.2 diperoleh:

i(r)

=

irf

_{i(lr) lxeI,x>c)}

=

sup{f(x)

lxel'x<c}

untuk fungsi naik.

Jika titik ujung

tiri

a dari I terletak palol, didefinisikan loncatan f di a yaitu

i(a)

= lim

f(x)

-

(a)

x-+a

Jika titik

ujung

kanan

b

dari

I

terletak pada

I,

didefinisikan loncatan

f

di b

yaitu

j(b): lim

(x)-f(b)

AnalTcis Rcal

_-

Funpi-fungsi Kontinu

c

Gambar

5.5.1

Loncatan f di c

5.5.4

Teorema

Misallan

Ic

&

I interval

danf:I-+R

naikpadal.

Jika c

el,

makaf

kontinu di c jika dan hanya

jikaj(c) =

0

Bulrti:

Jika c bukan titik ujung interval, ini trivial ( Akibat 2.5.1)

Jika c

e

[,

titik

ujung

kiri

dari

I,

maka

f

kontinu

di

c

jika

dan hanya

jika

f(c)

:

I i

m (x)

yang mana ini ekuivalen dengani(c)

:

0

x-)a*

Cara serupa untuk kasus c titik ujung kanan dari I.

Fungsi

lnvers

Akan ditentukan eksistensi dari invers untuk firngsi konr\tinu pada suuatu interw'al I

c R.

Perlu diingat kembali dari Analisis Real 1, bahwa fungsi

f:

I

-+

R

mempunyai suatu funggsi invers jika dan hanya jika fungsi

f

injektif

( satu-satu ) yaitu untuk setiap

4

y e I,

x

;c

y

maka f(x) :e

f(y)

atau untuk setiap x, y e I,

(*)

:

f(y) maka x =y.

Selarjufirya fungsi yang monoton

kuat

adalah satu-satu sehingga

mempunlai fungsi invers.

Pada tteorema berikut di bawah

ini,

ditunjukkan bahwa

jika

f:

I

-+

R flrngsi kontinu monoton kuat, maka f mempunyai suatu frrngsi invers g pada J = f(t)

=

{

f(x)

|

x e

I

}

dan fungsi invers g ini juga kontinu monoton kuat

pada J.

5.5.5

Teorcma lnverc Kontinu

Jika

I

g

R,

I

interval dcn f:

I

-->

R

monoton kuat dan kontinu pada

l,

malu fungsi invers

g

dari

f

adalah monoton

htat

dan kontinu pada

Analhit Real- Fangsi-fungsi Kontka

5.5.6

Bahan

Diskusi

l.

Susun suuatu bukti fomral untuk teorema 5.5,5 di atas!

2.

Tunjult<aa jika f dan g fungsi-fungsi naik positif pada suatu interval

I,

maka

pokalian f.g naik pada L

3.

Misalkan

f

g masing-masing fimgsi naik pada int€rval I

c

R, dan

(x)

> g(x) untuk setiap x e

I.

Jikay e f(D

^

g(D, tunjukkan

f-r

(y) <

g-'(y).

Petunjuk! Interpretasikan p€nryataan di attas secara geometris.

5.5.7

Latihan

t.

Jika I = _[a

b]

suaruintervaldant I

+ R

firngsi nnaikpadal maka

_titika

merupakan

titik

minimum mutlak dari

f

pada

I.

Jika

f

naik

kuat,

maka a satu-saturya ( _{unik )} merupakan titik minimum mutlak dari f pada I.

2.

Tunj\kkan bahwa fungsi f(x)

=

x

dan g(x)

= x

_-

1,

masing-masing merupakan firngsi naik kuat pada

I

= _[0,

1],

tetapi pokalian

fg

tidak naik pada I.

3.

Tunjul*an jika

I

= [q b] dan f: I -+

R

naik pada

I,

maka f kontinu di a jikadanhanyajikaf(a)

₌

_inf{f(x)

_lx

e(a,b]}.

4.

Misalkan I

:

_[0,

_U

dan

f

: I -+ R didefnisikan oleh f(x) = x untuk x rasional

dan

(x)

:

I -

x

untuk x irrasional. Tunjukkan, bahwa

f

firngsi satu-satu pada I

dan((x)

= xuntuk setiap

x e

I.

Tunjrrkkaor pula bahwa fkontinu hanya di titik x = 1/2 .

5.14isalkanf(x): xuntukxe_[0,1], dan f(x)

= l+x

untukxe(1,2].

Tuniiukkan bahwa

f

dan

f

- 1 naik kuat. Apakah

f

dan f

-'

kontinu di setiap titik?